Articles

 

A generalized equation of state with an application to the Earth's mantle

 

J. A. Robles–Gutiérrez^1*, J. M. A. Robles–Domínguez¹ and C. Lomnitz²

 

¹ Universidad Autónoma Metropolitana, Iztapalapa, 09340, Mexico City, Mexico.

² Instituto de Geofísica, Universidad Nacional Autónoma de México, Ciudad Universitaria, Del. Coyoacán, 04510, Mexico City, Mexico. * Corresponding author: nautilo68@yahoo.fr

 

Received: June 29, 2009
Accepted: February 4, 2010

 

Resumen

En este trabajo se muestra la pertinencia de incluir en la ecuación de estado de Kamerlingh–Onnes, interacciones múltiples no aditivas de fuerzas entre partículas. Estas fuerzas son de carácter electrodinámico. A partir de la ecuación de estado así generalizada se obtienen las isotermas en la vecindad del punto crítico y del punto triple para sistemas polares o no polares. Se desarrolla el ejemplo del agua. Se generaliza la ecuación de estado para el manto desarrollada por Birch, y en particular se obtiene la compresibilidad isotérmica para el manto terrestre. Se presentan las formas que toman, bajo esta generalización, algunas leyes de la mecánica y electrodinámica.

Palabras clave: Ecuación de estado, fases, energías no aditivas, energías binarias, isotermas, compresibilidad isotérmica.

 

Abstract

This study analizes the pertinency of including in the state equation of Kamerlingh–Onnes, non additive, potentials of multiple–interactiions of particles. These forces are indeed real and of a electrodinamic character. From the state equation no gerenalized, we obtained the isotherms in the vecinity of the critical point, and of the triple point for polar (or no polar) systems. We developed the example of water. We generalized the state equation for the mantle developed by Birch, and in particular, we obtained the isothermal compressibiliy for the earth mantle. We present, the forms that, under this generalization assume several laws of classical mechanism and electrodinamics.

Key words: Equation of state, phases, non–additive energies, additive binary energies, isotherms, isothermic compressibility.

 

Introduction

In an earlier paper (Robles–Dominguez et al., 2007) we derived the equation of state for a one–component fuid and in general, for a fuid of 1, 2, 3 . . . phases. This result was based on introducing inter–molecular potential energies such as additive binary, non–additive tertiary, non–additive quaternary interactions and so on:

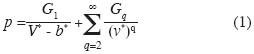
where p is pressure on a container of volume V, V* is the molar volume, b* is the molar volume of all molecules, G₁ , G₂ , ... are functions of absolute temperature T. Here G₁ is the mean feld of all rigid shells of a molecule, G₂ is the mean feld of all additive binary interactions between pairs of molecules, G₃ is the mean feld of all non–additive ternary interactions and so on. The term "non–additive" means that the interaction among, say, 4 particles is different from the other interactions so that they cannot be included in a sum of binary interactions or in a sum of interactions of three particles, and so on. We also consider the mean feld approximation for all these energies.

In Section II, we derive our equation (1) in a new basis of functions, which is (ρ*)^r, r = 1, 2, 3, ... , where ρ* is the molar density. In Section III, we obtain the isotherms in the vicinity of the critical point and of the triple point of any system, polar or not, and applied it to water as an example.

Section IV, provides exist, and it is shown that, the new forces develop a generalization of electrodynamics, classical mechanics, etc. In Section V, we derive the isothermal compressibility for the Earth's Mantle after Birch (1947). Section VI, contains the conclusions.

 

The equation of state in base (ρ*)^l, l = 1, 2, 3

If the 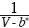term in Equation (1) is expanded in a Taylor series in terms of V^*–m, where V^* >> b^* and ΔV^* = –b^* , we fnd:

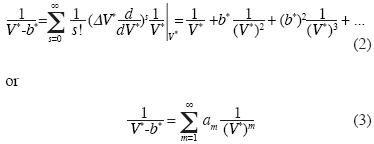
The coeffcients a_m are the same found by Ursell and Mayer (c.e., Uhlenbeck and Ford, 1963).

We replace (3) into (1) and we obtain:

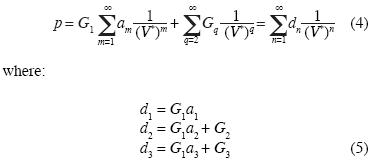
etc.

Note that the equation of state (4) contains linear independent vectors 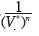, n=1,2,3,... thus the Kamerlingh–Onnes equation is derived from statistical mechanics. The parameters a_m and G₂ were calculated from additive binary potentials that contain all additive binary interactions (c.e., Uhlenbeck and Ford, 1963). The parameters G_q, q≥3, were obtained from non–additive potentials. Thus, d₃ ≠ a₃, d₄ ≠ a₄, and so on. Since d₃ = G₁a₃ + G₃, the quantity G₁a₃ is identical to the coeffcient of van der Waals, or Ursell & Mayer. Not so G₃, our coeffcient for non additive tertiary potentials. Also, G₄ is our coeffcient for non additive quaternary potentials, and so on.

If d_n = 0, n ≥ 2 equation (4) should become the equation for an ideal gas, namely:

where R is the universal gas constant. This is because:

If we set

where ρ* is the molar density, we may write (4) as:

 

The isotherms in the neighborhood of the critical and triple points of water

Equation (9) is an appropriate equation of state which yields the isotherms of polar or non polar fuids. Let us derive the critical isotherm by means of the well known conditions:

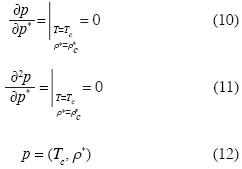
where ρ_c* is the critical molar density and T_c is the critical temperature. In equation (12), if we substitute p = p_c and ρ* = ρ_c*, we may use (10), (11) and (12) in order to obtain d_2c, d_3c, d_4cassuming d_nc = 0, for n > 4. Thus we obtain the critical isotherm in the neighborhood of the critical point:

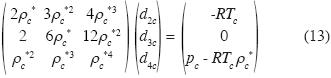
Now we calculate the solutions of these equations for water, using data of Black and Hartley. (1993):

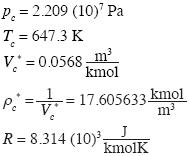
The solution of (13) is

For these values the non additives interactions between three and four molecules are necessary to explain the Critical Point, and the isotherm in the neighborhood of the critical point is:

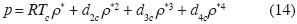
Van der Waals could not obtain this isotherm because he did not consider potentials of 3, 4. molecules respectively.

When a wider interval of molar densities is desired, more experimental data will be required; in this case the critical isotherm will be of degree n > 4 which will enable us to compute the values of d_nc to a higher precision.

We consider now the isotherm in the neighborhood of the triple point in a system, polar or otherwise. As an example we consider water. The minimum curve near the triple point to provide stability in (p₃, ρ*_g3, T₃), (p₃, ρ*_s3, T₃) y (p₃, ρ*_l3, T₃), must be of ffth degree. Let the right sub index 3 denote "triple point", and let g, s, and 1 be the three phases. The equation (8) is reduced to:

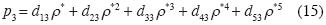
where

R is the Universal Gas Constant and T₃ the absolute temperature of the triple point in the system. The remaining four unknown constants in (15) may be determined as follows. Let the molar densities be ρ*_g3 < ρ*_d3 < ρ*_s3 < ρ*_b3 < ρ*_l3 where ρ*_s3 y ρ*_l3 are obtained by experiment from the solid and liquid phases of water at the triple point. The other molar densities are restrained by Maxwell's constructions for triple point:

According to Keenan and Keyes (1978) we have, for

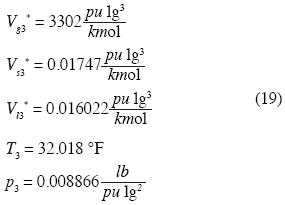
and recalling 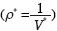we fnd:

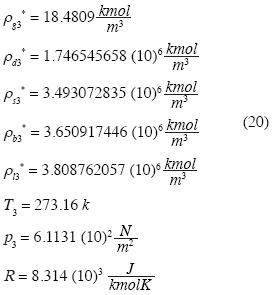
The system of equations is as follows:

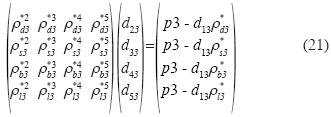
and the solution is:

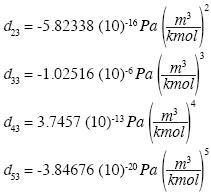
which yields the isotherm of water in the neighborhood of the triple point:

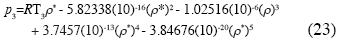
For these values the non–additive interactions between three, four and fve molecules are absolutely indispensable, for all fuids, to obtain the isotherm for the triple state; the explicit isotherm for the triple state for the water is equation (23), where the term of non–additive interactions between three molecules is the dominant term; this equation is derived, using statistical mechanics, for the frst time.

 

Existence of an infnity of new electromagnetic forces, and generalizations of electrodynamics, classical mechanics.

Robles–Domínguez et al. (2007) derived expression (1), the frst two terms of which reduce to the van der Waals equation. While van der Waals had considered all binary interactions in the fuid, his expression does not fit adequately the experimental data. We therefore considered additional interactions such as non–additive tertiary, non–additive quaternary and so on, which are the Fourier coeffcients of the development based on Functional Analysis (see Courant and Hilbert, 1953; and Kolmogorov and Fomin, 1957) which reproduce exactly the experimental isotherm. The new forces are real.

But in a fuid the interactions are electromagnetic. Therefore these new interactions are electromagnetic interactions. In equation (1), G₃ represents the mean feld of the non–additive interaction between molecular triplets. Coulomb could not obtain these results. Thus equation (1) contains an infnity of additional new electromagnetic forces. If these forces are not considered, e.g. by making G₃, G₄,... to vanish, functional analysis suggests that we may not succeed in reproducing the experimental results.

When those new felds are considered, in the Electromagnetic case, the Maxwell's Laws are generalized. Thus the fourth Law of Maxwell takes the form:

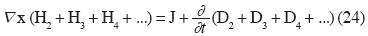
Where H is the Magnetic Field, D is the Electric Displacement Field, J is the Electric Current and subscript 2 is employed for binary additive felds, sub–script 3 is employed for ternary non–additive, etc.

In Classical Mechanics, Newton's Second Law is generalized to the form:

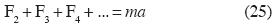
where F₂ is the resultant of the additive binary forces upon m, F₃ is the resultant of the non–additive tertiary forces upon m, and so on. Here m is mass and a is acceleration.

Generalized conservation of energy

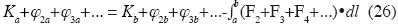
here K is kinetic energy, a and b are two points of the path of the particle, φ₂ , φ₃ , ... are the energies of all additive binary, non–additive ternary, non–additive quaternary conservative forces, and so on, and the integral is the total work done by all binary additive non–conservative forces, tertiary non–additive non–conservative forces, etc.

In Quantum Field Theory are obtained:

Generalized Klein–Gordon equation with electromagnetic feld

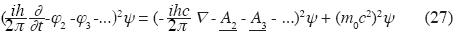
• φ₂ is the additive scalar potential energy operator

• φ₃ is the non–additive tertiary scalar potential energy operator.

• etc.

• A2 is the additive binary vector potential operator.

• A₃ is the non–additive ternary vector potential operator.

• etc.

All these operate on the Wave Function. (for the case with additive binary interaction only see Björken and Drell, 1964).

Generalized Dirac equation for the electromagnetic feld

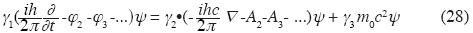
where γ_s = 1, 2, 3 are Dirac matrices (for the case with additive binary interaction only see: Björken et al, 1964).

 

Isothermal compressibility in the Earth's Mantle

The geophysicist F. Birch obtained a state equation for the Earth's Mantle (Birch,1947) which is:

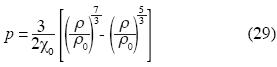
where p is pressure, χ is isothermal compressibility and ρ is the density of the Earth's Mantle; the sub–script zero is used for quantities evaluated to atmospheric pressure.

The density is:

where m is the mass and V the volume.

The mass can be expressed in terms of the moles number n:

where M is the molecular mass, and ρ can be expressed in terms of n as follow:

and the Molar Density ρ^* is:

then:

and:

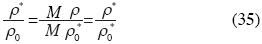
Birch's equation can be rewritten as follows:

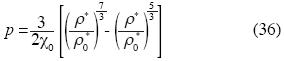
Our State Equation (1) is valid for gases, liquids and solids; of course Birch's Equation is a particular case of (1).

We can express that equation in the base {ρ^l, l = 0, 1, 2, 3, 4, 5, ...}developing it in Taylor series near ρ₀ :

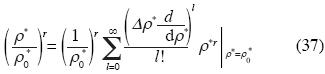
where r can take the values 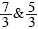, and Δρ^*=ρ^*– ρ₀

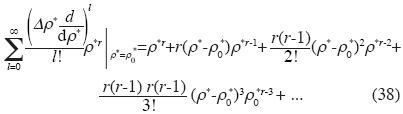
and Birch's equation is:

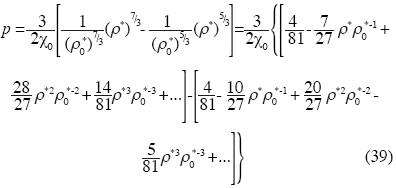
and Birch's state equation is:

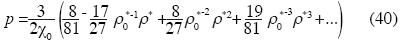
This state equation shows, at this approximation, that the non –additive interactions of three bodies are relevant.

The isothermal compressibility is:

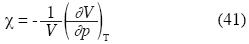
Or in terms of ρ*:

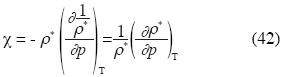
Implicit derivation applied to the last equation of p gives:

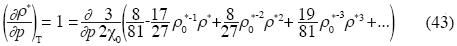
and the isothermal compressibility is expressed as follow:

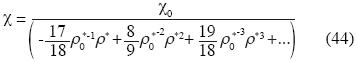
According to this equation, if the molar density increases the isothermal compressibility decreases.

We can use other equations for the Earth's Mantle, but Birch's equation is more simple and we want to show only the existence of the term of tertiary non–additive interactions in the Earth's Mantle.

 

Conclusions

In this paper we show that there is an infnite number of new molecular forces in a fuid; these forces are of electromagnetic nature. Here we present the corresponding generalization of the equations of electrodynamics and classical mechanics and quantum feld theory in which comprising these new forces. We propose that any feld in nature must be associated with a corresponding infnite set of new non–additive forces. Also, the Earth's Mantle equations must contain these new forces.

 

Acknowledgments

Critical review from two anonimous reviewer is acknowledged.

 

Bibliography

Birch, F., 1947. Finite Elastic Strain of Cubic Crystals, Phys. Rev., 71, 11, 809–824.        [ Links ]

Björken, J. D. and S. D. Drell, 1964. Relativistic Quantum Mechanics. McGraw–Hill Book Company, 300 p.        [ Links ]

Black, W. Z. and S. A. Hartley, 1993. Termodinámica, Editorial CECSA, México, 883 p.        [ Links ]

Courant, R. and D. Hilbert, 1953. Methods of mathematical physics. 1^st English ed., translated and rev. from the German original. New York, Interscience Publishers, p. 62.        [ Links ]

Keenan, J. H. and F. G. Keyes, 1978. Thermodynamics properties of water including vapor, liquid and solid phases. Ed. J. Wiley. New York, 156 p.        [ Links ]

Kolmogorov, A. N. and S. V. Fomin, 1957. Elements of the theory of functions and functional analysis. Translated from the 1^st Russian ed. by Leo F. Boron. Rochester, N. Y. , Graylock Press, 128 p.        [ Links ]

Robles–Domínguez, J. A. M., J. A. Robles–Gutiérrez and C. Lomnitz, 2007. An Equation of State for more than two phases, with an application to the Earth's mantle, Geofísica Internacional 40, 3, 155–161.        [ Links ]

Uhlenbeck, G. E. and G. W. Ford, 1963. Lectures in Statistical Mechanics in American Mathematical Society, Providence, R. I., 30 p.        [ Links ]