Services on Demand
Journal
Article
Indicators
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Geofísica internacional
On-line version ISSN 2954-436XPrint version ISSN 0016-7169
Geofís. Intl vol.46 n.3 Ciudad de México Jul./Sep. 2007
Articles
An equation of state for more than two phases, with an application to the Earth's mantle
J. A. M. Robles–Dominguez1,*, J. A, Robles–Gutiérrez1 and C. Lomnitz2
1 Universidad Autónoma Metropolitana, 09340 Iztapalapa, D.F., México. * Corresponding author: nautilo68@yahoo.fr Email: rodj@xanum.uam.mx
2 Instituto de Geofísica, Universidad Nacional Autónoma de México, 04510 México City, México.
Received: October 18, 2006
Accepted: July 27, 2007
Resumen
Se deriva una ecuación general de estado para fluidos de cualquier número de fases. La ecuación contiene a las principales ecuaciones de estado experimentales como casos especiales. Las energías no–aditivas de 3,4,... partículas deben también de ser consideradas, además de las energías binarias aditivas. Para derivar la isoterma en la vecindad de un punto crítico, se encuentra que la ecuación de estado debe contener al menos tres parámetros, incluyendo la energía potencial no–aditiva de tres cuerpos. Mostramos como obtener el espectro de interacciones de una ecuación de estado para el manto terrestre.
Palabras clave: Ecuación de estado, fases, energías no aditivas, energias binarias, isotermas.
Abstract
A general equation of state for fluids of any number of phases is derived. The equation contains the principal experimental state equations as special cases. The non–additive energies of 3, 4, ... particles must also be considered, plus the additive binary energies. In order to derive the isotherm in the vicinity of a critical point, it is found that the equation of state must contain at least three parameters, including the non–additive three–body potential energy. We show how to obtain the interaction spectra of an equation of state for the earth's mantle.
Key words: Equation of state, phases, non–additive energies, additive binary energies, isotherms.
Introduction
Recent experimental evidence suggests the presence of an infinity of new forces acting in the electromagnetic field. Three–body forces are also beginning to be considered in nuclear physics (Mermod et al., 2005; Amir–Ahmadi et al. (2007). It seems reasonable to expect that non–additive forces may exist in other fields of physics as well.
Single–component fluids feature isotherms belonging to several phases (Figure 1). In 1873 van der Waals published an empirical equation of state which assumes that the free Helmholtz energy contains up to binary potentials only. He assumed short–range repelling potentials and long–range attracting potentials. His equation contains two terms, and the two phases of the isotherms agree qualitatively but not quantitatively with experiment.

In 1901, Kamerlingh Onnes proposed an improved equation of state which contains an infinite series of negative powers of the molar specific volume v*, known as a virial expansion. While he did not evaluate the coefficients of the expansion, the two first terms are virtually identical with van der Waals' expression.
In 1930, Ursell and Mayer found that the expansion converged only for weak binary molecular interactions. The discrepancies found when one attempts to apply the Ursell–Mayer theory to both solids and fluids may be due to their introducing a small perturbation in the behavior of an ideal gas.
Another approach is functional analysis, where any function may be expressed as an expansion consisting in an infinite series of independent terms, such as an experimental isotherm of several phases. Such an isotherm would never be obtained by an Ursell–Mayer expansion. In order to obtain the missing terms in the van der Waals equation we shall consider the non–additive tertiary, quaternary,..., forces in the Helmholz free energy, i.e., all forces that are not included in the binary forces. A similar situation applies to the potential energies.
This is achieved in statistical mechanics by using the mean field. Any multiphase isothermal may be obtained directly by expansion in negative powers of the molar volume. The second term is associated to binary potentials, the third term with tertiary non–additive potentials, and so on. Note that the molar volume must exceed a thermodynamically compatible minimum molar volume for a given system, as otherwise the integrals will diverge.
Equations of state may be either empirical or theoretical. Empirical equations include the equations due to van der Waals or Berthelot. Theoretical equations of state, such as the Yang–Lee equation (Thompson, 1972), are mostly based on statistical mechanics. These equations do not address problems involving three or more different phases.
Some equations of state are obtained by fitting various functions to the experimental isotherms. An early example is Sugie and Lu (1971). This approach can successfully replicate the behavior of three–phase systems in specific ranges of thermodynamic space. It does not consider energy potentials, however; and the terms do not always have a physical meaning. In this paper we propose an equation of state derived from first principles, which attempts to overcome these shortcomings.
2. The model
Consider a system of N identical particles interacting by means of additive binary energy potentials, and non–additive energy potentials involving 3, 4, ... particles. The particles are contained in a variable volume V which is weakly coupled to a large heat reservoir at a temperature T.
The total additive binary potential energy between N particles is defined as the sum of all binary potential energies between pairs of particles. The total non–additive 3–particle potential energy that exists between N particles (N>3) is defined as the sum of all triads of particles. It is called non–additive because these energies cannot be included in the sum of binaries. The other non–additive potential energies are defined in a similar way.
In this paper it will be shown, from experiment, that the non–additive potential energies are both real and necessary for consideration in a thermodynamic system composed of liquids and solids. The system may be described by a canonical partition function QN(T, V) defined as follows (Uhlenbeck and Ford, 1963):

where h is Planck's constant, Γ stands for integration over phase space, β=(kT)–1, k is Boltzmann's constant, and E is the total energy of the system from classical mechanics, i.e.

where K is the total kinetic energy, U2 is the total additive binary potential energy from binary energy potentials between pairs of particles, U3 is the total non–additive 3–particle energy potential, and so on.
We integrate over the moments. The volume V is partitioned into cells in such a manner that all energy potentials remain approximately constant within any given cell. If Ni >> 1 is the number of molecules in the i–th cell we have

where λ, = h/(2πmkT), m is the mass of a particle, γ(N1) contains the short–range energy potentials and the summation is over all possible configurations, i.e., all distributions of N particles in all cells. Further, Ulm is the long–range contribution of the binary energy potential, Ulmn is the long–range contribution of three–particle energy potentials and so on. Every configuration must also obey the constraint

over the number of cells. Equation (3) may be rewritten as:

where

and γ(N1) is the volume Δ of a cell minus the volume of molecules in the cell. The volume of cells is assumed constant.
Let δ be the volume of a molecule. Ornstein (in van Kampen, 1964) assumed that the molecules are tightly packed as spheres in each cell so that

Substituting (7) into (6) and using Stirling's approximation we find

The restriction associated with equation (4) was considered by employing a Lagrange multiplier. In equation (8), all terms except for the term corresponding to the most probable configuration vanish. This term is the maximum in equation (8) which turns out to be for a uniform distribution of particles in V, i.e.

for all l. Thus, the partition function is practically the same as the one obtained when introducing (9) into (8), or

Now, the pressure p in an isothermal system may be written as p=–∂F /∂V, where F=–lnQN(T,V)β is the Helmholtz energy. Using the specific volume per mole v*, we obtain


 and so on; the specific molar volume v* is obviously larger than the molar volume of all particles. Let v*0 be the minimum value of v* which is characteristic of any given gas. The integration limits of v*are v*0 and ∞, thus the integrals will not diverge. As for ωq (T), q>2, it can be shown than ω2(Z) is the mean field produced by additive binary forces, ω3(Z) is the mean field produced by non–additive tertiary forces, etc.
and so on; the specific molar volume v* is obviously larger than the molar volume of all particles. Let v*0 be the minimum value of v* which is characteristic of any given gas. The integration limits of v*are v*0 and ∞, thus the integrals will not diverge. As for ωq (T), q>2, it can be shown than ω2(Z) is the mean field produced by additive binary forces, ω3(Z) is the mean field produced by non–additive tertiary forces, etc.
By functional analysis (Kolmogorov and Fomin, 1970; Morse and Feshbach, 1953) the functions ωq (T), q=2, 3,..., may be expressed on a base of linear independent functions

And, substituting eq.(12) into (11):
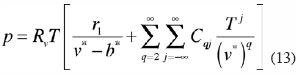

Another possible form of equation (13) is

where: Dqj = Ru Cqj , or


Equations (11), (13), (14) and (15) are expressions for a new equation of state which employs mean field potential energies—both additive and non–additive—between particles. As a result we have a base of linear independent functions (for v*> v*0) from functional analysis, being the spectra of interaction of the system. The parameters C may be obtained from experimental data for any particular gas. In conclusion, equation (13) reproduces exactly and completely all experimental properties, e.g. the values of the critical indices, the specific heat at constant volume, the isothermal compressibility near the critical point, etc.
On the other hand, the experimental critical indices α, β, γ,... (Reichl, 1977) may be obtained from the experimental equation of state (for example:  ). As equation (13) reproduces exactly the experimental equation we can also obtain the values of these experimental critical indices.
). As equation (13) reproduces exactly the experimental equation we can also obtain the values of these experimental critical indices.
3. Comparison with other equations
1.– Equation (13) reduces to the ideal gas equation if b* = 0, rq = 0 for q > 2:

2.– Equation (13) reduces to the van der Waals equation if 

3.– The virial equation Kamerlingh Onnes and equation (11) are equal if b*=0:
Discussion
Equation (13) is obtained from statistical mechanics. The base of the space of equations of state for simple fluids is formed by an infinite number of linear independent functions (where v* > v*0). From functional analysis, all equations of state can be expressed as linear combinations of the elements of this base.
For this functional space we may use an infinity of different bases but the one used in this paper for equation (13) is important because it expresses the equation of state as a convergent series which is a spectrum of mean field interactions. Thus the second term contains the binary (additive) mean field, the third contains the tertiary (non–additive) mean field, the fourth contains the quaternary (non–additive) mean field, and so on.
At a critical point an equation of state is restricted by three conditions:

Equation (11) can be used to obtain approximately the isotherm in the vicinity of the critical point, considering Cqj=0 for q>3, r1,=1, and defining a and c so that  for q=2 and
for q=2 and  . In this case the system of equations to be solved is
. In this case the system of equations to be solved is

where the subscript c denotes the critical values. We may rewrite this system as

from which the parameters bc*, r2c and r3c can be determined for a given gas.
Van der Waals attempted to solve the same problem. However, his equation of state failed to provide a solution for the critical point, because it contains only two unknowns. When substituting the van der Waals equation into (16) the system of equations has no solution, because van der Waals failed to consider non–additive forces.
As a simple example, in the case of water pc=2.209x107Pa, Tc =647.3K and v*c =0.0558m3/kmol. Introducing these values into (18) we find:

These values define the isotherm in the vicinity of the critical point. Inserting into (15) and solving this system of equations for pc, Tc, and v*c, we obviously obtain the values p=2.209xWPa, T=6473Kandv*=0.0558m3/kmol. Thus we have shown that the isotherm in the vicinity of the critical point is obtained by necessarily considering non–additive forces of three particles at the very least.
In the case of the isotherm of a triple point in a single–component gas (Figure 1), the curve acb represents coexistence of liquid and gas, and P3 is the pressure at the triple state. If we introduce the pressure at the triple point into equation (13) and we neglect the terms higher than the sixth order the result is a fifth–degree equation in v* as shown in Figure 2. This means that at the triple point there are contributions of non–additive potentials of 2,3,4,5 particles at least. Also it is necessary to employ two Maxwell constructions in order to fit the experimental curve.
5. An application to geophysics
The mantle of the Earth may be treated as a highly viscous convecting fluid. Birch (1947) proposed the following equation of state for the mantle:
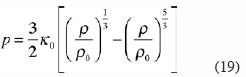
where κ is the compressibility, ρ is the density, and the zero subscript indicates evaluation at atmospheric pressure. Equation (17) in terms of specific volume v* per mole may be written

This equation can be expressed in the form of equations (11), (13), (14) or (15). As Birch's expression does not include temperature explicitly it is more convenient to use equation (15) expressed in the base of linear independent functions  . However, the coefficients are more easily obtained by using the orthonormal base after Gram–Schmidt (see Dennery and Krzywicki, 1995), as follows.
. However, the coefficients are more easily obtained by using the orthonormal base after Gram–Schmidt (see Dennery and Krzywicki, 1995), as follows.
In the bracket notation of functional analysis (Dennery and Krzywicky, 1995) the functions, also called vectors, being elements of base of linear independent functions in equation (11) yield  or, more simply,
or, more simply,  . For example,
. For example,  Thus elements of the new base will be orthonormal and may be written
Thus elements of the new base will be orthonormal and may be written 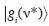 or simply
or simply  for i, j
for i, j 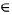 (1, ∞).
(1, ∞).
The inner product between two vectors  is defined as follows:
is defined as follows:

Two vectors are orthonormal if

for i, j 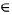 (1, ∞).
(1, ∞).
In the case of the vectors of the new base, these vectors must form an orthonormal set

Thus any equation of state given by an empirical equation or by means of experimental data can be expressed as

both bases are new in functional analysis in the domain considered.
If the equation of the Mantle is denoted by  and we use the orthonormal base the result is:
and we use the orthonormal base the result is:

or by reorganizing the terms in the non–orthonormal; base

where: c1=a1b1+a1b2a2a3, etc.
In conclusion, the Mantle has 1, 2, 3, 4,...phases and there is at least one critical point and one triple point.
Conclusions
We derive an equation of state which predicts several phases. Equations (11), (13), (14) or (15) can explicitly generate 1, 2, 3,... phases depending on the experimental data, by using non–additive many–body energy potentials. A treatment based on statistical mechanics will agree with the experimental data, for systems of 1, 2,...phases, if and only if it considers non–additive many–body energy potentials plus binary additive energy potentials. The fact that the non–additive many–body energy potentials are absolutely indispensable to explain the experimental data means that they really exist. Thus we find that the earth's mantle is composed of many phases and has at least one critical point and one triple point. Independent linear and orthonormal bases are not used in functional analysis in the domain considered.
Bibliography
AMIR–AHMADI, H. R. et al. 2007. Three–nucleon force effects in cross section and spin observables of elastic deuteron–proton scattering at 90 MeV/nucleon. Phys. Rev. C 75, 04100 (R). [ Links ]
BIRCH, F., 1947. Finite Elastic Strain of Cubic Crystals. Phys. Rev., 809–824. [ Links ]
DENNERY, P. and A. KRZYWICKI, 1995. Mathematics for Physicists (Dover Publications Inc.). [ Links ]
KOLMOGOROV, A. N. and S. V. FOMIN, 1970. Introductory Real Analysis (Dover Publications Inc.). [ Links ]
MERMOD, P. et al. 2005. Evidence of three–body force effects in neutron–deuteron scattering at 95 MeV. Phys. Rev. C 72, 061002 (R). [ Links ]
MORSE, P. M. and H. FESHBACH, 1953. Methods of Theoretical Physics (McGraw Hill Inc.). [ Links ]
REICHL, L., 1977. A Modern Course in statistical Mechanics (University of Texas Press, Austin). [ Links ]
SUGIE, H. and LU, B. C.–Y., 1971. AIChE Journal 17, 1068. [ Links ]
THOMPSON, C. J., 1972. Statistical Mechanics (McMillan, New York). [ Links ]
UHLENBECK, G. E. and G. W. FORD, 1963. Lectures in Statistical Mechanics (American Mathematical Society, New York). [ Links ]
VAN KAMPEN, N. G., 1964. Phys. Rev. A 135, 362. [ Links ]














