Artículos

 

Desenvolvimento do conhecimento didático de uma futura professora de matemática do 3.° ciclo¹: O confronto com a sala de aula na preparação e análise de tarefas de modelação matemática

 

Development of didactical knowledge of a future mathematics teacher of 7th to 9th grade: the confrontation with the classroom in the preparation and analysis of mathematical modeling tasks

 

Floriano Viseu*, Luís Menezes**

 

* Centro de Investigação em Educação-Universidade do Minho, Portugal. fviseu@ie.uminho.pt

** CI & DETS - Escola Superior de Educação de Viseu, Portugal. menezes@esev.ipv.pt

 

Recepción: Septiembre 13, 2013
Aceptación: Octubre 18, 2013.

 

Resumo

Este artigo discute a forma como uma futura professora de Matemática mobiliza e desenvolve o seu conhecimento didático, ao nível do conhecimento do conteúdo matemático e do conhecimento da prática letiva, na preparação e análise de tarefas de modelação matemática, recorrendo à tecnologia. Este trabalho foi desenvolvido na fase final da sua formação inicial, no momento em que realiza o seu estágio profissional. Trata-se de um estudo interpretativo, na forma de estudo de caso qualitativo, que mostra que a realização de tarefas de modelação matemática e a sua reflexão, recorrendo à tecnologia, durante o estágio profissional, constitui uma ocasião de desenvolvimento profissional da futura professora, tanto em relação ao seu conhecimento do conteúdo matemático, ao ativar conhecimento trabalhado durante a sua formação inicial, como do seu conhecimento instrucional. Desta forma, as tarefas de modelação permitiram que a estagiária compreendesse que, para além do modelo transmissivo, existem outros modelos de ensino, com um cunho exploratório, que passam pela proposta pelo professor de tarefas matemáticas abertas e com um grau de dificuldade mais elevado, que envolvem os alunos numa atividade matemática intensa e que podem redundar em aprendizagens matemáticas significativas.

Palavras chave: Formação inicial de professores de Matemática, Conhecimento didático, Tarefas de modelação matemática.

 

Resumen

El presente artículo aborda cómo una futura profesora de matemáticas moviliza y desarrolla sus conocimientos didácticos, en lo que se refiere al conocimiento del contenido matemático y al conocimiento pedagógico, en la preparación y análisis de tareas de modelación matemática recurriendo a la tecnología. Este trabajo se desarrolló durante la fase final de su formación académica, en el momento de la realización de las prácticas. Se trata de un estudio interpretativo, bajo la forma de estudio de caso cualitativo, que demuestra que la realización de tareas de modelación matemática y la reflexión sobre ellas, recurriendo a la tecnología, durante la fase de prácticas constituye una oportunidad de desarrollo profesional para la futura profesora, tanto en lo que tiene que ver con su conocimiento del contenido matemático, activando conocimiento adquirido durante su formación académica, como en lo relativo a su conocimiento pedagógico. En este sentido, las tareas de modelación han permitido que la profesora en prácticas entendiese que, además del modelo transmisivo, existen otros modelos de enseñanza con un carácter exploratorio que pasan por que el profesor proponga tareas matemáticas más abiertas y con un grado de dificultad mayor, que hacen partícipes los alumnos en una actividad matemática intensa y que pueden redundar en aprendizajes matemáticos significativos.

Palabras clave: Formación inicial de profesores de matemáticas, Conocimiento didáctico, Tareas de modelación matemática.

 

Abstract

This article discusses how a preservice teacher of mathematics develops and mobilizes their didactical knowledge, in the matter of mathematical content and of instructional knowledge, in the preparation and analysis of tasks of mathematical modeling, using technology. The work took place at the end of their initial education when they make their internship. It is an interpretive study in the form of a qualitative case study that shows that the performance of tasks of mathematical modeling and the thinking about it, using technology, during the internship it is an opportunity for professional development of the preservice teacher, both the level of their knowledge of the mathematical content, enabling knowledge worker during their initial training, as their instructional knowledge. At this level, the modeling task allowed the future teacher to understand that beyond the transmissive model, there are other models of teaching in an exploratory nature, in which the teacher proposes mathematical open tasks with a higher degree of difficulty, involving students in mathematical intense activity which may result in significant mathematics learning.

Key words: Preservice mathematics, teacher education, Didactical knowledge, Mathematical modeling tasks.

 

Résumé

Cet article discute la manière dont une future enseignante de mathématiques développe et mobilise son savoir didactique, au niveau de la connaissance tant du contenu mathématique que pédagogique, au cours de la préparation et l'analyse de tâches de modélisation mathématique qui font appel à la technologie. Ce travail s'est fait à la fin de sa formation initiale, au moment de la réalisation du stage professionnel. Il s'agit d'une étude interprétative, sous la forme d'une étude de cas qualitative. La conclusion est que l'exécution, pendant le stage, de tâches (accompagnées de réflexion) de modélisation mathématique, qui utilisent la technologie, favorise le développement professionnel des futurs enseignants. Sont ainsi développées les connaissances sur le contenu mathématique, en activant les acquis de la formation initiale, ainsi que celles au niveau pédagogique. Les tâches de modélisation ont permis au stagiaire de comprendre qu'il existe, en plus le modèle transmissif, d'autres modèles d'enseignement d'orientation exploratoire. Le professeur propose alors des tâches mathématiques plus ouvertes, de degré de difficulté plus élevé, dans lesquelles les élèves s'investissent dans une activité mathématique intense, ce qui peut permettre des apprentissages mathématiques significatifs.

Mots clés: Formation initiale des enseignants de mathématiques, Connaissance didactique, Tâches de modélisation mathématique.

 

1. INTRODUÇÃO

A prática letiva e a reflexão sobre essa prática constituem um binómio fundamental da formação de professores (Menezes & Ponte, 2009; Ponte & Chapman, 2008; Viseu, 2008; Viseu & Ponte, 2012). A atividade que resulta dessa interação é particularmente importante na formação inicial de professores, porque corresponde, habitualmente, à primeira oportunidade em que os futuros professores confrontam a realidade da sala de aula com as suas teorias pessoais, tanto as que se formam por processos experienciais (enquanto alunos) como por processos de formação de natureza estruturada ao longo do curso de formação de professores. Estes processos formativos, que incluem conhecimentos de diversas áreas disciplinares (em particular, da Matemática e da sua Didática), trabalhados ao longo do curso, e também o conhecimento que resulta da prática profissional, na situação de estágio, interrelacionam-se para formar o conhecimento didático do professor, donde se destacam o conhecimento do conteúdo matemático e o conhecimento da prática letiva. Esses dois tipos de saber refletem o conhecimento que o professor tem do currículo e também o conhecimento que o professor tem da forma como os alunos aprendem (Ponte, 1999, 2012).

Na aprendizagem dos alunos, a atividade matemática, incluindo os processos de abstração reflexiva, assume um papel decisivo (Sierspinska, 1998). Para que haja atividade matemática rica, que permita que os alunos resolvam problemas, raciocinem e comuniquem matematicamente, é fundamental que estes sejam confrontados com tarefas desafiantes (Canavarro, Oliveira & Menezes, 2012; Simon & Tzur, 2004). As tarefas de modelação matemática, recorrendo à tecnologia, constituem exemplos de propostas didáticas que reúnem essas caraterísticas, incorporando uma forte componente experimental (Stein & Smith, 1998). A relevância que este tipo de tarefas adquire nos documentos curriculares oficiais (Ministério da Educação, 2007), em publicações dirigidas a professores (por exemplo, Matos & Carreira, 1996) e a investigadores (Blum, Galbraith, Henn & Niss, 2007), faz com que os professores, em geral, e os futuros professores, em particular, devam conhecê-las e experimentá-las, para poderem vir a integrá-las nas suas práticas de ensino.

O estudo que aqui se apresenta surge na confluência dessas duas vertentes: a formação inicial de professores de Matemática e as tarefas de modelação matemática enquanto recurso para a aprendizagem da Matemática. Em particular, este estudo tem como objetivo compreender o papel que uma experiência de ensino, baseada na preparação e análise de tarefas de modelação, recorrendo à tecnologia, tem no desenvolvimento profissional de uma futura professora de Matemática, quando esta se encontra no seu ano de estágio profissional, numa escola portuguesa do 3.° ciclo do ensino básico (EB). Com essa finalidade, este estudo propõe-se responder à questão: Como se desenvolve o conhecimento didático (do conteúdo matemático e da prática letiva) de uma futura professora em resultado da sua participação numa experiência de ensino, durante o seu estágio profissional, com alunos do 3.° ciclo do EB, baseada na utilização de tarefas de modelação matemática com recurso ao uso de tecnologia?

 

2. CONHECIMENTO DO PROFESSOR E PROCESSOS DE FORMAÇÃO

A investigação em educação matemática tem dado um destaque especial ao conhecimento que o professor precisa para ensinar, a partir da posição crítica de Shulman (1986), em face à tendência da investigação para se preocupar mais com o conhecimento dos aspetos pedagógicos do que com o conhecimento do conteúdo. Ao reconhecer a existência de um conhecimento específico para ensinar, o autor organiza esse conhecimento em conhecimento do conteúdo, conhecimento pedagógico geral, conhecimento do currículo e conhecimento pedagógico do conteúdo. Destes conhecimentos, Shulman dá particular destaque ao conhecimento pedagógico do conteúdo, que consiste nas formas de representar e formular o assunto, de modo a torná-lo compreensível ao aluno. O interesse por este tipo de conhecimento deriva da ligação que é estabelecida entre o conhecimento do conteúdo e a prática de ensino, o que significa que as discussões sobre o conteúdo devem ser relevantes para o ensino e que as discussões sobre o ensino devem garantir que se dê atenção ao conteúdo (Ball, Thames & Phelps, 2008). Ponte e Chapman (2006) consideram que essa definição de Shulman remete mais para uma conceção declarativa do conhecimento do professor do que para uma conceção de conhecimento orientado para a ação ou inserido na prática. Face a esta polaridade entre pedagogia e conteúdo matemático, alguns autores adotam uma posição integradora e de síntese do conhecimento do professor, apresentando a ideia de conhecimento didático (Azcárate, 1999; Canavarro, 2003; Ponte, 1999, 2012; Viseu, 2008). Seguindo esta linha conceptual, Ponte (2012) assevera que esse conhecimento do professor de Matemática é orientado para a atividade de ensinar, apoiando-se em conhecimentos de natureza teórica e também de natureza social e experiencial, integrando quatro vertentes fundamentais: (i) conhecimento da matemática; (ii) conhecimento dos alunos e da aprendizagem; (iii) conhecimento do currículo; e (iv) conhecimento da prática letiva. O autor considera que este modelo do conhecimento do professor (ver figura 1) é diferente de outros aparentemente semelhantes, pois assume claramente a existência de um núcleo central, o conhecimento da prática letiva. O modelo, em vez de separar as diversas vertentes, distinguindo umas das outras, chama a atenção para o facto de que elas estão sempre presentes, de uma forma ou de outra, na atividade de um professor quando ensina Matemática.

A primeira vertente do conhecimento didático diz respeito à disciplina que se vai ensinar. O conhecimento do conteúdo, similar ao proposto por Shulman (1986), é determinante na seleção das tarefas matemáticas, na tomada de decisões sobre como e quando abordar um dado tópico, estabelecer conexões entre tópicos, orientar as atividades dos alunos, ouvir e comentar as ideias destes e determinar a validade de um argumento matemático. O conhecimento didático inclui também uma vertente que se refere aos processos de aprendizagem dos alunos, mais especificamente das formas como eles aprendem. A este respeito, conhecer os interesses dos alunos, os seus gostos, as suas referências culturais e como aprendem é decisivo para o trabalho de ensinar do professor.

Das outras duas vertentes do modelo de Ponte (2012), o conhecimento do currículo, tal como para Shulman (1986), diz respeito ao saber que o professor possui relativamente aos programas da sua área disciplinar, à variedade de materiais que pode ser utilizada no ensino, assim como às vantagens e desvantagens do uso desses programas e materiais na sua atividade profissional. Por último, o núcleo, o conhecimento da prática letiva, refere-se à preparação, condução e avaliação do processo de ensino-aprendizagem. Esse conhecimento do professor, com uma forte dimensão acional e que está bastante diluído na proposta de Shulman (1986), envolve a capacidade para planificar uma aula, selecionando tópicos matemáticos dos documentos curriculares, e organizar situações didáticas que permitam a aprendizagem dos alunos. Ponte (2012) reforça nesse conhecimento, ao qual também chama de relativo à instrução ou instrucional, o papel das tarefas matemáticas, organizadas em sequências didáticas, por permitirem o trabalho autónomo dos alunos e momentos de discussão e sistematização de conhecimentos. Em todo este tipo de ensino, o professor desempenha um papel ativo, mas com uma atividade completamente diferente da de um estilo de ensino transmissivo.

Neste estudo, utilizamos como marco teórico para estudar o conhecimento do professor de Matemática este modelo de Ponte (2012) que, embora inspirado em Shulman (1986), tem uma natureza mais dinâmica e explicativa, colocando o conhecimento da prática letiva no centro, em torno do qual surgem o conhecimento da matemática, o dos alunos e da sua aprendizagem e o do currículo.

Embora a preparação dos professores seja um desiderato de uma vida, é no período da formação inicial que é dado um impulso decisivo para a construção do conhecimento didático (Viseu, 2008). Os cursos de formação inicial de professores seguem modelos diversificados, desde aqueles que integram a prática e a teoria ao longo do curso, até aos modelos sequenciais, nos quais primeiro são tratadas as matérias teóricas (da Matemática e da Didática) e só depois há o estágio pedagógico. Em Portugal, a formação inicial de professores do começo do ensino básico (feita pelas Escolas Superiores de Educação e por algumas Universidades) adotava, até meados da primeira década de 2000, o modelo integrado, enquanto a formação de professores para o final do ensino básico e para o ensino secundário (feita exclusivamente por universidades) adotava um modelo sequencial. Atualmente, como resultado da adaptação do ensino superior português às determinações do processo de Bolonha, a formação inicial de professores de Matemática de todos os níveis de ensino é obtida através da realização de dois cursos sequenciais, o primeiro de licenciatura (com seis semestres) e o segundo de mestrado (com dois a quatro semestres). O curso de licenciatura fornece ao futuro professor o conhecimento na área de docência, neste caso, da Matemática. O curso de mestrado é orientado para a preparação dos licenciados em áreas de formação educacional geral, de didáticas específicas e de prática de ensino supervisionado. Ou seja, proporciona sobretudo o conhecimento relativo ao currículo, aos alunos e à aprendizagem, e à prática letiva. O estudo que agora se apresenta incide sobre o conhecimento didático no contexto de um tipo de formação inicial de professores pré-Bolonha, realizada através de um curso único de licenciatura (cinco anos, dez semestres), que incluía no quinto ano a prática de ensino (estágio).

 

3. TAREFAS DE MODELAÇÃO MATEMÁTICA

O papel das tarefas é cada vez mais reconhecido como impulsionador da atividade dos alunos e da dinâmica da sala de aula (Stein & Smith, 1998; Viseu & Ponte, 2009). As recentes reformulações, em Portugal, dos programas da disciplina de Matemática dos diferentes anos de escolaridade, dão conta da importância que a diversidade do tipo de tarefas tem na indução das interações na sala de aula. Na dinamização dessas interações, o professor tem ao seu dispor, em função dos objetivos que pretende atingir, diferentes tipos de tarefas. Ponte (2005) distingue as tarefas a partir do grau de desafio (elevado/reduzido) e de estrutura (aberta/ fechada), da duração (curta/média/longa) e do contexto (realidade/semirealidade/ matemática pura).

Quanto ao contexto, as tarefas podem enquadrar situações da realidade, puramente matemáticas ou situações aparentemente reais. Ponte refere que as tarefas de contexto semirealidade tendem a não considerar a maior parte das propriedades reais das situações, centrando a sua atenção nas propriedades "que interessam a quem enunciou o problema" (2005, p. 19), acabando por possuir um contexto quase tão abstrato como o contexto matemático.

Um tipo de tarefa que é consignada de contexto de realidade são as tarefas de modelação. Trata-se de tarefas de natureza problemática e desafiante, sob a forma de problema ou investigação, conforme o grau de estrutura do seu enunciado, e que procuram identificar a Matemática presente numa situação do dia-a-dia e dar resposta às questões que vão sendo formuladas (Ponte, 2005). Atendendo às suas características — elas têm que ser para os alunos um problema e não um exercício e têm que ser extraídas do mundo real (Barbosa, 2006) —, as tarefas de modelação são, muitas vezes, designadas por aplicações da Matemática (Kaiser & Sriraman, 2006). Kaiser e Maaß (2007) descrevem a modelação como um processo no qual uma problemática é resolvida através da aplicação da Matemática, o que Barbosa (2002) chama de utilização de "ideias e/ou métodos matemáticos para compreender e resolver situações-problema oriundas de outras áreas de conhecimento que não a matemática" (p. 1). Para Silva e Barbosa (2011), a modelação matemática tem o propósito de desenvolver a compreensão dos alunos de como a matemática é utilizada nas práticas sociais, através da análise crítica da cultura dominante através da matemática. Um ambiente de aprendizagem que incentiva a questionar e a investigar situações com origem noutras áreas da realidade envolve os alunos em atividades de "esquematizar, desenvolver operações aritméticas, gerar equações, fazer desenhos, traçar gráficos, e, principalmente, produzir discursos" (Silva & Barbosa, 2011, p. 199).

O que se entende por modelação matemática não é consensual na literatura (Barbosa, 2006; Blum, 1993; Kaiser & Sriraman, 2006). Partindo do pressuposto de que os alunos e os modeladores profissionais possuem diferentes condições e interesses e que as práticas conduzidas por eles são diferentes, Barbosa (2006) distingue a modelação matemática feita por modeladores profissionais da atividade de modelação que é realizada na sala de aula. Na sala de aula, a atividade de modelar consiste em analisar e evidenciar os elementos e as relações presentes numa dada situação, solucionar a situação com base na Matemática, interpretar os resultados e confrontá-los com o fenómeno em estudo e tirar as respetivas conclusões. Nessa atividade, Verschaffel, Greer e De Corte (2000) identificam uma sequência de fases, que podem ser repetidas tantas vezes quantas forem necessárias, para se obter o modelo mais próximo da situação em estudo:

Fase 1: Compreensão da situação em estudo: analisar uma dada situação para considerar e decidir que elementos são relevantes e que relações e condições podem ser estabelecidas (como por exemplo, através da recolha de dados experimentais, com recurso à calculadora e aos sensores);

Fase 2: Construção de um modelo matemático: analisar os elementos relevantes, as relações e as condições disponíveis na situação para traduzir a situação na forma matemática;

Fase 3: Trabalhar com o modelo: obter alguns resultados;

Fase 4: Interpretação dos resultados: chegar a uma solução para a situação que deu origem ao modelo matemático;

Fase 5: Avaliar o modelo: verificar se a solução é matematicamente adequada e razoável para o problema original;

Fase 6: Comunicar a solução do problema original.

A forma como as tarefas de modelação são trabalhadas na sala de aula levou Barbosa (2003) a classificá-las, do ponto de vista teórico, em três casos. No caso 1, é o professor quem apresenta o problema, com dados qualitativos e quantitativos, competindo aos alunos a sua investigação. No caso 2, perante o problema que lhes é proposto, os alunos têm que recolher dados fora da sala de aula. No caso 3, integram-se os projetos a serem desenvolvidos a partir de temas 'não matemáticos', que podem ser escolhidos pelo professor ou pelos alunos.

A inclusão de tarefas de modelação na sala de aula de matemática coloca questões ao ensino, ao aluno e ao professor, umas que resultam em dificuldades e outras em elementos catalisadores. Em relação ao ensino, a dificuldade mais notória é o cumprimento do programa (Carreira, 2011), uma vez que, para se desenvolverem tarefas dessa natureza na sala de aula, é necessário tempo para as compreender, executar e avaliar. Quanto ao aluno, visto que na construção de um modelo matemático é necessário ter em conta vários aspetos simultaneamente, aumenta a complexidade na compreensão da experiência e na interpretação de resultados. Relativamente ao professor, exige-se capacidade para gerir conhecimentos matemáticos e também relativos a outras ciências, de modo a assegurar a transdisciplinaridade de saberes. As tarefas de modelação constituem, assim, desafios para o professor, principalmente pela dinâmica da aula de matemática perante a diversidade de estratégias que os alunos podem gerar (Oliveira & Barbosa, 2011). A imprevisibilidade de processos e de respostas situa o professor, segundo estes autores, numa zona de risco. Para além dessas razões, Oliveira e Barbosa (2011) enumeram outras que condicionam o professor na integração de tais tarefas na sala de aula:

"Dilemas relacionados à compreensão das fases do processo de modelação, como considerá-las separadamente ou conjuntamente no desenvolvimento dos projetos; a compreensão do objetivo da modelação, como um objetivo educacional em si ou para os alunos aprenderem matemática; inseguranças em relação à tomada de decisões na organização e condução da modelação em sala de aula; incertezas em relação à maneira como os professores podem proceder diante das soluções dos alunos na resolução dos problemas." (p. 268)

Em termos de elementos catalisadores, Júnior e Santo (2006) apontam a modelação matemática como um instrumento para a "desfragmentação dos currículos matemáticos tradicionais" (p. 5) na introdução de temas, favorecendo o currículo flexível e transdisciplinar. O desenvolvimento de um currículo compartimentado e assente na imitação do que o professor faz dá lugar, através desse tipo de propostas, a um currículo baseado na conexão de saberes e em atividades de exploração e investigação. No que concerne ao aluno, o contacto com situações que são geradas a partir da realidade desponta maior curiosidade, capacitando-o para estabelecer relações entre essa realidade e a Matemática. A atividade do aluno com tarefas de modelação matemática fomenta hábitos de trabalho, bem como o espírito crítico nas situações com as quais se depara. Na promoção de uma formação crítica do aluno em aulas de matemática, Barbosa (2002), Santana (2010), Oliveira e Barbosa (2011) e Ruiz-Higueras e García (2011) defendem que os alunos devem ter a oportunidade de refletir e discutir sobre os modelos matemáticos que lhes são impostos na sociedade e sobre as implicações dos resultados matemáticos decorrentes de uma situação-problema na sociedade. Relativamente ao professor, a modelação matemática promove a evolução intelectual, bem como a sua formação através da troca de experiências com os alunos e o seu meio social (Júnior & Santo, 2006). Todo este processo valoriza o ambiente criado dentro da sala de aula, enquanto prática social, sendo assim propício à implementação de tarefas de modelação matemática com os alunos. Trata-se de uma forma de compreender a Matemática como uma ciência que é relevante para a vida quotidiana, com significados próprios, que se (re)constroem no contexto da atividade através da interação com os outros (Cantoral, Farfán, Lezama & Martínez-Sierra, 2012). Nesta perspetiva, a aprendizagem da Matemática proporciona um meio para compreender o mundo, enfrentar problemas do dia-a-dia e preparar para futuras profissões. Em termos epistemológicos, a aula de Matemática é vista como um espaço de construção de conhecimento uns com os outros, em detrimento de práticas que induzem no aluno a aceitar conceitos, factos ou técnicas matemáticas como um campo de conhecimento estabelecido.

A relevância dada pela educação matemática à atividade decorrente do uso de tarefas de modelação faz com que esse tipo de tarefas seja incluído nos cursos de formação inicial de professores. Em termos educativos, procura-se aplicar o que se aprende na disciplina de matemática em situações do quotidiano. Porém, Barbosa (2002) considera que os futuros professores tendem a manifestar ceticismo quanto à possibilidade de implementar tarefas de modelação na sala de aula. Tal ceticismo despertou a atenção deste autor, no sentido de estudar como futuros professores concebem a modelação nas suas futuras práticas de ensino. O autor trabalhou com um grupo de 10 futuros professores, os quais frequentavam pelo menos o 2.° ano da Licenciatura em Matemática. Durante onze sessões, Barbosa (2002) envolveu os candidatos a professor em atividades de modelação e de reflexão sobre a sua utilização em sala de aula. Conjuntamente com essas atividades, os participantes desenvolveram projetos de modelação em grupo sobre temas não matemáticos, recolheram informações, formularam e resolveram problemas matemáticos e criaram uma história de sala de aula que englobasse o seu tema. Embora considerem que as tarefas de modelação são desejáveis nas aulas de matemática, por motivar os alunos e os formar para a cidadania, os futuros professores manifestam insegurança em trabalhar em sala de aula tarefas dessa natureza, devido às dificuldades que antecipam na condução das atividades de modelação, no acompanhamento dos alunos e no domínio do conteúdo matemático, à organização da escola, às condições de trabalho do professor e às expetativas e possíveis reações dos diferentes intervenientes no processo educativo. O autor conclui que para se ganhar segurança com tarefas de modelação é preciso acumular experiência e familiaridade com o ambiente de aprendizagem que resulta da integração deste tipo de tarefas na sala de aula.

Num outro estudo, Doerr (2007) examina o conhecimento de modelação de futuros professores numa disciplina de um curso de formação, que teve por finalidade introduzir ideias e técnicas básicas de modelação matemática. Ao longo da disciplina, os futuros professores efetuaram leituras e discussões sobre modelação, fundamentalmente sobre as fases de modelação. Inicialmente, viam essas fases como uma descrição não problemática de como a modelação era processada. Eles concebiam essas fases como uma sequência. Durante a experiência, os futuros professores alteraram esta conceção, passando da atividade sequencial para cíclica, não linear. Nem sempre os futuros professores efetuaram uma análise de regressão dos dados e aplicaram muitas vezes de forma acrítica o ajuste de uma dada curva aos dados que trabalharam. Mesmo com software disponível para efetuarem esse ajuste, os futuros professores raramente usaram esse recurso e quando ajustavam os dados com uma curva atendiam ao significado das equações resultantes. Este resultado sugere que a natureza das tarefas de modelação, as ferramentas disponíveis, as normas para a argumentação e os padrões de qualidade de uma solução foram decisivos para influenciar os tipos de modelação que ocorreram em cada configuração. A autora conclui que através da reflexão sobre a própria atividade de modelação, os futuros professores compreenderam a natureza do ciclo do processo de modelação. O uso de modelos de regressão parece depender do tipo de atividades que os futuros professores experimentaram, o que implica que precisam de contactar com atividades de modelação que ofereçam oportunidades para explicar e justificar as decisões tomadas. A discussão sobre o modelo de regressão que melhor se ajusta aos dados experimentais sustenta a perspetiva de modelação adotada neste estudo. Seguindo as fases delineadas por Verschaffel et al (2000), a modelação é vista como um processo de resolução de problemas, cujo enunciado é aberto à recolha de dados, à procura do modelo que melhor se ajuste a esses dados e à discussão dos resultados em função do contexto do problema.

 

4. METODOLOGIA

Este estudo de caso, qualitativo e de natureza interpretativa, foca-se numa futura professora de Matemática, a quem foi atribuído o nome fictício de Vera, durante o seu quinto e último ano do curso de formação inicial. Vera foi escolhida por diversas razões: (i) pertencia ao grupo de estágio que tinha como supervisor o primeiro autor deste artigo; (ii) foi um dos elementos deste grupo de estágio em que mais foi patente o confronto entre a teoria e a prática de sala de aula; (iii) mostrou disponibilidade e interesse em participar na investigação. Neste quinto ano, Vera realizou o seu estágio profissional numa escola da zona norte de Portugal, no 3.° ciclo do EB, do qual fazia parte, e além da prática profissional na escola, a realização de um trabalho de projeto que incidisse em atividades relativas à Matemática e sua Didática que realçassem as relações da Matemática com outras ciências. O trabalho de projeto de Vera consistiu em analisar a aplicação de sete tarefas de modelação, com recurso à tecnologia, no ensino da Matemática no 3.° ciclo e a sua extensão no ensino secundário (ver Quadro 2 e anexo). Neste artigo, só nos debruçamos sobre duas tarefas do 3.° ciclo (Matemática por um canudo e Bola saltitante).

Algumas tarefas foram trabalhadas na sala de aula, nas turmas atribuídas ao orientador² da escola que acompanhou a prática pedagógica de Vera, e em turmas de 8.° e 9.° ano de outros professores que cederam um bloco de Estudo Acompanhado³. As tarefas foram elaboradas com base nas orientações dos programas de Matemática do 3.° ciclo do EB e do ensino secundário e na análise de publicações sobre experiências com tarefas de modelação com recurso à tecnologia, como por exemplo o trabalho do Grupo de Trabalho T³ (Associação Professores de Matemática, 2002). As tarefas escolhidas (em anexo) envolvem modelação matemática em situações do quotidiano dos alunos do 3.° ciclo do EB, tocando diversas áreas disciplinares, promovendo assim a interdisciplinaridade. No âmbito deste trabalho, recorreu-se a vários meios tecnológicos como calculadora gráfica, CBR (Calculator-Based RangerTM), CBL (Calculator-Based LaboratoryTM) e folha de cálculo.

Os dados recolhidos neste estudo resultam: (i) do relatório do trabalho de projeto desenvolvido pela estagiária; (ii) da planificação e reflexão de uma aula; e (iii) da entrevista realizada a Vera após a conclusão do estágio. Com o relatório, conseguiu-se uma descrição e fundamentação das situações de modelação, para além das que foram trabalhadas com os alunos nas aulas. Com a planificação e reflexão, obtiveram-se dados relativos à preparação, execução e avaliação da utilização de uma tarefa de modelação matemática em contexto de sala de aula. Com a entrevista, obtiveram-se dados relativos ao impacto que este trabalho teve no seu conhecimento didático, em particular no conhecimento de conteúdo matemático e no conhecimento da prática letiva.

A análise de dados assentou na análise de conteúdo de todo o material escrito, tomando como referência o quadro teórico relativo ao conhecimento didático (em particular, duas das vertentes consideradas por Ponte (2012), o conhecimento matemático e o conhecimento relativo à prática letiva) e às tarefas de modelação matemática.

 

5. A ESTAGIÁRIA VERA

5.1. A futura professora e as tarefas de modelação

Vera é uma futura professora de Matemática que inicia o seu estágio pedagógico sem ter qualquer experiência de ensino como professora. O estágio, que corresponde ao último ano do curso, ocorre quando Vera está prestes a completar 23 anos.

Vera relata que, durante todo o seu percurso escolar, "nunca trabalhei com tarefas de modelação, nunca me foram dadas a conhecer enquanto aluna do básico, do secundário ou do superior" (Entrevista (E), Nov. 2009). A aplicação e análise de tarefas de modelação no estudo de tópicos matemáticos do 3.° ciclo, durante o seu estágio pedagógico, constituiu, como refere, "um grande desafio, uma vez que para mim foi uma autêntica descoberta, o que levou a uma grande pesquisa e trabalho" (E). Este trabalho contribuiu para que a futura professora se apercebesse que a natureza das tarefas de modelação aponta, como sublinha, para estratégias de "ensinar Matemática de uma forma experimental e aberta (...) método que motiva os alunos e os torna mais participativos e empenhados" (E). Esta relação que a estagiária estabelece entre a natureza das tarefas e o tipo de estratégias de ensino reflete algumas das orientações metodológicas dos atuais programas de Matemática do ensino básico (PMEB)⁴.

A atividade experimental que é proporcionada aos alunos pelas tarefas de modelação leva Vera a afirmar que, através dela, os alunos realizam uma aprendizagem da Matemática mais sólida, e comprometida: "As tarefas de modelação permitem que os alunos, através de um trabalho experimental, construam as suas próprias aprendizagens, o que os motiva muito mais do que quando é o professor a transmitir-lhes os conteúdos" (E). Na perspetiva da futura professora, um estilo de ensino baseado nas tarefas de modelação, além de robustecer o envolvimento dos alunos nas atividades da aula, favorece o desenvolvimento do espírito crítico, a predisposição para aprender e ajuda a compreender a utilidade do que aprendem:

Com este método de ensino, os alunos desenvolvem o seu espírito crítico e estão mais predispostos para aprender conceitos novos. Este método permite mostrar aos alunos como a Matemática lhes é útil no seu quotidiano. Os alunos não ficam com uma visão tão limitada dos conteúdos matemáticos e através das tarefas de modelação articulam o que aprendem na sala de aula e colocam em prática na sua própria vida. (E)

Esta visão global que a estagiária desenvolve sobre o papel das tarefas de modelação no ensino da Matemática é resultado da sua experiência de estágio, ao longo de um ano letivo, em particular a forma como mobiliza e gera duas das principais componentes do seu conhecimento didático: conhecimento do conteúdo matemático e conhecimento da prática letiva.

 

5.2. Conhecimento do conteúdo matemático

A experiência que Vera realizou com as tarefas de modelação no seu estágio incidiu sobre vários tópicos matemáticos, tais como tratamento e análise de dados, proporcionalidade direta e inversa e funções (afim e quadrática). Para a estagiária, a experimentação pelos alunos das diversas fases do trabalho numa tarefa de modelação "favorece a compreensão dos tópicos matemáticos que são trabalhados" (E). Essa compreensão matemática resulta da atividade que se desenvolve desde a fase da recolha de dados até à discussão do modelo que melhor se ajusta aos pontos experimentais que traduzem esses dados. A integração destas tarefas na sala de aula faz com que, na perspetiva de Vera, o professor, além de ter bem presente os conteúdos matemáticos, saiba esclarecer os alunos de como encontrar esse modelo. Para o ilustrar, apoiando-se nas representações que coloca no relatório, Vera invoca um exemplo de uma aula relativo à constante de proporcionalidade inversa:

O professor ao conduzir a tarefa tem que estar bem seguro do que está a fazer. Aconteceu comigo, por exemplo, numa aula sobre proporcionalidade inversa⁵. Levei para a aula uns tubos com o mesmo diâmetro e comprimentos diferentes. O que se pretendia era que o aluno observasse através dos diferentes tubos uma fita métrica que estava colocada numa parede a um metro. À medida que o comprimento do tubo diminuía o campo de visão aumentava, o que indicia estarmos perante uma situação de proporcionalidade inversa. Admitindo que fosse este o melhor modelo que se ajustava aos dados experimentais, procurámos o valor da constante de proporcionalidade inversa. Até este momento funcionou tudo bem o problema foi a seguir. Os alunos fizeram o produto entre as grandezas e não obtiveram nem um valor igual.

A possibilidade que tínhamos para encontrar o modelo foi considerar a média dos produtos. Foi dessa forma que contornei a situação no momento. É um pouco desgostoso no final de uma tarefa que pensamos que executamos tudo na perfeição não encontrarmos o modelo pretendido, mas com a prática haverá sempre uma forma de contornar a situação. (E)

Na verdade, o trabalho que se realiza nas aulas de Matemática, ao longo do EB, habitualmente com tarefas de natureza fechada, leva os alunos a construir a conceção de que a atividade matemática se resume à aplicação de algoritmos, regras e propriedades para se obter um resultado. Vera, mesmo depois de ter frequentado grande parte do seu curso de Matemática, indicia alguma perplexidade e insegurança por a tarefa "Matemática por um canudo'" não lhe fornecer resultados com a precisão que esperava: "experimentei esta atividade diversas vezes e nunca consegui chegar à constante de proporcionalidade inversa. Sabendo que corria este risco, levei avante esta atividade muito por incentivo dos meus orientadores que acreditam que é necessário inovar e correr riscos" (Reflexão (R), Dez. 2008).

Por se tratar de uma tarefa de natureza experimental, fatores como a sensibilidade do óculo visual e também a precisão de manter o tubo de observação na horizontal podem influenciar os valores registados. A tarefa não gerou valores que permitissem obter um produto constante, como esperaria. O valor médio dos produtos obtidos foi a solução encontrada por Vera para resolver este problema matemático. Posteriormente, na discussão com o seu supervisor sobre a forma como explorou esta tarefa na aula, a estagiária vê-se confrontada com a possibilidade de alargar esta abordagem com a determinação do erro entre os valores experimentais e os valores gerados pelo modelo através da soma dos quadrados dos desvios entre estes valores:

Com recurso à folha de cálculo, Vera apercebeu-se da atividade que a tarefa proporcionaria na discussão de formas de minimizar o erro entre os valores gerados pelo modelo e os experimentais. Para além da exploração do valor médio dos produtos entre os valores das variáveis, o que fez na sala de aula com os seus alunos, o trabalho que realiza no contexto de supervisão permite-lhe compreender que a riqueza da tarefa proposta está na discussão sobre o efeito da variação da constante que se procura no erro entre os valores experimentais e os teóricos:

Como não tinha a certeza que este modelo seria o melhor que se ajustasse aos dados experimentais, procurei encontrar outros modelos que minimizassem o erro entre os valores determinados e os valores experimentais. Recorri então ao Excel para apurar a variabilidade do somatório dos erros. (Rel, Junho 2009)

Figura 3

Em vez de aplicar o método dos mínimos quadrados para cada valor que considerasse como constante, para poder comparar a soma dos quadrados dos desvios, a função solver da folha de cálculo permitiu-lhe encontrar o valor da constante que minimiza o erro dos quadrados de tais desvios. O conhecimento que adquire dessa abordagem permite que Vera trate os dados que recolhe com outras tarefas de modelação que realizou. A folha de cálculo fez emergir o significado de conhecimentos, em detrimento da componente instrumental, que Vera adquiriu durante o seu curso de formação inicial:

O trabalho passou por analisar cada uma das tarefas e estabelecer conexões entre os diferentes temas. Em todas elas me auxiliei na Estatística para encontrar o modelo pretendido, através do método dos mínimos quadrados. Para fazer este estudo pesquisei sobre o assunto para perceber o significado do que estava a utilizar. Trabalhar no Excel o método dos mínimos quadrados foi uma grande aprendizagem. Este era um conteúdo que tinha aprendido numa cadeira de Análise Numérica mas que não estava presente, muito menos trabalhá-lo com o auxílio do computador. Foi esta a forma que me permitiu discutir qual era o modelo que melhor se aproximava do modelo pretendido. (E)

Em complemento, Vera destaca a aprendizagem de conceitos matemáticos que as tarefas de natureza aberta lhe proporcionaram, especialmente aqueles que têm incidência direta em temas matemáticos dos anos de escolaridade onde irá lecionar futuramente:

Como não tive um ensino baseado em tarefas abertas posso dizer que os conteúdos abordados ao longo do meu curso me permitiu adquirir conhecimento acerca dos conteúdos que são necessários ensinar na prática pedagógica. Reconheço que após o trabalho com as tarefas de modelação, a visão de cada conceito abordado através de uma tarefa é muito mais abrangente. É mais compreensível que os conteúdos não sejam tratados de forma muito abstrata e tentando, sempre que possível, aproximar a matemática da realidade. (E)

Depreende-se, pois, que Vera desenvolveu, regra-geral, até ao seu estágio, o seu conhecimento matemático através de um ensino direto, com recurso a tarefas fechadas, seguindo um padrão baseado na repetição do apresentado e explicado previamente pelo professor.

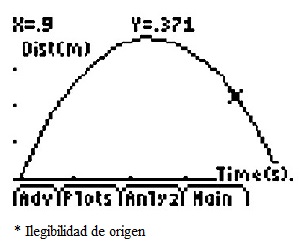
Na tarefa 'Bola Saltitante' (anexo), que Vera analisou no seu relatório do trabalho de projeto, com o auxílio de uma calculadora gráfica, um CBR e uma bola, são recolhidos dados referentes à queda vertical da bola, colocada a uma altura inicial de aproximadamente 0.7 m (Figura 4). Com os dados recolhidos representa graficamente a altura da bola em relação ao solo em função do tempo. Vera considera que "esta representação não é linear porque se trata de um movimento uniformemente acelerado; a velocidade da bola aumenta ao longo do movimento descendente e diminui no movimento ascendente" (Rel, Junho 2009).

Da análise dos dados, a estagiária apercebe-se que "os pontos máximos de cada uma das parábolas descritas pelo movimento da bola descrevem uma função exponencial" (Rel). Para averiguar a altura máxima que a bola atinge num determinado intervalo de tempo, Vera regista no seu relatório:

Restringi o domínio da experiência de modo a analisar uma das curvas que traduz o movimento da bola nesse intervalo. Fisicamente, a curva é uma parábola porque se trata do movimento de um corpo sujeito apenas à aceleração da gravidade.

Para este tipo de movimento verifica-se que é uma função representada por uma expressão do tipo y(t) =at² + bt+c. Recolhendo três pontos do gráfico obtido - (0.4; 0.301), (0.65; 0.632) e (0.9; 0.371) - e substituindo na expressão geral das funções do 2.° grau encontrei, através de um sistema com três equações a três incógnitas, a expressão y (t) = -4.741² + 6.3t-1.46. Esta expressão permite evidenciar o grau da função, a distinção das funções quadráticas completas das incompletas, a designação da sua imagem geométrica (parábola) e as unidades das variáveis. Permite ainda determinar, através da fórmula resolvente, os zeros da função e discutir o seu significado. (Rel)

A concretização de tarefas de modelação despertou em Vera alguns receios, devidos principalmente à imprevisibilidade dos resultados encontrados que dificultam a construção do modelo:

O meu maior receio surgiu ao nível prático, os resultados nem sempre são os pretendidos. Por exemplo, nas tarefas em que se pretendia estudar a proporcionalidade direta ou inversa, nem sempre as experiências nos davam valores constantes. Esta abordagem obrigou-me a um trabalho de pesquisa e de revisão de conceitos. Senti que alguns conceitos estavam esquecidos pelo facto de não serem trabalhados diariamente, como por exemplo conceitos das funções e de estatística ao nível do secundário. (E)

A imprevisibilidade dos resultados e do modelo mais adequado fez com que Vera sentisse a necessidade de rever e, sobretudo, de acomodar conceitos matemáticos abordados no estudo das funções e da organização e tratamento de dados. Esta acomodação de conceitos, aprendidos durante o seu curso, traduziu-se na atribuição de significado na interação teoria/prática.

 

5.3. Conhecimento da prática letiva

A tarefa "Matemática por um canudo" foi uma das que foram trabalhadas com os alunos na sala de aula, no estudo da função de proporcionalidade inversa. Na planificação da aula, Vera identifica os conhecimentos prévios dos alunos — "o conceito de função, representação de pontos no referencial cartesiano e operar com expressões com variáveis" (Plano de Aula (PA), Nov. 2008) — e formula um enunciado de um problema que pretende que desencadeie a atividade dos alunos:

A Rita ao visitar um museu de arte sentou-se diante de um quadro para descansar. Como tinha vários folhetos de diferentes comprimentos mas com a mesma largura resolveu contemplar um dos quadros com os tubos que formou com esses folhetos de igual diâmetro. Será que existe alguma relação entre o comprimento dos tubos e a porção do quadro contemplada pela Rita? (PA)

Para que os alunos pudessem resolver o problema, a futura professora propôs-lhes uma experiência através do seguimento de um conjunto de procedimentos:

Um elemento segura a fita métrica verticalmente encostada à parede; um outro elemento coloca-se a 1 metro dessa parede e olha através do tubo colocado paralelamente ao chão; um outro elemento regista o comprimento da fita visualizada. Alterando o comprimento do tubo, repetir o procedimento até preencher a tabela seguinte):

Vera adota uma abordagem exploratória, convidando os alunos a "recolher os dados, identificar e justificar as variáveis dependente e independente, recorrer a diferentes representações das funções, conjeturar e a generalizar" (PA). Refletindo sobre a ação instrucional do professor, Vera confronta esta sua estratégia de ensino com outras estratégias que remetem o aluno para um papel passivo e que dão prevalência a tarefas fechadas:

Quando o ensino é fechado, as próprias tarefas são fechadas. Neste tipo de ensino, o professor chega à sala de aula, transmite os conceitos que o aluno tem que ser capaz de reproduzir, faz alguns exercícios tipo e a aula termina. Desta forma, o aluno não tem tempo sequer de assimilar os conceitos. É esta a diferença entre este ensino e o ensino que aposta nas tarefas de modelação. (...) Na minha opinião é muito mais enriquecedor um ensino baseado em tarefas do que um ensino fechado que a maioria das vezes apenas recorre ao manual escolar. (E)

Por os alunos estarem mais habituados a tarefas fechadas, e também por ter ponderado sobre as suas próprias dificuldades no momento de preparação da tarefa, Vera sentiu necessidade de os alertar para a natureza dos resultados que poderiam obter:

Comecei a aula a dizer aos alunos que íamos colocar em prática uma atividade experimental mas que eles tinham de ter em atenção que esta poderia afastar-se um pouco daquilo que pretendíamos. Já tinha experimentado esta tarefa antes de a levar para a sala de aula e nunca tinha conseguido chegar à constante de proporcionalidade inversa que se pretendia. (R)

Este seu receio, que já vinha da fase de preparação da aula, levou-a a conduzir os alunos, orientando-os fundamentalmente a seguirem procedimentos, perdendo as potencialidades que tais valores divergentes poderiam trazer para a discussão coletiva:

Após o registo dos valores fizemos o produto entre os valores do comprimento do tubo e da fita observada e os alunos foram-se apercebendo que o valor não era constante. Sugeri que fizessem a média dos valores obtidos. Os alunos introduziram os dados na calculadora gráfica e efetuaram a representação gráfica da expressão cuja constante de proporcionalidade inversa era esse valor da média. Observámos que o gráfico só passava em apenas dois pontos. (.) Quanto ao que correu menos bem não posso dizer que tenha sido negativo o facto de não termos conseguido obter uma constante com o produto das variáveis. No entanto, se tivéssemos obtido uma constante ou valores muito próximos teria sido muito mais gratificante. (R)

Além de identificar vantagens das tarefas de modelação nas estratégias de ensino, Vera assume que existem obstáculos que dificultam esta integração curricular, tais como a necessidade de cumprimento dos programas, o ritmo de aprendizagem dos alunos e a sua própria inexperiência profissional:

Na minha opinião, é um pouco difícil apostar a cem por cento num ensino baseado em tarefas de modelação devido ao cumprimento dos programas. O mais certo é que dentro da sala de aula existam alunos com diferentes ritmos de aprendizagem. Uns precisam de mais tempo para assimilar os conteúdos que outros. Quando se levam tarefas de modelação para a sala de aula já se sabe de antemão que a execução da tarefa pode não correr como planificada. Todos estes fatores exigem tempo, mais tempo do que se pensar numa forma de transmitir um conceito mesmo que seja através de um exemplo da vida real. Se o programa não fosse tão extenso devia-se apostar muito mais neste tipo de ensino. (E)

Vera tem consciência que, apesar dessas dificuldades, que são agravadas pela sua condição de estagiária, é possível e desejável seguir um estilo de ensino que equilibre o trabalho dos alunos com tarefas de modelação e tarefas de natureza mais fechada:

Enquanto estagiária foi muito importante ter trabalhado com estas tarefas porque me fez ver o ensino com outros olhos mas também percebi que para ter a possibilidade desta prática letiva, outros conceitos tiveram que ser trabalhados de forma mais fechada para ser possível cumprir o programa. É certo que se o professor já tiver alguma prática, mais facilmente conseguirá gerir o programa de forma a implementar tarefas de modelação matemática com os seus alunos. (E)

Apesar de reconhecer que as tarefas de estrutura aberta tornam mais difícil a gestão da aula, Vera considera que as aulas são mais desafiantes quando os alunos se envolvem intensamente nas atividades de aprendizagem:

Acredito que para os alunos foram muito mais interessantes as aulas em que eles puderam participar de forma ativa na aula. Enquanto estagiária, posso afirmar que mesmo com toda a minha inexperiência e pelo facto de ter conduzido umas aulas de forma mais aberta (ou pelo menos essa era a minha intenção) e outras não tão conseguidas, as aulas em que foram os próprios alunos a tirarem as suas próprias conclusões foram muito mais satisfatórias. Mesmo por vezes ter-me sentido insegura por não saber o que um aluno me pudesse perguntar, achei muito mais desafiantes estas aulas. (E)

A estagiária tem consciência dos riscos que corre quando se trabalha na sala de aula com tarefas cujos resultados são inesperados. Ao assumir esse risco, identifica vantagens que essas tarefas têm na atividade matemática que os alunos realizam. Para além disso, desenvolve um conhecimento sobre a instrução em que repensa o papel do professor e dos alunos no ensino e na aprendizagem e o papel que as tarefas matemáticas, e a atividade que decorre da sua proposta, podem ter na aprendizagem dos alunos.

 

6. CONCLUSÕES

O confronto com a sala de aula, ao longo do seu estágio, através de uma prática baseada em tarefas de modelação matemática constitui para a futura professora uma ocasião de desenvolvimento profissional, tanto ao nível do seu conhecimento do conteúdo matemático para ensinar como do conhecimento do relativo à prática letiva (Ponte, 2012).

No âmbito do conhecimento do conteúdo matemático, a futura professora confronta o seu conhecimento matemático, aprendido durante a formação inicial (declarativo e axiomaticamente fundado) com situações da realidade, representadas por modelos matemáticos. Este choque provocado pelas tarefas de modelação matemática colocou a futura professora, em termos do conhecimento do conteúdo matemático, num terrento adverso de conflito cognitivo que rompeu com algumas das suas conceções sobre a matemática. A sua conceção da matemática-ciência, caracterizada por modelos puros e verdades objetivas e absolutas - evidência disso é a situação de proporcionalidade inversa em que o modelo matemático não se ajusta perfeitamente aos dados da realidade - dá lugar a uma matemática enquanto um corpo de conhecimentos em construção que resulta da interação entre os intervenientes, na qual a dúvida dá lugar à certeza e esta a novas dúvidas (Davis & Hersh, 1995). Além disso, as tarefas de modelação matemática trabalhadas no estágio colocam igualmente a futura professora numa situação desconfortável e de conflito cognitivo, porque elas mobilizam a matemática em situações abertas, onde impera a imprevisibilidade (ao contrário do que experienciou na sua formação inicial), o que para Oliveira e Barbosa (2011) coloca o professor numa zona de risco. A inexperiência profissional do futuro professor tende a determinar a preferência por tarefas que lhe permita antever processos e resultados.

A preparação, aplicação e análise das tarefas de modelação matemática tiveram impacto significativo no conhecimento do conteúdo matemático da futura professora, fazendo com que ganhasse em termos da sua própria compreensão matemática e também da melhor forma de o apresentar e tornar inteligível aos alunos, no sentido que Shulman (1986) dá quando se refere ao conhecimento pedagógico de conteúdo. Esses resultados reforçam estudos anteriores que dão conta da importância de os professores, durante a sua formação inicial, terem contacto com tarefas de modelação matemática, visando o desenvolvimento do conhecimento matemático e da conceção da própria matemática (Barbosa, 2002; Doerr, 2007; Júnior & Santo, 2006; Oliveira & Barbosa, 2011). Os resultados deste estudo mostram que isso deve acontecer desde cedo no curso de formação de professores e não no ano terminal (como foi o caso com esta futura professora). Em termos matemáticos, o estudo permite destacar o desenvolvimento do conhecimento relativo ao próprio processo de modelação matemática. Neste estudo, tal como em Doerr (2007), a futura professora evolui de uma conceção da modelação como uma atividade sequencial para uma concetualização em que esta surge como uma atividade não linear, o que parece resultar da formulação dos problemas que propõe nas aulas e da sua consciencialização de fatores que condicionam a recolha de dados, a problematização do modelo e dos resultados obtidos e a minimização do erro entre os valores teóricos e experimentais.

Em paralelo com este desenvolvimento no seu conhecimento do conteúdo matemático, a futura professora questiona a sua conceção sobre a forma de ensinar matemática, ou seja, o seu conhecimento da prática letiva (Ponte, 2012), inicialmente muito marcado pela sua experiência enquanto aluna (no ensino secundário e depois no ensino superior). Assim, reconhece que a utilização de tarefas de modelação matemática permite que os alunos tenham uma experiência matemática completamente diferente daquela que resulta de um ensino direto (Canavarro et al, 2012; Simon & Tzur, 2004), havendo no primeiro um ganho significativo em termos da qualidade da sua aprendizagem. Este reconhecimento resulta daquilo que observou nos seus alunos durante as aulas em que utilizou tarefas de modelação matemática, mas também de um certo isomorfismo entre o seu próprio processo de desenvolvimento do seu conhecimento matemático (a compreensão que ganhou de determinados tópicos matemáticos em resultado da preparação, realização e reflexão das aulas com tarefas de modelação), e aquilo que os seus alunos também experienciaram em termos da sua aprendizagem da Matemática (Viseu & Ponte, 2009, 2012).

A futura professora, apesar de reconhecer os méritos das tarefas matemáticas de modelação para a aprendizagem dos alunos, revela: (i) insegurança na sua capacidade para gerir este tipo de aulas; (ii) dúvidas sobre a possibilidade de cumprir o programa curricular de Matemática recorrendo assiduamente a tarefas de modelação matemática, dado serem muito exigentes em termos de necessidade de tempo. Trata-se de fatores de tensão da prática letiva que também foram salientados no estudo de Oliveira e Barbosa (2011) e na metaanálise de Silveira e Caldeira (2012). O facto de ser estagiária, faz com estes dois aspetos estejam muito ligados. O confronto com a prática, nas fases de preparação, execução e reflexão das aulas, é um momento importante da formação dos futuros professores (Cochran-Smith & Lytle, 1999; Viseu, 2008; Viseu & Ponte, 2012).

Neste estudo, a futura professora coloca em causa algumas das suas conceções sobre o modo de organizar a instrução, problematizando o papel do professor, dos alunos e das tarefas matemáticas. A questão do cumprimento do programa é um aspeto recorrente na gestão curricular, que esta futura professora coloca no outro prato da balança, neste momento de finalização da sua formação. O conhecimento relativo à prática letiva, que permite gerir a aula e promover a aprendizagem da Matemática, é um domínio em que os primeiros anos de carreira têm um papel fundamental (Viseu & Ponte, 2009, 2012).

Os resultados deste estudo, no qual foram registados progressos significativos no conhecimento do futuro professor em termos do conteúdo matemático (incluindo neste conhecimento, tanto o conhecimento matemático propriamente dito como o conhecimento relativo aos processos de trabalho matemático, como sejam a modelação matemática) e da instrução, consequência do confronto com a prática, na preparação, execução e reflexão de tarefas de modelação matemática, levam-nos a concluir da importância de proporcionar aos futuros professores experiências formativas que incluam desde cedo a possibilidade de ensinar. O modelo positivista que inspira modelos de formação inicial de professores sequenciais, em que a prática profissional deve ser precedida pela teoria (neste caso, o conhecimento didático, nas suas diversas vertentes) e apresentada de maneira formal, é seriamente questionado por este estudo, tanto no desenvolvimento do conhecimento da prática letiva, onde seria expectável, como, e sobretudo, no conhecimento matemático dos futuros professores.

 

REFERÊNCIAS BIBLIOGRÁFICAS

Associação Professores de Matemática Grupo de trabalho T3 (2002). Funções no 3.º ciclo com tecnologia. Lisboa, Portugal: Associação Professores de Matemática.         [ Links ]

Azcárate, P. (1999). El conocimiento profesional: naturaleza, fuentes, organización y desarrollo. Quadrante, 8, 111-137.         [ Links ]

Ball, D. L., Thames, M. H. & Phelps, G. (2008). Content knowledge for teaching: what makes it special? Journal of Teacher Education, 59(5), 389-407. doi: 10.1177/0022487108324554.         [ Links ]

Barbosa, J. C. (2002). Modelagem matemática e os futuros professores. In Reunião Anual da ANPED, Caxambu: ANPED. Acedido em 13 de Maio de 2013 de http://www.inf.unioeste.br/~rogerio/MM-Futuros-Professores.pdf.         [ Links ]

Barbosa, J. C. (2003). Modelagem matemática na sala de aula. Perspectiva, 27(98), 65-74.         [ Links ]

Barbosa, J. C. (2006). Mathematical modelling in classroom: a critical and discursive perspective. Zentralblatt für Didaktik der Mathematik, 38(3), 293-301. doi: 10.1007/BF02652812        [ Links ]

Blum, W. (1993). Mathematical modelling in mathematics education and instruction. In T. Breiteig, I. Huntley & G. Kaiser-Messmer (Eds.), Teaching and learning mathematics in context (pp. 3-14). New York, United States of America: Ellis Horwood.         [ Links ]

Blum, W., Galbraith, P. L., Henn, H. W. & Niss, M. (Eds.) (2007). Modelling and Applications in Mathematics Education -The 14^th ICMI Study. Berlin, Germany: Springer.         [ Links ]

Canavarro, A. P. (2003). Práticas de ensino da Matemática: Duas professoras, dois currículos. Tese de Doutoramento não publicada, Universidade de Lisboa, Lisboa, Portugal.         [ Links ]

Canavarro, A., Oliveira, H. & Menezes, L. (2012). Práticas de ensino exploratório da matemática: o caso de Célia. In P. Canavarro, L. Santos, A. Boavida, H. Oliveira, L. Menezes & S. Carreira (Ed.), Actas do Encontro de Investigação em Educação Matemática 2012: Práticas de ensino da Matemática (pp. 255-266). Portalegre, Portugal: Sociedade Portuguesa de Investigação em Educação Matemática.         [ Links ]

Cantoral, R., Farfán, R. M., Lezama, J. & Martínez-Sierra, G. (2006). Socioepistemología y representación: algunos ejemplos. Revista Latinoamericana de Investigación en Matemática Educativa, Número Especial 9(4), 83-102.         [ Links ]

Carreira, S. (2011). Looking Deeper into Modelling Processes: Studies with a Cognitive Perspective – Overview. In G. Kaiser, W. Blum, R. Borromeo Ferri & G. Stillman (Eds.), Trends in Teaching and Learning of Mathematical Modelling (Vol. 1, pp. 159-163). New York, United States of America: Springer. doi: 10.1007/978-94-007-0910-2_17        [ Links ]

Cochran-Smith, M. & Lytle, S. (1999). Relationships of knowledge and practice: Teacher learning in a communities. Review of Research in Education, 24, 249-305.         [ Links ]

Davis, P. J. & Hersh, R. (1995). A experiência matemática. Lisboa, Portugal: Gradiva.         [ Links ]

Doerr, H. (2007). What knowledge do teachers need for teaching mathematics through applications and modeling? In W. Blum, P. L. Galbraith, H. W. Henn & M. Niss (Eds.), Modelling and Applications in Mathematics Education -The 14 ^th ICMI Study (Vol. 10, pp. 69-78). Berlin, Germany: Springer. doi: 10.1007/978-0-387-29822-1_5        [ Links ]

Júnior, A. G. M. & Santo, A. O. E. (2006). A modelagem como caminho para "fazer matemática" na sala de aula. Acedido em 5 de Novembro de 2008 de http://www.ufpa.br/npadc/gemm/documentos/docs/A%20Modelagem.PDF        [ Links ]

Kaiser, G. & Sriraman, B. (2006). A global survey of international perspectives on modelling in mathematics education. Zentralblatt für Didaktik der Mathematik, 38(3), 302-310. doi: 10.1007/BF02652813        [ Links ]

Kaiser, G. & Maaß, K. (2007). Modelling in lower secondary mathematics classroom-problems and opportunities. In W. Blum, P. L. Galbraith, H. W. Henn & M. Niss (Eds.), Modelling and Applications in Mathematics Education -The 14 ^th ICMI Study (pp. 99-108). Berlin, Germany: Springer.         [ Links ]

Matos, J. F. & Carreira, S. P. (1996). Modelação e Aplicações no ensino da matemática: situações e problemas. Lisboa, Portugal: Instituto de Inovação Educacional.         [ Links ]

Menezes, L. & Ponte, J. P. (2009). Investigação colaborativa de professores e ensino da Matemática: caminhos para o desenvolvimento profissional. International Journal for Studies in Mathematics Education, 1(1), 1-31.         [ Links ]

Ministério da Educação (2007). Programa de Matemática do Ensino Básico. Lisboa, Portugal: Direcção-Geral de Inovação e de Desenvolvimento Curricular.         [ Links ]

Oliveira, A. M. P. & Barbosa, J. C. (2011). Modelagem matemática e situações de tensão na prática pedagógica dos professores. Boletim de Educação Matemática, 24(38), 265-296.         [ Links ]

Ponte, J. P. (1999). Didáticas específicas e construção do conhecimento profissional. In J. Tavares, A. Pereira, A. P. Pedro & H. A. Sá (Eds.), Investigar e formar em educação: Atas do IV Congresso da SPCE (pp. 59-72). Porto, Portugal: Sociedade Portuguesa de Ciências da Educação.         [ Links ]

Ponte, J. P. (2005). Gestão curricular em Matemática. In Grupo de Trabalho de Investigação (Ed.), O professor e o desenvolvimento curricular (pp. 11-34). Lisboa, Portugal: Associação de Professores de Matemática.         [ Links ]

Ponte, J. P. (2012). Estudiando el conocimiento y el desarrollo profesional del profesorado de matemáticas. En N. Planas (Coord.), Teoría, crítica y práctica de la educación matemática (pp. 83-98). Barcelona, España: Graó         [ Links ].

Ponte, J. P. & Chapman, O. (2008). Preservice mathematics teachers' knowledge and development. In L. D. English (Ed.), Handbook of international research in mathematics education (pp. 223 – 261). New York, United States of America: Routledge.         [ Links ]

Ponte, J. P. & Chapman, O. (2006). Mathematics teachers' knowledge and practices. In A. Gutierrez & P. Boero (Eds.), Handbook of research on the psychology of mathematics education: Past, present and future (pp. 461-494). Rotterdam, The Netherlands: Sense Publishers.         [ Links ]

Ruiz-Higueras, L. & García, F. J. G. (2011). Análisis de praxeologías didácticas en la gestión de procesos de modelización matemática en la escuela infantil. Revista Latinoamericana de Investigación en Matemática Educativa, 14(1), 41-70.         [ Links ]

Santana, T. S. (2010). Modelagem matemática na sala de aula: diálogos com a educação matemática crítica. In III Seminário Políticas Sociais e Cidadania. Acedido em 13 de Maio de 2013 de http://www.interativadesignba.com.br/III_SPSC/arquivos/sessao7/191.pdf.         [ Links ]

Shulman, L. (1986). Those who understand: Knowledge growth on teaching. Educational Researcher, 15(2), 4-14.         [ Links ]

Sierspinska, A. (1998). Three epistemologies, three views of classroom communication: Constructivism, sociocultural approaches, interactionism. In H. Steinbring, M. Bussi, & A. Sierpinska (Eds.), Language and communication in the mathematics classroom (pp. 30-62). Reston, United States of America: National Council of Teachers of Mathematics.         [ Links ]

Silva, J. N. D. & Barbosa, J. C. (2011). Modelagem matemática: as discussões técnicas e as experiências prévias de um grupo de alunos. Boletim de Educação Matemática, 24(38), 197-218.         [ Links ]

Simon, M. A. & Tzur, R. (2004). Explicating the role of mathematical tasks in conceptual learning: An elaboration of the hypothetical learning trajectory. Mathematical Thinking and Learning, 6(2), 91-104.         [ Links ]

Silveira, E. & Caldeira, A. D. (2012). Modelagem na Sala de Aula: resistências e obstáculos. Boletim de Educação Matemática, 26 (43), 1021-1047. doi: 10.1590/S0103-636X2012000300012        [ Links ]

Stein, M. K. & Smith, M. S. (1998). Mathematical tasks as a framework for reflection: from research to practice. Mathematics Teaching in the Middle School, 3 (4), 268-275.         [ Links ]

Verschaffel, L., Greer, B. & De Corte, E. (2000). Making sense of word problems. Lisse. The Netherlands: Swets & Zeitlinger.         [ Links ]

Viseu, F. (2008). A formação do professor de Matemática apoiada por um dispositivo de interacção virtual no estágio pedagógico. Tese de Doutoramento não publicada, Universidade de Lisboa, Lisboa, Portugal.         [ Links ]

Viseu, F. & Ponte, J. P. (2009). Desenvolvimento do conhecimento didático do futuro professor de Matemática com apoio das TIC's. Revista Latinoamericana de Investigación en Matemática Educativa, 12 (3), 383-413.         [ Links ]

Viseu, F. & Ponte, J. P. (2012). The role of ICT in supporting the development of professional knowledge during teaching practice. Mathematics Teacher Education and Development, 14 (2), 137-158.         [ Links ]

 

Notas

¹ O sistema de ensino português engloba 12 anos antes da entrada no ensino superior, assim como a generalidade dos países do mundo. Desses anos, os primeiros nove correspondem ao ensino básico e os três últimos ao ensino secundário. No ensino básico (formado por três ciclos: o primeiro de quatro anos, e com professor único, o segundo de dois anos, e o terceiro ciclo de três anos), o currículo da disciplina de Matemática é igual para todos os alunos. Nos tês anos de ensino secundário, no qual os alunos começam a ser encaminhados para um grupo de cursos do ensino superior, os currículos da disciplina de Matemática divergem, de acordo com os cursos de Ciências, Humanísticos, Tecnológicos ou de Artes.

² Os estagiários lecionam numa turma do professor orientador da escola, na qual realizam o estágio. Além deste orientador, contam também com um supervisor da universidade.

³ Trata-se de uma área não curricular que tem por finalidade promover a apropriação, por parte dos alunos, de métodos de organização, de trabalho e de estudo, assim como o desenvolvimento de atitudes e de capacidades que favoreçam a sua a autonomia.

⁴ O Ministério da Educação de Portugal aprovou em 2007 um novo programa de Matemática do ensino básico (PMEB). O trabalho de preparação deste documento, que começou a ser implementado a título experimental em 2008/09 e generalizado em 2010/11, foi coordenado por João Pedro da Ponte e Lurdes Serrazina e contou ainda com a participação de sete professores e investigadores portugueses.

⁵ Tarefa "Matemática por um canudo".