nova página do texto(beta)
Inglês (pdf)
Artigo em XML
Referências do artigo
Tradução automática
Enviar este artigo por email
Citado por SciELO 
Similares em
SciELO 
Permalink
1.Introduction
Nonlinear differential equations appear in many fields, such as in fluid mechanics, viscoelasticity, chemistry, physics, engineering, biology, fluid flow, signal processing, control theory, systems identification, fractional dynamics and finance. Nonlinear phenomena play a crucial role in applied mathematics and physics. It was stated in literature that the nonlinear wave phenomena of dissipation, diffusion, dispersion, reaction and convection have important roles in nonlinear wave equations. New exact solutions might be used to find new phenomena in this field. In the literature, there are many methods to find new exact solutions, such as the tanh-sech method 1, the functional variable method 2-4, the exp-function method 5,6,(G’/G)-expansion method 7,8, the generalized exponential rational function method 9-11, the reproducing kernel method 12, Hirota method 13,14 and the ansatz method 15,16.
In recent years, the importance of fractional (non-integers) differential equations has increased. Fractional calculus is as old as conventional calculus, but is not as popular in science and engineering as conventional calculus. In the last centuries this subject was studied only in mathematics, In recent years it has been used in many fields of engineering and science 17. Among the investigations for fractional differential equations (FDEs), research for finding approximate/exact solutions of FDEs is an important topic 18-22.
As a result, many methods had been developed such as, the exp-function method 23-26, the
Our goal in this work is to present the exact solutions of time-fractional Cahn-Allen equation, space-time fractional Klein-Gordon equation and space-time fractional Zakharov Kuznetsov Benjamin Bona Mahony (ZK-BBM) equation. In Chapter 2, we give preliminaries and notations, in Chapter 3 we describe the algorithm for using the generalized Kudryashov method with fractional complex transform to solve nonlinear FDEs. In Chapter 4, 5 and 6, we obtained exact solutions of time-fractional Cahn-Allen equation 40
space-time fractional Klein-Gordon equation 35
where γ and β are a non zero constants. The ZK-BBM equation 35
where α and b are arbitrary constants and α is a parameter describing the order of the fractional derivative.
2.Preliminaries and Notations
We give some basic concepts that we will use in this paper. Jumarie’s modified Riemann-Liouville derivative of order α is defined as 41:
Some important properties of the fractional modified Riemann-Liouville derivative were summarized in 42,43:
Similar to integer-order differentiation, the Jumarie’s modified fractional differentiation is a linear operation:
where a and b are constants. The last properties are
We will use these facts in some problems.
3.The generalized Kudryashov method and the fractional complex transform
For given general nonlinear FDEs for an unknown function u of
independent variables, x,
where
Li and He 44 45 developed a fractional complex transform to convert FDEs into ordinary differential equations (ODEs). With the help of this transformation, analytical methods devoted to the calculus can be easily applied to the fractional calculus.
We presented the main steps of the generalized Kudryashov method as follows 43:
Step 1: Firstly, we investigate the travelling wave solution of (9) as following form;
where k and c are non zero arbitrary constants.
Substituting (10) with (5) into (9), we can rewrite (9) in the following nonlinear ODE;
where the prime denotes the derivation with respect to
Step 2: The exact solutions of (11) can be obtained in the following form:
where
This function satisfies to first order the ordinary differential equation
We will use (14) to calculate the derivatives of the function
Step 3: We should calculate the derivatives of function
The higher order derivatives of function
Step 4: We substitute the expression (14) in (11). Later, we take
where
4.Applications
We obtained the exact solutions of three fractional differential equations by using the generalized Kudryashov method.
4.1.The time-fractional Chan-Allen equation
We consider the travelling wave solutions of (1) and we perform the
transformation
where k and c are nonzero constants. Plugging (18) in (1), the equation can be reduced to an ODE,
where
Thus, we have
By substituting (21) into (19) using (13) and then setting the coefficients of
Case 1:
Case 2:
Case 3:
Case 4:
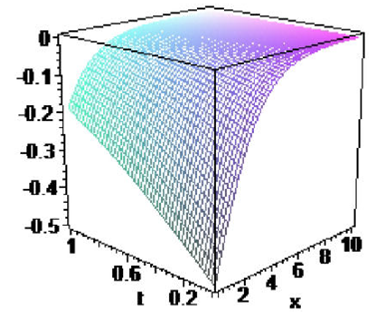
When we substitute (22)-(25), we have the following solutions of FDE (1):
Remark 1: We get the hyperbolic function solutions of the time-fractional Chan-Allen equation and these obtained exact solutions are soliton solutions.
4.2.The space-time fractional Klein-Gordon equation
We will investigate the travelling wave solutions of (2), for which we implement
the transformation
where k and c are nonzero constants. Combining (2) and (30) reduces the equation to an ODE,
where
Therefore, the solution of (32) can be expressed as
Upon substitution of (33) into (31), the use of (13) and setting the coefficients
of Fi
Case 1:
Case 2:
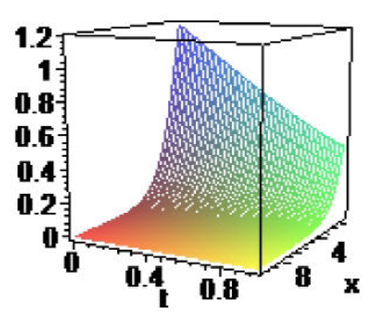
Inserting (34) and (35) into (33), we obtain the following exact solutions of (2):
Remark 2: We have the hyperbolic function solutions of the space-time fractional Klein-Gordon equation. These obtained exact solutions are soliton solutions and periodic solitary wave solutions.
4.3.The space-time fractional ZK-BBM equation
We want to find traveling wave solutions of the (3), reason for which we apply
the transformation
where
Substituting (13) and (39) into (38), collecting all coefficients for each power
of
Case 1:
Case 2:
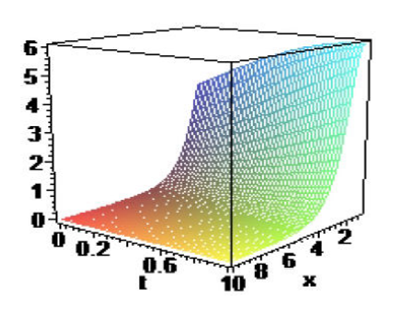
Inserting (40) and (41) into (39), we obtain the following exact solutions of (3):
Remark 3: We obtain the hyperbolic function solutions of the space-time fractional ZK-BBM equation. In particular, the soliton solutions, compacton solutions, peakon solutions and other solutions have been found for such physical problems.
5.Conclusion
In this paper, the generalized Kudryashov method has been successfully applied to find the solution of time-fractional Cahn-Allen equation, space-time fractional Klein-Gordon equation and space-time fractional ZK-BBM equation. Calculations in generalized Kudryashov method are simple, reliable and effective mathematical tool for solving fractional differential equations in science and engineering. As far as we know, the solutions obtained are new solutions that are not available in the literature. The solutions obtained will play a significant role in explaining many physical problems. According to the results obtained, this approach can be used to other nonlinear FDEs, nonlinear fractional equation systems, the fractional complex equations, the fractional difference equations, etc. All the solutions reported above have been verified using the symbolic computation system Maple.
