Introducción
El volumen maderable por aprovechar está en función del crecimiento y rendimiento de las especies que conforman los rodales forestales. En este contexto, es una práctica común la predicción del diámetro normal, el área basal, de la altura total o del volumen en función de variables predictoras tales como edad, densidad, calidad de estación, índices de competencia u otras que explican de manera alómetrica o biológica el crecimiento de los árboles (Briseño et al., 2020).
Desde hace varias décadas se han generado diversos modelos que simulan de forma lógica y precisa el crecimiento a nivel individual o de rodal a través del tiempo (Clutter et al., 1983; Corral y Návar, 2005; McCullagh et al., 2017); los modelos de Chapman-Richards, Schumacher, Weibull y Hosffeld I, en particular, tienen la propiedad de simular el crecimiento sigmoidal de las especies forestales maderables y reflejar la dinámica antagónica que ocurre entre los factores fisiológicos intrínsecos que estimulan el crecimiento y los del medio ambiente que lo limitan (Kiviste et al., 2002). Desde el punto de vista práctico, las ecuaciones que resultan del ajuste de los parámetros de esos modelos sirven para estimar el crecimiento de los árboles, cuyo conocimiento es fundamental en la toma de decisiones silvícolas eficientes que aseguran un aprovechamiento maderable sustentable (Santiago-García et al., 2013; Vargas-Larreta et al., 2013).
La modelación y predicción del crecimiento de rodales en bosques mezclados e irregulares es una tarea difícil, ya que estos bosques, además de reunir una variedad de especies, son irregulares en su estructura. En ellos, cada especie tiene diferente ritmo de crecimiento biológico como respuesta a la herencia genética y la adaptación a las condiciones ambientales donde se desarrolla (Diéguez et al., 2009; Fien et al., 2019). Con base en lo anterior, los modelos de crecimiento para árboles individuales facilitan la predicción al nivel de unidad de área, ya que la suma de los crecimientos de los árboles individuales que componen una unidad de superficie da como resultado el crecimiento total (Torres y Magaña, 2001). La técnica utilizada para obtener información y el de modelo por utilizar depende del tipo de bosque: puro, mezclado, coetáneo, incoetáneo, homogéneo o heterogéneo; y del intervalo de proyección (Diéguez et al., 2009; Hernández et al., 2018; Briseño et al., 2020).
Pinus pseudostrobus Lindl. y Pinus oocarpa Schiede ex Schltdl. se distribuyen ampliamente en todo el territorio forestal de la región centro del estado de Guerrero; forman manchones de una sola especie o de varias del género Pinus asociadas con encinos y algunas latifoliadas, además se consideran dentro de los seis taxones del género de mayor importancia comercial. Presentan buenas características para utilizarse en la fabricación de triplay, chapa, cajas de empaque, molduras, construcción y fabricación de muebles (Conafor, 2015).
Con el propósito de generar herramientas que ayuden a la toma de decisiones para contribuir a lograr un aprovechamiento sustentable de las especies maderables de la región centro del estado de Guerrero, el objetivo del presente estudio fue evaluar la bondad de ajuste de cuatro modelos de crecimiento en diámetro normal, área basal, altura total y volumen fustal de Pinus pseudostrobus y Pinus oocarpa, para seleccionar el más eficiente.
Materiales y Métodos
Área de estudio
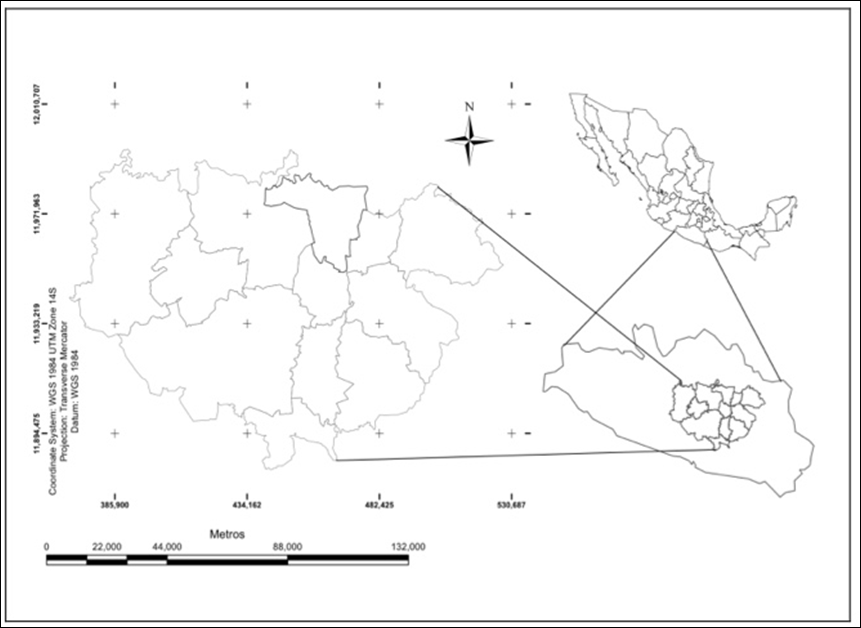
El área de estudio fue la Unidad de Manejo Forestal 1205 (Umafor-1205), la cual se ubica dentro del sistema montañoso Sierra Madre del Sur en la región centro del estado de Guerrero (Figura 1).
Los tipos de clima en las áreas forestales de coníferas varían de templado a semicálido con diferentes graduaciones de humedad. Sin embargo, el clima predominante es (A)C(w) (García, 2004).
Los suelos se clasifican como leptosoles, luvisoles, regosoles y cambisoles; de ellos, los leptosoles tienen la mayor distribución dentro del área de estudio (Inegi, 2016).
Muestreo
El método de muestreo selectivo se aplicó en las calidades de estación baja, media y alta de la Umafor-1205 para recolectar 27 árboles dominantes y 28 codominantes, sin daños físicos, con edades de 20 a 100 años. Del fuste de cada individuo se obtuvieron rodajas a 0.30 m, 0.60 m y 1.30 m de altura y posteriormente a cada 2.60 m hasta llegar a la parte de la punta para reconstruir 102 y 152 perfiles de árboles de Pinus pseudostrobus y Pinus oocarpa, respectivamente; y se aplicó la metodología descrita por Klepac (1983) para realizar los análisis troncales.
Variables
Las mediciones iniciales por árbol de cada especie fueron el diámetro normal con corteza obtenido a 1.30 m de altura con cinta diamétrica marca Lufking™ modelo 283D/5M, diámetro sin corteza de cada rodaja medido con regla Lufking™ y estimado como el promedio de dos medidas en cruz. Los anillos de cada rodaja se dividieron en grupos de 10 para medir el crecimiento radial a las diferentes alturas. La edad de cada uno de los árboles reconstruidos se determinó sobre el diámetro mayor de la rodaja obtenida a los 30 cm de altura del fuste. Para medir el diámetro normal y estimar el área basal de cada árbol reconstruido, los anillos de crecimiento se agruparon en edades de 10 años a partir del centro hacia la periferia (Klepac, 1983). La estimación de la altura verdadera se realizó mediante la fórmula de Carmean (1972) modificada por Newberry (1991), cuya expresión es:
Donde:
j = Número de anillos de crecimiento a partir del centro de cada rodaja
El área basal se determinó con la ecuación:
Donde:
Los volúmenes de cada troza se estimaron con la ecuación de Smalian y la del cono, respectivamente.
Donde:
La suma de los volúmenes de las trozas de cada árbol fue igual al volumen total sin corteza del fuste.
En el Cuadro 1 se muestran las estadísticas descriptivas básicas de las variables analizadas por especie.
Cuadro 1 Estadísticas descriptivas de las variables analizadas.
| Especie | Variable | N | Mínimo | Promedio | Máximo | Desviación estándar |
|---|---|---|---|---|---|---|
| Pinus pseudostrobus Lindl. | Diámetro (cm) | 102 | 1.3 | 19.84 | 41.5 | 10.65 |
| Área basal (m2) | 102 | 0.00013 | 0.03976 | 0.13526 | 0.03584 | |
| Altura (m) | 282 | 0.17 | 12.26 | 38.28 | 8.84 | |
| Volumen (m3) | 102 | 0.00042 | 0.45 | 2.32 | 0.5075 | |
| Pinus oocarpa Schiede ex Schltdl. | Diámetro (cm) | 152 | 1.3 | 20.23 | 45.5 | 10.0061 |
| Área basal (m2) | 152 | 0.00013 | 0.03999 | 0.16259 | 0.03305 | |
| Altura (m) | 257 | 0.17 | 10.05 | 28.3 | 6.90207 | |
| Volumen (m3) | 152 | 0.00022 | 0.37325 | 1.84337 | 0.35941 |
Análisis
A los datos de crecimiento en diámetro normal, área basal, altura y volumen se les ajustaron los modelos de crecimiento de Chapman-Richards (M1), Hossfeld I (M2), Weibull (M3) y Schumacher I (M4) citados por Kiviste et al., (2002) mediante regresión no lineal (Cuadro 2). Además, se generaron sus respectivas expresiones para determinar el incremento corriente anual (ICA) y el incremento medio anual (IMA). Los ajustes se realizaron al aplicar el procedimiento PROC MODEL del programa estadístico SAS (SAS, 2002). El criterio analítico para seleccionar la bondad del ajuste de los modelos consideró a la raíz del error medio cuadrático (REMC), el coeficiente de determinación ajustado (R 2 adj ) y las propiedades estadísticas de los parámetros estimados.
Donde:
Cuadro 2 Modelos de crecimiento evaluados y sus expresiones del ICA e IMA.
| Modelo | Expresión | ICA | IMA |
|---|---|---|---|
| Chapman-Richards |
|
|
|
| Hossfeld I |
|
|
|
| Weibull |
|
|
|
| Schumacher |
|
|
|
Finalmente, como factor determinante para seleccionar el mejor modelo se consideró el análisis gráfico de las curvas de crecimiento.
Dado que las mediciones del crecimiento a través del tiempo de cada variable evaluada dentro de cada árbol están correlacionadas, se evalúo la significancia de la autocorrelación de los modelos seleccionados como los mejores mediante la prueba de Durbin-Watson (DW) (Sharma et al., 2011; Quiñonez et al., 2018).
Donde:
Cuando esta prueba fue significativa, se aplicó el modelo autorregresivo CAR(X) (Zimmerman et al., 2001) para corregir el problema de autocorrelación y generar parámetros y errores estándar consistentes con los modelos. La estructura del modelo autorregresivo es:
Donde:
Una vez seleccionado el mejor modelo, se estimó el ICA máximo (ICA máx ) e IMA máximo (IMA máx ) para cada una de las variables y especies. Ambos incrementos corresponden a los valores más altos calculados con las ecuaciones del ICA e IMA.
Resultados
La estimación de los parámetros de los modelos sin considerar la estructura
autorregresiva del error para Pinus pseudostrobus presentó valores
de DW para el crecimiento en diámetro entre 0.9518 y 1.0028, área
basal de 0.6188 a 0.9390, altura de 0.3057 a 0.3324 y volumen de 0.9896 a 1.0343;
mientras que para Pinus oocarpa, los valores de DW
para el crecimiento en diámetro variaron de 0.5095 a 0.5912, área basal de 0.5814 a
0.6621, altura de 0.3437 a 0.3655 y volumen de 0.6211 a 0.6966; cifras que indican
autocorrelación. Los valores de DW estimados después de ajustar los
modelos de crecimiento con el modelo autorregresivo CAR(1), CAR(2) y CAR(3)
permitieron deducir que la autocorrelación de los residuales mejoró
significativamente (Cuadro 3). A su vez, los
estimadores de los parámetros
Cuadro 3 Estadísticos de ajuste de los modelos de crecimiento en las variables analizadas.
| Modelo | Pinus pseudostrobus Lindl. | Pinus oocarpa Schiede ex Schltdl. | ||||
|---|---|---|---|---|---|---|
| R2adj | RCME | DW | R2adj | RCME | DW | |
| Diámetro normal | ||||||
| M1 | 0.7403 | 5.427 | 1.653 | 0.8654 | 3.671 | 1.162 |
| M2 | 0.7230 | 5.605 | 1.746 | 0.9001 | 3.162 | 1.649 |
| M3 | 0.7831 | 4.960 | 1.480 | 0.8640 | 3.690 | 1.182 |
| M4 | 0.7400 | 5.431 | 1.654 | 0.8648 | 3.679 | 1.117 |
| Área basal | ||||||
| M1 | 0.7063 | 0.0194 | 1.489 | 0.9154 | 0.0096 | 1.590 |
| M2 | 0.6962 | 0.0197 | 1.591 | 0.9096 | 0.0096 | 1.660 |
| M3 | 0.7019 | 0.0196 | 1.514 | 0.9120 | 0.0097 | 1.509 |
| M4 | 0.7105 | 0.0193 | 1.500 | 0.9079 | 0.0100 | 1.515 |
| Altura | ||||||
| M1 | 0.9650 | 1.6093 | 1.661 | 0.9460 | 1.603 | 1.220 |
| M2 | 0.9338 | 2.2315 | 1.770 | 0.9441 | 1.631 | 1.300 |
| M3 | 0.9645 | 1.6224 | 1.692 | 0.9688 | 1.231 | 1.597 |
| M4 | 0.9275 | 2.3167 | 1.652 | 0.9695 | 1.204 | 1.598 |
| Volumen | ||||||
| M1 | 0.8544 | 0.1977 | 1.735 | 0.9321 | 0.0936 | 1.635 |
| M2 | 0.7426 | 0.2574 | 1.626 | 0.9240 | 0.0990 | 1.621 |
| M3 | 0.9338 | 0.0924 | 1.361 | 0.9338 | 0.0924 | 1.361 |
| M4 | 0.8500 | 0.1964 | 1.737 | 0.9305 | 0.0947 | 1.608 |
M1 = Chapman-Richards; M2 = Hossfeld I; M3 = Weibull; M4 = Schumacher; R 2 adj = Coeficiente de determinación ajustado; RCME = Raíz cuadrada media del error; DW = Durbin-Watson.
Cuadro 4 Estimadores de los parámetros y errores estándar de los modelos evaluados para Pinus pseudostrobus Lindl.
| Pinus pseudostrobus | Parámetros | ||||||
|---|---|---|---|---|---|---|---|
| Modelo | Estadístico |
|
|
|
|
|
|
| Diámetro | |||||||
| M1 | Estimador | 32.96137 | 0.07249 | 3.197013 | 1.00368 | ||
| E. E. | 2.86740 | 0.01540 | 0.83570 | 0.01100 | |||
| M2 | Estimador | 2.81260 | 0.12419 | 0.99036 | |||
| E. E. | 0.33320 | 0.00931 | 0.01450 | ||||
| M3 | Estimador | 30.8810 | 0.00095 | 2.09730 | 1.01299 | 0.97076 | 0.32513 |
| E. E. | 2.58110 | 0.00063 | 0.2283 | 0.00954 | 0.01740 | 0.21780 | |
| M4 | Estimador | 49.14015 | 24.38972 | 0.99762 | |||
| E. E. | 4.18750 | 2.49430 | 0.01210 | ||||
| Área Basal | |||||||
| M1 | Estimador | 0.08711 | 0.06955 | 4.85097 | 1.72976 | ||
| E. E. | 0.01440 | 0.02710 | 2.73200 | 8.73230 | |||
| M2 | Estimador | 92.12886 | 1.84175 | 0.09097 | |||
| E. E. | 15.33660 | 0.34970 | 0.45990 | ||||
| M3 | Estimador | 0.081866 | 0.000242 | 2.37926 | 0.878077 | ||
| E. E. | 0.0111 | 0.000388 | 0.51580 | 4.26000 | |||
| M4 | Estimador | 0.16539 | 40.21302 | 3.05171 | |||
| E. E. | 0.0267 | 5.8208 | 15.43200 | ||||
| Altura | |||||||
| M1 | Estimador | 26.26966 | 0.06274 | 1.77583 | 1.146894 | 0.97393 | |
| E. E. | 1.01290 | 0.00689 | 0.16550 | 0.01310 | 0.01190 | ||
| M2 | Estimador | 2.221376 | 0.15547 | 1.03211 | |||
| E. E. | 0.11780 | 0.00404 | 0.01310 | ||||
| M3 | Estimador | 25.82468 | 0.01108 | 1.43804 | 1.14903 | 0.97225 | |
| E. E. | 0.95930 | 0.00222 | 0.07600 | 0.01310 | 0.0119 | ||
| M4 | Estimador | 33.64891 | 16.64891 | 1.00452 | |||
| E. E. | 1.17250 | 0.83290 | 0.01420 | ||||
| Volumen | |||||||
| M1 | Estimador | 2.20766 | 0.02989 | 4.80571 | 4.203409 | ||
| E. E. | 1.54900 | 0.0185 | 2.27560 | 0.4316 | |||
| M2 | Estimador | -46.1913 | -0.14897 | 1.95681 | |||
| E. E. | 8.03150 | 0.14610 | 0.42170 | ||||
| M3 | Estimador | 0.81488 | 8.30x10-8 | 4.12430 | 10.62855 | 3.36962 | |
| E. E. | 0.06390 | 1.15x10-7 | 0.36980 | 1.33610 | 0.34480 | ||
| M4 | Estimador | 3.66476 | 82.53542 | 4.06032 | 2.38687 | ||
| E. E. | 0.90860 | 11.30020 | 0.39320 | 0.27590 | |||
M1 = Chapman-Richards; M2 =
Hossfeld I; M3 = Weibull; M4 =
Schumacher; E.E. = Error
estándar;
Cuadro 5 Estimadores de los parámetros y errores estándar de los modelos evaluados para Pinus oocarpa Schiede ex Schltdl.
| Pinus oocarpa | Parámetros | ||||||
|---|---|---|---|---|---|---|---|
| Modelo | Estadístico |
|
|
|
|
|
|
| Diámetro | |||||||
| M1 | Estimador | 33.30371 | 0.05272 | 2.78622 | 0.97376 | ||
| E. E. | 1.91760 | 0.00869 | 0.54060 | 0.01280 | |||
| M2 | Estimador | 3.53210 | 0.12302 | 0.98023 | 0.97631 | 0.93747 | |
| E. E. | 0.25640 | 0.00556 | 0.01490 | 0.01180 | 0.01910 | ||
| M3 | Estimador | 32.19344 | 0.00184 | 1.77252 | 0.97084 | ||
| E. E. | 1.71310 | 0.00092 | 0.16090 | 0.01300 | |||
| M4 | Estimador | 48.59111 | 30.57237 | 0.97336 | |||
| E. E. | 2.46550 | 2.04540 | 0.01310 | ||||
| Área Basal | |||||||
| M1 | Estimador | 0.11168 | 0.03658 | 3.81223 | 182509.8 | 1700.225 | 0.03670 |
| E. E. | 0.01520 | 0.00706 | 0.72260 | 642673.0 | 4436.2 | 0.12610 | |
| M2 | Estimador | 134.7345 | 1.65843 | 1.8093x108 | 101.28700 | 3.93x10-10 | |
| E. E. | 14.3358 | 0.23650 | 5.1302x108 | 278.70000 | 2.79x10-9 | ||
| M3 | Estimador | 0.08803 | 0.00010 | 2.36525 | 1.1768x108 | 13.08743 | |
| E. E. | 0.00915 | 0.00008 | 0.23610 | 3.07x108 | 34.40770 | ||
| M4 | Estimador | 48.59111 | 30.57237 | 0.97336 | |||
| E. E. | 2.46550 | 2.04540 | 0.01310 | ||||
| Altura | |||||||
| M1 | Estimador | 19.2500 | 0.01592 | 1.34003 | 1.05532 | 0.97638 | 0.90647 |
| E. E. | 0.54760 | 0.00334 | 0.07240 | 0.02130 | 0.01850 | 0.02060 | |
| M2 | Estimador | 2.17484 | 0.18839 | 0.96258 | |||
| E. E. | 0.10580 | 0.00343 | 0.01970 | ||||
| M3 | Estimador | 19.25000 | 0.01592 | 1.34003 | 1.05532 | 0.97638 | 0.90647 |
| E. E. | 0.54760 | 0.00334 | 0.07240 | 0.02130 | 0.01850 | 0.02060 | |
| M4 | Estimador | 23.34795 | 14.04075 | 1.06527 | 0.99418 | 0.93053 | |
| E. E. | 0.66200 | 0.69910 | 0.01990 | 0.01670 | 0.01650 | ||
| Volumen | |||||||
| M1 | Estimador | 0.90389 | 0.05058 | 6.86763 | 6.84513 | 4.00005 | 1.26232 |
| E. E. | 0.10200 | 0.00685 | 1.33010 | 1.32240 | 0.64170 | 0.33180 | |
| M2 | Estimador | -55.2519 | -0.39983 | 10.48295 | 2.96807 | 0.33751 | |
| E. E. | 6.34390 | 0.09880 | 1.63760 | 0.46260 | 0.16290 | ||
| M3 | Estimador | 0.81488 | 8.3x10-8 | 4.12430 | 10.62855 | 3.36962 | 0.33751 |
| E. E. | 0.06390 | 1.15x10-7 | 0.36980 | 1.33610 | 0.34480 | 0.16290 | |
| M4 | Estimador | 2.33633 | 80.82759 | 7.09319 | 4.19346 | 1.35311 | |
| E. E. | 0.30240 | 6.66230 | 1.35920 | 0.67930 | 0.36270 | ||
M1 = Chapman-Richards; M2 =
Hossfeld I; M3 = Weibull; M4 =
Schumacher; E.E. = Error
estándar;
Bondad de ajuste de los modelos
Los estadísticos R 2 adj y RCME indicaron que en Pinus pseudostrobus, el modelo de Weibull fue el que mejor se ajustó para estimar el crecimiento en diámetro y volumen y los de Chapman-Richard y Weibull en altura; a su vez, todos los modelos se ajustaron de manera similar en la estimación del área basal. En Pinus oocarpa, el modelo de Hossfeld I fue el que registró el mejor ajuste en diámetro, los de Chapman-Richard y Weibull en área basal, los de Schumacher y Weibull en altura, así como los de Chapman-Richard, Weibull y Schumacher en volumen (Cuadro 3).
Sin embargo, al considerar el nivel de significancia de los estimadores de los
parámetros (
Tendencias de las curvas de crecimiento
En la Figura 2 se observa que tanto el modelo de Chapman-Richards como el de Schumacher predicen crecimientos en diámetro normal muy similares para ambas especies hasta los 50 y 65 años. A partir de esas edades, la tasa de crecimiento predicha con el modelo de Chapman-Richards tiende a cero; mientras que con el modelo de Schumacher, el crecimiento continúa en sentido ascendente hasta alcanzar la asíntota. Los máximos crecimientos en diámetro estimados con el modelo de Chapman-Richards en Pinus pseudostrobus y Pinus oocarpa fueron menores a los predichos con el modelo de Schumacher; este último presentó tasas de crecimiento más plausibles en edades superiores a los 60 años y se le seleccionó para realizar las predicciones del crecimiento en diámetro de ambas especies.

Figura 2 Comparativo de las tendencias de las curvas de crecimiento que generan los modelos de Schumacher y Chapman-Richards con respecto a las series de crecimiento observadas para las variables analizadas.
En relación al área basal, el modelo de Schumacher fue el que mejor reflejó la tendencia en Pinus pseudostrobus; el de Chapman-Richards lo hizo en Pinus oocarpa durante el periodo evaluado. En la primera especie, el modelo de Schumacher predijo crecimientos menores en el área basal hasta una edad aproximada de 70 años; en Pinus oocarpa, esto mismo sucede sobre todo el periodo de crecimiento evaluado.
En el análisis gráfico del crecimiento en altura total, el modelo de Schumacher fue el que mejor predijo este crecimiento. El modelo de Hossfeld I exhibió una tasa de crecimiento mayor a partir de los 40 años en Pinus pseudostrobus y de los 60 años en Pinus oocarpa; mientras que los modelos de Chapman-Richards y Weibull la disminuyeron drásticamente a partir de los 50 años, y presentaron las asíntotas a edades tempranas.
Por su parte, las predicciones del crecimiento en volumen con el modelo de Schumacher en Pinus pseudostrobus y Pinus oocarpa fueron inferiores a las calculadas con el modelo de Chapman-Richards a lo largo del periodo de evaluación, en el que se programan las cortas intermedias; por lo que si se desea evitar sobrestimar el volumen aprovechable, se considera al modelo de Schumacher como el más apropiado para tales predicciones. A su vez, el modelo de Chapman-Richards presentó la asíntota a partir de los 60 años, y reflejó las estimaciones menores a partir de esa edad.
Máximos Incrementos Corriente Anual y Turno
Las estimaciones obtenidas con la ecuación derivada del modelo de crecimiento en diámetro normal de Schumacher indicaron que los ICA máx en diámetro en Pinus pseudostrobus y Pinus oocarpa se registraron a los 12 (1.09 cm) y 15 años (0.86 cm); los del área basal predichos con la ecuación derivada del modelo Chapman-Richards se obtuvieron a los 30 y 37 años (0.0017 cm), respectivamente. Los ICA máx en altura total determinados con la ecuación derivada del modelo de Schumacher ocurrieron a los 8 (1.15 m) y 7 años (0.90 m). A su vez, los ICA máx en volumen fustal predichos con las ecuaciones derivadas de los modelos de Chapman-Richards y Schumacher se presentaron a las edades de 38 (0.024 m3) y 41 años (0.018 m3) en Pinus oocarpa y Pinus pseudostrobus, respectivamente. La edad del turno físico del volumen estimada con la ecuación de Schumacher se determinó a los 82 años en Pinus pseudostrobus y 62 años en Pinus oocarpa (Figura 3).

Figura 3 Tendencias de las curvas del ICA-IMA que generan los modelos evaluados con respecto a las series de crecimiento.
Si ambos taxones están asociados en el mismo tipo de bosque, la diferencia en los patrones de crecimiento, el tiempo en que se registran los incrementos máximos y el turno es posible asumir que las dos especies responden de manera diferente a las mismas condiciones ambientales y niveles de productividad prevalecientes en este ecosistema. Las predicciones del crecimiento hechas con los modelos seleccionados sugieren que los individuos de Pinus pseudostrobus alcanzaron mayores dimensiones en diámetro, altura y volumen que los de Pinus oocarpa durante el periodo estudiado.
Discusión
Los estadísticos R 2 adj y las RCME fueron muy similares entre los modelos ajustados, por lo que el análisis de las tendencias de las curvas de crecimiento que cada modelo genera con respecto a las tendencias de crecimiento observadas fue fundamental para seleccionar el modelo que mejor representó el crecimiento biológico del diámetro normal, del área basal, de la altura total y del volumen fustal en ambas especies de interés. Los modelos de Chapman-Richards y Schumacher, seleccionados como los mejores, además de ser simples y parsimoniosos (Vanclay, 1994; Vanclay y Skovsgaard 1997) tienen un comportamiento asintótico y representan curvas biológicamente realistas (Alder, 1980; Salas et al., 2016).
De forma semejante a los resultados de este estudio, Arteaga (2000) registró que el modelo de Schumacher fue el que mejor se ajustó y representó el crecimiento en altura y volumen de Pinus pseudostrobus y el modelo de Chapman-Richards para el diámetro.
Monárrez y Ramírez (2003) indicaron que el mejor modelo para estimar el crecimiento en diámetro para Pinus durangensis Martínez fue el de Schumacher y para volumen el de Chapman-Richards; Corral y Návar (2005), al evaluar el comportamiento de diversos modelos determinaron que el modelo de Chapman-Richards se ajustó adecuadamente para estimar el crecimiento en diámetro, altura y volumen en cinco especies de Pinus del estado de Durango.
Martínez et al. (2014) al ajustar los modelos de Chapman-Richards y Schumacher para evaluar el crecimiento en diámetro, altura y volumen de Pinus hartwegii Lindl. consignaron que, aunque ambos modelos presentaron buen ajuste, el de Schumacher fue el que tuvo la mejor calidad predictiva. Pacheco et al. (2016) mediante el ajuste de los modelos de Schumacher, Chapman-Richards y Weibull decidieron aplicar el segundo para estimar el crecimiento, ICA e IMA en altura de Pinus montezumae Lamb.
Quiñonez et al. (2015) establecieron al modelo de Chapman-Richards como el más adecuado para generar familias de curvas de crecimiento en diámetro para Pinus lumholtzii Robins & Ferns; De Almeida et al. (2019) refirieron que los modelos de Chapman-Richards junto con el de Weibull mostraron los mejores ajustes para generar curvas de crecimiento en diámetro de cinco especies de pinos. A su vez, Hernández et al. (2018) documentaron que el modelo de crecimiento de Chapman-Richards fue el que mejor se ajustó para generar curvas de índice de sitio en Pinus ayacahuite Ehren.
Recientemente, Hernández et al. (2020) al trabajar los mismos modelos que se aplicaron en este estudio a tres especies de pino del estado de Chihuahua, concluyeron que los modelos de Chapman-Richards y Schumacher fueron los que mejor representaron el crecimiento en diámetro, área basal, altura y volumen.
Si se parte del hecho de que el diámetro normal es un indicador de las fases de crecimiento de las especies estudiadas (Imaña y Encinas, 2008), la edad a la que se calculó el valor del ICA máx sugiere que el periodo juvenil de Pinus pseudostrobus y de Pinus oocarpa culminó de manera natural a los 12 y 14 años, y alcanzaron diámetros de 7.5 y 6.3 cm, respectivamente. A partir de esas edades, ambas especies inician su periodo de madurez, que alcanzan a los 24 y 31 años; temporalidades relacionadas a crecimientos promedio en diámetro de 17.5 y 18.1 cm e intersecciones del ICA-IMA de 0.752 y 0.575 cm, respectivamente. La etapa senil inicia cuando se llega a la última edad de la madurez y se extiende hasta que los individuos logran su máximo crecimiento, el cual es igual al valor de la asíntota. Al proyectar las estimaciones del crecimiento en diámetro con el modelo de Schumacher, tanto Pinus pseudostrobus como Pinus oocarpa alcanzarían el máximo crecimiento (49 y 48 cm, respectivamente) después de los 200 años.
La intersección de las curvas del ICA con el IMA indica el tiempo en que ocurren los mejores rendimientos. Con base en lo citado por Martínez et al. (2014), las edades en que se registra el ICA máx del diámetro y la altura sirven de referencia para iniciar el programa de tratamientos intermedios, el cual termina un ciclo de corta antes de la aplicación de la corta de regeneración, edad de intersección de las curvas del ICA e IMA en volumen (turno físico). Por ello, si se desea aplicar un sistema de manejo regular se sugiere empezar la aplicación de las cortas intermedias cuando los individuos de las especies estudiadas tienen en promedio entre 10 y 15 años con el fin de promover la redistribución del agua, luz y nutrientes en los árboles residuales, para favorecer su crecimiento e iniciar la regulación de la estructura dimensional del bosque (Novák, et al., 2017).
Conclusiones
Los resultados del estudio indican que el modelo de Schumacher es el mejor para predecir el crecimiento en diámetro y altura tanto de Pinus pseudostrobus como de Pinus oocarpa; el área basal de Pinus pseudostrobus y el volumen de Pinus oocarpa; mientras que el modelo de Chapman-Richards es el mejor para predecir el crecimiento en área basal de Pinus oocarpa y el crecimiento en volumen de Pinus pseudostrobus. A su vez, Pinus pseudostrobus presenta mejores crecimientos en diámetro, altura y volumen que Pinus oocarpa. El turno físico del volumen predicho en Pinus oocarpa y Pinus pseudostrobus es de 65 y 85 años, respectivamente.











 texto en
texto en