Introducción
Los sistemas agroforestales (SAF) se originaron, de cierta forma, a partir de la observación de los agroecosistemas tradicionales en los que se integran distintos tipo de cultivos y plantaciones, particularmente en los trópicos. Su establecimiento ha sido promovido, en parte, con el propósito de mantener la biodiversidad de los bosques naturales (DaRocha, Neves, Dáttilo y Delabie, 2016), como alternativa a la agricultura de tala y quema, comúnmente practicada por pequeños agricultores (Kearney et al., 2017).
Debido a su conceptualización, estos sistemas se consideran sostenibles en relación con las actividades de agricultura y silvicultura convencionales, pues conservan la biodiversidad, aumentan la prestación de servicios ecosistémicos, no comprometen la productividad (Torralba, Fagerholm, Burgess, Moreno y Plieninger, 2016) y son capaces de asociar ganancias económicas a los beneficios ambientales (Kalita, Das y Nath, 2015), destacándose entre los métodos de cultivo que más contribuyen para el equilibrio entre economía, sociedad y medio ambiente.
Los estudios con SAF que utilizan varias especies, bajo diferentes aspectos, han sido desarrollados a escala mundial. En Brasil, la mayor parte de los trabajos están concentrados en la Amazonia (Lima, Leite, Oliveira y Costa, 2011), donde Swietenia macrophylla King, especie nativa, es utilizada para producción y suministro de materia prima maderable, debido a sus características tecnológicas y el alto valor comercial de la madera, sin embargo, no hay estudios sobre los patrones de su variabilidad espacial.
Mulkey, Kitajima y Wrightt (1996) afirman que caracterizar el comportamiento de la variación espacial, de modo que permita generalizaciones, está entre los principales desafíos para el conocimiento ecofisiológico de las especies tropicales. En ese sentido, métodos geoestadísticos pueden ser utilizados para caracterizar la variación espacial de diferentes variables dendrométricas y proporcionar informaciones que subsidien su manejo e, incluso, la planificación de su cosecha en áreas de SAF.
La geoestadística considera las características estructuradas y aleatorias de las variables espacialmente distribuidas para proporcionar estimaciones óptimas y sin tendencias (Weindorf y Zhu, 2010), siendo fundamentada en la teoría de las variables regionalizadas (Borssoi, Uribe-Opazo y Galea, 2011), pues considera que los valores resultantes de las parcelas muestreadas son dependientes entre sí en función de sus localizaciones en el espacio, pudiendo complementar o, incluso sustituir, eficientemente, la estadística clásica (Angelico, 2006). Cuando se considera la dependencia espacial, los errores aleatorios pueden ser reducidos por atribuir a ésta, parte de ese error (Mello, Lima, Silva, Mello y Oliveira, 2003).
La estadística clásica tiene como requisito la independencia de las unidades de muestreo y la ausencia de dependencia espacial (Kanegae Junior, Mello, Scolforo y Oliveira, 2007). Sin embargo, Miller, Franklin y Aspinall (2007) afirman que esto viola los principios básicos de la geografía, tales como la existencia de relación directa entre distancia y semejanza, así como de la teoría ecológica, en que los elementos de ecosistemas cercanos son más propensos a ser influenciados por el mismo proceso generador y, por lo tanto, serán similares.
La utilización de geoestadística para estimar recursos forestales disminuye los costos de operaciones en campo (Lundgren, Silva y Ferreira, 2016) porque permite obtener estimaciones mejores o similares con menor intensidad de muestreo, cuando se compara con las técnicas de estadística clásica (Lundgren, Silva y Ferreira, 2015). Esta técnica ha sido ampliamente utilizada para modelar e ilustrar la variabilidad espacial de diferentes variables dendrométricas por interpolación de los puntos muestreados en el espacio (Biondi, Myers y Avery, 1994; Bognola, Ribeiro Júnior, Silva, Lingnau e Higa, 2008; Scolforo, Scolforo, Mello, Mello y Ferraz Filho, 2015; Lundgren, Silva y Ferreira, 2017).
Desde hace más de dos décadas, Franklin (1995) en trabajo con mapeo predictivo de la vegetación, ya preveía la importancia futura de investigaciones con dependencia espacial. En las últimas décadas, el número de investigaciones que utilizan geoestadística para modelado predictivo de variables dendrométricas viene creciendo (Souza, Almeira, Ribeiro, Souza y Leite, 2015; Wojciechowski, Arce, Weber, Ribeiro Junior y Pires, 2017). Sin embargo, actualmente, son escasos los trabajos que analizan la variabilidad espacial de especies como Swietenia macrophylla que no pertenecen a los géneros Eucalyptus y Pinus, principalmente cuando se plantan en sistemas no convencionales.
Objetivos
Considerando la hipótesis de que las variables dendrométricas de árboles de Swietenia macrophylla, plantados en sistema agroforestal en el municipio de Tomé-Açu, Pará, Brasil, presentan dependencia espacial, este trabajo tiene como objetivos: obtener por regresión lineal la ecuación volumétrica que mejor represente la variabilidad de los datos y permita estimaciones confiables; y evaluar y mapear la variabilidad espacial, usando kriging ordinario, del diámetro a 1.3 m del nivel del suelo (dap), de la altura comercial del (hc) y del volumen comercial (vc).
Materiales y Métodos
Caracterización del área de estudio
Esta investigación fue realizada con datos de Swietenia macrophylla con 17 años de edad, en sistema agroforestal multi-estratificado en el Municipio de Tomé-Açu, en parea localizada entre las coordenadas geográficas 02°29'14 '' y 02°30'03 '' de latitud Sur y 48°23'10 ' y 48°22'22 '' de longitud oeste, en la Mesorregión Nordeste del Estado de Pará, Brasil.
De acuerdo con el mapa de clasificación climática de Köppen para Brasil (Alvares, Stape, Sentelhas, Gonçalves y Sparovek, 2013), el clima de la región es del tipo Af (sin estación seca definida), con precipitación pluviométrica acumulada a lo largo del año entre 2500 y 2800 mm, y temperatura media anual superior a 26 ºC. La altitud es de 45 m y con base en el Sistema Brasileño de Clasificación de Suelos de la Empresa Brasileña de Investigación Agropecuaria [Embrapa] (Santos et al., 2013), el suelo predominante es clasificado como latosol amarillo distrófico, equivalente al suelo Xanthic Ferralsol en clasificación de la FAO.
El sistema agroforestal fue implantado escalando las especies en el tiempo como es descrito a continuación, considerando los años a partir del inicio del proyecto. Primero fue plantada Piper nigrum (pimienta común), cultivada durante los tres primeros años, a los dos años fue establecida Swietenia macrophylla (caoba), a los tres años fue plantada Cocos nucifera (coco), como fuente alternativa de producción y finalmente, luego de nueve años y con el fin de que se beneficie de la sombra de la caoba, fue establecida Theobroma cacao (cacao).
Los individuos de pimienta, de coco y de cacao fueron plantados bajo los espaciamientos de 2.5 m × 2.5 m, 5 m × 7.5 m y 3 m × 3.5 m, respectivamente, y la plantación de caoba fue realizada con espaciamiento de 8 m × 6 m. El área total del sistema es 14.65 ha.
Toma de datos
En el área del estudio fue instalada una cuadrícula de 50 m × 50 m, resultando en 36 puntos de intersección muestreados sistemáticamente mediante parcelas circulares con área aproximada de 0.05 ha, totalizando 1.8 ha muestreadas. Dentro de cada parcela, fueron medidas a todos los árboles las variables dendrométricas diámetro a 1.3 m del nivel del suelo (dap), en centímetros y altura comercial (hc), en metros.
Luego del inventario forestal en las parcelas, fueron cubicados 108 árboles, tres por parcela, agrupados en tres clases diamétricas para representar la variación de la plantación agroforestal. Esta intensidad de muestreo proporcionó un error máximo del 1% con base en el cálculo descrito por Cochran (1965). La cubicación fue hecha en el árbol en pie por medio del método de Smalian, midiendo directamente las circunferencias con corteza en la base, a 1.3 m del nivel del suelo y en las alturas sucesivas de 2 m a lo largo del fuste, hasta alcanzar la altura comercial definida por la primera rama en el árbol.
Estimación del volumen por regresión lineal
El volumen comercial individual (vc), en metros cúbicos, de los árboles en las parcelas, fue estimado por la ecuación de mejor ajuste. Para ello, los datos muestreados fueron particionados aleatoriamente en las proporciones 65:35, siendo 65% utilizado para ajuste de los modelos volumétricos (Tabla 1) por medio de regresión lineal y 35% empleado para validación de las ecuaciones, probándose la capacidad de generalización de estas a nuevos datos.
Tabla 1 Modelos volumétricos utilizados para estimar el volumen comercial de los árboles de Swietenia macrophylla.
| N | V.I. | Fórmula | Autor |
| 1 | dap | Ln() = β0 + β1 Ln(dap) + εi | Husch |
| 2 | = β0 + β1 (dap2) + εi | Kopezky-Gehrhardt | |
| 3 | = β0 + β1 dap + β2 dap2 + εi | Hohenald-Krenm | |
| 4 | Ln() = β0 + β1 Ln(dap) + β2 (dap-1) + εi | Brenac | |
| 5 | dap; hc | = β0 + β1 (dap2 hc) + εi | Spurr |
| 6 | Ln() = β0 + β1 Ln(dap) + β2 Ln(hc) + εi | Schumacher-Hall | |
| 7 | = β0 + β1 (dap2) + β2 (dap2 hc) + β3 (hc) + εi | Stoat | |
| 8 | Ln() = β0 + β1 Ln(dap2 hc) + εi | Spurr Logaritmizado |
V.I.: variables independientes; β0, β1, β2 e β3: coeficientes de la ecuación de regresión; Ln: logaritmo neperiano; : volumen comercial estimado (m³); dap: diámetro a 1.3 m del nivel del suelo (cm); hc: altura comercial (m); εi: error aleatorio.
Fuente: adaptado de Loetsch et al. (1973).
Los coeficientes de las ecuaciones fueron determinados por el método de los mínimos cuadrados ordinarios, con ayuda del software Microsoft Office Excel 2016®, al igual que la validación de la mejor ecuación. Para verificar la presencia de heterocedasticidad en la distribución gráfica de residuos, fue utilizado Minitab® Statistical 18 (MINITAB Inc., 2010), versión trial.
Luego del ajuste, las ecuaciones fueron analizadas y comparadas por medio de las estadísticas de precisión: coeficiente de determinación ajustado (R2 aj.), error estándar de la media en porcentaje (EEM%) y desviación media en porcentaje (DMP%). La representación numérica de la heterogeneidad de los errores fue realizada por medio de la prueba de White-Noise, según Zhang (2016).
El Factor de corrección de Meyer fue utilizado para mitigar los errores sistemáticos de las estimaciones obtenidas por las ecuaciones que presentan variables transformadas en escala logarítmica, y de esta manera poder comparar los resultados con los demás modelos.
Las ecuaciones fueron validadas por el EEM% y la prueba Chi-cuadrado (X2) al nivel de 5% de significancia. La prueba X2 evidencia la existencia de igualdad o no entre valores (Siegel, 2016), por lo tanto, la hipótesis nula fue: valores estimados son iguales a los observados; y la hipótesis alternativa: los valores estimados no son igual a los observados. A pesar de que las medidas de precisión y la prueba de validación son indicadores importantes para la selección de la mejor ecuación, la distribución residual también fue analizada por considerarla esencial para evaluar posibles errores de tendencia en determinadas amplitudes de clase de la variable respuesta.
Análisis descriptivo
Los valores máximo y mínimo, medidas de posición (media y mediana) y de dispersión (desviación estándar y coeficiente de variación), asimetría y curtosis, se presentan para un mejor análisis de las variables medidas. Además, la hipótesis de normalidad en la distribución de las variables fue evaluada por la prueba de Kolmogorov-Smirnov (KS) al nivel de 5% de significancia, esto por medio de Minitab® Statistical 18, versión trial.
Análisis geoesadístico
El análisis geoestadístico por ajuste de semivariogramas fue utilizado para modelar la variabilidad espacial de las variables dendrométricas involucradas en esta investigación. Para cada variable, se realizaron cálculos de semivarianzas (Ecuación 1), considerando las distancias de separación de las muestras en el área estudiada (h) y las diferencias cuantitativas de las variables (Z), de acuerdo con Pelissari et al. (2017a). Los semivariogramas fueron demostrados gráficamente.
Donde:
y(h): semivarianza para el intervalo h
N(h): número de pares de valores separados entre sí por una magnitud h en la dirección de ese vector
Z(xi) - Z(xi + h): valor de la diferencia de un par de datos que distan h entre sí
Las semivarianzas fueron ajustadas, inicialmente, para cada variable en las direcciones 0 °, 45 °, 90 ° y 135º utilizando el software VARIOWIN (Pannatier, 1996), esto para verificar la presencia o ausencia de anisotropía. Constatada la isotropía de las semivariazas, todo el análisis posterior fue realizado para el caso isotrópico. Las inferencias para la variabilidad espacial se determinaron a partir de los modelos de semivariogramas y sus parámetros: efecto pepita (C0), varianza estructural (C), nivel (C0 + C) y alcance de la dependencia espacial (a).
Para la estimación de las semivarianzas entre las muestras, independientemente de la distancia, se introdujeron los parámetros "C0", "C" y "a" para el ajuste de los diferentes modelos de semivariogramas experimentales presentados en la tabla 2, esto con la ayuda del software VARIOWIN.
Tabla 2 Modelos de semivariogramas utilizados para la estimación de las semivarianzas entre las parcelas.
| Modelo de semivariograma | Fórmula |
| Gaussiano |
|
| Exponencial |
|
| Esférico |
|
y(h): semivarianza de la variable; h: distancia entre los dos valores medidos; C0: efecto pepita; C: varianza estructural; y a: alcance.
Luego del ajuste de los semivariogramas, el grado de dependencia espacial de las variables fue clasificado por el índice de dependencia espacial (IDE), según el método propuesto por Cambardella et al. (1994), en el cual, se considera como dependencia espacial fuerte los semivariogramas que tienen C0 ≤ 25% del C0 + C, moderada cuando está entre 25% <C0 ≤ 75% del C0 + C y débil para C0> 75% del C0 + C.
Después del ajuste de los modelos teóricos experimentales de semivariograma, se realizaron interpolaciones por el método de kriging ordinario con la herramienta Geoestatistical Analyst del software ArcMap® 10.4 (Esri INC, 2016).
La precisión de los valores interpolados fue evaluada por validación cruzada, siendo utilizadas las medidas: error absoluto medio (EAM), error cuadrático medio (ECM) y raíz del error cuadrático medio (RECM). Estos, en conjunto, permitieron seleccionar el semivariograma experimental que mejor se ajustó a los patrones espaciales de cada variable. Finalmente, fueron generados mapas temáticos de estimaciones e incertidumbres de las variables dendrométricas, con cinco y cuatro clases relativas, respectivamente.
Resultados
Regresión
El volumen comercial observado para los 108 árboles cubicados fue de 15.53 m3, con una media de 0.1438 m3 ± 0.0731 m3 por árbol, variando de 0.0104 m3 a 0.3676 m3, mientras que el dap y la hc variaron de 6.05 cm a 33.42 cm y de 1.60 m a 5.82 m, respectivamente.
En la etapa de ajuste, las ecuaciones presentaron R2 aj. superior a 0.7 y EEM% inferior al 27% (Tabla 3) y los valores de DMP que variaron entre 2.27% y 10.86% indican que todas las ecuaciones sobreestiman el volumen de los árboles muestreados.
Tabla 3 Coeficientes estimados de los modelos biométricos utilizados y sus respectivas medidas de precisión.
| N | Coeficiente | Ajuste | Validación | |||||||
| FCM | R 2 aj. | EEM (%) | DMP (%) | White-Noise (α) | EEM (%) | X 2 cal. | ||||
| 1 | β0 | -8.1991018* | 1.0323 | 0.7451 | 26.97 | 6.27 | 0.770 | 27.34 | 0.247ns | |
| β1 | 2.0125677* | |||||||||
| 2 | β0 | 0.0101686 | - | 0.7517 | 26.62 | 10.86 | 0.055 | 25.76 | 0.240ns | |
| β1 | 0.0002726* | |||||||||
| 3 | β0 | -0.0121223 | - | 0.7492 | 26.75 | 7.60 | 0.718 | 25.89 | 0.240ns | |
| β1 | 0.0023757 | |||||||||
| β2 | 0.0002153* | |||||||||
| 4 | β0 | -6.4001067* | 1.0318 | 0.7476 | 26.84 | 6.34 | 0.787 | 26.06 | 0.238ns | |
| β1 | 1.5391335* | |||||||||
| β2 | -6.9789310 | |||||||||
| 5 | β0 | 0.0104519 | - | 0.8507 | 20.64 | 5.98 | 0.590 | 26.95 | 0.235ns | |
| β1 | 0.0000723* | |||||||||
| 6 | β0 | -8.4784276* | 1.0198 | 0.8518 | 20.56 | 3.86 | 0.654 | 25.37 | 0.209ns | |
| β1 | 1.8423781* | |||||||||
| β2 | 0.6237952* | |||||||||
| 7 | β0 | -0.0098088 | - | 0.8552 | 20.33 | 2.27 | 0.858 | 26.61 | 0.215ns | |
| β1 | 0.0000896 | |||||||||
| β2 | 0.0000502* | |||||||||
| β3 | 0.0045745 | |||||||||
| 8 | β0 | -8.4332382* | 1.0216 | 0.8475 | 20.86 | 4.28 | 0.785 | 26.13 | 0.239ns | |
| β1 | 0.8633574* | |||||||||
β0, β1, β2 e β3: coeficientes de la ecuación de regresión; *: coeficiente significativo (p-valor ≤ 0.05); FCM: factor de corrección de Meyer; R2 aj.: coeficiente de determinación ajustado; EEM (%): error estándar de la media en porcentaje; DMP%: desviación media porcentual; α: significancia; X2 cal.: valor calculado del teste Chi-cuadrado; e ns: valor calculado no significativo (p-valor > 0.05).
En esta etapa, las medidas de precisión permiten separar claramente los modelos que utilizan solamente el dap como variable independiente, de aquellos que utilizan el dap y la hc, pues, de manera general, las ecuaciones que utilizan solamente dap generan estimaciones menos precisas, con menores R2 aj. y mayores EEM% y DMP.
El modelo de Stoat (7) se destacó por presentar mejor ajuste a la variabilidad de los árboles muestreados, con R2 aj. superior a 85.52% y apenas 14.48% no explicado por causa de la aleatoriedad de la variable respuesta. De forma contraria, el modelo de Kopezky-Gehrhardt (2) fue el que peor se ajustó, aunque presenta valores de R2 aj. y EEM% ligeramente mejores que el modelo de Husch (1), pero con peor DMP.
Las ecuaciones originadas a partir de modelos que utilizan solamente el dap como variable independiente, presentaron estimaciones para el conjunto de validación con EEM% similares a las del conjunto de ajuste. En contraste, esa semejanza no fue observada en las estimaciones de las ecuaciones de doble entrada (dap y hc) donde los valores aumentaron en aproximadamente 5.7%, lo que demuestra, en este caso particular, que la aplicación de las ecuaciones a nuevos datos resulta en estimaciones menos precisas que las realizadas con los datos del ajuste.
La prueba X2 evidencia que todas las ecuaciones presentaron valores estimados igual a los observados. En esta etapa, el modelo de Schumacher-Hall (6) presentó menores valores de EEM% y X2 calculados, resultando en el de mejor ajuste para estimación del vc. En general, se observa que todas las ecuaciones construidas tienden a sobreestimar la estimación para árboles con vc inferior a 0.18 m3 (Fig. 1), pues presentan mayor cantidad de residuos positivos en esa amplitud, siendo consistente con los valores ya presentados de DMP (Tabla 3).
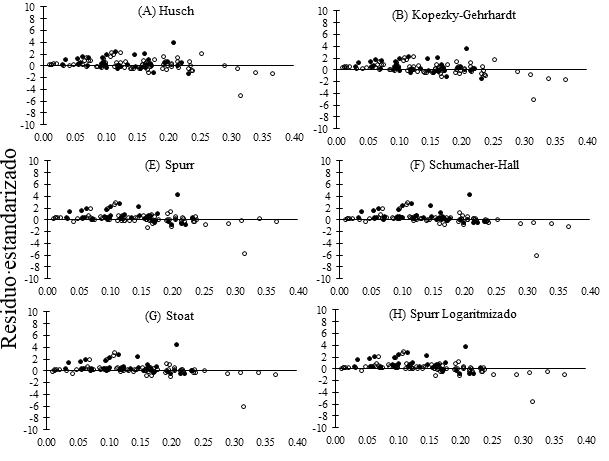
Volumen comercial real (m3)
○ Ajuste ● Validación
Figura 1 Dispersión de los residuos estandarizados para estimaciones del volumen comercial.
Al analizar la distribución residual en la etapa de ajuste, se observó la presencia de un outlier, lo cual puede ser atribuido a que la forma del fuste de este individuo es más afilada a partir de 1.3 m de altura en relación con los demás, y también fue observado un outlier en la etapa de validación. En esta última etapa, los modelos de Schumacher-Hall (Fig. 1F) y de log de Spurr (Fig. 1H), se distribuyeron con menor amplitud de variación al compararlos con los demás. Esto se puede atribuir a la transformación logarítmica de los valores, a la adición de la variable independiente hc y a la significancia de los coeficientes.
Los modelos de Stoat (Fig. 1G) y Schumacher-Hall (Fig. 1F) se ajustaron con mayor precisión a los datos muestreados, lo cual es comprobado por presentar las mejores medidas de precisión y distribución residual. Sin embargo, se optó por desconsiderar la ecuación 7 que corresponde al modelo de Soat, al igual que las ecuaciones 2, 3, 4 y 5 por presentar coeficientes no significativos, ya que esto indica que puede haber multicolinealidad entre las variables independientes.
En el caso del modelo de Stoat, solo uno de los cuatro coeficientes estimados, asociado con la variable combinada dap2hc, presentó significancia (p-valor ≤ 0.05), los tres coeficientes restantes no añadieron precisión al ajuste, haciendo este modelo equivalente al de Spurr (5).
Debido a lo anterior, la ecuación ajustada con el modelo de Schumacher-Hall (6) fue escogida para estimar el volumen comercial de los árboles de las parcelas georreferenciadas para posterior análisis geoestadístico. Se resalta que debe haber cautela para el uso generalizado de esa ecuación, pues el ajuste fue específico para las condiciones biofísicas del área en estudio.
Análisis descriptivo
A pesar de ser semejantes, las medias de dap y hc son levemente superiores a sus correspondientes medianas (Tabla 4). Esto indica que la distribución de los datos presenta cola a la derecha, y que la mayor parte de los árboles de la plantación presentan valores de dap y hc mayores o iguales al de sus respectivas medianas, lo cual es corroborado con el coeficiente positivo de asimetría de las variables.
Tabla 4 Estadística descriptiva de las variables dendrométricas utilizadas para el análisis de variabilidad espacial.
| Variables | Mín | X̄ | Med | Máx | s | CV% | AS | K | K.S. |
| dap (cm) | 12.30 | 21.39 | 21.14 | 30.68 | 3.20 | 14.96 | 0.04 | 2.22 | 0.42ns |
| hc (m) | 3.49 | 4.86 | 4.81 | 6.16 | 0.72 | 14.81 | 0.05 | -0.83 | 0.25ns |
| vc (m3) | 0.06 | 0.17 | 0.17 | 0.29 | 0.03 | 17.64 | 0.41 | 1.7 | 0.37ns |
dap: diámetro a 1.3 m del suelo (cm); hc: altura comercial (m); vc: volumen comercial (m3); Mín: valor mínimo; : media de los valores; Med: mediana de los valores; Máx: valor máximo; s: desviación estándar (m3); CV%: coeficiente de variación; AS: coeficiente de asimetría; K: coeficiente de curtosis; K.S.: valor calculado de la prueba de Kolmogorov-Smirnov; e ns: valor calculado no significativo (p-valor > 0.05).
De acuerdo con los resultados de la prueba K.S., las variables involucradas en esta investigación se aproximan a una distribución normal. Aunque la geoestadística no exige la normalidad de los datos, esta característica favorece las estimaciones.
Geoestadística
Los mejores modelos ajustados a los semivariogramas propuestos para las variables dendrométricas, demuestran fuerte dependencia espacial en el área experimental (Tabla 5), pues la varianza estructural representa más de 75% del nivel (C0 + C) y el efecto pepita (C0) está, en todos los casos, por debajo de 25%, demostrando que la cuadrícula utilizada fue eficiente para detectar las características espaciales de las variables estudiadas.
Tabla 5 Parámetros de los semivariogramas seleccionados para las variables dendrométricas utilizadas en el análisis de la variabilidad espacial.
| Variables | Modelo | C 0 | C 0 +C | a | IDE% | GDE | EAM | ECM | RECM |
| dap (cm) | Esférico | 3.00 | 12.50 | 91.00 | 24.0 | Forte | -0.0407 | -0.0118 | 3.5335 |
| hc (m) | Gaussiano | 0.14 | 0.67 | 180.00 | 20.9 | Forte | -0.0285 | -0.0381 | 0.5069 |
| vc (m3) | Esférico | 0.00 | 0.0022 | 104.00 | 0.0 | Forte | -0.0014 | -0.0299 | 0.0418 |
dap: diámetro a 1.3 m del suelo (cm); hc: altura comercial (m); vc: volumen comercial (m3); C0: efecto pepita; C0+C: meseta; a: alcance de la dependencia espacial (m); IDE%: índice de dependencia espacial; GDE: grado de dependencia espacial; EAM: error absoluto medio; ECM: error cuadrático medio; e RECM: raíz del error cuadrático medio.
El modelo esférico fue el que mejor se ajustó para explicar la estructura espacial del dap y el vc, seguido por el modelo gaussiano para la hc. Con el modelado, el valor más bajo de C0 fue observado para vc, seguido de hc y dap, ese orden creciente también fue observado para C0 + C. Las áreas cubiertas por los alcances de 91 m para dap, 180 m para hc y 104 m para vc, consideran que al menos 3, 7 y 4 puntos vecinos alrededor de la muestra, respectivamente, influyen en la estimación de un determinado punto en el espacio.
Por medio de los semivariogramas seleccionados para la estimación de la variabilidad espacial, es posible observar la dispersión de los valores reales en torno a la línea media estimada (Fig. 2), comprobando el fuerte grado de dependencia espacial de las variables.

y(lhl): semivarianza de la variable; y lhl: distancia entre valores medidos
Figura 2 Semivariogramas seleccionados para las variables dendrométricas utilizadas en el análisis de la variabilidad espacial.
Al aplicar los modelos ajustados, fueron generados por medio de kriging ordinario los mapas temáticos de predicción e incertidumbre de cada una de las variables dendrométricas, con cinco clases relativas (Fig. 3).

Sistema de coordenadas proyectado: Universal Transversal de Mercator - Datum: WGS84 - Zone: 22S
Figura 3 Mapas de predicción e incertidumbre de los semivariogramas seleccionados para las variables dendrométricas.
La mayor similitud entre las distribuciones espaciales de predicciones e incertidumbres fue encontrada para el dap y el vc, pues existe alta correlación entre esas variables, mientras que las amplitudes de los valores estimados para vc, hc y dap fueron mayores que las amplitudes observadas a partir del inventario, debido a los errores de la estimación. Se observó el predominio de la clase media (20.82 cm a 22.3 cm) para la estimación del dap, mientras que para la incertidumbre de la hc, hubo el predominio de la menor clase (0.21 m a 0.34 m), indicando que existe autocorrelación elevada entre las parcelas.
Discusión
La menor precisión de ajuste de los modelos que utilizan únicamente el dap como variable independiente es esperada, pues en éstos se asume que árboles del mismo diámetro tienen la misma altura (Rolim, Couto, Jesus y França, 2006). Entretanto, la mejora de los modelos ajustados para estimar el volumen con la incorporación de la variable altura junto al dap, es comprobada por varios autores (Higuchi y Ramm, 1985; Cysneiros, Pelissari, Machado, Figueiredo Filho y Souza, 2017), incluso para estimar otros recursos forestales (Chave et al., 2005; Marra et al., 2016).
El valor medio del volumen comercial por árbol de este estudio (0.17 m3) es inferior al estimado por la ecuación ajustada por Mayhew y Newton (1998) usando solo el dap medio en untrabajo realizado con más de 300 árboles de Swietenia macrophylla King en Sri Lanka, cuyo valor es 0.22 m3, indicando que, posiblemente, las estimaciones realizadas con dicha ecuación no resultarían en adherencia y, confirmando la necesidad de realizar ajuste específico para las condiciones del estudio.
La similitud de los valores de media y mediana de las variables dap, hc y vc, indica, de acuerdo con Silva, Lima, Xavier y Teixeira (2010), que las distribuciones de los datos presentan distanciamiento reducido en comparación con un valor central. Al evaluar el coeficiente de variación y conforme de la clasificación de Warrick y Nielsen (1980), el CV% de las variables entre 12% y 60% indica variabilidad media de los valores observados entre parcelas.
Los valores de efecto pepita pueden ser debidos a una combinación entre el error de muestreo y la variabilidad que ocurre en escala menor que el espaciamiento de la muestra más cercana (Zawadzki, Cieszewski, Zasada y Lowe, 2005), relacionándose directamente con la variabilidad aleatoria. Considerando lo anterior y asumiendo que no hubo errores de muestreo tendenciosos, los bajos valores de efecto pepita encontrados pueden estar relacionados con la dependencia espacial a pequeña escala.
En el caso del alcance, indica la distancia en la cual comienza la asíntota y la distancia máxima en que los datos son dependientes de forma estocástica (Zas, 2006), por lo tanto, las observaciones a distancias superiores al valor del alcance presentan independencia entre sí (Webster y Oliver, 2007). En la presente investigación, los resultados de este parámetro sugieren que es posible reducir el costo de trabajo en campo al demostrar que una cuadrícula de 90 m × 90 m es suficiente para el muestreo de todas las variables estudiadas, pudiendo incluso disminuir la intensidad de muestreo en hc e vc.
El modelo esférico, en el caso del dap y del vc, y el gaussiano, en el caso de la hc, demostraron la dependencia espacial de esas variables, posibilitando el desarrollo de mapas temáticos que pueden proporcionar informaciones para planeación de las actividades silviculturales y de la cosecha de madera. En otros estudios (Alvarenga, Mello, Guedes y Scolforo, 2012; Pelissari, Figueiredo Filho, Caldeira y Machado, 2014; Guedes et al., 2015; Pelissari et al., 2017b), los modelos clásicos de semivariogramas también describieron con precisión estadística los patrones espaciales de las variables dendrométricas de especies como: Tectona grandis L. f, Eucalyptus sp. y de otras del bioma Cerrado.
Conforme a los resultados, la generación de mapas temáticos es posible debido al fuerte grado de dependencia espacial que, de acuerdo con Assis, Mello, Guedes, Scolforo y Oliveira (2009), es una exigencia para la generación de mapas sin tendencia y sesgos, tornándolos más precisos en la espacialidad de las variables dendrométricas estudiadas.
Debido a que la media, comúnmente utilizada en la estadística clásica, no permite por si sola identificar con claridad la variabilidad espacial y los estratos de las variables dendrometrías estudiadas, se comprueba la necesidad de combinar el inventario forestal con la geoestadística para detectar esas distribuciones espaciales y posibilitar, de acuerdo con Guedes et al. (2012), ganancias de precisión en la estimación de las variables.
Conclusiones
Las variables dendrométricas dap, hc y vc de la especie Swietenia macrophylla, presentan dependencia espacial y pueden ser modeladas y estimadas con precisión usando técnicas geoestadísticas.
La ecuación ajustada a partir del modelo de Schumacher-Hall es la que mejor representa la variabilidad del volumen comercial de Swietenia macrophylla en el sistema agroforestal estudiado en la Amazonia brasilera.
La cuadrícula de 50 m × 50 m es eficiente para la generación de mapas de superficie que representan la variabilidad espacial de las variables dendrométricas estudiadas, por medio kriging ordinario, en el cual, el modelo de semivariograma esférico es el que mejor se ajusta para explicar la estructura espacial del dap y del vc y el modelo gaussiano para la hc.











 text new page (beta)
text new page (beta)


