1. Introduction
Materials are more or less dissipative and show phenomena such as creep, relaxation and damping. Viscoelastic constitutive models are often useful to model such behavior. Viscoelasticity theory describes processes in which the state of a mechanical system depends on a complete record of actions that were performed on it. Many polymers initially undergo fast relaxation followed by very slow relaxation. This behavior can be described effectively by using fractional order operators in the constitutive laws of viscoelasticity. Fractional viscoelastic model used to described the laws of deformation for modeling the viscoelastic behavior of real materials [7]. Fractional differential models in linear viscoelasticity allow the creep and relaxation processes to be described adequately by means of simple relationships between stresses and strains with a relatively small number of adjustable parameters [15]. Fractional viscoelastic models lead to the non-Debay relaxation behavior typical of numerous experimental observations [6]. Fractional differential models in linear viscoelasticity take into account stochastic (micro-Brownian) motion of molecules at the microlevel in the phenomenological description of viscoelastic media [15,16]. Viscoelastic materials exhibit both elastic and viscous characteristics when undergoing deformation [22]. For elastic response, the stressstrain relationship is rate independent. For viscous behaviors, the stress depends on deformation rate representing as a stiffer response at a larger loading rate. The viscoelastic response shows a dependence on the deformation history [12]. The mechanics of these viscoelastic materials can be modeled as arrangements of lossless elastic springs and lossy viscous dampers (dashpots). For a distributed material the stress due to the elastic element is proportional to the strain and the stress due to the viscous element is proportional to the time rate of change of strain. The commonly used viscoelastic material models are Maxwell model and Kelvin-Voigt model. These provide a useful description of relaxation, creep and stress rate dependence for some viscoelastic materials [13].
The Fractional calculus is a powerful tool to characterize the viscoelastic behaviors due to long-time memory and global correlation information. Fractional order derivatives are used in fractional calculus models, which represent a relatively simple way to describe dynamics in complex systems. In fractional viscoelastic models, a fractional dashpot is proposed to describe the dependence of viscous response on deformation history, while an elastic spring is used to represent the time-independent elastic response. Through different combinations of elastic springs and fractional dashpots, various fractional viscoelastic models have been constructed such as fractional Maxwell model, fractional Kelvin-Voigt model and fractional Zener model.
The rheological representative of fractional Maxwell model which is consisted of a spring in series with a fractional dashpot as shown in Fig. 1a). The relationship between stress σ and strain є of fractional Maxwell model can be expressed as
where E is the elastic modulus of the string and τ is the relaxation time of the fractional dashpot.
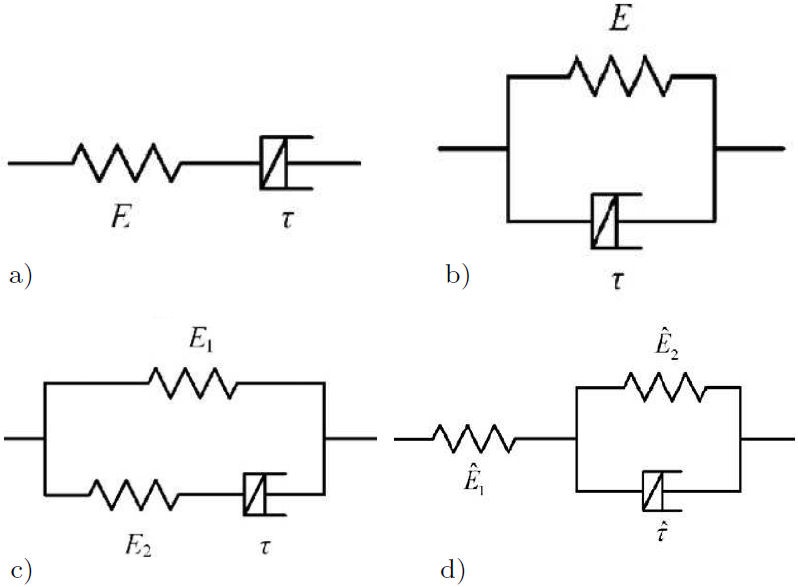
FIGURE 1 Fractional viscoelastic models: a) fractional Maxwell model, b) fractional Kelvin-Voigt model, c) fractional Zener model and d) fractional Poynting-Thomson model.
The fractional Kelvin-Voigt model is composed by a spring in parallel with a fractional dashpot as shown in Fig. 1b). The constitutive relationship has the following form
The fractional three-element models include the fractional Zener model and the fractional Poynting-Thomson model. The fractional Zener model is composed of an elastic spring and a fractional Maxwell model in parallel as shown in Fig. 1c). The stress is related with the strains as
where E 1 is the elastic modulus of the spring in the first branch, E 2 is the elastic modulus of the spring in the branch of the fractional maxwell element and τ is the relaxation time of the fractional dashpot. While the fractional Poynting-Thomson model is consisted of a spring and fractional Kelvin-Voigt element, which are arranged in series as shown in Fig. 1d). The corresponding constitutive relationship is represented
where
According to the general theory of linear viscoelasticity [25], given linear model can be expressed in terms of two equivalent forms, namely the creep and the relaxation representations. To each of these representations, two material functions G(t) and J(t) respectively called relaxation modulus and creep compliance can be associate. It is also important to stress that each of these two functions contains all the physical information about the viscoelastic model. In the Laplace domain, a given (linear) constitutive equation takes the following two equivalent forms [18,25]
These fractional viscoelastic models have been successfully applied to describe the viscoelastic behaviors of various material systems [10,11,20,24,25].
1.1. Fractional Calculus
In last decades, the concept of fractional calculus has been attracting the attention around the world due to its applications in complex systems. The model involving the fractional order derivatives gives a better prediction in comparison to model using integer order derivatives. Recently, the concepts of fractional differentiation and integration have both witnessed an historical development where the power law kernel was reviewed and replaced by exponential and Mittag-Leffler kernels [3,8,9,19]. These developments come from some arguments that were raised about the singularity of the power law around the origin zero. Generally speaking, a finite-time singularity will be observed when one input parameter or variable is time and the result of the output variable blow up toward infinity at a finite time. The notion of fractional differentiation with non singular kernel was then suggested to handle such natural occurrence and also to handle those physical problem where the singularities do not occur at the initial conditions. They have been applied in many fields of science with great success [2, 5, 21, 23]. While the concept of fractional derivative with constant order have been in fashion in the last decades, they have been found to be inefficient when dealing with anomalous diffusion therefore, the concept of variable orders was suggested. The variableorder fractional derivatives are very useful when investigating the memory properties which change with time and spatial location. Therefore, variable-order fractional derivative can be used to characterize variable memory effect of the system. Constant-order fractional operators are capable of describing some very relevant physical phenomena, it cannot capture important classes of physical phenomena where the order itself is a function of either dependent or independent variables. For example, the reaction kinetics of proteins has been found to exhibit relaxation mechanisms that are properly described by a temperature-dependent fractional order [17]. Thus, the underlying physics of the reaction kinetics (captured by the order of the relaxation mechanism) changes with temperature. Hence, it is reasonable to think that a differential equation with operators that update their order as a function of temperature will better describe the protein kinetics. This study suggests that there exist classes of physical problems that would be better described by variable-order fractional operators. The differential operators are excellent suggestion for anomalous diffusion, one will realizes that they cannot be used for analytical purpose [1,4].
Definition 1.1. The generalized Mittag-Leffler function
where (λ) n is the Pochhammer symbol defined by
Definition 1.2. Let f ∈ H 1(α,b) and 0 < δ ≤ 1, then Atangana-Koca derivative of fractional order in Caputo sense is given as [4]:
where the function g(δ) is well-defined such that
The Laplace transform for the Atangana-Koca fractional derivative (6) is given by
Definition 1.3. Let g(x) ∈ C 1[α,b] and f(x) a differential function in an open interval I. The Atangana-Koca fractional variable order derivative in Caputo sense is given by [1]
The Laplace transform for the Atangana-Koca fractional variable order derivative is given by
The m-th derivative of the function
The Laplace transform of the function
Delgado et al [26] applied a new fractional derivative with variable and constant order applied to a mass-spring-damper system. Gómez-Aguilar [14] obtained analytical solutions to electrical circuits of non-integer order via fractional derivatives with and without singular kernels.
2. Maxwell model with Atangana-Koca fractional derivative
In this section, we will investigate the analytic solutions of the relaxation modulus and creep compliance for fractional Maxwell model with fractional derivative of variable and constant order with non singular kernel.
Maxwell model with AKC fractional derivative with constant order
Let us consider (1) involving the AKC fractional derivative with constant order (6) as follows:
We apply Laplace transform to (11) and obtain the following relationship,
which gives
The Laplace transform of relaxation modulus can then be derived as
By applying the inverse Laplace transform to (14) and using (10), the relaxation modulus of fractional Maxwell model with Atangana-Koca fractional order derivative (6) is obtained as
The Laplace transform of the creep compliance can be estimated from
The creep compliance then be obtained through inverse Laplace transform of (16) as following
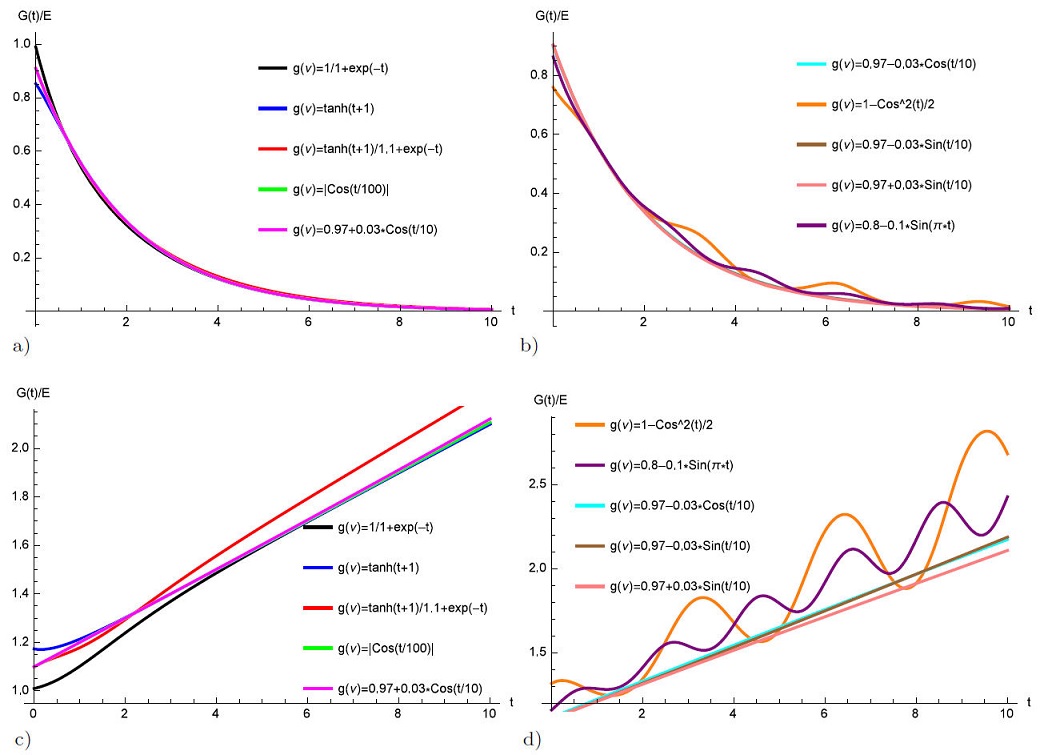
Figures 2a)-2b) shows the mechanical response of fractional Maxwell model involving the Atangana-Koca fractional derivative for several ν values, arbitrarily chosen.
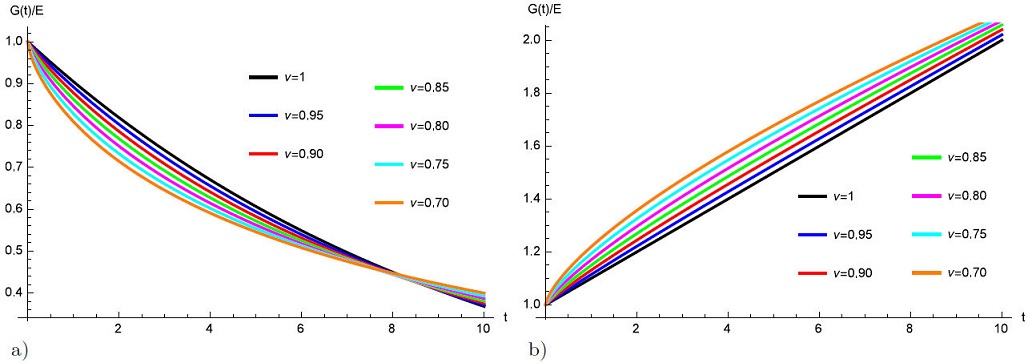
FIGURE 2 Mechanical properties of fractional Maxwell model involving the Atangana-Koca fractional derivative. In a) relaxation modulus and b) creep compliance for several ν values, arbitrarily chosen.
Maxwell model with AKC fractional derivative with variable order
Let us consider (1) involving the AKC fractional derivative with variable order (8) as follows:
We apply Laplace transform to (18) and obtain the following relationship,
which gives
By applying the inverse Laplace transform to (20) and using (10), the relaxation modulus of fractional Maxwell model with Atangana-Koca fractional variable order derivative (8) is obtained as
The Laplace transform of the creep compliance can be estimated from
The creep compliance then be obtained through inverse Laplace transform of (16) as following
Figures 3a)-3d) shows the mechanical response of fractional Maxwell model involving the Atangana-Koca fractional derivative with variable order for several g(ν) values, arbitrarily chosen.
3. Kelvin-Voigt model with Atangana-Koca fractional derivative
In this section, we will investigate the analytic solutions of the relaxation modulus and creep compliance for fractional Kelvin-Voigt model with fractional derivative of variable and constant order with non singular kernel.
Kelvin-Voigt model with AKC fractional derivative with constant order
Let us consider (2) involving the AKC fractional derivative with constant order (6) as follows:
We apply Laplace transform to (24) and obtain the following relationship,
which gives
The Laplace transform of relaxation modulus can then be derived as
By applying the inverse Laplace transform to (27) and using (10), the relaxation modulus of fractional Kelvin-Voigt model with Atangana-Koca fractional order derivative (6) is obtained as
The Laplace transform of the creep compliance can be estimated from
The creep compliance then be obtained through inverse Laplace transform of (16) as following
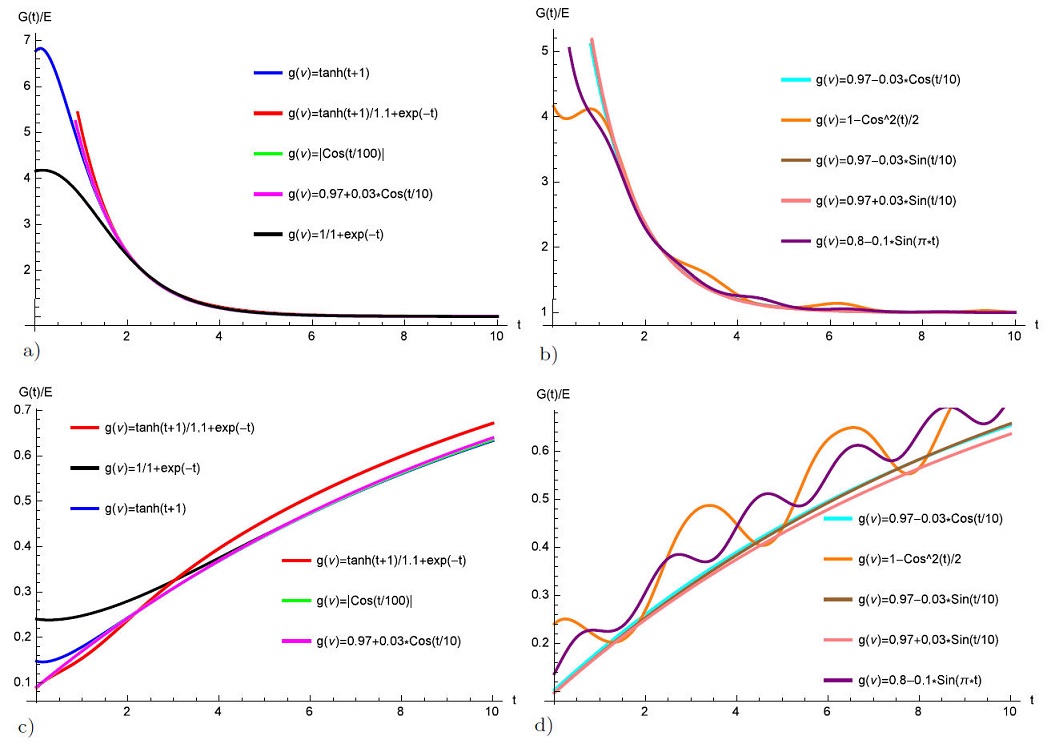
Figures 4a)-4b) shows the mechanical response of fractional Kelvin-Voigt model involving the Atangana-Koca fractional derivative for several ν values, arbitrarily chosen.
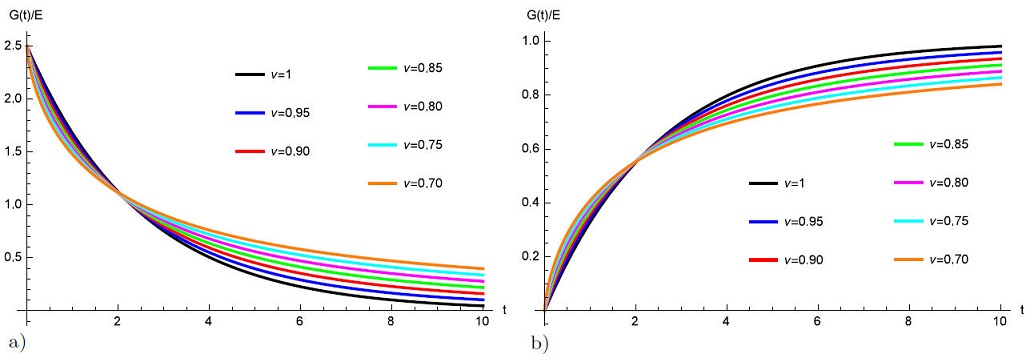
FIGURE 4 Mechanical properties of fractional Kelvin-Voigt model involving the Atangana-Koca fractional derivative. In a) relaxation modulus and b) creep compliance for several ν values, arbitrarily chosen.
Kelvin-Voigt model with AKC fractional derivative with variable order
Let us consider (2) involving the AKC fractional derivative with constant order (8) as follows:
We apply Laplace transform to (31) and obtain the following relationship,
which gives
The Laplace transform of relaxation modulus can then be derived as
By applying the inverse Laplace transform to (34) and using (10), the relaxation modulus of fractional Kelvin-Voigt model with Atangana-Koca fractional variable order derivative (8) is obtained as
The Laplace transform of the creep compliance can be estimated from
The creep compliance then be obtained through inverse Laplace transform of (36) as following
Figures 5a)-5d) shows the mechanical response of fractional Maxwell model involving the Atangana-Koca fractional derivative with variable order for several g(ν) values, arbitrarily chosen.
4. Three-element model with Atangana-Koca fractional derivative
In this section, we will investigate the analytic solutions of the relaxation modulus and creep compliance for fractional Zener model and fractional Poynting-Thomson model with fractional derivative of variable and constant order with non singular kernel.
Zener model with AKC fractional derivative with constant order
Let us consider (3) involving the AKC fractional derivative with constant order (6) as follows:
We apply Laplace transform to (38) and obtain the following relationship,
which gives
The Laplace transform of relaxation modulus can then be derived as
By applying the inverse Laplace transform to (41) and using (10), the relaxation modulus of fractional Zener model with Atangana-Koca fractional order derivative (6) is obtained as
The Laplace transform of the creep compliance can be estimated from
The creep compliance then be obtained through inverse Laplace transform of (43) as following
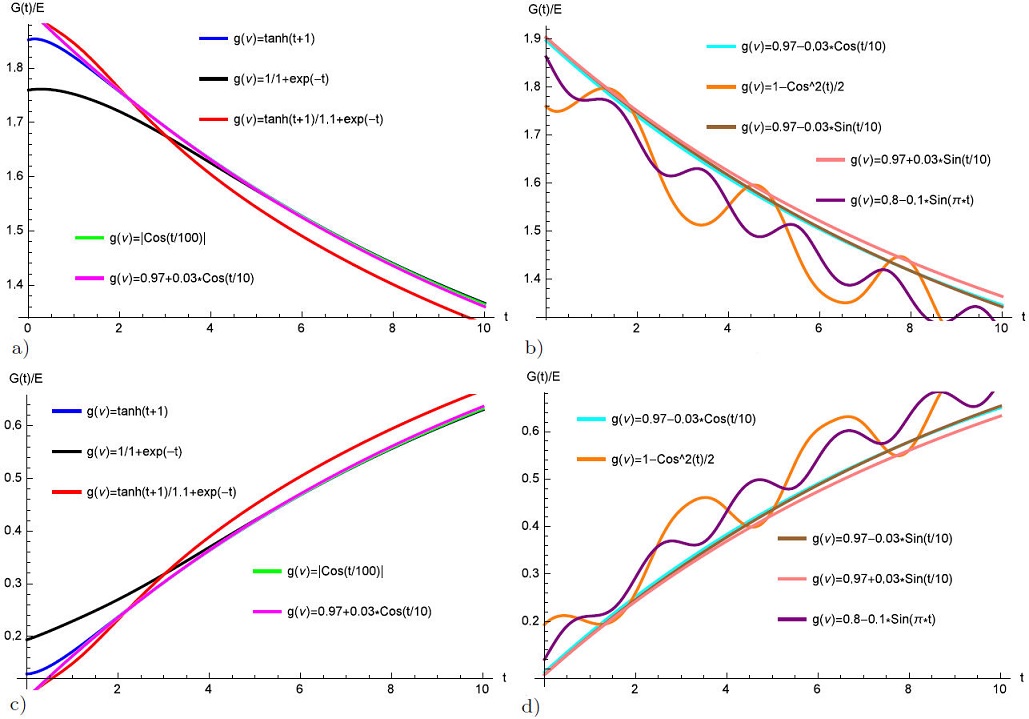
Figures 6a)-6b) shows the mechanical response of fractional Zener model involving the Atangana-Koca fractional derivative for several ν values, arbitrarily chosen.
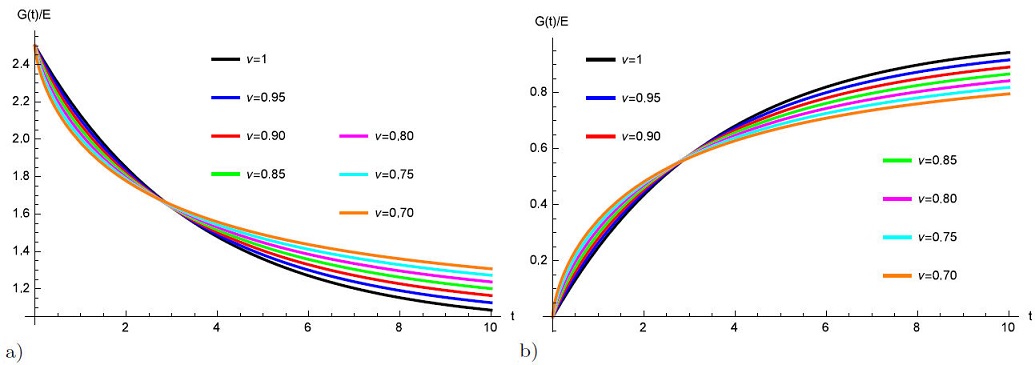
FIGURE 6 Mechanical properties of fractional Zener model involving the Atangana-Koca fractional derivative. In a) relaxation modulus and b) creep compliance for several ν values, arbitrarily chosen.
Zener model with AKC fractional derivative with variable order
Let us consider (3) involving the AKC fractional derivative with constant order (8) as follows:
We apply Laplace transform to (44) and obtain the following relationship,
which gives
The Laplace transform of relaxation modulus can then be derived as
By applying the inverse Laplace transform to (47) and using (10), the relaxation modulus of fractional Zener model with Atangana-Koca fractional variable order derivative (8) is obtained as
The Laplace transform of the creep compliance can be estimated from
The creep compliance then be obtained through inverse Laplace transform of (36) as following
Remark 4.1 If the materials constants E
1
, E
2
and
Figures 7a)-7d) shows the mechanical response of fractional Zener model involving the Atangana-Koca fractional derivative with variable order for several g(ν) values, arbitrarily chosen.
5. Results and discussions
In this section, we compare the performance of fractional viscoelastic models with fractional derivatives of constant and variable order of Atangana-Koca type. The mechanical response of Maxwell model with new fractional derivatives of constant and variable order are shown in Figs. 2a)-2b) and 3a)-3d) respectively. It can be seen from Figs. 2a)-2b) that creep compliances with Atangana-Koca constant order derivative decrease sharply as ν → 1. The Atangana-Koca fractional derivative of constant order ν results in slowest relaxation of viscoelastic materials as ν → 0, which can be used to characterize ultraslow relaxation of viscoelastic materials. Numerical solutions of Eq. (23) have been depicted in Figs. 3a)-3d), for different values of the fractional order g(ν). It is seen that the system exhibits behaviors such that the solution continuously depends on the time variables. The creep compliance of fractional Maxwell model with variable order derivative exponential increase with time instead of linear increase compared with fractional Maxwell-model with constant order fractional derivative. The numerical results indicate that the fractional order has an important influence on the relaxation modulus and the creep compliance and the general solution of the fractional equations depends on the parameter ν and when the order is a function rather than a constant of arbitrary order g(ν), respectively.
Figures 4a)-4b) and 5a)-5d) shows the mechanical response of fractional Kelvin-Voigt model with Atangana-Koca fractional derivative with constant and variable order. The creep compliance of fractional Kelvin-Voigt model exponential increase with time instead of linear increase compared with fractional Maxwell-model.
Figures 6a)-6b) plot the relaxation modulus and creep compliance for different ν of fractional Zener model with Atangana-Koca fractional derivative with constant, the relaxation modulus exponential decreases with increasing value of ν.
6. Conclusions
The analytical solutions of the stress relaxation modulus and creep compliance for fractional Maxwell model, fractional Kelvin-Voigt model, fractional Zener model and fractional Poynting-Thomson model are obtained. It is found that the fractional Zener model has similar performance as fractional Maxwell model. These solutions represent a new family of solutions for the viscoelastic models, which allows for the possibility of multiple solutions that are not observed in experiments (complex dynamic behaviors are observed). For different time periods we have different memory abilities. The representation of generalized viscoelastic models by variable-order and constant-order fractional derivative also allows a deeper insight into the physics behind fractional stress-strain relations. The variable-order fractional derivative can be used to characterize variable memory effect of the systems. It is shown that the constant-order model is not able to capture all the details of the variable-order solution, particularly in the areas of transition between dynamic regimes. We concluded that this new fractional variable-order operator is more suitable for modeling real-world complex problems than all existing fractional variable-order operators. The experimental verification of these models will be reported in a future paper.
Conflicts of Interest
The authors declare no conflict of interest.











 text new page (beta)
text new page (beta)