Introducción
El servicio de transporte público cuenta con una amplia y compleja red de infraestructura que surge de la creciente necesidad de la población de trasladarse hacia sus destinos ya sea de trabajo, escuela, salud, diversión, entre otros; es decir, propician el desarrollo económico de las regiones. De acuerdo con el Instituto Mexicano para la Competitividad [1] se sabe que más de 2/3 de los 22 millones de viajes diarios en la Ciudad de México se realizan en transporte público con 14.8 millones de usuarios que demandan un servicio de calidad.
La calidad del servicio de transporte se traduce en las necesidades que deben ser satisfechas por este, que en materia de sistemas de calidad se denominan voz del cliente o VOC por sus siglas en inglés (voice of customer). El estudio hecho por Gaskin, Griffin, Hauser, Katz y Klein [2], expresa que la VOC es una técnica de desarrollo de productos que genera un conjunto detallado de deseos y necesidades de los clientes, que se organizan en una estructura jerárquica, y luego se priorizan en términos de importancia relativa y satisfacción con las alternativas actuales. Por otro lado, también se sabe que de acuerdo con el estudio de El Poder del Consumidor[3] los usuarios están insatisfechos con el servicio de transporte público de la ciudad ya que dicho estudio revela que:
El 65% de los usuarios considera que la calidad del servicio es pésima o mala
Ocho de cada diez usuarios piensan que es inseguro
Nueve de cada diez coinciden que es incómodo
Siete de cada diez mencionan que es lento
Se han desarrollado propuestas de mejora en este sentido [4], en el cual, se propone una metodología en la que; por un lado, se aprovecha la experiencia de los dueños en cuanto a la administración de la operación y por otro, las necesidades de los viajeros referente a la calidad de servicio, logrando optimizar la operación del despacho de unidades o la minimización de los tiempos de espera. Esto permite detectar una problemática concreta.
Problemática
Una de las características más importantes de la prestación de servicios de transporte es que la oferta no se almacena. Esto es, la oferta debe ajustarse de acuerdo con la demanda en tiempo real o con un margen de ajuste relativamente corto, aumentando en las horas pico y disminuyendo en las horas valle, conjugando así un equilibrio entre la calidad y la rentabilidad del servicio. Los estudios que generalmente preponderan en la literatura son los relacionados con el establecimiento del cálculo de la demanda en un sistema de transporte público desde la perspectiva de la Ingeniería de tránsito. Y para ello, existen técnicas muy precisas, pero al mismo tiempo costosas, como lo son las de implementación de un sistema de control de entradas y salidas (por ejemplo, el uso de torniquetes); o bien a través del cálculo de aforos, que consiste en la obtención de una estimación a partir del conteo manual durante un número representativo de días. Sin embargo, de acuerdo con la Ley de Movilidad del Distrito Federal [5], los sistemas de transporte deben realizar periódicamente estudios que permitan conocer las necesidades de movilidad de sus usuarios y mejorar el servicio de acuerdo con estas, ajustando la oferta a la demanda, en el momento en que debe prestarse, además de la identificación de las variables que hacen del servicio uno bueno, pero nunca se especifican los factores o variables que logran un mejor servicio, como lo propuesto por [4] previamente señalado. En este estudio se determinan algunas de estas variables empleando la información de un sistema público concesionado de la Ciudad de México quien solicitó ayuda para efectuar un análisis que permita determinar las variables que pudieran afectar la afluencia de la demanda y en particular su disminución. El objetivo de la investigación es identificar las variables que alteran el comportamiento de la demanda en el sistema de transporte analizado y así tener herramientas para planear estrategias que mejoraren su funcionamiento, apoyándonos de la técnica VOC, que de acuerdo con [6] no existe una herramienta superior que permita la mejora de la calidad de un servicio ya sea público o privado en el que el transporte público no sea la excepción.
Metodología
1. Se consultaron las fuentes [3] y [7] para la identificación de las variables que afectan la afluencia, con un enfoque VOC y se concluye que los factores determinantes para identificar una buena o mala calidad del servicio son: inseguridad e incomodidad y lentitud del servicio. Sin embargo, es necesario determinar otras variables que inciden en la variabilidad de la demanda del servicio, específicamente de la empresa analizada.
2. También, se identificaron y analizaron los modelos econométricos que permitieran la agregación de todas las variables de las que se tiene información utilizando la teoría de modelos econométricos explicados en la fuente [8] y [9] y para la prueba de Granger, se utilizó como referencia el libro de causalidad en economía [10].
3. Captura de información. Para el análisis de la demanda, la empresa en cuestión disponía de los siguientes datos, con intervalos de tiempo diario, con una ventana de tiempo que inicia en enero de 2015 y termina en febrero de 2019:
demanda diaria del servicio
robos
accidentes
variación del costo del servicio
número de camiones diarios utilizados en el servicio
Se investigaron los datos de afluencia de la competencia directa.
Días de la semana se consideraron como variables explicativas dispuestas como variables ficticias.
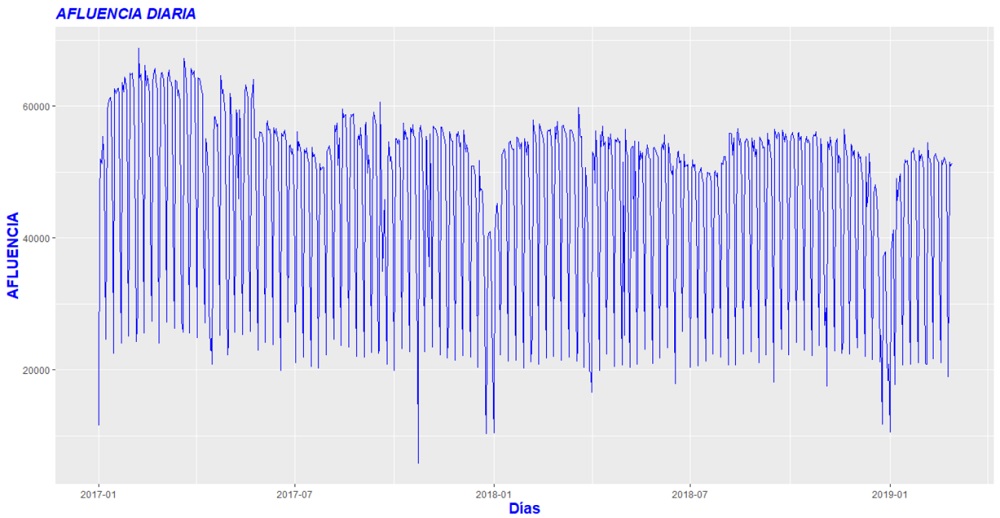
4. Se observaron cambios estructurales en la demanda durante los años 2015 y 2016, incluyendo casi la mitad del año 2017; se optó por recortar las series de demanda durante esos años y tomar sus valores diarios desde el 1 de enero de 2017 hasta el 27 de febrero de 2019 previos a la pandemia ocasionada por el Covid-19, con un total de 788 datos con frecuencia diaria. La figura 1 muestra los datos de la demanda diaria. La ventana de tiempo también fue ajustada para el resto de las series de datos de las variables empleadas.
Previo a la construcción del modelo es relevante la revisión del comportamiento de la variable de interés (afluencia diaria). En la figura 2, se puede observar que la serie presenta una tendencia negativa y un marcado comportamiento estacional; por lo que se necesita filtrar la serie para conocer de forma cuantitativa el valor correspondiente a la tendencia, así como los valores de sus factores estacionales. Por otra parte, es importante hacer notar los picos que apuntan hacia abajo, por lo que se analiza su comportamiento y posible causa.
En la tabla 1 y figura 3, se muestran los resultados obtenidos del cálculo de los factores estacionales tanto para los meses del año como los días de la semana.
Tabla 1 Valores de los Factores Estacionales por día y mes.
| Día | FE | Mes | FE | Mes | FE |
| Lunes | 1.10 | Ene | 0.99 | Jul | 0.95 |
| Martes | 1.17 | Feb | 1.05 | Ago | 1.05 |
| Miércoles | 1.17 | Mar | 1.03 | Sep | 0.99 |
| Jueves | 1,16 | Abr | 0.98 | Oct | 1.04 |
| Viernes | 1.13 | May | 1.01 | Nov | 1.01 |
| Sábado | 0.79 | Jun | 1.01 | Dic | 0.87 |
| Domingo | 0.48 |
En la tabla 1, se puede apreciar, por ejemplo, que la demanda se incrementa en un 5.71% cuando pasa de lunes a martes, en un 0.48% del martes al miércoles; mientras que del miércoles al jueves se decrementa en un 1.76%; y del jueves a viernes en un 2.63%; del viernes al sábado se presenta la caída más importante de la demanda en un 34.42%, y de igual manera, del sábado al domingo con un valor del 30.88%. Finalmente, el incremento de la demanda más grande se da del domingo al lunes con un 63.50%. Este comportamiento se repite cada semana, el cual se puede apreciar en la figura 3.
El cálculo de los factores estacionales también puede ser realizado para otros periodos, en este caso por mes para tener una idea del comportamiento de la serie a lo largo del año. La tabla 1 muestra los factores estacionales por mes y se puede observar que existen incrementos de la afluencia de enero a febrero del 5.75%; de abril a mayo del 2.87%; entre julio y agosto del 10.53%; septiembre a octubre del 5.31%; de diciembre a enero del 11.79% que resulta ser el incremento más grande entre los meses. Por otro lado, se presentan decrementos entre febrero marzo del 1.10%; de marzo a abril del 4.93%; de mayo a junio del 0.43%; de junio a julio del 6.08%; de agosto a septiembre del 6.31%; de octubre a noviembre del 3.20% y finalmente el decremento más grande se presentade noviembre a diciembre con un valor del 14.20%. Así mismo, de la figura 3 se puede apreciar que los meses de enero y septiembre comparten un comportamiento estacional similar, lo mismo ocurre con febrero y agosto. Finalmente, mayo, junio y noviembre tienden a tener el mismo valor de factor estacional.
En lo que respecta a los picos negativos estos se presentan en los días feriados y tienen impactos significativos en la demanda, no importando si son días laborales, entre semana de lunes a viernes, o fines de semana sábados y domingos. Para la muestra de los años 2017, 2018 y parte del 2019.
Una vez realizado este análisis y teniendo un mejor entendimiento del comportamiento de la serie en estudio se procede a la construcción del modelo.
Construcción del modelo
Con estas variables se construye el siguiente modelo de regresión lineal dada por la ecuación (1), sabiendo que a través de estas variables llamadas explicativas (x i) que, al calcularlas, se determina el valor de la variable explicada (y), que en este caso es la afluencia del servicio llamada demanda.
Donde:
y demanda número de usuarios registrados con frecuencia diaria.
X N : periodo secuencial con frecuencia diaria
X camiones : número de camiones registrados
X asaltos : número de asaltos registrados
X accidentes : número de accidentes registrados
X tasa : precio del servicio
X competencia : número de usuarios registrados por competencia directa
X domingo : valor de 1 si el día es domingo
X lunes : valor de 1 si el día es lunes
X martes : valor de 1 si el día es martes
X miercoles : valor de 1 si el día es miércoles
X jueves : valor de 1 si el día es jueves
X viernes : valor de 1 si el día es viernes
X sabado : valor de 1 si el día es sábado
β 0: es el valor del intercepto
β :1,2, …, 13: es el parámetro asociado a la correspondiente.
𝜀: Es el término de error.
Es necesario aclarar que las variables que se incorporaron para cuantificar el impacto de la estacionalidad presente en la serie en estudio fue el de los días de la semana, esto debido a que las decisiones que se toman son en un plazo muy corto. Así mismo si se hubieran agregado los meses del año para explicar el comportamiento del modelo esto hubiera generado una probabilidad mayor de caer en un problema de colinealidad. Finalmente, si se hubiera ingresado como variables explicativas a los meses del año junto con los días de la semana, el coeficiente independiente, en este caso la beta cero estimada, no se puede interpretar fácilmente. Una vez propuestas las variables es necesario determinar si estas explican la afluencia.
Solución del modelo propuesto: Determinación de contribución de cada variable a la demanda
Se procede a resolver el modelo de regresión lineal múltiple expresado por las ecuaciones (2) y (3) de la siguiente manera:
Para este modelo, se considera que los valores de y demanda son el resultado de las combinaciones lineales de las variables explicativas X i un término aleatorio. Primero se acomodan los valores de у t expresados en la ecuación (4)
Los valores de 𝑋 están ordenados en una matriz ampliada, en la que la primera columna está definida sólo por números uno, ecuación (5):
Se elimina la columna Χ sabado para evitar la dependencia lineal y problemas de colinealidad entre las variables explicativas. El valor de esta variable se expresará mediante β0 estimada.
La tabla 2 presenta los resultados de la regresión considerando un nivel significancia del 5% utilizando el análisis de datos de excel [11].
Tabla 2 Regresión estadística
| Coeficiente de correlación múltiple | 0.903174073 |
| Coeficiente de determinación | 0.815723406 |
| R2 ajustado | 0.812870091 |
| Error típico | 5852.756498 |
| Observaciones | 788 |
Fuente: Elaboración propia
El coeficiente de determinación ajustado nos indica que el 81.29% de la variación en la variable de respuesta se debe a un incremento de las variables explicativas, el resto se puede asumir al término de error. El resultado de los parámetros β estimados se muestran en la siguiente ecuación 6, así como los valores p:
Realizando el análisis de los coeficientes β estimados y sus respectivos valores p obtenidos de la regresión lineal, tenemos las siguientes afirmaciones:
A pesar de que el signo del coeficiente de la variable “asaltos” es consistente con el modelo, dicho valor no es estadísticamente significativo.
En el caso de “accidentes”, el signo de su coeficiente estimado no es consistente, pero al igual que el caso de la variable “asaltos” no es estadísticamente significativo.
El resto de los coeficientes resultaron ser estadísticamente significativos.
Análisis preliminar: determinar análisis de coeficientes inesperados.
Del análisis de los coeficientes previo a la prueba de significancia, se desprenden dos coeficientes con valores inesperados. El primero es el coeficiente β 4 estimado, relacionado con los “accidentes”, el signo esperado era negativo (-); ya que, como se ha explicado anteriormente, un accidente es contraproducente para un aumento de la afluencia. Sin embargo, el resultado que se obtuvo fue: "La afluencia aumenta en promedio 338.9645388 usuarios por un incremento de un accidente, manteniendo las demás variables constantes". Esto indicaría que la empresa, si quiere aumentar la demanda de su servicio, debe aumentar los accidentes, un análisis totalmente inesperado.
El segundo valor inesperado es el del coeficiente 𝛽 6 estimado, relacionado con la variación de la afluencia de la competencia ya que se espera que tenga un efecto inverso a la variación de la afluencia local; es decir, si la afluencia de la competencia aumenta, la afluencia local disminuye teniendo un signo negativo (-); sin embargo, el coeficiente obtenido de la regresión tuvo un signo positivo (+) dando como resultado: "La afluencia aumenta en promedio 0.295400417 usuarios por cada aumento de un usuario que utiliza el servicio ofrecido por la competencia, esto manteniendo las demás variables constantes". Esto indicaría que la empresa, si quiere aumentar la demanda de su servicio, debe incentivar a su competencia directa para que aumente la demanda de su servicio, situación que vuelve a caer en lo inesperado.
Por lo tanto, se necesita una prueba estadística para explicar este comportamiento y para tal efecto se utiliza la prueba de causalidad de Granger para ambas variables. Hasta ahora, hemos conseguido que la afluencia y sea una función de x Accidentes y xc ompetencia de la siguiente manera, expresado por la ecuación (7):
Es decir, la flecha de causalidad indica que Χ accidentes causa la afluencia y (Χ accidentes → y) y Χ competencia causa la afluencia 𝑦 Χ competencia → y); sin embargo, como mencionan Gujarati y Porter [10] es necesario considerar que la flecha de causalidad puede cambiar de dirección, siendo y causante de Χ accidentes (y → Χ accidentes ) y y causante de Χ competencia (y → Χ competencia ) expresada como: Χ accidentes , Χ competencia = f (y).
El resultado de la prueba de Granger efectuado en el software Eviews [12] para estas dos variables dicta el juicio de los resultados, indicando que tanto los accidentes como la competencia no pueden ser causados por la afluencia. Esto es un problema, ya que ambas variables seguirán sin tener una explicación estadística verificable, sin embargo, se pueden hacer suposiciones y a través de la recolección continua de datos se pueden verificar estas suposiciones.
Al reconstruir el modelo de regresión lineal múltiple considerando sólo las variables estadísticamente significativas, el modelo se muestra en la ecuación (9):
Se eliminan las variables x asaltos y x accientes por no ser estadísticamente significativas y se reasignan los coeficientes β estimados. Con el modelo de regresión lineal múltiple actualizado (ecuación 10), el cálculo de los coeficientes β estimados se realiza de nuevo mediante el análisis de datos de excel [9].
Resultados
Los resultados son los siguientes (se redondean los valores de los coeficientes al tratarse de usuarios):
"La afluencia es aproximadamente de 29,277 usuarios si el día es sábado".
"Existe una disminución en la afluencia a razón de 8 usuarios por cada día, lo que muestra una tendencia negativa; es decir, los usuarios han disminuido a través del tiempo".
"También se encontró que por cada unidad en el servicio se aumenta la afluencia a razón de 301 usuarios".
"El número de viajes se ve disminuido a razón de -2,597 usuarios por cada incremento en un peso MXN en el costo del servicio, lo que denota que la demanda es inelástica al precio del servicio".
"Por cada persona que utiliza el transporte ofrecido por la competencia el aforo aumenta en promedio 0.3 usuarios ".
"Si el día es domingo, comparado con el sábado, el flujo de personas se ve disminuido a razón de 7,530 pasajeros".
" Si los días son lunes, martes, miércoles, jueves y viernes el flujo de personas aumenta aproximadamente 25,995, 17,841, 16,935, 15,778 y 14,750 usuarios respectivamente si se compara con el sábado".
Otros valores que arroja la regresión son los estadísticos de regresión mostrados en la tabla 3:
Tabla 3 Regresión estadística actualizada
| Coeficiente de correlación múltiple | 0.902579362 |
| Coeficiente de determinación | 0.814649504 |
| R2 ajustado | 0.812264041 |
| Error típico | 5862.226375 |
| Observaciones | 788 |
Fuente: Elaboración propia
Para este trabajo se considera el valor del Coeficiente de determinación ajustado R 2 , el cual indica, qué tan bueno es el modelo construido. A diferencia del Coeficiente de Determinación no ajustado, el R 2 ajustado es fiable ya que muestra la variación del 𝑦 demanda por las variables explicativas y penaliza por cada variable agregada. El valor ajustado de R 2 fue de 81.23%, lo que indica que de las variables explicativas propuestas pueden explicar la variación de 𝑦 demanda ,. Sólo el 18.77% de la de la variación en la demanda es explicada por el término de error. Por lo tanto, se concluye que las variables explicativas del modelo reflejan el comportamiento de la demanda o afluencia en ese corredor con esa ruta.
El valor del 81.22% considera únicamente las variables x N , x camiones , x tasa , x competencia , x domingo , x lunes , x martes , x miércoles , x jueves , y x viernes , a pesar de que penaliza por cada variable ingresada, el valor es bastante aceptable. Si se hubiera considerado también x accidentes y x asaltos , el R 2 ajustado aumenta muy poco, llegando a un 81.28% de incremento, lo que nos parece importante teniendo en cuenta que ambas variables no son significativas.
Discusión
A partir de estos resultados, la empresa concesionaria debe atender y potenciar las variables de impacto positivo y generar políticas internas que mitiguen el impacto de las variables negativas. Ahora podemos saber qué variables son las determinantes de la fluctuación de la demanda y el responsable de la planificación estratégica de la empresa tiene la posibilidad de tomar decisiones concretas para mejorar el servicio y aumentar la demanda de este.
Se logra observar con claridad que conforme pasan los días de la semana la afluencia disminuye y entonces se pueden diseñar modelos que optimicen la flota de autobuses con base este conocimiento. También, se puede señalar que no existe suficiente evidencia que indique que los accidentes y asaltos no contribuyen a la variación de la afluencia de la demanda en esa ruta de la compañía concesionaria estudiada. Esto es, no se ha llegado a alcanzar un umbral en el que el número de accidentes y asaltos sean lo suficientemente grandes como para afectar la decisión de los usuarios en cambiar su modo de transporte.
También, resulta de interés que la afluencia de la competencia influye de manera positiva en la afluencia de la compañía estudiada. Esto podría ser explicado de la siguiente manera: el incremento en la competencia se puede deber a que consideran que hay un mercado insatisfecho que pueden tomar; sin embargo, en vez de reducir la demanda de la ruta estudiada, el hecho de que se presente la competencia indica al usuario que hay más opciones y esto tiene un efecto positivo ya que más usuarios optarán en escoger esa ruta.
A pesar de que el porcentaje de variación entre días de la semana empleando Factores Estacionales y el Modelo Lineal muestran diferencias, estas pueden adjudicarse al término de error y se puede considerar que no son tan grandes. Sin embargo, es de resaltar que el porcentaje de variación con una mayor diferencia es el que corresponde a la comparación del martes respecto al lunes como se muestra en la tabla 4.
Tabla 4 Comparación de incremento/decrementos de afluencia entre días de la semana empleando los Factores Estacionales de la serie y el Modelo de Regresión calculado.
| Días comparados | Con Factores Estacionales | Con Modelo Lineal |
| Lunes-martes | 5.71% | -14.75% |
| Martes-miércoles | 0.48% | -1.42% |
| Miércoles-jueves | -1.76% | -2.50% |
| Jueves-viernes | 2.36% | -2.28% |
| Viernes-sábado | -34.42% | -33.50% |
| Sábado-domingo | -30.88% | -25.72% |
| Domingo-lunes | 63.50% | 54.16% |
Fuente: elaboración propia.
Conclusiones
A través de este análisis se logra un modelo de regresión lineal múltiple que permite establecer las variables que explican el movimiento de la afluencia en un transporte público concesionado en la Ciudad de México desde la perspectiva de la voz del cliente que a diferencia de algunas de las metodologías de ingeniería de tránsito no la consideran. Consideramos que cada metodología tiene sus ventajas y desventajas, sin embargo, se considera que son complementarias, ya que por un lado se pueden medir los niveles de afluencia de manera precisa en ambas metodologías, pero no se sabe desde la percepción del usuario qué causa las variaciones en el número de viajes. Se observa por ejemplo que la competencia puede ser un factor positivo de aumento de estos, o bien, que los asaltos no son determinantes (al menos con los datos analizados) para que exista una disminución y que son conclusiones que no se tendrían con las metodologías de ingeniería de tránsito. Este análisis pude emplearse para hacer la planeación de la ruta considerada, sin embargo, esto debe ser comprobado con los datos post pandemia que se están generando. Además, conocer el porcentaje de variación entre días permitirá tener una decisión más precisa para estimar la demanda y por ende el número de unidades necesarias para atender a la misma.
Investigación futura
Se requiere de un análisis estadístico más profundo de la demanda cuando se presentan días feriados como un comportamiento que puede ser tipificado y estimar la caída en la afluencia esperada, lo que puede dar mayores herramientas en la toma de decisiones para estos días en particular, tenido en cuenta cuando estos caen entre semana o los fines de semana.
Se puede robustecer el estudio al incorporar intervalos de confianza en el análisis de los factores estacionales y los correspondientes al modelo de regresión, establecer su relevancia estadística en el estudio y explicar la diferencia tan grande en el porcentaje de variación entre los lunes y martes.
El estudio fue realizado previo al inicio de la pandemia que detono en China en diciembre del 2019, se puede suponer que actualmente en México se están retomando las actividades presenciales con todas las modificaciones que esto involucra y que el estudio realizado pude emplearse para hacer la planeación de la ruta. Sin embargo, esto debe ser comprobado con los datos post pandemia que se están generando.











 text new page (beta)
text new page (beta)