Artículos técnicos

 

Obtención de ecuaciones empíricas para estimación de crecientes de diseño en la Región Hidrológica Núm. 10 (Sinaloa) de México

 

Obtainment of empirical equations for design floods estimation in the Hydrological Region No. 10 (Sinaloa) of Mexico

 

Daniel Francisco Campos-Aranda*
Profesor jubilado de la Universidad Autónoma de San Luis Potosí,
*Autor de correspondencia.

 

Dirección institucional del autor

Dr. Daniel Francisco Campos–Aranda

Profesor jubilado
Universidad Autónoma de San Luis Potosí
Genaro Codina 240
colonia Jardines del Estadio
78280 San Luis Potosí, San Luis Potosí, México
campos_aranda@hotmail.com

 

Recibido: 19/07/12
Aceptado: 23/05/13

 

Resumen

Las crecientes de diseño (Q_Tr) son la estimación hidrológica más frecuente debido a que son básicas para dimensionar y revisar todo tipo de obras hidráulicas. Su estimación en cuencas sin datos de gasto máximo anual se basa en los métodos regionales, que emplean tal información de una región o zona geográfica para obtener resultados que son aplicables dentro de ella. Los procedimientos regionales son de dos tipos: los similares al índice de crecientes y el desarrollo de ecuaciones de empíricas. Los primeros se basan y deben su capacidad de predicción a la homogeneidad de la región; en cambio, el segundo método permite cierto grado de heterogeneidad, la cual es tomada en consideración en los propios modelos de regresión generados. Empleando como variables predictivas el área de cuenca (A), la longitud del cauce principal (Lcp) y las predicciones de lluvia máxima diaria (PMD), se establecieron cuatro ecuaciones empíricas, seleccionando dos, según sus índices de desempeño, para cada uno de los seis periodos de retorno establecidos. Se procesaron 23 registros de gastos máximos para obtener los valores de Q_Tr con base en la distribución general de valores extremos. Para la obtención de los coeficientes de ajuste de cada ecuación se emplearon tres métodos: el de mínimos cuadrados de los residuos en el dominio logarítmico, su corrección por sesgo y el de optimización numérica minimizando una función objetivo. Se obtuvieron seis ecuaciones empíricas para cada uno de los seis periodos de retorno analizados. El contraste numérico en seis estaciones hidrométricas no utilizadas en la deducción de las ecuaciones y en seis de las procesadas, las de mayor periodo de registro, indica una regularidad en las estimaciones y destaca la capacidad predictiva de las ecuaciones empíricas desarrolladas. Se recomienda aplicar el procedimiento propuesto en otras regiones para encontrar este tipo de ecuaciones, que permiten estimar las crecientes de diseño de manera sumamente fácil.

Palabras clave: regresión lineal múltiple, error relativo, índices de desempeño, algoritmo de Rosenbrock.

 

Abstract

Floods designing (Q_Tr) is the most common hydrological estimation, because it is basic to sizing and reviewing all types of hydraulic works. Its estimation in watersheds without annual maximum flow data is based on regional methods, which use such information from a region or geographical area, in order to obtain results that apply within it. There are two types of regional procedures: those related to the index flood and those that develop empirical equations. The first type is based on the homogeneity of the region, hence its predictability; whereas the second method allows some degree of heterogeneity, which is taken into account in the regression models generated. Four empirical equations were established, using as prediction variables: the watershed area (A), the main channel length (Lcp) and predictions of maximum daily rainfall (PMD). Only two equations were selected for each of the six return periods established. 23 records of maximum annual flow were processed to obtain values of Q_Tr based on the General Extreme Values distribution. To obtain the fit coefficients of each equation three methods were used: the least-squared residuals in the logarithmic domain, their bias correction and the numerical optimization minimizing an objective function. Six empirical equations for each of the six return periods analyzed were obtained. The regularity of the estimations was tested by numerically contrasting results from six gauging stations (not used in the derivation of the equations) and six of those processed (those with the longest period of record). Such analysis allowed to point out the predictive ability of the empirical equations developed. It is highly recommended to apply the proposed procedure in other regions to find such empirical equations for design flood estimation, because of their very simple application.

Keywords: multiple linear regression, relative error, performance indices, Rosenbrock algorithm.

 

Introducción

Las crecientes de diseño, conocidas de manera coloquial como avenidas máximas, son la estimación hidrológica más común, debido a que con base en ellas se dimensionan, en las etapas de planeación y/o diseño, todas las obras de infraestructura hidráulica; además, permiten la revisión de la seguridad asociada con tales obras cuando ya están construidas, sean éstas de aprovechamiento o de control (embalses), de protección (diques y encauzamientos) o de cruce (alcantarillas y puentes). El procedimiento más confiable para la estimación de las crecientes de diseño consiste en el ajuste de un modelo probabilístico al registro disponible de gastos máximos anuales, para obtener estimaciones o predicciones relativas a diversas probabilidades de excedencia, cuyo recíproco es el periodo de retorno o intervalo promedio en años entre la ocurrencia de un evento igual o mayor. El procedimiento citado se denomina de manera genérica análisis de frecuencia de crecientes (AFC) y actualmente emplea como modelos probabilísticos prescritos la distribución Log-Pearson tipo III, la General de Valores Extremos y la Logística Generalizada, ajustando éstas a través del método de momentos, de máxima verosimilitud o de momentos L.

La desventaja fundamental del AFC es la escasa disponibilidad de registros de crecientes en los sitios de interés. Por ello, se recurre al análisis regional de frecuencia de crecientes (ARFC), el cual utiliza la información de gastos máximos anuales disponible en una región o zona que puede ser considerada homogénea desde un punto de vista hidrológico. Las técnicas de ARFC utilizan de manera conjunta la información citada y sus resultados resultan aplicables a cualquier sitio o localidad ubicada dentro de la región homogénea. Por ello, el ARFC permite estimar crecientes de diseño en cuencas sin aforos. Entre los métodos clásicos del ARFC se tienen la técnica de las estaciones-años, el índice de crecientes, el ajuste de modelos probabilísticos con base en parámetros estadísticos regionales y la obtención de ecuaciones de regresión potencial, que relacionan las crecientes de diseño obtenidas en cuencas aforadas, con ciertas características fisiográficas o climáticas de éstas (Cunnane, 1988; GREHYS, 1996a; Escalante-Sandoval y Reyes-Chávez, 2002).

El GREHYS (1996a) indica que se puede establecer una distinción clara dentro de las técnicas del ARFC; por una parte, se tienen los métodos similares al índice de crecientes y por la otra al método que desarrolla ecuaciones de regresión empíricas. Los primeros se basan y deben su capacidad de predicción a la homogeneidad de la región y por ello la definición más precisa posible de ésta resulta fundamental. En cambio, el segundo método permite cierto grado de no homogeneidad, la cual es tomada en consideración en los propios modelos de regresión desarrollados. Entonces, si la región bajo estudio puede ser caracterizada con un alto grado de homogeneidad, los métodos semejantes al índice de crecientes serán preferibles; por el contrario, si existe incertidumbre al definir las regiones homogéneas o la zona estudiada está conformada por varias subregiones y no existe suficiente información hidrométrica en ellas para ser trabajadas de manera independiente, el método de las ecuaciones empíricas será la mejor opción dentro del ARFC.

El objetivo de este trabajo consistió en desarrollar el método regional de las ecuaciones de regresión empíricas en la Región Hidrológica Núm. 10 (Sinaloa) de México, para la cual se ha encontrado que está integrada por dos subregiones: una al norte y otra al sur, según Escalante-Sandoval (1998); o bien por tres subregiones: zona norte, de montaña y planicie costera (Gutiérrez-López et al., 2004; Campos-Aranda, 2008a). Se procesaron 23 registros de gastos máximos anuales, con amplitudes que oscilan entre los 19 y 56 años, con 36 años como valor medio. Se desarrollaron cuatro tipos de ecuaciones empíricas, cada una para seis periodos de retorno y todas se generaron con dos métodos básicos de ajuste, los mínimos cuadrados de los residuos en el dominio logarítmico y la optimización numérica multivariada no restringida, aplicada a través del algoritmo de Rosenbrock. Como las ecuaciones obtenidas por mínimos cuadrados fueron corregidas por sesgo, se generó un total de 72 ecuaciones empíricas, de entre las cuales se seleccionaron 36, por tener sus mejores indicadores de desempeño, éstas se probaron en seis estaciones hidrométricas no utilizadas en su deducción y en seis de las procesadas, las de registro amplio. Las conclusiones formuladas destacan la regularidad de las predicciones estimadas y sugieren el desarrollo de este tipo de modelos empíricos en otras regiones del país con base en los tres planteamientos de ajuste seguidos. Tales ecuaciones empíricas permitirán estimar fácilmente las crecientes de diseño en otras zonas geográficas del país.

 

Desarrollo

Ecuaciones de regresión potencial y su ajuste

En la ingeniería hidrológica es común el uso de ecuaciones empíricas para realizar estimaciones en sitios donde no existe información hidrométrica. En relación con la estimación de crecientes de diseño, la regresión potencial ha sido el modelo más utilizado para describir la relación entre las predicciones (Q_Tr), y ciertas características fisiográficas y climáticas (X_i) de las cuencas de las cuales proceden las estimaciones involucradas. Entonces, para una cierta región considerada homogénea, se tiene (McCuen et al., 1990; GREHYS, 1996a):

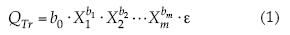
en donde b₀, b₁,..., b_m son los parámetros de ajuste y ε es el error multiplicativo del modelo. Para estimar los parámetros b_i ha sido práctica común linealizar la ecuación (1), tomando logaritmos y entonces estimar los coeficientes de una ecuación de regresión lineal múltiple (RLM):

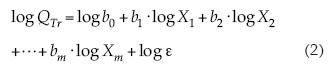
haciendo y = log Q_Tr, a₀ = log b₀, a_i = b_i y x_i = log X_i, con i = 1, 2,..., m, se obtiene la ecuación de la RLM:

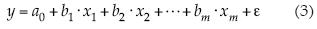
cuya solución matricial de mínimos cuadrados de los residuos (MCR) se puede encontrar en cualquier texto de métodos numéricos, por ejemplo, en Campos-Aranda (2003). El coeficiente b₀ es igual a o bien a , según si se utilizaron logaritmos decimales o naturales; los demás coeficientes tienen correspondencia directa. Cuando el error en la ecuación (1) es de adición, la RLM no se puede utilizar para estimar los parámetros de ajuste y entonces la optimización numérica ha sido empleada.

Corrección por sesgo para el ajuste de MCR

Desde principios de la década de los años setenta se comenzaron a desarrollar métodos para corregir los resultados del ajuste de la ecuación (1) a través de una ecuación de RLM debido a que el ajuste de mínimos cuadrados de los residuos minimiza a éstos en el dominio logarítmico, al emplear los logaritmos de las variables predictivas (X_i) y de la dependiente (Q_Tr), como se estableció en la ecuación (2). Lo anterior implica que el coeficiente de determinación (R²) encontrado está evaluado en el dominio logarítmico y por ello se cita después como log R².

McCuen et al. (1990) exponen y aplican tres procedimientos para corregir el coeficiente b₀, también llamado ordenada al origen, por la similitud entre la ecuación (3) y la fórmula de la línea recta. El primer método corrige la mayor parte del sesgo y su planteamiento consiste en obtener una estimación de b₀ no sesgada, haciendo cero los residuos (e_i) en el dominio real, es decir:

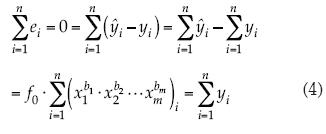
el estimador buscado será:

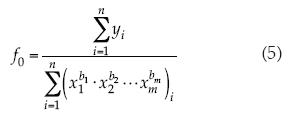
en la obtención de f₀ se está aceptando que el sesgo se puede corregir exclusivamente ajustando b₀, pero ello no conduce a unos coeficientes b_i poblacionales insesgados; en realidad, sólo b₀ es insesgado para la muestra utilizada. Este procedimiento de corrección por sesgo no altera el valor del coeficiente de determinación. Los otros dos procedimientos de ajuste de b₀ expuestos por McCuen et al. (1990) se basan en los residuos en el dominio logarítmico.

Ecuaciones empíricas por probar

Las ecuaciones de regresión potencial que han sido probadas y que conducen a resultados satisfactorios para estimar crecientes de diseño (Q_Tr) han utilizado el área de cuenca (A) como variable fisiográfica fundamental con la que están relacionados todos los procesos hidrológicos y a partir de la cual toman dimensión. Después del tamaño de la cuenca, la longitud del cauce principal (Lcp) también se ha utilizado para dar dimensión con una relación inversa, ya que a mayor longitud, las crecientes son menores (McCuen et al., 1990; Tasker et al., 1996; GREHYS, 1996b; Pandey y Nguyen, 1999). El uso de ambas variables origina un problema de multicolinealidad, ya que es común que exista correlación entre ellas (Montgomery et al., 2002).

Con respecto a las variables climáticas o meteorológicas empleadas, por lo general se han considerado las predicciones asociadas con la lluvia máxima diaria anual (PMD_Tr), por la mayor cobertura de las estaciones pluviométricas y la facilidad de obtención de tales datos, comparados, por ejemplo, con los registros pluviográficos. Con base en lo anterior, las cuatro ecuaciones que se propone investigar son:

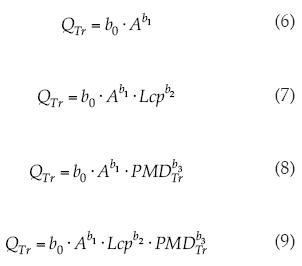
La comparación entre las dos primeras ecuaciones busca establecer si existe mejoría estadística al usar dos variables predictivas; en cambio, la comparación entre las siguientes dos ecuaciones potenciales propuestas se orienta a definir cuál resulta más conveniente en asociación con la tercera variable predictiva involucrada.

Índices de desempeño de las ecuaciones empíricas

Cuando se tienen varias ecuaciones de RLM, la selección de la más conveniente se puede buscar con base en varios indicadores en los residuos (Montgomery et al., 2002); es decir, en las diferencias entre la variable observada (y) y la estimada (ŷ) con la ecuación de RLM que se contrasta. Cuando se trabaja con los logaritmos de las variables, tales indicadores, como el coeficiente de determinación (R²) o la estadística C_p de Mallows no son confiables, pues los residuos se evalúan en el dominio logarítmico, como ya se ha indicado.

Por lo anterior, todas las ecuaciones potenciales empíricas que se obtengan a través de la RLM se evaluarán por medio de los siguientes tres índices de desempeño promedio, calculados en el dominio real (Pandey y Nguyen, 1999):

1. DAM es la desviación absoluta media con unidades de m³/s:

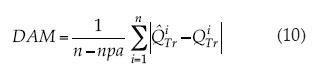
en la cual, y son las predicciones del gasto observado y estimado con la ecuación potencial empírica; n, el número de datos utilizados de cada variable en este estudio (23) (ver cuadro 1), y npa es el número de parámetro de ajuste, que variará de 2 a 4.

2. EEM es el error estándar medio, con unidades de m³/s:

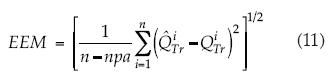
3. EREM es el error relativo estándar medio sin unidades:

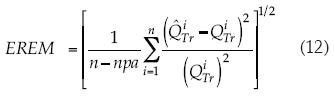
También se evaluarán tres índices de desempeño puntual, que son los errores relativos máximo (ERmáx), mínimo (ERmín) y mediano (ERmed). La expresión del error relativo es:

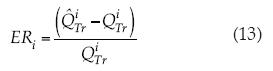
Cuando el ER resulta negativo indica que la estimación () resultó menor que la predicción observada o creciente de diseño calculada (, cuadro 2). Lógicamente, cuando ER es positivo ocurrió lo contrario.

Información hidrométrica procesada

En el cuadro 1 se citan las características generales de las 22 estaciones hidrométricas procesadas, cuyos datos de gasto máximo anual fueron obtenidos del sistema BANDAS (IMTA, 2002). Las estaciones están expuestas en orden decreciente de magnitud de cuenca. Los datos relativos a la estación San Francisco proceden del Boletín Hidrológico núm. 36 (SRH, 1970, 1975). Se observa que los registros anuales de tales estaciones fluctúan de 19 a 56 datos, con una media de 36 años. Las propiedades fisiográficas de área de cuenca (A) y longitud del cauce principal (Lcp) expuestas en el cuadro 1 proceden del Apéndice A de Escalante-Sandoval y Reyes-Chávez (2002). En la parte final del cuadro 1 se exponen otras cinco estaciones hidrométricas que serán empleadas en el contraste; sus registros no son confiables y se han integrado con base en el sistema BANDAS y los valores expuestos por Escalante-Sandoval y Reyes-Chávez (2002). En la figura 1 se muestran las cuencas de las 29 estaciones hidrométricas que serán utilizadas dentro de la Región Hidrológica Núm. 10 (Sinaloa).

Predicciones del gasto máximo anual (Q_Tr)

Los seis periodos de retorno que tendrán las crecientes de diseño que se estimarán con las ecuaciones empíricas por desarrollar son de 5, 10, 25, 50, 100 y 500 años. Estos intervalos de recurrencia cubren la mayoría de los que son empleados en los dimensionamientos y revisiones hidrológicas de las diversas obras hidráulicas. Se probó la calidad estadística de los 23 registros procesados, verificando que estuvieran exentos de componentes determinísticas, para buscar obtener predicciones confiables. En el cuadro 2 se exponen las predicciones del gasto máximo anual (Q_Tr), obtenidas con base en el ajuste de la distribución General de Valores Extremos (GVE), a través de los cuatro métodos siguientes (Campos-Aranda, 2001): momentos, sextiles, máxima verosimilitud y momentos L, adoptando los resultados del que condujo al menor error estándar de ajuste (Kite, 1977).

Predicciones de la lluvia máxima diaria (PMD_Tr)

Campos-Aranda (2008a) procesó los registros de precipitación máxima diaria anual de 67 estaciones pluviométricas de la Región Hidrológica Núm. 10 (Sinaloa) y expuso sus predicciones de periodos de retorno de 2, 5, 10 y 100 años. Como no existe correspondencia entre estos periodos de retorno y los seleccionados para las predicciones de gasto máximo anual, se decidió emplear la lluvia máxima diaria de 10 años en los tres primeros intervalos de recurrencia del gasto y la lluvia con frecuencia de 100 años en los siguientes tres (ecuaciones (8) y (9)). En cada una de las 29 cuencas de las estaciones hidrométricas que fueron empleadas se localizaron las estaciones pluviométricas procesadas y se buscó obtener su predicción promedio. Lógicamente, en las cuencas pequeñas sólo existe la estación pluviométrica ubicada en donde está la hidrométrica, es decir, a la salida de la cuenca, tal fue el caso de Bamícori, La Tina, Pericos y Choix. En otros casos se localizaron dos estaciones pluviométricas dentro de la cuenca, como en Badiraguato, Naranjo y Guamúchil. Por último, en las cuencas medianas y grandes se ubicaron tres o más estaciones pluviométricas. Los valores calculados para cada cuenca se tienen en las dos últimas columnas del cuadro 2.

Ecuaciones empíricas obtenidas por MCR

En los cuadros 3 y 4 se exponen los parámetros de ajuste obtenidos en el dominio logarítmico mediante MCR, para las ecuaciones (6) a (9) y cada uno de los seis periodos de retorno analizados; por ello, el primer indicador de desempeño es el coeficiente de determinación, indicado como log R². También en tales cuadros se citan los otros índices de desempeño promedio y puntual (ecuaciones (10) a (13)). Las predicciones observadas y estimadas, así como los errores relativos obtenidos en cada una de las 23 estaciones hidrométricas procesadas en los periodos de retorno extremos analizados, es decir, 5 y 500 años, se muestran en los cuadros 5 y 6.

Ecuaciones empíricas obtenidas por MCR con corrección por sesgo

Los resultados de la aplicación de la ecuación (5) para estimar el coeficiente b₀ corregido, es decir f₀, en las cuatro ecuaciones empíricas propuestas y para los seis periodos de retorno analizados, se muestran en los cuadros 7 y 8, en los cuales se ha suprimido log R², por ser igual al indicado en los cuadros 3 y 4. También se tienen en los cuadros 7 y 8 los indicadores de desempeño definidos en las ecuaciones (10) a (13). Nuevamente, las predicciones observadas y estimadas, así como los errores relativos obtenidos en cada una de las 23 estaciones hidrométricas procesadas en los periodos de retorno extremos analizados se muestran en los cuadros 9 y 10.

Ecuaciones empíricas obtenidas con optimización numérica

Desde el inicio de los años noventa (McCuen et al., 1990; GREHYS, 1996a) se ha sugerido emplear la optimización numérica para ajustar modelos de regresión potencial (ecuación (1)) en el dominio real y así evitar los inconvenientes de la transformación logarítmica. También desde tal fecha se ha sugerido utilizar como función objetivo (FO) minimizar la suma de los errores relativos al cuadrado por medio del algoritmo de múltiples variables no restringidas de Rosenbrock (Rosenbrock, 1960; Kuester y Mize, 1973; Campos-Aranda, 2003).

Con el propósito de tomar en cuenta el número de parámetros de ajuste (npa), el cual cambia en las ecuaciones (6) a (9) de dos a cuatro, se consideró conveniente emplear como FO el error relativo cuadrado medio (ERCM), cuya expresión es:

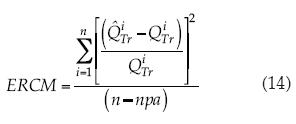
Las condiciones iniciales que se utilizaron para poner a funcionar el algoritmo de Rosenbrock fueron las dos siguientes de acuerdo con cada ecuación (6) a (9), cuya FO se estaba minimizando: (1) se empleó el b₀ y los respectivos b_i y (2) se cambió sólo al b₀ por f₀. En los cuadros 11 y 12 se tienen los nuevos valores de los coeficientes de ajuste, así como otras magnitudes asociadas con el funcionamiento del algoritmo de Rosenbrock, como son FO inicial y final, número de etapas y de evaluaciones de la FO. Cuando se trabajó con las ecuaciones (6) y (7), la mayoría de las veces los coeficientes de ajuste de MCR condujeron a la FO más baja (cuadro 11). En cambio, cuando procesan las ecuaciones (8) y (9), en la mitad de los casos la segunda condición de inicio es la que lleva a la menor FO (cuadro 12).

Análisis y selección de ecuaciones empíricas

La comparación del desempeño entre las ecuaciones (6) y (7) se tiene en el cuadro 3, e indica que en el dominio logarítmico, el coeficiente de determinación (R²) es escasamente superior en la ecuación (7). Los índices de desempeño DAM y EEM son también ligeramente mayores en la ecuación (7), quizás debido al mayor número de parámetros de ajuste. El índice adimensional EREM (ecuación (12)) indica que la ecuación (6) tiene mejor desempeño en los primeros tres periodos de retorno y en los siguientes tres la (7). Lo mismo se puede decir para la comparación entre las ecuaciones (8) y (9) del cuadro 4, pero la ecuación (8) sólo es recomendable en los dos primeros periodos de retorno, es decir, en 5 y 10 años. En los cuadros 3, 4, 7, 8, 11 y 12, los coeficientes de ajuste de las ecuaciones empíricas seleccionadas se muestran sombreados.

Respecto a la comparación mostrada en el cuadro 7 y de acuerdo con el índice de desempeño EREM, se concluye que la ecuación (6) con f₀ es mejor en los cuatro primeros periodos de retorno y la ecuación (7) en los dos últimos, es decir, en 100 y 500 años. Para la comparación del cuadro 8 y nuevamente con respecto al índice EREM, la ecuación (8) con f₀ resulta recomendable sólo en los dos primeros periodos de retorno y la ecuación (9) en el resto.

El algoritmo de Rosenbrock en todos los casos operó y minimizó la FO inicial (ecuación (14)) definida con base en los resultados del método de MCR o de MCR con corrección por sesgo, sus resultados (cuadros 11 y 12), es decir, las ecuaciones (6) a (9) ajustadas a cada uno de los seis periodos de retorno serán sometidas al mismo proceso de selección, en este caso adoptando la que condujo al mejor ERCM o menor FO. Para el cuadro 11, la ecuación (6) es la mejor en los tres primeros periodos de retorno y la ecuación (7), en los tres siguientes. Respecto al cuadro 12, la ecuación (8) es la más conveniente en los dos primeros periodos de retorno y la ecuación (9) en los cuatro siguientes, es decir, en 25, 50, 100 y 500 años de intervalo de recurrencia.

En el cuadro 13 se exponen las 36 ecuaciones empíricas obtenidas bajos los tres planteamientos seguidos de: (1) mínimos cuadrados de los residuos (MCR) en el dominio logarítmico, (2) MCR con corrección por sesgo y (3) optimización numérica de una función objetivo (FO = ERCM).

Contrastes numéricos de las 36 ecuaciones empíricas seleccionadas

Se realizaron dos contrastes numéricos. El primero en las seis estaciones hidrométricas indicadas al final de los cuadros 1 y 2, las cuales no fueron utilizadas en la deducción de las ecuaciones empíricas, porque sus registros no son confiables. Para el segundo contraste se emplearon las estaciones hidrométricas con registro más amplio de gasto máximo anual, mismo que varía de 45 a 56; se eliminó Huites por tener un área de cuenca que está fuera de las expectativas de aplicación de las ecuaciones empíricas dentro de la Región Hidrológica Núm. 10. Debido a que se han seleccionado seis ecuaciones empíricas para cada uno de los seis periodos de retorno procesados, se optó por obtener su valor mediano para definir la predicción estimada y contrastarla con la observada.

En el cuadro 14 se tienen los resultados del primer contraste. Respecto a las predicciones observadas en la estación Piaxtla, éstas se consideran sumamente elevadas, pues son superiores a las observadas en la estación Ixpalino, que tiene un área de cuenca mayor un 16%. Por lo anterior, las predicciones de las ecuaciones empíricas están más acordes con los valores probables. Lo contrario ocurre en la estación Urique II, cuyas predicciones observadas son en extremo bajas, como se comprueba al compararlas con las de Chinipas, cuenca vecina y adyacente, con un 27% más de área. Nuevamente, las predicciones de las ecuaciones empíricas se consideran más aproximadas a las crecientes probables.

En las estaciones Tecusiapa y Cazanate todas las predicciones de las ecuaciones empíricas están por debajo de las observadas, pero dentro del orden de magnitud. Lo contrario, pero mucho más acusado, ocurre en las dos últimas estaciones contrastadas: Los Molinos y Chico Ruiz. Para la primera ya se ha demostrado que su registro de gastos máximos anuales tiene valores que no están acordes con su tamaño de cuenca (Campos-Aranda, 2008b) y respecto a la segunda, la cuenca contigua de Pericos, que tiene un 31% menos de tamaño, reporta predicciones mayores, intuyendo que quizás en el registro corto de Chico Ruiz todavía no se han presentado los valores extremos grandes, pero sí los menores (1991 con 10 m³/s y 1999 con 17 m³/s). Respecto al cuadro 14, las predicciones estimadas con las ecuaciones empíricas son consideradas más apegadas a la realidad que las derivadas de sus registros, pues éstos no son confiables. Las aplicaciones numéricas del cuadro 14 ilustran los beneficios del método regional desarrollado.

En relación con los resultados del cuadro 15, se concluye de manera general una excelente aproximación entre las predicciones observadas y las estimadas, en los periodos de retorno menores de 100 años. Exclusivamente, en la estación Naranjo se tienen errores relativos por defecto mayores del 20% en los periodos de retorno mayores de 50 años. En el resto de las estaciones hidrométricas contrastadas, los errores relativos por exceso no son importantes, pues llegan a un máximo del 38% en Santa Cruz en el periodo de retorno de cinco años. En las estaciones Ixpalino y El Bledal se tienen los errores relativos más bajos en todas sus predicciones, en la primera por exceso y en la segunda por defecto, pero ambos menores del 8.5%.

 

Conclusiones

Se estableció encontrar sólo cuatro tipos de ecuaciones potenciales para las crecientes de diseño de periodos de retorno de 5, 10, 25, 50, 100 y 500 años, empleando como variables predictivas dos propiedades fisiográficas, el área de cuenca y la longitud del cauce principal, y una característica climática, la precipitación máxima diaria de periodo de retorno de 10 y 100 años. Sin embargo, sólo se seleccionan dos ecuaciones para cada intervalo de recurrencia: las de mejor desempeño estadístico. Al emplear tres procedimientos de obtención de los parámetros de ajuste, se obtiene un total de 36 ecuaciones empíricas, expuestas en el cuadro 13.

Los dos primeros métodos de ajuste, el de mínimos cuadrados de los residuos en el dominio logarítmico y su versión corregida por sesgo en el dominio real conducen a cuatro ecuaciones empíricas en cada periodo de retorno, que son únicas; por el contrario, el tercer procedimiento de ajuste, basado en optimización numérica (algoritmo de Rosenbrock) permite obtener muchas ecuaciones empíricas con sólo cambiar la función objetivo (FO) a minimizar. En este trabajo, únicamente se aplicó como FO el error relativo cuadrado medio.

Los dos contrastes realizados, el primero en seis estaciones hidrométricas no usadas en la deducción de las ecuaciones empíricas y, el segundo, en las seis estaciones de aforos con mayor registro, destacan la regularidad de las predicciones estimadas, cuyo valor mediano se considera una aproximación aceptable a los valores probables de las crecientes de diseño en cualquier sitio y su cuenca dentro de la Región Hidrológica Núm. 10 (Sinaloa) de México. Por lo anterior, el procedimiento seguido para obtener las ecuaciones potenciales que permiten estimar predicciones de gasto máximo anual o crecientes de diseño se sugiere aplicarlo o desarrollarlo en otras regiones o zonas geográficas para obtener tales herramientas de estimación hidrológica (ecuaciones empíricas), cuya aplicación es extraordinariamente simple.

 

Referencias

CAMPOS-ARANDA, D.F. Introducción a los métodos numéricos: software en Basic y aplicaciones en hidrología superficial. Capítulo 5, Ajuste de curvas, y capítulo 9: Optimización numérica. San Luis Potosí, México: Librería Universitaria Potosina, 2003, pp. 93-127 y 172-211.         [ Links ]

CAMPOS-ARANDA, D.F. Contraste de cinco métodos de ajuste de la distribución GVE en 31 registros históricos de eventos máximos anuales. Ingeniería Hidráulica en México. Vol. XVI, núm. 2, abril-junio de 2001, pp. 77-92.         [ Links ]

CAMPOS-ARANDA, D.F. Estudio de la precipitación máxima diaria anual en la Región Hidrológica No. 10 (Sinaloa), con base en Distancias Euclidianas. Investigaciones Geográficas. Núm. 65, abril-junio, 2008a, pp. 56-67.         [ Links ]

CAMPOS-ARANDA, D.F. Calibración del método Racional en ocho cuencas rurales menores de 1,650 km² de la Región Hidrológica No. 10 (Sinaloa), México. Agrociencia. Vol. 42, núm. 6, 2008b, pp. 615-627.         [ Links ]

CUNNANE, C. Methods and merits of regional flood frequency analysis. Journal of Hydrology. Vol. 100, 1988, pp. 269-290.         [ Links ]

ESCALANTE–SANDOVAL, C. Multivariate extreme value distributions with mixed Gumbel marginals. Journal of the American Water Resources Association, Vol. 34, No. 2, 1998, pp. 321-333.         [ Links ]

ESCALANTE-SANDOVAL, C. y REYES–CHÁVEZ, L. Técnicas Estadísticas en Hidrología. Capítulo 8: Análisis regional hidrológico y Apéndice A. México, D.F.: Facultad de Ingeniería de la UNAM, 2002, pp. 157-202 y 291-298.         [ Links ]

GREHYS (GROUPE DE RECHERCHE EN HYDROLOGIE STATISTIQUE). Presentation and review of some methods for regional flood frequency analysis. Journal of Hydrology. Vol. 186, 1996a, pp. 63-84.         [ Links ]

GREHYS (GROUPE DE RECHERCHE EN HYDROLOGIE STATISTIQUE). Inter-comparison of regional flood frequency procedures for Canadian rivers. Journal of Hydrology. Vol. 186, 1996b, pp. 85-103.         [ Links ]

GUTIÉRREZ-LÓPEZ, A., LEBEL, T. y DESCROIX, L. Reflexiones sobre el concepto de cuencas hidrológicamente homogéneas. Memorias del XXI Congreso Latinoamericano de Hidráulica, Sao Paulo, Brasil, 2004, 10 pp.         [ Links ]

IMTA. Banco Nacional de Datos de Aguas Superficiales (BANDAS). Ocho CD. Jiutepec, México: Comisión Nacional del Agua-Secretaría de Medio Ambiente y Recursos Naturales-Instituto Mexicano de Tecnología del Agua, 2002.         [ Links ]

KITE, G.W. Frequency and Risk Analyses in Hydrology. Chapter 12: Comparison of frequency distributions. Fort Collins, USA: Water Resources Publications, 1977, pp. 156-168.         [ Links ]

KUESTER, J.L. and MIZE, J.H. Optimization Techniques with Fortran. ROSENB algorithm. New York: McGraw Hill Book Co., 1973, pp. 320-330.         [ Links ]

McCUEN, R.H., LEAHY, R.B., and JOHNSON, P.A. Problems with logarithmic transformations in regression. Journal of Hydraulic Engineering. Vol. 116, No. 3, 1990, pp. 414-428.         [ Links ]

MONTGOMERY, D.C., PECK, E.A., y VINING, G.G. Introducción al Análisis de Regresión Lineal. Capítulo 10: Multicolinealidad. México, D.F.: Compañía Editorial Continental, 2002, pp. 291-342.         [ Links ]

PANDEY, G.R. and NGUYEN, V.T.V. A comparative study of regression based methods in regional flood frequency analysis. Journal of Hydrology. Vol. 225, 1999, pp. 92-101.         [ Links ]

ROSENBROCK, H.H. An automatic method of finding the greatest or least value of a function. Computer Journal. Vol. 3, 1960, pp. 175-184.         [ Links ]

SRH. Boletín Hidrológico No. 36. Tomos I y VI. Región Hidrológica No. 10 (Sinaloa). México, D.F.: Secretaría de Recursos Hidráulicos, Dirección de Hidrología, 1970 y 1975.         [ Links ]

TASKER, G.D., HODGE, S.A., and BARKS, C.S. Region of influence regression for estimating the 50-year flood at ungaged sites. Water Resources Bulletin. Vol. 32, No. 1, 1996, pp. 163-170.         [ Links ]