Introducción
Los productos forestales no maderables (PFNM) son de gran importancia como bienes y servicios, esencialmente en las comunidades rurales, pues tienen diferentes usos: alimenticio, cultural, medicinal e industrial; y, en general, son de alta demanda en el comercio extranjero (Chandrasekharan et al., 1996).
El área de distribución nativa de Litsea parvifolia (Hemsl.) Mez. (laurel) es el noreste de México, con siete especies reconocidas del género; habita en zonas húmedas, bosques de pino-encino y matorral semidesértico; se desarrolla en altitudes de 1 000 a 3 000 m, pero con distribución restringida en los estados de Coahuila, Nuevo León y Tamaulipas (Van Der Werff y Lorea, 1997; Jiménez-Pérez y Lorea-Hernández, 2009).
De acuerdo con la Comisión del “Código Alimentario” (CODEX Alimentarius) de la Organización de las Naciones Unidas para la Agricultura y la Alimentación (FAO) y la Norma Oficial Mexicana PROY-NOM-000-SCFI/SADER-2019, referente a Especias y Hierbas Culinarias o Aromáticas, las hojas secas del laurel, en forma entera, rota, quebrada o molida son de uso culinario por sus propiedades de sabor, aroma y aspecto visual, cuya función primaria es sazonar alimentos en forma fragante, aromática o pungente (CODEX, 2017).
Desde el punto de vista medicinal, se prepara en forma de infusión para aliviar problemas estomacales, como diarrea e indigestión; así como fiebre y el nerviosismo; además, el macerado en alcohol se usa para sanar el reumatismo. En algunos casos la planta se utiliza como ceremonial y ornamental (Jiménez-Pérez et al., 2011).
La biomasa es la cantidad de materia orgánica viva presente en tallos, hojas y corteza (biomasa aérea), así como en las raíces (biomasa subterránea) (Brown, 1997). En el ámbito forestal, la biomasa se emplea para conocer el contenido de carbono por unidad de superficie y de esta manera calcular la capacidad de fijación por los ecosistemas (Ordóñez et al., 2015).
Los modelos alométricos son herramientas para predecir componentes de biomasa de la planta (hojas, ramas, raíces, etcétera), a partir de una o más variables de fácil medición (diámetro, altura) y así, expresar su contenido medio a nivel género o especie (Avery y Burkhart, 1983; Picard et al., 2012; Gaillard et al., 2013). Una tabla de producción resume estos cálculos; sin embargo, su aplicación se restringue a regiones con características ecológicas similares a donde se elaboró (Ramos-Uvilla et al., 2014).
En las zonas áridas se han generado algunos modelos alométricos predictivos para la biomasa de árboles y arbustos como Prosopis glandulosa Torr. (Méndez et al., 2012), Acacia pennatula (Schltdl. & Cham.) Benth. (López-Merlín et al., 2003), Larrea tridentata (DC.) Coville (Ludwig et al., 1975), Atriplex canescens (Pursh) Nutt. var. canescens (Thomson et al., 1998), Lippia graveolens Kunth (Villavicencio et al., 2018); así como en especies productoras de fibra: Yucca carnerosana Trel. (Villavicencio y Franco, 1992), Agave lechuguilla Torr. (Berlanga et al., 1992; Velasco et al., 2009) y Nolina cespitifera Trel. (Sáenz y Castillo, 1992), incluso para predecir el peso del tallo o “piña”, en Dasylirion cedrosanum Trel. (Cano et al., 2006).
Dado que las hojas de L. parvifolia son uno de los componentes más aprovechados y comercializados en las zonas áridas, el objetivo del presente estudio fue determinar la o las variables dasométricas de la planta que están correlacionadas directamente con la biomasa foliar seca de la hoja, a partir de la selección del modelo alométrico que mejor se ajuste para predecir el peso de hoja seca y con base en él elaborar una tabla de producción que sirva para evaluar las poblaciones naturales de laurel existentes en el municipio Saltillo, Coahuila, México.
Materiales y Métodos
Área de estudio
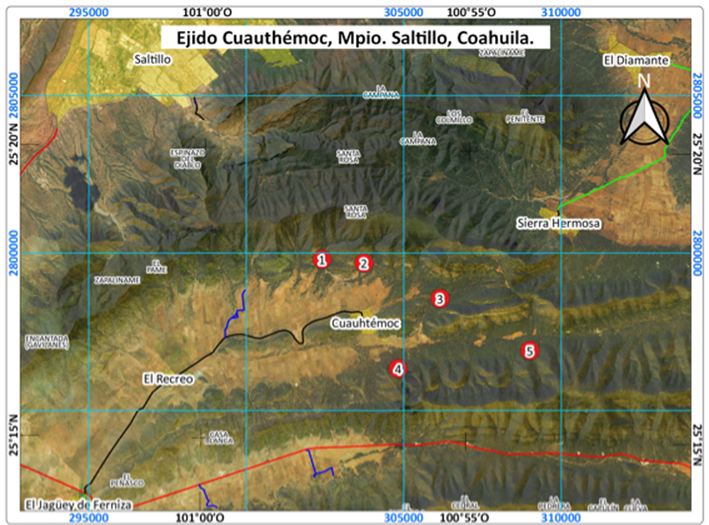
El estudio se realizó en el ejido Cuauhtémoc, Saltillo, Coahuila, ubicado en las coordenadas 25°17'3.61" N y 100°56'57.99" O (RAN, 2018) (Figura 1). El suelo es de tipo Leptosol (Inegi, 2006a); el clima corresponde al BS1kw (Semiárido, templado); la temperatura media anual fluctúa entre 12 y 18 °C y la precipitación de 500 a 800 mm (Inegi, 2006b; Inegi, 2007; Inegi, 2008). La vegetación está compuesta por bosque de coníferas, matorral rosetófilo, matorral submontano y pastizales (Profauna, 2008).
Diseño de muestreo y obtención de variables
Acorde a un muestreo dirigido, un total de 156 plantas de L. parvifolia fueron seleccionadas, considerando todas las categorías de altura y diámetro de copa. Las variables medidas fueron altura total desde el nivel del suelo (H, cm), diámetro mayor (DM) y menor de la copa (Dm), las cuales se hicieron con un flexómetro profesional Pretul® 21601. El diámetro promedio (Dp) de la cobertura foliar del arbusto se calculó en función de la medición de dos diámetros perpendiculares (DM y Dm) de cada arbusto, ambos expresados en centímetros (cm). Se aplicó un muestreo destructivo, en el que se cortaron los tallos y hojas de cada planta elegida. Las muestras e guardaron en bolsas de papel con su etiqueta correspondiente; posteriormente, se deshidrataron en el invernadero del Campo Experimental Saltillo del Centro de Investigación Regional Noreste del Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias, a temperatura ambiente durante cinco días; después, los tallos y las hojas secas se separaron. La biomasa foliar seca (Bfs) se determinó con una balanza analítica digital marca ADAM, con una precisión de 0.001 g. De esta manera la variable dependiente fue Bfs y las independientes H y Dp.
Análisis estadístico
Los datos de biomasa foliar seca y las variables altura y diámetro promedio se analizaron con el programa SAS (Statistical Análisis System) versión 9.4, mediante el procedimiento PROC MODEL (SAS, 2017), con regresión por Mínimos Cuadrados Ordinarios (MCO); se ajustaron nueve modelos alométricos, que previamente se han evaluado en estudios semejantes con orégano (Villavicencio et al., 2018), lechuguilla (Velasco et al., 2009), mezquite (Méndez et al., 2012) y acacias (López-Merlín et al., 2003) (Cuadro 1); estos modelos describen perfectamente la relación de variables dasométricas con la biomasa.
Cuadro 1 Modelos ajustados para predecir la biomasa foliar seca de Litsea parvifolia (Hemsl.) Mez. en el ejido Cuauhtémoc, Saltillo. Coahuila.
| Modelo | Nombre | Ecuación |
|---|---|---|
| 1 | Alométrico |
|
| 2 | Coeficiente mórfico constante |
|
| 3 | Australiano |
|
| 4 | Variable combinada lineal |
|
| 5 | Spurr |
|
| 6 | Schumacher-Hall |
|
| 7 | Potencia |
|
| 8 | Takata |
|
| 9 | Thornber |
|
Fuente: Segura y Andrade (2008); Picard et al. (2012).
Bfs = Biomasa foliar seca (g); Dp = Diámetro promedio de la copa (cm); H = Altura total (cm); Β 0 ..., β n = Coeficientes de regresión, Exp = Exponencial de la expresión.
Criterios de selección del modelo
Los parámetros estadísticos para la selección del mejor modelo fueron: valor
mayor en el coeficiente de determinación ajustado (
Donde:
EMP = Error medio porcentual
Y i = Valores observados
Y est =Valores estimados
DA = Diferencia agregada
Resultados y Discusión
En el área de estudio, L. parvifolia promedió 40.99 g de biomasa foliar seca por planta, con una variación de 1.80 a 246.32 g; y se evidenció que la variación morfológica y factores como la competencia determinaron su producción (Foroughbakhch et al., 2009), además es indicadora de la productividad del ecosistema forestal como lo refieren Huff et al. (2018) (Cuadro 2).
Cuadro 2 Estadística descriptiva de Litsea parvifolia (Hemsl.) Mez. en el ejido Cuauhtémoc, Saltillo, Coahuila.
| Variable | Promedio | Mínimo | Máximo | S | CV |
|---|---|---|---|---|---|
| H (cm) | 71.25 | 27.00 | 201.00 | 26.59 | 37.32 |
| Dp (cm) | 53.54 | 16.50 | 120.50 | 22.09 | 41.26 |
| Bfs (g) | 40.99 | 1.80 | 246.32 | 44.05 | 107.47 |
H = Altura total; Dp = Diámetro promedio de copa (DM + Dm) /2; Bfs = Biomasa foliar seca; S = Desviación estándar (g); CV = Coeficiente de variación (%).
Acorde a los resultados de los nueve modelos ajustados: siete tuvieron una R 2 aj. mayor a 0.70, lo cual indica que la variabilidad de biomasa foliar seca de L. parvifolia es explicable 70 % a partir del diámetro de copa promedio y la altura total de la planta. El S xy varió de 17.56 a 25.81 g y el CV fue de 42.84 a 62.96 % g (Cuadro 3). De acuerdo con los criterios de selección, el modelo de Schumacher-Hall (6) fue el que mejor estimó la biomasa foliar de L. parvifolia.
Cuadro 3 Coeficientes de regresión y estadísticos de bondad de ajuste de los modelos para predecir biomasa foliar seca de Litsea parvifolia (Hemsl.) Mez. en el ejido Cuauhtémoc, Saltillo, Coahuila.
| ModelO | Coeficiente | Estimado | Valor de P | R 2 aj | S xy | CV | SCR |
|---|---|---|---|---|---|---|---|
| 1 | β 0 | 0.0070 | 0.062 | 0.6568 | 25.81 | 62.96 | 93243.4 |
| β 1 | 1.0482 | <0.0001 | |||||
| 2 | β 1 | 0.0001 | <0.0001 | 0.6794 | 24.94 | 60.86 | 87731.7 |
| 3 | β 0 | -15.4778 | 0.0116 | 0.8391 | 17.67 | 43.11 | 43090.8 |
| β 1 | 0.0119 | <0.0001 | |||||
| β 2 | 0.1977 | 0.0206 | |||||
| β 3 | 0.0000 | 0.4754 | |||||
| 4 | β 0 | 11.6173 | <0.0001 | 0.7206 | 23.28 | 56.80 | 75898.5 |
| β 1 | 0.0001 | <0.0001 | |||||
| 5 | β 1 | 0.0039 | 0.0266 | 0.7754 | 20.95 | 51.11 | 61452.8 |
| β 2 | 0.7516 | <0.0001 | |||||
| 6 | β 0 | 0.0029 | 0.0174 | 0.8411 | 17.56 | 42.84 | 42853.1 |
| β 1 | 2.0836 | <0.0001 | |||||
| β 2 | 0.2512 | 0.0006 | |||||
| 7 | β 0 | 0.0043 | 0.0196 | 0.8275 | 18.29 | 44.63 | 46857.4 |
| β 1 | 2.2459 | <0.0001 | |||||
| 8 | β 0 | 3767.9430 | <0.0001 | 0.7163 | 23.46 | 57.24 | 77069.7 |
| β 1 | 44.1444 | <0.0001 | |||||
| 9 | β 0 | 0.000138 | <0.0001 | 0.7915 | 20.1176 | 49.08 | 56660.5 |
| β 1 | -0.704540 | <0.0001 |
R 2 aj = Coeficiente de determinación ajustado; S xy = Error estándar del modelo (g); CV = Coeficiente de variación (%); SCR = Suma cuadrada de los residuales.
El modelo Schumacher-Hall por su simplicidad y por su buen ajuste es de amplio uso para predecir el volumen, contenido de carbono (Cruz et al., 2016) y biomasa foliar en taxones arbustivos (Villavicencio et al., 2018). En modelos generados para especies aromáticas como orégano (Villavicencio et al., 2018) y tomillo (Belmonte y López, 2003), las variables altura y diámetro también son las mejores predictoras de la biomasa, como ocurrió con L. parvifolia.
El estadístico (d) de Durbin-Watson (2.03) con una
n de 142,
Cuadro 4 Factores de ponderación para el modelo de Schumacher-Hall, pruebas de homocedasticidad y de normalidad de los residuales.
|
|
Variable | Sxy |
|
|
Heteroscedasticidad | Normalidad | ||
|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|||||
|
|
|
17.75 | 0.8376 | 2.15 | 53.39 | <0.0001 | 0.96 | 0.0006 |
|
|
0.97 | |||||||
|
|
|
17.83 | 0.8361 | 2.25 | 55.45 | <0.0001 | 0.96 | 0.0002 |
|
|
0.98 | |||||||
|
|
|
18.82 | 0.8174 | 1.81 | 5.69 | 0.7702 | 0.95 | <0.0001 |
|
|
1.02 | |||||||
|
|
|
19.26 | 0.8089 | 1.95 | 14.81 | 0.0962 | 0.94 | <0.0001 |
|
|
1.02 | |||||||
|
|
|
17.63 | 0.8399 | 2.19 | 61.28 | <0.0001 | 0.96 | 0.0002 |
|
|
2.01 | |||||||
|
|
|
18.04 | 0.8324 | 2.19 | 40.90 | <0.0001 | 0.96 | 0.0008 |
|
|
0.23 | |||||||
|
|
|
18.42 | 0.8252 | 2.03 | 16.20 | 0.0629 | 0.97 | 0.0011 |
|
|
0.03 | |||||||
|
|
|
17.79 | 0.8368 | 2.22 | 54.88 | <0.0001 | 0.96 | 0.0004 |
|
|
0.98 | |||||||
|
|
|
19.23 | 0.8094 | 1.87 | 6.42 | 0.6977 | 0.94 | <0.0001 |
|
|
1.02 | |||||||
F. P. = Factor de ponderación; Dp = Diámetro promedio de cobertura foliar del arbusto; H = Altura total; c y k = Parámetros del modelo de varianza; Resid. = Residuales; Bfs = Biomasa foliar seca.
Regresión ponderada con estructura de varianza
Para corregir la heteroscedasticidad del modelo de
Schumacher-Hall se probaron varios factores de ponderación
de acuerdo con Álvarez-González (2007),
Gómez-García (2013) y Pedrosa et al., (2015);
para ello se emplearon las variables (Dp y H)
como factor de ponderación (

Figura 2 Biomasa foliar seca de Litsea parvifolia (Hemsl.) Mez. estimada sin ponderación (a) y con ponderación (b); residuales calculados sin ponderación (c) y con factor de ponderación (d).
Se observaron diferencias entre los valores predichos ponderados y sin ponderar, en términos absolutos (observados menos predichos). El primero sobreestima en 9.5 g; mientras que el segundo solo en 6.3 g, menos de 0.10 % de la biomasa foliar total. No obstante, el cumplimiento de los supuestos de los modelos de regresión (para el caso del modelo ponderado) es preferible, puesto que asegura que las predicciones sean eficientes. Dado que el modelo Schumacher-Hall corrige totalmente la heteroscedasticidad y es confiable estadísticamente (P < 0.0001), puede ser usado para predecir la producción de biomasa foliar seca de L. parvifolia.
Los estadísticos de bondad de ajuste corregidos fueron: R 2 aj . de 0.8252, error de estimación de 18.42 g (Cuadro 4) y significancia estadística en todos los parámetros (P ≤ 0.05). Estos resultados se ajustan a lo requerido por Picard et al. (2012) para la selección de un modelo; además, están dentro del intervalo citado por Návar et al. (2002) y Návar et al. (2004) para 18 especies arbustivas del matorral tamaulipeco, en donde se generaron modelos de predicción de biomasa foliar con una R 2 de 0.56 a 0.93, error entre 0.026 a 0.396 kg y C.V. de 14 a 81 %. Valores similares también se han documentado para taxones arbustivos de uso forrajero, leña y medicinal, en los que la R 2 varía de 0.45 a 0.99 (Foroughbakhch et al., 2005; Foroughbakhch et al., 2009). Huff et al. (2018) consignan una S xy de 33.2 a 441.9 g para arbustos. En la mayoría de los casos, el diámetro y cobertura fueron las variables independientes utilizadas para predecir la producción de biomasa foliar; en el presente estudio se corrigió la heteroscedasticidad con la inclusión de la variable altura.
Ante la falta de normalidad y presencia de heteroscedasticidad, como se presentó
en L. parvifolia, autores como Gómez-García (2013) realizaron una regresión ponderada con modelo de
varianza, a partir del diámetro, la altura (
Modelo para predecir biomasa foliar seca de Litsea parvifolia (Hemsl.) Mez.
Modelo Schumacher-Hall sin ponderación:
Modelo Schumacher-Hall corregido por factor de ponderación:
Los resultados evidenciaron una diferencia agregada (DA) de 0.06 g de error promedio en la estimación de la biomasa foliar seca por planta, con un error medio porcentual (EMP) de 0.16 %. De acuerdo con Prodan et al. (1997) una EMP menor a 1 % asegura la validez del modelo; por lo que el Modelo Schumacher-Hall es adecuado para el intervalo de valores observados, y cumple estadísticamente para predecir la biomasa foliar seca de L. parvifolia.
A partir de las variables seleccionadas en el modelo Schumacher-Hall se construyó una tabla de doble entrada, cuyo intervalo de operación es de 5 a 120 cm, para ambas variables independientes (H y Dp). Dentro de este existen intervalos cada 5 cm, en los que es factible predecir la biomasa foliar seca (Bfs) (g) de plantas en pie de L. parvifolia (Cuadro 5). Dicha tabla de predicción facilita la cuantificación en el campo y es de fácil uso.
Cuadro 5 Biomasa foliar seca (g) Litsea parvifolia (Hemsl.) Mez. para rodales naturales del ejido Cuauhtémoc, municipio Saltillo, Coahuila, México.
| Diámetro (cm) | Altura (cm) | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 | 105 | 110 | 115 | 120 | |
| 5 | 0.1 | 0.1 | 0.1 | 0.2 | 0.2 | |||||||||||||||||||
| 10 | 0.3 | 0.5 | 0.5 | 0.6 | 0.7 | 0.8 | ||||||||||||||||||
| 15 | 0.7 | 1.0 | 1.2 | 1.4 | 1.6 | 1.7 | ||||||||||||||||||
| 20 | 2.2 | 2.5 | 2.8 | 3.1 | 3.3 | 3.5 | ||||||||||||||||||
| 25 | 3.9 | 4.4 | 4.8 | 5.2 | 5.5 | 5.9 | ||||||||||||||||||
| 30 | 6.3 | 6.9 | 7.5 | 8.0 | 8.4 | 8.9 | 9.3 | 9.7 | 10.1 | |||||||||||||||
| 35 | 9.4 | 10.1 | 10.8 | 11.5 | 12.1 | 12.7 | 13.2 | 13.8 | 14.3 | 14.8 | 15.2 | |||||||||||||
| 40 | 12.3 | 13.2 | 14.1 | 15.0 | 15.8 | 16.5 | 17.3 | 17.9 | 18.6 | 19.3 | 19.9 | 20.5 | 21.1 | |||||||||||
| 45 | 15.5 | 16.7 | 17.9 | 18.9 | 19.9 | 20.9 | 21.8 | 22.7 | 23.5 | 24.4 | 25.1 | 25.9 | 26.6 | 27.4 | 28.1 | |||||||||
| 50 | 20.6 | 22.1 | 23.4 | 24.6 | 25.8 | 26.9 | 28.0 | 29.0 | 30.1 | 31.0 | 32.0 | 32.9 | 33.8 | 34.6 | 35.5 | 36.3 | 37.1 | 37.9 | ||||||
| 55 | 25.0 | 26.7 | 28.3 | 29.8 | 31.2 | 32.6 | 33.9 | 35.1 | 36.3 | 37.5 | 38.7 | 39.8 | 40.8 | 41.9 | 42.9 | 43.9 | 44.9 | 45.8 | ||||||
| 60 | 31.7 | 33.6 | 35.4 | 37.1 | 38.7 | 40.3 | 41.8 | 43.2 | 44.6 | 46.0 | 47.3 | 48.6 | 49.8 | 51.0 | 52.2 | 53.3 | 54.5 | |||||||
| 65 | 39.4 | 41.5 | 43.5 | 45.4 | 47.3 | 49.0 | 50.7 | 52.3 | 53.9 | 55.5 | 57.0 | 58.4 | 59.8 | 61.2 | 62.6 | 63.9 | ||||||||
| 70 | 45.7 | 48.1 | 50.5 | 52.7 | 54.8 | 56.8 | 58.8 | 60.7 | 62.5 | 64.3 | 66.0 | 67.7 | 69.4 | 71.0 | 72.5 | 74.1 | ||||||||
| 75 | 52.4 | 55.2 | 57.9 | 60.4 | 62.9 | 65.2 | 67.4 | 69.6 | 71.7 | 73.8 | 75.8 | 77.7 | 79.6 | 81.4 | 83.2 | 85.0 | ||||||||
| 80 | 59.7 | 62.8 | 65.8 | 68.7 | 71.5 | 74.1 | 76.7 | 79.2 | 81.6 | 83.9 | 86.2 | 88.4 | 90.5 | 92.6 | 94.7 | 96.7 | ||||||||
| 85 | 70.9 | 74.3 | 77.6 | 80.7 | 83.7 | 86.6 | 89.4 | 92.1 | 94.7 | 97.2 | 99.7 | 102.2 | 104.5 | 106.8 | 109.1 | |||||||||
| 90 | 83.3 | 86.9 | 90.4 | 93.8 | 97.0 | 100.1 | 103.2 | 106.1 | 109.0 | 111.8 | 114.5 | 117.1 | 119.7 | 122.3 | ||||||||||
| 95 | 96.8 | 100.7 | 104.4 | 108.1 | 111.5 | 114.9 | 118.2 | 121.4 | 124.5 | 127.5 | 130.5 | 133.4 | 136.2 | |||||||||||
| 100 | 115.7 | 119.7 | 123.6 | 127.3 | 130.9 | 134.5 | 137.9 | 141.3 | 144.5 | 147.7 | 150.9 | |||||||||||||
| 105 | 136.2 | 140.3 | 144.3 | 148.2 | 152.0 | 155.7 | 159.3 | 162.8 | 166.3 | |||||||||||||||
| 110 | 153.9 | 158.3 | 162.6 | 166.8 | 170.8 | 174.8 | 178.6 | 182.4 | ||||||||||||||||
| 115 | 177.7 | 182.2 | 186.6 | 191.0 | 195.2 | 199.3 | ||||||||||||||||||
| 120 | 198.4 | 203.2 | 207.9 | 212.5 | 217.0 | |||||||||||||||||||
Conclusiones
El modelo de Schumacher-Hall es el que mejor predice la biomasa foliar seca de los arbustos en pie de Litsea parvifolia (Hemsl.) Mez., a partir mediciones sencillas de variables como el diámetro promedio de la copa y altura total del arbusto. La tabla de predicción de doble entrada generada es aplicable en zonas que posean plantas de esta especie con estructuras de diámetro, altura y condiciones climáticas similares a las observadas en este estudio.











 text in
text in