Introducción
La Moringa oleifera es la especie más ampliamente cultivada del género moringa, siendo la única del género de la familia Moringaceae según Quattrocchi (2000) es considerado uno de los árboles más útiles del mundo, se puede utilizar como alimento o para aplicaciones medicinales por ser una importante fuente de caroteno, vitamina C, proteínas, hierro, potasio, calcio y fósforo. De acuerdo con Olson (2011) dicha planta comúnmente se seca, se tritura y se almacenan sin refrigeración durante meses sin pérdida de valores nutricionales. Con un valor nutritivo tan poderoso, estas hojas podrían evitar el azote de desnutrición y otras enfermedades relacionadas (Mathur, 2005). Por los beneficios que ofrece la moringa, resulta importante su conservación postcosecha mediante el secado, lo cual le permite ser comercializada en lugares donde no se cultivan.
El secado es una de las técnicas más antiguamente utilizadas para la conservación de alimentos desde los principios de la humanidad ya que proporciona la posibilidad de subsistencia en épocas de carencia Fito et al. (2001). Aunque el secado natural es el más económico, presenta algunas limitaciones. En condiciones normales tarda de dos a tres días; sin embargo, en épocas de baja radiación solar y de lluvias el tiempo de secado se prolonga a 5 días o más, además el producto puede ser afectado negativamente por agentes biológicos. Debido fundamentalmente a estas desventajas es recomendable considerar el empleo de secadores solares.
De acuerdo con Heldman y Lund (2007) el secado se define como la remoción de humedad debido a la transferencia simultánea de calor y masa. Asimismo, Sharma et al., (2003) señalan que la cinética de secado de alimentos es un complejo fenómeno y requiere modelos fiables para predecir dicho proceso. Según Andrade et al. (2003) estos modelos son herramientas útiles para estimar el tiempo necesario para reducir el contenido de agua del producto en diferentes condiciones y la temperatura idónea, mejorando así la eficiencia del proceso. Midilli et al. (2002) describen diversos modelos matemáticos para la cinética de secado de productos agrícolas. Hasta ahora, no se han realizado estudios de cinética de secado de Moringa oleifera, es por ello que esta investigación se enfoca al estudio de la cinética de secado de dicha planta.
Materiales y métodos
Las hojas de Moringa oleifera se obtuvieron de plantíos de un rancho hidropónico ubicado en la ciudad de Chiapa de Corzo, Chiapas, el cual se comercializan capsulas de moringa seca, sometiendo a dicha planta a un proceso de secado tradicional o natural.
Después se trasladó la planta a los laboratorios del Centro de Investigación y Desarrollo Tecnológico en Energías Renovables (CIDTER) de la Universidad de Ciencias y Artes de Chiapas (UNICACH), se procedió a realizar una selección microbiológica de las hojas, lavarlas, removerle el exceso de agua y finalmente someterlas al proceso de deshoje. Se elaboraron charolas de papel aluminio, taradas en una balanza analítica marca Velab, modelo VE-24, en ella también se pesaron las hojas de moringa obteniéndose muestras entre 9 y 10 gramos aproximadamente, que fueron colocadas en las charolas.
Equipo de secado
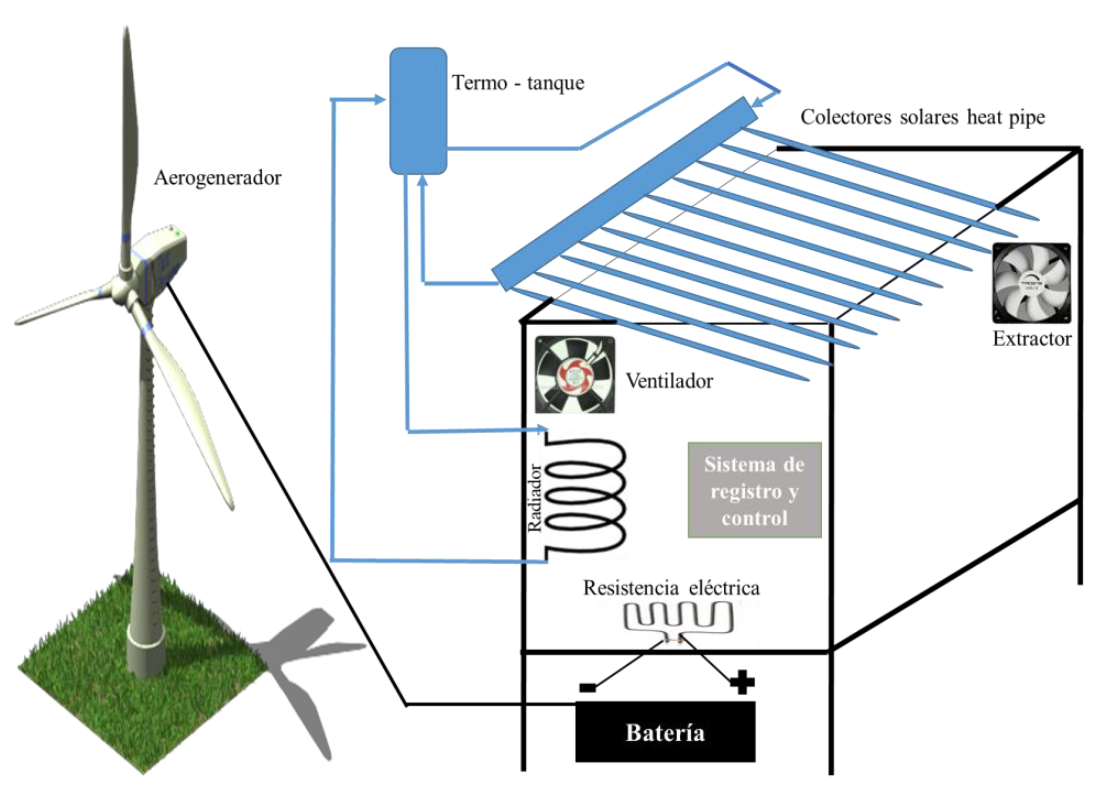
El proceso de secado se realizó en un secador solar híbrido (Figura 1), que tiene la particularidad de mantener la temperatura de la cámara constante. Presenta para ello un sistema de calentamiento de agua constituido de dos colectores solares heat pipe, un termo- tanque, un intercambiador de calor colocado en el interior de la cámara de secado y una bomba que recircula el agua entre el termo-tanque y el intercambiador de calor. Además, cuenta con un generador eólico de respaldo para recargar un banco de baterías que se descargas a través de resistencias eléctricas colocadas en la cámara. También la cámara tiene un ventilador para la recirculación de aire y un extractor de aire para remover el aire húmedo desde dentro de la cámara hacia el ambiente.
Proceso de secado
El secador cuenta además con un sistema de registro y control de datos donde se monitorean y registran en una tarjeta SD los valores de temperatura y humedad del aire en la cámara y la temperatura del agua del termo-tanque. Los experimentos del secado de las hojas de moringa se realizaron a 40 °C, 50 °C y 60 °C. Para determinar la humedad inicial de la muestra de moringa, se empleó una termo-balanza marca Velab, modelo VE-50-5.
Se prepararon cuatro muestras de Moringa oleifera para cada experimento. Dichas muestras se colocaron dentro de la cámara de secado (previamente calentada a temperatura de estudio constante). Durante el secado se registraron las variaciones de la masa de la moringa cada 30 min hasta que esta fuera mínima o nula.
Determinación de humedad y velocidad de secado
Para la obtención de las curvas de secado y de velocidad de secado se utilizó el método de Geankoplis (1983), determinándose el contenido de humedad en base seca en cada instante (
Donde:
Con el por ciento de humedad de equilibrio del producto (
En relación con lo anterior, se calculó la velocidad de secado mediante la ecuación (3), donde:
Modelación matemática de las curvas de secado
Para el modelado de la cinética de la Moringa oleifera se ajustaron modelos matemáticos a los datos experimentales, siendo los de Newton, Page, Henderson y Verma (Cuadro 1) los seleccionados ya que son los que más caracterizan la cinética de secado de plantas nutrimentales y medicinales (Corrêa et al., 2007).
Cuadro 1 Lista de modelos utilizados y sus referencias.
| Nombre del modelo | Modelo | Referencia |
|---|---|---|
| Newton | Xa(t)=exp(-kt) | Mujumdar (1987) |
| Page | Xb(t)=exp(-ktn) | Diamante and Munro (1993) |
| Henderson | Xc(t)=a exp(-ktn) | Henderson and Pabis (1961) |
| Verma | Xe(t)=a exp(-kt)+(1-a) exp(-gt) | Verma et al. (1985) |
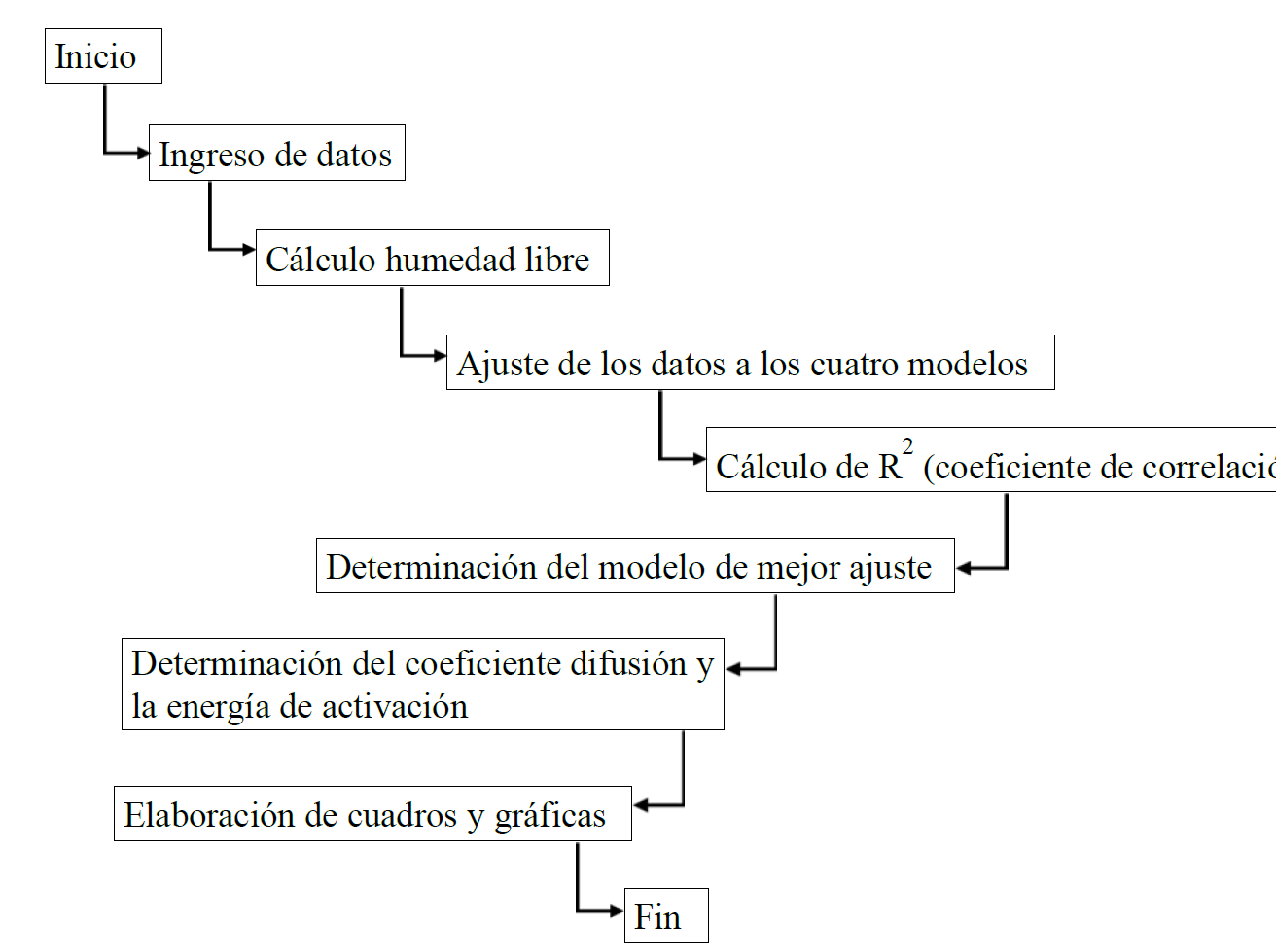
Mediante un programa elaborado en Matlab, cuyo funcionamiento se describe en la Figura 2, permitió encontrar el modelo que mejor describe el comportamiento de su cinética de secado, utilizando el coeficiente de correlación (R2) como principal criterio para seleccionar el de mejor ajuste.
Determinación del coeficiente de difusión (Def)
El coeficiente de difusión (Def)es una difusividad efectiva cuyo valor es calculado a través del modelo matemático ajustando los valores experimentales. Puede entenderse como la facilidad con que el agua es removida del material, esta varia conforme cambia las condiciones de secado (temperatura y velocidad del aire), no es intrínseca al material (Giraldo y Arévalo, 2010). Los valores del coeficiente de difusión se obtuvieron a través de la correlación logarítmica de los datos experimentales (
Para el cálculo de la difusividad efectiva se usó la ecuación de Fick para geometría laminar en una dirección.
Donde:
Según Da Rocha et al., 2012 la solución de la ecuación de Fick para la geometría de a moringa (lamina) y utilizándose ocho termos de serie es.
Se supuso que el primer término de la sumatoria es el único que tiene significación, así que para n=0, la ecuación resultante queda así:
Mediante la regresión lineal, se obtienen los valores de los parámetros asociados con la mejor curva de ajuste, para los datos experimentales de humedad libre
Mediante una transformación lineal, aplicando logaritmos neperianos se obtiene una ecuación lineal:
Por analogía a la ecuación de una recta
Energía de activación
La energía de activación representa la energía requerida para iniciar la difusión de la humedad durante el secado y da un indicio de la influencia de la temperatura en el proceso, la cual puede describirse por la ecuación (10) de Arrhenius.
En la que
Mediante la regresión exponencial se obtiene la energía de activación como sigue.
Por analogía a la ecuación de la recta
Donde:
Evaluación sensorial descriptiva de la moringa
Por ser este un producto nuevo se evaluó el nivel de preferencia y aceptabilidad usando este método por ser fácil y rápido de procesar y analizar. Para lo cual se encuentran a 50 individuos para establecer no solo la diferencia entre muestras sino la magnitud de la misma. Estas encuestas permitieron determinar el nivel de aceptabilidad en sabor, textura, olor y color de las muestras. (Liria, 2007). Todo esto en colaboración con la Escuela de Nutrición de la UNICACH.
Resultados y discusión
La Moringa oleifera presentó una humedad inicial de 70.3%. En el Cuadro 2 se presenta el tiempo de secado y la humedad libre para las temperaturas de estudio. Estos resultados coinciden con la relación entre temperaturas elevadas y menores tiempos de secado.
Cuadro 2 Tiempo de secado y humedad libre de la moringa para las tres temperaturas.
| Temperatura de secado (oC) |
Tiempo de secado (h) | Humedad de libre (kg de agua/kg de solido seco) |
|---|---|---|
| 40 | 6:30 | 0.13 |
| 50 | 4:00 | 0.02 |
| 60 | 2:15 | 0.12 |
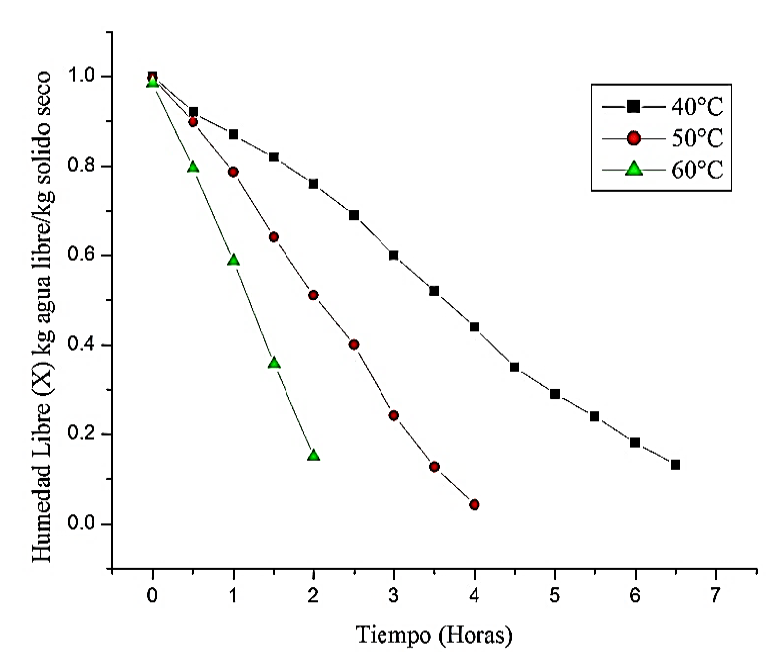
En las Figura 3 y 4 se muestran las curvas de variación del por ciento de humedad y de velocidad de secado para las tres temperaturas de estudio respecto al tiempo.
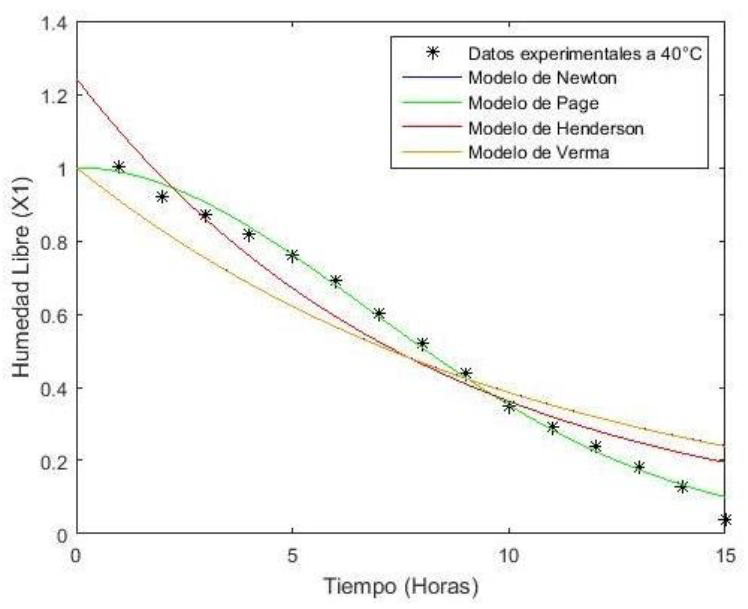
Como resultado del modelado de los datos experimentales, en el Cuadro 3 se presentan los coeficientes obtenidos de cada uno de los modelos empleados, así como el coeficiente de correlación. Como se observa el modelo que más se ajustó a los datos experimentales fue el modelo Page con un coeficiente de correlación promedio para las tres temperaturas de R2 = 0.9957, esto queda comprobado en las gráficas descritas en las Figuras 5, 6 y 7, seguido por el modelo de Verma, Henderson y Newton en ese orden. Por tanto, se usará el modelo Page para la determinación del coeficiente de difusión y la energía de activación.
Cuadro 3 Coeficientes por modelos matemáticos de acuerdo a los datos experimentales.
| Modelo y ecuación | 40 °C | 50 °C | 60 °C | |||||
|---|---|---|---|---|---|---|---|---|
| Coeficientes | R2 | Coeficientes | R2 | Coeficientes | R2 | |||
| Newton | k= 0.0952 | 0.8704 | k= 0.1561 | 0.8234 | k= 0.2147 | 0.7798 | ||
| Page | k= 0.01201 n= 1.94 | 0.9946 | k= 0.01911 n= 0.03818 | 0.995 | k= 0.03818 n= 2.399 | 0.9439 | ||
| Henderson | k= 0.1235 a= 1.244 | 0.9385 | k= 0.2227 a= 1.369 | 0.9337 | k= 0.3445 a= 1.45 | 0.9439 | ||
| Verma | k= 0.244 a= -36.47 g= 0.2362 | 0.9819 | k= 0.4186 a= -49.15 g= 0.4075 | 0.9779 | k= 0.6805 a= -14.28 g= 0.6174 | 0.7798 | ||
Como se puede observar en el Cuadro 4, existe una similitud entre los valores del coeficiente de difusión calculados a partir del modelo de Page y los obtenidos del mediante la correlación logarítmica de las temperaturas de 40, 50 y 60 °C. Se puede notar que para mayores temperaturas del secado mayor son las velocidades; de esta manera, el aumento de la temperatura favoreció la transferencia de masa y como consecuencia el aumento del coeficiente de difusión.
Cuadro 4 Coeficientes de difusión (Def) obtenidos para el Ln(X)y por el modelo de Page.
| Temperatura (°C) | (Def) | |
|---|---|---|
| Ln (X) | Page | |
| 40 | 9.68678E-08 | 9.8894E-08 |
| 50 | 1.5008E-07 | 1.6966E-07 |
| 60 | 2.69933E-07 | 2.7581E-07 |
Para la energía de activación para el modelo Page es muy similar a los datos experimentales por lo que se refirma que esté es el model/o de mejor ajuste (Cuadro 5).
Cuadro 5 Energía de Activación para el modelo de Page y la correlación logarítmica.
| Modelo | Pendiente (B) | Intercepto(A) | Do = exp (A) | Ea= -B*(kJ mol-1) |
|---|---|---|---|---|
| Correlación o Ln(X) | -5.33607 | 0.86084 | 2.365146583 | 44.36408598 |
| Page | -5.35133 | 0.96307 | 2.619726702 | 44.49095762 |
La energía necesaria para iniciar el proceso de secado de moringa se encuentra en el rango desde 44.36 a 44.49 kJ mol-1. Una energía de activación alta corresponde a una velocidad de reacción muy sensible a la temperatura (la representación de Arrhenius tiene una pendiente grande) y al revés, una energía de activación pequeña corresponde a una velocidad de reacción relativamente insensible a cambios de temperatura (Figura 8).
En el Cuadro 6 se muestra una comparación del coeficiente de difusión obtenidos en este experimento con moringa con los reportados en estudios de plantas similares.
Cuadro 6 Comparación del coeficiente de difusión y energía de activación para varios productos.
| Menta (Mentha crispa L.) Park et al. (2002) | Epazote (Dysphania ambrosioides) Kane et al. (2008) | Tomillo (Thymus) Da Rocha et al. (2012) | Moringa | ||||
|---|---|---|---|---|---|---|---|
| Temp | Def (m2 s-1) | Temp | Def (m2 s-1) | Temp | Def (m2 s-1) | Temp | Def (m2 s-1) |
| 40 °C | 9.281E-13 - 1.125E-12 |
- | - | 40°C | 7.760E-12 | 40 °C | 4.8677E-08 |
| 50 °C | 2.261E-12 - 2.295E-12 |
50 °C | 3.7116E-09 - 4.598E-09 |
50°C | 2.089E-11 | 50 °C | 7.7453E-07 |
| - | - | 60 °C | 5.4772E-09 - 1.044E-0 |
60°C | 5.626E-11 | 60 °C | 1.5474E-07 |
Evaluación sensitiva
Para la evaluación organoléptica se numeraron las muestras como sigue: 1, secada a 40 °C; 2, secada a 50 °C; 3, secada a 60 °C y 4, producto comercial del Rancho de Chiapas de Corzo que se seca tradicionalmente; los resultados de dicha evaluación se muestran en el Cuadro 7. El novel de agrado se evaluó integralmente, ósea los sentidos evaluados se resumen en aguardo o desagrado con dos términos intermedios como se muestra en el Cuadro 7.
Conclusiones
Se puede concluir que tanto en la cinética de secado como en la evaluación organoléptica, la temperatura óptima de secado para la Moringa oleifera es a 60 °C, presentando un tiempo de secado de dos horas, siendo el modelo de Page el que mejor describe el proceso; con un coeficiente de difusión de 1.54745E-08 y una energía de activación (











 text in
text in