Introducción
El desarrollo de las boquillas está ligado al surgimiento de los primeros transformadores en 1890. Eran de tipo sólidas, diseñadas con un conductor central rodeado por un aislante. Fueron muy exitosas porque su construcción era muy simple, pero al aumentar cada vez más la demanda energética se volvió impráctico su uso, por encima de los 34.5 kV, ya que a mayores niveles de tensión se requería incrementar las dimensiones radiales de la boquilla, lo que hacía al dispositivo demasiado grande y pesado.
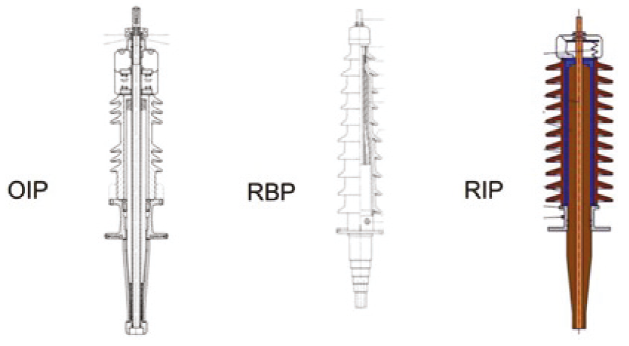
A partir de 1908 la compañía americana Westinghouse comienza a desarrollar las primeras boquillas con capacitancia, al mismo tiempo la compañía sueca ASEA, (Allmänna Svenska Elektriska Aktiebolaget, cuya traducción al español es: Compañía Eléctrica General Sueca), produce las primeras boquillas tipo capacitivas. Después de la Segunda Guerra Mundial, ocurre un aumento considerable de energía eléctrica y para satisfacer estas demandas se necesitó de boquillas capaces de operar a mayor tensión. Hasta esa fecha se utilizaba la tecnología de papel aglomerado con resina (RBP) que operaba hasta 69 kV, pero esta no pudo aplicarse con éxito para niveles más altos, entonces surge la tecnología constructiva de papel impregnado en aceite (OIP), la cual soportaba niveles de 170 kV. Sobre el año 1950 se desarrollaron las boquillas condensadoras, que se construían con la tecnología de papel impregnado en resina (RIP), esta podía soportar niveles hasta de 765 kV (Ellis, 2011).
La Figura 1 muestra las diferentes tecnologías de construcción de boquillas (Ellis, 2011).
A finales de la década del 1950, comienza en Estados Unidos la campaña antimonopolios y se vivieron escándalos en la fijación de los precios, lo que obligó a los productores de componentes eléctricos a reducir los costos en todos sus productos, esto trajo como consecuencia un aumento en la tasa de fallas de estos y se redujo también la calidad y confiabilidad de todos los dispositivos. La compañía fabricante suiza, Haefely, en el año 1991, diseña la primera norma de la IEEE para la construcción de boquillas, su tecnología creció constantemente y se introdujo en los mercados de boquillas de Estados Unidos y Canadá (Ellis, 2011).
Este proceso de desarrollo continuo es la base de las diferentes tecnologías de boquillas que se conocen y se utilizan en la actualidad, que hacen del dispositivo un elemento indispensable para el correcto funcionamiento de los transformadores.
Este trabajo se estructura de la siguiente manera: en la sección 2 se describen los diferentes tipos de boquillas existentes y su clasificación; en la sección 3 se hace una descripción del modelado de la boquilla en estudio; en la sección 4 se analizan las ecuaciones que se resuelven para el cálculo del campo eléctrico, además se brinda información sobre la utilización del software COMSOL Multiphysics®; en la sección 5 se muestran las simulaciones y gráficos obtenidos, así como la comparación del modelado en 3D y axisimétrico-2D; y en la sección 6 se presentan las conclusiones sobre el estudio realizado.
Clasificación de las boquillas
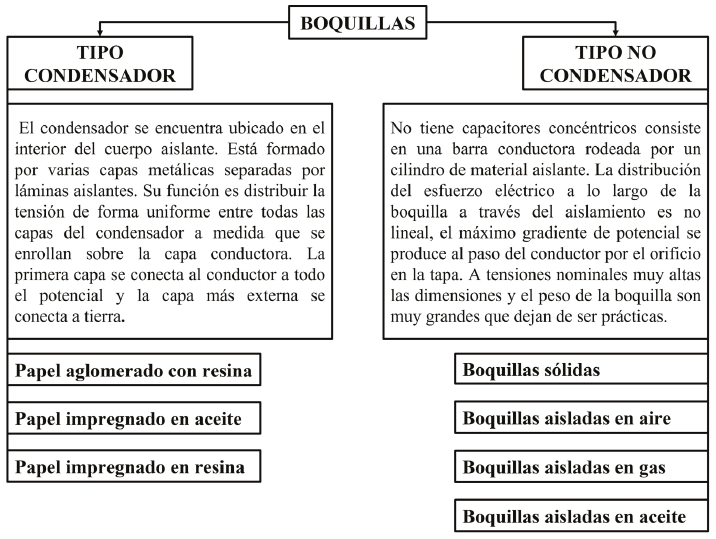
La Figura 2 muestra la clasificación de las boquillas según su tipo (Ellis, 2011), (CFE, 2006).
Los diferentes tipos de boquillas tienen las siguientes características (Ellis, 2011):
Papel aglomerado con resina. El papel utilizado para la construcción de esta boquilla se recubre primero con resina fenólica o epóxica, después se enrolla en forma cilíndrica con calor y presión, insertando las capas en intervalos apropiados. Debido a esta configuración, el dispositivo va a contener una gran cantidad de aire que se distribuye entre las fibras del papel y en los bordes de la capa atenuada. Su uso se ha limitado a baja tensión, principalmente en interruptores, ya que, al aumentar los niveles de tensión, aumenta considerablemente el ancho del papel utilizado en su construcción y el peligro de inestabilidad térmica del aislamiento debido a las pérdidas del material.
Papel impregnado en aceite. El papel utilizado para la construcción de esta boquilla debe ser lo suficientemente poroso para permitir la impregnación eficiente con aceite mineral y así mantener la rigidez dieléctrica adecuada, la cual se logra mediante un proceso de secado al vacío que asegura baja humedad y bajo contenido de gas. Se utilizan hasta los niveles de tensión más altos, debido a su construcción y su bajo punto de congelación se pueden utilizar instalaciones a baja temperatura.
Papel impregnado en resina. El papel utilizado para la construcción de esta boquilla se seca a una temperatura estrictamente controlada y se le realiza una impregnación al vacío con resina epóxica y tratamiento de curado, donde se controla la contracción del material para evitar la producción de grietas debido a esfuerzos mecánicos internos, esto asegura bajas pérdidas dieléctricas.
Boquillas sólidas. En su construcción interna solo presentan el conductor central y el envolvente de porcelana o polímero. Su utilización se limita para niveles nominales de voltaje menores de 34.5 kV en transformadores y generadores de potencia. No necesitan graduación de campo eléctrico debido a los gradientes eléctricos reducidos con los que trabaja.
Boquillas aisladas en aire. Son de tipo sólido en su construcción, pero utilizan aire a presión atmosférica entre el aislante y la barra conductora. Se utilizan solamente en equipos aislados en aire, donde uno de los extremos de la boquilla se encuentra expuesto a las condiciones medioambientales y el otro no, se tiene en cuenta una distancia de fuga considerable en el extremo externo, para que soporte la contaminación y las lluvias.
Boquillas aisladas en gas. En su construcción utilizan gas presurizado como aislante entre la barra conductora y aislante principal. Utilizan una pantalla aterrada que funciona como mecanismo de control de los campos eléctricos y no tienen graduación capacitiva. En algunos casos se construyen con un núcleo hecho de una película plástica compatible con el gas Hexafluoruro de Azufre SF6, lo que le da al núcleo del dispositivo propiedades capacitivas. Su uso generalmente es en subestaciones aisladas completamente en SF6.
Boquillas aisladas en aceite. Son de tipo sólido en su construcción, pero en su interior poseen un ducto de aceite que funciona como material aislante y refrigerante, que separa la barra central conductora del aislamiento principal. Son generalmente las que más se utilizan, con mayores aplicaciones en transformadores de potencia, a tensiones nominales no mayores de los 34.5 kV.
Descripción del modelado de la boquilla
Para realizar un correcto análisis es necesario que el modelado de las boquillas en el software COMSOL Multiphysics® sea lo más cercano posible a la realidad, por lo que las características tanto eléctricas como estructurales son de gran importancia para obtener buenos resultados y predecir con exactitud el comportamiento del dispositivo (Madrid et al., 2013).
La boquilla que analizar es de tipo sólido y en su construcción interna tiene un tubo de mylar que divide un ducto de aceite permitiendo la circulación de este y que funciona como material aislante. Esta se ubica en el lado de baja tensión del transformador a 34.5 kV (H-J, ENTERPRISES); su función es proteger el conductor que va del devanado del transformador a la línea de transmisión y permitir su conexión eléctrica de forma segura (CFE, 2007). El transformador donde está ubicada la boquilla entrega una potencia de 30 MVA, con voltajes de 115/34.5 kV.
Se construyó la boquilla mediante la utilización de un plano proporcionado por la empresa H-J, donde se desglosan los materiales usados en su construcción, además se colocó una estructura que simula el tanque del transformador y otros elementos que están cerca de la parte sumergida en aceite de la boquilla (H-J, ENTERPRISES). La Figura 3 muestra los elementos que conforman la boquilla:
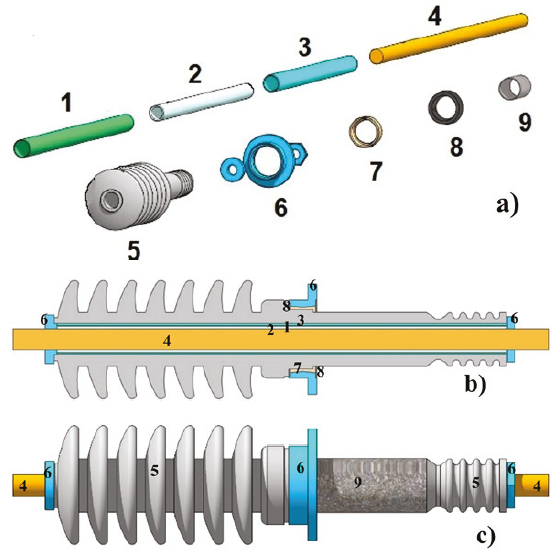
Figura 3 Boquilla H-J: a) Elementos que conforman la boquilla en estudio, b) Corte transversal, c) Vista exterior
Especificaciones geométricas y propiedades físicas
Esta boquilla tiene una longitud de 41.38 pulgadas, el cuerpo de cerámica aísla al conductor, las campanas que lo forman tienen un diámetro de 9.06 pulgadas. La barra central conductora de cobre tiene un diámetro de 1.625 pulgadas y es el elemento de unión entre los devanados y la línea exterior (H-J, ENTERPRISES), (CFE, 2007). El tubo de mylar es de poliéster, con una elevada resistencia dieléctrica, además es extremadamente resistente y constituye una barrera mecánica entre el aceite que pega a la barra y el que está cerca de la cerámica. Las tuercas y arandelas son el sistema que aprieta una junta de neopreno conocidas como empaques, realiza un cierre hermético con la cerámica que evita la salida de aceite de la boquilla y del transformador. La brida de montaje de aluminio se adhiere al cuerpo de cerámica mediante el pegamento y constituye el mecanismo de fijación que permite que la boquilla esté rígidamente unida al tanque del transformador, y también permite la conexión a tierra del dispositivo (CFE, 2007), (Rahman & Nirgude, 2019).
Modelado del campo eléctrico
El estudio a realizar para esta investigación es electrostático, esto indica que no van a existir variaciones respecto al tiempo, se desprecia la circulación de corriente y por ende la existencia del campo magnético. Se utilizan las ecuaciones de Maxwell para los cálculos del campo electrostático, estas son, en su forma diferencial:
Donde:
E = fuerza del campo eléctrico en volt por cada metro (V/m).
D = densidad de campo eléctrico en Coulomb por cada metro cuadrado (C/m2).
ρ = densidad volumétrica de carga eléctrica en Coulomb por cada metro cúbico (C/m3).
La ecuación constitutiva que va a relacionar los dos campos presentes es:
Donde ε es la permitividad del material en (F/m).
La intensidad del campo eléctrico se define como el gradiente del potencial eléctrico escalar:
Se agrega un signo negativo en la ecuación anterior para dar sentido físico al potencial, se define como el trabajo realizado en contra del campo eléctrico.
Sustituyendo (4) en (3) y luego en (2):
Se obtiene entonces la ecuación de Poisson:
Como en el caso de estudio no existe carga, entonces:
La ecuación (6) se conoce como la ecuación de Laplace, es la expresión que se va a resolver para calcular los valores del campo eléctrico en la boquilla (Madrid et al., 2013).
Método de Elementos Finitos (MEF)
El MEF es un procedimiento muy eficaz que permite la resolución de una gran variedad de problemas complejos. En sus inicios, se utilizó con más intensidad en el campo del análisis de estructuras mecánicas, pero en la actualidad su aplicación se extiende en las diferentes áreas de la ingeniería, como análisis electromagnéticos, de calor, acústicos, dinámicos, biomédicos, entre otros.
Esta herramienta computacional se basa en la resolución numérica de un sistema de ecuaciones diferenciales parciales y funciones suaves continuas por partes, para aproximar las cantidades desconocidas. Propone un método de solución matemática donde se divide un dominio continuo en pequeños subdominios finitos llamados elementos, este proceso es conocido como discretización. Los elementos se conectan entre sí por una cantidad de puntos llamados nodos. Para el caso lineal, el dominio se divide mediante puntos para problemas bidimensionales mediante líneas y tridimensionales mediante superficies imaginarias, de forma tal, que el dominio total en estudio se aproxime mediante el conjunto de elementos en que se subdivide. El conjunto que se forma entre elementos y nodos recibe el nombre de malla (Illias et al., 2010).
El MEF es una herramienta numérica que se aplica a objetos que tienen forma irregular, compuestos de diferentes materiales y con variadas condiciones de fronteras. Se pueden obtener soluciones en estado estacionario o variantes en el tiempo, así como problemas que involucren materiales con propiedades no lineales. La precisión de los resultados depende de la calidad del mallado que se realice, para esto hay que tener en cuenta la geometría del sistema en estudio, las condiciones de frontera, las incógnitas y variables que se calculan, entre otros detalles que favorecen el correcto modelado del problema (Rahman & Nirgude, 2019).
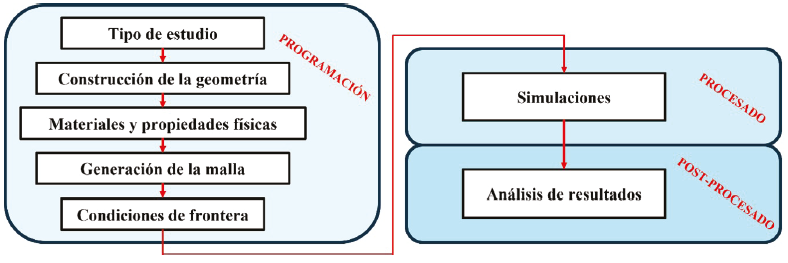
La Figura 4 muestra los pasos a seguir para poder realizar la construcción, modelado y análisis de la boquilla en el software COMSOL Multiphysics® (Madrid et al., 2013).
Mallado de la geometría
Cuando se realiza una simulación en cualquier software que use el MEF, el mallado de la geometría del objeto de estudio, es uno de los factores más importantes en la estabilidad y precisión de los cálculos numéricos. Para esto se deben tener en cuenta las características físicas del problema que se va a analizar, también se debe considerar el tiempo necesario para crear la malla y los costos computacionales que esto conlleva.
COMSOL Multiphysics® ofrece un escenario de mallado interactivo, se pueden mallar fácilmente las caras individuales o dominios. Este software contiene la función de adaptación y estimación de error, muy eficaz para estudios estacionarios, que adapta automáticamente la malla con base en las estimaciones de errores incorporados y se refina en las regiones críticas del estudio. El software tiene un asistente que pide al usuario las características del mallado, se ajusta la malla controlada por la física del problema y se selecciona el tamaño del elemento (Madrid et al., 2013).
El proceso automático de mallado genera una solución basada en una malla inicial gruesa, luego refina la malla en áreas de alta densidad de errores y genera una nueva solución. Cuando los parámetros seleccionados convergen dentro de un límite deseado, el software se sale del ciclo (Madrid et al., 2013; Patil & Pangarkar, 2018).
En el mallado de la boquilla se eliminan los elementos considerados de mala calidad, superficies con ángulos obtusos; se aumenta la densidad de la malla en las regiones de interés en el modelo: Barra central de cobre, tuercas, arandelas y brida de montaje; y se observa una distribución progresiva entre los elementos adyacentes.
La Figura 5 representa la malla propuesta para la geometría, en 3D y en axisimétrico-2D.
Para el caso en 3D se ajusta el tamaño del elemento en “normal”, tiene: 456 elementos de vértices, 4400 elementos de aristas, 22069 elementos de contorno para un total de 63718 elementos y se tarda 2.73 segundos en construirse. Para el caso axisimétrico-2D se ajusta el tamaño de la malla en “extrafina”, tiene: 113 elementos de vértice, 6680 elementos de contorno, 6509 elementos de contorno para un total de 174491 de elementos.
Condiciones de frontera del modelo
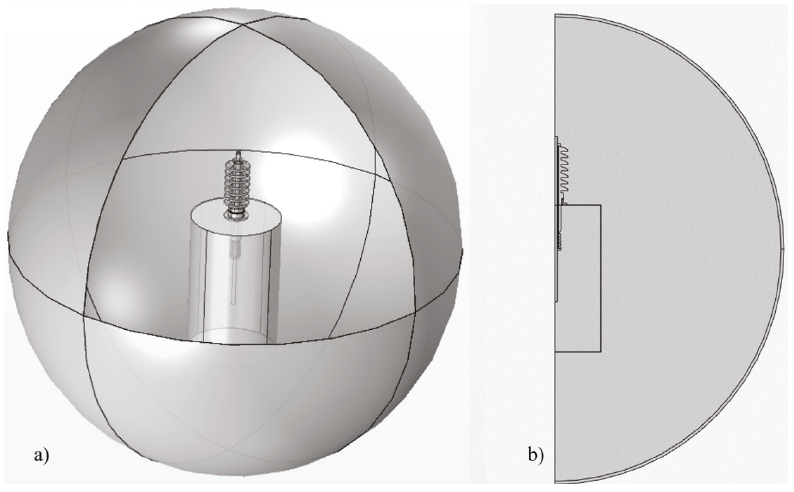
Para la realización de las simulaciones, tanto para el modelo en Axisimétrico-2D, como para el 3D, se asume una superficie esférica sólida de 80 pulgadas de radio, con una capa de 0.2 pulgadas, que envuelve toda la geometría de la boquilla. El interior de esta esfera representa la región de aire que hace contacto con los diferentes dispositivos que conforman el transformador. A la capa externa se le agrega la condición de frontera de dominio de elementos infinitos, como se observa en la Figura 6, concepto que simula que un espacio infinito alrededor de nuestro objeto sea infinito, para ello, hace que los campos que llegan a esta capa no reboten y sean totalmente absorbidos, simulando que el campo o la onda sigue propagándose (Illias et al., 2010).
Para obtener resultados con mayor precisión se evalúa todo el dominio de estudio, la excitación del modelo se aplica a la barra central de cobre con voltaje nominal
Simulaciones
Para hacer el estudio se propone acoplar la boquilla a un dominio cilíndrico que representa el tanque del transformador simulando las distancias dieléctricas hacia los componentes internos, de tal forma que la parte que hace contacto con la brida de sujeción es la pared del tanque del transformador, conectada a tierra. El dominio interno representa el aceite del transformador, y el alargamiento de la barra central simula el cable de la boquilla hacia la bobina. Se dibuja un conductor recto para que no existan distorsiones apreciables del campo eléctrico en la zona de la cola de la boquilla. Se calculan los valores del campo eléctrico para los modelos 3D y Axisimétrico-2D propuestos. El estudio es estacionario, la distribución del campo eléctrico en los materiales que conforman la boquilla indicará en qué zonas existe el mayor esfuerzo eléctrico. Las condiciones iniciales son simplemente los voltajes aplicados para la prueba, la barra central de la boquilla se encuentra a voltaje nominal, 19.9185 kV. Las condiciones de operación del transformador son a tensión nominal y sin carga.
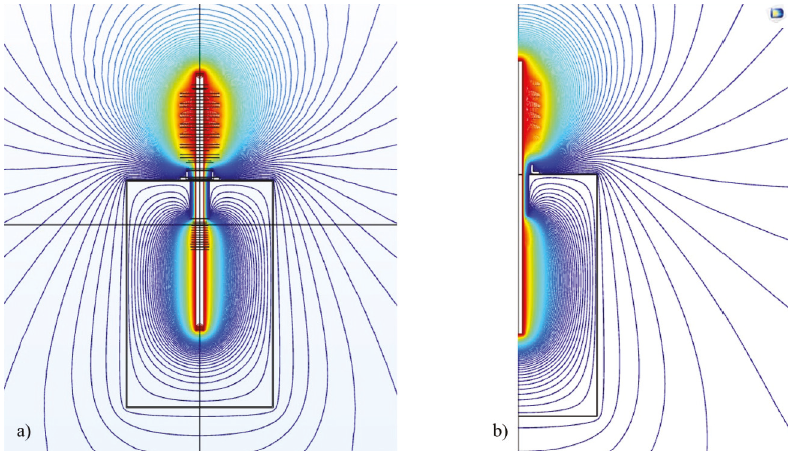
La Figura 7 muestra las líneas equipotenciales para los modelados en 3D y Axisimétrico-2D. En el primer caso, aprovechando la simetría de la boquilla, se muestra un corte transversal en el plano z, para una mejor visualización. Se observa que las líneas de potencial son concéntricas al conductor central y van disminuyendo de valor conforme se acercan a las regiones conectadas a tierra, estas nunca van a cruzar los electrodos aterrizados, pues se encuentran a potencial cero.
La distribución del potencial en ambos modelos tiene el mismo comportamiento. El valor máximo de potencial, de 19.9185 kV, se observa en la región del conductor central. En la Figura 7 se observa que las líneas equipotenciales se concentran en la zona cercana a la brida de montaje, esto indica que en esas zonas se tendrá la mayor concentración de campo eléctrico. La pintura semiconductora es la referencia a tierra en la parte inferior de la boquilla, por lo que, en esa región, también el potencial es cero.
La Figura 8 muestra la distribución del potencial eléctrico en ambos modelos, en escala de colores en lugar de líneas equipotenciales, para una mejor visualización. Se nota como el conductor central se encuentra en color rojo intenso, a 19.9185 kV, indicando el máximo valor de potencial, esto representa la conducción de la barra central, como se definió anteriormente. Se observa la distribución del potencial en todo el espacio y materiales, en función de la geometría y la permitividad relativa de cada material. Se obtiene el mismo comportamiento para el modelado 3D y Axisimétrico-2D.
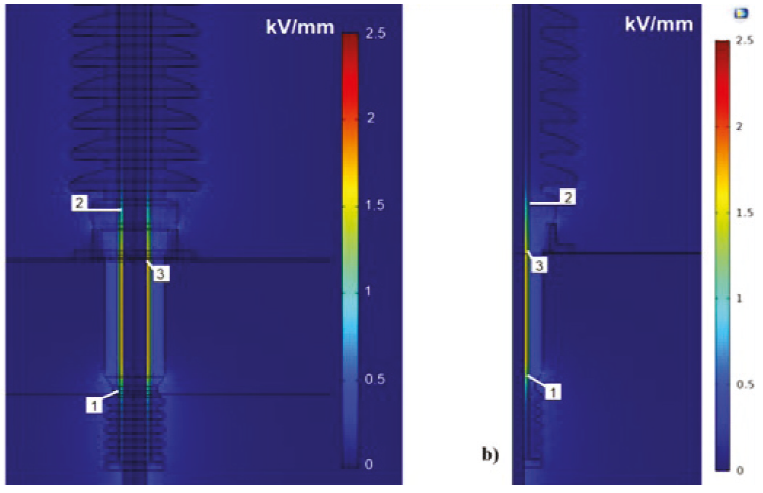
La Figura 9 muestra la concentración del campo eléctrico para el modelo en 3D y Axisimétrico-2D. Al realizar las simulaciones, se obtiene que las mayores concentraciones de campo eléctrico ocurren en el aceite que circula cercano a la barra central de conducción. Al observar la distribución en las zonas 1 y 2, correspondientes al aceite, se detecta que comienza a intensificarse el campo eléctrico con valores de 1 kV/mm, para ambos modelos.
El máximo valor de campo eléctrico obtenido, zona 3, es de aproximadamente 2 kV/mm, en la región del aceite que pega a la barra, cerca de la brida de montaje que funciona como aterramiento de la boquilla. Se observa que este material es el más afectado, por ende, es el que mayor esfuerzo eléctrico soporta. Esto debido a que, en la construcción de la boquilla, el aceite es el material que menor permitividad eléctrica posee (ε = 2.3), entonces el esfuerzo eléctrico incrementa de manera inversa al valor de permitividad
La Figura 10 muestra un corte radial realizado a la boquilla, en la zona correspondiente a la brida de montaje. Se observan los valores del campo eléctrico en las diferentes fronteras de los materiales respecto a la longitud radial del dispositivo. Esas magnitudes de campo eléctrico están directamente relacionadas con los valores de permitividad eléctrica de cada material.
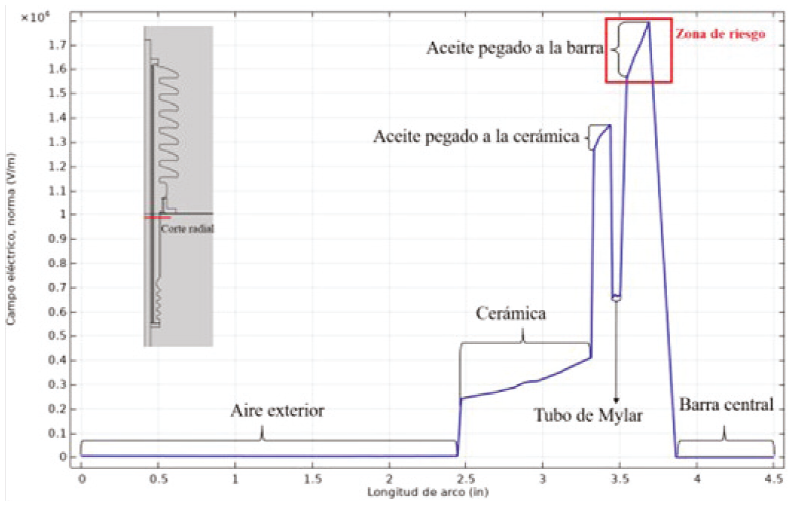
Figura 10 Campo eléctrico determinado en las fronteras de los materiales que conforman la boquilla en la zona de la brida de montaje
El área externa de la boquilla no presenta variación del campo eléctrico, este comienza a crecer una vez que se llega a la cerámica, mostrando valores que varían de 0.2 a 0.4 kV/mm.
El campo aumenta al llegar al aceite cercano a la cerámica, alcanzando los 1.3 kV/mm. Al llegar a la región del tubo de mylar, los valores disminuyen hasta 0.65 kV/mm, esto demuestra la función de este elemento, es un material de poliéster con elevada resistencia dieléctrica de 133 kV/mm, que reduce el tamaño del ducto, además funciona como una barrera mecánica entre la barra central y la cerámica, dividiendo el conducto de aceite en dos, permitiendo la circulación de este dentro del dispositivo.
El material más afectado por el campo eléctrico es el aceite, específicamente el que circula cercano a la barra central de conducción. Esto se debe a sus valores de permitividad relativa, menor que los demás materiales. Los valores de campo eléctrico son de aproximadamente 2 kV/mm, por lo cual es considerada la zona de mayor atención y con mayor riesgo de una ruptura del aislamiento en caso de que existan condiciones favorables para la generación de descargas parciales (burbujas de aire, humedad el aceite o partículas contaminantes).
Conclusiones
En el presente trabajo se realizó el cálculo del potencial y el campo eléctrico en una boquilla de tipo sólida, marca H-J, utilizando el método de elementos finitos considerando un modelo en 3D y otro en 2D-axisimétrico. Al observar las diferentes figuras mostradas, se concluye que los resultados para el modelo en 3D y en axisimétrico-2D son prácticamente iguales, con un 0.05 % de error. El hecho de completar la geometría de la boquilla en 3D es muy complejo, ya que hay que tener en cuenta muchos detalles de construcción, evitar la intersección de superficies y diferentes planos de trabajo, y un conocimiento más profundo de las herramientas del software utilizado; por lo que deja de ser práctico. Además, la geometría de la boquilla permite, de forma mucho menos laboriosa, el trabajo en axisimétrico-2D. Si bien las simulaciones realizadas en 3D no exceden los 7.0 minutos de cómputo, al resolver utilizando la axisimétrico-2D, se disminuye considerablemente el tiempo empleado, menos de 1.0 minuto, lo que demuestra que este modelado es mucho más eficiente y de la misma forma, permite obtener resultados correctos.
Utilizando el modelado de la boquilla y gracias a las simulaciones realizadas, se pueden ubicar las zonas donde hay mayor concentración de campo eléctrico. Los gráficos y los resultados obtenidos arrojan, que las mayores concentraciones de estrés eléctrico ocurren en el interfaz del aceite aislante con la barra central de conducción, zona que se ubica cerca de la brida de montaje.
Las boquillas estructuralmente están sometidas a elevados campos eléctricos, existen varios mecanismos que van a ir debilitando su aislamiento gradualmente, uno de los más importantes y que en la actualidad es una de las principales fallas que afecta a las boquillas y por consiguiente al transformador, son las descargas parciales.
Una vez ubicadas estas zonas de concentraciones de campo eléctrico, como trabajo futuro, se pretende realizan un análisis del fenómeno de descargas parciales, observar su comportamiento y los efectos que este proceso causa en el deterioro del aislamiento de la boquilla de baja tensión en estudio.











 text new page (beta)
text new page (beta)