Introducción
El cálculo aritmético de números complejos es un punto clave en los sistemas modernos de comunicación digital, de radares y ópticos (Wang y Tull, 2004). Muchos algoritmos basados en convolución, correlación y filtros complejos requieren la multiplicación de números complejos. El procesado de la información se hace mediante circuitos digitales como: los microprocesadores, computadoras personales y procesadores digitales de señales (DSP’s).
Un DSP es un circuito integrado que contiene un procesador digital y un conjunto de recursos complementarios capaces de manejar digitalmente las señales analógicas del mundo real. Estos dispositivos surgieron a principios de la década de los 80’s y se comercializaban varios modelos desarrollados por Texas Instrument, NEC e Intel. En la actualidad Texas Instrument mantiene el liderazgo del mercado de DSP’s (Angulo, 2006).
En sí, un DSP puede considerrse como un controlador clásico, pero incorporando recursos especiales para el control óptimo de los requerimientos específicos y los algoritmos manejados en el procesamiento digital de señales analógicas.
Con la introducción de los FPGA’s (Field Programmable Gate Array), es posible diseñar e implementar sistemas en un chip programable (SoPC de System on a Programmable Chip). Estos dispositivos permiten integrar un procesador, módulos de memorias, periféricos de entrada/salida, y aceleradores hardware a la medida, dentro de un mismo circuito integrado. Además de eso, cuentan con grandes capacidades, poseen una alta eficiencia hardware y la facilidad de realizar una implementación por software, facilitando así la implementación de nuevas propuestas de arquitecturas de DSPs (Tessier y Burleson, 2001). Entre las mejoras que se han apreciado con el uso de estas nuevas tecnologías, es que apoyan la optimización de energía, reducción de costos y rendimiento, respecto al tiempo de ejecución.
En los últimos años ha existido un incremento en el diseño y desarrollo de núcleos o cores, los cuales son para distintas aplicaciones. Entre dichos cores están los de procesadores de propósito general y los de propósito específico. En Hernández et al. (2015) y García et al. (2010) se presentan cores de preprocesadores de propósito general, con una arquitectura RISC. En Sosa et al. (2009), se presenta un core que implementa el algoritmo de Levinson-Durbin, empleado en el protocolo de comunicación TCP/IP, para la transmisión de voz. Finalmente en Sosa et al. (2012), se presenta un core para el cálculo del flujo óptico, donde se detecta el movimiento aparente de los objetos.
En este trabajo se presenta el diseño de una arquitectura soft-core para el procesamiento de números complejos de 16 bits. La arquitectura es RISC, tipo Harvard y posee, entre otras cosas: una pila hardware de 8 niveles, una memoria de programa de 64K × 29 bits, dos bancos de registros independientes y una memoria de datos, segmentada en 2 partes para almacenar la parte real e imaginaria, además de una unidad DSP.
Desarrollo
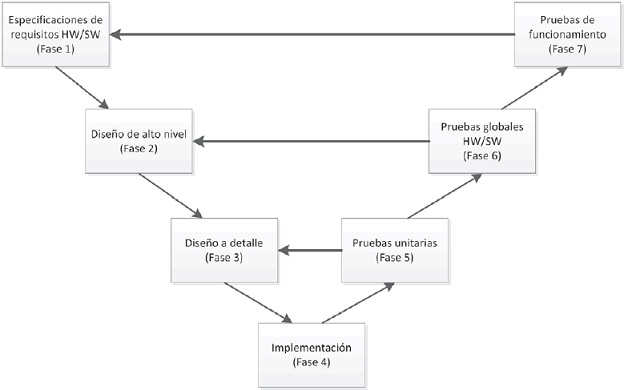
La metodología de diseño empleada en el desarrollo de este trabajo fue la metodología en V (Perez, 2006) para sistemas embebidos, como se muestra en la Figura 1.
En el diseño se emplearon las herramientas CAD-EDA (de diseño asistido por computadora para la automatización del diseño electrónico): ISE™ WebPACK 10.1™ de Xilinx, la tarjeta Spartan-3A™ (que tiene la FPGA XC3S700A), el lenguaje de descripción de hardware VHDL y una computadora personal, con sistema operativo Windows®.
Diseño
Siguiendo la metodología en V, se determinaron las especificaciones hardware y software de la arquitectura. Se estudiaron arquitecturas de microcontroladores y DSPs, de marcas comerciales, donde se encontraron dos diferencias importantes: la estructura de memoria que poseen y las unidades de ejecución. En la primera, en un microcontrolador es posible encontrar una memoria lineal, en la que se almacenan tanto datos como instrucciones de programa. Esto obliga a generar programas que no sobrepasen límites de tamaño, ya que podrían sobrescribirse datos por instrucciones o viceversa. En cambio, un DSP posee dos bloques separados e independientes de memoria, cada uno con su propio bus de acceso. Esta estrategia permite al procesador ir a buscar la siguiente instrucción y dato en el mismo ciclo de reloj (Fetch).
La segunda diferencia existente, incluso entre diferentes DSP’s, es la cantidad de unidades de ejecución que poseen, lo que permite ejecutar operaciones en paralelo. Por ejemplo: algunas arquitecturas, además de la Unidad Lógica Aritmética (ALU), también cuentan con Bloques de Multiplicación y Acumulación (MAC) y se encuentran también bloques solo para corrimientos (shifters). Otro claro ejemplo, se puede ver en la arquitectura del DSP TMS320F241, de Texas Instrument®. Este dispositivo cuenta con una arquitectura con 3 unidades de cálculo: una que realiza las operaciones lógicas y aritméticas (CALU), otra que realiza cálculos sobre registros auxiliares para direccionamientos indirectos tanto a memoria de datos como de programa (ARAU) y la tercera que realiza la multiplicación y corrimientos.
De esta menara y en función de las arquitecturas estudiadas, se propone el diseño de una arquitectura que cuente con las siguientes características:
Arquitectura de un conjunto de instrucciones reducido (RISC), con formato de instrucciones fijo, de 25 bits
2 archivos de 16 registros de 16 bits c/u
Arquitectura Harvard: mem. de programa 64K × 25 bits y mem. de datos 128K × 16 bits
Manejo de operaciones de números complejos
Tipo de direccionamiento especiales
Formato de instrucciones
El conjunto de instrucciones tiene un formato de 25 bits, y pueden realizar operaciones con tres operandos. Existen tres tipos de instrucciones: tipo Registro (R), tipo Inmediato (I) y tipo Salto (J).
El formato tipo R, tiene todas las instrucciones cuyos operandos son registros. Los 25 bits de la instrucción se distribuyen en los campos, como se muestra en la Tabla 1.
Tabla 1 Formato de instrucción tipo registro
| Formato de instrucción tipo R (Registro) 1 | |||||
| 24…………20 | 19…………16 | 15……………12 | 11………8 | 7……………………5 | 4…………0 |
| OPCODE | Rd | Rt | Rs | S/U | FUNCT |
| 5 bits | 4 bits | 4 bits | 4 bits | 3 bits | 5 bits |
| Formato de instrucción tipo R (Registro) 2 | |||||
| 24…………20 | 19…………16 | 15……………12 | 11………8 | 7……………………5 | 4…………0 |
| OPCODE | Rd | Rt | SHAMT | SELAC/CHAD | FUNCT |
| 5 bits | 4 bits | 4 bits | 4 bits | 3 bits | 5 bits |
En donde:
OPCODE |
= Código de operación |
Rd |
= Registro operando destino |
Rt |
= Primer registro operando fuente |
Rs |
= Segundo registro operando fuente |
FUNCT |
= Código de función, aquí se selecciona una variante de la instrucción indicada en el opcode |
SELAC/CHAD |
= Selecciona el acumulador deseado de la unidad DSP o el tipo de modificación a la dirección contenida en el registro que indica Rt (incremento, decremento, reversión de bits) |
SHAMT |
= Cantidad de bits a desplazar en las instrucciones de corrimiento |
S/U |
= sin uso |
El formato tipo I, tiene todas las instrucciones donde uno o dos de los operandos es un número de 16 ó 12 bits que dependiendo de la instrucción representa una constante o dirección. Los 25 bits de la instrucción se distribuyen en los campos, como se muestra en la Tabla 2.
Tabla 2 Formato de instrucción tipo inmediato
| Formato de instrucción tipo I (Inmediato) 1 | |||
| 24……………20 | 19……………16 | 15…………………12 | 11……………………………………………………………0 |
| OPCODE | Rd | Rt | Constante o dirección |
| 5 bits | 4 bits | 4 bits | 12 bits |
| Formato de instrucción tipo I (Inmediato) 2 | |||
| 24……………20 | 19……………16 | 15………………………………………………………………………………………………0 | |
| OPCODE | Rd | Constante | |
| 5 bits | 4 bits | 16 bits | |
El formato tipo J, tiene todas las instrucciones donde uno o dos de los operandos es un número de 16 ó 12 bits que dependiendo de la instrucción representa una constante o dirección. Los 25 bits de la instrucción se distribuyen en los campos, como se muestra en la Tabla 3.
Conjunto de instrucciones
La arquitectura cuenta con un conjunto de 50 instrucciones, las cuales se pueden dividir en 8 grupos: instrucciones de carga y almacenamiento, instrucciones DSP de números complejos, instrucciones de procesamiento de números reales, instrucciones lógicas, instrucciones para el manejo del acumulador de DSP, instrucciones de saltos condicionales e incondicionales, instrucciones de corrimiento e instrucciones de manejo de subrutinas.
Aquí, en la Tabla 4, solo se presentan las instrucciones de DSP de números complejos. Es importante resaltar que se omitió a propósito presentar el resto de las instrucciones, por razones de espacio en el documento. En este caso se presentan las instrucciones: suma entre dos números complejos (ADD.c), resta de dos números complejos (SUB.c), suma acumulada de dos números complejos (ACC.c), resta acumulada entre dos números complejos (SUC.c), multiplicación acumulada entre dos números complejos (MAC.c) y multiplicación de dos números complejos (MUL.c).
Tabla 4 Instrucciones de números complejos
| Inst. | Ejemplo | Significado | Código de operación | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 24-20 | 19-16 | 15-12 | 11-8 | 7-5 | 4-0 | Tipo | |||
| ADD.c | ADD.c Rd, Rt, Rs | RdR = RtR + RsR | 00 | Rd | Rt | Rs | S/U | 6 | R |
| RdI = RtI + RsI | S/U | ||||||||
| SUB.c | SUB.c Rd, Rt, Rs | RdR = RtR - RsR | 00 | Rd | Rt | Rs | S/U | 7 | R |
| RdI = RtI - RsI | |||||||||
| ACC.c | ACC.c Rt | ACCR = RtR + ACCR | 00 | S/U | S/U | Rs | S/U | 8 | R |
| ACCI = RtI + ACCI | |||||||||
| SUC.c | SUC.c Rt | ACCR = RtR - ACCR | 00 | S/U | S/U | Rs | S/U | 9 | R |
| ACCI = RtI - ACCI | |||||||||
| MAC.c | MAC.c Rs, Rt | ACCR = RtR*RsR - | 00 | S/U | Rt | Rs | S/U | 10 | R |
| RtI*RsI + ACCR | |||||||||
| ACCI = RtR*RsI + | |||||||||
| RtI*RsR + ACCI | |||||||||
| MUL.c | MUL.c Rt, Rs | R1R:R0R = RtR*RsR | 00 | S/U | Rt | Rs | S/U | 11 | R |
| - RtI*RsI | |||||||||
| R1I:R0I = RtR*RsI | |||||||||
| + RtI*RsR | |||||||||
Diseño de la arquitectura
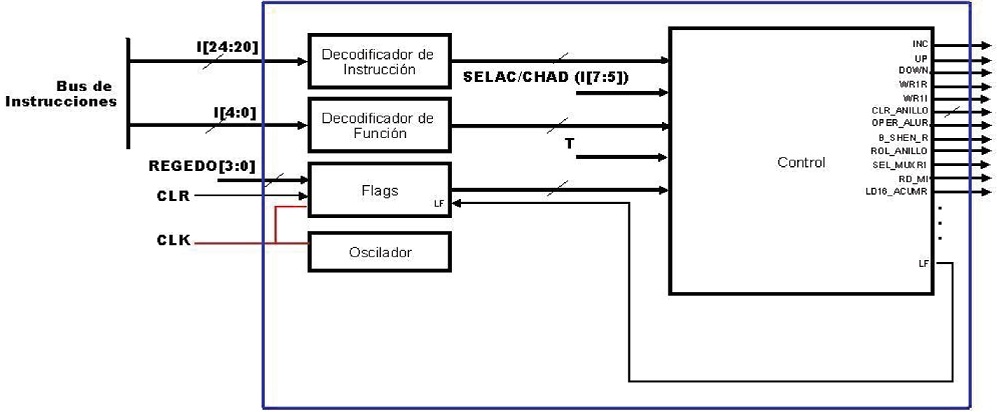
La arquitectura se constituye básicamente por 8 bloques y un bus de interconexión, como el que se muestra en la Figura 2. Todos ellos se diseñaron en el lenguaje de descripción de hardware VHDL y empleando el IDE de Xilinx.
El primer bloque, de izquierda a derecha, es una PILA en hardware de 8 niveles. Con ella se ejecutan las instrucciones de saltos o llamadas a subrutinas mediante el uso de 8 registros Contadores de Programa (PC). En el mismo bloque incluye una Instrucción de Incremento (INC), para determinar si el contador de programa debe esperar otro ciclo.
El segundo bloque es la memoria de programa. En ella se almacenarán las instrucciones a ejecutarse. Es de 64kB × 25 bits, por lo que puede almacenar hasta 64 k instrucciones. La instrucción que sale de esta memoria se distribuye hacia la unidad de control, el archivo de registros, la unidad DSP y a las 2 memorias de datos.
El tercer bloque es la unidad de control. Esta unidad es la que indica cuál es la siguiente instrucción a ejecutarse, de dónde se tomarán los datos y en dónde se almacenará el resultado. Como puede observarse en la Figura 3, la unidad de control consta de un decodificador de instrucción y un decodificador de función, para las instrucciones que contienen ese campo y junto con las banderas (Flags) y los bits SELAC/CHAD toma la decisión de las señales de control que habrá de habilitar. Esta unidad tiene 29 bits de entrada y 48 señales de control. Estas señales de control se pueden clasificar en 10 clases, como se indica en la Tabla 5.
Tabla 5 Señales de control de salida
| UP, DW, WPC, INC | Señales de control del Bloque de Pila |
| SRR, SWDR, SRI, SOPR2, SDIM, SAMR, SDOMR, SDOMI | Señales de selección de multiplexores de la Arquitectura |
| WR1R, WR2R, WR1I, WR2I | Señales de control de escritura en los Archivos de Registros. |
| CLR_ANILLO, CLR_ACUMR, CLR_ACUMI | Señales CLR´s asíncronas de registros por instrucción |
| OPER_ALU1, OPER_ALUR, OPER_ALUI | Señales de control de Operación de ALU´s en el core DSP |
| SEL_DMUX1, SEL_MX1, SEL_MX2, SEL_DMUXR, SEL_DMUXI, SEL_MUXR_S, SEL_MUXI_S, SEL_MXR1, SEL_MXR2, SEL_MXI1, SEL_MXI2 | Señales de selección de multiplexores y demultiplexores dentro del core DSP |
| LD_REG1, LD_REG2, LD32_ACUMR, LD32_ACUMI, LD16_ACUMR, LD16_ACUMI | Señales de carga de registros internos y acumuladores del core DSP |
| B_SHEN_R, B_SHEN_I, B_SHDIR_R, B_SHDIR_I | Señales de control del Barrel Shifter |
| WD_MR, RD_MR, WD_MI, RD_MI | Señales de lectura y escritura en memorias de Datos |
| LF | Señal de carga de banderas para el Registro de Estado |
El cuarto y quinto bloque son los archivos de registro. Son dos, debido a que en uno de ellos se almacena la parte real y en el otro la parte imaginaria, con ello se plantea facilitar y maximizar la velocidad en el procesamiento de datos. Cada uno de estos archivos se constituye por 16 registros, de 16 bits cada uno, y en ellos se pueden almacenar los resultados de las operaciones que así lo requieran. Otra función de los registros de trabajo es contener direcciones de los operandos, es decir, tienen la función de apuntar al inicio del bloque en memoria de datos sobre el cual se vayan a efectuar operaciones en forma iterativa usando direccionamiento indirecto.
Entonces, el archivo de registros real se usa para realizar operaciones ordinarias entre reales, ya sean aritméticas o lógicas, pero para nuestros propósitos de manipular números complejos, y crear un tipo de dato complejo dentro de la arquitectura, decidimos duplicar el archivo de registros y separarlos en un archivo de registros para la parte real de un número complejo, y otro que almacene la parte imaginaria de dicho número.
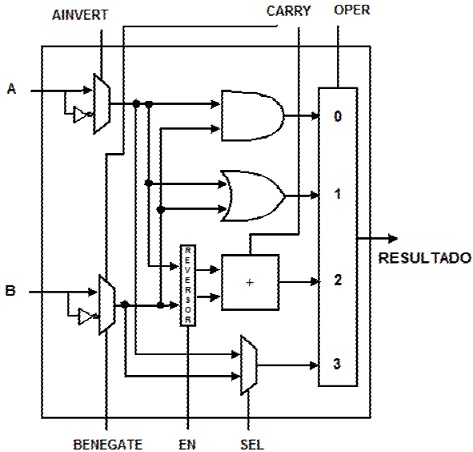
El sexto bloque es la etapa principal y la parte más compleja de este trabajo. En este bloque se procesan los números complejos. Por ello se denomina Unidad DSP o Core-DSP. Esta unidad se conforma por la Unidad Lógica Aritmética (ALU), por multiplicadores, registros intermedios, para la segmentación de las etapas de ejecución, extensores de signo de 16 a 32 bits, circuitos sumadores/restadores, acumuladores de 32 bits, registros de desplazamiento, entre otros componentes menores, como se puede apreciar en la Figura 4.
Para el diseño de la ALU, se parte de las operaciones lógicas y aritméticas que se pretenden ejecutar, excluyendo la multiplicación, puesto que esa operación se ejecutará de manera dedicada. De esta manera, tenemos que las operaciones aritméticas son: suma (real y compleja), resta (real y compleja) y las operaciones lógicas: AND, NAND, OR, NOR y NOT. El diseño de la ALU para un bit, se muestra en la Figura 5. La entrada OPER selecciona el tipo de operación a realizar, de esta menara si OPER = 00 ejecuta la operación lógica (A AND B), en cambio, si OPER = 10, entonces realizará la operación de suma o resta, según el valor de CARRY. Si CARRY =0 indica que es una suma y si CARRY =1, entonces la entrada B se complementa y al circuito sumador se le suma un uno, por el acarreo de entrada.
La implantación del sumador se realizó mediante el algoritmo de acarreo anticipado, de esta manera el tiempo de ejecución de la operación se minimiza a un tiempo constante. En cambio, una implementación de acarreo en cascada el tiempo de ejecución dependerá del tamaño de los operandos a sumar. La ecuación de suma y acarreo de salida, para una suma con acarreo anticipado, está dada por la ecuación 1.
donde
Gi se denomina como generador de acarreo y produce un acarreo de salida cuando tanto Ai como Bi son uno, haciendo caso omiso del acarreo de entrada. Pi se denomina propagador de acarreo, puesto que él es el término asociado con la propagación del acarreo de Ci a Ci + 1.
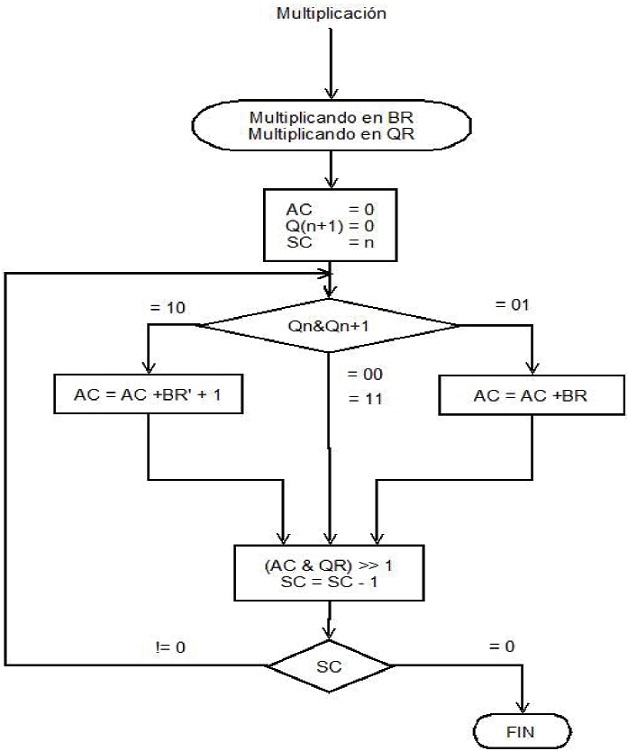
Para el diseño del circuito multiplicador, se empleó el algoritmo Booth. Dicho algoritmo proporciona un procedimiento para multiplicar enteros binarios en representación de complemento a 2 con signo. Opera con base en que las series de números 0 en el multiplicador no requieren suma, solo corrimiento, y que una serie de dígitos 1 en el multiplicador de una ponderación de bit de 2k a una ponderación 2m puede tratarse como 2k+1 - 2m. Por ejemplo, el número binario 001110 (+14) tiene una serie de dígitos 1 de 23 + 22 + 21 (k = 3, m = 1). El número puede representarse como 2k+1 - 2m = 24 - 21 = 16 - 2 = 14. Por lo tanto, la multiplicación M × 14, donde M es el multiplicando y 14 el multiplicador, puede realizarse como M × 24 - M × 21. Como resultado, el producto puede obtenerse al ejecutar el corrimiento del multiplicando binario M cuatro veces a la izquierda y restar una vez M recorrido a la derecha.
Como en todos los esquemas de multiplicación, el algoritmo de Booth requiere un examen de los bits del multiplicador y ejecutar un corrimiento del producto parcial. Antes del corrimiento, puede sumarse el multiplicando al producto parcial, restarse o dejarlo sin cambio, de acuerdo con las siguientes reglas:
El multiplicando se resta del producto parcial cuando se encuentra el primer 1 menos significativo en una serie de dígitos 1 en el multiplicador.
El multiplicando se suma al producto parcial cuando se encuentra el primer 0 (siempre y cuando exista un 1 anterior) en una serie de dígitos 0 en el multiplicador.
El producto parcial no cambia cuando el bit multiplicador es idéntico al bit multiplicador anterior.
El diagrama de flujo del algoritmo se puede apreciar en la Figura 6.
El diseño de los acumuladores de 32 bits surge de la necesidad de un acumulador de mayor longitud. Esto debido a que las operaciones de la unidad DSP involucran multiplicaciones entre números de 16 bits, que arrojan resultados de 32 bits, y las operaciones de acumulación requieren que la precisión en los registros sea mayor. El acceso a los 2 acumuladores de la unidad DSP se realiza mediante instrucciones de carga y almacenamiento (Load y Storage), que acceden a la parte alta (ACCXH) o baja (ACCXL) del acumulador, accesando a solo una parte a la vez.
Debido a las instrucciones de corrimiento sobre registros y a la necesidad de hacer corrimientos sobre los acumuladores del Core-DSP, se diseñó un circuito de corrimientos lógicos de 32 bits. Para no agregar un bit más en el formato de instrucción fue que se propusieron dos instrucciones de corrimiento, para especificar la dirección del corrimiento.
Para el diseño de la ruta de datos, durante la ejecución de las operaciones MAC, se realizó por separado para la parte real y la parte imaginaria. Esto se puede apreciar claramente en la Figura 4.
Finalmente el séptimo y octavo bloque, de la Figura 2, corresponden a la memoria de datos. La memoria de datos se encuentra dividida en 2 bloques de memoria de 64 k localidades y son denominadas memoria real y memoria imaginaria, para ser congruente con el diseño de la arquitectura.
La operación de la memoria de datos real dependerá de las instrucciones que se estén ejecutando, ya que actúa junto con la memoria de datos imaginaria para almacenar números complejos en caso de que así se requiera. Además de eso, también almacena valores en caso de que se trabaje solo con números reales y en su estructura encontramos mapeados 2 puertos y 2 registros de configuración, como son: REGEDO (Registro de Estado) y REGSUM (Registro de Suma).
La memoria de datos imaginaria almacena la parte imaginaria de los números enteros complejos, cuando se usan instrucciones del tipo ST.C o LD.C. Esta memoria también contiene mapeados los dos registros que apuntan al final e inicio de un buffer de datos, usados en la implantación del direccionamiento por buffer circular, así como otros 2 puertos. APINI (Registro del Apuntador de Inicio de Buffer) y APFIN (Registro del Apuntador de fin de buffer).
Implementación y simulación
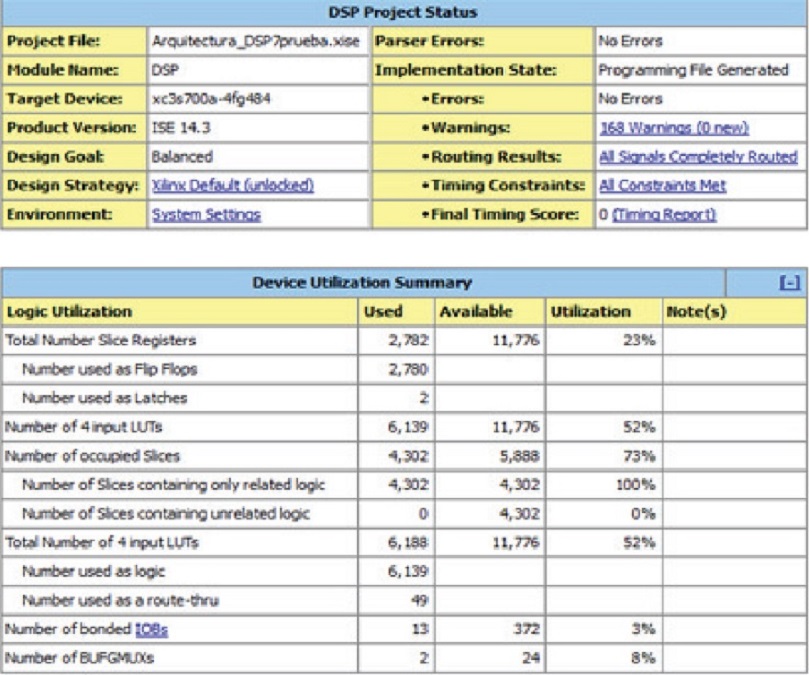
La arquitectura se implementó y se probó realizando una suma y una multiplicación de números complejos. Los resultados de su síntesis se presentan en la Figura 7.
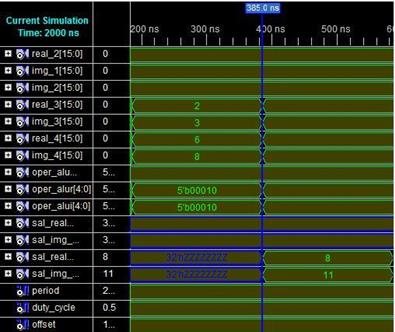
Primero se realizó la suma de números complejos: (2 + 3i) + (6 + 8i) = 8 + 11i, y se realizó la simulación, como se muestra en la Figura 8.
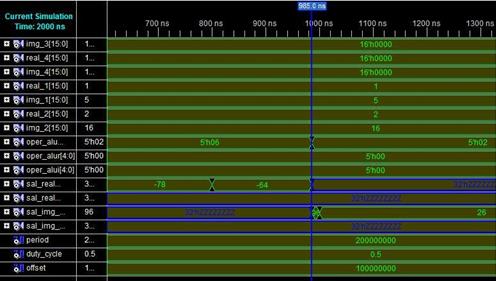
La segunda prueba fue una operación de multiplicación de números complejos: (1+5i) * (2+16i) = -78 + 26i, teniendo el resultado mostrado en la Figura 9. La rutina programada para la multiplicación de los números complejos fue:
RUTINA DE MULTIPLICACIÓN DE COMPLEJOS
LDR R4, #0x0000 --R4=0 APUNTADOR AL BUFFER 1
LDR R5, #0x000A --R5=10 APUNTADOR AL BUFFER 2
LDR R6, #0x0014 --R6=20 APUNTADOR AL BUFFER RESULTADO
LDR R7, #0x0015 --R6=21 FIN DE BUFFER
SIGMUL: (5)
LD.C R2, [R4++] --CARGA UN COMPLEJO DEL BUFFER 1
LD.C R3, [R5++] --CARGA UN COMPLEJO DEL BUFFER 2
MUL.C R2, R3 --R1:R0=R2*R3 MULTIPLICA DOS COMPLEJOS
ST.C R0, [R6++] --GUARDA LA PARTE BAJA DEL RESULTADO
CMP R7, R6
BNE SIGMUL
CICLO: (11)
NOP
BRA CICLO
Una vez que se observó un correcto funcionamiento se procedió a implementar algoritmos empleados en otras arquitecturas y comprarlos con los resultados de la arquitectura aquí propuesta.
Comparación con otras arquitecturas
Se realizó una comparación con dos arquitecturas: la arquitectura diseñada en Guarneros (2006), llamada PPG y la arquitectura comercial DSPic, empleada en Angulo (2006). En dichas arquitecturas se programaron los mismos algoritmos y los resultados se compararon con los obtenidos por la arquitectura diseñada en este trabajo, previamente programada con los mismos algoritmos.
Para la primera prueba, se empleó una función que cumple con la ecuación 2.
Los resultados se pueden observar en la Tabla 6. En donde la arquitectura propuesta requiere de menos ciclos de reloj para ejecutar una multiplicación compleja. Es decir, es 200% más rápido en relación con la arquitectura no optimizada (PPG) y 100% más rápido que la arquitectura comercial DSPic. Otra ventaja es que la arquitectura aquí desarrollada posee una arquitectura expandible y la arquitectura DSPic tiene una arquitectura cerrada.
Tabla 6 Ciclos de reloj para ejecutar la operación de la ecuación 2
| PPG | DSPic | Arquitectura aquí propuesta | |
|---|---|---|---|
| (Guarneros, 2006) | (Angulo, 2006) | ||
| Operaciones | 4 multiplicaciones | 4 multiplicaciones acumuladas | 1 multiplicación acumulada de complejos |
| Requeridas | 2 sumas | ||
| Núm. Ciclos | 6 ciclos | 4 ciclos | 2 ciclos |
Otro algoritmo que se comparó fue el cálculo de una mariposa, del algoritmo de la Transformada Rápida de Fourier (FFT), obteniendo los resultados de la Tabla 7.
Tabla 7 Ciclos de reloj para ejecutar la Transformada Rápida de Fourier
| PPG | DSPic | Arquitectura aquí propuesta | |
|---|---|---|---|
| (Guarneros, 2006) | (Angulo, 2006) | ||
| Operaciones | 4 multiplicaciones | 4 multiplicaciones acumuladas | 1 multiplicación única de complejos |
| Requeridas | 6 sumas | 4 sumas | 2 sumas de complejos |
| Núm. Ciclos | 10 ciclos | 8 ciclos | 4 ciclos |
Para este caso el rendimiento sigue siendo el mismo, se reduce a la mitad el número de ciclos respecto al DSPic y es 2.5 veces más rápido que la arquitectura de propósito general (PPG).
Discusión y análisis
Las comparaciones presentadas se hacen en función del número de ciclos del reloj, necesarios para un tipo de función específica, resulta clara la ventaja de realizar las multiplicaciones en paralelo aunque ello requiera de una mayor cantidad de recursos de hardware.
Se podrá comparar el trabajo aquí desarrollado, con otras arquitecturas, siempre que especifiquen los ciclos de reloj o tiempos de ejecución de funciones. En muchos trabajos solo comparan la arquitectura, respecto a otras arquitecturas, con los recursos utilizados de la FPGA. Sin embargo, los principales fabricantes de FPGAs, Xilinx y Altera, no guardan una similitud entre celdas lógicas y elementos lógicos por lo cual será necesario que la comparación se realice empleando el mismo FPGA aun cuando se trate del mismo fabricante, dado que algunos cuentan con diferentes tipos de FPGAs, los cuales pueden poseer elementos dedicados, como son las memorias de doble puerto, que otras FPGAs no tienen.
Conclusiones
Se implementó el núcleo de una arquitectura para procesar números complejos. Se diseñó empleando el lenguaje de descripción de hardware VHDL, por lo que se puede implementar en cualquier tipo de FPGA, sin importar el fabricante. Para este caso se empleó la FPGA XC3S700A-4FG484, de Xilinx. Este dispositivo posee 13 mil celdas lógicas, y utilizó 52% de sus celdas y 23% de los bits de memoria que incorpora el mismo dispositivo. Es importante mencionar que la FPGA empleada es un dispositivo que posee pocos recursos, comparándola con la Spartan 6 (XC6SLX150T), que posee 147 mil celdas lógicas. Esto significa, que junto al procesador, aquí desarrollado, es posible implementar otra etapa para una aplicación específica que se requiera, creando así un sistema más complejo, comúnmente llamados SoPC. De esta manera disponemos de un recurso para construir sistemas de procesamiento digital de señales ad hoc, es decir un DSP de propósito específico sin depender de DSP’s de uso general. Recordando la eficiencia demostrada del núcleo desarrollado en este trabajo en cuanto a los ciclos de reloj requeridos para cada operación.
Para este prototipo, el procesador trabaja a una frecuencia de reloj de 12 MHz, por lo que será necesario, en versiones futuras, segmentar la ruta de datos de la arquitectura y el multiplicador, poniendo una etapa de pipeline con la finalidad de aumentar la frecuencia de operación y por consiguiente el rendimiento del procesador. Otro punto a mejorar es la creación de un compilador para la traducción de las instrucciones al código máquina.











 text new page (beta)
text new page (beta)