Introducción
Un aspecto importante en hidrología es saber cuánta agua fluirá en una corriente como respuesta a un evento de lluvia. Al no estar disponibles los datos de escurrimientos o al ser insuficientes para una interpretación o extrapolación fiables, las relaciones lluvia-escurrimiento pueden ser muy útiles porque permiten generar la información del escurrimiento con los registros de la precipitación (OMM, 1994). Un modelo adecuado de la relación entre precipitación y escurrimiento permite una buena estimación de los escurrimientos en una cuenca y se puede usar en el diseño de obras para controlar inundaciones o para hacer pronósticos oportunos. También puede servir para operar obras existentes y emitir alarmas para movilizar a la población asentada en zonas en riesgo (Domínguez et al., 2008).
Los modelos de simulación hidrológica tienden a integrar diferentes procesos que antes se estudiaban por separado. Su fuerte dependencia con datos espaciales ha llevado a acoplarlos con sistemas de información geográfica (SIG), incluso a integrarlos bajo una sola plataforma (Domínguez et al., 2008; Guzmán et al., 2011; Bhatt et al., 2014; Fotakis et al., 2014). Es el caso de los modelos físico-hidrológicos de parámetros distribuidos, cuyo objetivo es ser una herramienta de pronóstico, ayudar a comprender el sistema físico y proporcionar un método de análisis de los fenómenos involucrados. Así, Mobayed y Cruickshank (1998), Mobayed y Ortiz (2000) y Mobayed (2009) desarrollaron el modelo hidrológico distribuido HIDRAS, el cual integra bajo una misma plataforma el procesamiento de la información digital climatológica, hidrométrica, fisiográfica y topográfica para la estimación de parámetros hidrológicos y tiene implementados algoritmos de cálculo de las diferentes etapas del proceso lluvia-escurrimiento.
El objetivo de este estudio fue simular el escurrimiento directo a escala de evento en cuencas pequeñas, implementando en el modelo HIDRAS procedimientos basados en métodos hidrológicos para el cálculo de hidrogramas aplicables a los casos de estudio; previa la calibración y validación de este modelo.
Materiales y métodos
El modelo HIDRAS
El modelo hidrológico distribuido HIDRAS usa la información de los modelos digitales de elevación (MDE), no sólo para definir direcciones de flujo y la acumulación de elementos para configurar la red de drenaje, sino también para hacer el escalado de la cuenca en celdas geomorfológicas (Mobayed y Cruickshank, 1998), esto es una agrupación mínima y suficiente de elementos que dan forma a una superficie tributaria. Tal agrupación corresponde al área mínima (threshold area) capaz de formar un cauce incipiente de escurrimiento.
Para la escorrentía pluvial, cada unidad produce un hidrograma incipiente o propio, equivalente a la precipitación en exceso de cada unidad. El tránsito de avenidas por los cauces se basa en una forma integral de la ecuación dinámica de advección-difusión que corresponde a una simplificación de las ecuaciones de Saint-Venant para flujo 1D transitorio a superficie libre (Diskin y Ding, 1994). Dado que la forma y el tamaño de una celda geomorfológica pueden modificar el hidrograma definido solo en función de la lluvia en exceso, se usa un esquema de convolución para caracterizar el efecto regulatorio del área tributaria. Y para valorar el efecto que producen las áreas de inundación, se toma en cuenta el cambio que experimentan los coeficientes de celeridad y difusión cuando la escorrentía ocurre en la sección modificada del área (planicie) de inundación. Los hidrogramas que produce un tránsito de avenidas sin efecto de regulación sirven como elemento de referencia para cuantificar los volúmenes de retención y retorno a los cauces, por comparación con los hidrogramas regulados para estimar la retención global y la asociada a cada elemento de la red de drenaje.
Precipitación en exceso, hidrogramas y su tránsito
En el modelo HIDRAS la precipitación efectiva (Pe), es decir, la parte de la precipitación total que participa en el escurrimiento, se calcula con la expresión propuesta por el Servicio de Conservación de Suelos de los Estados Unidos (SCS, 1993), en donde P es la precipitación total y S es la retención potencial (ambas en mm):
Para estandarizar el método se define el número adimensional CN, tal que 0<CN≤100, siendo máximo para superficies impermeables y menor para terrenos naturales. Este número y la retención potencial S se relacionan por:
Las ecuaciones anteriores son válidas cuando la abstracción inicial (Ia) es menor que la precipitación total (P). Al estudiar los resultados de muchas cuencas experimentales pequeñas, el SCS encontró la siguiente relación empírica para estimar la abstracción inicial:
Para la transformación de la precipitación efectiva (Pe) en escurrimiento directo se implementaron en el modelo HIDRAS el método de Haan et al. (1994) y el propuesto por Sánchez y Gracia (1997), los cuales se exponen a continuación.
Haan et al. (1994) propusieron la siguiente relación adimensional para generar las ordenadas (q u ), en el tiempo (t), como una función del tiempo pico (tp), el gasto máximo (qp) y un parámetro adimensional K H :
De acuerdo con estos autores, el hidrograma unitario adimensional propuesto por el SCS se reproduce adecuadamente por medio de la ecuación (4)cuando K H ≈3.77.
Sánchez y Gracia (1997) basaron su método en la siguiente hipótesis: las pérdidas, como la salida, son proporcionales al almacenamiento. Con base en esta suposición, la ecuación de continuidad y las relaciones entre el coeficiente de escurrimiento (CE), las pérdidas (CP), la lámina que escurre (BE) y la que se pierde (BP), dedujeron la siguiente expresión para calcular la variación de la lámina h del tiempo t al t+1:
donde i t es la intensidad de lluvia en el tiempo t y BC=BE/CE. puesto que h t+1 =h t +Δh, hay un criterio que permite calcular rápidamente las alturas de lámina de lluvia de la cuenca, si se conoce BE. El cálculo de este coeficiente se puede obtener por un método numérico, de manera que al llegar al último intervalo de tiempo, el tamaño de la lámina h final sea menor que un cierto límite de tolerancia cercano a cero, donde se verifique que:
Los gastos de salida, es decir las ordenadas del hidrograma, que involucran el área (A) de la cuenca, están dados por la expresión:
El tránsito de avenidas se efectúa con el método propuesto por Diskin y Ding (1994). La solución integral no requiere de una subdivisión de los cauces para transitar una avenida; se expresa como una función impulso respuesta, esto es, que se puede aplicar directamente a un valor de entrada I para obtener el de salida Q.
En este caso Q j , es una ordenada de la curva de salida asociada al tiempo jΔt mientras que I k se refiere a la entrada en el tiempo kΔt. El valor de u se estima mediante la ecuación para el tiempo t=(j-k+1)Δt, la distancia L entre hidrogramas, y para valores medios de los coeficientes de celeridad y difusión, C y D, respectivamente. La metodología para la caracterización de C y D se puede consultar en el estudio de Mobayed y Ortiz (2000).
Calibración de parámetros
El modelo HIDRAS utiliza el método de optimización conocido como evolución diferencial (Storn y Price, 1997) para encontrar los valores de los parámetros involucrados en los métodos de cálculo hidrológico con los cuales se obtiene el mejor valor del índice de Nash Sutcliffe (1970), cuya expresión es la siguiente:
donde, NS es índice de Nash Sutcliffe; NQ es el número de ordenadas del hidrograma calculado; Qc(i) y Qo(i) son el gasto calculado y el observado, respectivamente, en el intervalo de tiempo i;
Casos de estudio
Hay información suficiente para realizar la modelación hidrológica de dos cuencas experimentales: Mixcoac, en el valle de México; y Cerro Blanco, en los límites de Chiapas y Tabasco, México. La cuenca del río Mixcoac tiene una superficie de 31.5 km2, donde predominan suelos de media y muy alta permeabilidad, y vegetación densa propia del bosque de oyamel. La unidad de escurrimiento Cerro Blanco pertenece a la subcuenca del río de la Sierra, tiene una superficie aproximada de 0.67 ha, la cubierta vegetal del suelo es pastizal cultivado de buena permeabilidad y el uso es para actividades agrícolas. Los datos pluviométricos e hidrométricos utilizados en este estudio se obtuvieron de Domínguez et al. (2008) y Granada et al. (2014).
Procesamiento de la información
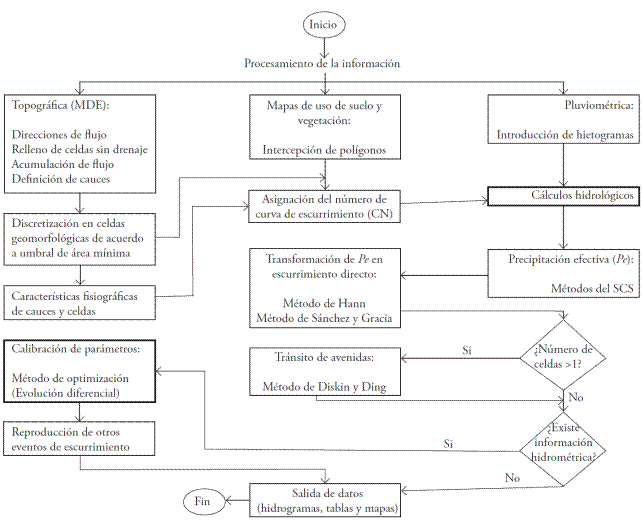
En este estudio se siguió el proceso metodológico del diagrama de flujo de la Figura 1, el cual muestra la forma de operar del modelo HIDRAS. Los Modelos Digitales de Elevación (MDE), del Instituto Nacional de Estadística y Geografía (INEGI), se usaron con resolución de celda de 5 m y escala 1:10 000; también mapas vectoriales, que incluyen tablas descriptivas, de cobertura de suelo en escala 1:50 000.
La cuenca del río Mixcoac se trabajó con un esquema de modelo distribuido de parámetros, se definió un umbral de área mínima de 10 800 celdas (0.27 km2), y se obtuvo una red de cauces y un total de 92 celdas geomorfológicas, con áreas (A) en el intervalo de 0.375≤A≤77.40 ha y valores asignados de número de la curva de escurrimiento (CN) entre 31≤CN≤91. En el caso de la unidad de escurrimiento Cerro Blanco, debido a su tamaño, no se realizó una discretización del área de estudio, por lo que el modelo utilizado fue de tipo global, con un único cauce, sin tránsito de avenidas y el número de curva de escurrimiento (CN) asignado fue de 69.
Resultados y descusión
Para probar la fiabilidad de los algoritmos formulados por cada uno de los métodos de cálculo de hidrogramas, se simularon eventos de lluvia escurrimiento con el modelo HIDRAS. El evento (E1) elegido fue el registrado el 28 de julio de 1998 en la cuenca del río Mixocac, con una precipitación (P) de 31.97 mm y 4.5 h de duración. En la unidad de escurrimiento Cerro Blanco se trabajó con el evento de tormenta registrado el 11 de octubre de 2011 (E2), con P de 46.4 mm y duración de 9.75 h. Se realizaron dos simulaciones por cada evento, la primera empleando valores de parámetros iniciales y una segunda después de ejecutar el proceso de calibración de parámetros; éste último se aplicó, en cada caso de estudio, sólo al método de formulación de hidrogramas que presentó los mejores resultados. El Cuadro 1 muestra los valores de los parámetros iniciales y los resultantes del proceso de calibración. El proceso de calibración se realizó con base en los resultados de la simulación con los parámetros iniciales. Durante esta simulación los mejores resultados en el cálculo del escurrimiento directo en la cuenca del río Mixcoac se obtuvieron aplicando el método de Haan al evento de lluvia E1. El resultado fue un hidrograma similar en forma y volumen al hidrograma medido pero con diferencias en los valores de tiempo base, el cual sobreestima, tiempo pico y gasto pico; estos dos últimos adquieren valores menores a los registrados. Con base en este resultado el proceso de calibración involucró el parámetro de forma K H , el cual una vez calibrado mejoró el índice de bondad de Nash Sutcliffe (NS), de 0.13 a 0.75 (Cuadro 1). El método de Sánchez y Gracia, antes de calibrar, produjo un gráfico de escorrentía muy similar al registrado en la unidad de escurrimiento Cerro Blanco el 11 de octubre de 2011, el cual coincidió con ciertos desfases en el tiempo y la forma de ocurrencia de los gastos, aunque no así con los volúmenes. Así la calibración, que se inició con un valor de NS de 4.98, afectó principalmente a los parámetros que modifican el volumen, como es la abstracción inicial (Ia), la cual redujo su valor a poco más de la mitad (Cuadro 1); y el número de curva (CN) que, al incrementarse después de la calibración (Cuadro 1), refleja condiciones de humedad precedente mayores a las supuestas. Esto se verifican al revisar los registros de lluvias de fechas previas al evento analizando, y así resulta mayor el volumen de escurrimiento directo, lo que mejora la función objetivo NS a un valor de 0.83.
Cuadro 1 Parámetros y variables.
| Parámetro | Mixcoac | Cerro Blanco | ||
| Inicial | Calibrado | Inicial | Calibrado | |
| Número de curva | 31 ≤ CN ≤ 91 | - | 69 | 77.5 |
| Abstracción inicial (mm) | 5.0 ≤ Ia ≤ 113.0 | - | 22.8 | 10.2 |
| Coeficiente de Haan K H | 3.77 | 3.00 | 3.77 | - |
| Nash - Sutcliffe NS | -0.13 | 0.75 | -4.98 | 0.83 |
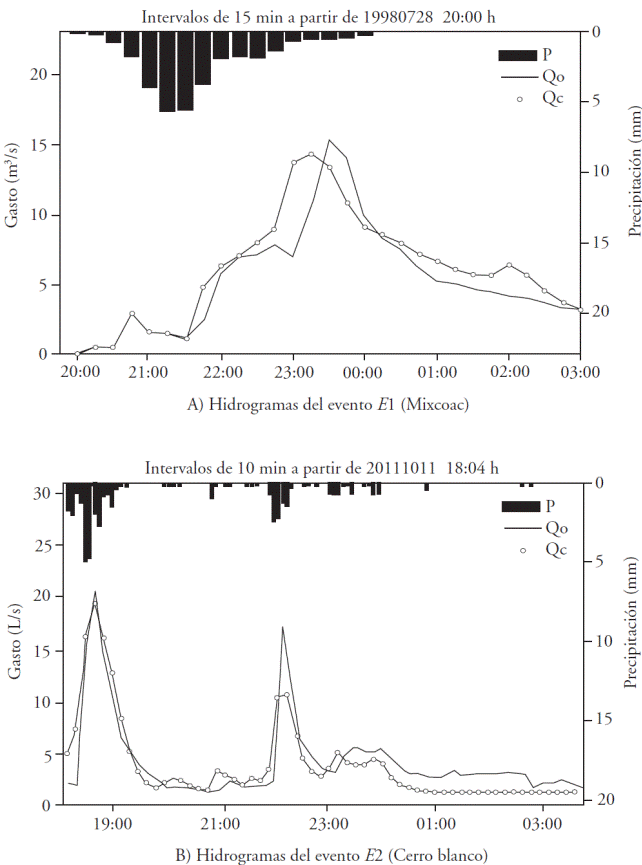
Los resultados de la simulación con los parámetros resultantes de la calibración se muestran en la Figura 2, la cual presenta de manera conjunta los hidrogramas de gasto total calculado (Qc) y observado (Qo), parte inferior, y el hietograma de entrada (P), en la parte superior, para cada uno de los escenarios de simulación. En el caso del río Mixcoac (Figura 2A) el hidrograma simulado se obtuvo con el método de Hann, resultando un gasto máximo 14.30 m3 s-1, el cual presentó un desfase de un intervalo de tiempo (15 min) con el tiempo pico medido que, comparado con los 15.42 m3 s-1 de gasto máximo medido, representa un error de 7.3 % y se obtuvo un índice de bondad de ajuste NS de 0.75. En la unidad de escurrimiento Cerro Blanco, el hidrograma muestra gastos expresados en unidades de L s-1, los cuales se registran y estiman cada 10 min (Figura 2B). Cabe señalar que en ambos hidrogramas el gasto base se separó del gasto total mediante procedimiento gráfico convencional y sumado al escurrimiento directo, porque aún no está implementada una subrutina para calcular este componente del escurrimiento.
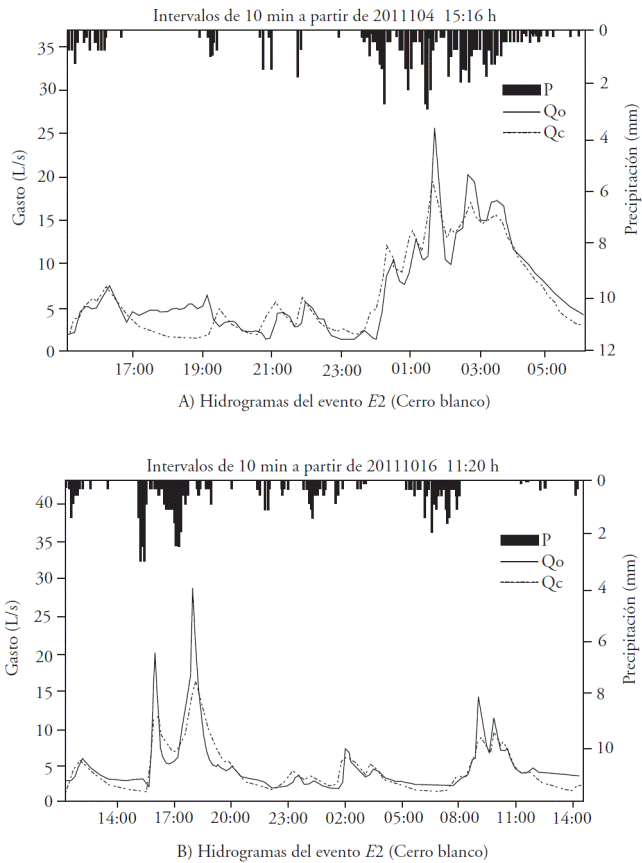
Gracias a la amplia base de datos hidrométricos y pluviométricos disponible en la unidad de escurrimiento Cerro Blanco, es factible validar los parámetros calibrados para el método de Sánchez y Gracia. En este caso mediante la simulación de dos eventos, uno antes y otro después que el usado durante el proceso de calibración (11 de octubre del 2011). Los resultados de la validación se muestran en la Figura 3, donde puede observarse que el método empleado, al usar los parámetros calibrados, simula de forma aceptable los hidrogramas medidos, en los que se obtiene un índice de bondad NS de 0.81 en el evento del 04 de octubre (Figura 3A) y NS de 0.74 para el del 16 de octubre (Figura 3B). El proceso de validación no pudo realizarse en el caso de la cuenca del río Mixcoac por la falta de otros registros de escurrimiento.
Al analizar los tres hidrogramas medidos en la unidad de escurrimiento Cerro Blanco (Figura 2B y 3), se observó que el escurrimiento ocurre casi inmediatamente después de iniciada la precipitación, lo cual implica que es poca o despreciable la abstracción inicial, o elevada la saturación del suelo. Esto coincide con la hipótesis del método de Sánchez y Gracia, que define a las pérdidas y al caudal como proporcionales a la tasa de precipitación, sin tomar en cuenta el efecto del retardo inicial que produce el déficit de humedad antecedente y puesto que las dimensiones del área no favorecen la regulación de los volúmenes pluviales, este método produce un gráfico de escorrentía muy similar al registrado.
Conclusiones
En la cuenca del Río Mixcoac, el método de Haan logró reproducir con un índice de bondad de ajuste aceptable (NS=0.75) el hidrograma del evento registrado. Mientras que en la unidad de escurrimiento Cerro Blanco, por sus características y homogeneidad, en cuanto a topografía, uso y tipo de suelo, respondió mejor al método de Sánchez y Gracia (NS=0.83).
El modelo HIDRAS, que cuenta con distintos métodos de cálculo para el proceso lluvia-escurrimiento y un código semi-abierto, permitió agregar los algoritmos necesarios para encontrar el que proporciona la mejor respuesta hidrológica. Lo cual apoya la conveniencia de implementar métodos hidrológicos diferentes a los tradicionales, en particular cuando no se cumplen del todo las hipótesis para las cuales se desarrollaron y probaron. La falta de suficientes datos hidrométricos es común en el país, por lo cual es indispensable contar con modelos hidrológicos para estimar la escorrentía que se puede generar dado un evento de lluvia.











 text in
text in