Introducción
La visualización de datos, o data visualization (DataViz), ha tomado una gran importancia en el mundo (Bertling et al., 2021; Brigham, 2016), ya que tiene diversas aplicaciones que van desde hacer perceptible el vaivén de un producto específico en una cadena de autoservicio hasta asistir en los procesos administrativos de las instituciones, la movilidad urbana, la educación, y la salud; haciendo visible tanto a grupos especializados de trabajo como a la población general, información compleja resultante de estos mismo procesos que de otro modo sería complicada de explicar y entender.
En este texto se entiende a la visualización de datos como un área aplicada del diseño de información (DI), en donde se busca dar forma a datos no estructurados mediante procesos de gestión de información, como son: analizar, depurar, organizar, clasificar y catalogar, de tal manera que estos pueden ser transformados en información útil mediante una configuración visual que haga más accesible el entendimiento de un fenómeno en cuestión. Dicha visualización puede tomar muchas formas, desde una gráfica de barras que permite hacer comparaciones entre un par de unidades de valor hasta gráficos más sofisticados que muestren correlaciones, desviaciones, distribuciones, magnitudes, flujos. Además, permite visualizar muchos otros fenómenos donde intervienen datos complejos, ya sea cuantitativos o cualitativos, y facilita interpretar una situación, lo que a su vez da pie a que las personas puedan tomar decisiones y llevar a cabo acciones particulares.
Entonces, es necesario que haya profesionistas capacitados para hacer visualizaciones efectivas (Donohoe & Costello, 2020), lo que nos lleva a plantear que desde la formación universitaria se puede desarrollar la pericia en el conocimiento y habilidades en esta temática. Si bien existen muchas áreas del conocimiento que pueden abordar el DataViz, una de ellas es particularmente el diseño gráfico, pues en su perfil los practicantes tienen dos grandes ventajas: hacen comunicación visual y pueden implementar la gestión de datos desde el diseño de información. Por ello, es necesario contar con programas educativos que permitan formar estudiantes con habilidades y conocimientos competitivos, actualizados a las necesidades de las comunidades, que se integren como factores de cambio en la sociedad, generando nuevos paradigmas ante los retos actuales desde una perspectiva humanista.
En las instituciones educativas, la enseñanza debe tener un efecto no solo en el aprendiz sino también en el medio en que se desarrolla la práctica de esta. Los autores coincidimos con Boyer (1990) en que el trabajo docente solo tiene sentido si este es entendido por otros, en referencia tanto al aprendiz como a los colegas docentes, así como al personal administrativo que es parte del sistema institucional. De esta manera, el proyecto que se presenta en este artículo busca focalizar el proceso de enseñanza al puntualizar que se requiere centrarlo en el aprendizaje del estudiante, y en donde el docente debe cuestionarse frecuentemente cómo es la pedagogía, cómo sucede el aprendizaje y bajo qué circunstancias específicas ocurre (Harrington et al., 2021). De esta manera, al provocar un acto de constante reflexión, se puede tener un entendimiento fundamental que contribuya a mejorar la teoría y la práctica educativa, que incida en el estudiante, en los académicos, en los administrativos y consecuentemente en la institución educativa (Shawa, 2020).
Como parte de su proceso de transformación, crecimiento y consolidación, la Benemérita Universidad Autónoma de Puebla (BUAP) ha identificado las necesidades educativas de la sociedad e implementado el Modelo Universitario Minerva (MUM), el cual, desde el constructivismo social, se centra en los cambios constantes del contexto local, nacional e internacional; reconociendo nuevas formas de aprendizaje y enseñanza a través de la investigación y el trabajo colaborativo, así como la vinculación constante del conocimiento, de manera horizontal y transversal (Dirección de Educación Superior BUAP, 2022). Esto es congruente con la pertinencia curricular como respuesta a las necesidades sociales por medio de los planes de estudio y programas de educación, lo que conlleva la revisión constante de ellos en beneficio de la mejora disciplinar y su ejecución como un agente de cambio en el ámbito de la educación superior y con la calidad educativa desde la perspectiva internacional (Luna & Montané, 2020; Medina & Montané, 2019). Así, en la práctica académica, los docentes de diseño gráfico evalúan la necesidad de actualización de los programas de asignatura, y de forma colaborativa, por especialidad, revisan cada unidad temática considerando la pertinencia curricular, recomendaciones de acreditadores y fuentes bibliográficas actualizadas con el fin de generar la propuesta de rediseño que se envía a la coordinación de la academia para su presentación, revisión y aprobación por las instancias institucionales competentes.
El MUM plantea ejes transversales que generan competencias generales en los estudiantes y establece que los nuevos conocimientos esenciales deben incorporarse y actualizarse a lo largo de la currícula de diseño gráfico como réplica que da solución a la necesidad de representación de información que la sociedad demanda; ya que, los estudiantes de diseño gráfico, como especialistas de comunicación visual, tendrán la responsabilidad profesional de difundir información veraz, confiable y, sobre todo, fácil de comprender; con un especial enfoque en una comunicación clara hacia la población general, los grupos vulnerables y los especialistas que toman decisiones que impactan a la sociedad.
Por ello, a lo largo de la licenciatura, el estudiante aprende a resolver problemas visuales derivados de datos cuantitativos, los cuales están relacionados con la disciplina mediante métodos matemáticos que le permiten desarrollar una argumentación coherente basada en estudios de tipo cuantitativo, particularmente a través de la disciplina de la estadística. En la licenciatura de diseño gráfico, el primer acercamiento a esto se da durante la asignatura de Matemáticas para el diseño, cuyo objetivo es lograr que el estudiante identifique la relación que existe entre la disciplina del diseño y las matemáticas, a través de temáticas como: geometría plana y del espacio, geometría fractal y probabilidad y estadística, que son abordados en el programa de la asignatura. El propósito de la asignatura es que el estudiante resuelva problemas relacionados con la disciplina del diseño mediante métodos matemáticos; por consiguiente, se establece como competencia profesional el uso e incorporación de conceptos y métodos matemáticos que permitan al estudiante argumentar la toma de decisiones para la resolución de problemas o proponer mejoras en proyectos del área de diseño, cuya finalidad es la de justificar la eficiencia, eficacia y viabilidad de estas (Tabla 1).
Tabla 1 Resumen del programa de la asignatura Matemáticas para el Diseño.
| Propósito | |||
| Resolver problemas relacionados con la disciplina del diseño gráfico mediante la utilización de diversos métodos matemáticos, evaluando la importancia de la implementación de los métodos matemáticos como herramienta para el desarrollo de la habilidad de lógica del pensamiento en los profesionales de la disciplina del Diseño Gráfico. | |||
| Competencias | |||
| Desarrolla flexibilidad de pensamiento para la toma de decisiones sobre propuestas y acciones en función de la mejora del proyecto de diseño mediante técnicas de conceptualización y estudios de tipo cuantitativo y cualitativo.
Define e implementa una estrategia metodológica adecuada a las variables de tipo social, cultural, económico, político y religioso implicadas en el contexto del proyecto de diseño para una óptima interpretación de las necesidades de comunicación a través de la aplicación de técnicas de comunicación, mercadotecnia y gestión. | |||
| Temas | Subtemas | Productos de aprendizaje | Evaluación |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fuente: Elaboración propia a partir del programa de asignatura de matemáticas para el diseño del Colegio de Diseño Gráfico, BUAP (2022).
Entonces, se presenta la necesidad de hacer representaciones gráficas, manejar datos complejos y producir una explicación visual coherente, así como lograr el entendimiento en los usuarios y que estos sean capaces de usar la información para lograr sus metas. Todas ellas son circunstancias que pueden ser resueltas desde la práctica del DI.
De acuerdo con el mapa curricular vigente aprobado por la BUAP, la asignatura enfocada al aprendizaje del diseño de la información, designada como Taller V, se encuentra ubicada en el periodo formativo dentro de los niveles de competencia asignados al proceso educativo, mientras que la asignatura Matemáticas para el diseño pertenece al periodo básico (Figura 1). Uno de los principales objetivos disciplinares de la clase Taller V es que los estudiantes interioricen los principios que actúan en y guían el pensamiento del diseño de información hacia la elaboración de visualizaciones que sean intuitivas, eficaces, dinámicas, y que empoderen la comunicación de datos e información hacia el público general o especializado (Franconeri et al., 2021).
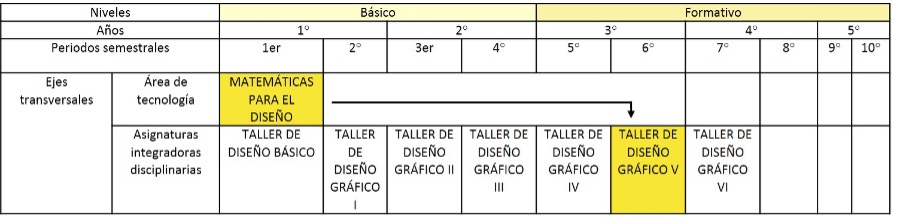
Fuente: Elaboración propia a partir de BUAP (2020).
Figura 1 Versión sintetizada del plan de estudios de la licenciatura en Diseño Gráfico.
Desde el pensamiento del DI, una visualización mal diseñada va a generar confusión, interpretaciones incorrectas, malentendidos y desconfianza en los lectores, especialmente en aquellos con una baja alfabetización visual. Por otro lado, un buen trabajo en el diseño de la visualización de datos aumenta el potencial comunicativo de la información, permitiendo a los lectores identificar patrones y acceder al conocimiento en la ciencia, la salud, la educación, las políticas públicas, etc., y aplicarlo en aspectos utilitarios y necesarios para llevar a cabo nuestra vida cotidiana (Franconeri et al., 2021). Entonces, el DataViz se vuelve un asunto de interés público debido al beneficio que implica su presencia prevalente en nuestra vida y reafirma la necesidad de tener profesionistas preparados, cuyo bagaje de conocimientos les permita explorar el potencial de esta área para obtener productos informativos de calidad.
Se ha encontrado un vínculo educativo importante, pues si bien se aprende el arte y oficio de la visualización de datos en la clase de Taller V, es durante el primer semestre en la clase de Matemáticas para el diseño donde se pueden establecer las bases conceptuales que van a permitir a los estudiantes configurar el pensamiento analítico, la estadística, el manejo de numerales y los procesos de interpretación de datos, que son la base para aprender a hacer DataViz, además de habilitarlos para resolver un amplio abanico de casos donde intervienen datos en forma estadística.
Matemáticas y diseño tienen una relación ancestral, pues la primera aporta a la segunda importantes herramientas, como un pensamiento ordenado, estrategias metodológicas y una perspectiva objetiva (Ponce, 2016). Coincidentemente, todas estas son características necesarias en el área del diseño de la información y deseables en el perfil de quien ejerce en esta área del diseño, por lo que podemos establecer una empatía entre ambas disciplinas. Especialmente, las matemáticas en la práctica del DataViz y en la formación de los diseñadores gráficos ayudan a entender grupos de datos abstractos y poder depurarlos y clasificarlos, al mismo tiempo que aportan el lenguaje estadístico para entender cómo interpretar esos mismos grupos de datos y determinar los beneficios de los diferentes tipos de gráficos estadísticos que pueden utilizarse (Brigham, 2016). Además, para la vida en general, las matemáticas aportan el conocimiento para leer e interpretar la información que se presenta de forma estadística en los medios informativos (Bertling et al., 2021).
Actualmente no se aprovecha el potencial del vínculo entre estas dos asignaturas, de ahí que la idea de este escrito sea documentar una primera experiencia docente que sirva para indagar cómo establecer las bases de contenido y estrategias educativas para la enseñanza de los estudiantes noveles en un primer acercamiento a la visualización de datos, de tal manera que se puedan establecer lineamientos o una logística para proponer reformas al plan de estudio de la asignatura Matemáticas para el diseño. Esto se hace con la finalidad de que los estudiantes tengan un aprendizaje significativo que les sirva como fundamento al llegar a la clase de Taller V y que logren ser más proficientes en esta área del diseño cuando tengan que resolver proyectos enfocados en el DataViz.
Revisión de literatura
Recibimos una gran cantidad de información a través de diferentes medios de comunicación, por lo que la habilidad de leer y entender datos estadísticos se ha convertido en una necesidad para comprender nuestro propio contexto social, siendo entonces indispensable la alfabetización estadística, la cual es un derecho ciudadano, pues una persona que sea estadísticamente diestra posee habilidades que le permiten leer datos y tablas, hacer interpretaciones de encuestas y gráficos, comparar y organizar datos, pensar críticamente, comunicar y explicar su interpretación, evaluar la información estadística respecto a los contextos en los cuales se desenvuelve y tomar alguna acción en correspondencia (Bertling et al., 2021; Estrella & Olfos, 2012; Zapata, 2011).
El desarrollo de las ciencias dio paso al surgimiento de los gráficos estadísticos, objetos informativos que sirven para analizar datos mediante la representación visual y que pueden ser interpretados, analizados y entendidos de forma más ágil por el lector (Fantino, 2021). Sus primeros usos surgieron como soporte para la cartografía y se fueron incorporando a otras áreas del conocimiento (Instituto Nacional de Estadística de España, 2010); así, estos gráficos se convirtieron en una necesidad para la evolución de las ciencias.
Respecto a la enseñanza moderna de este tipo de gráficos matemáticos, según el National Council of Teachers of Mathematics (2000), desde el comienzo de la educación escolarizada la curricula propone la inclusión de experiencias con análisis de datos donde los estudiantes aprendan a clasificar, organizar y representar datos. Posteriormente, se les enseñan métodos de recolección de datos y comparación de diferentes grupos de los datos. Y en niveles más avanzados, los estudiantes deberán proporcionar evidencia y explicar predicciones basadas en su interpretación de los datos, así como delinear estudios para mejorar las implicaciones y predicciones. Como señala Eudave (2009), en México, desde hace varios años se han incorporado contenidos que buscan fomentar habilidades para la lectura e interpretación de datos estadísticos en la educación básica, que permitan al estudiante comprender el valor y sentido de tablas y gráficas en la toma de decisiones en diversos contextos.
Podemos establecer un modelo cognitivo respecto a la educación estadística que abarca: el conocimiento previo de los estudiantes, manifestado en su entendimiento básico sobre cálculo, así como su capacidad de expresar este conocimiento; el razonamiento estadístico, que abarca la capacidad de primero entender y luego hacer procedimientos básicos; y, finalmente, el pensamiento crítico sobre estadística, que se manifiesta en una persona con una alfabetización suficiente en el área, para hacer procesos avanzados, entender las reglas de funcionamiento, integrar el pensamiento analógico e inductivo y explicar con certeza los resultados (Estrella & Olfos, 2012; Garfield, 2002). Lo anterior permite que el estudiante transite en este proceso desde la escuela básica al nivel universitario, de usuario a productor de estadística. En la actualidad, en México, los planes y programas de estudio para la educación básica de la Secretaría de Educación Pública (SEP) están conformados por dos áreas (SEP, 2017): Campos de formación académica (Lenguaje y comunicación, Pensamiento matemático y Exploración y comprensión del mundo natural y social) y Área de desarrollo personal y social (Artes, Educación socioemocional, Educación Física). Dentro de la sub-área de Pensamiento matemático se consideran tres ejes temáticos: (1) Número, algebra y variación; (2) Forma, espacio y medida; y (3) Análisis de datos, siendo en este último donde podemos observar los aprendizajes esperados por grado escolar enfocados a la estadística (Tabla 2).
Tabla 2 Aprendizajes esperados por nivel en la educación básica en el eje de análisis de datos dentro del pensamiento matemático.
| Nivel | Aprendizaje esperado por nivel escolar |
| Preescolar | Cuenta del 1 al 10, contesta preguntas en las que necesite recabar datos y los organiza a través de dibujos que interpreta para contestar las preguntas planteadas. |
| Primaria | Recolecta, registra, lee datos en tablas, lee pictogramas sencillos, lee graficas de barras y circulares, usa e interpreta la moda, la media aritmética y el rango de un conjunto de datos. |
| Secundaria | Recolecta, registra y lee datos en gráficos circulares, histogramas, polígonos de frecuencia, y graficas de línea. Usa e interpreta las medidas de tendencia central (moda, media aritmética y moda), y dispersión (rango y desviación media) de un conjunto de datos y decide cuál de ellas conviene más en el análisis de los datos en cuestión. |
Por otra parte, en la Educación Media Superior se establecen competencias genéricas, disciplinares y profesionales con base en el Acuerdo Secretarial 444 para el Marco Curricular para el Sistema Nacional de Bachillerato (Diario Oficial de la Federación [DOF], 2008), el cual se subdivide en cuatro áreas disciplinares: matemáticas, ciencias experimentales, ciencias sociales y comunicación. Dentro de las competencias disciplinares de matemáticas se busca que el estudiante pueda razonar matemáticamente, argumentar y estructurar sus ideas, siendo clave para estas competencias el desarrollar y producir diversos tipos de gráficas, elaborar tablas y mapas y generar diagramas, así como interpretar lecturas con símbolos matemáticos y científicos.
El resultado global de los esfuerzos en los diferentes niveles educativos es poner énfasis en las competencias derivadas de la alfabetización procedente del aprendizaje matemático (Ilhan et al., 2019). De acuerdo con lo anterior, se espera que los estudiantes, al llegar a nivel licenciatura, ya cuenten con un andamiaje en su conocimiento previo suficiente para ser versados en el pensamiento matemático, lo que debería reforzar su paso por la asignatura de Matemáticas para el diseño, facilitando una conexión con el tema de DataViz, para que puedan abordar la resolución de problemas visuales donde se presentan datos cuantitativos.
Se puede clasificar a las personas que tienen competencias desde la alfabetización estadística en tres grupos: (1) quienes activamente producen datos, (2) aquéllos que son consumidores de estos y (3) quienes se encargan de comunicarlos a los demás (Serradó, 2013). Dadas las características del perfil que debe tener el diseñador gráfico, es importante que desarrolle las habilidades para formar parte de estos grupos, siendo la construcción de gráficos estadísticos una de las principales, pues la importancia de que la población general tenga a su alcance visualizaciones estadísticas entendibles y cognitivamente accesibles es imperante.
En este contexto, se calcula que de un 3% a un 6% de la población padece discalculia, que es la dificultad en el aprendizaje de las matemáticas por la forma en la que el cerebro procesa y entiende el trabajar con números. Algunas señales de este padecimiento son: usar los dedos para contar, olvidar procesos elementales, sufrir inconvenientes al manejar dinero, tener dificultades para leer la hora desde el reloj analógico, confundir la derecha con la izquierda, tener conflictos con números secuenciales y patrones, no comprender conceptos de mayor o menor, tener problemas para asociar palabras y símbolos o tener dificultad para recordar tablas de multiplicar (Delgado, 2020). Lo anterior se traslada a la interpretación de la información que se nos proporciona en forma de gráficas por diferentes medios a los que tenemos acceso y lo que hacemos con los datos numéricos. Y si consideramos que esto es esencial para la vida, por ejemplo, en cuestiones que van desde formarnos una opinión sobre un tema que afecta a nuestra comunidad, tomar decisiones con base en datos estadísticos, elaborar un plan de acción o simplemente saber cuándo nos están diciendo la verdad y cuándo no al momento de ver una gráfica, entonces se vuelve indispensable que las visualizaciones estén hechas para darle a las personas la ayuda necesaria para solucionar estas situaciones.
Dentro del DataViz encontramos que los gráficos estadísticos son recursos para representar tendencias y comportamientos de datos mediante barras, líneas, áreas o puntos (Instituto Nacional de Estadística y Censos [INEC], 2017), por lo que sus formas básicas son accesibles para que los diseñadores gráficos los utilicen para presentar información de forma clara. Por tanto, se vuelve necesario aprender las bases para interpretar datos, y que los diseñadores obtengan habilidades que les permitan visualizar el comparar datos, identificar cambios de comportamiento a lo largo del tiempo, hacer relaciones entre dos variables, reconocer cómo se encuentra un elemento en comparación con el total o cómo se distribuyen los elementos y sus diferencias.
Dentro de la Licenciatura de Diseño Gráfico, las matemáticas son una disciplina fundamental, ya que “el diseño es un proceso de creación visual con un propósito” (Wong, 2008). Por ello, es esencial que se comprendan los principios visuales de la composición geométrica, como los sistemas clásicos de las proporciones (sección aurea, razones y proporciones), los cuales permiten tener una visión del proceso de diseño y aportan coherencia al diseño mediante la estructura visual, lo que da como resultado un proyecto bien elaborado no solo desde el punto de vista estético sino también funcional (Elam, 2003). Por esa razón se imparte la asignatura de Matemáticas para el diseño, es decir, por su estrecha relación con la geometría y la aritmética. Esta asignatura cuenta con siete unidades: (1) Ángulo y rectas, (2) Figuras geométricas complejas, (3) Circunferencia, (4) Cuerpos geométricos, (5) Razones y proporciones, (6) Razón aurea y geometría fractal y (7) Probabilidad y estadística. De estas, las primeras seis centran su contenido de aprendizaje en las necesidades de geometrización y composición visual, y en la última unidad se revisan conceptos básicos de probabilidad y estadística que permiten determinar grupos humanos, necesidades del usuario, tendencias, análisis de fenómenos, etc., es decir, información que permite la toma de decisiones para perfilar una solución visual a un determinado problema.
Dentro de los gráficos más utilizados en el área de diseño para representar información, están los gráficos de barras, circular o pastel y línea, además de una extensa gama de otros tipos de gráficos que pueden ser de utilidad para facilitar la comprensión de la información. En ese sentido, es necesario que los diseñadores los conozcan y que entiendan cómo se construyen. Entre las habilidades y conocimiento que debe hacer suyo quien hace DI y visualiza información, se encuentra comprender que un gráfico útil debe tener claro quién será el grupo humano y determinar el mensaje que debe comunicar, así como la naturaleza de este, con el fin de construir un gráfico que, además de captar la atención del lector, logre comunicar un mensaje claro (Brigham, 2016). Hay gran variedad en los tipos de gráficos, pero todos tienen elementos básicos para su comprensión (título, cuerpo y pie de gráfico), además de que poseen componentes de apoyo para facilitar su interpretación, a saber: título de leyenda, eje de valores, eje de conceptos, código o número de gráfico y fuente de donde se obtienen los datos. Todo lo anterior es conocimiento necesario que debe tener un estudiante desde el inicio de su aprendizaje para poder aplicarlo con mayor efectividad durante su formación, especialmente al resolver problemas desde el diseño de información.
Revisando la literatura especializada, se han analizado proyectos en la línea temática de investigación y se han retomado sus principales aportaciones para nutrir el trabajo. Por ejemplo, se busca obtener un nivel interpretativo competitivo al trabajar con datos estadísticos (Wolfe, 2015); dicho de otra manera, se pretende adquirir habilidades para la selección de los datos y la capacidad para hacer una interpretación válida. Esto da pie a que la enseñanza en diseño busque generar estos aprendizajes en los alumnos para que desarrollen habilidades que los fortalezcan en su práctica (Uyan, 2014), es decir, un pensamiento organizado y sistemático, la capacidad de detectar patrones, una visión multidisciplinaria y el reconocimiento de diversos objetos resultado de la capacidad de visualizar información a partir de datos. Estas habilidades que se espera sean resultado del aprendizaje en la asigatura darán a la comunidad de estudiantes de diseño competencias para relacionarse con los números, de manera que puedan desarrollar sus propias estrategias para vincularse con estos y así poder dar soluciones efectivas a problemas complejos, trabajando con principios que guíen el trabajo desde una perspectiva matemática que apoya el proceso de pensamiento de diseño (Simon, 2020).
Actualmente, en la clase de Matemáticas para el diseño, aunque se hace uso de conceptos estadísticos como las medidas de tendencia central para conocer gustos y necesidades de los usuarios, y en los cuales se usan gráficos estadísticos, no se profundiza en la construcción de estos como medios de representación visual, sino que son utilizados meramente como fuentes de consulta. Si bien los avances tecnológicos permiten el uso de mecanismos más eficientes para recopilar, gestionar y evaluar datos, es la creciente generación de datos la que hace necesario que existan mejores métodos que permitan la representación visual para facilitar su interpretación, por lo que el diseñador gráfico debe ser capaz no solo de leer e interpretar gráficos estadísticos sino de integrarlos de manera correcta. Esto hace necesario replantear la forma en que se enseñan las matemáticas a los diseñadores, para así poder proponer una renovación en la curricula de la asignatura de la Licenciatura en Diseño Gráfico de la BUAP, que permita actualizar los conocimientos y saberes, identificar las habilidades que se requiere desarrollar, fortalecer el vínculo entre asignaturas en distintos niveles y vislumbrar las dificultades que implica la enseñanza desde la visualización de datos para poder proponer, además de un cambio de contenidos, estrategias pertinentes que apoyen el proceso de enseñanza y aprendizaje.
Materiales y métodos
Este trabajo tuvo un enfoque cualitativo con dos líneas asociadas: por un lado, la exposición de los temas de parte de la docente a cargo de la clase, en donde se siguió la guía constructivista determinada por el MUM para generar el conocimiento de parte de los estudiantes en los temas de interés; por otro lado, la propia investigación, en donde se llevó un proceso guiado por la investigación-acción (IA) para elaborar el plan, los materiales necesarios y dar seguimiento del desarrollo investigativo general. Es necesario apuntar que estas dos vertientes se fueron entrecruzando a lo largo del tiempo que duró el proceso hasta completarlo. Finalmente, hay que señalar que en los contenidos se eligió trabajar únicamente con la unidad temática dedicada a la estadística, dada su estrecha relación con el DataViz.
La IA es un método que permite el encuentro del docente con el estudiante, siendo el primero un organizador de las dinámicas que suceden al interior del aula (análoga o digital), facilitando los procesos, catalizando los conflictos y estando siempre presente para el estudiante como una guía y fuente de consulta (Intriago et al., 2018). En este trabajo se le ha dado mayor realce a la perspectiva del docente, pero sin descuidar la voz del estudiante, pues al ser un proyecto que propone la renovación de un curso, entrelazando sus intersecciones con otra asignatura ubicada en un nivel distinto, las estrategias surgen desde la iniciativa de quien imparte el curso, de su análisis de cómo se va insertando al estudiante y del efecto que la práctica va teniendo. Así, la investigación desde las prácticas docentes adquiere el potencial para transformar la realidad, buscando ayudar al estudiante y generar una educación que responda a las demandas sociales (Stecanela et al., 2019).
Mediante la IA es posible lograr avances teóricos y ampliar el conocimiento práctico sobre el campo temático estudiado, a través del análisis y diagnóstico de la situación o problema identificado para después formular estrategias y aplicarlas en una secuencia de mejora e ir refinando estas estrategias hasta alcanzar el objetivo, resultando en un acercamiento crítico, mejorando con esto la práctica docente y el aprendizaje del estudiante (Intriago et al., 2018; Stecanela et al., 2019). En todo esto es importante señalar que la IA está alineada con el espíritu del modelo constructivista, además de que es socializante (Intriago et al., 2018), con lo que empata perfectamente con el MUM.
Al considerar a la IA una táctica que ayuda al investigador a realizar mejoras en su entorno, esta apoya a construir el camino para lograr el objetivo primario de las instituciones educativas: la constante adecuación y actualización de la calidad de sus servicios, que deben ser sometidos a una constante evaluación informada a través de las necesidades y cambios de la sociedad, cuya finalidad es tener un impacto en las estrategias y políticas institucionales que contribuya a mejorar sus programas educativos, pues esto comprende que se ha revisado y analizado la eficacia curricular de lo que se enseña, así como las estrategias didácticas y los materiales que permiten una experiencia educativa reflexiva para todos los actores involucrados (Cabrera, 2017; Hernández, 2019; Roushan et al., 2016).
Para diseñar la prueba, colaboraron una docente con amplia experiencia en la enseñanza de las matemáticas para diseñadores, un experto en diseño y visualización de información (ambos colaborando en la selección de los sets de datos, los tipos de gráficos que se enseñaron, en la redacción de la problematización de los ejercicios y en el desarrollo de los diferentes cuestionarios implementados durante el proceso) y un estudiante del área de físico matemáticas que apoyó puntualmente en algunos rubros. De esta manera, se planteó un experimento que comprendía la exposición del tema de parte de la docente a cargo de la materia, una prueba práctica, un examen para medir la retención del conocimiento en la memoria y un test para conocer cualitativamente la opinión sobre la experiencia de aprendizaje de los estudiantes en la resolución de problemas matemáticos mediante el DataViz.
La idea, por un lado, es fomentar el pensamiento de diseño al promover en el estudiante la aplicación sistemática del conocimiento aprendido, y que por medio de este pueda hacer una comprobación metódica de la eficacia de las posibles soluciones (Sánchez et al., 2020) al hacer supuestos predictivos sobre cuál sería el mejor tipo de visualización para representar los datos dados. Otro punto importante de esta experiencia es para los docentes, que tienen la oportunidad de ensayar estrategias que permitan un mejor aprendizaje de las matemáticas y su aplicación en la visualización de datos, pues de esta manera es que pueden proponer un rediseño al plan de contenidos de la asignatura, así como afinar la propuesta didáctica para asegurar una calidad de aprendizaje, y con esto generar en el estudiante un conocimiento que perdure para ser aplicado y afinado al llegar a la asignatura de Taller V.
Es decir, se busca comprobar qué tanto el estudiante podía observar, diagramar y cuantificar la problemática que debía resolver, externando un análisis guiado por un pensamiento concreto, objetivo y preciso que daba como resultado un proceso de diseño de información al producir un tipo de visualización concreta (Ponce, 2016). De acuerdo con esto, previamente, los docentes involucrados seleccionaron seis tipos de gráficos (barras, área, circular, radial, histograma, líneas), y de estos, de acuerdo con el tipo de datos proporcionados y con el objetivo enunciado en cada problema de visualización presentado a los estudiantes, había tres que correspondían a un resultado óptimo y tres que eran soluciones no tan precisas. Participaron en el estudio tres grupos de estudiantes de la asignatura de Matemáticas para el diseño del periodo Otoño 2021 (Figura 2); sin embargo, durante la aplicación en cada parte de la secuencia participaron un número diferente de estudiantes debido a que algunos presentaron problemas con su red de internet o tuvieron que vacunarse por la pandemia Covid-19. Aquéllos que estuvieron presentes resolvieron los ejercicios de forma análoga, sin la ayuda de algún software especializado.
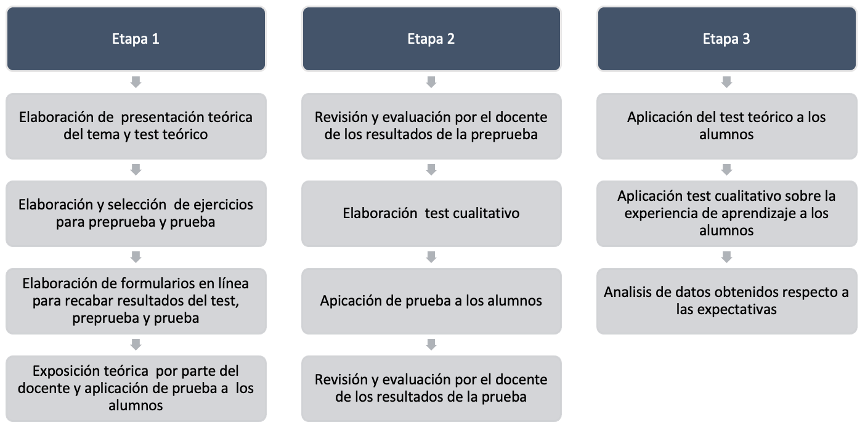
El estudio consistió en tres etapas (Figura 3) que a continuación se describen.
La primera etapa consistió en una presentación del tema con información teórica sobre conceptos básicos, tipos de variables que pueden graficarse y la clasificación de gráficos. Se explicaron cada uno de los seis tipos de gráficos elegidos, y se proporcionó una serie de recursos didácticos (lecturas especializadas y videos) de los que los estudiantes pudieran apoyarse para resolver los ejercicios propuestos.
Se elaboró una presentación teórica sobre conceptos básicos de estadística, la clasificación de los diferentes tipos de gráficos, especificando sus componentes y esquemas, además de un análisis sobre cuándo utilizar cierto modelo de gráfico basado en el objetivo de representación de la información. Esta se presentó a los estudiantes durante la primera etapa del proceso de enseñanza. Al mismo tiempo que se elaboró la presentación, se fueron generando las preguntas que correspondían al test teórico que se aplicaría a los estudiantes al finalizar el experimento.
Después, se procedió a seleccionar los datos que se utilizarían en los ejercicios de las pruebas, para ello se analizaron diferentes fuentes confiables en internet:
-La base de datos México en Cifras, del Instituto Nacional de Estadística y Geografía;
- La base de datos mundial sobre la desigualdad en la educación, de la Organización de las Naciones Unidas para la Educación, la ciencia y la Cultura (UNESCO);
- El sitio web de la Asociación de Internet en México, que provee diversos estudios sobre comercio electrónico, hábitos de internet de los internautas, comercio móvil, entre otros.
Las anteriores fueron las principales bases de datos que se consultaron para extraer los datos que conformarían los ejercicios, y para complementarlas se buscaron libros y artículos que proporcionaran datos comprensibles que fueran interesantes para los estudiantes.
Después, se llevó a cabo una reunión con los investigadores donde se discutieron los diferentes ejercicios propuestos. En esta sesión se analizó conjuntamente la pertinencia de estos ejercicios y se eligieron los que se utilizarían para la preprueba (ejercicios guiados por el docente), así como los pertenecientes a la prueba. También se dilucidaron los contenidos que debían pertenecer a la posprueba. Finalmente, se generó un formulario para cada prueba a través de la herramienta Forms de Microsoft.
Posteriormente, en una sesión del curso, se proporcionó un ejercicio para resolver cada tipo de grafico seleccionado para el experimento, el cual fue guiado por la docente, con treinta minutos para la resolución de cada gráfica, y en donde se consideró la experiencia previa del estudiante en la construcción de gráficos.
Para la segunda etapa, se solicitó al estudiante documentarse a partir de los materiales elegidos y proporcionados por la docente a través de la plataforma digital utilizada en la asignatura. En la clase subsiguiente se aplicó la prueba integrada por tres ejercicios previamente seleccionados, donde el estudiante debía analizar la información y decidir qué tipo de gráfico utilizaría para la representación visual de los datos y entonces llevar a cabo el proceso de construcción de la solución visual. Para la elaboración y evaluación de cada ejercicio, la lógica del procedimiento seguía esta secuencia: al estudiante se le presentan tres ejercicios, cada uno con una solución correcta, determinada por la enunciación del problema, el cual se acompañaba de un set de datos, y había en total seis tipos de gráficas a elegir para resolver el problema. De esta manera, la evaluación tenía el parámetro de que una solución se consideró correcta cuando el estudiante desarrollaba una visualización eligiendo el tipo de gráfico idóneo, el que mejor representaba la información de acuerdo con lo que se solicitaba en el problema; y la respuesta era incorrecta cuando se desarrollaba un tipo de gráfico distinto. Cabe mencionar que la determinación acerca de qué tipo de gráfico era la solución idónea se hizo de acuerdo con lo hallado en las revisiones de la literatura sobre el uso de cada tipo de gráfico y considerando los acuerdos en las sesiones de los investigadores (todo estuvo alineado con la explicación que se les dio a los estudiantes en la sesión teórica.)
En la tercera etapa, se aplicó una prueba sobre los conceptos teóricos para saber si el estudiante retuvo el conocimiento, además, se aplicó un test cualitativo para conocer cómo fue su experiencia de aprendizaje de estos temas. Terminado esto, de parte de los investigadores se procedió a analizar los datos obtenidos, a la luz del marco teórico y de las expectativas que se tenían.
De acuerdo con lo revisado en la literatura, para este estudio se consideró que, a lo largo del proceso educativo de los estudiantes, durante la educación básica a nivel primaria, secundaria y bachiller, el estudiante ha generado experiencia en el área matemática en general y en particular de la estadística, desde procesos de lógica, operaciones básicas, recolección de datos, representación y graficación de datos y evaluación de aspectos importantes de los datos.
Resultados
Parte del objetivo de la prueba era determinar cómo, a partir de las estrategias didácticas aplicadas por la docente, los estudiantes habían asimilado el conocimiento que se podía hacer visible en la aplicación de sus propias estrategias y herramientas para trabajar, hacer algo y dar una solución visual a los sets de datos que se les proporcionaron bajo un esquema de problema matemático.
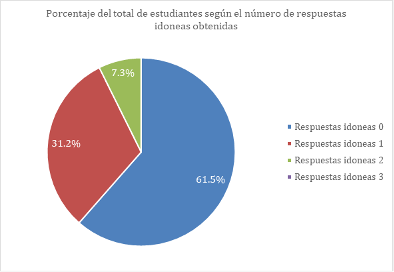
Si bien los resultados obtenidos no son óptimos (Figura 4), los rubros de práctica y de retención en la memoria, interpretados desde los resultados de los cuestionarios de prueba práctica y prueba de conocimiento, señalan que los estudiantes tuvieron dificultades debido a la falta de asertividad en escoger el tipo de visualización y a la poca retención en la memoria. Esto es porque, para la elección del gráfico adecuado, el estudiante no solo debe memorizar conceptos matemáticos, sino realizar un análisis que permita determinar el tipo de gráfico idóneo para transmitir el mensaje deseado; es decir, debe ser claro para qué se necesita. Además, de acuerdo con Infogram (2022), organización especializada en visualización de datos, una persona con conocimiento en el tema debe también poder identificar cuántas variables quiere mostrar, cuántos puntos desea visualizar y qué escala sería adecuada.
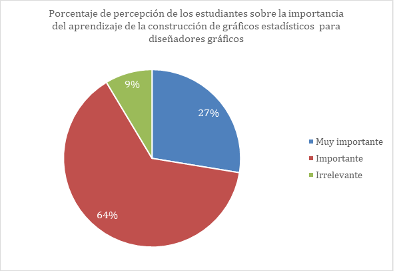
Por otro lado, el cuestionario donde se les preguntó sobre su experiencia con el tópico (Figura 5) es un indicador de que el tema tiene un sentido y los estudiantes lo perciben; sin embargo, esto no se alinea con su desempeño.
De la propuesta de solución que los estudiantes presentaron, podemos observar que su principal desafío fue decidir qué tipo de gráfico estadístico era el idóneo para representar los datos solicitados. Además, se puede distinguir que en algunos casos se omitió colocar el título del gráfico o su descripción no fue clara, no se utilizaron líneas de división, no se determinaron las leyendas, tampoco se usaron etiquetas, y se omitió el uso de pie de gráfico (Figura 6).
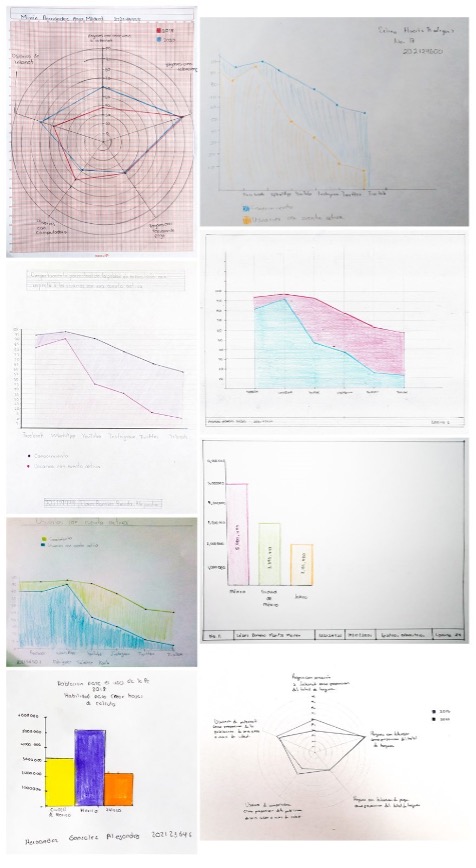
Fuente: Registro fotográfico de los autores.
Figura 6 Ejemplos del material desarrollado por los estudiantes.
Para el análisis del problema, se requiere de la capacidad de razonamiento del estudiante para poder extraer, agrupar y representar datos en un gráfico. Sin embargo, podemos identificar que, a pesar de utilizar el tipo de grafico idóneo, no en todos los casos el estudiante comprende lo que se le solicita representar, como se puede ver en la Figura 7.
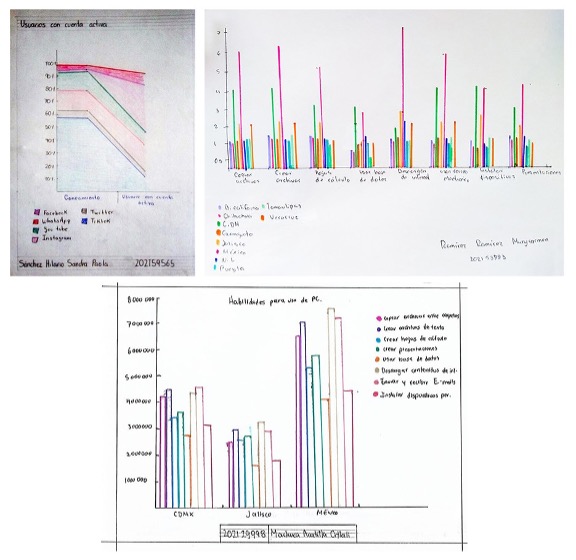
Fuente: Registro fotográfico de los autores.
Figura 7 Ejemplos de gráficas idóneas resueltas erróneamente.
Estos resultados dan información para identificar los puntos de atención que se deben considerar tanto en la propuesta de rediseño de la asignatura como en las estrategias educativas específicas a implementar durante el proceso de enseñanza y aprendizaje de la asignatura.
Al tomar como punto de referencia a los estudiantes que obtuvieron los mejores resultados (Figura 8), estos fueron los que mostraron evidencia de relacionarse más con los materiales proporcionados como apoyo, así como de ser más consistentes en su desempeño durante las actividades de la clase. Con esto se evidencia que, al implementar estrategias de trabajo durante las sesiones normales de clase, estas estrategias se deben emparejar con evidencia que refuerce la importancia del tema, por ejemplo, evidencia derivada de aplicaciones del DataViz en diferentes medios, o que los alumnos investiguen por su cuenta para reforzar la percepción y la actitud al desarrollar los ejercicios, de manera que impacte en su práctica y retención del conocimiento.
Discusión
El INEC (2017) menciona que las habilidades necesarias para tener información estadística de calidad son: relevancia, exactitud, credibilidad, oportunidad, accesibilidad, interpretabilidad y coherencia. Basado en esto, es de suma importancia que el estudiante de la licenciatura en diseño gráfico adquiera conocimientos y desarrolle habilidades encaminadas con dicho objetivo.
Según Arteaga et al. (2016) y Friel et al. (2001), los estudiantes deben conocer los elementos estructurales de construcción de los gráficos usados para visualizar los datos, como usar etiquetas y títulos para identificar el tema y que aportan información sobre el contenido contextual del gráfico y sus variables representadas. Además, deben conocer los procesos que dan pie a transformar la información de datos sueltos a unidades informativas, las unidades de las magnitudes en juego e identificar los ejes, escalas y marcas de referencia necesarias para elaborar y leer la gráfica. Todo esto se les indicó a los estudiantes durante la sesión de clase y estaba presente en los materiales asignados, pero no tuvo una retención óptima en su memoria.
Esto repercutió en la forma en que crearon sus soluciones visuales, alineándose con lo que dice la literatura. Por ejemplo, una de las principales problemáticas de los estudiantes que mencionan Arteaga et al. (2016) es que utilizan gráficos incorrectos al tipo de problema o a la variable que están manejando; además, el autor mostró que persisten errores de convención en títulos, etiquetas, ejes, escalas y proporcionalidad en pictogramas, situación que pudimos corroborar durante el desarrollo de este experimento. En la revisión de los resultados, detectamos complicación para interpretar los datos, errores en los títulos y etiquetas y confusión entre tipos de gráficas parecidas, pero que explican información distinta.
Los resultados obtenidos indican que, para crear un vínculo más fuerte entre la asignatura de Taller V y la de Matemáticas para el diseño, el camino está en replantear los contenidos de la asignatura de Matemáticas para el diseño, al hacer hincapié en proponer unidades conceptuales con menor extensión en cantidad de temas, pero con mayor profundidad del conocimiento y buscando establecer una conexión significativa entre los datos y su relación con el mundo real, tal y como dice la literatura (Bertling et al., 2021). El proceso de enseñanza requiere de un aprendizaje progresivo al encaminar a los estudiantes por los diferentes tipos de gráficos matemáticos, que se apropien de los conceptos estadísticos, enfocando la enseñanza en las propiedades y ventajas de cada visualización, enfatizando que la elección debe hacerse de acuerdo a objetivos de comunicación de la información y a pensando en un contexto y grupos humanos específicos.
El lograr que los estudiantes se apropien del conocimiento básico de estadística y matemáticas para la clase de Taller V significa actualizar el desarrollo de proyectos a través del conocimiento previo, para establecer ejercicios que aporten experiencias significativas que den pie a un conocimiento con mayor profundidad y que vaya de la mano con el desarrollo de una mayor pericia para resolver las demandas requeridas de diversas áreas laborales en la actividad del diseño.
Como parte de la discusión, es valioso señalar que se han identificado las siguientes debilidades en el proceso realizado: se requiere tener mayor cantidad de ejemplos visuales que fomenten el interés en la visualización de los datos, desarrollar estrategias para organizar los tiempos de la clase y dedicar más espacio para el tema de estadística, así como buscar estrategias para motivar a los alumnos en el tema. Dentro de las limitaciones que tiene este estudio, se encuentra que, al ser un primer acercamiento, y al haber aplicado implementaciones tan solo a tres grupos, durante un único periodo de tiempo, no se pueden hacer conclusiones que sean generalizables al problema; sin embargo, este es un primer paso, y los resultados obtenidos ayudan a establecer el camino a seguir.
Durante este estudio se han identificado la áreas de oportunidad para mejorar la planificación de la estrategia docente: desarrollar materiales educativos que refuercen la estructura técnica de la construcción y composición de cada gráfico; tener en mente la tendencia de los alumnos a confundir la función de los gráficos; reforzar, durante las explicaciones y los ejercicios en clase, para qué sirve cada gráfico; implementar herramientas en la forma de pre-pruebas para conocer con mayor detalle el conocimiento previo de cada estudiante, así como post-pruebas para conocer su experiencia y generación de conocimiento sobre temas específicos de estadística; y mostrar más ejemplos que vinculen las posibilidades que existen en la visualización de información, reforzando así el vínculo con la clase de Taller V.
Se espera que al considerar todo esto, los hallazgos realizados permitan que se aumente el nivel de calidad del proceso de enseñanza y aprendizaje, entendiendo esto como la facilidad que tengan los alumnos para identificar el tipo de gráfica idónea de acuerdo con el problema enunciado, una lectura, manejo y selección eficiente de los sets de datos, además de una solvencia en la interpretación de gráficas estadísticas que puedan encontrar en su vida en general.
Ha de decirse que tal vez el principal hallazgo sea que los estudiantes perciben la importancia del tema, es decir: conocer sobre estadística y saber gestionar datos, pero hace falta tanto la motivación personal como el desarrollo de estrategias educativas que faciliten el acercamiento a un tema que resulta complicado. Si se rompen estas barreras, esto permitirá generar un aprendizaje significativo que se lleva de la mano con el desarrollo de habilidades valiosas para la práctica en diseño.
Los autores coincidimos en que “a través de estrategias de aprendizaje es posible lograr buenos resultados para combatir la ansiedad hacia las matemáticas y ayudar a los estudiantes a aproximarse a los números de manera que puedan entenderlos y aplicarlos en su práctica profesional” (Ponce, 2016). Asimismo, estamos de acuerdo en que la adquisición de competencias sucede entre todos los co-participantes del proceso educativo, estudiantes y profesores, pues solo reconociendo esta relación intrínseca es que podemos hablar de una auténtica enseñanza. Este reconocimiento va a resultar en una dinámica que motive a estos actores hacia un verdadero encuentro (Intriago et al., 2018), tanto entre ellos como con el tema y el área de conocimiento estudiado, es decir, con el cruce entre las matemáticas y el diseño.
Las habilidades que se pueden desarrollar al sistematizar el pensamiento del diseño de información permiten madurar el pensamiento crítico, y esto aporta competencias relacionadas con la investigación, la resolución de problemas de forma visual, una mejor argumentación en el proceso de diseño y, a nivel personal, al establecer un juicio sobre la información con la que interactuamos, se logra una mayor independencia y libertad (Ponce, 2017). Todos estos son beneficios que se pueden desarrollar desde la formación temprana básica del diseñador, para que así se potencie su efecto a lo largo de su proceso educativo universitario.
Conclusiones
El DataViz es un área estratégica para el diseñador gráfico que hace diseño de información, y su base es el pensamiento matemático y el diálogo que debe existir con los numerales que conforma la estadística. Debe desarrollarse desde etapas tempranas de su formación profesional, pues esto facilitará el acercamiento a un pensamiento que dé forma a soluciones creativas con los datos y que estas no solo sean estéticamente aceptables, sino que cumplan una función comunicativa y promuevan el entendimiento de lo que se está mostrando.
Esto es posible al replantear los vínculos que existen desde el nivel básico de la educación universitaria en diseño, para que, al llegar a otros periodos formativos, se tengan las habilidades elementales para trabajar con información numérica. Esta prospectiva de cambio hace necesaria la actualización curricular, ya que los estudiantes al ser especialistas en comunicación visual deben ser capaces no solo de leer e interpretar datos, sino de producir representaciones de estos de forma eficaz.
Aplicar la investigación-acción permitió una dinámica de trabajo en donde se escucha la voz de los participantes en el proceso de enseñanza y aprendizaje. En particular, IA fue útil para guiar la investigación dando un énfasis en las experiencias cualitativas de los docentes involucrados, para modernizar los contenidos de la asignatura de Matemáticas para el diseño, enfatizando su vínculo con la asignatura de Taller V.
Se reconoce que los estudiantes presentan dificultades para acercarse al tema, los problemas detectados son: tener un conocimiento previo insuficiente, se requiere de mayor dedicación durante las sesiones y para consultar los materiales proporcionados, así como tener mayor concentración al abordar las actividades y pruebas. Y de parte del docente, se identificaron las siguientes áreas de mejora: dedicar mayor tiempo a la asesoría, apoyarse con materiales didácticos personalizados para las necesidades de cada grupo y aplicar más actividades de solución de ejercicios previas a la evaluación, lo que implica que se debe considerar reestructurar las secuencias didácticas en la planeación y ejecución de actividades, buscando promover la profundidad de contenidos en lugar de la cantidad de temas vistos.
Las contribuciones de este artículo son, para la literatura, aumentar el cuerpo de conocimiento sobre la relación entre matemáticas y diseño; para la docencia, se contribuye a entender el tipo de estrategias a seguir durante el proceso de enseñanza y aprendizaje de los diseñadores cuando aprenden el vínculo entre estadística y visualización; y para la gestión educativa, se puntualiza la necesidad de actualización de los planes de estudio en relación a las demandas sociales de empleadores-egresados. Finalmente, un tema central es que el tópico del artículo pone atención en el desarrollo de saberes y habilidades que ayuden a los estudiantes a ser participantes sociales activos y críticos de la información que reciben en distintos medios.
Este estudio identifica las áreas de intersección entre la enseñanza de las matemáticas con la aplicación de la visualización de datos desde el diseño de la información, para mejorar la educación de los diseñadores gráficos, al plantear un primer diagnóstico para mejorar el proceso de enseñanza y aprendizaje, buscando elevar el nivel de alfabetización de los estudiantes y cómo se puede mejorar su desempeño en estas áreas.
Si bien todavía hay un camino por recorrer para un resultado óptimo, la resolución de este tema tiene un gran impacto en el proceso formativo, lo que se espera conlleve a personas mejor preparadas para resolver los problemas que enfrenten, es decir, que sean profesionistas con herramientas conceptuales y prácticas que les permitan diseñar soluciones más eficientes y ciudadanos conscientes que puedan tener una mejor interpretación de la información estadística que reciben de su entorno.
Conflicto de interés
Los autores no tienen conflictos de interés con instituciones u organizaciones gubernamentales, académicas o privadas relacionadas con los temas que trata esta investigación.











 text new page (beta)
text new page (beta)