1. Introduction
Recently, there have been several scientific studies and research either experimental or theoretical have focused on the various physical properties of half Heusler materials and their large-scale applications. These studies enable us to identify the various fields in which they can be used. We have discovered that these materials have important properties that can be used in diverse technologies and industrial domains as in: optics, semiconductor, spintronic applications, solar cells, optoelectronic devices and thermoelectrics [1-7]. Half Heusler materials are an interesting category of ternary in-termetallic materials having a general formula XYZ. These materials crystallize in a face centered cubic crystal structure MgAgAs structure type) in F-43m (216) where X and Y are transition metals or metal elements while Z comes from the main group element [8,9]. Compounds containing elements such as Ni, Bi, Y and Sc in their composition have great interest in half Heusler materials, this is why we see that many researchers are studying its different characteristics, Romaka et al. [10] analyzed several properties of half Heusler Y-Ni-Sb and Tm-Ni-Sb and found that these materials are semiconductors. Sarwan et al. [11] discuss the physical properties of half-Heusler YNiPn, the calculated values show that YNiPn is mechanically stable, ductile and observed in electronic properties that YNiPn are indirect narrow bandgap semiconductors provoking a potential candidate for many semiconducting and thermoelectric Applications. Guo [12] study the effects of spin-orbit coupling on the electronic structures of half-Heusler ANiB (A = Ti, Hf, Sc, Y; B = Sn, Sb, Bi), the study reveals that the strength of SOC influences on valence and conduction bands near the Fermi level is shown by the related gaps and in removing the band degeneracy. Majumder et al. [13] justify the crystal stability and origin of transport properties in half Heusler ScPtBi, the obtained calculation shows that ScPtBi has good alloying ability as well as structural stability. Winiarski et al. [14] investigated the electronic structures of half Heusler Alloys XNiBi, the results exhibit features that promote an occurrence of high thermoelectric power factors. A.Bano [15] discuss the Strain effect on electronic and elastic properties of ScNiBi, they found that Sc-NiBi at small strain, shows dynamic stability but for higher strain the material show instability.
In this investigation and based on first-principles calculation, we study the structural, electronic, optical and elastic properties of half Heusler compounds MNiBi (M = Sc and Y). We have identified which approximations among LDA and GGA can give us the best possible value of lattice parameter and allows us to obtain good results for the structural properties. We used the Tran-Blaha modified Beck Johnson exchange (TB-mBJ) potential [16,17], which yields band gaps in better estimation compared to LDA and GGA approximations. Optical parameters like the real and imaginary dielectric constant, reflectivity, absorbtion, refractive index, and extension coefficient were calculated as a function of EM radiation energy. Our compounds have a semiconductor character, for this reason we have neglected the intraband transitions in this study. In addition, this study gives us an overview of the elastic and mechanical properties of our half Heusler alloys MNiBi (M = Sc and Y).
This paper is divided as follows: Section 2 describes the methodology details, the obtained results and discussion are presented in Sec. 3 and finally, the conclusion is given in Sec. 4.
2. Methodology details
For investigating the structural, electronic, optical and elastic properties of our half Heusler compounds MNiBi with (M=Sc and Y), we have used the technique of the Full Potential Linearly Augmented Plane Wave (FP-LAPW) [18] as implemented in the WIEN2k package [19], we have treated effects of the exchange-correlation (XC) using both the local density approximation LDA [20] and the generalized gradient approximation GGA of Perdew-Burke-Ernzerhof (PBE) [21]. To get a good result in electronic properties, Tran and Blaha modified Becke-Johnson potential (TB-mBJ) [22] is employed to enhance the calculations of the bandgap.
In this scheme, the kinetic energy cut off which separated the core and valence states is chosen to be -6Ry. The angular momentum is set to be lmax = 10 , Furthermore, the RMT * Kmax = 9 was used where RMT is the smallest of the (MT) sphere radii and Kmax is the largest reciprocal lattice vector used in the plane wave, K-Points in the first Brillouin zone is selected as 6000 and Gmax is set to be 12. We have calculated by optimization method the muffin-tin radii (RMT) of different atoms in the unit cell, the values found are: Sc :1.9; Ni:2.2; Bi:2.5 for ScNiBi and Y:2.2; Ni:2.0; Bi:2.5 for YNiBi. The convergence criterion was considered when we obtained total energy less than 10-5 Ry.
In order to better understand and interpret the results that will obtain from these technical considerations, we declare the electronic configuration of each of the elements that form our compounds ScNiBi and YNiBi.
Sc: [Ar] 4s2 3d1
Y: [Kr] 5s2 4d1
Ni: [Ar] 4s2 3d8 or [Ar] 4s1 3d9
Bi: [Xe] 6s2 4f14 5d10 6p3
We used for calculations of elastic constants the package IRelast modeled by M. Jamal [23]. This package is integrated with WIEN2K.
3. Results and discussion
3.1. Structural properties
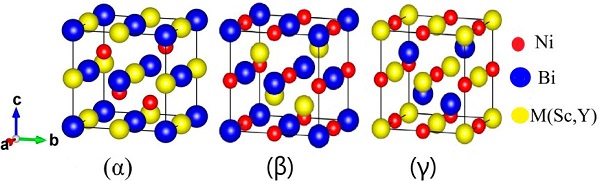
The half-Heusler alloys crystallize in the structure of non-centrosymmetric cubic C1 b phase having a structural formula XYZ with space group F-43 m (No. 216), in this case there may be three ways (phases α, β and γ) to locate the X, Y and Z atoms in the unit cell. The location of atoms is given in Table I. The Crystal structure of ScNiBi and YNiBi half-Heusler alloys for three phases (α, β and γ) is illustrated in Fig. 1.
Table I he sites occupied by the M(Sc and Y) , Ni and Bi atoms in the α, β and γ phases.
| Compounds | M(Sc and Y) | Ni | Bi |
|---|---|---|---|
| α phase | 4b(12, 12, 12) | 4c(14, 14, 14) | 4a(0,0,0) |
| β phase | 4c(14, 14, 14) | 4a(0,0,0) | 4b(12, 12, 12) |
| γ phase | 4a(0,0,0) | 4b(12, 12, 12) | 4c(14, 14, 14) |
Using the LDA and GGA approximations, the calculated total energies of ScNiBi and YNiBi compounds are plotted as a function of the unit cell volume for different phases (α, β and γ). The results are shown in Fig. 2. From Fig. 2 we can see that for each compound, the lowest total energy is shown in phase α compared to the other phases β and γ. And according to this, it can be stated that phase a is the most stable structure. The calculated total energies versus volume are fitting to Murnaghan's equation of state [24]:
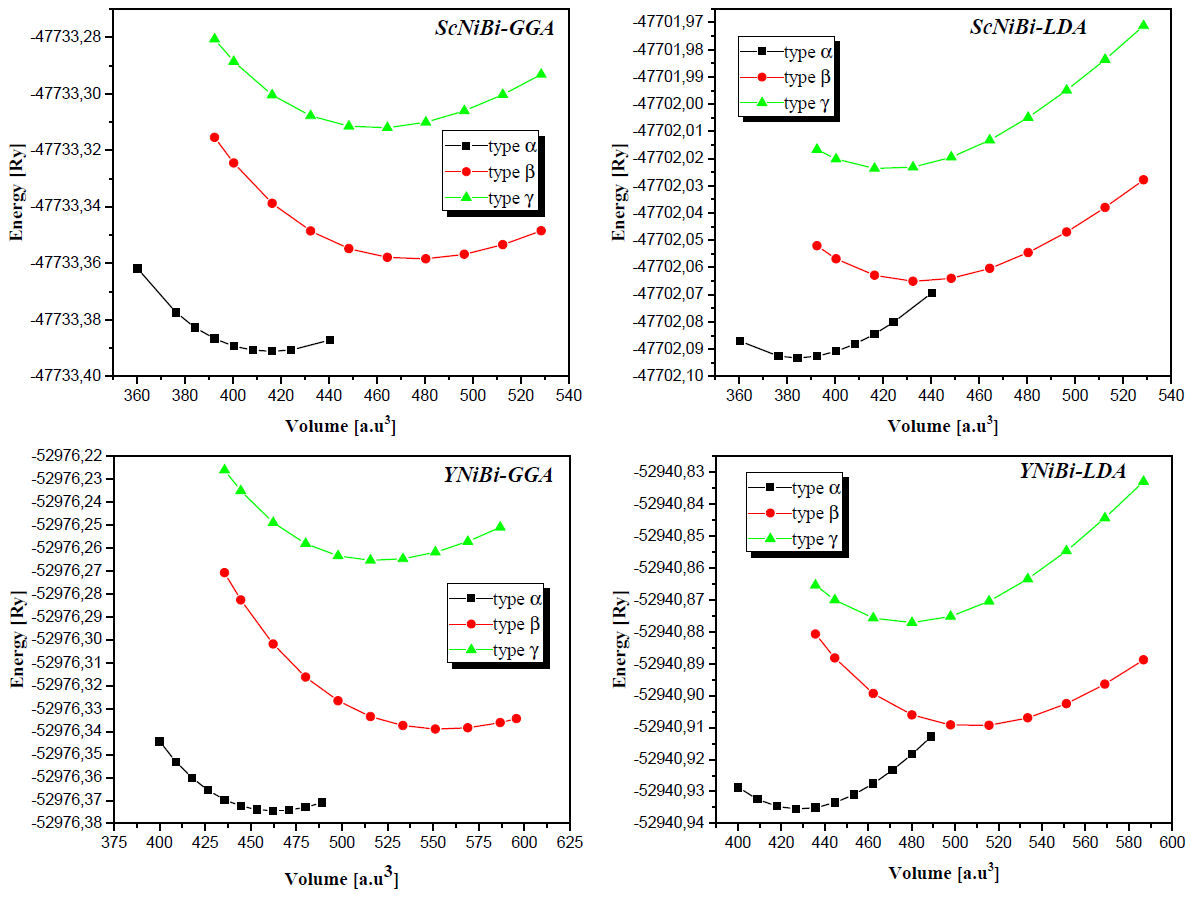
Figure 2 Total energy as a function of volume in three type of atomic arrangements for the MNiBi (M= Sc and Y) alloys.
where E is the equilibrium energy, V the atomic volume, V0 the atomic volume at P = 0 GPa, B0 and B'0 are the bulk modulus and its pressure derivative respectively. We have fitting this equation in order to determine different structural properties at the optimized state such as the lattice parameter a (Å), bulk modulus B (GPa) and the derivative of the bulk modulus B' (GPa).
The calculated values are summarized in Table II where we can observe clearly that the equilibrium lattice parameter is higher for YNiBi than ScNiBi and this in both approximations LDA and GGA, this is due to the high value of Z for Y(Yttrium) than the Sc (Scandium). We can see also from Table II that values of lattice parameter for ScNiBi are 6.115 Å and 6.269 Å for LDA and GGA approximation respectively, and for YNiBi are 6.330 Å and 6.498 Å for LDA and GGA approximation respectively. From this result, values of lattice lattice parameter are better matched in GGA approximation than LDA approximation, our values obtained for both compounds are in overestimation about Δ = + 1.01% in GGA and Δ = + 1% in LDA compared with experimental [25-27] and theoretical result [12,14,28,29]. The values obtained of the Bulk modulus for both compounds ScNiBi and YNiBi in LDA and GGA approximations means that ScNiBi and YNiBi are incompressible alloys.
Table II Calculated values of structural parameters for MNiBi (X = Sc and Y) at the optimized state.
| Compounds | Lattice constant, ao(Å) | Bulk modulus, B(GPa) | Derivative of B, B' |
|---|---|---|---|
| ScNiBi-LDA | 6.115 | 109.57 | 4.729 |
| ScNiBi-GGA | 6.269 | 89.45 | 4.363 |
| Other theor/exp | 6.191 [28],[12], 6.101 [14], | ||
| 6.1785 [27] | |||
| YNiBi-LDA | 6.330 | 97.12 | 4.549 |
| YNiBi-GGA | 6.498 | 79.46 | 4.345 |
| Other theor/exp | 6.411 [28],[12], 6.475 [29], | 75.30 [11], | 4.67 [11] |
| 6.328 [14], 6.411 [26], | 80.9 [29] | ||
| 6.4122 [25]> |
3.2. Electronic properties
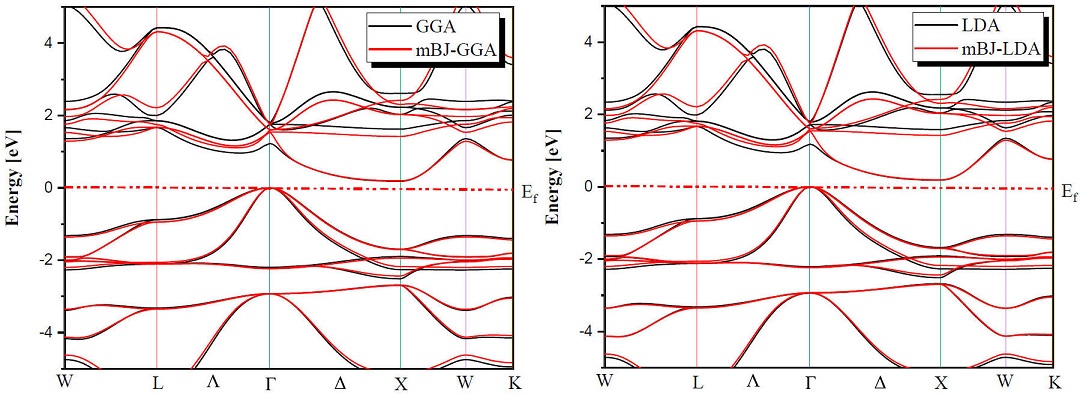
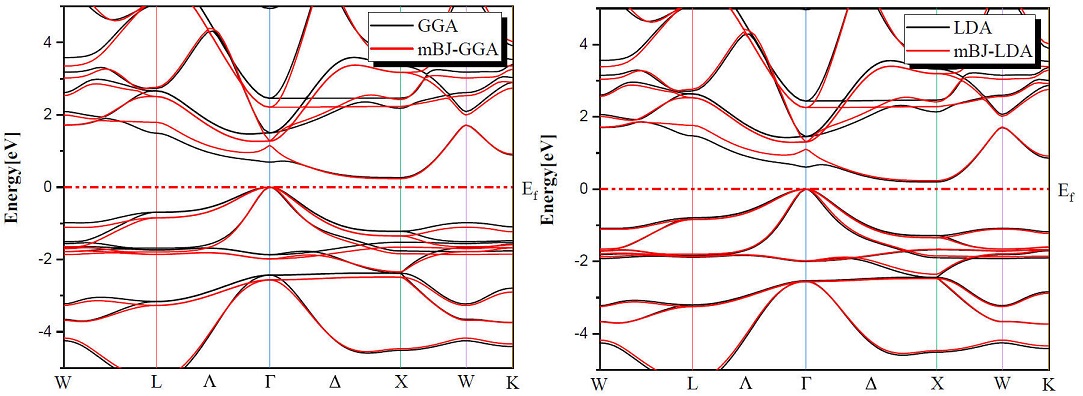
Determination of electronic properties guides us to determine the nature of the studied crystalline solids. In this section we presented the electronic properties of our half Heusler alloys MNiBi (M = Sc and Y) using the equilibrium lattice constants found at the optimized state and examined them by LDA, GGA and TB-mBJ (modified Becke-Johnson) exchange correlation functionals for the comparison between them. Figures 3 and 4 shows the band structures of ScNiBi and YNiBi by using LDA, GGA and TB-mBJ, the Fermi level, which separates valence and conduction states is set at 0 eV. As observed in Figs. 3, 4 The conduction band minimum (CBM) and the valence band maximum (VBM) are not located at the same symmetry point, CBM falls at the X point and VBM situated at the Γ point, therefore both half-Heusler alloys (ScNiBi and YNiBi) show indirect bandgap (Γ⟹X).
The calculated indirect band gaps are recapitulated in Table III. We can observe clearly from Table III that the band gap is increasing when going from LDA and GGA to TB-mBJ, consequently, the usage of TB-mBJ potential in contrast to the LDA and GGA approximation increases the bandgap. The energy gap is a very important indicator for optoelectronic applications, our value found using mBJ-LDA deviates by 5.45% from the experimental value and by 6.66% from the Ref. [12], from mBJ-GGA; our value is closed of Ref. [12]. According to this result, we can see easily that the use of the TB-mBJ approach improves the value of the bandgap. The values obtained in this investigation indicate that our study alloys ScNiBi and YNiBi present a semiconducting nature and this result is in reasonable agreement with previous studies [11,12,14,15,25,28].
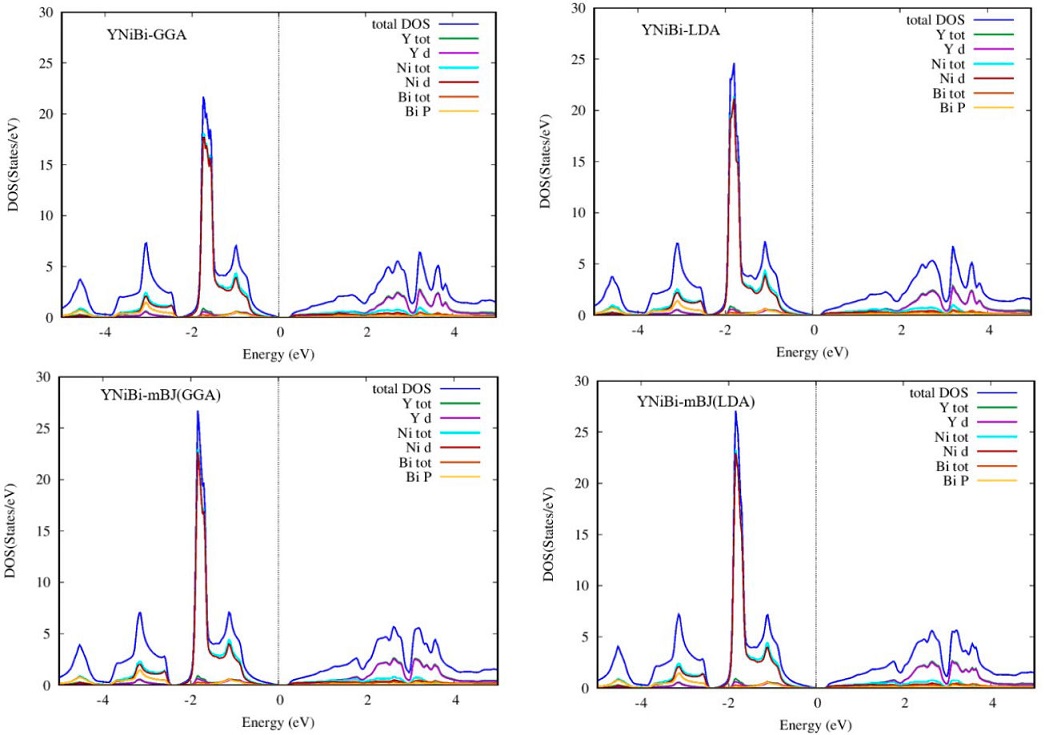
In order to better understand the nature of the electronic band structure, we analyze the contribution of different atomic states and for this, we calculate the total and partial density of states (DOS) of our HH ScNiBi and YNiBi Compounds with LDA, GGA and TB-mBJ functionals. Figures 5 and 6 display the total and partial density of states. It can be observed in LDA, GGA and TB-mBJ approach for both compounds ScNiBi and YNiBi that in the valence band with energy range from -5 eV to 0 eV, the dominating contribution is coming from d state of Ni hybridized with a small contribution of the p state of Bi. whereas the d state of both Sc and Y in all approaches used in this study are dominating majorly in the conduction band region ranging from 0 to 5 eV.
3.3. Optical properties
In this section and based on GGA exchange correlation functionel, we analyzed the optical properties of our cubic half Heusler compounds ScNiBi and YNiBi. Optical properties allow us to understand the interaction that can occur between electromagnetic radiation (EM) and materials and the applications of this materials in various optoelectronic technologies. from the complex dielectric function ϵ(ω) given by Ehrenreich and Cohen [30] (2), we can deduce almost of optical properties such as dielectric function ϵ(ω), optical conductivity σ(ω), absorption coefficient α(ω), extinction coefficient κ(ω) refractive index n(ω):
where ϵ1(ω) represents the electronic polarizability [31] under incident electromagnetic radiation and ϵ2(ω) describes the real transition between the occupied states in valence band and unoccupied states in conduction band while we can express ϵ2(ω) from [32]:
where P, ω, e and m represent the dipole matrix, photon frequency, electron charge and electron mass respectively. Ei is the electron energy of the initial state (the valence band), Ej is the electron energy of the final state (the conduction band), and fi signifies the Fermi distribution.
The real part ϵ1(ω) are determined from the imaginary component of dielectric tensor ϵ2(ω) by using the Kramers-Kronig relations [33,34]:
where M is denoted as the base value of the integral.
Absorption coefficient α(ω) and refractive index n(ω) and other optical parameters are determined with the help of ϵ1(ω) and ϵ2(ω) of the dielectric function [35]:
For the equilibrium ground state of our compounds MNiBi (M=Sc, Y), the optical parameters have been calculated with energy up to 13 eV of the incident EM radiation and they are presented in Figs. 7-12.
3.3.1. Dielectric functions
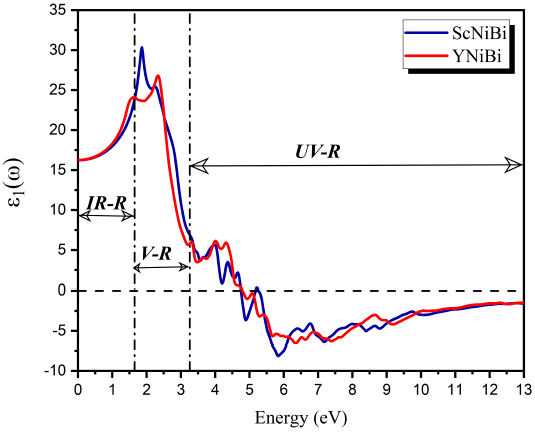
From Fig. 7, we can clearly observe that at ω = 0, the value of ϵ1(ω) that is called static dielectric is 16.23 and 16.26 for ScNiBi and YNiBi respectively. From this symbolic point, the curve increases and takes positive values in IR-R and V-R which mean that EM radiation spreads through the compounds under study, seeing for the two compounds a rapidity in the increase until the curve reaches the maximum in the Visible region V-R, showing a peak with value of 30.3 at 1.86 eV for ScNiBi and a peak with value of 26.81 at 2.33 eV for YNiBi. Proceeding from this value, we noted that the curve decreases from V-R to ultraviolet region UV-R until canceled in 4.75 eV for ScNiBi and 4.79 eV for YNiBi. from the canceled point in the UV-R, we observe that ϵ1(ω) takes negative values what we can explained that our study compounds reflects all incident EM radiation and our compounds ScNiBi and YNiBi exhibits a metallic behavior.
The imaginary part ϵ2(ω) of the dielectric tensor elucidate the absorption of EM radiation [36]. Figure 8 illustrate the variation of ϵ2(ω) in function of EM radiation energy. The threshold energy is observed at zero frequency. For ScNiBi is noted ΔEog = 0.201 eV and for YNiBi is ΔEog = 0.231 eV. This values indicates an optical band edge of both compounds MNiBi (Sc, Y) at the equilibrium state which was due to transition Γv → Xc between the highest valence band and lowest conduction band. This result of optical band edge of our study compounds is perfectly matches with that obtained by band structure. We notice from this figure that there is a rapid rise of the curve in V-R that reaches its highest values such as 25.12 in 2.92 eV for ScNiBi and 24.87 in 2.6 eV for YNiBi, and from this maximum a decrease with some important peaks in the UV-R in interval from 3.9 to 5.5 eV. These peaks due to the different electronic transition inter-band between valence band and conduction band.
From these findings, it's can be concluded that our compounds MNiBi (M=Sc, Y) have a great absorption in the visible region V-R.
3.3.2. Refractive index
The refractive index reports how light propagates in materials, that's why it's important for photoelectric applications. The curve of refractive index n(ω) of both compounds Sc-NiBi and YNiBi are presented in Fig. 9. From Fig. 9 we can clearly derive the value of static refractive index at frequency zero which is almost the same n(0) = 4.03 for both compounds under investigation. from the Eq. (5) at low frequency, when ω → 0 we obtain the following relation: n2(0) = ϵ1(0), Penn model [37]. Our obtained results satisfy this relation and therefore the accuracy of optical properties result. It is clear from Fig. 9 that refractive index increases to get the highest value in visible region V-R of 5.55 and 5.42 in peak located at 1.86 eV and 2.38 eV and this for ScNiBi and YNiBi respectively. After this maximum, the curve decreases with remarks of some smaller peaks in UV-R.
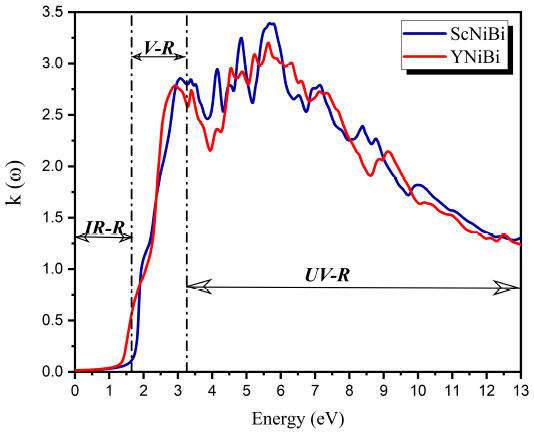
3.3.3. Extinction coefficient
Figure 10 shows the extinction coefficient κ(ω) of ScNiBi and YNiBi. The evolution of the extinction coefficient κ(ω) for both compounds shows that the curve reach a peak in the visible region located at around 3 eV and other important peaks in UV-R in interval from 3.3 to 6.2 eV.
3.3.4. Optical conductivity
Optical conductivity is a parameter which allows us to measure and estimated the amount of optical reflecting from matter and the character of the dependent frequency. Figure 11 shows the optical conductivity as a function of incident EM energy for both compounds ScNiBi and YNiBi. The greater value of optical conductivity is observed in UV-R in the energy range of 4.2 to 5.8 eV with maximum value of 12690 Ω-1cm-1 and 11685.5 Ω-1cm-1 for ScNiBi and YNiBi respectively. We notice that there is a remarkable peak invisible region V-R with value of 9953.87 Ω-1cm-1 for ScNiBi and 9023.47 Ω-1cm-1 for YNiBi.
We deduce that MNiBi compounds have height optical conductivity in V-R and in the region near to V-R included in UV-R.
3.3.5. Absorption
The absorption coefficient determines penetration of incident EM radiation into a material before its absorbed for determining the adequate using in the optical devices. The absorption coefficient α(ω) curve of our alloys are displayed in Fig. 12, It can be seen that the curves are almost compatible for both the alloys, with very minor variations.
From the plotted in Fig. 12, we can see that the highest absorption for both compounds MNiBi comes from UV-R in the range of 5.2 eV to 9.5 eV with values around 180 × 104cm-1. Also, we observed some amount of absorption in the V-R has values of about 82 × 104cm-1.
Our compounds ScNiBi and YNiBi have a high absorption in UV-R and V-R, for this it can be used to absorb visible solar light or UV radiation.
From a global view of the available information, we can't make a comparison of our result because there are no experimental or theoretical data focus the optical properties of our study compounds.
3.4. Elastic properties
For the purpose of understanding the elasticity and the hardness of our crystal studied and to see how this crystal reacts with the deformations and see how resists the different stress applied, we use the precious tools the elastic properties. The half Heusler compounds ScNiBi and YNiBi were investigated in this study have a cubic structure which indicated due of its symmetry that in the tensor Cij we need only three elastic constants, therefore, they are C11 allow us to recognize the degree of elasticity, C12 indicates the strength of shear tensile and C44 demonstrating the strength of diagonal tensile. From these elastic constants, we will be able to know and understand the elastic and mechanical properties of our study compounds such as bulk modulus B, shear modulus G, Young's modulus E, anisotropy factor A and the Poisson's ratio v, by utilizing following formula using the Viogt-Reuss-Hill method [38]:
where GR and GV are the Reuss shear modulus and the Voigt shear modulus respectively, which are given by :
The results we have obtained in structural and electronic properties indicate that the use of the GGA approximation is more compatible with previous experimental and theoretical studies than the LDA approximation. For this, we will use the exchange correlation functional GGA to determine the elastic properties of our half Heusler alloys ScNiBi and YNiBi.
The calculated elastic parameters are summarized in Table IV. From these values of constants elastic, we can see that both compounds ScNiBi and YNiBi satisfies the stability criteria of Born et al. [39], C11 > 0, C44 > 0, C11 - C12 > 0, C11 + 2C12 > 0, Therefore, our half Heusler compounds MNiBi (M = Sc and Y) are mechanically stable.
Table IV Calculated elastic constants Cij(GPa), bulk modulus B(GPa), shear modulus G(GPa), Young's modulus E(GPa), Poisson's ratio v, B/G and Anisotropy factor A, of the half- Heusler alloys MNiBi (M = Sc, Y).
| Compounds | C11 | C12 | C44 | B | G | E | v | BG | A |
|---|---|---|---|---|---|---|---|---|---|
| ScNiBi | 166.2192 | 51.3751 | 58.7116 | 89.656 | 58.194 | 143.528 | 0.233 | 1.54 | 1.02 |
| YNiBi | 161.9927 | 38.4293 | 46.6197 | 79.617 | 52.683 | 129.488 | 0.228 | 1.51 | 0.75 |
The C11 value is higher than C12 and C44, which indicates that these compounds exhibit high resistance to compression. The Bulk modulus values are 89.656 GPa and 79.617 GPa for ScNiBi and YniBi respectively which are in accordance with the values obtained from fitting the Murnaghan's equation of state. The comparison between the two results indicates the accuracy of elastic calculations.
The shear modulus (G) indicates the resistance of compounds to shear deformation, from Table IV we observed that ScNiBi (58.194 GPa) is stiffer than YNiBi (52.683 GPa).
Young's moduli E displays the ratio of linear stress and strain, Table IV illustrates that the ScNiBi have high stiffness (143.528 GPa) compare to YNiBi (129.488 GPa).
We analyzed the elastic anisotropy by utilizing Zener anisotropy factor [40] symbolized by A for both compounds ScNiBi and YNiBi and the result are recapitulated in Table IV. If the obtained A factor equals to 1, it's mean that our compound is isotropic, while when the obtained value is around 1, the compound is elastically anisotropic.
In our calculation, ScNiBi Show a value equal to 1 which indicates that this compound is isotropic. Moreover, YNiBi Display a value less than 1 which means that this compound is elastically anisotropic.
The ductility and the brittleness of a compound are estimating using the ratio of Pugh [41] B/G and the Poisson's ratio v. For the ratio of Pugh, if is bigger than 1.75 the compound is ductile, otherwise, it will be brittle, the obtained values of B/G ratio for our half-Heusler ScNiBi and YNiBi is smaller than 1.75, indicating that our compounds are brittle.
For the Poisson's ratio v which allow us to verify the ductility and brittleness according to the Frantsevich rule [42], if the value v > 0.26, the material is ductile, and if v < 0.26, the material is brittle, and also Poisson's ratio can verify bonding forces contribution in solids [43]. Based on the results for v in Table IV, we can say that the both alloys ScNiBi and YNiBi had an ionic bonding, and also we observe from the values of v that our compounds ScNiBi and YNiBi are brittle.
The Cauchy pressure CP: CP = C12 - C44 can be used either on determination of brittleness or ductility of materials, or to characterize the existing bonding type in materials [44]. If we obtained a positive value, the material has ductile character. Otherwise, is brittle. Based on our calculation, both compounds ScNiBi and YNiBi gives negative values which confirmed the brittleness of our compounds. Furthermore, the negative value obtained indicates an ionic bonding characteristic, which confirms the result obtained with the calculation of the Poisson's ratio.
To the best of our knowledge, There are no theoretical and experimental data available for comparing the calculated results. Thus, we consider this study as a theoretical prediction.
4. Conclusion
In this study, we have investigated the structural, electronic, optical and elastic properties of half Heusler compounds MNiBi (M= Sc and Y) by first-principles calculations using FP-LAPW method within the LDA, GGA and TB-mBJ exchange correlation functionals. GGA functional has given a lattice parameter value and other structural properties identical to the available experimental and theoretical data than using LDA. For this reason, we have adopted it for calculating the elastic and optical properties.
The electronic band structures of our half Heusler compounds ScNiBi and YNiBi show an indirect bandgap with an energy range from 0.185 eV to 0.230 eV indicating a semiconducting nature. It is clear from the obtained result that utilizing the functional TB-mBJ provides a better estimation of the bandgap energies as compared to those computed with LDA and GGA.
We observed from the obtained result ofelastic properties that our half Heusler alloys fulfill the criteria of stability and therefore are mechanically stable.
The calculation of electronic, optical and elastic properties shows that both compounds ScNiBi and YNiBi have an indirect bandgap semiconductor character with high absorptivity of the electromagnetic radiations in visible and ultraviolet region and also they are brittle compounds, consequently these compounds can be used to absorb visible solar light or EM radiation with ultraviolet wavelength in optoelectronic devices like solar cell technologies.











 text new page (beta)
text new page (beta)