1. Introduction
Quantum chromodynamics (QCD) theory can explain mesons and baryons (and thus multiquark states) [1-8]. The only requirement for these states, according to QCD [9], is that they are colour singlets, and diquark interactions appear to be essential in hadron physics. In 1964, Murray Gell-Mann and George Zweig suggested the quark hypothesis in their papers. Since the composition of their quarks and/or their spin/parity is unknown, several reported exotic states are being studied for a study of hypothetical exotic states [10-12]. Ground-state mesons and baryons, on the other hand, are well-defined experimentally. Other than the quark model, multiquark states like tetraquarks (qˉqqˉq or qqˉqˉq), pentaquarks qˉqqqq), and structures containing more quarks have been proposed for years [13-15].
A Tccˉcˉc state might split into two charmonium states, each consisting of a ˉcˉc pair, such as J/ψ mesons. It's also possible to decay into a J/ψ meson plus a heavier charmonium state, or two heavier charmonium states, with the heavier states decaying into a J/ψ meson and associated particles. The masses of Tccˉcˉc states are predicted to range between 5.8 and 7.4 GeV/c2, which is higher than the masses of known charmomia and charmonium-like exotic states but lower than the masses of bottomonium hadrons [16].
The fully-charm tetraquark state ccˉcˉc has an energy range that is significantly larger than the experimentally known range for charmonium, which is in the range of 3-4.5 GeV. This is due to the XYZ state's energy range corresponding to the mass range of ordinary charmonium levels, which can cause problems in these systems [17]. The discovery of a possible ccˉcˉc structure sparked a lot of theoretical research [18-21]. So far, no observations on the side of bbˉbˉb structures have been made. According to experimental research, the entire bottom tetraquark state bbˉbˉb exists, with a global significance of 3.6 σ and a mass of about 18.4 GeV, nearly 500 MeV below the ϓϒ threshold [22]. The LHCb Collaboration, on the other hand, proposed an intriguing study looking for the unusual bbˉbˉb tetraquark in the ϒ(1S)μ+ μ— state, but no further research was conducted [23]. The theoretical existence of the bbˉbˉb state was investigated both before and after these experimental studies [24-26].
This work determines the masses of tetraquarks in the ground state, with a tetraquark being a bound state of one diquark and one antidiquark. The unification of any two quarks to generate a colored quasi-bound state is the physical principle behind the diquark concept. This approach enables us to first consider the potential of applying the diquark concept in this situation, and then to obtain relatively brief formulations for the masses. We have used the non-relativistic Bethe-Salpeter equation with the logarithm potential, linear potential, harmonic potential, and spin-dependent potential. The logarithm potential was used to measure the masses of pentaquarks [27]. To the best of our knowledge, no previous research has employed the logarithm potential to estimate tetraquark masses. We have provided numerical results for the ground masses. The following is how the paper is structured: The Bethe-Salpeter equation is obtained in the current potential in Sec. 2. The numerical results and discussion are included in Sec. 3, and the conclusion is found in Sec. 4.
2. The theoretical model
One heavy diquark and one heavy antidiquark are thought to be bonded together to form tetraquarks. As a result, this two-body structure can be described using the Bethe-Salpeter equation in QCD. By considering the natural units (where ℏ=c=1), the Bethe-Salpeter equation [28] is derived.
where m1 and m2 are the masses of the two-body structure components, V(r) is the potential, M is the bound state mass and ψnl(r) is the wave function. Applying Eq. (1) to heavy interacting particles at p < μ, as shown in Ref. [29], is a basic method of dealing with the non-local behavior of the kinetic energy operator.
where μ= m1m2/(m1+m2) is the reduced mass and α= m1m2/(m1m2-3μ2). Taking up to terms of instructions just 1/μ3 in the given equation. This is a strong approximation for heavy interacting particles that employs the operator p2=-∇2 and p4=4μ2[E-V(r)]2, where E=M-m1-m2 the energy of the bound state. It is possible to rewrite Eq. (1) in spherical coordinates as
For each two-body interaction, the logarithm potential, linear potential, harmonic potential, and spin-spin interaction are all included in the potential considered in Eq. (3).
The parameter A is coupled to the strong constant coupling αs in the one gluon exchange approximation. The spins of the interacting particles in the spin-spin interaction are S1 and S2, respectively. S1.S2=(1/2)[S(S+1)-S1(S1+1)-S2(S2+1)], and S is the total spin. The parameters for the logarithm potential are given in Table I.
The interaction potential of two coloured objects usually includes two contributions. This potential is illustrated by colour interaction, which is specified by a virtual model inspired by the Cornell potential VCor=-(a/r)+br+c presented in Ref. [30] for the value of parameters α = 0.63, b = 0.18 GeV2 and c = -0.22 GeV and gives a good description for masses of tetraquark as in Ref. [32] in comparison with experimental data. But it has been replaced in the present study by the logarithmic potential as in Eq. (5). Figure 1, shows a relationship between two potentials that results in similar behavior for both.
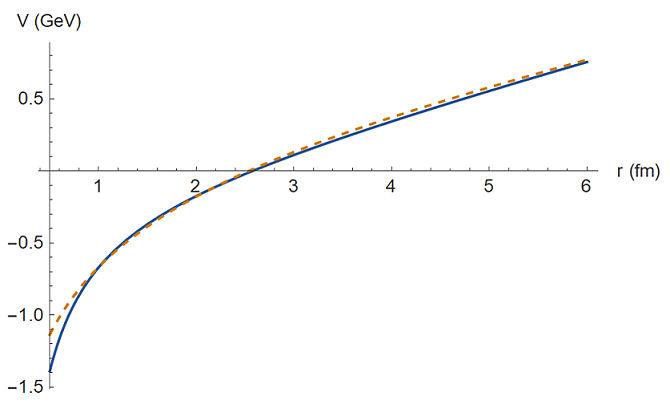
Figure 1 The Cornell potential [30] and the logarithm potential are plotted as a function of r. The blue line represents the Cornell potential and the dotted line represents the logarithm potential.
By presenting ψnl(r)=Xnl(r)r-1 and using the potential in Eq. (4), then Eq. (3) can defined as;
We use the basic approximation to solve the previous equation analytically, taking into consideration that r < 1 fm. Function approximation e-σ2r2≈1-σ2r2+… and function log[r/r0]≈-[3/2]+[2/r0]r-[1/2r20]r2… leading to the possible equation of potential as follows:
where
for which Eq. (7) becomes
where
Since Eq. (10) can be solved analytically.
Where
where
then we get,
The mass equation is found by solving Eqs. (15)-(17) with Eq. (11).
where
The diquark masses are calculated using Eqs. (18) and (19), as shown in Table II.
3. Numerical results and discussion
The mechanism underlying unusual state binding is currently unknown. The following three types of models can be used to ascribe various interpretations. (i) The molecular model of mesons and baryons, or their mixing. A chiral effective Lagrangian technique, the color-screen model, the QCD sum rules, and the scattering amplitudes approach were used to estimate the energy spectrum for this model. (ii) Diquark (triquark) interaction models, including compact diquark-triquark model and the diquark-diquark-antiquark model. As a result, the diquark-triquark model, as described in Ref. [38], is possible. In addition, as shown in Refs. [39,40], a classification of all possible pentaquark states QQqqˉq is based on the mass predictions and the related quantum numbers. To explore the tetraquark system in terms of diquark states, we plan on building a diquark-antidiquark system as a four-particle, i.e. two-body system. The method for prescribing the quantitative masses of particular tetraquark states is derived using the idea of tetraquarks as diquark-antidiquark systems. This is accomplished by first studying a quark-antiquark system and characterizing its Hamiltonian with an unperturbed one-gluon exchange (OGE) potential and a perturbation term that takes into account the system's spin. As a result, a model having four free parameters is developed and then fitted to meson data. Second, diquarks, which are composite quark-quark complexes, are utilized (the antiquark-antiquark systems are called antidiquarks). Finally, once the masses of the diquarks have been calculated, the first stage of the model explaining quark-antiquark systems is applied to diquark-antidiquark systems, which are construed as tetraquark bound states [32].
Only diquarks in the ground state N2S+1 LJ = 13 S1 are considered, and the diquark total spin must be 1 to preserve the Pauli exclusion principle. As a result, the diquark's total wave function will be anti-symmetric. These are known as axial-vector diquarks, and Jaffe [41] called these excellent diquarks.
In Table II, we noted that the diquark was slightly greater than the sum of its constituent quarks. Since we deal with diquark (quark-quark) as a bound state which required the binding energy to build them which gives by E = M - m1 - m2. They differ by no more than 200 MeV from the values for the diquark masses given in Table II and are actually in good accord with the findings in Refs. [32,34,37], which is proposed in the framework of non-relativistic quark systems. The Bethe-Salpeter and the Schwinger-Dyson equations, which take into account kinetic energy and also splittings in the spin-orbit, spin-spin, and tensor interactions, are used to study the diquark masses in Ref. [35]. Their diquark masses are estimated to be about 300 MeV higher than ours. Relativistic models based on QCD sum rules, as those in Ref. [36], projected smaller diquark masses. (With the cc diquark mass excluded, this indicates a higher mass).
In Table III, the tetraquark ground state mass spectrum is shown. Overall, lighter tetraquarks have a greater range of energy eigenvalues than heavier ones, resulting in a greater relative difference in mass between states for lighter tetraquarks compared to heavier ones. We analyze systems with the use of the various parameters of principal quantum number, orbital angular momentum, spin, and total angular momentum. Tetraquarks with total spins of 0, 1, and 2 are produced using a combination of spins, spin 1 diquark, and spin 1 antidiquark. In this non-relativistic method, quantum mechanic couplings were introduced, where the orbital angular momentum LJ couple into total angular momentum JT and total spin S.
Table III The masses of tetraquark in N2S+1 LJ (in GeV).
| Tetraquark | N2S+1 LJ | M(our) |
|---|---|---|
| qcˉqˉc | 11 S0 | 4.049 |
| 13 S1 | 4.053 | |
| 15 S2 | 4.069 | |
| 11 P0 | 4.213 | |
| 13 P1 | 4.370 | |
| 15 P2 | 4.441 | |
| 11D0 | 4.675 | |
| 13D1 | 4.91 | |
| 15 D2 | 5.03 | |
| ccˉcˉc | 11 S0 | 6.609 |
| 13 S1 | 6.611 | |
| 15 S2 | 6.629 | |
| 11 P0 | 6.531 | |
| 13 P1 | 6.611 | |
| 15 P2 | 7.034 | |
| 11D0 | 6.464 | |
| 13D1 | 6.52 | |
| 15 D2 | 7.22 | |
| qbˉqˉb | 11 S0 | 11.0164 |
| 13 S1 | 11.032 | |
| 15 S2 | 11.049 | |
| 11 P0 | 11.013 | |
| 13 P1 | 11.061 | |
| 15 P2 | 11.173 | |
| 11D0 | 11.009 | |
| 13D1 | 11.05 | |
| 15 D2 | 11.23 | |
| bbˉbˉb | 11 S0 | 20.012 |
| 13 S1 | 20.016 | |
| 15 S2 | 20.028 | |
| 11 P0 | 20.01116 | |
| 13 P1 | 20.0162 | |
| 15 P2 | 20.078 | |
| 11D0 | 20.013 | |
| 13D1 | 20.017 | |
| 15 D2 | 20.104 |
Table IV, shows our projected values for tetraquark masses as well as those from other studies. The results reported in Refs. [42,43] for qcˉqˉc tetraquarks are similar and the relative variation between the masses of this type of tetraquark states in Refs. [42,43] is generally small about 200 MeV with this type. In our model, the masses of qcˉqˉc tetraquarks are in excellent agreement with those in Ref. [32]. The masses calculated for qcˉqˉc tetraquarks agree well with those found in Refs. [34,44]. In comparison to Ref. [45], the 1S state differs by roughly 400 MeV. Furthermore, the calculated masses for qbˉqˉb tetraquarks are in good consistent with other tetraquarks of the same type. The predicted masses of bbˉbˉb tetraquarks are very close to those found in Refs. [34,45], yet our values are higher than those in Refs. [32,44]. In Refs. [32,45], the same model with a Cornell potential and spin-spin interaction potential are considered, but the Schrödinger equation is numerically solved in Ref. [32], and the variation principle is used to solve it in Ref. [45]. The color-magnetic interaction is used to compute the masses in Ref. [44]. The non-relativistic model of Hulthen potential, linear confining potential, and spin-spin interaction are considered in Ref. [34], and the solution of the Schrodinger equation is obtained.
Table IV Comparison of tetraquarks masses (in GeV) in the ground state N2S+1 LJ with other works.
| Tetraquark | N2S+1l | M (our) | Ref. [32] | Ref. [42] | Ref. [43] | Ref. [34] | Ref. [44] | Ref. [45] |
|---|---|---|---|---|---|---|---|---|
| qcˉqˉc | 11 S0 | 4.0497 | 4.076 | 3.849 | 3.852 | — | — | — |
| 13 S1 | 4.053 | 4.156 | 3.822 | 3.890 | — | — | — | |
| 15 S2 | 4.069 | 4.262 | 3.946 | 3.968 | — | — | — | |
| ccˉcˉc | 11 S0 | 6.609 | 6.198 | — | — | 6.322 | 6.487 | 7.016 |
| 13 S1 | 6.611 | 6.246 | — | — | 6.354 | 6.50 | 6.899 | |
| 15 S2 | 6.629 | 6.323 | — | — | 6.385 | 6.524 | 6.956 | |
| qbˉqˉb | 11 S0 | 11.0164 | 10.445 | — | 10.473 | — | — | — |
| 13 S1 | 11.032 | 10.472 | — | 10.494 | — | — | — | |
| 15 S2 | 11.049 | 10.523 | — | 10.534 | — | — | — | |
| bbˉbˉb | 11 S0 | 20.012 | 18.754 | — | — | 19.666 | 19.322 | 20.275 |
| 13 S1 | 20.016 | 18.768 | — | — | 19.673 | 19.329 | 20.212 | |
| 15 S2 | 20.028 | 18.797 | — | — | 19.68 | 19.341 | 20.243 |
4. Conclusion
The non-relativistic Bethe-Salpeter equation is used to describe a tetraquark with two heavy-valence quarks by the current potential, that contains the logarithmic, linear and harmonic potentials and spin-spin interaction. The approach includes computing diquark masses from single quark interactions, then computing the four-quark state mass formed by one diquark and one antidiquark, which results in the tetraquark as shown in Fig. 2. Results in the literature that accurately characterize tetraquarks were compared to our findings and found to be in good agreement. Our results of the heavy tetraquark may be useful for future experimental data.
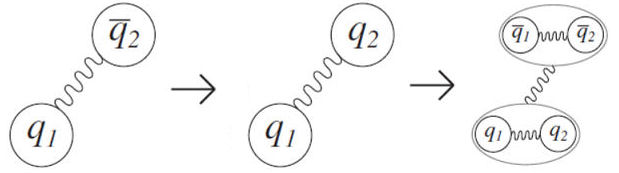
Figure 2 A diagram illustrating the modelling process. First, take the q1ˉq2 model of the quark-antiquark system. Second, expanding the model to include the q1 q2 quark-quark (or diquark) system. Finally, similar to the quark-antiquark system, except with diquarks and antidiquarks as constituents of model a tetraquark q1q2ˉq1ˉq2 [32].











 text new page (beta)
text new page (beta)


