2.1. Analysis of ⁹Be+²⁰⁸Pb

The ⁹Be+²⁰⁸Pb data in the energy range of 37.0-75.0 MeV is reanalyzed from the phenomenological point of view using OM. Then, this nuclear system is analyzed semi-microscopically using double folding optical model (DFOM). In this model, the real part of the potential was constructed by folding the density distributions of ⁹Be and ²⁰⁸Pb with nucleon- nucleon interaction potential of the M3Y form with and without taking into consideration the effect of rearrangement term, namely, DFOM and DFOM-RT, in addition to a phenomenological WS imaginary potential of parameters fixed to those obtained from OM analysis. Finally, the ⁹Be + ²⁰⁸Pb data in the aforementioned energy range is subjected to a fully microscopic analysis based on cluster folding model (CFM) for both real and imaginary parts. The cluster folding calculations were constructed based on the ⁷Li + d cluster structure of ⁹Be. The required ingredients to prepare the cluster folding potential for both the real and imaginary parts are: the ⁷Li + ²⁰⁸Pb and d + ²⁰⁸Pb potentials at appropriate energies as well as the ⁷Li + d binding potential. As the experimental data for ⁹Be + ²⁰⁸Pb elastic scattering angular distribution at E_lab (⁹Be) = 75.0 MeV is the highest energy under consideration, the required potentials are: ⁷Li + ²⁰⁸Pb potential at E_lab (⁷Li) = 7/9 x 75 = 58.3 MeV and the d + ²⁰⁸Pb potential at E_lab (d) = 2/9 x 75 = 16.7 MeV. Fortunately, there are available experimental measurements for ⁷Li + ²⁰⁸Pb angular distribution at E_lab = 63 MeV²⁶ which is close to the required 58.3 MeV, and for d + ²⁰⁸Pb at E_lab = 63 MeV²⁷ which is close to the required 16.7 MeV. The real and imaginary cluster folding parts of the ⁹Be + ²⁰⁸Pb potential can be defined on the basis of ⁷Li + ²⁰⁸Pb and d + ²⁰⁸Pb potentials as follows:

where W7Li-208Pb, W7Li-208Pb, and Wd -208Pb are the optimal real and imaginary potentials for the ⁷Li + ²⁰⁸Pb and d + ²⁰⁸Pb channels, respectively, which were taken the same as those in Ref.^26,27. The term (⁷Li _d (r) is the inter-cluster wave function for the relative motion of ⁷Li and d in the ground state of ⁹Be and r is the relative coordinate between the centers of mass of ⁷Li and d. The ⁷Li - d bound state form factor represents a 2S₁ state in a real Woods-Saxon potential with V₀ = 79.0 MeV, R = 1.15 fm, a = 0.7 fm. The generated cluster folding potential for ⁹Be+²⁰⁸Pb is shown in Fig. 1.

Figure 1 Real and imaginary parts of ⁹Be+²⁰⁸Pb cluster folding potential constructed on the ⁷Li + d cluster structure for ⁹Be. 

2.2. Analysis of ¹⁰Be+²⁰⁸Pb

The available experimental angular distributions for ¹⁰Be+²⁰⁸Pb elastic scattering at energies E_lab = 38.4, 39, 39.9, 42.6, and 43.9 MeV¹⁰ are reanalyzed from the phenomenological and the semi-microscopic point of view. Firstly, the OM analysis was performed utilizing OM potential consisting from real and imaginary volume parts, each having the conventional WS form in addition to a Coulomb part “see Eq. (1)”. The analysis was performed using fixed radii parameters. Then, on the basis of the ⁹Be + n cluster structure of ¹⁰Be, the considered data are reanalyzed using cluster folding model. The required ingredients to perform cluster folding calculations for ¹⁰Be + ²⁰⁸Pb by considering the proposed ⁹Be + n cluster structure of ¹⁰Be are: the ⁹Be + ²⁰⁸Pb potential at E_lab (⁹Be) = 9/10 x E_lab (¹⁰Be), n + ²⁰⁸Pb potential at E_lab (n) = 1/10 x E_lab(¹⁰Be) and n + ⁹Be binding potential. For ¹⁰Be + ²⁰⁸Pb elastic scattering angular distributions in the energy range 38.4 - 43.9 MeV, the highest energy under consideration is E_lab (¹⁰Be) = 43.9 MeV. Fortunately there are available experimental measurements for ⁹Be + ²⁰⁸Pb angular distribution at E_lab(⁹Be) = 39.6 MeV¹¹. The real and imaginary cluster folding parts of the ¹⁰Be + ²⁰⁸Pb potential can be defined on the basis of ⁹Be + ²⁰⁸Pb and n+²⁰⁸Pb potentials as follows:

where V9Be-208Pb, W9Be-208Pb, Vn-208Pb, and Vn-208Pb are the optimal real and imaginary potentials for the ⁹Be + ²⁰⁸Pb and n + ²⁰⁸Pb channels, respectively, which were taken the same as those in Ref.^11,28. The term (⁹Be _n (r) is the inter-cluster wave function for the relative motion of ⁹Be and n in the ground state of ¹⁰Be, and r is the relative coordinate between the centers of mass of ⁹Be and n. The bound state potential which bind the core (⁹Be) with the valence particle (n) orbiting this core was taken of phenomenological Woods-Saxon potential of diffuseness a_b = 0.7 fm and radius r_b =1.15 fm. The potential depth V_b was found by fitting to the cluster binding energy (B.E=6.812 MeV).

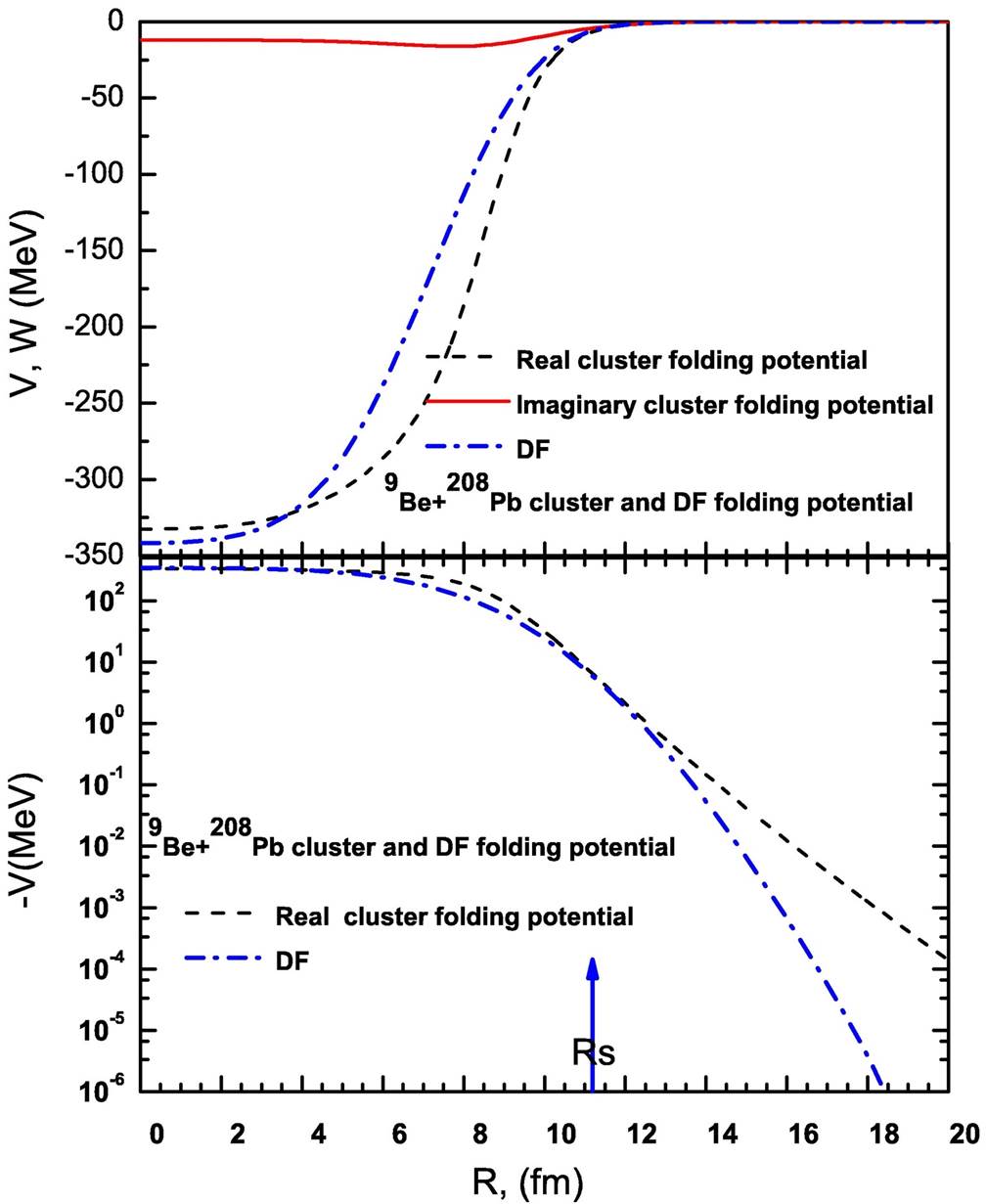
The generated cluster folding potential for ¹⁰Be+²⁰⁸Pb is shown in Fig. 2. To validate our analysis, we plotted expression (11) for ⁹Be+²⁰⁸Pb at 75 MeV and expression (13) for ¹⁰Be+²⁰⁸Pb at 48.3 MeV, respectively, against the DF potential with finite-range exchange contribution for the densities under consideration, as shown in Figs. 1 and 2. At (R=0), (V^Cluster (0)/V^DF (0)) ≈ 0.95, this means that the scattering is sensitive to the real potential for both the considered systems. These two figures show that, the DF potential is about 5% deeper than the cluster potential at(R = 0), while they are similar for radial distances R ranging from 0.5 fm to 7 fm.

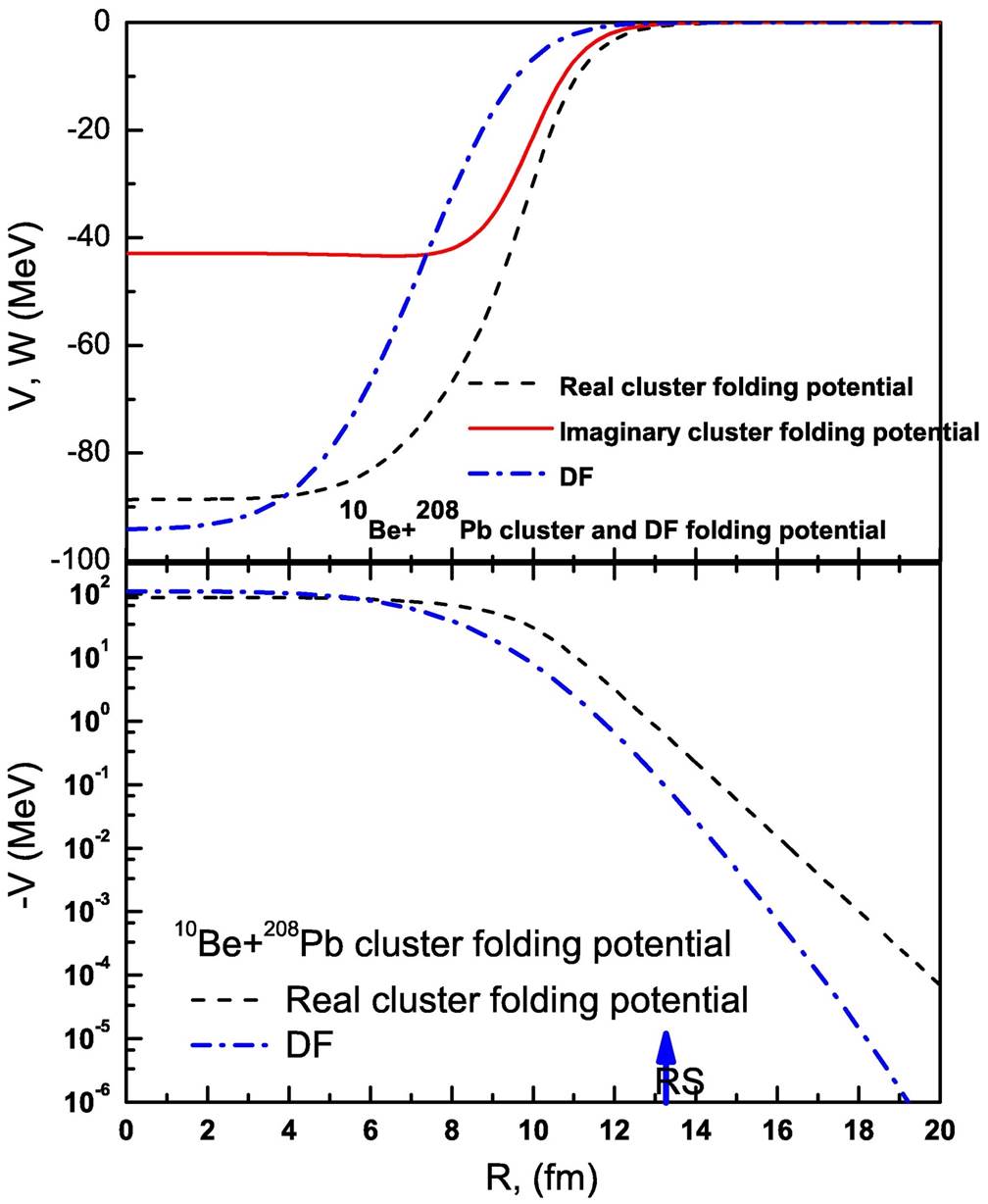
Figure 2 Real and imaginary parts of ¹⁰Be+²⁰⁸Pb cluster folding potential constructed on the ⁹Be + n cluster structure for ¹⁰Be. 

A strong absorption radius R_S (closest approach) through the surface radial region can be defined as the distance between colliding particles in terms of the transmission coefficient T_1/2, which is a function of the partial wave and momentum L_1/2, as well as the Sommerfield parameter η and the projectile wave number k¹³. We can see that the different DF and cluster potentials agree with each other near the strong absorption radius R_S where R_S =11.1 fm for the ^9,10Be +²⁰⁸Pb reaction.

3.1. ⁹ Be+²⁰⁸ Pb nuclear system

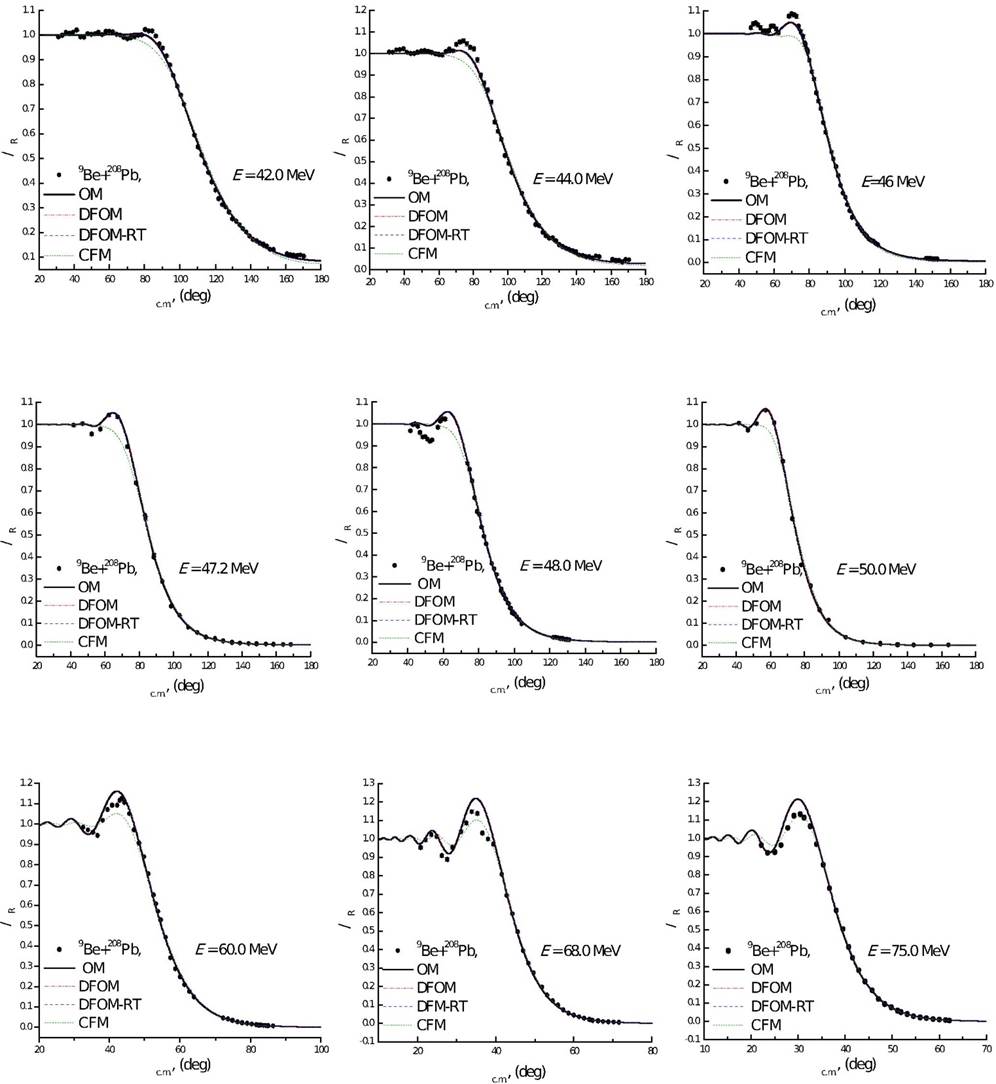
The comparison between the experimental ⁹Be+²⁰⁸Pb elastic scattering angular distributions in the energy range 37.0-75.0 MeV and the OM, DFOM, DFOM-RT, and CFM calculations performed using FRESCO code²⁹ are shown in Figs. 3 and 4 using the potential parameters listed in Table I. In OM calculations, the analysis was performed using two adjustable parameters real and imaginary potential depths V₀ and W₀, while the real and imaginary radius and diffuseness parameters were kept fixed at 1.24 and 0.63 fm respectively. The potential parameters considered in Ref.¹¹ for both the real and imaginary parts of potential were taken as starting parameters. It is clearly shown in Figs. 3 and 4, that the agreement between experimental data and OM calculations is fairly good even in the angular range where the Coulomb rainbow phenomenon is well presented. Although similar OM calculations were performed for ⁹Be+²⁰⁸Pb system in the energy range 37.0-50.0¹¹, it was necessary also in the current study to start our analysis from the pure phenomenological point of view in order to extract the optimal OM parameters for ⁹Be+²⁰⁸Pb system in the whole considered energy range. The optimal extracted imaginary potential parameters were implemented in the semi-microscopic analysis. In DFOM calculations, two approaches were used: DFOM and DFOM-RT in order to study the effect of introducing the rearrangement term. As expected, in order to describe ⁹Be+²⁰⁸Pb data, the strength of the real part should be reduced by (25-28%. The extracted average renormalization factor for the real part of the potential is 0.72±0.095 and 0.75±0.099 from DFOM and DFOM-RT calculations, respectively. The experimental data is reasonably reproduced by DFOM with nearly the same good fitting as shown in Figs. 3 and 4, whereas the DFOM-RT clearly provides a poorer description, particularly in the Coulomb rainbow region.

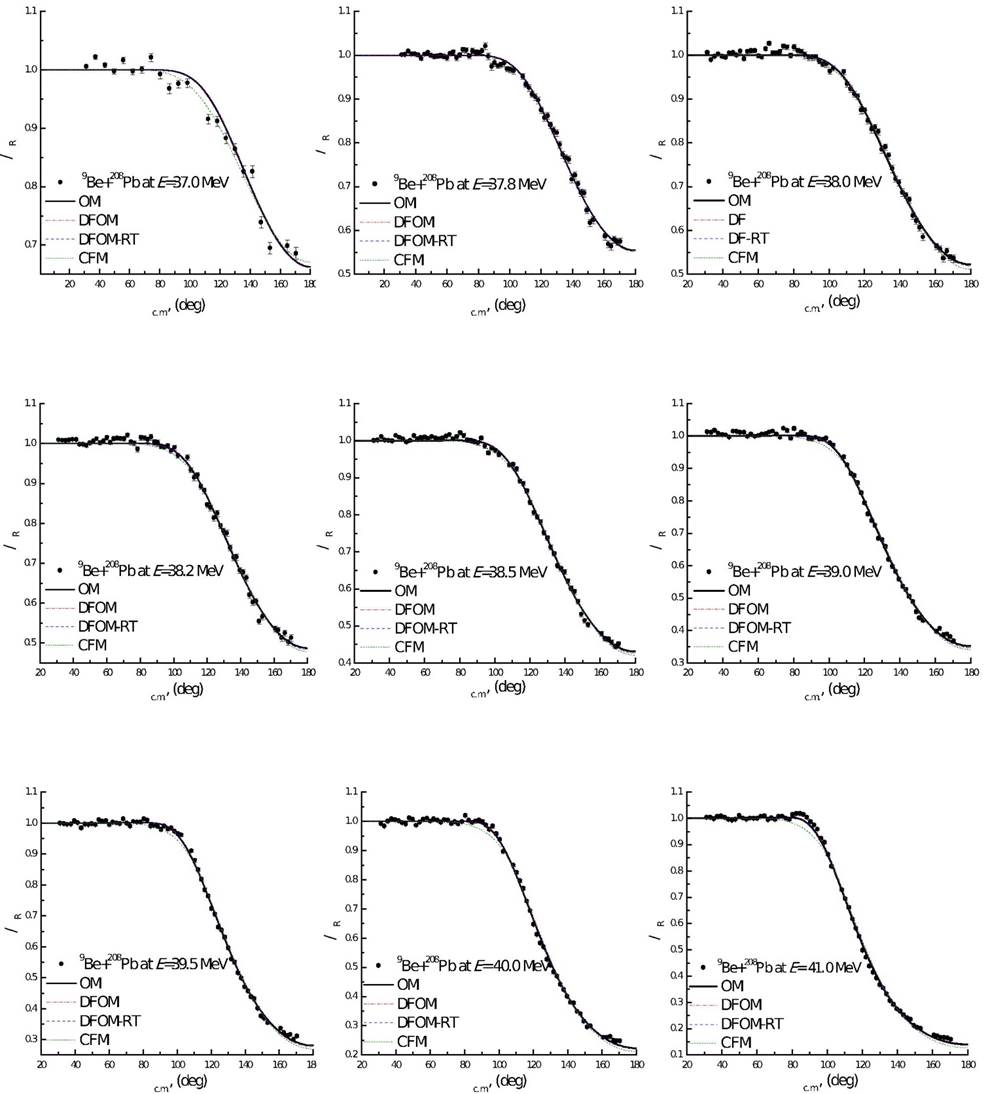
Figure 3 Comparison between ⁹Be+²⁰⁸Pb elastic scattering angular distributions at E_lab = 37.0; 37.8; 38.0; 38.2; 38.5; 39.0; 39.5; 40.0, and 41.0 MeV and theoretical calculations using OM (solid lines), DFOM (dash dot lines), DFOM-RT (dash lines), and CFM (short dash lines). 

Figure 4 Same as Fig. 3 but at E_lab = 42.0; 44.0; 46.0; 47.2; 48.0; 50.0; 60.0; 68.0, and 75.0 MeV. 

Finally, the ⁹Be+²⁰⁸Pb elastic scattering angular distributions in the energy range 37.0-75.0 MeV are analyzed within the framework of CFM. The CFM analysis was performed using two free parameters N_RCF and N_IFC, namely renormalization factor for the real and imaginary cluster folding potential, respectively. These two parameters are allowed to be freely changed in the range 0.2-1.3 till reach the best agreement the experimental data and the theoretical calculations by minimizing the X²/N value. As shown in Figs. 3 and 4, the comparison between the experimental angular distributions for ⁹Be+²⁰⁸Pb nuclear system and theoretical calculations within the frame work of CFM is fairly good except in the angular range where Fresnel peak is presented especially at energies less than 60 MeV. At higher energies greater than 60 MeV, the CFM calculations reproduce well the Fresnel peak. In order to reproduce the experimental data using CFM, the strength of the real cluster folding parts should be reduced by (0.45%. The extracted average N_RCF and N_IFC values are 0.55(0.18 and 0.45(0.13, respectively. These results emphasize the weak nature of ⁹Be.

As shown in Fig. 5, the Coulomb rainbow phenomenon (Fresnel peak) which resulted from the interference between Coulomb and nuclear potential is well presented at energies above 40 MeV. It is obvious that with increasing the projectile energy, the position of Fresnel peak is shifted towards smaller angles.

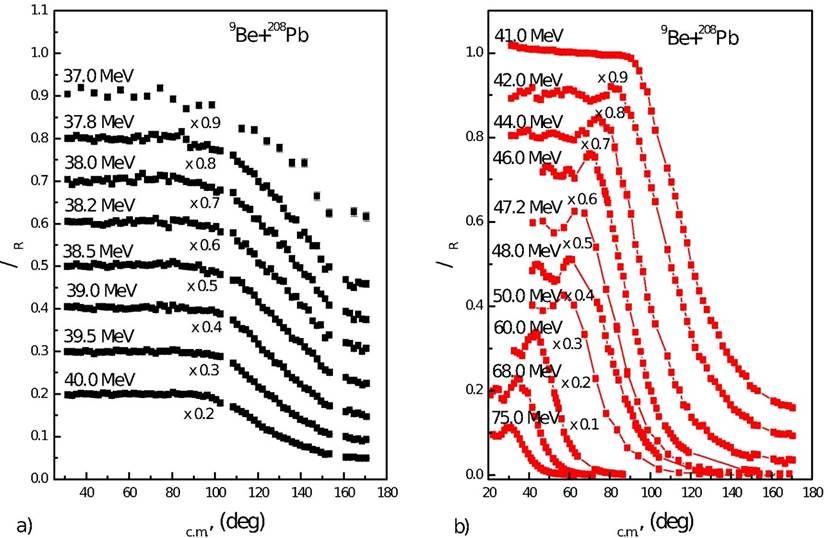
Figure 5 Angular distributions for ⁹Be+²⁰⁸Pb elastic scattering in the energy range 37.0-75.0 MeV. Data are displaced by 0.1 for the sake of clarity. Left panel for energies 37.0-4.0. MeV where Coulomb rainbow phenomenon is not observed. Right panel for energies 41.0- 75.0 MeV where Coulomb rainbow phenomenon is observed. 

3.2. ⁹Be+²⁰⁸Pb nuclear system

The comparison between the experimental angular distributions for ¹⁰Be+²⁰⁸Pb nuclear system and theoretical calculations within the frame work of OM in the energy range 38.4 - 43.9 MeV is shown in Fig. 6. The OM calculations were performed by fixing radii parameters r_V and r_W to the values 1.355 and 1.338 fm, respectively and by allowing the other four parameters (real ands imaginary potential depth and diffuseness) to be changed freely till reach the best agreement between the experimental data and the theoretical calculations by minimizing the (²/N value as shown in Table II. The CFM analysis was performed using two free parameters N_RCF and N_ICF. These two parameters are allowed to be freely changed in the range 0.2-1.2 till reach the best agreement between the experimental data and the theoretical calculations as shown in Fig. 6 using potential parameters listed in Table II. In order to reproduce the data within the frame work of CFM, the strength of real part of potential should be reduced by about 74 % which reflect the weak nature of ¹⁰Be.

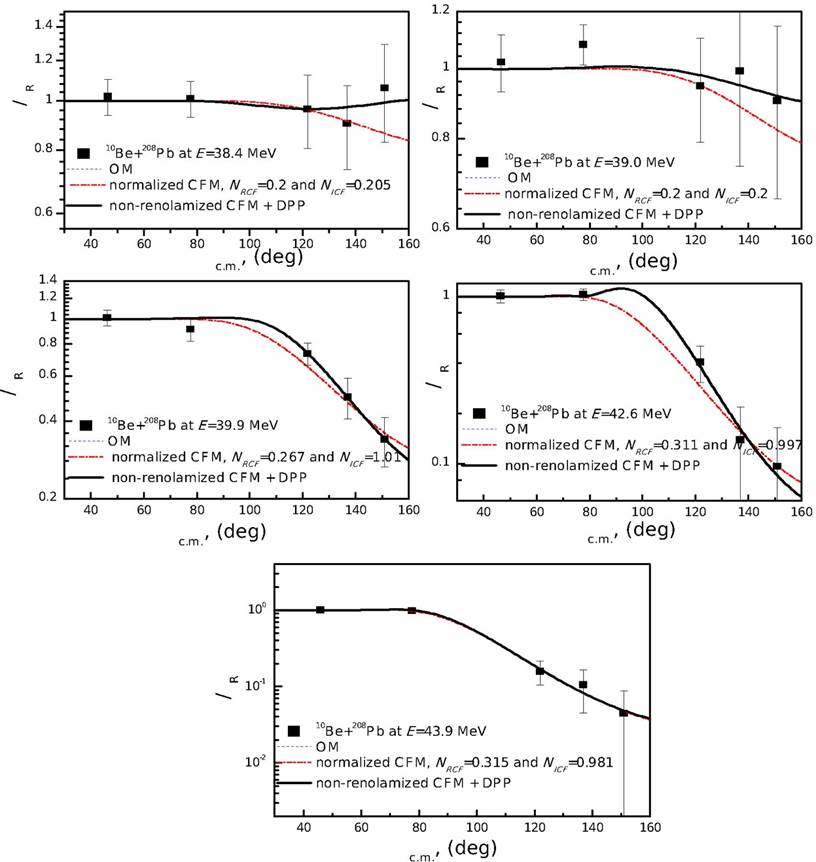
Figure 6 Comparison of elastic scattering angular distributions of ¹⁰Be+²⁰⁸Pb at E_lab = 38.4, 39.0, 39.9, 42.6, and 43.9 MeV with theoretical calculations using OM, CFM, and CFM+DPP. 

Finally, ¹⁰Be+²⁰⁸Pb elastic scattering angular distributions in the aforementioned energy range are reanalyzed using the previously created cluster folding potential but without renormalizing the real and imaginary cluster potential parts (N_RCF and N_ICF = 1) plus a dynamical polarization potential DPP in the form of Woods-Saxon and has a repulsive surface nature, namely CFM+DPP, to compensate the observed reduction in the strength of real and imaginary CF parts of potential. The dynamical polarization potential for both the real and imaginary parts has been fixed (r_Vpol = r_Wpol = 1.24 fm) and (a_Vpol = aW_pol = 1.24 fm). Two parameters are allowed to be changed freely until they achieved the best agreement between data and calculations: real and imaginary dynamical polarization potential depths, V_pol and W_pol. The comparison between the experimental angular distributions for the ¹⁰Be+²⁰⁸Pb nuclear system and the CFM+DPP calculations is shown in Fig. 6 using the potential parameters listed in Table III.

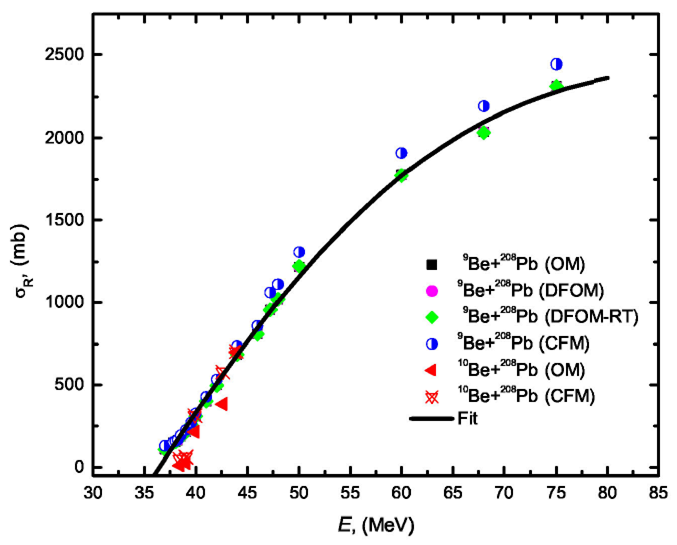
As the total reaction cross section σ_R is a useful quantity to test the validity of calculations, the energy dependence on σ_R is studied for the two systems- ^9,10Be+²⁰⁸Pb - under consideration. As shown in Fig. 7, it is found that the extracted (_R values for ^9,10Be+²⁰⁸Pb systems utilizing the different considered approaches (OM, DFOM, DFOM-RT and CFM) are close to each other and can be expressed by quadratic polynomial function σ_R (E) = -370+196 E - 1.431 E².

Figure 7 Energy dependence on reaction cross sections for ^9,10 Be+²⁰⁸Pb systems based on the different considered ap- proaches (OM, DFOM, DFOM-RT and CFM).