1. Introduction
In material science, surface analysis has enabled an enormous progress concerning the deep understanding of materials properties for several applications including biology, nano-electronics, semiconductors, photonics and magnetic media. Basically, backscattering coefficient (BSC) is defined as the ratio between the backscattered electrons to the total number of the primary incident electrons while; secondary electrons (SE) are the escaped electrons due to inelastic interaction between the primary electron and the targets atoms when high energies up to 40eV are considered. The BSC associated with thin-film targets is regarded as an important parameter, which is involved in many surface analysis applications, including scanning electron microscopy, electron probe microanalysis and electron lithography1-4. However, analyzing the materials surface properties using thin-film deposition and characterization techniques by means of experimental approaches is found very expensive and time consuming. In this context, Monte Carlo simulations is considered efficient for the accurate modeling of electrons backscattering behavior associated with several materials including polymers, oxides and others. This technique can serve as predictive simulation of the materials backscattering behavior, offering the possibility to avoid costly experimental characterization. In addition, this technique enables exciting opportunities for simulating the materials BSC as well as the energy distribution of both backscattered and secondary electrons.
In this framework, this subject has triggered a great deal of attention, where models dedicated to the materials backscattering behavior dependence on both the atomic number of a massif target and the primary energy of the electron beam was proposed by many research groups Everhart5, Archard6, Dapor7, Vicanek and Urbassek theory8 and August et al9.However, their expressions are valid only for thicknesses to which the target can be considered as semi-infinite solid, making the developed models inappropriate for investigating the material surface properties in wide thin-film thickness ranges. On the other hand, the BSC dependence on the film thickness for low energy electrons has been investigated in literature10-12. However, these studies targeted only a few materials for different thicknesses. Surprisingly, there is a lack of information concerning the electron backscattering coefficients associated with thin-film materials, where only a few studies focused on investigating the electron backscattering in some bulk materials at low energies were carried out16-22. To the best of our knowledge, no analytical expression has been proposed to calculate the backscattering coefficient for all thicknesses of all materials (monoatomic) at a given electron energy. In this framework, our aim is to generalize the expression of the electron backscattering coefficient for thin-films as a function of the primary energy, the atomic number and the thickness of the target as well. To achieve this goal, we carried out a scaling study based on both the Monte-Carlo simulation using the Penelope code and the interpolation techniques. The obtained results are compared to the experimental and theoretical data, showing an excellent agreement, which confirms the accurateness of the developed model. Furthermore, several thin-film materials are considered in probe analysis of the electrons backscattered behavior using the proposed model, demonstrating a great promise in reproducing the experimental results. It is found that our proposed model enables identifying the thin-film critical thickness showing the same electron backscattering behavior as that of a semi-infinite solid. Therefore, the developed models considered universal, being able to determinate the electron backscattering coefficient of various thin-film materials with dissimilar thicknesses with energy up to 30 keV, thus providing a pathway toward carrying out efficient surface analysis of various thin-films.
2. Monte Carlo procedure
The Monte Carlo method has been used to study the electron transport in thin-film solid targets by identifying the trajectories followed by the incident particle. So, in the present work, we used the Monte Carlo method with the Penelope code13 (Penetration and Energy Loss Positrons and Electron) for modeling the electron paths within the targets. In this context, the target was studied as an infinite thin-film with thickness equal to δ. The electron particles path was made with respect to an orthonormal reference (oxyz). It is selected as follows: the outer surface (in) is taken on the plane (oxy), the point “o” (origin of axes) is the entry point of the incident particle by the input surface and the normal direction is taken on the “oz” axis directed into the target.
A magnitude of 106 incident electron particles is simulated, to achieve a relative statistical uncertainty less than 10−3%. Thus, the electron << i >> (i = 1 to N) in the target is identified by its energy-coordinates (Ei, xi, yi, zi), where Ei is the electron << i >> energy and (xi, yi, zi) their Cartesian coordinates within the target. Only two values (Ei and zi) could define the state of the particle either backscattered or absorbed or transmitted under the following conditions:
For Zi > δ the particle is transmitted;
For Zi < 0 the particle is scattered;
For 0 < Zi ≤ δ and Ei < Ecut the particle is absorbed where Ecut is the cutoff energy.
Our simulation parameters of the input file used in Penelope code were included as follows:
SIMPAR 1.0e2 1.0e21.0e2 0.05 0.05 1.0e2 1.0e2 [EABSs, C1, C2, W cc, W cr]
where EABSs refers to energies associated with electron, photon and positron, which are assumed to be effectively stopped and absorbed in the medium, C1 and C2 represent the allowed values of the elastic-scattering parameters, which are confined within the interval of [0,0.2]. Besides, Wcc and Wcr are the cutoff values dedicated to consider inelastic collisions with energy loss W < Wcc and emission of bremsstrahlung photons with W < Wcr as soft stopping interactions13.
The geometry of the simulation is achieved according to the following configuration: the incident electron beam is perpendicular to the target entrance surface, i.e. along the axis (oz). The electron source is located at the point that has the coordinates (0,0,-1).
Principally, the backscattering coefficient is defined as the ratio of the number of primary backscattered electrons to those incidents. For a thin-film, the transmission probability (Tr), the absorption probability (Abs) and the backscattering coefficient (Bsc) are linked by the following relationship
It is implied for a semi-infinite target δ → ∞ that Tr(∞) = 0. Accordingly, we have Bsc(∞) + Abs(∞) = 1.
In order to study the variation of the backscattering coefficient as a function of atomic number, energy and thickness, we have considered 9 samples (Al, Au, Cu, Cr,Ge, Ni, Pt, Pd, Si), and for each material, the primary energy of the electron beam is varied from 1 keV up to 30 keV. The latter energy range is carefully selected according to the surface analysis requirements.
For each material and energy value, the thickness of the target could be varied from δ = 0.1R to δ = R (R is the range of electron. By definition is the path length that the electron travels until its energy is entirely dissipated away to the solid). Otherwise, we took in consideration the thickness where the rapport (δ/R) is the same for all 9 studied samples.
3. Results and discussion
To make our study more general, it is convenient to calculate two ratios noted X and Y of the two quantities: the thickness δ of the thin film compared to the range R and the backscattering coefficient of a thin film noted BSC(X) compared to that of a massive semi-infinite solid η. We summarize this later as follows
With δ and R are the film thickness and the electron range, respectively. δ denotes the electron-backscattering coefficient for semi-infinite target. Y represents the normalized backscattering coefficient (Ymax = 1).
This choice will provide us with almost universal interpolation parameters.
3.1. Analytical model of the backscattering coefficient of thin films
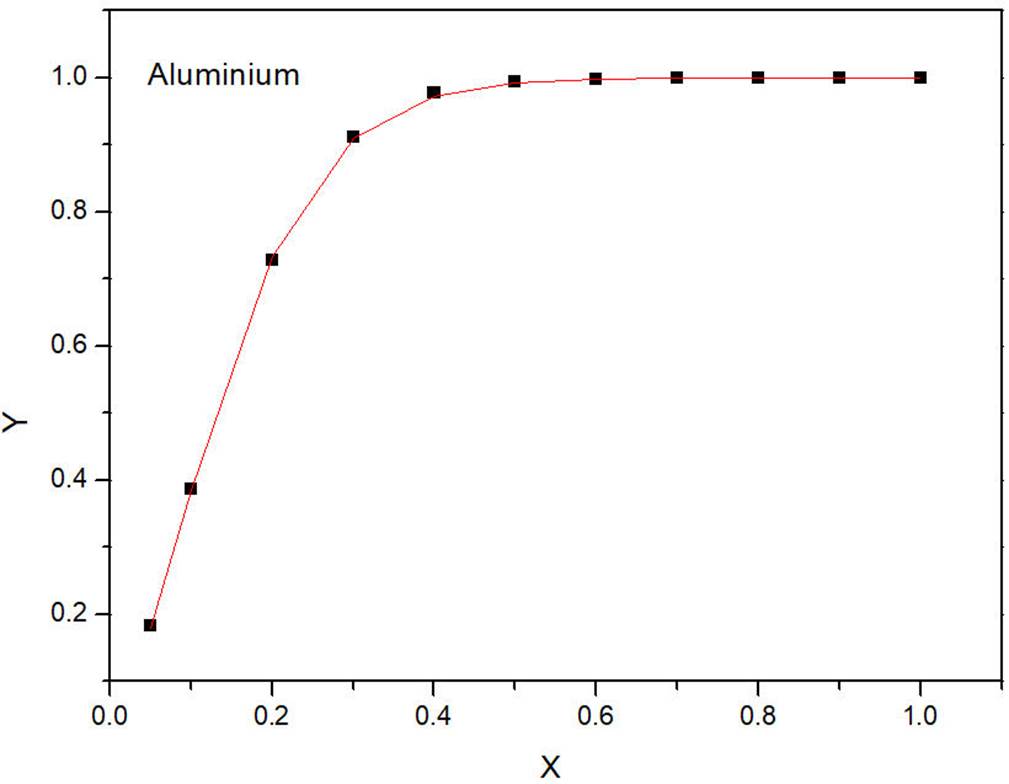
In order to develop an analytical model of thin-films backscattering coefficient, we present in Fig. 1 the BSC of Aluminum as a case study for an incident electron beam with energy of 10 keV. This figure shows the variation of backscattering coefficient as function of the film thickness. It can be seen from this figure that the BSC increases quickly from 0 to 1 with the thin-film thickness increase. It is revealed that Y(X) behaves like a sigmoidal function, which can be given by the following expression
This sigmoidal function contains 4 adjustment parameters namely A1, A2, A3 and A4. Accordingly, it is believed that for achieving a more reliable assessment regarding the thin-film backscattering behavior, the number of fitting parameters should be highly reduced14-15. For this purpose, it seems of great importance to reduce the number of fitting parameters associa ted with the obtained sigmoidal function. In our study, we were able to reduce the adjustment parameters from four parameters to a single parameter through two steps:
The first step: application of the boundary conditions
Therefore, the ratio Y can be expressed in the following form
Therefore, the application of boundary conditions allowed reducing the Y function with 4 parameters to a function with only two parameters A1 and A4.
By introducing the parameters P1 = A1 and P2 = 1/A4, the Y ratio function is given by:
Thus, the obtained Y(X) function is now containing only two adjustable parameters namely P1 and P2.
The second step: dependency on atomic number Z
In order to further reduce the number of the associated fitting parameters to a single parameter, the parameter P1 is fixed at its average value (P1 = 0.3) obtained for all the materials and the selected energy range. In this case, the behavior of Y = BSC/η is governed by the following model:
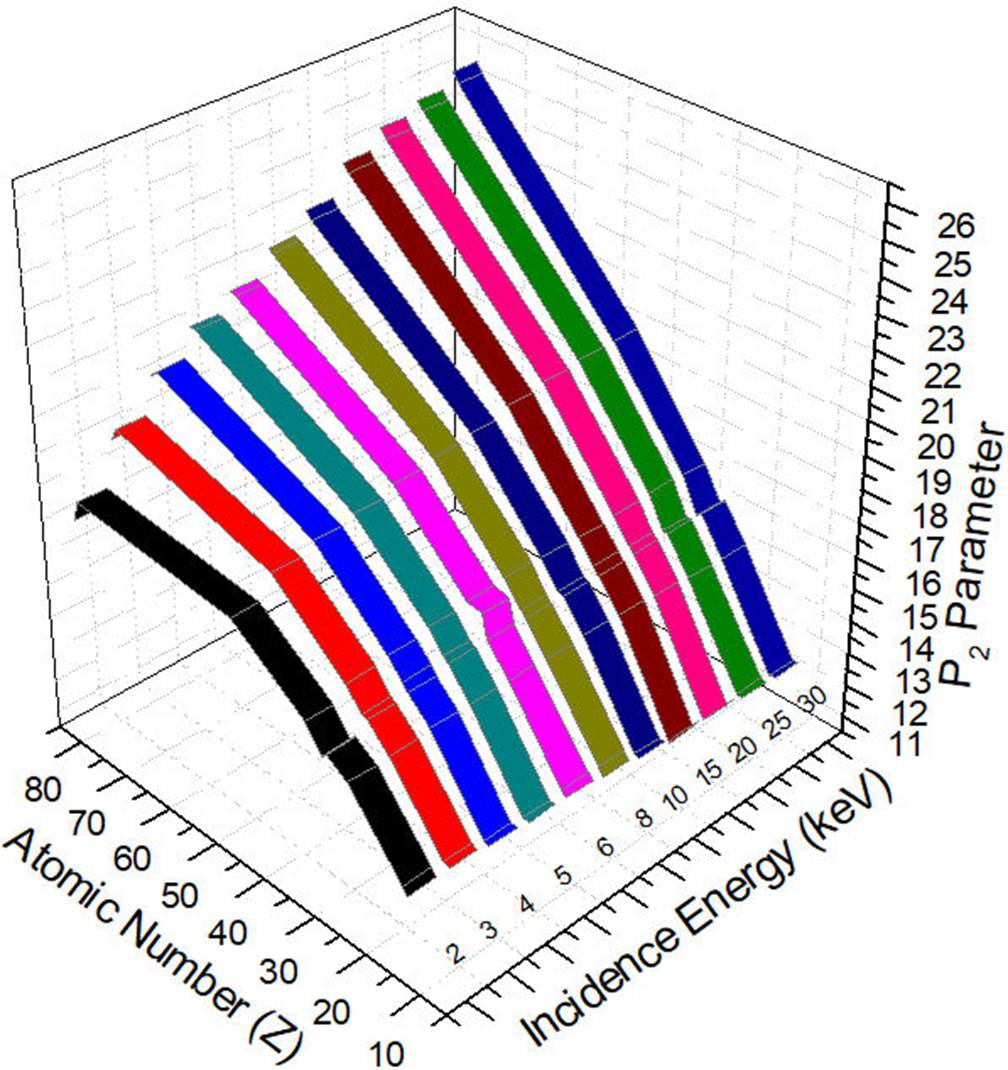
The next step is to study the variation of P2 according to the atomic number Z of the target and the energy of the incident electron as it is shown in Fig. 2. The latter figure demonstrates that the parameter P2 exhibits significant changes when varying both the atomic number and energy, emphasizing its complex behavior. Therefore, it is quite difficult to determine a general function describing well this behavior by passing from one target to another (when E is a variable).
On the other hand, the same figure shows a harmony of the behavior of P 2 as a function of the atomic number and by varying the energy. Accordingly, it is possible to interpolate P2 parameter as a polynomial law as follows:
Therefore, the backscattering coefficient can be expressed by the following analytical equation:
Table I summarizes the values of a, b and c parameters obtained for different energies, which can be considered as a grid for energies from 1 keV to 30 keV. Thus, we propose the use of Table I as a data base. In other words, for any given energy E for which E1 < E < E2, we can use the spline interpolation between two successive energy values (E1 and E2) of the data base for determining the corresponding values of the parameters a(E), b(E) and c(E).
Table I a, b and c parameters as function of the incidence energy.
| E(keV) | A | B | c |
|---|---|---|---|
| 1 | 0.0017 | 0.1865 | 10.7484 |
| 2 | 0.0019 | 0.2489 | 10.0236 |
| 3 | 0.0018 | 0.2649 | 9.7496 |
| 4 | 0.0017 | 0.2729 | 9.4968 |
| 5 | 0.0016 | 0.2746 | 9.3834 |
| 6 | 0.0016 | 0.2865 | 9.2499 |
| 7 | 0.0014 | 0.2779 | 9.2277 |
| 8 | 0.0014 | 0.2760 | 9.2169 |
| 9 | 0.0014 | 0.2792 | 9.1022 |
| 10 | 0.0014 | 0.2878 | 8.8261 |
| 15 | 0.0013 | 0.2963 | 8.4723 |
| 20 | 0.0012 | 0.2963 | 8.4003 |
| 25 | 0.0011 | 0.2943 | 8.3428 |
| 30 | 0.00095 | 0.28961 | 8.30008 |
3.2 Empirical formula of the electron backscattering coefficient of thin films
In fact, there are many empirical formulas proposed in the literature for determining both η and R. In this work, we used for η the August and Wernisch formula9 and for the range we have utilized our previously developed model16. In this perspective, the empirical expression associated with the η formula proposed by August and Wernisch is given by9
with
The range formula presented in our previous works is given by16
Where σTr and σel are the transport cross-section and the elastic cross-section, respectively. In our lastly published work, the mean value for σel/( σel − σTr) is given by
where α and n are two universal constants and ρ is the mass density (where ρ is expressed in [µg cm−3] and R is expressed in cm) of the material target given by16:
Consequently, our proposed model allows calculating the BSC (as a function of thickness, atomic number and energy) using simple expressions without going through stochastic models based on Monte Carlo calculation or complicated analytical models (such Boltzmann transport equation).
To validate our empirical model, the obtained results are summarized Table II and compared with those provided by Penelope code for different energies in the case of aluminum, which can be generalized for other materials. This table indicates that the deviation between the results obtained from our model and those provided by Penelope code does not exceed 6% for X ≥ 0.2. This clearly shows the validity of the proposed model especially for high thicknesses and low energies. In this context, this table recapitulates the following parameters RPn : the range by using Penelope code. R: the range expressed by Bentabet16. ηPen, η, ηExp: The backscattering coefficient of the semi-infinite aluminum target by using Penelope code, the backscattering coefficient proposed by August and Wernisch9 and the backscattering coefficient of the experimental data.
Table II Backscattering coefficient as function of the Aluminum film thickness.
| E(keV) | 1 keV | 2 keV | 3 keV | 4 keV | 5 keV | 6 keV | 7 keV | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RPen (nm) | 30.9 | 91.5 | 176.7 | 284.6 | 413 | 560.9 | 727.4 | |||||||
| RPW (nm) | 29.7 | 91.5 | 177 | 282.9 | 407 | 547.9 | 704.6 | |||||||
| ηPen | 0.216 | 0.203 | 0.196 | 0.191 | 0.187 | 0.184 | 0.182 | |||||||
| ηPW | 0.215 | 0.199 | 0.19 | 0.183 | 0.179 | 0.175 | 0.172 | |||||||
| ηExp | 0.19 | 0.175 | 0.170 | 0.165 | 0.158 | 0.158 | 0.158 | |||||||
| X=δ/R | YPen | YPw | YPen | YPw | YPen | YPw | YPen | YPw | YPen | YPw | YPen | YPw | YPen | YPw |
| 0.05 | 0.183 | 0.173 | 0.170 | 0.173 | 0.161 | 0.173 | 0.155 | 0.171 | 0.150 | 0.170 | 0.147 | 0.170 | 0.143 | 0.168 |
| 0.1 | 0.386 | 0.377 | 0.369 | 0.379 | 0.356 | 0.378 | 0.346 | 0.373 | 0.340 | 0.371 | 0.335 | 0.372 | 0.328 | 0.368 |
| 0.2 | 0.728 | 0.737 | 0.739 | 0.739 | 0.746 | 0.737 | 0.741 | 0.732 | 0.741 | 0.729 | 0.739 | 0.730 | 0.736 | 0.725 |
| 0.3 | 0.912 | 0.915 | 0.932 | 0.916 | 0.941 | 0.915 | 0.944 | 0.912 | 0.945 | 0.910 | 0.948 | 0.911 | 0.945 | 0.908 |
| 0.4 | 0.978 | 0.975 | 0.990 | 0.976 | 0.994 | 0.975 | 0.994 | 0.974 | 0.993 | 0.973 | 0.996 | 0.974 | 0.990 | 0.973 |
| 0.5 | 0.994 | 0.993 | 0.998 | 0.993 | 0.4 | 0.993 | 1.000 | 0.993 | 0.998 | 0.992 | 1.001 | 0.992 | 0.998 | 0.992 |
| 0.6 | 0.998 | 0.998 | 0.998 | 0.998 | 0.5 | 0.998 | 1.000 | 0.998 | 1.000 | 0.998 | 1.000 | 0.998 | 0.997 | 0.998 |
| 0.7 | 0.999 | 0.999 | 0.998 | 0.999 | 1.000 | 0.999 | 0.998 | 0.999 | 0.999 | 0.999 | 1.002 | 0.999 | 0.999 | 0.999 |
| 0.8 | 0.999 | 1.000 | 1.000 | 1.000 | 1.002 | 1.000 | 0.999 | 1.000 | 0.998 | 1.000 | 1.003 | 1.000 | 1.000 | 1.000 |
| 0.9 | 0.999 | 1.000 | 0.999 | 1.000 | 0.999 | 1.000 | 1.001 | 1.000 | 1.001 | 1.000 | 1.002 | 1.000 | 1.000 | 1.000 |
| 1 | 1 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| E(keV) | 8 KeV | 9 Kev | 10 KeV | 15 KeV | 20 KeV | 25 KeV | 30 keV | |||||||
| RPen(nm) | 912.1 | 1114.2 | 1333.5 | 2671.8 | 4394.3 | 6475.2 | 8892.9 | |||||||
| RPW(nm) | 876.2 | 1061.2 | 1261.2 | 2445.9 | 3914.4 | 5638.2 | 7597.2 | |||||||
| ηPen | 0.179 | 0.177 | 0.175 | 0.167 | 0.163 | 0.161 | 0.158 | |||||||
| ηPW | 0.169 | 0.167 | 0.165 | 0.157 | 0.152 | 0.148 | 0.145 | |||||||
| ηExp | 0.15 | 0.148 | 0.147 | 0.16 | 0.148 | 0.153 | ||||||||
| X | Pen | Pw | Pen | Pw | Pen | Pw | Pen | Pw | Pen | Pw | Pen | Pw | Pen | Pw |
| 0.05 | 0.140 | 0.168 | 0.138 | 0.167 | 0.135 | 0.164 | 0.126 | 0.161 | 0.119 | 0.160 | 0.115 | 0.159 | 0.112 | 0.158 |
| 0.1 | 0.324 | 0.367 | 0.320 | 0.365 | 0.313 | 0.359 | 0.303 | 0.352 | 0.294 | 0.350 | 0.286 | 0.348 | 0.281 | 0.346 |
| 0.2 | 0.735 | 0.724 | 0.733 | 0.721 | 0.733 | 0.713 | 0.728 | 0.703 | 0.727 | 0.700 | 0.721 | 0.697 | 0.719 | 0.694 |
| 0.3 | 0.949 | 0.907 | 0.946 | 0.905 | 0.944 | 0.901 | 0.950 | 0.895 | 0.954 | 0.893 | 0.950 | 0.891 | 0.951 | 0.889 |
| 0.4 | 0.999 | 0.972 | 0.993 | 0.971 | 0.991 | 0.969 | 1.000 | 0.967 | 0.997 | 0.966 | 0.996 | 0.965 | 0.995 | 0.964 |
| 0.5 | 1.004 | 0.992 | 0.998 | 0.992 | 0.998 | 0.991 | 1.004 | 0.990 | 1.002 | 0.990 | 0.998 | 0.989 | 0.997 | 0.989 |
| 0.6 | 1.002 | 0.998 | 0.998 | 0.998 | 0.998 | 0.997 | 1.003 | 0.997 | 1.004 | 0.997 | 0.999 | 0.997 | 0.997 | 0.997 |
| 0.7 | 1.000 | 0.999 | 1.001 | 0.999 | 1.000 | 0.999 | 1.003 | 0.999 | 1.002 | 0.999 | 0.995 | 0.999 | 0.999 | 0.999 |
| 0.8 | 0.998 | 1.000 | 1.001 | 1.000 | 1.003 | 1.000 | 1.002 | 1.000 | 1.005 | 1.000 | 0.998 | 1.000 | 1.001 | 1.000 |
| 0.9 | 1.000 | 1.000 | 0.999 | 1.000 | 0.998 | 1.000 | 1.003 | 1.000 | 1.004 | 1.000 | 1.001 | 1.000 | 0.997 | 1.000 |
| 1 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
Since the thickness of a thin-film is an essential parameter determining its properties, let us ask a very important question (which will be very useful for the experimenters): When the properties characterized from the backscattered electron beam will be the same as those of a massive body?
Our response: Everyone knows that the backscattered electrons can be used as a probe to characterize the physical properties of a thin film. For instance, to get surface analysis information concerning the texture of the thin film on the surface, like the presence of agglomerates.
In this part we will show that beyond a critical film thickness noted δ (, it will be highly recommended to use a different way than the backscattered electron, because the physical properties to be characterized by using backscattered electron beam as a probe give the same characters as those of a massive body. In other words, the use of the backscattered electron beam as a probe requires films with thicknesses very much lower than that critical value δ∞. Therefore, we believe that calculating BSC(δ)/η is the best way to answer this question. This can be justified by the fact that if BSC(δ)/η ≈ 1, we can infer that there is no statistical difference between a thin-film and a massive body regarding the backscattered electrons. Otherwise stating, the backscattering coefficient, energy distribution and spatial (or angular or profile) backscattered electrons associated with thin-film will be the same in the case of a bulk.
In fact, it is worth process the following steps.
From a definite thickness δ ( then: BSC(δ) becomes independent of the thickness when δ ≥ δ(. We can express it as follows: ∀δ ≥ δ( ⇒ BSC(δ)/η ≈ 1, where δ( is defined as the thickness for which the thin-film acts as a semi-infinite solid.
In our work, we make as a condition δ = δ( |BSC(δ)/η-1| ≤ 1%. It is very important to note that in our simulation we found for all the studied cases that
This result seems very important and remains valid only for the study of the backscattered electrons. However, in the case of absorption or transmission phenomena, it is suitable to consider higher thickness values δ > 1.5 R. Our results emphasize that only less penetrating electrons have a high probability to backscatter.
To validate this later (δ( = (3/5)R) we presented in Fig. 3 our results of the backscattering coefficient by using Eq. (15), where δ( = (3/5)R, compared to those of semi-infinite solids. In this context, a good agreement between our results and those of experimental and theoretical data is achieved which is the proof of the validity of our model.
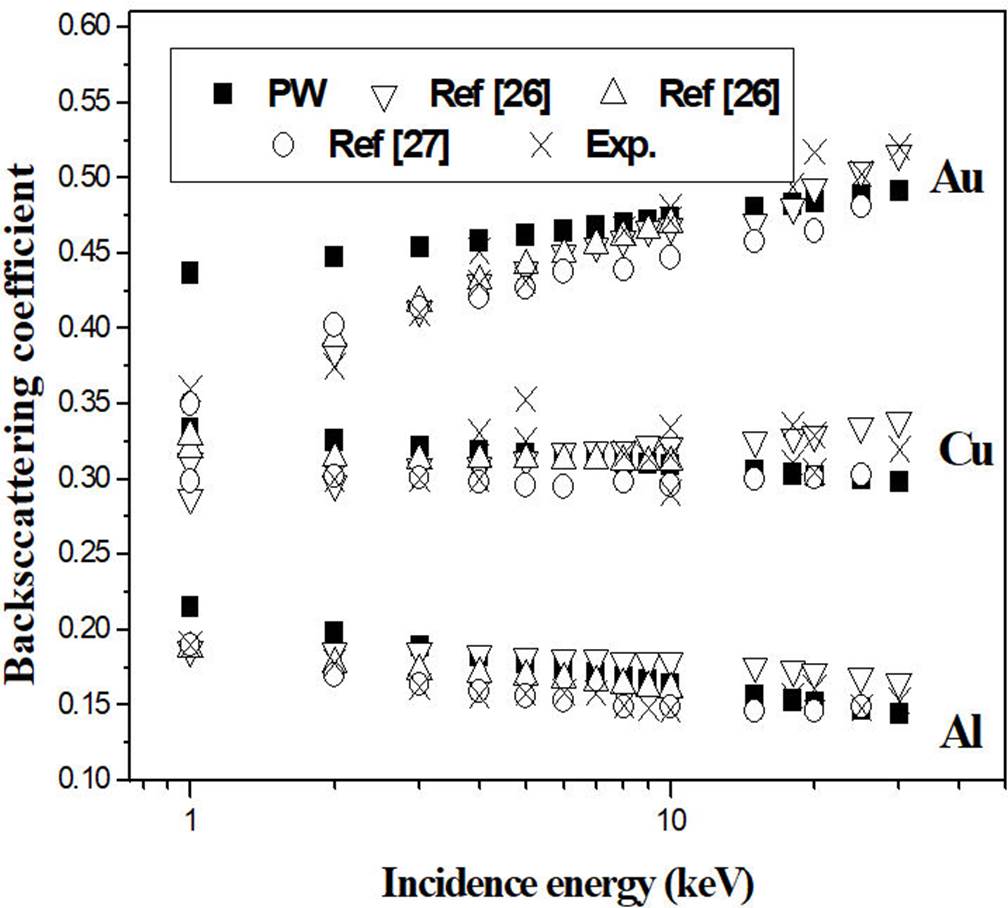
Figure 3 BSC of Al, Cu and Au vs. electron primary energy. PW: our results using Eq. (15). Exp.: the experimental data estimated from the curves reported in Ref.23 and published results reported in Refs.24-27.
There is another important question: why we develop an empirical formula for the backscattering coefficient of thin films knowing that the Monte Carlo simulation is possible?
The answer is:
It is not sure that everyone holds a sufficient knowledge about the tool;
Our results are in good agreement with those available;
The use of Monte Carlo simulation needs certainly long time compared to that by using an analytical expression;
Our model collects important quantities commonly used in the electron beam transport study in solids (η, the range R, the atomic number Z, the incidence energy E and the film thickness δ). Therefore, the calculation of one quantity of the above-mentioned parameters becomes a valuable process by reversing the problem via this equation. Conversely, this relationship can be very useful in the experiment for example: the measurement of BSC allows us either the thickness evaluation (δ) or the target identification (Z).
4. Conclusion
In the present study, an accurate model of the electron-backscattering coefficient of the thin film target for energy up to 30 keV is developed. The proposed model predicts the backscattering coefficient, without going through complicated analytical pathways (those based on the Boltzmann transport equation or those based on stochastic models of Monte Carlo).To the best of authors’ knowledge, no theoretical expression of the electron backscattering coefficient depending on both the film thickness and the atomic number targets has been reported so far. Moreover, our results are in good agreement with the experimental and theoretical calculation. Regarding the backscattering phenomena, we concluded that for thicknesses higher than (3/5R), no differences could be observed between the thin-film and the massive target. The use of the proposed empirical model allows performing efficient predictive simulation of thin-film backscattering behavior at a very low time as compared to that of complicated Monte Carlo time-consuming simulation. Therefore, the presented model can be implemented to accurately calculate the electron backscattering coefficient of various thin-film materials with large range of thickness and energy, making it suitable for surface analysis applications.











 text new page (beta)
text new page (beta)