1.1 Computational details

Using the full-potential linearized augmented plane-wave (FP-LAPW) method ^[15-17] implemented in the WIEN2k package ^[18], we have calculated the electronic properties, magnetic structures, mechanical stability and thermoelectric properties of a series of LiAlX (X = C, Si, Ge, Sn) half-Heusler compounds. The electronic exchange-correlation energy was treated using the generalized gradient approximation parameterized by Perdew-Burke-Ernzerhof (GGA-PBE) ^[19,20]. In addition, the modified Becke-Johnson (mBJ) approximation ^[21] was employed to predict the band gaps more precisely. The total energy dependence on the cell volume was fitted to the modified Murnaghan equation of state ^[22].

The cut-off parameter RMT*K_max in the basis set was chosen to be 8 ^[23], where K_max is the plane wave cut-off and RMT is the smallest muffin-tin radius. 2000 k-points have been used in the calculations, where the cut-off energy separating the core and the valence states was set at -6.0 Ry. For the elastic constants, we have employed the Thomas Charpin method ^[24]. While the thermoelectric properties were calculated using the Boltzmann theory as implemented in BoltzTrap code ^[25].

2.1 Structural properties

The ternary half-Heusler compounds crystallize in three different structural phases labelled as Type 1, Type 2 and Type 3. These phases differ according to the positions of atoms in the cubic lattice structure. The optimal structural parameters of the LiAlX (X = C, Si, Ge, Sn) compounds were calculated in the nonmagnetic and ferromagnetic states for each structural phase. The total energy as function of the unit cell volume are shown in Figs. 1 and 2. We present as well the equilibrium lattice parameters, calculated band gaps, bulk modulus and its pressure derivative in Table I.

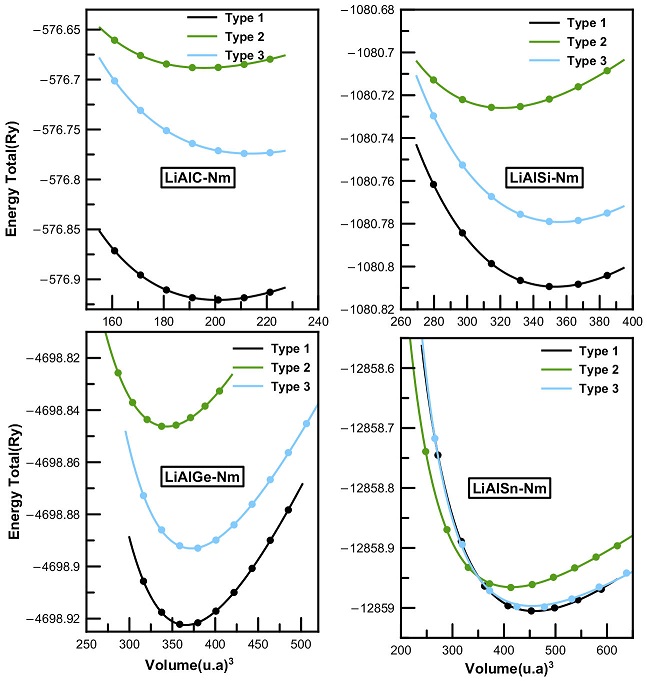
Figure 1 Volume optimization curves for LiAlX(X=C, Si, Ge, and Sn) compounds in Type 1, 2 and 3 half-Heusler structures in the nonmagnetic state. 

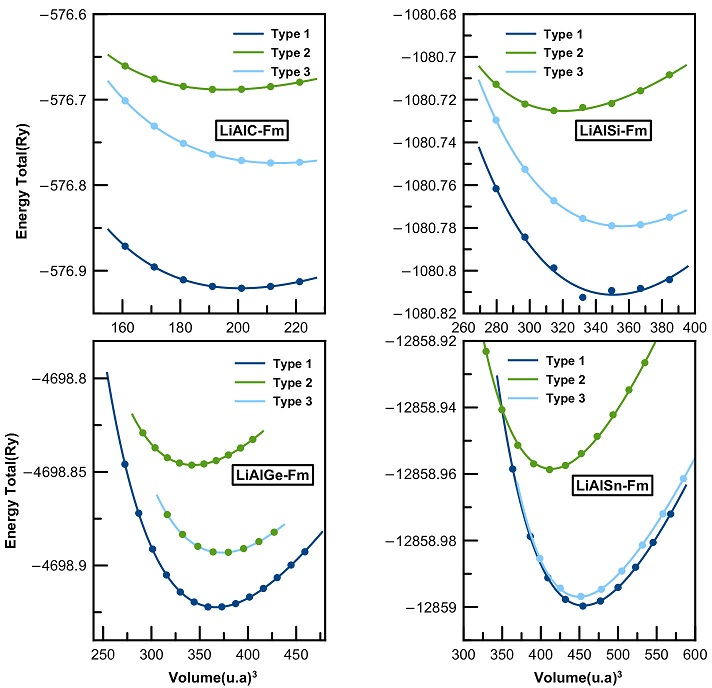
Figure 2 Volume optimization curves for LiAlX (X=C, Si, Ge, and Sn) compounds in Type 1, 2 and 3 half-Heusler structures in the ferromagnetic state. 

Both Figs. 1 and 2 show that Type 1 structure is the most stable among all the structural phases. Furthermore, the minimum energy corresponds to the nonmagnetic state, which indicates a paramagnetic behavior of the studied compounds. The remaining properties will be estimated for the Type 1 nonmagnetic most stable structure for all four Li-based systems.

The resulting lattice parameters are in good agreement with other published experimental data ^[26,27]. From Table I, we notice that the lattice parameter increases downward in the Mendeleev periodic table from LiAlC to LiAlSn, while the bulk modulus decreases.

2.2 Mechanical properties

The study of the mechanical stability and durability of a crystal against applied forces is very important to determine the strength and resistivity of any material. The three independent elastic constants C₁₁, C₁₂ and C₄₄ of the cubic LiAlX (X = C, Si, Ge, Sn) structures were calculated at normal pressure and under hydrostatic pressure. The calculations of the stability criteria and the evolution of C_ij, bulk B, shear G and Young modulus E were also illustrated as function of pressure in Fig. 3. From this figure it can be observed that with the rise in compression the value of all elastic constants increases and we notice that the stability criteria are verified for all LiAlX alloys with changing pressure.

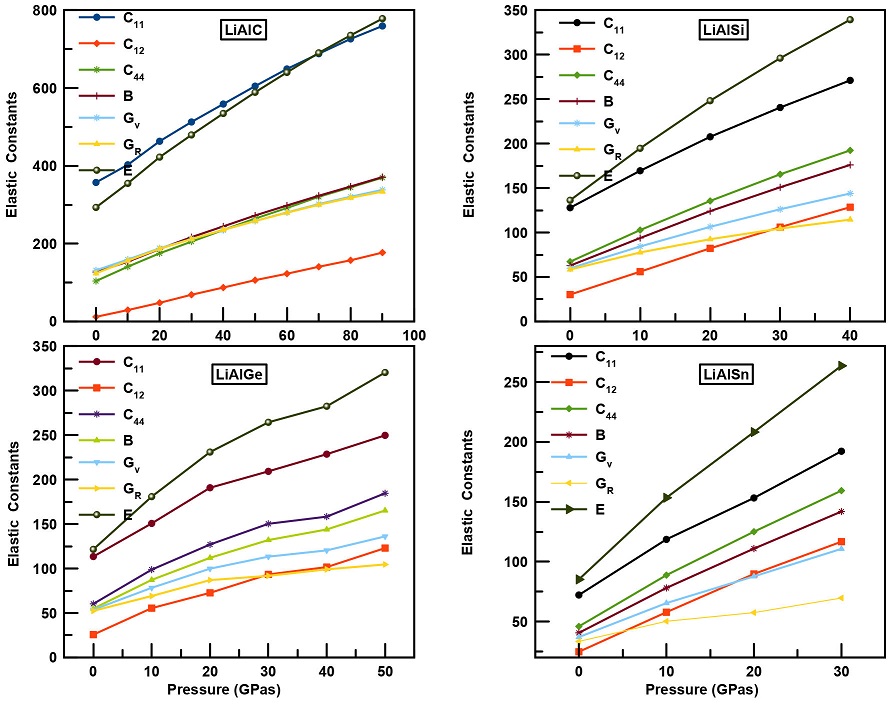
Figure 3 Variation of the elastic parameters as function of pressure for LiAlX (X= C, Si, Ge, Sn) alloys. 

The constant C₁₁, related to the linear elasticity, increases with pressure, signaling that pressure enhances the tensile strength of all compounds. The C₄₄ elastic constant, which is related to shape deformation, becomes less affected against rising pressures, indicating less bond strength enhancement.

The stability of cubic systems at zero pressure can be studied using the Born-Huang stability conditions ^[28]

However, Born’s elastic stability criteria are inapplicable when the pressure is different from zero. The calculated values of the elastic constants under hydrostatic pressure were compared with the generalized stability criteria ^[29] using the following relations:

Figure 4 shows the pressure dependence of the generalized stability criteria for LiAlX(X = C, Si, Ge, and Sn) compounds. Our calculations show that G' increases progressively with the pressure, while G decreases with pressure except for the compound LiAlC which remains approximately linear. These alloys are then mechanically stable and can maintain their stability along a wide range of pressures, especially LiAlC, which retains its structural stability in a pressure range of 0 to 90 GPa. In contrast, LiAlSi, LiAlGe and LiAlSn become unstable over a pressure superior of 40, 50 and 30 GPa, respectively.

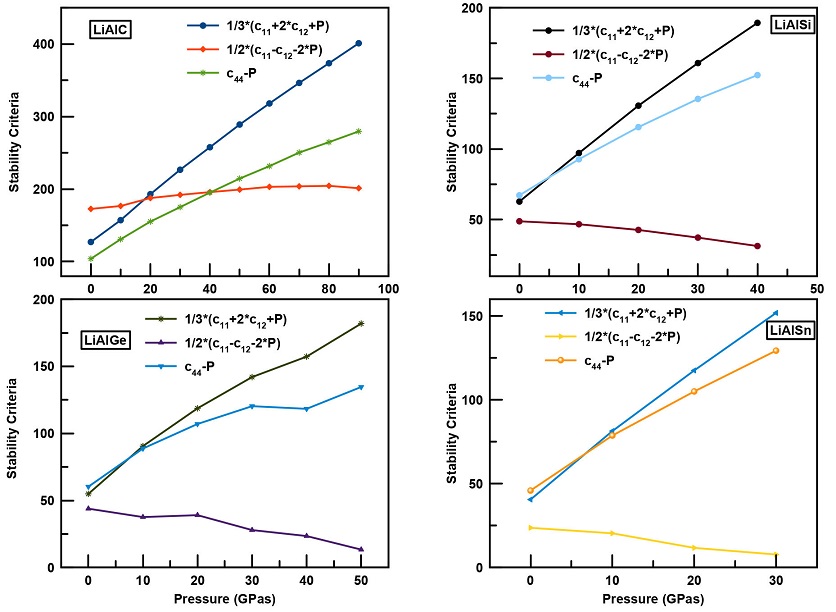
Figure 4 Generalized stability criteria as function of pressure for LiAlX (X= C, Si, Ge, Sn) alloys. 

From the elastic constants, we have derived the rest of the mechanical parameters. The bulk values of LiAlX alloys that were extracted from the Murnaghan equation of state are very close to the values calculated using the elastic constants at zero pressure for all alloys. It is well known that the shear modulus G represents the resistance of a material against plastic deformation, while Young’s modulus Y ^[30] is associated with the stiffness of a solid. From Fig. 3, we notice that, at zero pressure, LiAlC has a larger shear modulus than the rest of materials, which confirms its high stiffness. By increasing the pressure, the values of G and E increase as well. In fact, the higher the pressure, the higher the stiffness of these materials as well as their resistivity against deformation.

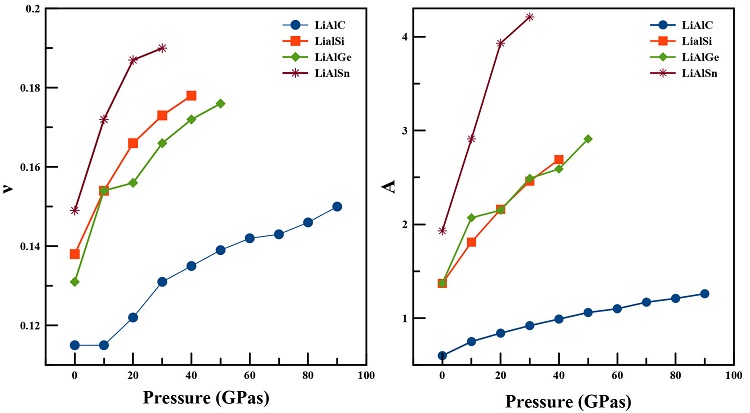
The ductility and brittleness of a material is also explained by Pugh’s ratio (k) defined by B/G ^[31]. A material is brittle if B/G < 1.75,otherwise it behaves as a ductile system. From the previous tables, it is evident that the four systems are brittle at ambient pressure. Even when increasing pressure, Pugh’s ratio increases gradually but the brittle behavior is still dominant in all four alloys. The negative Cauchy pressure Cp(C 12<C 44) also confirms the brittle nature in these materials. Poisson’s ratio serves in knowing the compressibility of a crystal as well as the bonding type (covalent or metallic bonding). For covalent bonding, Poisson’s ratio is about v = 0.1 and it increases for ionic crystals up to v = 0.25 ^[32,33]. The resulting values of Poisson’s ratio barely change (less than 0.2) with increase of pressure(see Fig. 5), which reflects the covalent characteristics of the studied materials. Another important factor is the elastic anisotropy A ^[34], presented in Fig. 5, that correlates to the possibility of inducing micro-cracks during the growth of materials; a large value of A is related to the instability of the lattice structure. At ambient conditions, all alloys possess small values of shear elastic anisotropy. Following an increase of pressure, the values of A are not very much affected, which confirms the stability of the Type 1 structure. The anisotropy factor is also a measure of the degree of elastic anisotropy in solids and since the resulting anisotropy values are different from unity, these systems can be considered as anisotropic. For LiAlSn, we notice that the values of A increase the most with increase of pressure as compared to the rest three compounds. This indicates that the degree of elastic anisotropy in this compound grows when the pressure increases.

Figure 5 Variation of the Poisson’s ratio v and elastic anisotropy A as function of pressure for LiAlX (X= C, Si, Ge, Sn) alloys. 

2.2.1 Electronic properties

The band structures of the semiconducting LiAlX alloys are presented in Fig. 6, where an indirect band gap characterizes the four Li-based alloys, with the valance band maximum at Γ point and the conduction band minimum at X point. The resulting band gaps calculated for LiAlC, LiAlSi and LiAlGe with either GGA or mBJ-GGA are very close to other theoretical data ^[35]. For LiAlSn, no theoretical or experimental data were available to compare the structural parameters of this compound.

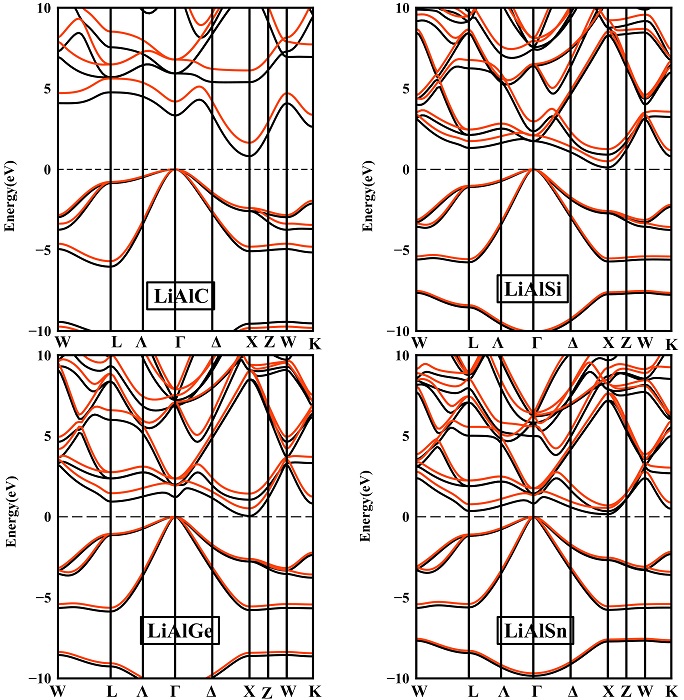
Figure 6 Electronic band structure in cubic (MgAgAs-type) phase for LiAlX (X=C, Si, Ge, Sn) alloys. The black lines represent GGA calculations and the red lines refer to the GGA-mBJ approximations. 

Along Γ—X direction, the highest band gap was obtained for LiAlC with a value of 0.81 eV and 1.64 eV using GGA and mBJ-GGA, respectively, at zero pressure. When replacing C by Si, Ge or Sn, we found small narrow gaps that almost touch both valence and conduction bands. These gaps were corrected using the modified Becke-Johnson approximation and the estimated values were in the proximity of 0.5 eV.

LiAlX compounds possess three types of transitions: two of which are indirect along Γ—X and Γ—L directions and the last one is direct along Γ— Γ direction. Unlike the lattice constant, we notice that the Γ— X band gaps decrease when going from LiAlC to LiAlSn alloy at zero pressure.

Studying the influence of external pressure on the gap of the crystal structure was also one of the main interests in this paper. For this reason, we have tabulated the variations of the band gaps within different values of pressures for the four LiAlX (X = C, Si, Ge, Sn) compounds in , Tables II, III, IV and V, respectively. From these Tables, we notice that these half-Heuslers are characterized by an indirect band gap that does not change for the pressure values considered. Similarly, to LiAlSi, the direct band gap of LiAlSn and LiAlGe compounds is the largest among the three possible transitions at ambient conditions. However, the Γ— Γ band gap decreases gradually in these alloys with an increase of pressure. For LiAlC, the values of the band gap along Γ — L direction are the widest at ambient conditions.

The energy gap along Γ — X direction decreases for all four compounds with increasing pressure. As for Γ — Γ and Γ — L directions, the band gaps increase for LiAlC, LiAlGe and LiAlSn with increasing pressure (see , Table II, IV and V, respectively) and decrease for the LiAlSi alloy (see Table III).

2.2.2 Thermoelectric properties

The Lithium based half-Heusler ompounds are known to be very promising in converting heat into power due to their large figure of merit (ZT) ^[36], which can be expressed as the following:

For this particular reason, we have estimated the Seebeck coefficient S,f igure of merit as well as the power factor PF for these LiAlX (X = C, Si, Ge, Sn) compounds, as illustrated in Fig. 7 and 8, respectively.

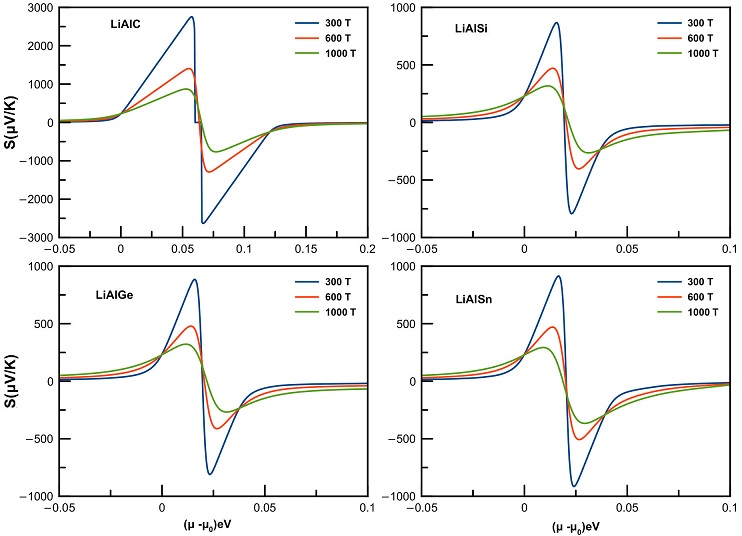
Figure 7 The Seebeck coefficient S dependence on chemical potential μ for LiAlX(X=C, Si, Ge, and Sn) compounds at three different temperatures. 

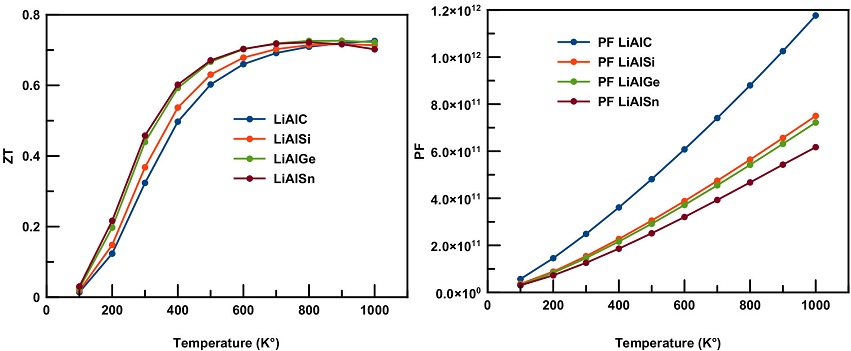
Figure 8 Temperature dependence of figure of merit (ZT) and power factor (PF) for LiAlX (X=C, Si, Ge, and Sn) compounds. 

In the considered range of chemical potential, the Seebeck curve shows almost equal values in both negative and positive regions, meaning that both types of charge carriers may be involved. We notice as well that the large values of thermopower are obtained in low ranges of chemical potential (Fig. 8). The greatest value of the Seebeck reached 2755 micro V⋅K -1 for the LiAlC compound, while LiAlSi, LiAlGe and LiAlSn showed a maximum of 867 micro V⋅K -1, 885 micro V⋅K -1 and 913 micro V⋅K -1, respectively.

When the temperature increases from 300 K to 900 K, the maximum value of thermopower in all four compounds decreases dramatically for both n- and p-type regions.

In order to predict the amount of power generated by the current Li-based materials, we have estimated the variation of the power factor within temperature as can be seen in Fig. 8. The curve of the power factor shows a linear increment with increase of temperature for all four compounds. At 1000 K, LiAlX (X = C, Si, Ge, Sn) compounds show the maximum values 1.18 × 10¹² WK^-2m^-1s^-1, 7.5 × 10¹¹ WK^-2m^-1s^-1, 7.2 × 10¹¹ WK^-2m^-1s^-1 and 6.2 × 10¹¹ WK^-2m^-1s^-1, respectively.

The effective thermal conductivity has a contribution from two parameters namely electronic thermal conductivity k 𝑒 and lattice thermal conductivity kl, where: ktot=ke+kl. Here, the lattice thermal conductivity kl was estimated using the Slack equation ^[37]:

where A is a physical constant (A ~ 3.1 × 10^-6), γ is the Grüneisen parameter θ_D the Debye temperature, V is the volume per atom, n is the number of atoms in the primitive unit cell, and m is the average mass of the atoms in the crystal.

The thermoelectric efficiency of the studied materials was also measured within temperature variation as can be seen in Fig. 7. An exponential increasing behavior is observed in the ZT curve of all compounds. The figure of merit increases sharply with increase of temperature until 700 K, where it shows a slow growth. The maximum values of figure of merit were found to be 0.73 for LiAlC and LiAlGe, and 0.72 for LiAlSi and LiAlSn alloys, respectively. These values correspond to a temperature in the range of 800 to 1000 K.