1. Introduction
The importance of technology and technological applications are the main reason for most experimental and theoretical physical studies. Materials having Chemical formula ABO3 materials have been of interest to many researchers to discover their physical and chemical properties and the extent of their technological applications [1,2]. It has a structure of cubic perovskite with space group 221 pm-3m, at room temperature. This ideal structure displays a wide variety of structural instabilities in the various materials. The interaction between these instabilities represents a rich group of photoelectric and ferroelectric and antiferroelectric behaviors. Useful properties of the ABO3 type perovskite can be obtained by some modifications of the ideal structure. In 2001, Shende et al. claim that SrTiO3 can be used in high voltage applications because of their high breakdown strengths [7], and Semiconductive ceramics, Pyroelectric far-infrared detectors. The effects of doping and alloying on the electronic structure of strontium titanate SrTiO3 have been discussed in previous experimental and theoretical studies [3-5] but, ab initio calculations of Sr(1-x)Be(x)TiO3 properties have not been performed yet (to our best knowledge). Beryllium has become an increasingly important material for a wide range of commercial and governmental applications because of its unmatched combination of qualities [6]. The simple cubic structure of SrTiO3 crystal is described mainly using the Pm3m space group [7.8]. The beryllium is potentially effective, which can improve the electrical or catalytic properties of SrTiO3. So, the results of FP-LAPW DFT calculations, elastic properties, and the electron density carried out for the structures of beryllium doped strontium titanate provide additional theoretical information that may aid in elucidating experimental results in the future. A few perovskites solid solutions were experimentally synthesized by the mean of the foreign ions substitution (see cations between parentheses), like (Ba, Sr)TiO3, Ca(Ti, Zr)O3, and (La, Sr)(Co, Fe)O3,etc. [9-10]. Sr 0.5 Be 0.5 TiO3 is one of them. The analysis of mechanical properties remains an untreated subject on such materials. The calculations of bandgap depict a possible use of the investigated compound in many UV device applications. In this study, the coordinate origin has been placed in Sr vacancy, which corresponds to the P4/mmm space group (Fig. 1). The purpose of this work is to provide information regarding Sr(1-x)Be(x)TiO3, x = 0.5 properties. Section 2 concerns the procedure calculation. The results are reported and discussed in Sec. 3. Finally, we present our conclusions in Sec. 4.
2. Theoretical method
Density functional theory (DFT) has been very popular for calculations in the ground-state properties of electronic systems (metals, semiconductors, and insulators) since the 1970s. At the beginning of the 1990s, DFT was considered accurate enough for calculations in quantum chemistry, when the approximations used in the theory were greatly refined to better model the exchange and correlation interactions [11,12].
In the current research worksheets, we have calculated the structural, electronic, electronic charge density, and elastic properties of pure (Sr,Be)TiO3 perovskite using the full potential linearized augmented plane wave (FP-LAPW) method implemented in the WIEN2k code as part of the DFT [13,14]. We used the generalized gradient approximation (PBEsolGGA) Perdew 08 et al., [15]. And the modified BeckeJohnson (mBJ) potential [16] is an empirical potential of the form (1)
where, c = 1 ⇒ Original
For the electronic properties and electronic charge density: A 1 × 1 × 2 supercell was constructed from the primitive cell of SrTiO3 cubic structure (space group Pm3 − m); the first atom Sr was replaced by beryllium atom (Be). The new compound Sr 0.5 Be 0.5 TiO3 has space group P4/mmm (N◦123), a (Å) = b(Å), and c > a. The electronic configuration and chemical composition of strontium beryllium titanate are given in Table I. The cell of Sr 0.5 Be 0.5 TiO3 can be schematically described by a sequence of successive layers perpendicular to the c−axis (see Fig. 1a), b). Input data is essential for Wien2K code such as: the elements in the materials. The crystalline lattice system of bravais, (space group). Radius of the atomic spheres RMT (MT: muffin-tin). The positions of the atoms.
TABLE I The electronic configuration and chemical composition of Sr0.5Be0.5TiO3.
| Element | Content (%) |
| Strontium [Kr] 5s2 | 30.38 |
| Beryllium 1s2 2s2 | 03.12 |
| Titanium [Ar] 3d2 4s2 | 33.20 |
| Oxygen [He] 2s2 2p4 | 33.30 |
These input parameters are grouped in Table II. The wave functions in the interstitial parts were developed in plane waves with a cutoff of RMT. Kmax = 7 and set 18 × 18 × 9 Monkhorst and Pack grid point in the (IBZ) Brillouin zone sampling with smearing occupations [18], corresponding to 3000 points in the (IBZ). We optimized the structures for the value of remaining force which was less than 0.0001 Ry/Bohr. We performed a self-consistent calculation of total energy as a function of volume and c/α ratio. The lattice constants (α = b and c), bulk modulus (B), and its pressure derivative (B’) for Sr0.5Be0.5TiO3 are determined after adjusting the total energy E(V) obtained from the Murnaghan state equation [19].
TABLE II Wyckoff positions, space group, and the atomic sphere radii of Sr 0.5Be0.5TiO3.
| Material | Space group | Atom | RMT (Bohr) |
Atomic position |
||
| x | y | z | ||||
| Sr0.5 Be 0.5 TiO3 | P4/mmm | Sr | 2.50 | 0.0 | 0.0 | 0.0 |
| (N◦ 123) | Be | 1.50 | 0.0 | 0.0 | 0.5 | |
| Ti | 1.87 | 0.5 | 0.5 | 0.75 | ||
| O 1 | 1.69 | 0.0 | 0.5 | 0.25 | ||
| O 2 | 1.69 | 0.5 | 0.5 | 0.0 | ||
| O 3 | 1.69 | 0.5 | 0.5 | 0.5 | ||
To evaluate the elastic parameters (elastic constants, bulk, shear, Young’s moduli, Poisson’s ratio, etc.) of Sr 0.5 Be 0.5 TiO3, for tetragonal symmetry. We have used the IRelast method developed by J. Morteza integrated into the Wien2K code [20] called Tetra-elastic.
3. Results and discussion
3.1. Structural and electronic properties
Using the data shown in Table II as the starting point for geometrical optimization for the Compound Sr 0.5 Be 0.5 TiO3. The total energy volume and c/α curves are shown in Fig. 3. Our results are reported in Table III. We note, for the calculations using (GGA-PBEsol, LDA) approximations of Sr 0.5 Be 0.5 TiO3, that there are any theoretical or experimental data for comparison, but we remark that the substitution of atom Sr by atom Be. Causes a noticeable decrease in the lattice parameter a(Å). We know that for SrTiO3, α exp = 3.91 A◦[21] for cubic structure. This is acceptable considering that the ionic radius of Sr2+ (1.18 Å) bigger than Be2+ (0.45 Å). To the best of our knowledge, there were no comparable studies done on the SrBeTi2O6 compound. And so, we calculated the formation energies (E form) of the proposed systems according to the equation of the reaction considered for the creation of the system.
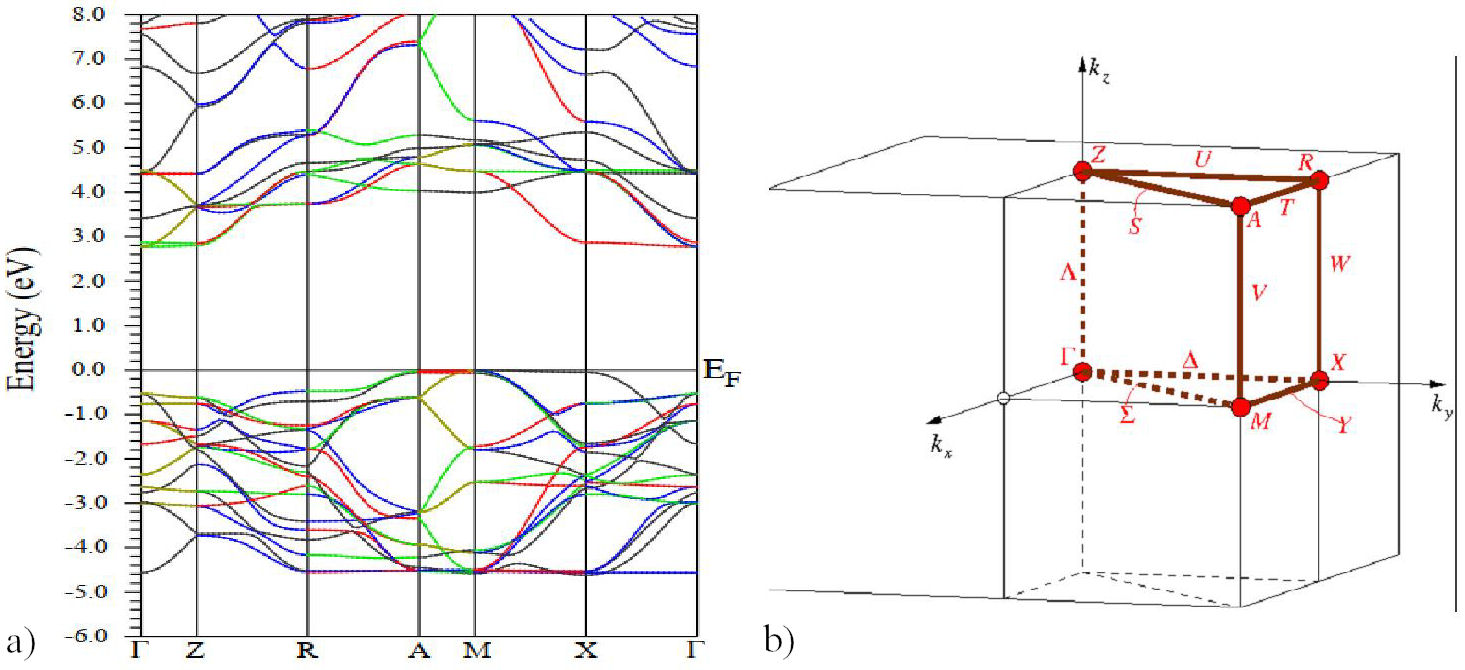
FIGURE 3 Electronic band structure of Sr 0.5 Be 0.5 TiO3 by using mBj-GGA potential. And the the high-symmetry points in the Brillouin zone, Γ, Z, R, A, M, X.
TABLE III Volume optimized (Ao) , The lattice parameters (α, b, c) (Å), bulk modulus B(GPa) and its pressure derivative B’.
| Material | Approximation | optimized volume | Parameters | ||||
| V0p | α = b | c | c/α | B | B’ | ||
| Sr0.5 Be0.5 TiO3 | GGA-PBEsol | 113.837 | 3.849 | 7.684 | 1.996 | 191.996 | 4.92 |
| LDA | 111.057 | 3.819 | 7.615 | 1.994 | 203.95 | 2.00 | |
| averaged value | 112.447 | 3.834 | 7.649 | 1.995 | |||
Which defined as the difference between the total energy of SrBeTi2O6 phase and the total energy of isolated atoms Sr, Be, Ti, and O. Using the following equation:
where Etot(Sr), Etot(Be), and Etot(Ti), Etot(O) correspond to the total energy per atom for Sr, Be, and Ti, O atoms, respectively, calculated by the same method used for E total (SrBeTi2O6). We found that the calculated formation energy is -4.757 Ry, which indicates that the (SrBeTi2O6) alloy is thermodynamically stable due to its negative formation energy. The calculation of the electronic properties is very important to determine the other physical properties. For accuracy, we have applied the possibility of using the averaged value as the volume optimized, VAvg, where VAvg = (VopLDA + VopGGA )/2, and the averaged value for the ratio c/α (avg) in Table III. Here VLDA (VGGA-PBEsol) is the volume optimized obtained from an LDA (GGA-PBEsol) optimization procedure.
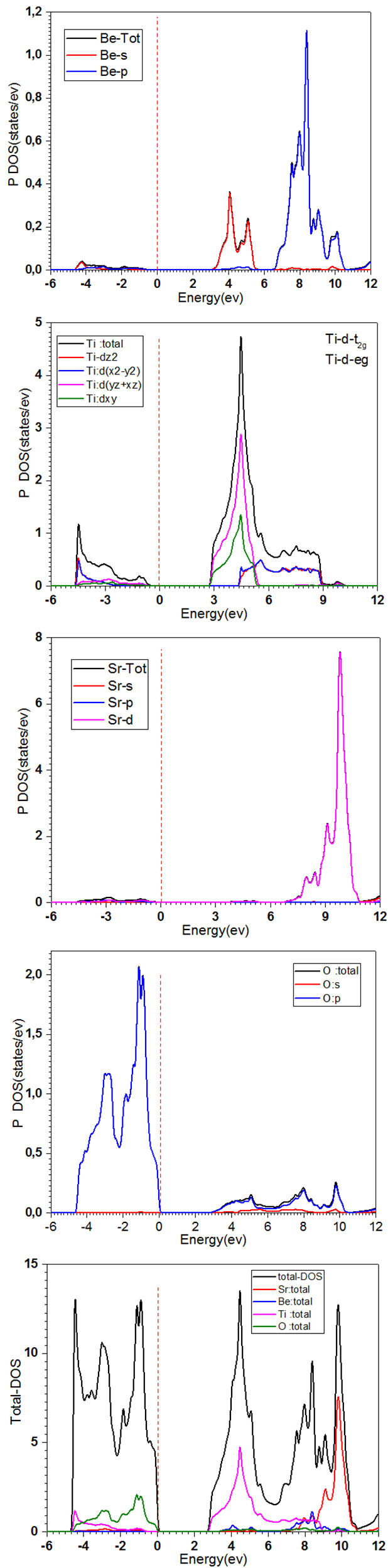
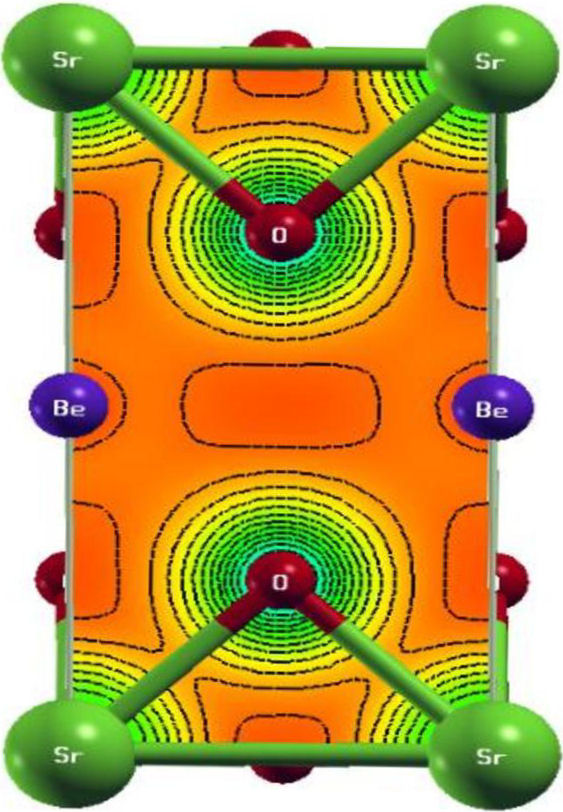
When V Avg and c/α (avg) ratio is used as input into the Wien2k code implemented with the mBJ potential, a better agreement of the bandgap value is obtained as compared to the results with either approximation LDA or GGAPBEsol. So this procedure turns out to give better results than the one recommended by Tran and Blaha, and its extra computational cost is relatively low [22]. The band structure calculated with this approach obtained along with the high symmetry directions for space group P4/mmm(N◦123) in the zone Brillouin, with k-vector. Description with the following [23]: GM(0,0,0); Z(0;0;1/2); R(0,1/2,1/2); A(1/2,1/2,1/2);M(1/2,1/2,0); X(0,1/2,0) of Sr 0.5 Be 0.5 TiO3 is schematized in Fig. 3. We note that our calculations outputted an indirect bandgap (Γ−X) equal to 2.77 eV, using mBj approximation, which indicates a semiconductor behavior. The contribution of atomic total densities to the total crystal density is shown in Fig. 4. This shows that the DOS and PDOS of Sr0.5Be0.5TiO3 consist bandgap (E g = 2.77 ev) and we note that the density of states at Fermi level is zero, which gives a material having a semiconductor character, the valence bands formed by the hybridization between O-2p and Ti-3d. The conduction bands are dominated by three-fold degenerate Ti-3d-t 2g orbitals, which hybridize with Sr-3d and O-2s and Be-3s Table IV, show the Comparison of our calculated bandgap values with different types of approximations. Electron density indicates the nature of the bond among different atoms [27]. Figure 5 exposures the charge density behaviors in 2D, which is determined in the (100) plane for our compound, indicating the sign of the covalent bond in the studied compound.
TABLE IV Show Comparison of our calculated band gap values with different types of approximations.
| band gap Eg (ev) | |||||
| Material (with space group N◦123 P4/mmm) |
SrTiO3 | Sr0.5 Be 0.5 TiO3 | |||
| Experiment | |||||
| Different types of approximations | .GGA-PBEsol | 1.87 | 1.73a | 3.4a | 1.25 |
| .LDA | 1.82 | 1.34 | |||
| . mBj- GGA | 2.80 | 2.77 | |||
3.2. Elastic properties
To obtain the elastic constants Cij, we used in the calculations the equilibrium structure of the standard volume [24]. The calculated elastic constants for several tetragonal structure compounds using the Tetra-elastic package are presented in Table V, the focus was on the Voigt-Reuss-Hill (VRH) approximation for its widely used [28]. The Pugh’s criterion (G/B ratio) was proposed as an empirical malleability measure of polycrystalline materials [27]: if G/B< 0.5, a material behaves in a ductile manner, and vice versa, if G/B> 0.5, a material demonstrates brittleness. In our case, according to this indicator (G/B∼ 0.7), Sr 0.5 Be 0.5 TiO3 will behave as a Brittle material. The stability criteria for tetragonal crystals are:
TABLE V Elastic constants (Cij, in Gpa).bulk modulus (B, in GPa), compressibility (β, in GPa−1), shear modulus (G, in GPa), Pugh’s indicator (G/B), Young’s modulus (Y, in GPa), Poisson’s ratio (ν), with in the Voigt-Reuss-Hill (VRH) approximation.
| Method | XC | C11 | C12 | C13 | C33 | C44 | C66 |
| Sr0.5 Be0.5 TiO3 FP-LAPW | PBE | 300.91 | 55.85 | 196.83 | 490.12 | 61.26 | 122.53 |
| BVRH | GVRH | β | YVRH | νVRH | G/B | ||
| 199.18 | 86.46 | 0.0084 | 226.59 | 0.31 | 0.72 |
The calculated elastic constants are positive and satisfy the criteria of generalized elastic stability [26]. We can confirm that Sr 0.5 Be 0.5 TiO3 is mechanically stable.
4. Conclusions
According to the calculations in tetragonal space group no123 structure of at zero temperature, using the fullpotential linear augmented plane-wave method (FP-LAPW) within the known Wien2k code. Has been exercised to probe the ground state properties such a structural, electronic, and elastic constant stability of the compound. The conclusions we can observe are:
The new compound Sr 0.5 Be 0.5 TiO3 represented by forming a supercell 2 × 1 × 1 of SrTiO3 cubic structure is a tetragonal structure with space group P4/mmm n◦123.
The narrowing of Sr 0.5 Be 0.5 TiO3 lattice calculated with PBEsol-GGA was inferred from the sharp decrease in unit cell volume V 0, due to the small ionic radius of Be+2 compared with the ionic radius of Sr+2.
An additional hybridization between Be-2s and Ti3d-2g in the conduction band narrowed the band gap calculated from 2.80 ev for SrTiO3 to 2.77 ev for Sr 0.5 Be 0.5 TiO3.
From Pugh’s ratio (B/G) we classify Sr0.5Be0.5TiO3 as brittle material while to that Poisson’s ratio suggests (0.3) Sr 0.5 Be 0.5 TiO3 its brittle nature.
The elastic constants C ij satisfy the mechanical stability criterion for tetragonal structure.











 text new page (beta)
text new page (beta)