1. Introducción
La curva de retención de humedad, que relaciona la carga de presión del agua en el suelo con el contenido de agua, y la curva de conductividad hidráulica, que relaciona la conductividad hidráulica con el contenido de agua, son de fundamental importancia en el estudio de las transferencias de agua en el suelo. Debido a que la determinación de estas curvas generalmente consume tiempo y es costosa, se han propuesto métodos indirectos de estimación; la curva de conductividad hidráulica se estima a partir de la curva de retención de humedad a través de modelos capilares, y la curva de retención a partir de propiedades más accesibles del suelo como la curva granulométrica, densidad volumétrica y contenido de materia orgánica, entre otras. Nuestro interés en este trabajo es establecer posibles relaciones entre las curvas de retención de humedad y granulométrica.
La curva de retención θ(ψ) induce una curva porosimétrica, Fv (R), ya que la carga de presión del agua en el suelo (ψ) está asociada a un radio (r) o diámetro (R) equivalente de poro a través de la ley de Laplace:
en donde la escala capilar está definida por
Las curvas porosimétrica y granulométrica se han ligado mediante una relación de similitud y una relación entre los tamaños de poros y partículas del suelo 2-6.
En el modelo de Arya y Paris 2, la curva
granulométrica Fs (D)
es discretizada en clases, de modo que la clase i-ésima, representada por el
diámetro equivalente de partícula Di,
contiene una masa ∆Fsi y un número de partículas
en donde (∆Nsi)1−α, con α ≥ 1, es un factor de alargamiento que resulta de la consideración de que cada una de las partículas contribuye más a la longitud que el diámetro de una esfera equivalente; estos autores recomiendan el valor medio de α = 1.38, obtenido mediante la calibración del modelo sobre algunos suelos.
Haverkamp y Parlange 7, hacen la observación
fundamental de que la relación entre R y D de Arya
y Paris 2, proporcionada por la
Ec. (2), no es única ya que
depende del número de clases; este hecho puede verse fácilmente cuando la curva es
discretizada de modo que cada clase contenga la misma cantidad de la masa unitaria
de suelo ∆Fi = 1/N
c con i = 1, 2, ...,
Nc, donde
Nc es el número de clases; en
tal situación
donde γHP es un coeficiente de empaquetamiento.
En el análisis realizado por Hwang y Powers 6, en suelos arenosos del catálogo UNSODA 8, se utiliza la ley potencial, estudiada por Rouault y Assouline 9:
donde u y υ son parámetros empíricos a determinar. Los autores señalan que la relación lineal es insuficiente incluso en suelos arenosos, ya que υ es definitivamente diferente de la unidad.
El objetivo del presente trabajo es el establecimiento de algunas posibles relaciones entre los tamaños de poros y partículas del suelo basadas en los modelos de medio poroso propuestos por Arya y Paris 2, y Fuentes 4,5.
2. Teoría
Se acepta la hipótesis de que la curva granulométrica Fs (D) y la curva porosimétrica Fv (R) admiten las funciones densidades fs (D) y fv (R), y que el número de partículas Ns (D) y el número de poros Nv (R) admiten las funciones densidades ns (D) y nv (R), definidas de manera que 10:
las funciones Fs (D) y Fv (R) se encuentran normalizadas, es decir Fs (∞) = 1 y Fv (∞) = 1.
Las funciones densidades fs (D) y ns (D) pueden relacionarse entre sí, considerando que el volumen de partículas en el intervalo (D − dD/2, D + dD/2) es proporcionado por:
donde
Una relación análoga puede ser obtenida entre las funciones densidades fv (R) y nv (R) del espacio poroso, a saber:
donde
2.1. Relación de similitud
La consideración de una relación de vacíos constante se traduce en:
de donde dVv /Vvt = dVs /Vst, lo que permite establecer la relación de similitud entre las curvas porosimétrica y granulométrica:
2.2. Relación entre los tamaños de poros y partículas
2.2.1. Modelo I
Se puede argumentar una relación entre D y R a partir de la aplicación de los conceptos de tortuosidad de las trayectorias de flujo y de la geometría fractal.
El factor de tortuosidad en las trayectorias de flujo se define como T = dLf /dL, donde L es la trayectoria rectilínea y Lf la trayectoria real en el medio poroso. Considérese un empaquetamiento de partículas y poros cuyos diámetros equivalentes se encuentran incluidos respectivamente en los intervalos (D − (dD/2), D + (dD/2)) y (R − (dR/2), R + (dR/2)) y en número ns (D)dD = −dNs (D) y nv (R)dR = −dNv (R); puesto que las partículas están ubicadas en todas las direcciones, se denotan por Tx = dxf /dx, Ty = dyf /dy y Tz = dzf /dz los factores de tortuosidad en las tres direcciones; un valor medio del factor de tortuosidad se obtiene haciendo (dL)3 = dxdydz y (dLf)3 = dxf dy f dzf, es decir T3 = Tx Ty Tz. Es claro que T3 representa la razón entre los volúmenes ‘tortuoso’ (dVf) y físico (dV) del paquete, es decir dVf /dV =T3.
El volumen físico del paquete (dV) se relaciona con el volumen de los sólidos por dV = (Ht /Hs)3dV s, y de acuerdo con la Ec. (9) se tiene dV = (ℜ,D) = (π/6)ℜ3 ns (D)dD, donde ℜ=Ht (D/Hs). Esto quiere decir que el paquete puede ser caracterizado por esferas de diámetro equivalente ℜ en un número igual al de las partículas; la fase sólida es la que define la estructura del suelo. El volumen tortuoso del paquete (dVf) puede ser caracterizado por las mismas esferas de diámetro equivalente ℜ, pero en número igual al de los poros ya que las trayectorias de flujo ocurren en el interior de los mismos, o sea dVf (ℜ,R) = (π/6) ℜ3 nv (R)dR. Se tiene dV/dNs = dVf /dNv, es decir:
La combinación de las Ecs. (9), (10) y (11) permite obtener la relación entre R y D siguiente 5:
Se ha argumentado que el factor de tortuosidad sigue una ley potencial 5,11:
donde Tv es un factor de tortuosidad de referencia; s es una función de la porosidad, de modo que s → 1/2 cuando ϕ → 0 y s → 1 cuando ϕ → 1,y está definido como s = Df /3, donde es la dimensión fractal de la superficie de las partículas o de la interfaz entre partículas y poros.
Las Ecs. (14) y (15) proporcionan la siguiente relación entre D y R:
Como ilustración, la curva de retención de Brooks y Corey 12, proporciona Fv (R) = (R/Rb)λ donde λ ≥ 0, y de las Ecs. (12) y (16) se deduce:
con λ < Λ. Así, en principio los parámetros λ y ψb de la curva de retención de Brooks y Corey pueden ser estimados a partir de la curva granulométrica usando las Ecs. (17) y (18) siempre y cuando el parámetro Tv sea conocido.
Es claro que el factor de tortuosidad induce una relación específica entre D y R, una ley en potencia de T (R) induce una relación en potencia entre D y R. Enseguida se investigan otras posibles relaciones para describir el factor de tortuosidad a partir de una reconceptualización del modelo de Arya y Paris.
2.2.2. Modelo II
En el modelo discreto de Arya y Paris el volumen de los vacíos es definido mediante la asimilación del espacio poroso a un tubo cilíndrico con una sección diferente en cada clase de partículas. En la adaptación de esta idea en el modelo presentado por Fuentes 4, se introduce la función densidad de la longitud de las partículas ℓs (D):
de modo que la longitud de las partículas con diámetros mayores que D, Ls (D), queda definida por:
El volumen de los vacíos quedaría definido por dVv (R) = (π/4) R2 τ (D) ℓs (D) dD, donde se ha introducido el factor τ (D) para alargar el diámetro de las partículas.
La relación entre R y D se deduce considerando las Ecs. (9) y (11):
de modo que la longitud de los poros de diámetros mayores que R, Lv (R), es proporcionada por:
El factor de alargamiento τ (D) se define como:
Con las Ecs. (21) y (23), la Ec. (10) se escribe como dVv (R) = (π/6) R 2τ (D) ℓs (D) dD. La relación entre R y D resultante es la siguiente:
Esta relación es solamente conceptual ya que se desconoce τ (D), razón por la cual es necesario investigar las posibles funciones que puedan representar la dependencia del factor de alargamiento con respecto al diámetro de partícula o de poro.
La combinación de las Ecs. (14) y (24) proporciona una relación entre los factores de alargamiento y tortuosidad:
y utilizando las Ecs. (15) y (16) se deducen las leyes en potencia siguientes:
Donde
Se puede establecer otra expresión del factor de alargamiento aceptando que τ
(D) es proporcional a
Para corregir este incoveniente se propone τ (D) = κs [Dns (D)]β [F s (D)]−c, la cual permite obtener Λ = λ(2 + 3β) / [2+λ(β−c)], que satisface λ ≤ Λ si c=β. La expresión para el factor de alargamiento toma la forma siguiente:
La relación Λ = λ [1 + (3/2) β] también es obtenida de la Ec. (28) si en lugar de F s (D) se utiliza Df s (D), pero en tal caso, en virtud de la Ec. (9), el resultado es equivalente al ya indicado por la Ec. (27), es decir τ (D) = τs (H s /D) 3β = τ s [n s (D) /f s (D)]β.
La Ec. (28), considerando la Ec. (9) y la pendiente en escala log-log de la curva granulométrica definida por 4:
toma la forma:
la cual contiene a la Ec. (27) tomando a τs (D) como una constante.
El sistema de Ecs. (12), (24), (27) y (30) constituye una relación entre las curvas porosimétrica y granulométrica; si se propone una representación analítica de alguna de ellas la otra queda definida por este sistema. Si se proporciona Fs (D), la curva porosimétrica Fv (R) queda representada como Fv = Fs (D) y R = R (D), en donde la relación entre R y D se obtiene de las Ecs. (24) y (30):
Cuando se proporciona la curva porosimétrica el sistema de ecuaciones permite obtener la expresión que define, con β > 0, la curva granulométrica:
donde R(Fs) representa la función inversa de Fs (R).
2.2.3. Modelo III
Otra relación posible entre el factor de alargamiento y las funciones de distribución de los poros análoga a la Ec. (27), es:
Esta última, en virtud de la Ec. (10), puede ser escrita como:
donde ξv (R) es la pendiente en escala log-log de la curva porosimétrica definida por:
Es claro que la Ec. (34) contiene la Ec. (26) haciendo τv (R) una constante.
La relación entre D y R correspondiente se obtiene de las Ecs. (24) y (34):
con 0 ≤ γ ≤ 2/3.
El sistema de Ecs. (12), (24) y (34) constituye otra relación entre las curvas porosimétrica y granulométrica. Si se proporciona Fs (D) la curva porosimétrica Fv (R), para γ < 2/3, queda definida por:
donde D (Fs) representa la función inversa de Fs (D). Si se proporciona la curva porosimétrica Fv (R), la curva granulométrica queda representada como Fs = Fv (R) y D = D (R), en donde la relación entre D y R está definida por la Ec. (32) y (36).
La obtención de formas analíticas cerradas a través de la Ec. (32), modelo II, o de la Ec. (37), modelo III, de Fs (D) a partir de Fv (R) en el primer caso, o de Fv (R) a partir de Fs (D) en el segundo, no es evidente para funciones más complejas que la función potencial de Brooks y Corey.
En estudios de la transferencia de agua en el suelo, generalmente es la curva de retención la que es representada analíticamente; la curva granulométrica correspondiente es difícil de obtener en forma cerrada a partir de la Ec. (32), sin embargo ella puede ser representada en forma parámetrica con el modelo III. En tal caso se puede utilizar la Ec. (14), modelo I, con el factor de tortuosidad que se obtiene de la combinación de las Ecs. (25) y (33) o (34). Haciendo
la cual representa una alternativa a la Ec. (13). La representación de la curva granulométrica queda como Fs =Fv (R) y D = D (R), esta última es similar a la Ec. (14), en donde Tv se reemplaza por:
2.2.4. Algunas funciones de distribución
Además de la ecuación de Brooks y Corey 12, se han propuesto diversas ecuaciones para representar la curva característica de humedad y en consecuencia la curva porosimétrica, como las de Brutsaert 15, van Genuchten14,Braddock et al. 16 y la distribución log normal. Muchas de estas ecuaciones pueden ser construidas a partir de ω (ρ) = ωmρλ, que se denominará distribución canónica y que tiene la estructura de la ecuación de Brooks y Corey; la escala adimensional está definida por ρ = R/Rm y ω = ω (1) con Rm un valor de referencia.
Se puede mostrar a partir de la identidad
que la distribución admite una función densidad del logaritmo de las escalas. En efecto, la transformación τ = ln(ρ) permite escribir la distribución canónica como ω(τ)=ωm exp(λτ) y su densidad p(τ) = dω/dτ = λω(τ), de donde d ln[ω(τ)] = λdτ y ω(τ) = p(τ)/λ; resultados que llevados a la identidad conduce a
a la cual se le impone la condición de normalización ω (∞) =1.
La ecuación de Brutsaert 15, se deduce considerando que la densidad tiene la forma
la cual es una distribución logística simétrica, en donde el término [1 − ω (τ)] impide el crecimiento sin bornes de ω(τ). La ecuación de van Genuchten 14, puede obtenerse a partir de una distribución logística asimétrica
donde m > 0 es un parámetro de asimetría, y haciendo n = λ/m. La ecuación de Braddock et al. 16, se obtiene a partir de
a saber:
donde n = λ/(1−ε)m y Rd = Rmω-1/λ (1−ω1/m)1/n.
Con ε = 0 se obtiene la ecuación de van Genuchten y de ésta la de Brutsaert con m = 1.
La distribución gaussiana fue establecida por A. Einstein en sus estudios de las fluctuaciones de una variable aleatoria a partir de la entropía 18, definida por S* (τ) = −ln[ω(τ)], de donde SE (τ) ≡ S*(0) - S*(τ) = ln[ω(τ)/ωm]. Considerando la distribución canónica se tiene p(τ) = λωm exp[SE (τ)]; SE (τ) es máxima en τ = 0, es decir S′E (0) = 0yS′′E (0) < −ε < 0, de modo que su desarrollo en potencias alrededor de τ = 0 y hasta el término cuadrático implica S* (τ) = S* (0) + ετ2 /2 , y en consecuencia p(τ) = λωm exp -ετ 2/2 . Esta densidad ha sido establecida para valores pequeños de τ, pero en razón de su rápido decrecimiento cuando |τ| → ∞, su aplicación puede extenderse sobre todo el dominio de integración, resultando de la normalización ε = 2π(λωm)2 y por lo tanto ω(τ) = [1+erf√πλτ/2)]/2, puesto que ω(τ = 0) = ½ = ωm; erf (x) es la función de los errores. Se tiene:
La distribución puede ser presentada en su forma usual ya que la variancia geométrica es proporcionada por σ 2=2/πλ 2.
El desarrollo de la densidad de Gauss alrededor de τ = 0 y hasta el término cuadrático es p (τ) = λωm (1− (ετ2 /2)), este desarrollo corresponde también a la densidad de Cauchy p(τ) = λωm (1+ ετ2/2)). En esta última la condición de normalización proporciona ε = 2 (πλωm)2 y en consecuencia ω (τ) = {1 + [2 arctan (πλτ /2) /π]} /2, ya que ω(τ = 0) = 1/2=ωm. Se tiene
Se pueden construir otras funciones de distribución proporcionando la función Φ(τ) en la siguiente perturbación de la distribución canónica: dω/dτ = λωm exp[λτ −Φ(τ)]. Con la función Φ(τ)=Φ0 +(μeλτ)1/p se obtiene ω(τ) = γ[(μeλτ )1/p ;p] y ωm Γ(1+p) = μeΦ0, donde γ(x;p) es la función gamma incompleta normalizada de variable x y parámetro p y Γ(p) es la función gamma (completa) de Euler; cuando p = 1/2 se deduce el caso estudiado por Fuentes 5: ω(τ) = erf (μeλτ) . En general se tiene:
el parámetro μ queda definido por
A la función
corresponde
y ωm pΓ(1 + p) ς (1 + p) = μ1+(1/p) eΦ0, donde ςI [x;s] es la función zeta incompleta normalizada de variable x y parámetro s y ς (s) es la función zeta (completa) de Riemann. Se tiene:
el parámetro μ queda definido por
3. Aplicaciones
Las características hidrodinámicas de los suelos son de fundamental importancia en los estudios de infiltración, precipitación, evaporación, drenaje y redistribución del agua en el suelo. A continuación se presenta la validación de los modelos fractales de medio poroso de Fuentes I, II y III; en donde se establecen las relaciones entre los tamaños de poros y partículas del suelo. El análisis se extiende de forma expresa a dos grupos de suelos de propiedades conocidas.
3.1. Suelos analizados por Hwang y Powers
En el trabajo de Hwang y Powers (6), se estudia la relación entre las curvas de retención y granulométrica representadas por una distribución lognormal y aplicada a suelos arenosos. Estas curvas de acuerdo con la Ec. (40) pueden escribirse como:
donde ψm es la presión asociada a
Rm y
Dm, S =
θ/θs es el grado de saturación,
Sr =
θr
/θs;
θs y
θr son los contenidos de
humedad a saturación y residual, respectivamente. Las desviaciones estándares
geométricas correspondientes están definidas por
La relación utilizada entre el diámetro de partícula y el radio de poro (r = R/2) es la ley potencial definida por la Ec. (4). De las Ecs. (45) y (46) se obtiene σψ = σD /υ o equivalentemente λ = υΛ.
La comparación de la Ec. (4) con la Ec. (18) proporciona el siguiente significado de los parámetros u y υ:
Los valores medios de los parámetros u y υ obtenidos en 79 suelos arenosos de la base de datos UNSODA, son los siguientes (Tabla IV de Hwang y Powers, 6): i) en 40 arenas u = 1.380 y υ = 0.70 , ii) 20 arenas francosas u = 0.991 y υ = 0.69, y iii) 19 francos arenosos u = 1.618 y υ = 0.68; D y R están en centímetros. Se debe notar que υ es casi una constante en las tres clases de suelos; de hecho, si se calcula υ a partir de los valores medios de los parámetros σD y σψ reportados en la Tabla III de Hwang y Powers 6, que para las tres clases de suelos son respectivamente: σD = 0.635, 0.913, 1.415 y σψ = 0.946, 1.360, 2.110, se obtiene el valor único de υ ≅ 0.67. Con el valor medio de la porosidad de las tres clases de suelos, ϕ ≅ 0.4, las Ecs. (13) y (48) predicen el valor de υ ≅ 0.65, valor cercano al obtenido precedentemente.
3.2. Suelos de Arya y Paris
Para el análisis de los suelos de Arya y Paris 2 se utiliza la distribución definida por la Ec. (40), a la cual corresponde la curva de retención siguiente:
donde Θ=(θ−θr)/(θs −θr) y ψd es la presión asociada a Rd.
La curva porosimétrica asociada a la Ec. (49), considerando θr = 0, es:
La pendiente en escala log-log de la curva porosimétrica se obtiene de la Ec. (50):
con ε = 1 − (λ/mn).
La curva granulométrica resultante es la siguiente:
donde
con Fsd = Fvd y Fvd definida por
La relación entre R y D definida por la Ec. (39) corresponde a γv = 2(2s−1)/3 en las Ecs. (52) y (53) y la relación definida por la Ec. (16) a γv =0 y κt = Tv.
La curva de retención definida por la Ec. (49) contiene tres parámetros de forma {λ, m, n} y pueden ser reducidos a uno, sin pérdida en la calidad de representación de los datos experimentales. En efecto, haciendo λ = mn las funciones θ (ψ) y Fv (R), Ecs. (49) y (50), se vuelven explícitas y corresponde la primera a la curva de retención de van Genuchten con dos parámetros de forma {m, n}; en este caso la función Fs (D) definida por la Ec. (52) es explícita sólo cuando γv = 0. Con una relación entre m y n el número de parámetros de forma se reduce a uno {m}; se acepta aquí la relación m = 1 − (2/n) (van Genuchten, 14; Fuentes et al., 17).
Los supuestos anteriores son utilizados para el análisis de los suelos B, D y F de Arya y Paris 2. La densidad de las partículas es tomada como ρ 0 = 2.65 g/cm3 lo que induce Hs = 8965.72 μm. Los valores de los parámetros Dd y m son reportados en la Tabla I, así como los valores de la porosidad; se debe observar que los valores predichos del parámetro α a partir de la porosidad son muy parecidos a los obtenidos por Arya y Paris 2, el valor medio teórico α teo = 1.385 (βteo = 0.385) es bastante cercano al valor de α = 1.38 recomendado por estos autores. El parámetro θs es tomado de Haverkamp et al. 13, y sobre los datos de las curvas de retención es calibrado el parámetro ψd y a partir de éste se obtienen los valores de τs y Tv que permiten el paso entre las curvas porosimétrica y granulométrica; los resultados se muestran en la Tabla II.
Tabla I Parámetros característicos de los suelos B, D y F.
| Suelo | ϕ(cm3 /cm3) | s | υ | κ | β = α - 1 | Dd (μm) | Tυ |
|---|---|---|---|---|---|---|---|
| B | 0.4717 | 0.6883 | 0.6234 | 0.6041 | 0.4027 | 220.31 | 0.0563 |
| D | 0.4415 | 0.6820 | 0.6360 | 0.5724 | 0.3816 | 277.12 | 0.0846 |
| F | 0.4264 | 0.6789 | 0.6422 | 0.5571 | 0.3714 | 300.35 | 0.1235 |
Tabla II Parámetros de la curva de retención de los suelos B, D y F y sus parámetros de calibración τs y Tv.
| Suelo | θs (cm3/cm3) | Rd (μm) | |ψ d | (cm) | m | Tυ |
|---|---|---|---|---|---|
| B | 0.4645 | 32.37 | 92.07 | 0.0563 | 0.7996 |
| D | 0.4112 | 29.48 | 101.07 | 0.0846 | 1.1157 |
| F | 0.3582 | 25.08 | 118.82 | 0.1235 | 1.3716 |
El parámetro τs o Tv fue calibrado de modo de minimizar la suma de cuadrados de los errores entre el contenido de humedad observado y el predicho por el modelo; en la Ec. (9) se ha considerado θ = θs F (D), para poder incluir el efecto del aire atrapado. En las Fig. 1, 2 y 3 se muestra la relación entre las curvas granulométrica y de retención para los suelos utilizados. En (a) se presenta el ajuste de la curva granulométrica del suelo a partir de su función de distribución Fs (D) definida en la Ec. (52), donde Fs (D) es la frecuencia acumulada basada en el peso de las partículas, cuyos diámetros son inferiores o iguales a D. En (b) se muestra la relación entre el contenido volumétrico de agua y la presión del agua, llamada curva característica de humedad o curva de retención en el suelo. El potencial de presión por unidad de peso se llama también presión efectiva del agua con respecto a la presión atmosférica o simplemente presión del agua, siendo denotada también por h(cm) que evoca la altura de una columna equivalente en agua. En un medio no saturado el potencial de presión varía con respecto al contenido de humedad; a medida que la presión aumenta el contenido de humedad se incrementa. El contenido volumétrico cuando los poros contienen agua o porosidad volumétrica parcial es denotado como (cm3/cm3), es decir volumen de agua por unidad de volumen de suelo y que en un suelo parcialmente saturado es función del potencial de presión del agua en el suelo. La curva característica de humedad es fuertemente afectada por la textura y la estructura del suelo. Por la textura, mientras mayor es el contenido de arcilla mayor es la retención del agua para un valor de la presión y más gradual es la pendiente de la curva, y por la estructura, se afectan los valores altos de presión donde los efectos capilares son los predominantes. En la Fig. 1 se muestra la relación entre las curvas granulométrica y de retención de humedad en el suelo B, con un factor de tortuosidad Tv = 0.7996. En la Fig. 2 se muestra la relación entre las curvas granulométrica y de retención de humedad en el suelo D, con un factor de tortuosidad Tv = 1.1157. En la Fig. 3 se muestra la relación entre las curvas granulométrica y de retención de humedad en el suelo F, con un factor de tortuosidad Tv = 1.3716.
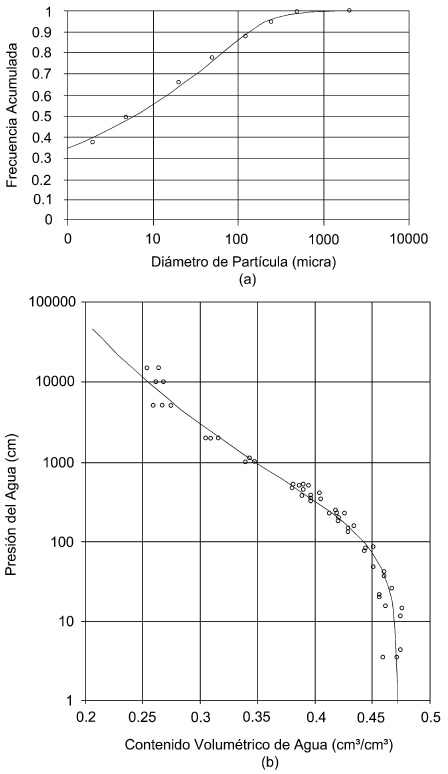
Figura 1 Relación entre las curvas (a) granulométrica y (b) de retención de humedad en el suelo B, con Tv = 0.7996.
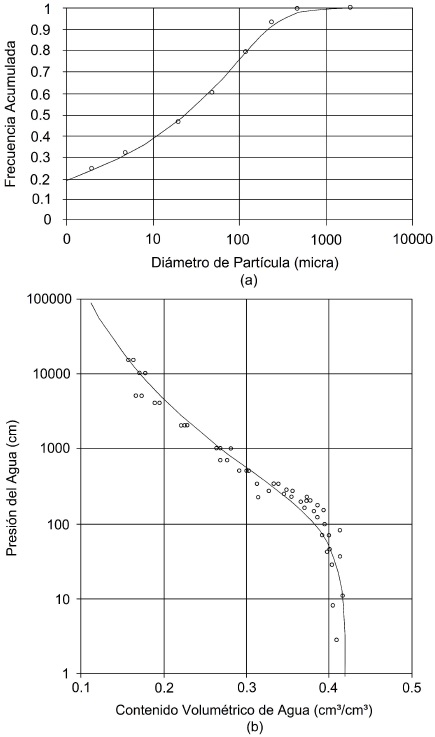
Figura 2 Relación entre las curvas (a) granulométrica y (b) de retención de humedad en el suelo D, con Tv = 1.1157.
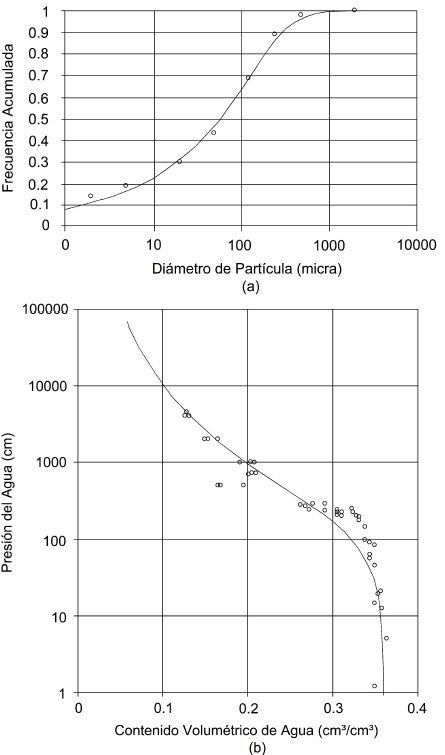
Figura 3 Relación entre las curvas (a) granulométrica y (b) de retención de humedad en el suelo F, con Tv = 1.3716.
En los modelos anteriores la representación de la histéresis en el suelo puede ser atribuida a la no uniformidad geométrica de los poros individuales, que son generalmente de forma irregular interconectados por pequeños pasajes, resultando un efecto de tintero. En el rango de potenciales altos, el efecto de histéresis es, en general, más pronunciado en suelos de textura gruesa que en los de textura fina. Finalmente la histéresis ha sido generalmente omitida en la teoría y en la practica de la física de los suelos, esto puede ser justificado en los procesos que envuelven sólo alguna rama de la curva como la infiltración (mojado) o evaporación (secado), pero el efecto de histéresis puede ser importante en el caso de procesos compuestos en lo que ocurre simultáneamente o secuencialmente el mojado y el secado en varias partes del perfil del suelo.
4. Conclusiones
Se ha expuesto la curva de retención o características de humedad del suelo que relaciona el contenido de humedad con la presión del agua. También se ha presentado una relación entre las curvas porosimétrica y granulométrica basada en el supuesto de una relación de vacíos constante en los diferentes empaquetamientos de las partículas del suelo y en una relación entre los tamaños de poro y partícula de los suelos. En la relación entre los tamaños de poro y partículas se hace intervenir el factor de tortuosidad de las trayectorias de flujo basado en el modelo de Fuentes o un factor de alargamiento de las partículas basado en el modelo de Arya y Paris. Puesto que la curva porosimétrica está asociada a una curva de retención de humedad del suelo, la relación propuesta puede ser utilizada para estimar esta última a partir de la curva granulométrica. La relación entre las curvas es validada con los suelos B, D y F de Arya y Paris, con buenos resultados. Con el valor medio de la porosidad de los suelos considerados por Hwang y Powers se pudo predecir los valores de los parámetros empíricos de empaquetamiento y forma de las partículas y poros. Finalmente, la curva de retención ha sido seleccionada a través de modelos fractales con la curva de distribución del tamaño de las partículas o curva granulométrica. Los autores recomiendan como trabajo futuro realizar revisiones de los modelos planteados empleando suelos con características distintas a los consideradas.











 text new page (beta)
text new page (beta)


