nueva página del texto (beta)
Inglés (pdf)
Artículo en XML
Referencias del artículo
Traducción automática
Enviar artículo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
1 Introduction
These days, circuit model-based quantum computers require some type of active error correction, because states in theoretically advantageous quantum algorithms acquire errors as they are prepared, manipulated by gates, and measured, reducing efficiency. For this reason, the characterization and correction of errors is of vital importance to obtain an acceptable result [2]. Although there are quantum error correction methods, as Fault-tolerant quantum error protocols [3], these are expensive from a computational point of view. In the current situation, i.e. a noisy intermediate-scale quantum era, it is important to characterize and analyze error models, for a possible future corrections.
The central idea of the article, is to use the isotropic index proposed in [1], that separates the model error into one part related to unitary deviation, due systematic errors, from another part which represents the loss of information. This last errors, due to decoherence, cannot be corrected without redundancy, while in principle systematic errors could be.
Two methods are proposed to model systematic errors. The first method determines the density matrix of the experimental output of a n qubit state, which requires about 4 n projective measurements (Quantum state tomography) and uses the isotropic index to find a unitary rotation, while the second method uses only 3n projective measurements. This last method is less general and works only for algorithms in which the output expected state, of each input basis state, is completely separable in all qubits.
With this intention, we analyze a particular algorithm: the Quantum Fourier Transform (QFT) [4], finding the unitary rotation that models the systematic error. The (QFT) is an important part of some quantum algorithms, such as the famous Shor’s factorization algorithm [5] and the quantum phase estimation algorithm [6]. However, the effect of noise on (QFT) is less studied. [7, 8].
This article is divided into three main sections. After the introduction, in Sec. 2, we present the Quantum Fourier Transform Algorithm (QFT), and its matrix model representation. In Sec. 3, we discuss both correction methods for general quantum algorithms. We explain how the unitary matrix model is determined for an n qubit state. Finally, in 4 we present, as an example, the experimental results of running the QFT algorithm for a two qubit system on IBM Q machine: ibmq_santiago, and some conclusions.
2 The quantum fourier transform algorithm
2.1 QFT Algorithm
The Fourier transform is used in a wide range of classical problems from signal processing to complexity theory. The QFT is the quantum generalization of the Discrete Fourier Transform (DFT) where the inputs are the amplitudes on a computational basis of a wave function. It is part of many quantum algorithms, most notably Shor’s factoring algorithm [5] which makes use of the QFT for period finding.
The classical DFT maps an input vector (x0,...,xN-1) to the output vector (y0,...,yN-1) according to Eq. (1):
where
Meanwhile the QFT acts on an input pure n-qubit quantum state x
where N=2n, and {j} is the standard computational basis, and maps it to the output state y according to
where ωjkN is the same as the classical case, Eq. (2).
2.2 Circuit implementation
Experimental quantum computers nowadays generally use a small set of universal quantum gates in order to generate quantum circuits. The quantum IBM computer (IBM Q) is no exception and only works with certain quantum gates, which made translating the matrix in Eq. (4) to quantum gates an essential task.
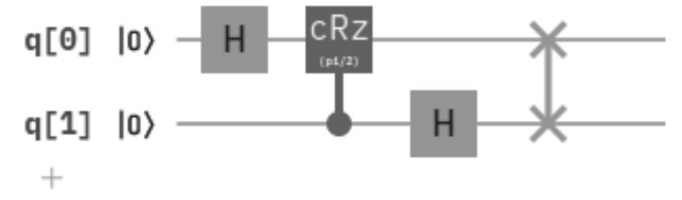
As an example, for a two qubit state, the quantum gate representation of the algorithm requires a few basic gates: the Hadamard transform and a controlled rotation of angle π/2 around the z axis, Rz, whose matrix representations are shown in Eq. (5) and (6), respectively.
where Rz is
the QFT circuit UQFT=(I⊗H).cRz.(H⊗I) is shown in Fig. 1.
3 Systematic error model
3.1 Error model using the density matrix and the isotropic index
In order to model the systematic error, the first step is to reconstruct the resulting density matrix ρexp, measuring the experimental projections from the data obtained from IBM Q, using Quantum State Tomography (QST) [4]. To recover the density matrix state, measurements must be made in the three basis (axes) of space, X,Y and Z whose matrices are defined:
For example, for any 2 qubit state its matrix ρ is given by
where σ0=I, σ1=X, σ2=Y, σ3=Z and the values of tr(ρσi⊗σj) are obtained, measuring the state several times in order to approach the expected value by the statistical average.
3.2 Isotropic index
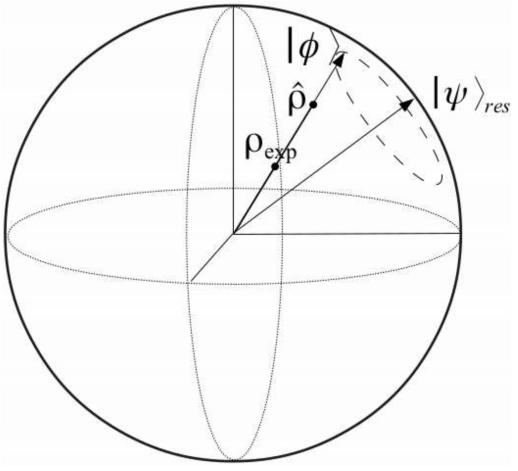
The isotropic index is useful to separate the global loss of information, called weight ω, from the misalignment A with respect to a reference pure state. While nothing can be done about the loss of information, the misalignment (coming from systematic errors), could be corrected, hence the importance of separating these two type of errors.
Considering the pure reference state |ψ⟩, ρψ = |ψ⟩⟨ψ| and the decomposition of a state ρ after a noisy process,
the double index is defined as:
where λ is the smallest eigenvalue of ρ,
where Fid is the fidelity between states [4], and ρψ⊥=I-ρψ/2n-1 is the isotropic mixed state orthogonal to |ψ⟩.
The misalignment takes values in the interval [-1,1], where 1 means the resulting state is completely aligned with the reference state ρψ and -1 means the resulting state is completely misaligned i.e. aligned with ρψ⊥. Moreover, ω takes values in the interval [0,1]: when ρ is a pure state ω=0, and when the loss of information is total, ω=1.
Consider now the state |ψ⟩ as the reference state of the resulting theoretical state from the application of QFT to some basis state, and ρexp the obtained experimental matrix state from the same input state. Decomposing the ρexp
it is always possible to obtain ω and ˆρ.
In the particular case where ˆρ is a pure state, i.e., ˆρ=|ϕ⟩⟨ϕ|, one could partially correct the error with a unitary matrix that takes |ϕ⟩ to the state |ψ⟩.
Unfortunately, generally the state ˆρ is not a pure state, so it is necessary to find the pure state |ϕ⟩, closest to ˆρ, and with maximal alignment with it, i.e., |ϕ⟩ should satisfy Eq. (14)
where A is the alignment index. These states can be graphically seen in Fig. 2.
In order to find |ϕ⟩ that satisfied the requirement, optimization methods were used. Once |ϕ⟩ was found, a rotation matrix U that takes |ϕ⟩ to theoretical |ψ⟩, is easy to write out, for any basis initial state. It is a corresponding matrix U i and |ϕi⟩ for each input canonical basis state |i⟩. Hence, the complete model is defined as a control unitary rotation Uc , and n ancillary qubits, that simultaneously correct the n basis states, and so any input state. An example of Uc for two qubits Hilbert space, is given in Sec. 4 (see Fig. 3). Although this method is more exact, it has a high computational cost since the resulting state needs to be measured in all 4n local projections, where n is the number of qubits. In Sec. 3.3 we will analyze another method that manages to estimate the necessary correction by measuring only 3n projections.
3.3 Error model using only 3n projection’s
Since determining the density matrix ρexp using the QST method is computationally expensive, another method is proposed to avoid this step. The idea is to find the pure state ϕ, closest to the ρexp measuring only those projections relevant for the correct functioning of the algorithm. This is, those that maximally differentiate each of the states resulting from the application of the QFT, on each of the 2 n initial basis states.
Fortunately, in the case of the QFT algorithm, the theoretical output state for each input basis state is separable on all qubits. Although the mixed state ρexp is generally not, we assumed the hypothesis that the error is expected to affect in such a way that the resulting state stays close to the theoretical one, and we shall discuss if this assumption proved right experimentally. We assume that a good estimate in this case is to find the reduced density matrix of ρexp in each qubit i, ρiexp, i.e., measuring the projections X,Y,Z, of this qubit, in total 3n measurements.
Once we have obtained the reduced density matrices of each qubit i, the eigenvector with the highest eigenvalue is extracted |ϕ⟩i without optimization. In the case of a one qubit matrix state, the decomposition in (13), ˆρ is a pure state and is always the most aligned.
Similarly to the previous method, the unitary rotation matrices are determined for each input basis state U=U1⊗U2...Un, that takes the state |ψ⟩ to |ϕ⟩. Finally the total U c matrix is defined similarly to previous method as in Fig. 3.
As an example, the resulting unitary matrix for two qubits on IBM Q computer ibm_santiago, are shown in the next section and the results are compared to those of the first method.
4 Analyzing experimental results
The procedure will be explained for one of the basis input state of the algorithm |01⟩, the other basis state were treated similarly.
Running the QFT algorithm in IBM Q computer ibm_santiago, we estimate the resulting probabilities of measuring the projections in all basis. The mean values are obtained from 8192 shots for each projection, and shown in Tables I and II.
Table I Experimental results for the basis input state |01⟩ in ibm_santiago, measuring a single qubit.
| Basis | 0 | 1 |
|---|---|---|
| IX | 4103 | 4089 |
| IY | 7923 | 269 |
| IZ | 2230 | 1866 |
| XI | 162 | 3934 |
| YI | 2274 | 1822 |
| ZI | 4115 | 4077 |
Table II Experimental results for the basis input state |01⟩ in ibm_santiago, measuring two qubits.
| Basis | 00 | 01 | 10 | 11 |
|---|---|---|---|---|
| XX | 202 | 120 | 3981 | 3889 |
| XY | 231 | 182 | 7266 | 513 |
| XZ | 158 | 147 | 4272 | 3615 |
| YX | 2299 | 2166 | 1874 | 1853 |
| YY | 4350 | 101 | 3587 | 154 |
| YZ | 2433 | 2016 | 2023 | 1720 |
| ZX | 2213 | 2052 | 2039 | 1888 |
| ZY | 4078 | 111 | 3875 | 128 |
| ZZ | 2204 | 1996 | 2167 | 1825 |
4.1 Experimental results with the isotropic index
Performing the QST on this data we obtained the experimental reconstructed density matrix for ibmq_santiago, which was deemed too large to fit this article.
The theoretical output state corresponding to input |01⟩ is |ψ⟩01=-⊗|+y⟩, where |+y⟩=|0⟩+i|1⟩. For this state, the pure state |ϕ⟩01 with the maximum alignment with ρexp is found:
Finally the unitary rotation matrix U 01 is calculated which maps the state |ϕ01⟩ to the output theoretical state |ψ⟩01. Similarly, the pure states |ϕ⟩ij obtained for the other input basis states are presented in the Table III.
Table III Optimal pure state |ϕ⟩ for ibm_santiago.
| |ϕ⟩00 | |ϕ⟩10 | |ϕ⟩11 |
|---|---|---|
| .565 | 0.559 | 0.586 |
| .450 + 0.031i | -0.480 - 0.006i | -0.026 - 0.453i |
| .485 - 0.010i | 0.534 + 0.021i | -0.498 |
| .488 - 0.063i | -0.414 + 0.015 | 0.015 + 0.450i |
This procedure was performed for the four resulting states, obtaining the four unitary transformations. Using two ancillary qubits, a unitary transformation U c is defined that controls which element of the unitary set should be applied, so that the model works for any input state. This model is shown in Fig. 3.
In order to model the decoherence, a total Depolarizing Chanel is applied on the theoretical state |ψ⟩, and the resulting state
is compared with the transformation of the experimental state under U:ρ'=UρexpU†. Although the decoherence error generated by the computer does not have to fit with a chosen Depolarizing Channel, this simple error model does not change the alignment of the states and can estimate the effect of decoherence.
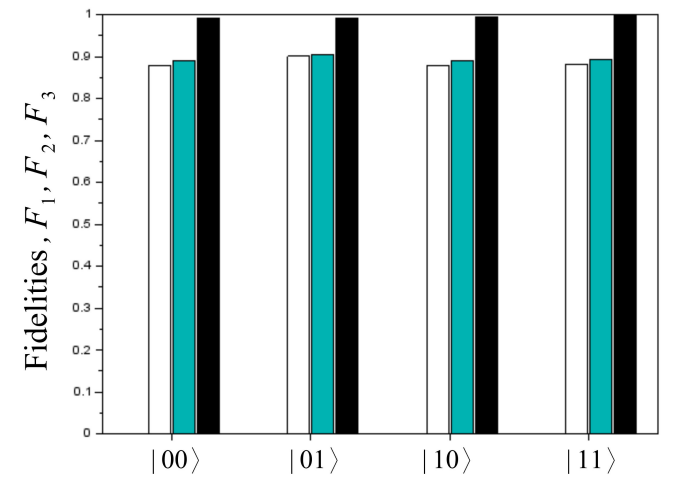
Finally in Table IV and as shown in Fig. 4, the results are compared. This comparison is done by calculating the fidelity in each step F 1, F2, F3 defined as:
where |ψ⟩ is the expected theoretical state and ρ'=UρexpU†.
Table IV Fidelities, Eq. (??) of the second method, using 4n projections, for ibm_santiago.
| Input state | F1 | F2 | F3 |
|---|---|---|---|
| |00〉 | 0.87940 | 0.88928 | 0.99213 |
| |01〉 | 0.90030 | 0.90551 | 0.99236 |
| |10〉 | 0.87870 | 0.88957 | 0.99553 |
| |11〉 | 0.88217 | 0.89308 | 0.99589 |
4.2 Experimental results Using only 3n projections
In contrast with the previous method, now we look for an estimate of the state |ϕ⟩, closer to the state ρexp without the explicit representation of the density matrix, using only 3n projective measurements. Those projections are chosen so that the unitary matrix brings the state ρexp closer to the particular basis state, and as far as possible from the other three basis states. The idea is to look for the pure state that is most aligned with each of the reduced one qubit matrices. With this purpose we measured the projections X,Y,Z in each of the qubits, and found the one qubit reduced matrices. To get the pure state with most alignment, no optimization is needed, because for one qubit matrices the principal eigenvector |ϕi⟩ (the eigenvector with maximal eigenvalue) is the state with most alignment, getting |ϕ⟩=|ϕ⟩1⊗|ϕ⟩2.
Finally the desired separable unitary rotation for each basis state U=U1⊗U2 is found, and similarly to the previous method a Depolarizing Chanel is applied on the theoretical state |ψ⟩, and the resulting state ρDch=ϵ(|ψ)⟩ is compared with the transformation of the experimental state under U: ρ'=UρexpU†. The fidelity between ρDch and ρ' is shown for the four input states in Table V and shown in Fig. 5.
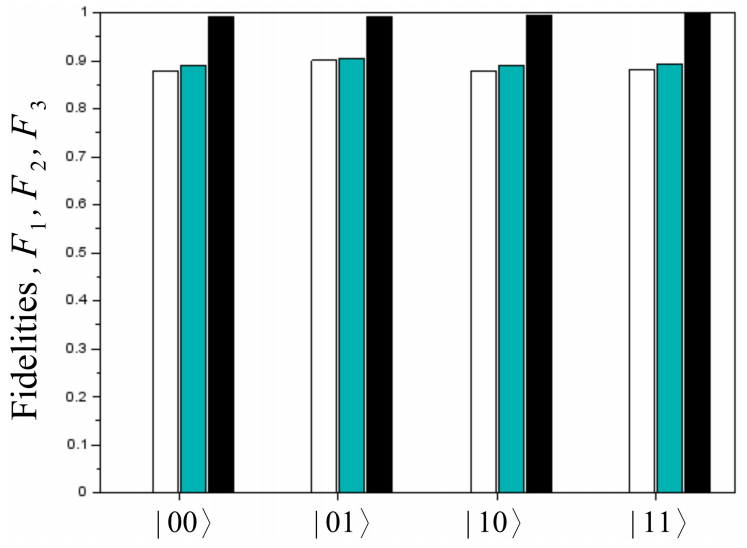
Table V Fidelities, Eq. (??) of second method, using 3n projections, for ibmq_santiago.
| Input state | F2 | F3 |
|---|---|---|
| |00〉 | 0.88471 | 0.98792 |
| |01〉 | 0.90541 | 0.99226 |
| |10〉 | 0.88857 | 0.99460 |
| |11〉 | 0.89133 | 0.99426 |
5 Conclusions
In this paper we have managed to study the performance of the Quantum Fourier Transform algorithm in a real quantum computer. The loss of information due decoherence effects, could be corrected by adding redundancy as in quantum correcting codes, but in general could be computationally expensive.
We propose two methods to model systematic errors: the first method uses the isotropic index that separates the loss of information, by decoherence, from the systematic error, that potentially could be correctable determining a unitary transformation that could correct any input state. The method needs to reconstruct the density matrix from 4 n measurements, and uses the alignment to determine the unitary correction matrix for each input basis state. Meanwhile, in the second method it is only necessary to measure 3n projections, taking advantage of the fact that the theoretical output of the QFT algorithm of each basis state, is separable in all qubits. The first method, although very expensive from a computational point of view, is more general and can be used to model systematic errors of any algorithm, the second can be only used for algorithms with separable output states as the QFT. Even though the theoretical output state of the QFT algorithm is separable, experimental errors can introduce some entanglement. Nonetheless, the experimental result is expected to be reasonably close to being separable for minor errors. As can be seen in Figs. 4 and 5, the results are very similar which seems to support this assumption.
As can be seen in these same figures, in actual IBM Q computers, the unitary errors are much less relevant than the decoherence errors. Nevertheless, this method could be used as calibration via software, using the U c matrix, once it is determined experimentally, regardless other methods are needed to correct decoherence error.
Even though this analysis shows correcting systematic errors at the current state of the art IBM Q computers is of minor importance, this models could be used to visualize (5) the weight of the different types of errors that affect quantum computation and could prove especially useful in educational contexts.
