1. Introducción
La nueva geografía económica (NGE) surge para explicar la distribución espacial de la actividad económica en los países, que responde, entre otros factores, a políticas de comercio e industriales (nacionales y regionales). Durante las últimas décadas muchos países en desarrollo han experimentado profundos cambios en este sentido. El caso de México es de los más estudiados puesto que estos han generado un importante reacomodo espacial de la actividad económica (Hanson, 1996, 1997 y 1998; Chamboux-Leroux, 2001; Dávila, 2004; Mendoza y Pérez, 2007; Hernández, 2007 y 2013, y Unger, 1996 y 2012).
En este trabajo se demuestra que la apertura comercial en México significó el debilitamiento de la fuerza centrípeta constituida por la integración vertical insumo-producto nacionales, lo que provocó un reacomodo de la actividad económica hacia los estados del norte del país, próximos al mercado estadounidense.
Este resultado es importante en dos dimensiones. Por un lado, hace una contribución a los escritos empíricos de la NGE sobre los determinantes clave de la concentración industrial. Por otro lado, el proceso de desintegración vertical de las actividades productivas ha generado que la economía mexicana se haya vuelto vulnerable a los cambios en los precios de los insumos importados (Cuadra, 2008 y Kim, 2013). Hay dos vertientes en la bibliografía sobre el tema que enfatizan distintos determinantes de la concentración industrial. Mientras que las teorías tradicionales del comercio (TTC) se concentran, como su nombre lo indica, en factores tradicionales como las diferencias en productividad o teoría ricardiana y en dotaciones de factores a través de las regiones como el modelo de Hecksher-Ohlin, la NGE subraya las economías a escala y la intensidad en el uso de bienes intermedios en las industrias (Krugman, 1992).
Mediante un análisis econométrico con datos de panel1 y efectos fijos, en este artículo se demuestra que las economías de escala y la intensidad en el uso de insumos intermedios nacionales son los factores que de manera más importante explican la concentración industrial absoluta en el país. En cambio, los determinantes propuestos por las TTC no aportan explicación significativa a la concentración industrial del país.
El resultado más importante radica en la relación significativa entre la concentración industrial y el uso de bienes intermedios nacionales. En general, la NGE sostiene que la intensidad en el uso de bienes intermedios nacionales debe relacionarse positivamente con la concentración industrial, debido a que los vínculos insumo-producto generan una fuerza centrípeta que incentiva tanto a los productores intermedios como a los productores finales a localizarse cerca unos de otros. En este artículo se comprueba empíricamente la existencia de esta fuerza durante el periodo previo a la apertura comercial. Quizás más interesante aun es el hecho de que, en aparente contradicción con la NGE, la relación entre la concentración industrial y la intensidad en el uso de bienes intermedios nacionales se torna negativa para el periodo posterior a la apertura comercial.
La razón de este comportamiento diferenciado antes y después de la apertura se origina con la disminución del precio relativo de los insumos intermedios importados. Esto generó incentivos en las industrias a ubicarse cerca de los productores de insumos más baratos, lo que se tradujo en un reacomodo de la actividad económica desde el centro del país hacia la frontera norte. Tal cambio estructural impacta en la relación de la concentración industrial con la intensidad en el uso de bienes intermedios nacionales. Para entender esto, se muestra cómo antes de la apertura comercial, la relación positiva entre ambas variables obedecía a que el centro capturaba la mayor parte de la actividad económica y las industrias más concentradas eran las más vinculadas verticalmente, tal cual lo predice la NGE. En cambio, después de la liberalización comercial, gran parte de la actividad económica se traslada hacia la frontera norte y, por tanto, las industrias más concentradas se convierten en las que importan más insumos, esto es, las menos vinculadas verticalmente con insumos nacionales. También puede observarse que aunque el resultado está en aparente contradicción con la NGE, el origen de este radica en la fuerza centrípeta que enfatiza la NGE: el deseo de estar cerca de insumos baratos.
Este fenómeno de desintegración vertical con insumos nacionales y vinculación con insumos importados es el origen de la alta vulnerabilidad que presenta la economía mexicana a los cambios en los precios de estos bienes. Así lo documenta Cuadra (2008), quien muestra que hay una fuerte correlación negativa entre el tipo de cambio y el PIB en México, en tanto que Kim (2013) señala que este mecanismo es crucial para explicar gran parte de las fluctuaciones de corto plazo en economías pequeñas y abiertas. En su artículo, el autor cuantifica que tales cambios explican alrededor de 50% de las fluctuaciones del PIB en Corea.
Una segunda contribución del presente artículo, y que lo hace diferente a otros en la bibliografía empírica de geografía económica, es que analiza el patrón de evolución de la concentración industrial en México con una perspectiva de muy largo plazo, desde 1981 hasta 2004, en la que pueden compararse periodos suficientemente amplios antes y después de los cambios en la política comercial.2 El principal resultado obtenido es que a nivel nacional se presenta una disminución de 20% en el grado de concentración industrial manufacturero.
Trabajos relacionados. Este artículo se ubica como parte de la bibliografía de la “nueva geografía económica” que, como se mencionó, es la rama de la economía que se ocupa de explicar dónde ocurren las cosas (Krugman, 1992; Krugman y Livas, 1996; Puga y Venables, 1996; Venables, 1996; Fujita, et al., 1999; Combes, et al., 2008). Esta empieza con la observación de que algunas industrias están concentradas geográficamente mientras otras se encuentran dispersas, y se enfoca en entender dicho fenómeno. Muestra cómo en regiones con un estructura productiva similar pueden llegarse a formar de manera endógena tanto los centros como las periferias, ya sea por la movilidad de los trabajadores o por la movilidad de las empresas, que demandan bienes intermedios.
Los estudios empíricos sobre esta línea de investigación están en proceso de desarrollo, tratando de verificar las principales predicciones que se deducen de los modelos teóricos, centrándose sobre todo en el caso de la Unión Europea. El primer trabajo empírico que estudia los determinantes de la concentración industrial en Estados Unidos es el de Kim (1995). Para la Unión Europea se han desarrollado trabajos como el de Amiti (1999), Haaland, et al. (1999), Brülhart (1998), Knarvik, et al. (2000 y 2001), y Redding, et al. (2003). A nivel país, estudios similares son lo de Paluzie, et al. (2001), Tirado, et al. (2002), Bai, et al. (2003), Traistatu y Volpe (2003 y 2006), Sanguinetti y Volpe (2004), Díaz y Gillmore (2004), Falcioglu y Akgüngör (2006) y Sala (2008). En todos ellos, los factores que explican en mayor medida la distribución espacial de las industrias son las economías de escala, el uso de bienes intermedios, diferencias en dotación de factores y productividad laboral, entre otros.
En este sentido, nuestro análisis confirma las hipótesis planteadas por el modelo teórico de Krugman y Livas (1996), que sólo habían sido parcialmente verificadas por Hanson (1997). Sin embargo, a diferencia de Hanson que se centraba en el análisis del gradiente salarial regional y su evolución al compás de los cambios en la política comercial en México, el presente análisis aborda por primera vez de forma explícita el papel de los enlaces verticales insumo-producto en la concentración y verifica de forma sólida las hipótesis teóricas planteadas por Krugman y Livas (1996).
El artículo está estructurado de la siguiente manera. En la primera sección, se describe el patrón de comportamiento de la concentración industrial en México, utilizando un índice de distribución. En el segundo apartado se explican las variables que se utilizarán para elaborar el modelo con base en las teorías del comercio y la NGE, y la concentración geográfica del personal ocupado de las industrias. La tercera sección presenta la estimación y el análisis del grado de influencia de estas variables sobre la concentración espacial de las industrias. En el cuarto apartado se realiza una prueba de cambio estructural para México. En la última parte de esta investigación se expresan las principales conclusiones sobre el tema y posibles líneas de investigación.
I. Comportamiento de la concentración industrial en México, 1981-2004
En el aspecto de distribución espacial de la actividad económica, la política de sustitución de importaciones condujo a una gran concentración urbana en la Ciudad de México e hizo de esta región el mayor mercado del país, atrayendo con ello una gran proporción de nuevas empresas industriales, con lo que se consolidó y se volvió autosostenido el proceso de concentración regional de las manufacturas. Con ello, se creó un patrón centro-periferia que se mantuvo hasta los años setenta.
El ingreso de México al Acuerdo General sobre Aranceles Aduaneros y de Comercio (GATT) en 1986, planteó la eliminación de barreras comerciales y fue una vía para garantizar el compromiso de liberalizar la economía nacional.3 La apertura de los mercados alcanzó su punto culminante con la puesta en marcha del Tratado de Libre Comercio de América del Norte (TLCAN) en 1994, que fue parte de una evolución internacional en la que se han multiplicado los procesos de integración regionales o continentales.
Como resultado de ello, los sectores económicos de base urbana han ido modificando su peso específico regional y nacional al irse reubicando en las regiones periféricas, quebrantándose de este modo la concentración en la zona centro del país.
A raíz de los procesos de apertura comercial en diversos países, este tipo de políticas ha influido de diferente manera en la distribución espacial de la estructura productiva según las características de las regiones y su nivel de desarrollo económico. Por esta razón, en esta sección nos planteamos describir los cambios en el patrón de concentración de la industria manufacturera mexicana en el periodo de la liberalización comercial mediante el índice de Gini absoluto.4,5
El índice de Gini, para el estudio de la concentración industrial, proporciona una medida de la desviación de los patrones geográficos del empleo de un sector industrial respecto a lo que sería si dicha actividad se comportará de manera homogénea en los estados de la República. Este indicador se obtiene a partir de la siguiente expresión:
Donde εij es el empleo de la industria j=1…32, ∑nj=iac(εij) corresponde al personal ocupado acumulado por industria i en el estado j, r es el numero total de industrias, μ la media del empleo total del estado j respecto del total de ramas.6 Los resultados señalan que cuando el valor es cero, el empleo de la industria está distribuido de manera uniforme en las áreas geográficas, mientras que el valor uno significa que el empleo está concentrado en una única unidad geográfica.
El caso mexicano es interesante ya que durante más de 40 años el gobierno mantuvo protegidas a empresas dedicadas a abastecer al mercado interno. A partir de la firma del GATT, la política económica se dirigió a fortalecer las industrias dedicadas al sector exportador. Esto ha provocado que a nivel nacional la industria manufacturera presente una disminución de 20% en el grado de concentración industrial de 1981 a 2004.7
Para cada par de años se analiza el índice de concentración industrial; como un resumen del patrón de cambios, en el siguiente Cuadro I.1. se observa que de 1989 a 1994 se presentaron los niveles más bajos de este indicador (en promedio el cambio fue de 5.73%), hecho que puede relacionarse con con el cambio de política dirigida hacia una mayor apertura comercial que se venía gestionando desde mitad de los años ochenta. En general, se percibe que en promedio 70% de las manufacturas disminuyeron su grado de concentración de 1981 a 2004. Diversos autores han encontrado una tendencia similar para un periodo más corto o para datos más agregados.8 No obstante, es importante subrayar que no todas las industrias manufactureras presentan la misma tendencia.
Cuadro 1 Cambios en el Índice de Gini de concentración industrial absoluta
| Número de industrias (promedio de cambio) | ||||
|---|---|---|---|---|
| Periodo | Incremento del Gini | Decremento del Gini | ||
| 1981-1986 | 13 | (3.50%) | 41 | (-5.47%) |
| 1986-1989 | 20 | (2.01%) | 34 | (-4.91%) |
| 1989-1994 | 8 | (3.39%) | 46 | (-5.73%) |
| 1994-1999 | 19 | (3.82%) | 35 | (-4.23%) |
| 1999-2004 | 22 | (4.11%) | 32 | (-5.11%) |
Nota: los porcentajes entre paréntesis señalan el cambio promedio del periodo.
Fuente: Elaboración propia a partir de los censos económicos del INEGI de 1981, 1986, 1989, 1994, 1999 y 2004.
Por ello, se realizó el siguiente ejercicio en donde se dividen las 54 ramas manufactureras en cinco grupos, acorde con el siguiente criterio: primero se tomarán las 18 industrias que muestran altos niveles de concentración en 1981 (es decir, un tercio del total), dividiendo ese grupo entre las que aún siguen concentradas en 2004 (CC) y las que disminuyeron su grado de concentración (CD). Segundo, se toman las 18 industrias con menores niveles de concentración en 1981 y se separan las que permanecen igual al final del periodo (DD) y las que incrementaron sus niveles de concentración (DC). El resto de las industrias que no entran en este criterio se sitúan en un grupo que se denominará residual (Knarvik, et al. 2000).9
En el Gráfico I.1 se presentan las tendencias en el tiempo de los primeros cuatro grupos y el promedio de las 54 industrias (observándose una tendencia decreciente), y en el Cuadro I.2 se enlistan las industrias de cada grupo con su nivel de tecnología. Las diferencias en el comportamiento de los grupos seleccionados son claras; posteriormente se explica cada una a detalle.
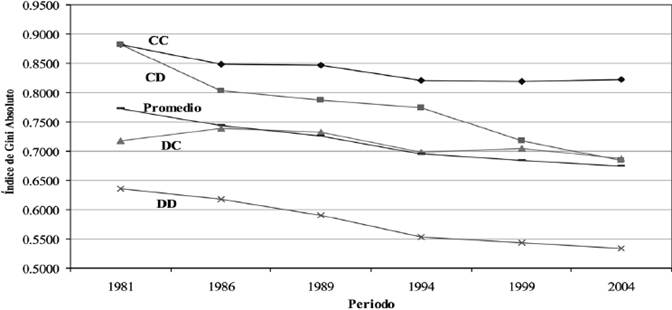
Fuente: Elaboración propia a partir de los censos económicos del INEGI de 1981, 1986, 1989, 1994, 1999 y 2004.
Gráfico 1 Índice de Gini de concentración industrial, agrupado por niveles y cambios en concentración, 1981-2004
I.1 Industrias concentradas que permanecen concentradas en el tiempo (CC)
Entre las manufacturas que permanecen con altos niveles de concentración del empleo a través de los años analizados se encuentran: cacao, tabaco, textil de fibras duras y cordelería de todo tipo, calzado, petroquímica básica, fibras artificiales y/o sintéticas, farmacéutica, otras sustancias y productos químicos, vidrio y sus productos, básicas de metales no ferrosos, máquinas de oficina, e instrumentos y equipo de precisión. Gran parte de estas industrias disminuyeron sus niveles de concentración desde 1986 (véase el Gráfico I.1), excepto la petroquímica básica y la farmacéutica, que presentan mayores niveles de concentración y comenzaron a notarse cambios en sus estructuras en 1989. A partir de 1994, todas las industrias presentan una caída en el índice de concentración excepto en la industria del tabaco.
La mayoría de estas ramas manufactureras se concentran en pocos estados, y pertenecen al sector de sustancias químicas, productos derivados del petróleo, del carbón, hule y plástico. Se puede resaltar que industrias como la farmacéutica, otras sustancias y productos químicos, máquinas de oficina, e instrumentos y equipos de precisión presentan, además, elevados niveles de tecnología.10
I.2 Industrias concentradas que se dispersaron en el tiempo (CD)
Hay un tipo de manufacturas que inicialmente tenían elevados niveles de concentración en los años ochenta, sin embargo, se observa que a partir de 1986 estos fueron disminuyendo. El grupo está comprendido por tejidos de punto, refinación de petróleo, productos de plástico, muebles metálicos, otros productos metálicos, y aparatos y accesorios de uso doméstico.
La mayoría de estas industrias carecen de tecnología avanzada y se localizan en la región centro (Ciudad de México, Estado de México y Puebla), en Jalisco y Nuevo León, que siguen siendo los estados con mayor concentración de la actividad productiva a nivel nacional, pero que han ido disminuido durante este periodo de estudio. Antes de la apertura comercial, las industrias pertenecientes a este bloque concentraban una mayor proporción del personal ocupado, pero al caer las barreras comerciales es muy probable que estas manufacturas se dispersaran hacia otros estados del país o disminuyeran su tamaño debido la competencia extranjera.
I.3 Industrias dispersas que se han concentrado en el tiempo (DC)
Las industrias que forman parte del tercer grupo son: aceites, grasas comestibles y materiales de arcilla para la construcción. Su grado de concentración comenzó a incrementarse en 1986; en el siguiente periodo presentan una disminución en los niveles de concentración y a partir de 1994 se han mantenido casi constantes, superando el promedio manufacturero. Estas dos ramas presentan una presencia baja o media baja de tecnología. La industria de aceites se concentra en los estados de México, Jalisco, Sonora y Veracruz; y la de arcilla está localizada en Nuevo León, Puebla y Guanajuato, principalmente.
Cuadro 2 Principales resultados del índice de concentración industrial manufacturero 1981-2004
| Industrias concentradas que permanecen concentradas en el tiempo (CC) |
Nivel de tecnología |
Industrias concentradas que se dispersaron en el tiempo (CD) |
Nivel de tecnología |
|---|---|---|---|
| 3119 Cocoa, chocolate y artículos de confitería | B | 3214 Tejidos de punto | B |
| 3140 Tabaco | B | 3530 Refinación de petróleo | MB |
| 3211 Textil de fibras duras y cordelería de todo tipo | B | 3560 Productos de plástico | MB |
| 3240 Calzado | B | 3813 Muebles metálicos | MB |
| 3511 Petroquímica básica | MB | 3814 Otros productos metálicos | MB |
| 3513 Fibras artificiales y/o sintéticas | MB | 3833 Aparatos y accesorios de uso doméstico | A |
| 3521 Farmacéutica | A | ||
| 3522 Otras sustancias y productos químicos | MA | ||
| 3620 Vidrio y productos de vidrio | MB | ||
| 3720 Básicas de metales no ferrosos | MB | ||
| 3823 Máquinas de oficina, cálculo y procesmiento informático | |||
| 3850 Instrumentos y equipo de precisión | A | ||
|
Industrias dispersas
que se han concentrado en el tiempo (DC) |
Nivel de tecnología |
Industrias dispersas
que ha permanecido dispersas en el tiempo (DD) |
Nivel de tecnología |
| 3117 Aceites y grasas comestibles | B | 3111 Carne | B |
| 3612 Materiales de arcilla para la construcción | MB | 3112 Productos lácteos | B |
| 3113 Conservas alimenticias | B | ||
| 3114 Beneficio y molienda de cereales y otros productos agrícolas | B | ||
| 3115 Productos de panadería | B | ||
| 3116 Molienda de nixtamal y tortillas | B | ||
| 3121 Otros productos alimenticios para el consumo humano | B | ||
| 3122 Alimentos reparados para animales | B | ||
| 3130 Bebidas | B | ||
| 3212 Hilado, tejido y acabado de fibras blandas | B | ||
| 3220 Confección de prendas de vestir | B | ||
| 3311 Productos de aserradero y carpintería | B | ||
| 3312 Envases y otros productos de madera y corcho | |||
| 3320 Muebles principalmente de madera | B | ||
| 3812 Estructuras metálicas, tanques y calderas industriales | MB | ||
| Grupo residual |
Nivel de tecnología |
Grupo residual |
Nivel de tecnología |
| 3118 Azucarera | B | 3710 Hierro y del acero | MB |
| 3213 Confección con materiales textiles | B | 3811 Fundición y moldeo de piezas metálicas, ferrosas y no ferrosas | MB |
| 3230 Cuero, pieles y sus productos | B | 3821 Maquinaria y equipo para fines específicos | A |
| 3410 Manufactura de celulosa, papel y sus productos | 3822 Maquinaria y equipo para usos generales | A | |
| 3420 Imprentas, editoriales e industrias conexas | B | 3831 Maquinaria, equipo y accesorios eléctricos | A |
| 3512 Sustancias químicas básicas | B | 3832 Equipo electrónico de radio, televisión, comunicaciones | A |
| 3540 Coque | MB | 3841 Automotriz | MA |
| 3550 Hule | MA | 3842 Equipo de transporte y sus partes | MA |
| 3611 Alfarería y cerámica. Excluye materiales de construcción | MB | 3900 Otras industrias manufactureras | B |
Nota: B = Nivel de tecnología bajo; MB = Nivel de tecnología medio bajo; MA = Nivel de tecnología medio alto; A= Nivel de tecnología alto, con base en la clasificación proporcionada por la Organización para la Cooperación y el Desarrollo Económicos (OCDE).
Fuente: Elaboración propia a partir de los censos económicos del INEGI de 1981, 1986, 1989, 1994, 1999 y 2004. La clasificación de niveles de tecnología se hizo con base en los datos proporcionados por la OCDE.
1.4 Industrias dispersas que continúan dispersas en el tiempo (DD)
Las ramas tradicionales y las menos intensivas en tecnología son las que presentan bajos niveles de concentración, es decir, una dispersión espacial que se mantiene a lo largo de todo el periodo.11 Los niveles de concentración de este grupo han disminuido desde 1986, en donde más de 50% de las manufacturas pertenece al sector de productos alimenticios, bebidas y tabaco y por lo general se ubican en los estados más grandes e importantes del país (Estado de México, Ciudad de México, Jalisco y Nuevo León).
II. Determinantes de la concentración industrial en México, 1981-2004
La evolución del índice de concentración industrial concuerda estrechamente con los cambios en las políticas comerciales adoptadas en el país, con lo que vuelve oportuno identificar las fuerzas que determinaron este comportamiento y verificar si la redistribución geográfica de la actividad económica actual es consecuencia de tales medidas.
Tanto las teorías del comercio como las de la integración económica señalan los efectos en las estructuras productivas de los países en proceso de integración. Con base en estas teorías se construyen algunas de las principales variables que constituyen una aproximación a las características de las industrias, las cuales podrían influir en su concentración.
II.1 Diferencias en productividad (o tecnología)
La teoría de comercio tradicional señala que el comercio entre países y la concentración de la actividad económica está determinada por las diferencias en la dotación de factores de las regiones o países que poseen ciertas ventajas comparativas en la producción de algunos bienes.
El modelo de David Ricardo argumenta que el comercio se ve fortalecido a consecuencia de las diferencias relativas en productividad. Cuanto más difiera relativamente en la dotación tecnológica se asume un mayor grado de concentración de la industria. Tales diferencias en tecnología son capturadas por las diferencias en la productividad del trabajo (PRODi) definida como el valor añadido por empleado de la industria i:
Donde, VAij corresponde al valor añadido de la industria i en la región j; εij es el empleo de la industria i en la región j; n es el numero de regiones (32 estados) y m es el numero de industrias (54 ramas). El primer término de la ecuación mide la productividad del trabajo en la industria i en la región j relativa al promedio de la productividad del trabajo total en esta industria entre las regiones; en tanto que el segundo término proporciona el promedio de la productividad del trabajo en la región j relativa al total de regiones.
Cuanto más significativas sean las diferencias en la productividad relativa entre los estados, más elevado será el valor de PRODi . Es decir, un índice alto significa que la industria i puede ser altamente productiva o extremadamente ineficiente en relación con el resto. Ambos casos arrojan un alto valor de esta medida. De acuerdo con la teoría ricardiana, cuanto más elevado sea este indicador de una industria en particular, tendrá mayores niveles de concentración geográfica.
II.2 Dotación de factores
El segundo modelo relevante en la teoría tradicional del comercio es el de Heckscher-Ohlin, que explica cómo la liberalización comercial permite que los países con abundancia relativa en trabajo se especialicen en industrias intensivas en ese factor y, a su vez, los que poseen abundancia relativa en capital se especializan en sectores intensivos en el uso de capital, lo que les permite comerciar. Como predice esta teoría, podría esperarse que las industrias con intensidad en el uso ya sea de capital o de trabajo, posean elevados niveles de concentración geográfica.12
En este caso, para medir la importancia de la dotación relativa de recursos se empleará el indicador utilizado en Amiti (1999). Este trabajo propone una aproximación que mide la desviación de la intensidad del uso del trabajo de la industria en las regiones con respecto al nacional. Esta medida ha sido utilizada en diversos estudios empíricos (Kim, 1995; Brülhart, et al., 1998; Haaland, et al., 1999; Paluzie, et al., 2001 y Traistaru, et al., 2004):
En donde, LCij son las remuneraciones al trabajo y VAij el valor añadido para las ramas i y las regiones j; n es el numero de regiones (32 estados) y m es el numero de industrias (54 sectores). DFi se define como la diferencia entre la proporción de la remuneración del factor trabajo respecto del valor agregado total de la industria, y la proporción de la remuneración del trabajo respecto del valor añadido en el país. Un valor elevado de este índice implica que la industria en cuestión difiere del promedio industrial en términos del uso relativo del trabajo: esta podría ser intensiva en trabajo o en capital (Haaland, et al., 1999). En cualquier caso, se espera que la industria esté concentrada. Mientras, un valor pequeño indicaría que la utilización (mucha o poca) de este insumo es similar entre las industrias en el país.13
II.3 Economías a escala
A medida que se observaba cómo la teoría del comercio convencional no explicaba la realidad de los intercambios comerciales debido a que incluían el intercambio de bienes diferenciados y no de bienes similares, en los años ochenta surge la NTC, que aporta el supuesto de la competencia imperfecta, movilidad de empresas e inmovilidad del factor trabajo, lo que dio lugar a la incorporación de las economías de escala en la explicación del comercio de bienes similares entre países, también similares.
En contra de lo que suponía la teoría clásica, la existencia de economías de escala implica que los países presentan incentivos para la búsqueda de la especialización, aún cuando no existan diferencias en tecnología o dotación de factores. Esta variable podría influir los patrones de concentración de las industrias, debido a que es un componente importante que afecta a otras variables, tales como el tamaño del mercado.
Las economías de escala han sido calculadas de diversas formas en los textos empíricos. Haaland, et al. (1999) emplea el porcentaje de reducción en el costo promedio por cada porcentaje de incremento en el producto. En tanto Kim (1995), Amiti (1999), Paluzie, et al. (2001) y Traistaru, et al. (2003), entre otros, utilizan el tamaño promedio de la industria como una aproximación para medir esta variable. Por tanto, con base en estos estudios, se trata de capturar los efectos de la NTC, de la siguiente manera:
Este indicador calcula el tamaño medio de la industria i, a partir del empleo total (εij) y del número de empresas (NEij) con las que cuenta cada industria en los estados. Los resultados se tienen que interpretar con precaución, por que las economías de escala indican la habilidad de la industria para explotar el poder del mercado, y el tamaño medio no refleja realmente esta habilidad. En principio, se espera que cuanto más altas sean las economías de escala de una industria en particular, esta poseerá mayores niveles de concentración geográfica. La razón es que en este tipo de industrias se necesitan pocas plantas para satisfacer la demanda.
II.4 Intensidad en el uso de bienes intermedios nacionales
La NGE enfatiza la magnitud de los efectos del mercado nacional y de las economías de escala sobre la concentración de la actividad manufacturera. En los modelos desarrollados por Krugman y Venables (1995) y Venables (1996) se destaca la importancia de la integración vertical -las cadenas productivas- entre las empresas como fuerza de aglomeración.
Cuando las empresas se encuentran en la parte superior de la estructura vertical de la cadena productiva (upstream) tienden a localizarse en donde hay un mayor número de empresas de la parte inferior de la estructura (downstream). De esta manera, mejoran su acceso a la demanda (integraciones hacia atrás). Por otra parte, cuando existe un mayor numero de empresas upstream, las downstream tienen a beneficiarse debido a que sus insumos intermedios los obtienen a costos más bajos (integraciones hacia adelante). Estas integraciones de demanda y costos son fuertes cuando la intensidad en el uso de los bienes intermedios es alta. La implicación de esta teoría es que sí las industrias requieren una alta proporción de insumos intermedios nacionales están probablemente más concentradas geográficamente (Amiti, 1999).
Para medir la intensidad de la utilización de los bienes intermedios nacionales entre las industrias, se construyó el siguiente índice:
En donde, Xij es la producción total de la industria i en la región j, VAij es el valor añadido de la industria i en la región j, y la diferencia entre estas dos variables es el consumo intermedio del sector i en todas las regiones j. IBIi es el consumo intermedio como proporción de la producción generada por la rama i en todo el país, a precios de mercado. Un alto IBIi implica una elevada integración vertical, lo que puede traducirse en una elevada concentración geográfica y viceversa.14 Esto pudo observarse tanto para México como para la mayoría de los países en desarrollo, en donde las grandes metrópolis fueron consecuencia de las integraciones hacia adelante y hacia atrás (Krugman y Livas, 1996).
III. Análisis de la concentración industrial en México, 1981-2004
Con el análisis del comportamiento de las variables proporcionadas por las diferentes teorías del comercio y de la NGE, se vuelve relevante observar si los patrones de concentración geográfica en México concuerdan con lo que predicen estas teorías; para ello se realiza un análisis de datos de panel para el periodo 1981-2004.
Estos modelos tienen una serie de ventajas: permiten enriquecer la información para estudiar los procesos dinámicos de ajuste, identificar efectos individuales y temporales que no pueden reconocerse con datos de sección cruzada o de series temporales; puede controlarse la existencia de heterogeneidad individual no observable, proporciona estimadores con mayor cantidad de información, mayor grado de variabilidad y menor nivel de colinealidad entre los regresores e incrementan los grados de libertad, dando lugar a estimaciones más eficientes.
III.1 Selección del modelo
En esta sección se describe el mecanismo a seguir para determinar el modelo que se ajuste mejor a los datos. En primer lugar, se buscan estimadores15 que arrojen el mayor poder explicativo posible y que tengan las propiedades deseables de eficiencia y consistencia. Como es sabido, la tarea consiste en determinar la naturaleza del término de error del modelo propuesto. El método de búsqueda que se utiliza es el de contrastar diversos estimadores provenientes de distintas especificaciones a través de las pruebas de hipótesis.
Como primer paso, es necesario determinar si la presencia de variables no observadas deteriora las propiedades de los estimadores de MCO. Cuando existen este tipo de variables, MCO es incapaz de aislar su efecto, por lo que los estimadores de las variables incluidas en el modelo resultan con propiedades indeseables.
Modelo MCO:
Como era de esperar, al realizar las pruebas de hipótesis correspondientes, se determinó que tales efectos están presentes y que MCO no es un estimador adecuado. (Véase Cuadro III.1 y Cuadro III.2).
Cuadro 3 Determinantes de la concentración industrial absoluta en México. Análisis de datos panel, 1981-2004
| Variables independientes | MCO | Efectos fijos por industria | Efectos aleatorios por industria | Efectos fijos por periodo | Efectos aleatorios por periodo | Efectos fijos por industria y periodo | Efectos aleatorios por periodo |
|---|---|---|---|---|---|---|---|
| Constante | 0.3446*** | 0.4001*** | 0.3569*** | 0.3577*** | 0.3568*** | 0.5588*** | 0.5138*** |
| (0.0319) | (0.0454) | (0.0412) | (0.0305) | (0.0421) | (0.0335) | (0.0352) | |
| Productividad | 0.0391** | 0.0090 | 0.0143 | 0.0448*** | 0.0444** | 0.0144 | 0.0177** |
| (0.0178) | (0.0118) | (0.0116) | (0.0177) | (0.0176) | (0.0089) | (0.0089) | |
| Dotación de factores | 0.0070 | 0.0030 | 0.0034 | 0.0031 | 0.0034 | -0.0025 | -0.0021 |
| (0.0071) | (0.0043) | (0.0043) | (0.0069) | (0.0069) | (0.0031) | (0.0031) | |
| Economía de escala | 0.0676*** | 0.0508*** | 0.0607*** | 0.0641*** | 0.0643*** | 0.0328*** | 0.0426*** |
| (0.0069) | (0.0094) | (0.0077) | (0.0067) | (0.0066) | (0.0069) | (0.0063) | |
| Intensidad de los bienes intermedios | -0.1187*** | 0.0392* | 0.0152 | -0.1480*** | -0.1480*** | 0.0053 | -0.0105 |
| (0.0280) | (0.0226) | (0.0217) | (0.0278) | (0.0276) | (0.0181) | (0.0179) | |
| Pruebas | |||||||
| Fcalculado Ftablas* | 19.68 Prob > F = 0.0000 1.36 | 8.54 Prob > F = 0.0000 2.24 | 39.33 Prob > F = 0.0000 1.36 | ||||
| Breusch- Pagan χ2tablas* | 405.94 Prob > χ2 = 0.0000 3.84 | 83.63 Prob > χ2 = 0.0000 3.84 | 540.41 Prob > χ2 = 0.00 3.84 | ||||
| Hausman χ2 tablas* | 25.34 Prob > χ2 = 0.0000 9.48 | 0.54 Prob > χ2 = 0.9691 9.48 | 24.64 Prob > χ2 = 0.0034 16.91 | ||||
| R2 | 0.3884 | 0.7982 | 0.7545 | 0.1411 | 0.2167 | 0.8958 | 0.8654 |
| Nº de observaciones | 324 | 324 | 324 | 324 | 324 | 324 | 324 |
Nota: (***) Significativa al 1% ; (**) Significativa al 5% ; (*) Significativa al 10% .
Los números que están entre paréntesis son los errores estándar.
Fuente: Elaboración propia a partir de los censos económicos del INEGI de 1981, 1986, 1989, 1994, 1999 y 2004.
El segundo paso consiste en determinar la naturaleza de la relación entre los efectos individuales (ramas) no observados y las variables independientes. Si la correlación entre estos es distinta de cero, entonces el estimador adecuado es el que se conoce comúnmente como de “efectos fijos”; en el caso de que la correlación sea cero, el estimador adecuado es el de “efectos aleatorios”.
Modelo de efectos fijos:
En este modelo las diferencias entre estados son constantes o fijas. En donde ai corresponde a los dummies16 de las industrias que representan efectos no observables, nt son los dummies temporales, es decir, para cada año, que capturan eventos comunes a todas las industrias durante un periodo. El modelo de efectos fijos se estima con diferentes especificaciones: variables dicotómicas por industria, periodo y de forma conjunta.
Para determinar cuál modelo aporta mayor explicación a la concentración industrial del país se utiliza la prueba de F entre el modelo MCO y el de efectos fijos.17 La prueba de F, con significancia del 5 % reporta que se rechaza la hipótesis nula en las tres modalidades, lo que implica que los estimadores que produce en MCO son insesgados e inconsistentes, por lo cual es mejor utilizar el modelo de efectos fijos. (Greene, 2002).
Otra manera de modelar el carácter individual de cada estado y periodo, es mediante efectos aleatorios Este modelo se define a continuación:
Modelo efectos aleatorios:
En donde λi corresponde a las variables dicotómicas de las industrias que representan efectos no observables aleatorios, m t son las dummies de tiempo. Este modelo se estima con variables dicotómicas por industria, periodo y de forma conjunta.
Analizando la ecuación con efectos aleatorios (4), si la varianza de λi y m t son iguales a cero, entonces no existe diferencia relevante entre la ecuación (1) y (4). Para probar si es mejor utilizar el modelo (4) que el MCO, se utiliza la prueba del multiplicador de Lagrange, que formularon Breusch y Pagan. Los resultados señalan que la hipótesis nula se rechaza (véase el Cuadro III.1), es decir, que sí existen discrepancias relevantes con un grado de significancia del 5 %, por lo cual es preferible utilizar la estimación de efectos aleatorios que la MCO.
Como se observa en el Cuadro III.1, las variables explicativas no son robustas ante las diferentes especificaciones de modelos, excepto por la variable que mide las economías de escala, que son significativas en todo momento a un nivel de 1 %.
Las pruebas de significancia F para efectos fijos y la de Breusch-Pagan para efectos aleatorios indican que estos modelos son mejores que el MCO. Sin embargo, ahora la cuestión es cuál de los dos modelos debe utilizarse para cada tipo de especificación. La respuesta depende de la posible correlación entre los regresores y los efectos no observables representados por las variables dicotómicas. El modelo de efectos fijos supone que esta correlación es diferente de cero, mientras que el de efectos aleatorios infiere que la correlación es cero.18
A través de una prueba, Test de Hausman, se obtiene que el estimador de efectos fijos es el más adecuado dada la naturaleza de los datos. Adicionalmente, con la prueba de F se verifica si la inclusión de efectos fijos por periodo agrega poder explicativo al modelo, el resultado es que dichos efectos también son importantes.
De los modelos estimados, el que logra explicar mejor la concentración industrial del país es el de efectos fijos por industria y periodo. La estimación de éste muestra que la ESCALA es el factor que mayor efecto tiene en la concentración geográfica de las ramas manufactureras, mientras que PROD, DF e IBI no parecen ser significativas.
Este último resultado es sorprendente debido a que en México había fuertes integraciones verticales entre las industrias antes de la apertura comercial, que fueron debilitándose debido a la intensa importación de insumos intermedios para la manufactura de bienes finales (véase resultados Cuadro III.4). Es interesante observar que este determinante cuenta con un efecto indirecto que hace que cambie su grado de significancia dependiendo del modelo estimado; al incluir en la ecuación el tiempo como variable dicotómica hace que IBI resulte no significativa. Lo contrario pasa con PROD, que se vuelve significativa.
Es posible que PROD y DF no expliquen gran parte de la concentración absoluta de las industrias, debido a que como señalan Haaland, et al. (1999) y Gordo, et al. (2003), estos factores se relacionan mejor con los índices de concentración relativa. Otra posible explicación es que algunos estados son muy similares y esto hace que no haya diferencias significativas entre ellos.
III.2 Corrección de problemas de especificación
Una vez seleccionado el modelo adecuado se procede a corregir otro tipo de problemas comunes, tales como heterocedasticidad y autocorrelación, entre otros. Una de las características de la base de datos con que se cuenta en este estudio, es que es corta en tiempo y larga en corte transversal, es decir, tiene la forma T<N, por lo tanto, no es posible corregir (en su caso) los problemas de autocorrelación y correlación contemporánea. Sin embargo, se sugiere que estos problemas son mínimos debido a que el periodo de análisis es largo (más de dos décadas), y que es espaciado (cada 5 años aproximadamente).
Finalmente, se procede a examinar y corregir la existencia de heterocedasticidad. Usando las pruebas adecuadas, se comprueba que los datos no son homocedásticos y, por lo tanto, es necesario corregir el modelo ya sea mediante mínimos cuadrados generalizados (GLS, por sus siglas en inglés) o por errores estándar corregidos para panel (PCSE, por sus siglas en inglés).
De acuerdo con la aportación de Beck y Katz (1995) se demuestra que los errores estándar resultado de la estimación por PCSE son más precisos que los GLS. Sin embargo, continua el debate entre cuál de estos dos métodos es mejor. Por esta razón, se considera oportuno en esta investigación estimar ambas opciones.
En el Cuadro III.2 pueden observarse las estimaciones del modelo corregidas por heterocedasticidad para las dos opciones: con efectos fijos por industria y efectos fijos por industria y periodo.19 En estos nuevos resultados se refleja nuevamente que ESCALA es el determinante más importante de la concentración industrial del país. También, es importante señalar como PROD agrega información significativa al modelo cuando se controla con dummies por industria y periodo; mientras que IBI sólo resulta significativa cuando se estima el modelo con PCSE, controlando con dummies por industrias.
Cuadro 4 Determinantes de la concentración industrial absoluta en México. Análisis de datos de panel corregido por heterocedasticidad, 1981-2004
| Variables independientes |
Efectos
fijos por industria y periodo |
Efectos
fijos por industria |
||
|---|---|---|---|---|
| Modelos | GLS | PCSE | GLS | PCSE |
| Constante | 0.2086*** | 0.3584*** | 0.2713*** | 0.5138*** |
| (0.0452) | (0.0332) | (0.0386) | (0.0352) | |
| Productividad | 0.1318* | 0.0144* | 0.0000 | 0.0090 |
| (0.0050) | (0.0080) | (0.0057) | (0.0085) | |
| Dotación de factores | -0.0022 | -0.0024 | 0.0021 | 0.0030 |
| (0.0018) | (0.0027) | (0.0027) | (0.0039) | |
| Economía de escala | 0.0369*** | 0.03288*** | 0.0398*** | 0.0508*** |
| (0.0049) | (0.0068) | (0.0059) | (0.0084) | |
| Intensidad de los bienes intermedios | -0.0137 | 0.0053 | 0.0148 | 0.0392** |
| (0.0115) | (0.0164) | (0.0181) | (0.0207) | |
| Nº de observaciones | 324 | 324 | 324 | 324 |
Nota: (***) Significativa al 1%; (**) Significativa al 5 %; (*) Significativa al 10 %.
Los números que están entre paréntesis son los errores estándar.
Fuente: Elaboración propia a partir de los censos económicos del INEGI de 1981, 1986, 1989, 1994, 1999 y 2004.
En resumen, los resultados obtenidos de los modelos anteriores (Cuadros III.1 y III.2) señalan que el factor más importante que determina la concentración de las ramas manufactureras en México son las economías de escala (ESCALA). Por su parte, se encuentra que los determinantes propuestos por las teorías tradicionales del comercio no aportan explicación significativa a este hecho (PROD y DF). Sin embargo, en este análisis sorprende el comportamiento de la variable intensidad del uso de bienes intermedios nacionales (IBI) ante distintas especificaciones. En particular, es de resaltar que IBI cambia de significancia y signo cuando se agregan dummies por periodo; esto nos ha llevado a concluir que la variable IBI y el periodo deben estar correlacionados.
III.3 Efectos de la liberalización comercial en la concentración industrial
Dada la observación anterior, la sospecha es que la variable IBI ha ido cambiando en el tiempo debido principalmente al efecto de la apertura comercial. Por esta razón, se realiza un nuevo modelo en el cual interactúan la variable IBI con el periodo de tiempo para explicar la concentración de la industria manufacturera.
A través de este análisis de interacción en periodos se demuestra que la relación entre la IBI y el índice de concentración industrial no es invariable en el tiempo. Antes de la liberalización comercial, la relación positiva entre la variable IBI y la concentración obedecía a que el centro del país capturaba la mayor parte de la actividad económica y las industrias más concentradas eran las que estaban más integradas verticalmente. Después de la apertura comercial, gran parte de la actividad económica se desarrolla en la región norte y las industrias más concentradas son ahora las que importan una mayor cantidad de insumos (ya que su precio disminuyó), y las que se localizan cerca de la frontera con Estados Unidos. Por esta razón, la relación se vuelve negativa.
III.3.1 Indicador de frontera
Como se ha venido mostrando, la variable IBI no es robusta ante las diferentes especificaciones de cada modelo estimado; para explicar este posible cambio en significancia se construye el índice de frontera,20 indicador que captura el efecto no observable que se presume existe entre IBI y la importancia adquirida en la zona fronteriza en el transcurso de los años.21
Desde el inicio de la liberalización comercial ha sido más conveniente para las empresas localizarse cerca del mercado al que van a vender su producto, así se disminuyen costos de transporte (que en el país aún siguen siendo una parte importante de los costos de las industrias). Para estas industrias ya no es rentable ubicarse cerca de sus proveedores de insumos intermedios, debido a que la mayor parte de estos son importados, ni cerca de los estados que tengan mayor población, ya que los trabajadores tienen libre movilidad en el país.
En el Cuadro III.3 se puede determinar que existe una relación positiva que ha ido creciendo a lo largo del tiempo (aún no significativa) entre la concentración de la industria y el índice de frontera.22 Si una industria está más concentrada en los estados fronterizos a medida que pasa el tiempo, se vuelve importante para la explicación de la concentración industrial del país. Este cambio ha sido gradual en donde la concentración de la industria pasó de los estados del centro a los de la frontera norte de México.
Mientras, la relación entre la intensidad del consumo de bienes intermedios nacionales y en el índice de frontera es negativa y significativa. Esto implica que las ramas que concentran mayor personal ocupado en los estados fronterizos han estado utilizando en menor medida el IBI del país. Una explicación factible es que al abrirse las fronteras a la libre competencia, se incrementaron las importaciones de insumos intermedios, fragmentando las integraciones verticales de los años ochenta.
Este análisis confirma que existe un efecto indirecto que afecta la variable propuesta por la NGE, que no logra capturarse con las estimaciones de sección cruzada por año.
Cuadro 5 Correlación entre el índice de frontera y concentración industrial absoluta e intensidad de insumos intermedios, 1981-2004
| Índice de frontera |
1981 | 1986 | 1989 | 1994 | 1999 | 2004 |
|---|---|---|---|---|---|---|
| Localización industrial | 0.0892 | -0.0307 | 0.0356 | 0.1833 | 0.1876 | 0.2248 |
| Intensidad de los inputs intermedios | -0.4244*** | -0.0560 | -0.2808** | -0.4824*** | -0.4820*** | -0.3361** |
Nota: (***) Significativa al 1%; (**) Significativa al 5% ; (*) Significativa al 10 %
Fuente: Elaboración propia a partir de los censos económicos del INEGI de 1981, 1986, 1989, 1994, 1999 y 2004.
III.3.2 Indicador de la apertura comercial
A continuación se estima una nueva variante de modelo en donde se diferencian los periodos previos y posteriores de la apertura comercial, para lo cual se crea una variable dummy denominada BTLC, que toma el valor de uno 1 para los años anteriores de la apertura comercial (1981 y 1986) y el valor de cero para el resto de los años. Esta variable se pone a interactuar con la variable de consumo intermedio, con el fin de capturar su impacto en la concentración de la industria.
El modelo que se estima es el siguiente:
En el Cuadro III.4 se observan los resultados de este ejercicio, donde la variable BTLC tiene un efecto positivo y significativo sobre la concentración absoluta de las manufacturas mexicanas. Esto indica que la apertura tiene un impacto importante en la estructura productiva del país, mientras que la interacción de BTLC con IBI presenta un efecto negativo debido a que la apertura comercial provocó la desintegración vertical de las industrias, originado por la disminución del precio relativo de los insumos intermedios importados. Además, al enriquecer el modelo con esta variable, se confirma lo que predijo la NGE tanto en la estimación por GLS como por PCSE corregida por heterocedasticidad. Así, una vez que se controla por la apertura comercial, la variable IBI, al igual que la variable ESCALA logran explicar la concentración absoluta de la industria manufacturera en el país.
Se elabora otro ejercicio similar para observar el efecto de cada año en la variable IBI, donde la ecuación sería la que se presenta a continuación:
El análisis de los resultados presentados en el Cuadro III.4 reflejan que la interacción de la variable IBI por año explica la relación positiva que mantenía IBI con la concentración de las manufacturas en los años ochenta va perdiendo importancia, volviéndola negativa a partir de 1994, tal como argumentan Krugman y Livas (1996). En su trabajo puramente teórico afirman que, con la liberalización de los mercados, las integraciones verticales iban a ser menos importantes para la explicación de la concentración de la industria.
Este resultado era esperable debido a que el modelo de sustitución de importaciones creó fuertes vínculos entre proveedores y productores nacionales con una gran concentración de la actividad económica en los estados del centro del país, ya que el incentivo era localizarse cerca de los insumos. Desde la apertura comercial se generaron fuertes cambios en la estructura productiva, caracterizada al principio por una desconcentración de la industria y por una desintegración de las cadenas productivas en años posteriores, sustituyendo los insumos nacionales por importados. La entrada en vigor del TLCAN trajo consigo mayor importación de insumos y, debido a la integración con Estados Unidos y Canadá, las industrias empezaron a localizarse en los estados de la frontera norte, cerca del mercado al que venden sus productos.
Cuadro 6 Determinantes de la concentración absoluta industrial. Análisis de datos de panel con interacción entre IBI y la apertura comercial
| Variables independientes | GLS BTLC | PCSE BTLC | GLS AÑO | PCSE AÑO |
|---|---|---|---|---|
| Constante | 0.2209*** | 0.2084*** | 0.3129*** | 0.2821*** |
| (0.0307) | (0.0345) | (0.0309) | (0.0394) | |
| Productividad | 0.0009 | 0.0009 | 0.0092* | 0.0083 |
| (0.0059) | (0.0075) | (0.0052) | (0.0084) | |
| Dotación de factores | -0.0029 | -0.0025 | -0.0028 | -0.0034 |
| (0.0024) | (0.0032) | (0.0023) | (0.0035) | |
| Economía de escala | 0.0440*** | 0.0434*** | 0.0288*** | 0.0361*** |
| (0.0056) | (0.0069) | (0.0054) | (0.0080) | |
| Intensidad de los bienes intermedios | 0.0282** | 0.0476** | 0.0827*** | 0.0712*** |
| (0.0148) | (0.0209) | (0.0141) | (0.0227) | |
| Dummy apertura comercial | ||||
| BTLC |
0.0981*** (0.0060) |
0.1050*** (0.0084) |
||
| BTLC* IBI |
-0.0684*** (0.0157) |
-0.0629** (0.0216) |
||
| Dummy por año | ||||
| IBI* 1986 |
-0.0375** (0.0153) |
-0.0014 (0.0232) |
||
| IBI* 1989 |
-0.0747*** (0.0157) |
-0.0517** (0.0237) |
||
| IBI* 1994 |
-0.1507*** (0.0162) |
-0.1261*** (0.0261) |
||
| IBI* 1999 |
-0.1861*** (0.0190) |
-0.1687*** (0.0283) |
||
| IBI* 2004 |
-0.2098*** (0.0176) |
-0.2044*** (0.0282) |
||
| Nº. de observaciones | 324 | 324 | 324 | 324 |
Nota: (***) Significativa al 1% ; (**) Significativa al 5% ; (*) Significativa al 10 %.
Los números que están entre paréntesis son los errores estándar.
Fuente: Elaboración propia a partir de los censos económicos del INEGI de 1981, 1986, 1989, 1994, 1999 y 2004.
Como se observó con el indicador de frontera, la relación entre las industrias concentradas en los estados de la frontera y el uso de insumos intermedios nacionales es negativa y significativa. Lo anterior explica por qué la variable IBI cambiaba de signo cuando se incluían dummies por año en el modelo.
IV. Cambio de la estructura productiva en México, 1981-2004
Con el fin de hacer evidentes estos cambios en la distribución espacial de la actividad económica, se aplica la Prueba de Chow a los datos de panel que fueron estimados. Esta prueba permite comparar datos de panel mediante el estadístico F de Fisher haciendo uso de la suma de cuadrados del error (SCE) de las mismas. Se consideraron dos subperiodos: 1981 - 1986, antes de la apertura comercial, y 1989 - 2004, después de que México se integrara al GATT y firmara el TLCAN.
Los resultados sugieren que esta prueba rechaza la hipótesis nula de estabilidad estructural con un nivel de significación de 1%, confirmando así que en México, a raíz de la liberalización comercial, tuvo lugar un cambio en la estructura productiva de la manufactura.23 Este hecho también se comprobó cuando se llevó a cabo la estimación mediante la variable dicotómica BTLC que representaba la apertura comercial. El resultado fue un efecto positivo y significativo en la concentración absoluta, determinando así que existe un impacto en la geografía económica como consecuencia del cambio de política económica instrumentada en el país.
V. Conclusiones
El análisis descriptivo de la concentración industrial en México revela cómo el grado de concentración del personal ocupado ha ido disminuyendo a partir de la liberalización comercial.
También se aporta evidencia de que las manufacturas que cuentan con un mayor grado de concentración son las ramas de los sectores de sustancias químicas, productos derivados del petróleo, del carbón, hule y plástico, así como de textiles, prendas de vestir e industria del cuero. Mientras que las industrias pertenecientes al sector de productos alimenticios, bebidas y tabaco fueron las que mostraron menor grado de concentración y se caracterizan por tener bajos niveles de uso de tecnología.
Este análisis confirma lo postulado por Krugman y Livas (1996), cuando en su artículo mencionan que en un país como México, una disminución en las barreras al comercio provocaría que las industrias disminuyeran sus niveles de concentración. Asimismo, se comprueban las expectativas de Hanson (1997) hacia una mayor desconcentración de la industria.24 Sin embargo, es importante remarcar que a partir del TLCAN, los niveles de concentración permanecen casi sin movimiento.
La contribución más importante de este trabajo es el análisis empírico de los determinantes de la concentración industrial, el cual no se ha realizado con anterioridad para el caso mexicano. Los resultados de este análisis indican que las economías de escala y la intensidad en el uso de insumos intermedios nacionales son los factores que de manera más importante explican la concentración industrial absoluta en el país. En cambio, los determinantes propuestos por las teorías tradicionales del comercio no aportan explicación significativa a la concentración industrial. De hecho, como han destacado otros estudios, las ventajas comparativas, que son los factores considerados por la teoría clásica del comercio internacional, se relacionan mejor con un índice relativo de concentración.
Un resultado clave del análisis indica que antes de la apertura comercial, la intensidad en el uso de insumos intermedios nacionales y la concentración industrial se relacionaban positivamente mientras que con el tiempo y debido a la apertura comercial, esta relación se volvió negativa.
Así, en este trabajo se confirma que la concentración industrial pasó del centro a la frontera norte del país y claramente se evidencia que este cambio estructural se ve reflejado en la relación de la concentración con la intensidad en el uso de bienes intermedios nacionales. Antes de la apertura comercial, la relación positiva entre ambas variables obedecía a que el centro del país capturaba la mayor parte de la actividad económica y las industrias más concentradas eran las que tenían una mayor vinculación vertical. Después de la liberalización comercial, gran parte de la actividad económica se desarrolló en la frontera y las industrias más concentradas, son ahora las que importan más insumos, las cuales se localizan cerca de la frontera.
En este sentido, nuestro análisis confirma las hipótesis planteadas por el modelo teórico de Krugman y Livas (1996), las cuales solo habían sido parcialmente verificadas por Hanson (1997). Sin embargo, a diferencia de Hanson que se centraba en el análisis del gradiente salarial regional y su evolución al compás de los cambios en la política comercial en México, el presente análisis aborda por primera vez de forma explícita el papel de los enlaces verticales insumo-producto en la concentración y verifica de forma sólida las hipótesis teóricas planteadas por Krugman y Livas (1996).
De este modo, en México, la apertura comercial significó el debilitamiento de la fuerza centrípeta constituida por los enlaces verticales insumo-producto nacionales característicos del periodo de sustitución de importaciones, provocando una desconcentración de la actividad económica en el espacio y una relocalización de la actividad hacia las regiones del norte, próximas al mercado estadounidense.
Sería interesante poder actualizar este trabajo homologando los censos económicos para un periodo de años más extenso, y así poder analizar cómo afectarán las actuales negociaciones al TLCAN en la distribución espacial de las actividades económicas del país.











 text new page (beta)
text new page (beta)


