INTRODUCCIÓN
Del teorema de Thales se destaca su relación con numerosos contenidos mate-máticos: la proporcionalidad numérica y las fracciones, la homotecia, la semejanza, la trigonometría, las ecuaciones de la recta y el cálculo infinitesimal... Para algunos autores su comprensión supone un hito para pasar de la idea de fracción aritmética a la de número racional (Filloy y Lema, 1996). Muchos destacan su potencial para relacionar lo numérico y lo geométrico (Michonneau y Pfaff, 1990), al suponer el paso del registro figural al registro algebraico (igualdad entre razones de segmentos) y de este al registro numérico (cuando reemplazamos los segmentos por sus medidas de longitud) (Lemonidis, 1992). Su papel de nexo entre con-tenidos y sus aplicaciones puede justificar que, pese a ser objeto de debate en reformas curriculares a nivel internacional, su estudio se haya mantenido en el currículo de Secundaria de distintos países (Escudero, 2005; Duperret, 1995).
Sobre el teorema de Thales se ha estudiado principalmente su aprendizaje (e.g. Lemonidis, 1991, 1992), poniéndose de relieve que los alumnos lo compren-den a un nivel de manipulación numérica, sin percibir sus propiedades geométricas (Michonneau y Pfaff, 1990). El aprendizaje del teorema suele reducirse a la aplicación del cálculo algebraico que emana de igualdades basadas en proporcionalidades (Laguerre, 2005).
El teorema de Thales puede verse como una aplicación de la semejanza de figuras o un precursor de esta. Así, en las Bases Curriculares para la asignatura de Matemáticas en Chile (MINEDUC, 2016a 6) el estudio del teorema de Thales se ubica en primer año de educación media (14-15 años), precedido por el concepto de homotecia, cuyo abordaje se realiza mediante proporciones y vectorialmente. Al teorema de Thales le sigue el estudio de la semejanza de figuras planas con aplicaciones a la vida diaria u otras asignaturas. Sin embargo, en las anteriores Bases Curriculares (MINEDUC, 2009), la semejanza se planteaba como un tema previo al teorema de Thales, ambos en segundo año medio (15-16 años), sin incluir la homotecia como tema de estudio. El Programa de Estudio vigente de primero medio (MINEDUC, 2016b) especifica que los estudiantes deben ser capaces de reconocer razones proporcionales y la necesidad de paralelismo en las rectas que intersecan, explicar el teorema de Thales mediante la homotecia y resolver problemas de aplicación del teorema. Por otro lado, en el tratamiento de la semejanza no se menciona de forma explícita el teorema, pese a que se presentan situaciones con las configuraciones de este. Se espera que los estudiantes puedan relacionar la geometría con los números y el álgebra armoniosamente mediante diferentes actividades. En el eje de geometría en el que también se inserta, se introduce gradualmente el concepto de demostración desde el planteamiento de conjeturas y las comprobaciones de propiedades.
La riqueza epistemológica del teorema y las dificultades de su aprendizaje requieren de la reflexión del profesor. Así, en Gualdrón (2011) se constatan carencias en la comprensión de la semejanza y del teorema de Thales de un profesor de Secundaria, en relación con conexiones con otros contenidos y en configuraciones de Thales no típicas.
El tratamiento del teorema de Thales supone, a su vez, una oportunidad de abordar la demostración en el aula de Secundaria. La multiplicidad de relaciones con otros contenidos posibilita distintas aproximaciones para ello. Además, el planteamiento de la demostración permite que los estudiantes puedan compren-der los conceptos que moviliza y desenvolver capacidades para desarrollar demostraciones (Alfaro-Carvajal, Flores-Martínez y Valverde-Soto, 2019).
Este estudio pretende aportar en la comprensión de cómo conciben los profesores este contenido, considerado como objeto de enseñanza y aprendiza-je. En concreto, su objetivo es describir el conocimiento que sustenta la práctica de aula de un profesor cuando enseña el teorema de Thales, identificando relaciones entre elementos de dicho conocimiento.
MARCO TEÓRICO
La práctica de aula ha sido analizada desde múltiples perspectivas con foco en el profesor (e.g. estudiando su capacidad de percibir y dar sentido a lo que ocurre, Mason, 2002, o fijándose en procesos de cambio, Liljedahl, 2010). Entre estas perspectivas se sitúa el interés por el conocimiento del profesor de mate-máticas. Una muestra del creciente interés en el estudio del conocimiento del profesor es que, de los cuatro focos en los que Ponte y Chapman (2006) organizan su revisión de la investigación presentada en el PME sobre el profesor, dos de ellos se refieren a su conocimiento. Además, en la siguiente revisión de la producción del PME, el capítulo dedicado a la investigación sobre profesores (Lin y Rowland, 2016) se centra en su conocimiento y desarrollo profesional.
Conocimiento especializado del profesor de matemáticas
El conocimiento del profesor puede ser entendido como un recurso que, junto con sus orientaciones y objetivos, permite explicar lo que hace y por qué (Schoenfeld, 2010).
La investigación sobre el conocimiento del profesor de matemáticas se ha centrado en refinar la conceptualización de las componentes diferenciadas por Shulman (1986) más específicas de la materia: Subject Matter Knowledge y Pedagogical Content Knowedge.
Entre los modelos que pretenden explicar el conocimiento del profesor de matemáticas, encontramos el Mathematics Teachers’ Specialised Knowledge (MTSK). Este modelo, además de diferenciar subdominios en el conocimiento del profesor relacionado directamente con la matemática como objeto de enseñanza y aprendizaje, aporta un sistema de categorías para cada subdominio (Carrillo et al., 2018). La posibilidad de refinar el análisis de la actuación de un profesor en el aula a partir de estas categorías y la consideración de la especialización del conocimiento del profesor de matemáticas como algo global, más que propio de un subdominio, y desde una perspectiva intrínseca al profesor de matemáticas (Scheiner et al., 2019), nos lleva a mirar el conocimiento del profe-sor desde el MTSK.
En el MTSK se diferencian tres dominios: el conocimiento matemático, el conocimiento didáctico del contenido y, las concepciones sobre la matemática y su enseñanza y aprendizaje. Daremos aquí una breve descripción de los mismos (Carrillo et al., 2018, y Zakaryan et al., 2018). El conocimiento matemático considera tres subdominios: El conocimiento de los temas (KoT) contempla el conocimiento del contenido matemático que se está enseñando en relación con las definiciones, las propiedades y su fundamentación, los procedimientos, los registros de representación y las situaciones que dan sentido al contenido. El conocimiento del profesor en relación con conexiones entre contenidos mate-máticos de distintos temas da sentido al subdominio conocimiento de la estructura de la matemática (KSM), diferenciándose entre conexiones de simplificación, de complejización, transversales (grandes ideas que relacionan contenidos diversos, como la idea de igualdad, que está presente en la expresiones numéricas y algebraicas y se relaciona con la congruencia de figuras geométricas y la semejanza) y auxiliares (contenidos de un tema que sirven como herramienta para resolver situaciones propias de otro tema, por ejemplo, las ecuaciones en el estudio de una función). Del tercer subdominio, conocimiento de la práctica matemática (KPM), nos ocuparemos después.
En el conocimiento didáctico del contenido se consideran también tres sub-dominios. El conocimiento de la enseñanza de la matemática (KMT) recoge el conocimiento del profesor de teorías sobre la enseñanza de contenidos mate-máticos, de recursos, y de estrategias, técnicas, tareas y ejemplos. El conocimiento de las características del aprendizaje de las matemáticas (KFLM) alude al conocimiento de teorías, fortalezas y dificultades, formas de interacción de los estudiantes con el contenido, y expectativas e intereses de los estudiantes hacia este, todo ello en relación con el aprendizaje de contenidos matemáticos. Final-mente, el conocimiento de los estándares de aprendizaje de las matemáticas (KMLS) se refiere al conocimiento sobre expectativas de aprendizaje, nivel de desarrollo conceptual o procedimental esperado, y secuenciación de temas.
Por último, respecto del tercer subdominio del MTSK, las concepciones del profesor en relación con la matemática pueden ser entendidas en términos de las visiones de la matemática platonista, instrumental, y de resolución de problemas (Ernest, 1991; Carrillo y Contreras, 1994). Asimismo, las concepciones sobre su enseñanza y aprendizaje recogen las ideas sobre cómo se enseña y aprende matemáticas, cuál es el sentido de la materia, el rol del alumno y del profesor y, su evaluación (Carrillo y Contreras, 1994).
Dado que la lección que analizamos en este artículo aborda la demostración del teorema de Thales, en lo que sigue desarrollaremos las bases teóricas para poder analizar el conocimiento del profesor sobre demostrar y sobre dicho teorema.
Conocimiento en relación con la práctica matemática de demostrar
El conocimiento de la práctica matemática (KPM) ha sido uno de los subdominios más complejos en su categorización, debido a las dificultades de cata-logar las prácticas matemáticas. Los avances en esta tarea se han producido mediante investigaciones que coinciden en que demostrar es una de estas prácticas y que el conocimiento sobre la demostración debe ser considerado como parte del conocimiento especializado del profesor (Alfaro-Carvajal et al., 2019; Delgado-Rebolledo y Zakaryan, 2019).
El término práctica matemática es utilizado en referencia a las actividades matemáticas realizadas para la creación y comunicación de conocimiento mate-mático. En este sentido, la demostración es considerada una práctica habitual y socialmente aceptada entre la comunidad matemática (Alfaro-Carvajal et al., 2019), generadora de conocimiento y que le son atribuidos otros papeles o funciones, como las de probar y explicar.
La demostración tiene los roles de: verificación respecto a la verdad de una proposición, explicación del porqué es o no verdadera, sistematización como estructuración de resultados desde la axiomática, descubrimiento de nuevos conocimientos y comunicación de estos conocimientos (De Villiers, 1993). Flores-Medrano (2016) señala que la demostración tiene también un rol de convencimiento personal o a otros en su carácter comunicativo, como una mezcla entre la verificación y la explicación, lo que permite relacionarla con el conocimiento de la enseñanza de las matemáticas cuando aparece en las aulas de matemáticas e integrar sus diferentes funciones en el conocimiento especializado del profesor (Delgado-Rebolledo y Zakaryan, 2019).
La enseñanza de la demostración moviliza otros conocimientos matemáticos, por lo que su inclusión en la clase de matemáticas requiere del profesor cono-cimiento de diferentes subdominios del MTSK. Al enseñar la demostración, el profesor también pone en juego sus conocimientos sobre representaciones, sobre la enseñanza, sobre los ejemplos, contraejemplos y sobre la conexión de conceptos matemáticos (Lesseig, 2016; Delgado-Rebolledo y Espinoza-Vásquez, 2019). Como señalan Sosa, Flores-Medrano y Carrillo (2016), esta elección del profesor sobre los ejemplos deja ver otros de sus conocimientos que se relacionan con la enseñanza de la matemática (KMT). Se ha observado que el KPM condiciona al KMT con respecto a la estrategia de enseñanza de una demostración y que, en las explicaciones del profesor, se evidencia su conocimiento sobre las dificultades que presentan sus estudiantes (KFLM) al comprender cierto tipo de demostraciones, sustentado por el KPM (Delgado-Rebolledo y Zakaryan, 2019).
Por tanto, resulta interesante estudiar el conocimiento sobre la demostración como parte del conocimiento especializado del profesor de matemáticas.
El teorema de Thales como objeto de enseñanza y aprendizaje
En la literatura de investigación podemos encontrar distintos trabajos sobre el teorema de Thales y la semejanza en relación con su análisis epistemológico, con aproximaciones a su enseñanza y con su aprendizaje por parte de alumnos generalmente de secundaria. Destacaremos los elementos tomados de algunas de estas investigaciones que nos servirán para analizar el conocimiento especializado del profesor respecto del teorema de Thales.
Lemonidis (1992) cita aproximaciones a la enseñanza del teorema a lo largo de la historia: una clásica, siguiendo la tradición de la geometría euclídea, donde se presentan razones de segmentos colineales para pasar al teorema, y luego a la semejanza de triángulos y la homotecia; desde la geometría afín; y desde la geometría vectorial. Análogamente, se presentan perspectivas de la semejanza (Lemonidis, 1991): como relación intrafigural (se destaca la relación entre los elementos de una figura y los correspondientes de su semejante, sin estar presente la idea de transformación), como transformación geométrica vis-ta como herramienta o como objeto matemático. Por su parte, Brousseau (1995) presenta tres aproximaciones usuales al teorema de Thales, apoyándose en una encuesta. Las dos primeras aproximaciones se basan en la idea de que “rectas paralelas determinan sobre dos rectas secantes segmentos correspondientes proporcionales” (p. 12), mientras que la tercera se apoya en la homotecia. Brousseau (1995) es crítico con las aproximaciones que se reducen al trabajo con configuraciones prototípicas.
Como hemos mencionado, el teorema de Thales puede introducir el estudio de la semejanza de triángulos, considerándose como objeto generador de nuevos conceptos (semejanza de triángulos, criterios de semejanza, figuras homo-téticas, etc.), o bien ser una consecuencia de la semejanza, donde su función principal es su aplicación en situaciones de ampliación y reducción y medidas indirectas (Escudero, 2005).
En relación con las representaciones figurales ligadas al teorema, Lemonidis (1992) diferencia representaciones homotéticas de tipo “pico” o triángulos anidados, y de tipo “mariposa”. La configuración más conocida por los alumnos, concluye este estudio, es la de tipo “pico”, restringiendo su comprensión de la igualdad de la razón en triángulos homotéticos. No conocen ni diferencian tipos de razones en representaciones homotéticas (de escala entre los dos triángulos homotéticos; entre los elementos de los dos triángulos; de proyección; o entre segmentos homólogos sobre los lados oblicuos) y automatizan la transformación del registro figural al algebraico. Este estudio y el de Duperret (1995) muestran la necesidad de trabajar en el teorema de Thales simultáneamente con registros figural, simbólico y numérico; enriquecer el registro figural, incluyendo configuraciones de triángulos no homotéticos; y comprender las distintas interpretaciones del teorema.
Respecto a la enseñanza, Escudero y Sánchez (2007) clasifican las tareas escolares relativas a la semejanza: de cálculo de un valor desconocido, de cálculo-comparación (determinar si se da una proporción entre cuatro números dados), de cálculo mixto (dados dos valores conocidos y dos desconocidos, calcular la razón entre los desconocidos para que todos constituyan una pro-porción), de construcción o de demostración.
En relación con el conocimiento del profesor, Zakaryan et al. (2018) muestran relaciones entre el conocimiento de una profesora de Secundaria sobre el aprendizaje de la semejanza de triángulos y su conocimiento sobre su enseñanza.
Gualdrón (2011), como se mencionó, muestra las posibles dificultades en la comprensión de estos contenidos por parte del profesor de Secundaria. Por su parte, Escudero y Sánchez (2007) describen el conocimiento de dos profesores de secundaria. Para uno de ellos el teorema de Thales precede a la semejanza, sirviendo para visualizar la proporcionalidad numérica (y relacionar lo numérico y lo geométrico), incluye aspectos de homotecia y de semejanza, y presenta variedad de configuraciones geométricas, conociendo las dificultades de los alumnos. Por contra, el otro profesor enfatiza un tratamiento algorítmico e introduce el teorema con una tarea de verificación numérica para que los alumnos confíen en el resultado. Usa configuraciones de rectas secantes cortadas por paralelas señalando solo el aspecto de proyección y sin considerar dificultades de aprendizaje.
Si bien, como hemos mencionado, existen estudios previos sobre el conocimiento de profesores sobre el teorema de Thales, en este trabajo esperamos aportar mayor detalle en la descripción de dicho conocimiento, valiéndonos de las categorías de los subdominios del MTSK, y a partir de este mostrar una visión integrada de dicho conocimiento, en la que se evidencien relaciones entre distintos elementos.
METODOLOGÍA
Puesto que intentamos comprender el conocimiento especializado que evidencia un profesor cuando aborda el teorema de Thales en el aula, esta investigación es de corte cualitativo y se realiza desde el paradigma interpretativo (Bassey, 1999). Se trata de un diseño de estudio de caso (Stake, 2007), donde el caso es un profesor de matemáticas de secundaria de un liceo público chileno, participante en un taller formativo.
La investigación se enmarca en el desarrollo de un proyecto sobre Formación Continua Docente en una universidad pública chilena, que contempla una etapa de trabajo colaborativo entre tres investigadores y los profesores de matemática que atienden diferentes niveles educativos en un liceo público, quienes participa-ron voluntariamente en el proyecto. Esta etapa se organizó en talleres cuyo objetivo era proporcionar herramientas de análisis colaborativo al profesor de matemáticas, relativas a su práctica en el aula, a través de la discusión sobre la ejemplificación en geometría. Se generó un espacio de reflexión y acompañamiento a la práctica docente, atendiendo el rediseño de actividades de instrucción y aprendizaje que los profesores usualmente aplican en sus cursos.
El taller se desarrolló en seis sesiones de julio a diciembre de 2018. Durante las cinco primeras sesiones, además de presentarse el taller y sus objetivos, se les pide seleccionar por grupos una actividad introductoria para algún tema de geometría que hayan planificado realizar en el nivel que atienden, presentarla a los otros grupos, y reformularla considerando alguno de los elementos teóricos que se les aportó para la reflexión en la segunda sesión del taller (entre ellos, Espacios de Trabajo Matemático, Kuzniak y Richard, 2014, y Conocimiento Especializado del Profesor de Matemáticas, Carrillo et al., 2018, que fueron mostrados de manera general). El rol del taller, y de los investigadores en estas sesiones, era generar un espacio colaborativo de reflexiones en torno a las prácticas habituales de los profesores y a sus posibles mejoras considerando alguno de estos elementos teóricos. Entre las sesiones 4 y 5 del taller, un profesor de cada grupo implementó en el liceo la sesión reformulada. Esta sesión fue video grabada y se analizó en las dos últimas sesiones (conviene aclarar que hay un encuentro posterior, que es la entrevista al profesor).
La lección que presentamos corresponde a la implementada por un grupo, una vez reformulada, que abordó el teorema de Thales y su demostración en el primer año de educación media (14-15 años). Para este grupo, la actividad original consistía solamente en presentar la demostración del teorema de Thales a los estudiantes, mientras que la reformulación propuso incorporar softwares dinámicos y una mayor participación de los estudiantes al establecer las relaciones planteadas en el teorema. Por su parte, el profesor que implementó la sesión es contador auditor de profesión, habiendo realizado cursos de regularización en un centro de educación superior para dar clases en el Sistema Educacional Chileno. Esta situación no es habitual entre el profesorado de matemáticas chileno, pues, en general, los profesores de matemáticas han egresado de las carreras de pedagogía (en matemáticas) impartidas por las universidades nacionales. El profesor se mostró dispuesto a participar en esta investigación y comprometido con el taller. Asimismo, estuvo abierto a compartir sus prácticas habituales y a incluir nuevos elementos en su práctica de aula. Lo anterior motivó la selección de la sesión y del profesor para este reporte.
La principal fuente de datos fue la videograbación de la clase reformulada por el profesor. Esta clase fue observada de modo no participante y grabada por uno de los investigadores. La grabación fue transcrita y llevada a una planilla electrónica para su tratamiento donde cada intervención de los estudiantes o del profesor se enumeró correlativamente. La sesión fue dividida en episodios (descritos más adelante) que ayudan a describir el contenido de la misma. Los episodios están determinados por los objetivos propuestos explícitamente por el profesor o que se pueden inferir de su quehacer, con un principio y un fin iden-tificables. Se realizó un análisis de contenido (Bardin, 1996), definiendo como unidades de análisis las intervenciones, orales o escritas, del profesor. En los resultados se exponen los extractos incluyendo el número que identifica la intervención dentro de la transcripción.
Los subdominios y categorías del modelo MTSK (Carrillo et al., 2018) sirvieron de herramienta para el análisis y la identificación de conocimiento especializado en los datos recolectados. Para ello, usamos la distinción entre indicio y evidencia de conocimiento (Flores-Medrano, 2015) para referirnos a la sospecha de un conocimiento especializado del profesor -que debe ser confirmado por otros indicios o evidencias- o a la presencia de información que asegure que el profesor posee cierto conocimiento relativo a algún subdominio del MTSK, respectivamente. Tres investigadores expertos y dos familiarizados con el modelo analizaron de manera individual la transcripción de la sesión para luego contrastar y llegar a acuerdos respecto de la identificación del conocimiento especializado del profesor estudiado, buscando así la triangulación por investigadores como lo señala Flick (2007). En este reporte se incluyen los resultados de ese consenso.
DESCRIPCIÓN DE LA LECCIÓN
La sesión observada aborda el teorema de Thales y puede dividirse en 3 episodios. En el primero, el objetivo es comprobar empíricamente el teorema, antes de demostrarlo en el episodio 2 y, el 3 se dedica a la resolución de ejercicios de aplicación del teorema.
Durante la sesión se proyecta sobre el pizarrón lo que el profesor trae pre-parado. Los alumnos están sentados y es el profesor quien escribe en la pizarra. En general, las intervenciones parten del profesor, que explica y plantea cuestiones, y los alumnos resuelven individualmente, respondiendo desde sus pues-tos. Las correcciones se hacen en alto, con el profesor preguntando y escribiendo en la pizarra lo que los alumnos indican, haciéndose una única resolución de cada ejercicio.
Pasamos a describir brevemente los episodios, extendiéndonos en los dos primeros por ser los más ricos respecto a la intervención del profesor y evidencias de su conocimiento.
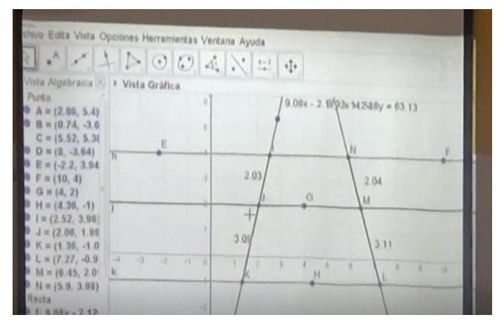
Episodio 1. Comienza la clase y se ve proyectada una imagen de GeoGebra (figura 1).
El profesor enuncia el objetivo de la clase: “Comprender y resolver ejercicios del
teorema de Thales”, anunciando que primero lo van a hacer de forma empírica y
después con una demostración. Relaciona el teorema de Thales con la semejanza y,
evocando lo que hacían en situaciones de semejanza de triángulos, les pide que
comprueben que
Episodio 2. Pasa entonces a la demostración, aunque dice que de forma empírica ha quedado prácticamente demostrado.
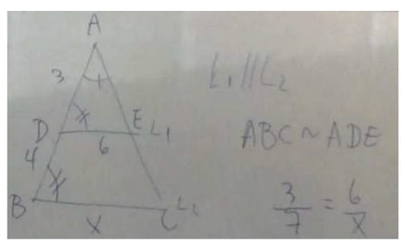
Parte de dos triángulos como los de la figura 2 (dibujados en la pizarra):
Comienza considerando que los triángulos ABC y ADE son semejantes, y establece
relaciones proporcionales en los triángulos, es decir, BA/DA=AC/AE, luego
En el Episodio 3 el profesor propone seis ejercicios de aplicación del teorema. Enfatiza las posibles dificultades de los alumnos en la resolución de las ecuaciones implicadas. El profesor propone cada problema, los alumnos lo resuelven individualmente y el profesor lo corrige en el pizarrón.
En el epígrafe siguiente presentaremos los resultados integrando evidencias e indicios de los episodios, siendo el hilo conductor los elementos de conocimiento del profesor y no los episodios en sí mismos.
RESULTADOS
Desde el enunciado del objetivo (“comprender y resolver ejercicios del teorema de Thales”) se observa la finalidad que el profesor parece otorgar a la enseñanza del teorema en la sesión: aplicarlo en situaciones de cálculo de un dato desconocido. Se aprecia así un énfasis procedimental que observaremos en toda la sesión. Y se puede observar su conocimiento sobre lo que espera que sus estudiantes aprendan del tema, adaptando los objetivos que se incluyen en las Bases Curriculares. La incorporación de las habilidades comprender y resolver en el objetivo atiende a los indicadores de evaluación que propone el currículo chileno sobre el desarrollo del teorema de Thales y la resolución de problemas geométricos, respectivamente. La comprensión conceptual queda relegada al entendimiento de las hipótesis del teorema de Thales como condición necesaria para aplicarlo, sin embargo, los ejercicios propuestos abordan, principalmente, lo procedimental. El planteamiento de tal objetivo permite observar que el profesor conoce que el teorema de Thales es un tema que debe enseñarse en el nivel que atiende y expone su idea sobre qué se espera que aprendan los alumnos al respecto. Todo lo anterior muestra conocimiento de los estándares de aprendizaje de las matemáticas (KMLS -nivel de desarrollo conceptual y procedimental esperado).
El profesor relaciona el teorema con la semejanza de figuras planas, en concreto de triángulos semejantes (KoT, definiciones, propiedades y sus fundamentos): “La verdad, el teorema de Thales se desprende básicamente de la semejanza de triángulos o de figuras planas”, episodio 1, I5).7 El teorema es para él una consecuencia de la semejanza, y su función, más que generador de otros contenidos, es la de aplicación al cálculo de medidas desconocidas. Esta fundamentación del teorema le sirve para su demostración (como aplicación de la semejanza de triángulos). Cabe señalar que esta secuencia difiere del currículo chileno actual, donde el teorema de Thales aparece asociado a las homotecias y a la proporcionalidad de segmentos, ubicándose la semejanza inmediatamente después del teorema de Thales, y muestra su conocimiento de una secuenciación de los temas (semejanza antes que el teorema de Tha-les) (KMLS - secuenciación con temas anteriores y posteriores). De este modo, el KMLS del profesor difiere de la propuesta del currículo oficial y parece relacionarse con su conocimiento matemático, en el que el teorema de Thales se explica desde la semejanza (KoT), sin que se observen manifestaciones de relaciones con la homotecia.
Además, la relación que establece entre semejanza y teorema de Thales en el aula es una relación procedimental (evocar la semejanza sirve para que los alumnos repitan el procedimiento de comparar razones):
| Profesor (P): | …quiero que hagamos un cálculo, ¿se acuerdan cómo lo hacían en semejan-zas? […] comparábamos dos razones, ¿cierto?; y aquí vamos a hacer lo mismo, pero cuando el trazo […] de este segmento, partido por este segmento, y lo vamos a igualar. Ya chiquillos, calculadora, celular, vamos dividiendo esto por esto. [episodio 1, I9-11] |
La intervención anterior se refiere al principio de la comprobación empírica del
teorema, en el episodio 1, y les pide en primer lugar que dividan
| P: | ¿Se acuerdan del teorema de ángulo a ángulo?
Decíamos que L1 era paralelo a L2 [escribe en la pizarra L1 //
L2 y alude a la igualdad del ángulo A en ADE y ABC, y de los
ángulos D y B -Figura 3]. Y
decíamos, por ejemplo, si acá yo tenía 3, 4, 6 y x, ¿cómo
hacíamos? [un alumno empieza a hacer referencias a los lados]
con números, con números… [Los alumnos le van indicando y él
escribe |
El profesor muestra, por otro lado, conocer una caracterización de la semejanza de figuras y de triángulos (algunos postulados como el teorema ángulo-ángulo, KoT -definiciones, propiedades y sus fundamentos en relación con la semejanza). Se refiere a la semejanza como una situación de comparación, mostrando indicios de haber descomprimido el concepto (en el sentido de Ball, 2003, lo que asociamos a los fundamentos del concepto -KoT) (“Resulta que estoy comparan-do dos triángulos, este triángulo es éste, y su lado homólogo ¿cuál era?”- episo-dio 1, I23). Observamos indicios de que el profesor está considerando la noción de proporcionalidad como idea transversal (conectando transversalmente la semejanza y la proporcionalidad numérica y vinculando el trabajo geométrico con el aritmético) y de que la fracción es considerada una herramienta en el trabajo en situaciones de proporcionalidad (estableciendo una conexión auxiliar entre fracción y semejanza), cuando hace explícito que una razón hace referencia a una situación de comparación, que se expresa mediante una fracción (“… acá vamos a hacer algo parecido, vamos a comparar esto con esto, haga la fracción” -episodio 1, I25). Ambos elementos corresponden a conocimiento de la estructura de la matemática (KSM).
En este primer episodio, el profesor va dando las indicaciones sobre las razones que deben calcular y comparar, y él mismo enuncia la condición de paralelismo que deben cumplir las tres rectas correspondientes. Se refuerza así que el fin del episodio es la comprobación numérica del teorema, más que los alumnos conjeturen sobre posibles propiedades, lo que parece coherente con el énfasis procedimental señalado.
La comparación de segmentos es vista como una comparación numérica llevándola a la
representación como cociente entre sus medidas, donde prima el registro numérico (de
hecho, la igualdad que escribe en la pizarra el profesor en relación con la figura 1 es directamente
El trabajo geométrico se traslada al ambiente numérico-aritmético, estableciendo con ello una conexión de tipo auxiliar entre la proporcionalidad de segmentos y la aritmética de los números racionales (KSM -conexión auxiliar)
| P: | Ahora, esa fracción la puedo separar en dos
fracciones ¿cierto? Recuerden que cuando yo sumo fracciones de
igual denominador […] Se conserva el denominador y se suman los
numeradores […] [Escribe: |
Vuelve de este modo a evocar un conocimiento anterior enfatizando una analogía de procedimientos desde un punto de vista puramente instrumental.
En la mayor parte de la sesión, se usa GeoGebra para proyectar una figura que el profesor trae ya hecha, lo que muestra que sabe usar el recurso para representaciones geométricas. Sin embargo, en dos ocasiones, el profesor usa el recurso en su carácter dinámico: desplaza una de las rectas paralelas de la figura 1, obteniendo otra recta paralela, e intenta desplazar esta recta de modo que su dirección no sea la misma, sin conseguirlo. Parece que aprecia el poten-cial del dinamismo en la configuración del teorema de Thales y la agilidad en el procesamiento de información numérica que permite el recurso (todo ello conocimiento del recurso, KMT). Sin embargo, parece estar poco familiarizado con el recurso, en el sentido de haber reflexionado sobre la posibilidad de mover un objeto eliminando una de las condiciones geométricas con las que ha sido creado. Cabe también la duda de si ha reflexionado sobre las posibles limitaciones del recurso a la hora de probar una igualdad entre medidas, por la aproximación de decimales que usa (“No da lo mismo. Qué raro, pero eso tiene que ser un error, básicamente, del GeoGebra porque está sacado como un paralelo”. [episodio 1, I41]).
El profesor usa un lenguaje matemáticamente preciso en general, haciendo uso de los términos (“lados homólogos”, “razones”…) y notación propios del tema. En este sentido, muestra conocimiento del tema en relación con registros de representación (KoT - registros de representación). Destaca, además, la necesidad de precisión en la notación. Así, cuando evoca una situación de semejanza de triángulos enfatiza la necesidad de considerar los triángulos como tripletas de puntos ordenados: “Decíamos que el triángulo ABC era semejante al triángulo ADE (en relación con la figura 3), en ese orden, ¿cierto?” (episodio 1, I15).
Al mismo tiempo, tenemos indicios de su KPM sobre cómo proceder en matemáticas cuando se busca conjeturar una propiedad mediante el examen de algunos casos posibles (usa la configuración del teorema de Thales para establecer las proporciones, sin embargo, las medidas de los segmentos son arbitrarias). Evidencia también conocimiento sobre el rol de las hipótesis en la comprobación de una propiedad (el paralelismo de las rectas en este caso) y sobre cómo se demuestra en matemáticas (así muestra conocer el significado de una condición “si y solo si”, y la diferencia entre teorema y corolario). Asimismo, evidencia conocer la diferencia entre una demostración y una comprobación (en su primera intervención en la sesión anuncia: “primero lo vamos a ver de forma empírica y después lo vamos a ver a través de una demostración” -episodio 1- y el segundo episodio se explica por esta diferencia) y atribuir importancia a las demostraciones en matemáticas. Sin embargo, en el aula no demuestra el teorema general de Thales sino el particular, considerando el segundo como un caso particular del primero y usándolo para justificar su demostración (KoT -definiciones, propiedades y sus fundamentos). El propio profesor llama la atención sobre este hecho, que decide no abordar para no dedicarle más tiempo:
| P: | Aunque éste básicamente no es el teorema de Thales, es un caso especial, porque el teorema de Thales, básicamente, es éste [dibuja una representación del tipo de la figura 1]. [episodio 2, I92]. |
Además, hace explícito su conocimiento de cierta evolución en la práctica mate-mática, donde se pueden aceptar demostraciones hechas con computador para cierto tipo de problemas y su conocimiento de demostraciones basadas en el estudio de casos particulares (KPM):
| P: | Ahora vamos a la demostración […] a muchos no les gustan las demostraciones, pero a mí me encanta saber de dónde vienen las cosas, y el por qué, ¿ya? Porque de esta forma empírica queda prácticamente demostrado, […] a nivel computacional ahora se pueden ocupar muchas cosas. [episodio 2, I66]. |
El extracto anterior también da cuenta, por una parte, del conocimiento del profesor acerca de la relación entre los estudiantes y las demostraciones matemáticas (“a muchos no les gustan las demostraciones”, KFLM -intereses y expectativas). Este conocimiento pareciera influir en cómo ha organizado la clase, partiendo de un trabajo sobre el cálculo de razones para introducir la demostración. Por otro lado, se observa el rol de explicación que el profesor asigna a la demostración, usada para comunicar y convencer a los estudiantes que lo planteado por el teorema es cierto (KPM).
Por otra parte, hace explícito a los alumnos cuándo están usando uno u otro resultado
matemático (“Esto es distinto a lo que decíamos, este segmento partido por este
segmento no se parecía a la semejanza del triángulo […] pero lo que vamos a hacer
ahora, sí” -episodio 1), mostrando su conocimiento de cómo proceder en el trabajo
matemático y la rigurosidad necesaria en la argumentación (KPM). En el fragmento
citado, el profesor diferencia explícitamente las razones entre segmentos homólogos
sobre los lados oblicuos
Parece que el profesor usa la comprobación y los casos concretos como facilitador del aprendizaje, mostrando de este modo indicios de KMT (estrategia y ejemplos) en relación a su KPM. Esto parece explicar el sentido para el profe-sor del primer episodio: los alumnos comprenderán mejor la propiedad tras una comprobación numérica del mismo. Además, en ocasiones propone que sean los propios alumnos los que elijan las medidas del ejemplo, mostrando así conocimiento de cómo aprenden los alumnos (KFLM, interacción con el contenido) (si los alumnos eligen los valores es más evidente para ellos que pueden ser cualesquiera). Además de ejemplos, el profesor propone a los alumnos contraejemplos (es el caso de la comprobación en el episodio 1 con rectas no paralelas -I51) mostrando su conocimiento de la necesidad de que en el conjunto de ejemplos se muestren también contraejemplos o no ejemplos (KMT -ejemplos).
En el episodio 3, el profesor enfatiza en todo momento que se use el teorema, frente a posibles procedimientos alternativos que no se comparan. La finalidad en la comprensión instrumental sigue evidenciándose en relación al objetivo de la clase y su KMLS. En los ejercicios presentados en este episodio se muestra su conocimiento de la aplicación del teorema de Thales a la medición de distancias desconocidas (KoT -fenomenología). Si consideramos el conjunto de las tareas propuestas a los alumnos (KMT) podemos diferenciar una tarea inicial de cálculo-comparación (la que sirve en el episodio 1 para introducir el teorema), una de cálculo mixto (el ejercicio 4 propuesto en el episodio 3, en el que se conocen dos términos de una proporción y se pide la justificación de la relación con los otros dos términos, requiriéndose identificar que Formula) y el resto de tareas de cálculo de valor desconocido (restantes ejercicios abordados en el episodio 3). El mayor peso de las tareas de cálculo de valor desconocido parece coherente con la finalidad que atribuye al teorema. La aproximación que se hace al teorema de Thales (KMT) corresponde a una relación intrafigural (se destacan las relaciones entre elementos de una figura y los de su semejante, sin hacer referencia a transformaciones), donde en los registros figurales se hace uso de representaciones de dos rectas secantes cortadas por paralelas (sin que se represente el punto de corte de las secantes) y de representaciones de triángulos homotéticos de tipo “pico”, estableciéndose la relación entre ambas representaciones. En la interpretación de estas representaciones se trata el aspecto de homotecia, estando ausente el de proyección (KoT). El conocimiento de estas configuraciones del teorema es parte del KoT (representaciones) y permite utilizarlas para el diseño de los ejercicios que plantea (KMT, tareas) de acuerdo a lo que espera aprendan sus estudiantes (KMLS, nivel de desarrollo procedimental).
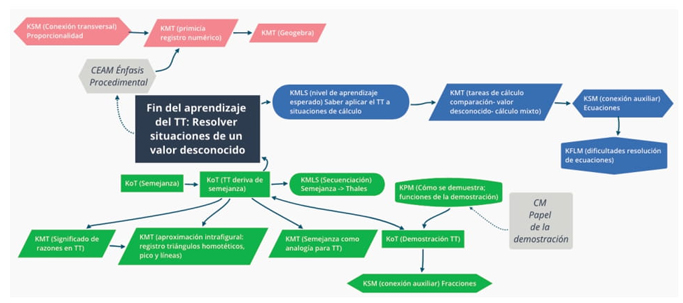
La figura 4 trata de representar gráficamente el conocimiento que asociamos al profesor en relación con la sesión analizada.
DISCUSIÓN Y CONCLUSIONES
En la interpretación de la sesión sobre el teorema de Thales identificamos tres núcleos de conocimiento principales, en el sentido de Sherin 1996 (citado en Sherin, Sherin y Madanes, 2000), quien alude a complejos de conocimiento del contenido, como estructuras de conocimiento en los que se muestran fuerte-mente conectados elementos del conocimiento de contenido y didáctico del contenido (a los que añadimos concepciones) que se desarrollan con la experiencia del profesor. Estos vienen definidos respectivamente por: 1) la relación que el profesor establece entre el teorema de Thales y la semejanza (núcleo verde), 2) el énfasis en el registro numérico (núcleo rosa), y 3) sus expectativas de aprendizaje en relación con el teorema (núcleo azul) (ver figura 4).
En el primer núcleo (verde) observamos que, para el profesor, el teorema de Thales deriva de la semejanza, lo que a la vez se relaciona con el conocimiento de la demostración del teorema en las diferentes configuraciones (particular y general) y explica los tipos de razones que activa en la enseñanza del teorema (entre segmentos homólogos sobre los lados oblicuos y de escala entre triángulos homotéticos), la aproximación intrafigural (relaciones en una figura, sin considerar transformaciones de una figura en otra) y el uso de registros figurales de triángulos homotéticos tipo “pico” y de líneas cortadas por paralelas que evocan a la configuración del mismo tipo. Las restricciones en las representaciones figurales del teorema y en las razones que se consideran podrían contribuir a las dificultades en la comprensión del contenido por parte de los alumnos evidenciadas en Lemonidis (1992) y Brousseau (1995), y coinciden con las carencias detectadas por el profesor del estudio de Gualdrón (2011), quien, consciente de las dificultades de los estudiantes en la comprensión de las demostraciones, organiza su estrategia de enseñanza en torno a tareas que buscan establecer conjeturas para luego presentar una aproximación a la demostración del teorema.
Respecto de la demostración del teorema, este conocimiento se ve influenciado a su vez por su conocimiento sobre cómo se demuestra en matemáticas y por la conexión auxiliar que establece entre las fracciones y la demostración del teorema (de modo que puede evocar a las operaciones con fracciones para operar con razones en registro algebraico). El profesor atribuye el rol de verificación y explicación a la demostración (De Villiers, 1993), lo que influye sobre su conocimiento de la enseñanza del teorema y de la misma demostración (Delgado-Rebolledo y Zakaryan, 2019). Coincidimos con Lesseig (2016) y Delga-do-Rebolledo y Zakaryan (2019) en que la enseñanza de la demostración moviliza conocimientos del profesor de diferentes subdominios del MTSK. En concreto, podemos observar cómo su conocimiento de la práctica matemática en relación con la demostración y los roles que le atribuye a esta en el aula, junto con su visión del teorema como una consecuencia de la semejanza, explican el conocimiento que evidencia sobre sus representaciones, su interpretación del teorema y las conexiones que establece entre este y las fracciones. En este sentido, destacamos el rol de la demostración como una práctica matemática que es parte del conocimiento especializado del profesor, ubicada en el subdominio menos explorado hasta ahora (KPM) del modelo MTSK. De este modo, esta investigación aporta evidencias de conocimientos que contribuyen a profundizar en el estudio del KPM y a la comprensión del conocimiento especializado del profesor de matemáticas, relacionando los subdominios KoT, KSM, KMT y KMLS (núcleo verde en figura 4) en diferentes categorías. El conocimiento sobre la demostración constituye un punto de partida desde el cual es posible indagar sobre la integración de diferentes tipos de conocimientos que el profesor pone en juego durante la enseñanza, particularmente, del teorema de Thales.
Finalmente, la conexión entre el teorema y la semejanza que realiza el profesor no permite distinguirlos como temáticas diferentes o ligados por la homotecia como propone el currículo chileno (MINEDUC, 2016a), usando la razón de semejanza como analogía procedimental de acuerdo a la secuenciación que él propone para estos temas.
En el segundo núcleo (núcleo rosa en la figura 4) observamos que si bien las representaciones que usa en el profesor en la lección se ubican en los registros figural y numérico, se enfatiza el tratamiento numérico. Aunque el profesor usa también el registro algebraico durante la resolución de las distintas tareas, como paso intermedio entre el figural y el aritmético, este parece aproblemático para él. Lo que puede explicar el uso que hace del GeoGebra, centra-do en la vista gráfica en la que se presenta el registro numérico y en las razones entre las medidas de las longitudes de los segmentos correspondientes. El profesor parece considerar la proporcionalidad como un contenido transversal que le permite enlazar el registro geométrico con el numérico y la fracción como una herramienta en situaciones de proporcionalidad, observándose su conocimiento sobre conexiones interconceptuales entre ecuaciones, operatoria con números racionales, semejanza y teorema de Thales, usando como idea transversal la proporcionalidad.
Por último, el tercer núcleo (en la figura 4) muestra que el profesor espera que los alumnos logren aplicar el teorema para resolver diferentes situaciones. Esto se observa a lo largo de toda la sesión, especialmente cuando traza el objetivo de la clase. Las tareas que propone son mayoritariamente de cálculo de valor desconocido, salvo la inicial de cálculo-comparación, cuyo objetivo es introducir el teorema, y una de cálculo mixto. En su gestión de dichas tareas también incide el conocimiento de una conexión auxiliar entre la resolución de ecuaciones de primer grado y la resolución de tareas de aplicación de Thales de cálculo de valor desconocido.
Así como cada núcleo descrito involucra conocimientos de diferentes sub-dominios y dejan ver el carácter especializado del conocimiento del profesor (Scheiner et al., 2019), otras particularidades del conocimiento del profesor que se evidencian en esta sesión también nos resultan llamativas. Por un lado, los aspectos que muestra conocer sobre cómo aprenden los alumnos y posibles dificultades no se refieren directamente al propio teorema (a diferencia del estudio de Zakaryan et al., 2018), sino a contenidos relacionados con el tipo de tarea que propone (como dificultades en la resolución de ecuaciones).
Por otro lado, el profesor muestra un tratamiento algorítmico del contenido. La presentación del teorema a partir de una tarea de cálculo-comprobación numérica, el tratamiento intrafigural con configuraciones de rectas secantes cortadas por paralelas y la no evidencia de conocimiento sobre características del aprendizaje de este contenido específico concuerdan con los resultados de Escudero y Sánchez (2007) y evidencian la finalidad instrumental del aprendizaje del teorema y su visión de la relación entre semejanza y teorema de Thales (donde pesa mucho su KoT) que puede reforzar esa finalidad instrumental. A pesar del papel de la demostración esperado en esta lección, el KPM manifestado por el profesor no resulta tan determinante en relación con su acción en el aula, como la finalidad que parece atribuir al teorema. Así, el teorema no llega a demostrarse realmente y la lección se centra más en su aplicación que en su demostración.
Consideramos que, al intentar dar respuesta a nuestro objetivo, hemos podido aportar una interpretación plausible de la misma en términos del conocimiento del profesor, mostrando lo que evidencia conocer de manera relacionada. Aquí aportamos el detalle en la descripción de dicho conocimiento que nos posibilita MTSK. Nuestro estudio añade a otros trabajos previos sobre el conocimiento del profesor sobre el teorema de Thales, además del detalle mencionado, la identificación de relaciones entre distintos aspectos de dicho conocimiento, mostrándolo de forma organizada.
Esta interpretación desde su conocimiento contribuye a dar una explicación parcial de la sesión, que podrá tener otras explicaciones, como por ejemplo las interacciones en el aula. Hemos de tener presente, además, que puede tener otros conocimientos especializados sobre el tema que, o no se han activado en la sesión, o no hemos encontrado evidencias.
Pensamos que esta visión de la sesión desde el conocimiento del profesor contribuye a mejorar nuestro conocimiento sobre cómo los profesores conocen un contenido (en este caso el teorema de Thales), tan importante para el formador de profesores como el conocimiento sobre el aprendizaje matemático lo es para el profesor de matemáticas. En ese sentido, reivindicamos la necesidad de estudios sobre la comprensión de profesores de distintos contenidos matemáticos. Los resultados de estudios como este pueden ser útiles en procesos de formación de profesores. Asimismo, a partir de este podemos plantearnos posibles cuestionamientos con profesores sobre la enseñanza de este contenido. Las relaciones identificadas en el conocimiento del profesor de nuestro estudio, pueden servir a su vez para pensar en posibles aspectos clave sobre los que hay que incidir en la reflexión del profesor (por ejemplo, la relación entre el teorema de Thales y la semejanza o sus expectativas de aprendizaje en relación con el teorema). Por otra parte, el análisis del conocimiento de los profesores participantes puede ser el punto de partida de un proceso formativo que parta de sus posicionamientos, así como una herramienta.











 nueva página del texto (beta)
nueva página del texto (beta)