Introduction
By and large, economists adhering to different theoretical persuasions agree that, in the long-term, productive activity is bounded by exogenous factors stemming from either the demand side or the supply side of the economy. According to Thirlwall (1979), the balance of payments (BoP), specifically the growth rate of exports and the income elasticity of the demand for imports, are the main restrictions limiting economic expansion. Solow (1956), in turn, argues that the quantity of capital and labor and productivity factors determine potential output growth in the long-run. Paul Romer (1986) and other authors of the so-called new endogenous growth theory also maintain that capital accumulation and technological progress are the main engine of economic growth.
The aim of this paper is to empirically inquire the relative influence of both demand side and supply side variables on the Mexican economy’s growth dynamics between 1951 and 2014. In particular, we consider that capital accumulation and the growth rate of capital productivity could affect the growth rate of the demand for imports because imported capital goods generate economic capacity which, in turn, could generate an import substitution process. Therefore, apart from the growth rate of exports, capital accumulation and the growth rate of capital productivity are determinants of the long-run growth rate of output which is consistent with BoP equilibrium.
This paper is organized as follows. The first section presents the essence of Thirlwall’s model, the second one summarizes Clavijo’s and Ros’s model of a small open economy in which capital accumulation is the engine of economic growth; this model is then compared with Thirlwall’s. Section three displays our model in which capital accumulation and the growth rate of capital productivity determine the long-run growth rate of output which is consistent with a constant position of the BoP. Such a model is applied to the analysis of the Mexican economy for the period 1951 - 2014 in the fourth section. Our empirical analysis led us to argue that Mexico’s low economic growth rate, seen ever since the foreign debt crisis of 1982, is deeply rooted in a pattern of low capital accumulation and low rate of capital productivity. Mexico’s dull economic performance also stems from increased demand and external constraints. The last part of the paper concludes.
1. The balance-of-payments constrained growth model.
Thirlwall (1979) and Thirlwall and Hussein (1982) obtain a balance-of-payments constrained growth model as follows:
where pd, pf and e stand, respectively, for the growth rates of the domestic price of exports in domestic currency, the foreign price of imports in foreign currency and the exchange rate measured as the price (in domestic currency) of the foreign currency; g, h, i, and m denote the share of imports financed by export income streams, the price elasticity of exports, the price elasticity of imports and the income elasticity of exports, z is the growth rate of foreign income, while c is the growth rate of nominal capital flows measured in domestic currency and y is the income elasticity of the demand for imports.
Now, suppose a small open economy for which the growth rate of exports (x) is exogenously given (x=x 0 ) and the growth rate of imports (m), measured in domestic output, is a function of the growth rate of output (g):
Assuming constant relative prices and current account equilibrium (exports = imports), Thirlwall (1979) derives his fundamental equation, which yields a long-run balance of payments equilibrium growth rate of output:
Equation (3) presents a demand-side determined economic growth model. Thirlwall’s model has recently been subject to criticisms on the grounds that it omits supply-side factors and capital accumulation plays no role whatsoever (cf. Clavijo and Ros, 2015).
2. Capital accumulation as the growth engine of a small open economy.
Ros and Clavijo (2015) argue that capital accumulation is the main engine of the long-run growth rate of output. According to them, Japan’s output growth rate exceeded that of Great Britain during the post-war period and today’s Chinese economy has grown much faster than Mexico’s over the last thirty years not because of trade specialization and the ensuing differences in income elasticities of the demand for both exports and income, but because of both Japan and China having far greater rates of capital investment (Ros and Clavijo, 2015: 81, own translation).
Clavijo and Ros (2015) develop a supply-side model where the long-run growth rate of a small open economy is determined by capital accumulation and capital flows are endogenous to domestic savings. Hence output growth is constrained neither by the demand side nor by the balance of payments equilibrium. Their model assumes a small open economy with an unlimited supply of labor and a given (in terms of domestic output) real wage (W/P); this economy produces only one good (Y) using capital (K), labor (L) and technology (A); the production process is captured by the following production function:
where α and 1-α are capital and labor elasticities of output respectively. The domestic output is used as a consumption good (C) and as an export good (X), whilst all the investment goods are imported (all imports are investment goods). Firms maximize profits; therefore, their demand for labor rises up to the point where the marginal product of labor (MgPL) is equal to W/P:
For simplicity, workers do not save at all, whilst firms save a fraction (sП) of profits (П). Under these assumptions, equilibrium in the domestic goods market is:
or
or, using equations (4) and (5):
solving equation (6’’) for X, yields:
where σ stands for capital productivity. It can readily be seen that, since
(W/P) is given, σ is also given. Therefore, X
and Y proportionally depend directly on K. Now,
suppose that the real exchange rate, defined as the price ratio of domestic output
to imported capital goods (P/P*), is given. This implies that the
profitability rate (r) in terms of (P*) is also
given, because (W/P) is fixed. Assume, further, that the growth
rate of capital is composed of two parts, an autonomous component (
where h is the profitability elasticity of net capital accumulation. So, the growth rates of X, Y and total imports are equal to the growth rate of K. It is worth noting that, starting from an initial trade deficit, such deficit will increase over time in absolute terms. Yet, this will not be a problem as Clavijo and Ros (2015) assume capital flows are endogenous to domestic savings.
Clavijo’s and Ros’ model implicitly assumes that y = 1. Although, clearly, such an assumption is not to be found in Thirlwall (1979), we follow it just for the sake of comparison. Both, Clavijo and Ros (2015) and Thirlwall (1979), consider that the long-run growth rate of output is equal to the growth rate of exports. However, the former maintains that causality runs from investment to exports and output, whilst, conversely, the latter states causality runs from exports to output.
3. Capital accumulation, long-run output growth and the balance of payments.
Clavijo and Ros (2015) rejects Thirlwall’s result of the existence of a balance of payments equilibrium constraint setting an upper limit to long-run economic growth. Thirwall (1979), in turn, does not include an explicit role for capital accumulation. In what follows we build a model combining capital accumulation and the growth rate of capital productivity as determinants of the long-run growth rate of output which is consistent with a constant position of the balance of payments (BoP) as a percentage of GDP, i.e., with a BoP constraint. In particular, the effect of capital accumulation on the growth rate of the demand for imports is dealt with.
Capital accumulation has played a major role in the literature on the determinants of the long-run growth rate of output. Particularly, Nurkse (1953) maintains that capital scarcity is the main hindrance in developing economies. In fact, capital accumulation exerts a double effect on the external restriction on economic growth: on the one hand, it imparts a negative effect as some capital goods must be imported; on the other hand, there is a positive effect arising from the import substitution that would become possible through the generation of economic capacity provided the new capital produces goods that otherwise would have to be imported2 . Clearly, capital accumulation and the demand side of the economy interact so as to determine the long-term position of the economy.
In our model the growth rate of exports is (given) equal to x0 and the growth rate of the demand for imports is determined as follows:
where I/K, ce, ε, and ψI denote the gross capital accumulation, the growth rate of economic capacity, the real exchange rate elasticity of the demand for imports and the gross capital elasticity of the demand for imports respectively. The above specification of the demand for imports accounts for the critique -with regards the specification given by equation (2)- put forth by Ibarra (2015:43, our translation): “suppose […] a slow rate of capital accumulation […]The capacity to produce competitive exportable goods for the world market will deteriorate, as will the capacity to produce domestic goods competing with importable goods. Given an increase in world demand, exports will grow slowly, impaired by the low productive capacity resulting from low capital accumulation… Likewise, in the face of an increasing domestic demand, the production of domestic goods competing with imports will respond weakly […]”. In such a case, we would empirically witness a high growth rate of global demand combined with a low growth rate of exports and a high growth of imports vis-à-vis domestic demand. Thus, if we run regressions assuming that the growth rates of exports and imports are solely explained by the behavior of external and domestic income, we would get coefficients revealing a low income elasticity of demand for exports and a high income elasticity of demand for imports.
Following Ibarra’s critique (2015), it can be argued that the estimation of the income elasticity of demand for imports based on equation (2) would be biased. Suppose an (non-domestically produced) imported good z with an income elasticity of demand ψz. Using equation (2) to estimate ψz, would obtain an unbiased estimation. Now, suppose, alternatively, that all the required amount of good z is domestically produced and none is imported. In this alternative case, the estimated value of ψz obtained by equation (2) would be zero, which is a biased estimation. Yet, if we use the specification given by equation (9) instead, the estimated value of ψz need not be zero; it would be obtained through the excess (shortfall) of the growth rate of output with respect to the growth rate of economic capacity.
Furthermore, even in the latter case (i.e., no imports of good z ) the estimation of ψI would indicate the percentage increase of imports of capital goods required to increase by 1% the capital stock for the production of good z.
There is yet one more particular issue with Thirlwall’s Law that, to the best of our knowledge, has not hitherto been thoroughly discussed: contrary to Pugno´s interpretation (1998), the long-run growth rate of output which is consistent with the BoP restriction is not a steady state position, unless y = 1. Consider the ratio exports-to-output (X/Y) when the growth rate of output is equal to gtb (equation (3)). The growth rate of the ratio X/Y is equal to:
which is higher (equal or lower) than (to) zero when ψ is higher (equal or lower) than (to) zero. The ratio X/Y is constant only when ψ = 1; when ψ > 1, X/Y is increasing and, eventually, it will be equal to one, so the economy will be producing just for the external market and the domestic demand for domestic production will be zero, which is implausible. When ψ < 1, the ratio X/Y is decreasing and, eventually, it will be very close to zero, so the economy will become a closed economy and a BoP restriction will not have any sense, apart from the fact that, actually, there is no closed economy in the real world.
Now, the problem is not so much that the composition of the aggregate demand is changing. In fact, we think that it is very important to bear in mind the endogenous change of the composition of the aggregate demand. However, the problem is that we do not observe economies transiting to become either actual closed economies or ones producing just for the external market. Instead, there is always some domestic demand for domestic goods as well as some external demand for domestic goods. Hence the specification represented by equation (9) will help us understand why, although y ≠ 1, the economy would not transit to become a closed economy or one solely producing for the external market. On the other hand, it is also very important to understand the changes in the composition of the aggregate demand because those changes involve winners and losers of the growth regime of the economy. So, in order to consider the composition of the aggregate demand, the growth rate of output is disaggregated in the specification of the growth rate of demand for imports3:
where id is the growth rate of internal demand for domestic goods and ω and 1-ω stand for the fractions of the total imports derived from the income generated by the internal demand for domestic goods and from the external demand for domestic goods respectively. Now, it is important to take into account that the trade balance of the economy is not always in equilibrium; its position, especially if initially it exhibits a deficit, will not increase as a percentage of output (see McCombie and Thirlwall, 1997; Moreno-Brid, 1998a; and Barbosa-Filho, 2001). With the aim of accounting for this characteristic, we postulate the dynamic condition required to maintain a constant position of the BoP as a percentage of the output:
where
Before explaining the above equation, let us assume that the growth rate of economic capacity is equal to the net capital accumulation plus the growth rate of capital productivity:
where δ is the depreciation rate of capital and
For the sake of explaining our result in a simple manner, let’s assume, following
Thirlwall (1979), that the trade balance
is in equilibrium (it means that
Substituting equation (15) into equation (16) obtains:
Again, aiming for a simple explanation of our result, assume that the trade balance
is in equilibrium (it means that
Now, given x0, if ψ is higher (equal or lower) than (to) ψI, an
increase in I/K will impart a positive (null or negative) effect on
gtbI (see Figures 1a, 1b and 1c),
whilst
Moreover, using equation (17) it can
be shown that the ratio X/Y does not just depend on ψ; it also
depends on ψI, x0, I/K,
Therefore, even when ψ > 1, X/Y will be decreasing if ψ is higher
than ψI and I/K and
4. Economic growth, capital accumulation and balance of payments in Mexico.
Graph 1, below, shows the output performance of the Mexican economy from 1951 to 2014. On average, the growth rate of Mexico’s GDP averaged 6.51% during 1951-1981, a period that encompasses the golden age of the country´s industrialization (1940-1970), the loss of macroeconomic stability in the seventies and the oil boom period (1978-1981) (Moreno-Brid and Ros, 2009). Mexico’s economic activity lost momentum after the foreign debt crisis of 1982: the average growth rate of GDP declined to 2.27% in 1982-2014. Moreover, the North American Free Trade Agreement (NAFTA) only brought an average growth rate of output equal to 2.59% during 1994-2014.4 The economic liberalization strategy has hitherto failed to deliver a higher growth rate of GDP commensurate with that of the import substitution industrialization era.
According to the balance-of-payments constrained growth approach, the sharp deceleration of Mexico’s output growth rate can be looked upon in two ways. One is through a decrease of the growth rate of exports; the other is through an increase in ψ (cf. Moreno-Brid, 1998b and 1999; López and Cruz, 2000 and Guerrero de Lizardi, 2006). As far as exports is concerned, the data say that their average growth rate, though slightly, did increase throughout the trade liberalization period vis-á-vis the import substitution industrialization epoch: exports grew at an average annual rate of 7.94% during 1982-2014, at 7.73% during 1986-2014 and 8.34% from 1994 to 2014, compared to 6.65% during 1951-1981 (see graph 2). Thus, a faster average growth rate of exports coincided with a slower growth rate of GDP during 1982-2014, while output growth acceleration overlapped with (slightly) lower exports.
Now, determining -in a very simple way- a value of ψ consistent with a dynamic BoP equilibrium, we divide the growth rate of exports by the effective growth rate of GDP5. It can be shown that the implied ψ was 1.02 during 1951-1981, 3.50 during 1982-2014, 3.06 in 1986-2014 and 3.23 during 1994-2014 (see table 1). Therefore, the income elasticity of demand for imports consistent with a dynamic BoP equilibrium more than tripled after the foreign debt crisis of 1982.
Table 1 Implied income elasticity of demand for imports, 1951-2014.
|
Subperiod |
1951- 1981 |
1982-2014 |
1986-2014 |
1994-2014 |
|
Growth rate of GDP (average) |
6.51% |
2.27% |
2.53% |
2.59% |
|
Growth rate of exports (average) |
6.65% |
7.94% |
7.73% |
8.34% |
|
Implied income elasticity of demand for imports |
1.02 |
3.50 |
3.06% |
3.23 |
Source: Authors’ calculation using data from INEGI.
Note: The implied income elasticity of demand for imports is equal to the growth rate of exports-to-the effective growth rate of GDP ratio
Yet, as mentioned above, according to our model both capital accumulation and the growth rate of capital productivity are also important in determining the long-run growth rate of the economy. As can be seen from graph 3, the growth rate of net capital followed the same pattern of behavior as the growth rate of GDP: its annual average growth rate was 5.91% during 1951-1981, 3.34% in 1982-2014, 3.22% during 1986-2014 and 3.41% during 1994-2014. After the foreign debt crisis of 1982 the path of net capital accumulation faltered, it fell down 2.57 percentage points, and the NAFTA did nothing to improve it.
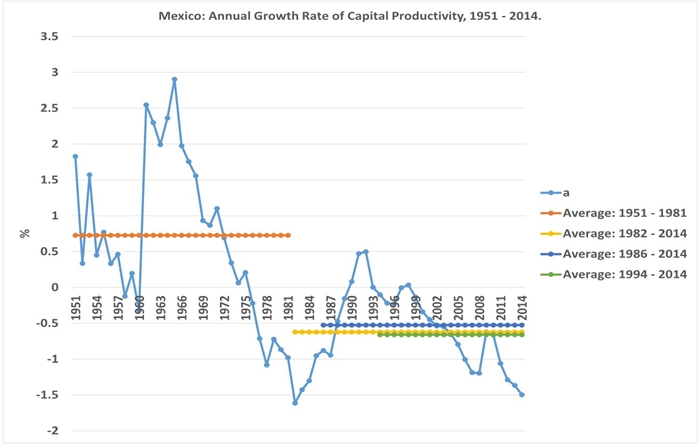
On the other hand, capital productivity6 grew at an annual average rate equal to 0.73% during 1951-1981, and at negative rates afterwards: -0.62% in 1982-2014, -0.53% during 1986-2014 and -0.66% during 1994-2014 (see graph 4).
Bearing in mind the above stylized facts, we apply our model estimating the following equation for the determinants of the annual growth rate of the demand for imports:
where t stands for time, DU represents a Dummy variable in the relevant cases (see below), βi are the parameters to be estimated and u t is a white noise. Our results of the ordinary least square method of estimation of equation (19) are shown in table 2.
Table 2 Dependent variable: m t
|
Subperiod |
1951-1981 |
1982-2014 |
1986-2014 |
1994-2014 |
Independent variable |
||||
|
-0.61* (-3.87) |
-0.84* (-9.05) |
-0.59* (-4.28) |
-0.66* (-2.34) |
|
|
It/Kt |
0.69* (5.45) |
0.86* (5.50) |
0.84* (4.89) |
0.80* (6.44) |
|
idt-cet |
1.94* (4.18) |
1.56* (3.02) |
1.50* (3.05) |
1.19* (3.23) |
|
xt-cet |
0.48* (4.09) |
0.74* (7.17) |
0.75* (10.46) |
|
|
D51 |
15.67** (2.61) |
|||
|
D58 |
-11.93*** (-2.08) |
|||
|
D79 |
11.81*** (1.95) |
|||
|
D80 |
13.52** (2.22) |
|||
|
D83 |
-22.30* (-4.37) |
|||
|
D86 |
25.45* (4.92) |
15.02** (2.51) |
||
|
D88 |
17.48* (3.74) |
20.52* (4.26) |
||
|
D94 |
10.43** (2.26) |
|||
|
D95 |
17.57** (2.51) |
|||
|
D13 |
-7.29** (-2.34) |
|||
|
Jarque-Bera test |
0.87 |
0.31 |
0.16 |
4.04 |
|
LM test |
0.99 |
0.98 |
0.79 |
0.33 |
|
White test |
0.40 |
0.95ϯ |
0.88 |
0.14 |
|
Ramsey test |
0.53 |
0.73 |
0.32 |
0.31 |
|
Numbers of observations |
31 |
33 |
29 |
21 |
*Statistically significant at 1% level.
** Statistically significant at 5% level.
***Statistically significant at 10% level.
Source: Authors’ calculation using data from Hofman (2000), World Penn Table, Banxico and INEGI.
Notes: D?? means a Dummy variable with value = 1 in the year 19?? (20??) and zero otherwise.
The LM test was includes one lag.
The White test includes cross terms, except in the case marked with †.
The Ramsey test includes one fitted term.
In the appendix we show the unit root test for the time series used.
Now, the estimated parameters of equation (19) are used to determine the long-run growth rate of internal demand for domestic goods which is consistent with a constant position of the balance of payments as a percentage of the GDP; β1, β2, β3, and β4 represent ε, ψp, ωψ and (1-ω)ψ respectively. Therefore, idtb can be determined as:
where t indicates the number of years of each subperiod for which the econometric
model was run. In order to derive gtbI we just use equation (17). Our estimations for ψp,
ψ, idtbI and gtbI for each subperiod using the annual average
values of β0,
Table 3 Long run growth rates of internal demand for domestic goods and of output and their determinants.
|
Subperiod |
ψI |
ψ |
DU |
x |
I/K |
|
idtb |
DU |
x |
I/K |
δ |
Capital acumulation |
||||
Annual averages values |
Contribution |
|||||||||||||||
1951-1981 |
0.69 |
1.94 |
0.94 |
-1.83 |
6.65 |
8.76 |
0.73 |
3.11 |
5.53 |
-0.54 |
-0.64 |
3.06 |
6.32 |
0.81 |
-3.47 |
3.65 |
1982-2014 |
0.86 |
2.04 |
1.47 |
0.88 |
7.94 |
6.60 |
-0.62 |
3.47 |
2.24 |
-0.88 |
0.44 |
3.02 |
4.64 |
-0.76 |
-4.22 |
-0.34 |
1986-2014 |
0.84 |
2.23 |
1.23 |
-0.94 |
7.73 |
6.49 |
-0.53 |
3.49 |
0.57 |
-0.78 |
-0.36 |
1.64 |
5.79 |
-0.75 |
-4.98 |
0.06 |
1994-2014 |
0.80 |
1.94 |
-0.35 |
-0.18 |
8.34 |
6.75 |
-0.66 |
3.56 |
1.73 |
0.28 |
-0.10 |
1.93 |
6.31 |
-1.05 |
-5.65 |
-0.39 |
Subperiod |
DU |
x |
I/K |
δ |
gtb |
DU |
x |
I/K |
δ |
Capital acumulation |
||||||
Annual average values |
Contribution |
|||||||||||||||
1951-1981 |
0.69 |
1.94 |
0.94 |
-1.83 |
6.65 |
8.76 |
0.73 |
3.11 |
5.59 |
-0.51 |
-0.61 |
3.26 |
5.96 |
0.77 |
-3.28 |
3.45 |
1982-2014 |
0.86 |
2.04 |
1.47 |
0.88 |
7.94 |
6.60 |
-0.62 |
3.47 |
3.37 |
-0.70 |
0.35 |
4.00 |
3.72 |
-0.61 |
-3.91 |
-0.28 |
1986-2014 |
0.84 |
2.23 |
1.23 |
-0.94 |
7.73 |
6.49 |
-0.53 |
3.49 |
2.10 |
-0.61 |
-0.28 |
2.94 |
4.55 |
-0.59 |
-3.91 |
0.05 |
1994-2014 |
0.80 |
1.94 |
-0.35 |
-0.18 |
8.34 |
6.75 |
-0.66 |
3.56 |
3.43 |
0.21 |
-0.07 |
3.58 |
4.69 |
-0.78 |
-4.20 |
-0.29 |
Source: Authors’ calculation using data from Hofman (2000), INEGI, Banxico and the World Penn Table.
First and foremost, according to our empirical estimations, contrary to some received accounts for the sharp deceleration of Mexico’s growth rate of GDP after the debt crisis of 1982 and the advent of trade liberalization in the late 1980s, a more accurate elucidation of the dismal performance of the Mexican economy must embed the interaction of the balance-of-payments constraints elements and the influence of capital accumulation. Our empirical results show that y increased from 1.94 to 2.23 between 1951-1981 and 1986-2014, although during the NAFTA sub-period it went down to 1.94 again. Moreover, the gross capital elasticity of demand for imports -not relevant in the balance-of-payments constrained growth model- remains more or less constant throughout the whole period under analysis. Likewise, the autonomous growth rate of the demand for imports, measured by the Dummy variables, and the rate of annual variation of the real exchange rate are not very important in the determination of idtbI and g tbp ; their contributions are lower than one percentage point for each of the subperiods considered (see table 3). Hence, it can be argued that the increase in y contributes to explain the slowdown of Mexico’s GDP growth beyond the debt crisis of 1982, but such increase in y does not explain the whole story.
The contribution of the growth rate of exports to idtbI was very similar in 1951-1981 (3.06 percentage points) and during 1982-2014 (3.02 percentage points), while it was lower during 1986-2014 (1.64 percentage points) and 1994-2014 (1.93 percentage points). The contribution of x to gtbI , instead, was a bit higher: 3.26 percentage points in 1951-1981; 4 percentage points during 1982-2014; 2.94 percentage points during 1986-2014 and 3.58 percentage points in 1994-2014. So, the blame for the dismal performance of the economy cannot be laid on the behavior of exports.
Finally, we consider the contribution of capital accumulation to id tbI
and gtbI taking into account its three components: I/K,
Another way of looking upon the importance of capital accumulation in the determination of g tbI stems from the disaggregation of the determinants of m. Table 4 shows that the autonomous growth rate of the demand for imports is positive, although low, for all the subperiods, except for the NAFTA one in which the annual average value is -0.35%. The real exchange rate, in turn, exhibits a low effect in the determination of the growth rate of the demand for imports for each of the subperiods under analysis. Given that the income elasticities of the demand for imports for each subperiod is almost the same, it is normal to see that the growth rate of the demand for imports, derived from the growth rate of income, was lower after the debt crisis of 1982. Lastly, the net effect of capital accumulation on the demand for imports was negative during 1951-1981 (-6.32%), but positive during 1982-2014 (0.58%). It is important to bear in mind the behavior of the income and gross capital accumulation elasticities of the demand for imports, if one is to understand that the problem of the Mexican economy was a sharp reduction in the net capital accumulation and the growth rate of capital productivity, combined with an increase in y.
Table 4 Determinants of the growth rate of imports.
Subperiod |
Autonomous |
I/K |
g |
I/K (Import substitution) |
Total |
|
1951-1981 |
0.94 |
1.11 |
6.03 |
12.62 |
-12.35 |
8.34 |
1982-2014 |
1.47 |
-0.74 |
5.67 |
5.71 |
-5.09 |
7.02 |
1986-2014 |
1.23 |
0.56 |
5.43 |
7.84 |
-5.54 |
9.52 |
1994-2014 |
-0.35 |
0.12 |
5.37 |
7.71 |
-4.90 |
7.95 |
Source: Authors’ calculation using data from Hofman (2000), INEGI, Banxico and the World Penn Table.
With the aim of checking the robustness of our results, we contrast the differences between id and id tbI and between g and g tbI with the annual average change of the trade balance as a percentage of GDP, ∆xmy (see table 5). It can be readily seen that when the effective values are higher (lower) than the values consistent with a constant position of the BoP as a percentage of the GDP, the annual average change of the trade balance as a percentage of the GDP is negative (positive). It is worth noting that during 1982-2014 the Mexican economy has grown a bit more than 1% less than the growth rate which is consistent with a constant position of the BoP as a percentage of the GDP.
Table 5 Deviation of the growth rate of output and annual average change of the trade balance as a percentage of GDP.
|
Subperiod |
id-idtb |
g-gtb |
Δ(xmy) |
|
1951-1981 |
0.99 |
0.92 |
-0.10 |
|
1982-2014 |
-1.02 |
-1.11 |
0.15 |
|
1986-2014 |
0.86 |
0.42 |
-0.09 |
|
1994-2014 |
-0.51 |
-0.84 |
0.07 |
Source: Authors’ calculation using data from Hofman (2000), INEGI, Banxico and the World Penn Table.
Final remarks
The balance-of-payments constrained growth model put forth by Thirlwall (1979) and extended by Thirlwall and Hussain (1982) and others does not envision capital accumulation as a determinant of the long-run growth rate of output, whereas Clavijo and Ros (2015) neglect the role of the demand side and the balance of payments equilibrium in the economy’s long-term dynamics. Clavijo and Ros (2015: 81) play down the relative merits of several patterns of trade specialization, income elasticities of both exports and imports and, alternatively, stress the importance of the rate of investment in the long-run dynamics of the economy.
Looked at in this way, there is a dichotomy in the theory of economic growth. Yet, this need not be so. We argued, in this paper, that there is no adequate reason for drawing such a sharp line of distinction between the relevance of those variables in the determination of the long-term growth position of a small open economy. Capital accumulation played a major role in the slowdown of the Mexican economy in the aftermath of the 1982 debt crisis. The growth rate of net capital accumulation dropped from 5.66% to 3.12% between 1951-1981 and 1982-2014 and, consequently, the growth rate of capital productivity diminished from 0.73% to -0.62% over the same years. While the income and gross capital stock elasticities of the demand for imports and the growth rate of exports changed somewhat over the same periods, the bulk of the explanation of Mexico’s low economic growth rate corresponds to a faltering process of capital accumulation. It is worth mentioning that the role of adjustment variable for both controlling the growth rate of aggregate demand and moderating the external restriction has been assigned to the internal demand for domestic goods: the annual average growth rate of internal demand was 6.52% during 1951-1981, and 1.23% in 1982-2014. This phenomenon could be reflecting not only the bad performance of the non-tradable sector, but also the strict policy control over real wages required for the central bank (the Banco de Mexico) to meet its inflation target.
All in all, our empirical analysis points out that capital accumulation and the balance of payments interact with one another so as to determine the dynamic position of the Mexican economy in the long-period. A number of policy implications and research topics for further inquiry ensue from this main result, for instance the impact of a progressive fiscal policy reform on public investment, capital accumulation and balance payments stability.











 nova página do texto(beta)
nova página do texto(beta)