Introduction
The educational teaching process admits different evaluations. Within evaluating education, study plans and programs, teachers, educational institutions or students’ learning evaluations can be referred. This work focus precisely on the evaluation of students’ learning, which is the essential and basic reference to perform all other assessments.
The evaluation of learning is not an external activity, nor an isolated component of the teaching-learning process. It is an organic part and an endogenous condition of that process, and is closely related to the elements that make it up: objectives, content, methods, forms of organization and teaching methods. Every evaluation system corresponds to a conception of learning.
The evaluation, in its comprehensive sense, includes other categories such as control, verification, qualification and accreditation, among others, where a hierarchical relationship takes place; evaluation is the unifying superior concept, while the others are subordinated concepts.
The evaluation must be oriented, with a formative purpose, to the assessment, the qualitative analysis of the processes, their intermediate stages, and the products to propose a personalized construction of what has been learnt. The evaluation does not have a unique time and space, but it comes alive in each of the stages of the educational process.
Learning should be understood as the process by which the student appropriates (or builds) the knowledge, develops the skills and abilities and is formed by values and attitudes, correspondent to the objectives of the programs and the curriculum.
In the conception of the teaching-learning process, students occupy the central place, being responsible for their own learning, building knowledge by themselves and no one can replace them in this task. This highlights the active role of the subject in learning, by emphasizing the contribution necessarily made by the person that learns in the learning process itself.
Meaningful learning requires the effort of the students, under the guidance of the teacher, to relate the new knowledge to the relevant concepts they already possess, that is to say, the student learns when he is able to construct (through the activity) meanings about the object of study content, from the interactions student-content-teacher.
In this type of learning, teamwork, research and performance of tasks by students play an important role, enabling them to self-assess and evaluate the entire educational process and the factors involved in it. Significant learning implies that curricula do not constitute limitations or obstacles to creativity and the student's research possibilities. Likewise, the contents and methods of teaching and learning must be oriented, so that the student interrelates theory and practice; theoretical knowledge allows them to understand the social and material reality of it in daily life (Rojas Maldonado, 2017 b ).
“A concern of educational mathematicians has to do with finding ways to intervene and improve the learning processes of students in Math classes, so that school mathematical knowledge, when it is learned by students, actually becomes meaningful and functional knowledge, so it can be integrated into the world of life to transform it and transform the subject that learns, reconstructing and enriching meanings permanently” (Córdoba, 2011,p.13 ).
In the same way, the teacher has the difficulty of evaluating mathematical knowledge and even confusing the students with the mechanization of procedures, that can also cause confusion with the algebraic abilities.
The research shown here is based on the practice of mathematization for Biotechnology degree Differential and Integral Calculus learning, which shows the impact it had on students when used as a teaching strategy.
According to (Tall, 1995), appropriate situations cause cognitive conflict, provoking an imbalance that leads to the overcoming of epistemological obstacles present in the teaching of any mathematical concept. Integration of the three representations -graphic, numerical and symbolic- should be favored.
Schoenfeld (2016) and Tall (2008) stated that people think differently, even when they have been exposed to the same environment and instruction. Likewise, although the mathematician in his daily practice develops a very particular point of view about the world, it is difficult to find two mathematicians who give an identical description of his mathematical thought.
For (Edwards, Dubinsky, & McDonald, 2005) -who proposed the definition for advanced mathematical thinking- thinking that requires deductive and rigorous reasoning about mathematical notions is not entirely accessible to us through our five senses. They discuss which kind of thinking may be required, depending on the size of a mathematical problem, including problems involving infinity and the available types of models.
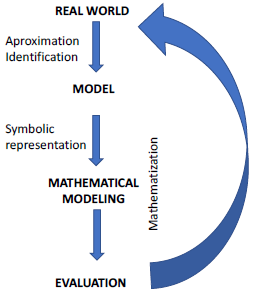
It is convenient to show that there is confusion about mathematization and mathematical modeling. Authors like Martínez, Cobos, and Torres (2015), made an analysis between the concepts. They mentioned that mathematization is to bring mathematical language to real or concrete situations, while mathematical modeling (Vera and Moreno, 2015) is defined as an articulating practice between two entities with the aim of intervening each on the opposite. The diversity of both entities intervening in the articulation, as well their nature, makes possible to identify modeling as a recurrent practice in different communities. Modeling practice allows building bridges between what is done in school and in communities outside schools.
Objective
To evaluate the learning of students after the strategy of mathematization and mathematical modeling.
Methodology
The selected approach to carry out this research corresponds to the qualitative-interpretative methodology, based on the complexity of the object of study: the evaluation of learning,
looking forward to “establish the five identity traits: Holistic, Inductive, Flexible, Emic, Indexable” (Barraza Macías, 2017).
A field investigation was carried out, for which the survey and in-depth interview techniques were used. With these techniques, relevant information provided by the subjects involved in the evaluation process was obtained.
Participants were exposed during a semester (6 months) to the process of teaching by mathematization and mathematical modeling in the subject of Differential and Integral Calculus in the Biotechnology degree at Universidad Michoacana de San Nicolás de Hidalgo (Morelia, Mexico) at the end of the intervention. Willing to be participants in the research project, they were interviewed in a random way. The data was collected at a non-experimental single time.
For the collection of data, the survey was carried out through a questionnaire applied in July 2017 through Google Forms -with no ordering of dimensions in a group with nine students- and the semi-structured in-depth interview -to six students- by means of a non-probabilistic discretionary sample in a dynamic way, flexible, non-directive and open, as well as the observation of the researcher during the project.
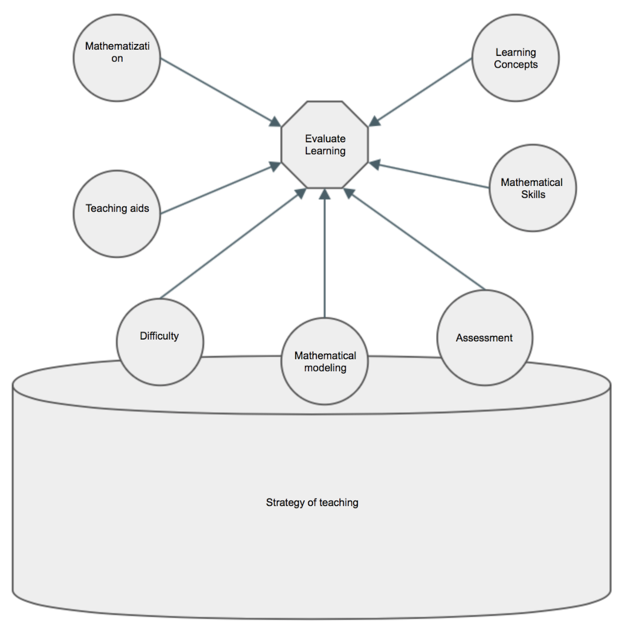
Likert scale was used to measure the variables, where the dimensions addressed were:
Learning concepts of Calculus
Empathy with teaching strategy
Mathematical modeling
Mathematization
Development of mathematical skills
Teaching support
Assessment
Difficulty of learning on previous Mathematics courses
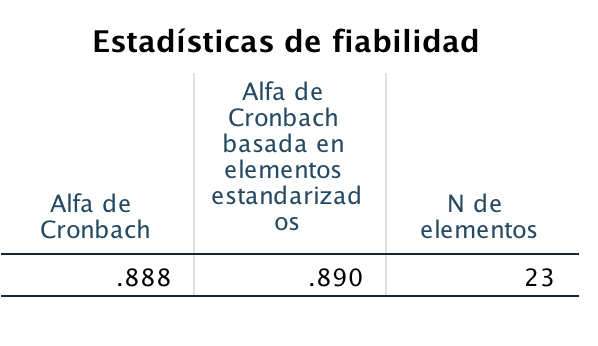
In this experiment, 0.88 Cronbach’s Alpha was obtained from the SPSS software, which shows that the test is reliable.
Results
It is important to notice that students are in an Exact Sciences career linked to practice, so they are aware of the importance of Mathematics within and for their field of work.
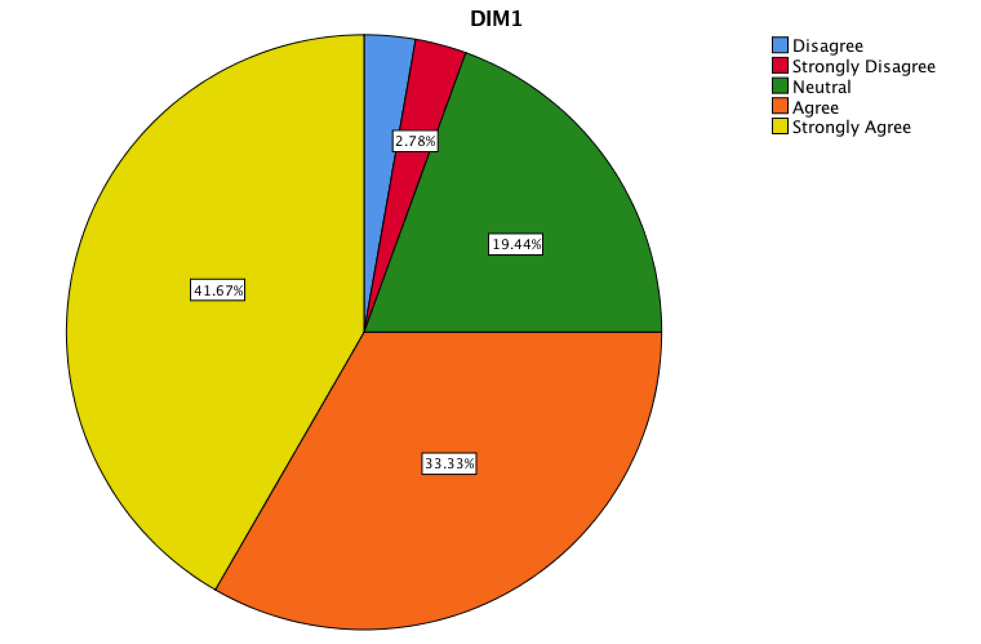
The DIM1 corresponds to learnt concepts of Calculus. It was the sum of frequencies of items one, two, 20 and 21.
The students showed a critical and reflective analysis of learning after being exposed to the strategy of mathematization, where the difficulties to be developed were exposed. In the same way, to establish Mathematics as a science that would allow solving a daily problem, the need to establish some mathematical concepts to support the idea of the phenomenon and express it through algebraic language was shown.
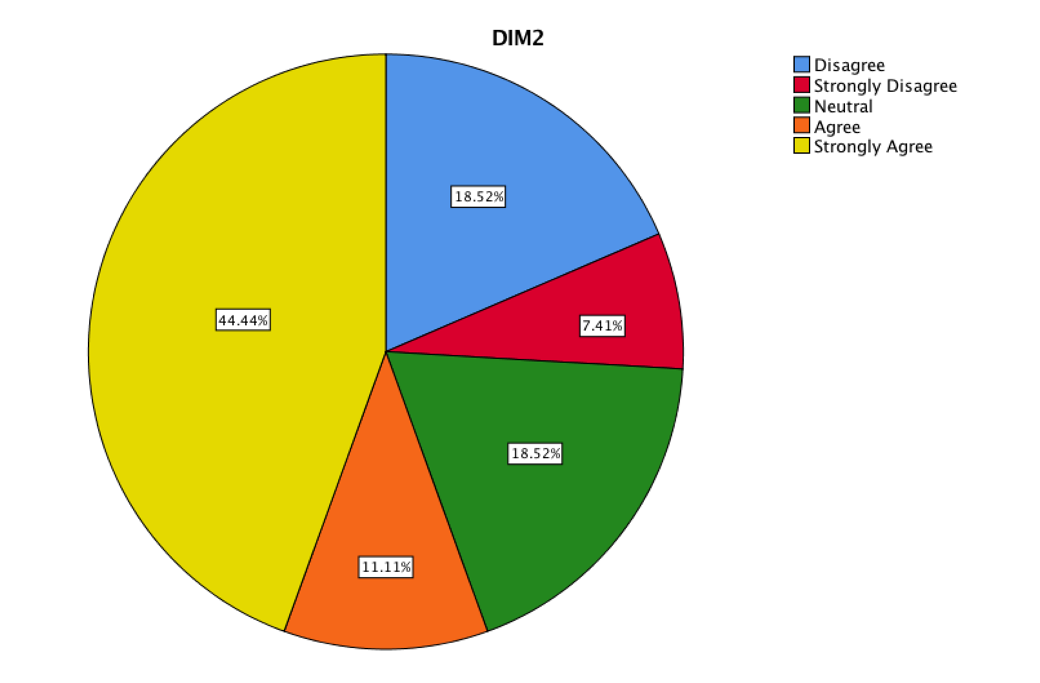
The DIM2 corresponds to the empathy with the teaching strategy. It is important to mention that if the student is satisfied with the teaching strategy, the pleasure of knowing and understanding is reflected in learning. That is why it is important to know the empathy that students feel with the way they are taught. It is convenient to show that if empathy did not exist, the research project would fall down.
That was the sum of frequencies of the items three, four, five.
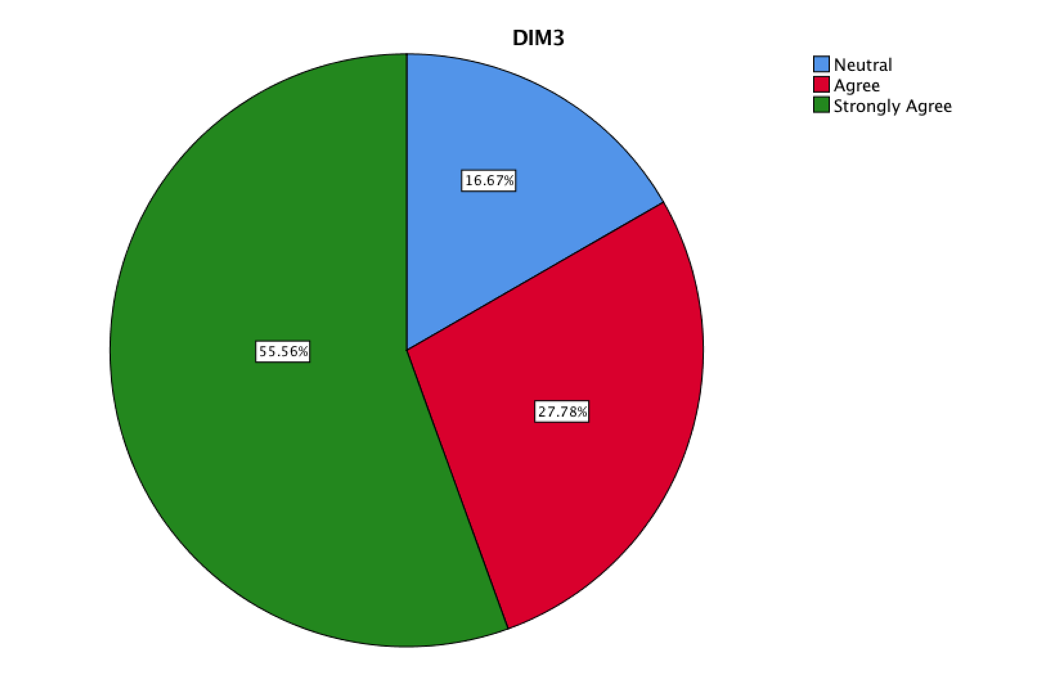
The DIM3 was considered with the items six and seven.
This figure shows the degree of acceptability in a self-critical and reflective way, regarding the learning of Calculus with physical phenomena of daily life, allowing to establish correlation with the mathematical world.
The DIM4 corresponds of the items eight-i and 23
It shows the percentage of mathematical language and interpretation of mathematical functions understanding applied in everyday problems and to model some problems.
The DIM5 corresponds of the items nine-i, 10, 13i and 22.
It represents the acquired mathematical techniques and skills which were developed through this strategy. This simulation was evaluated through a symbolic and algebraic management of mathematical variables, as well as conceptualization of function to establish the problem to solve.
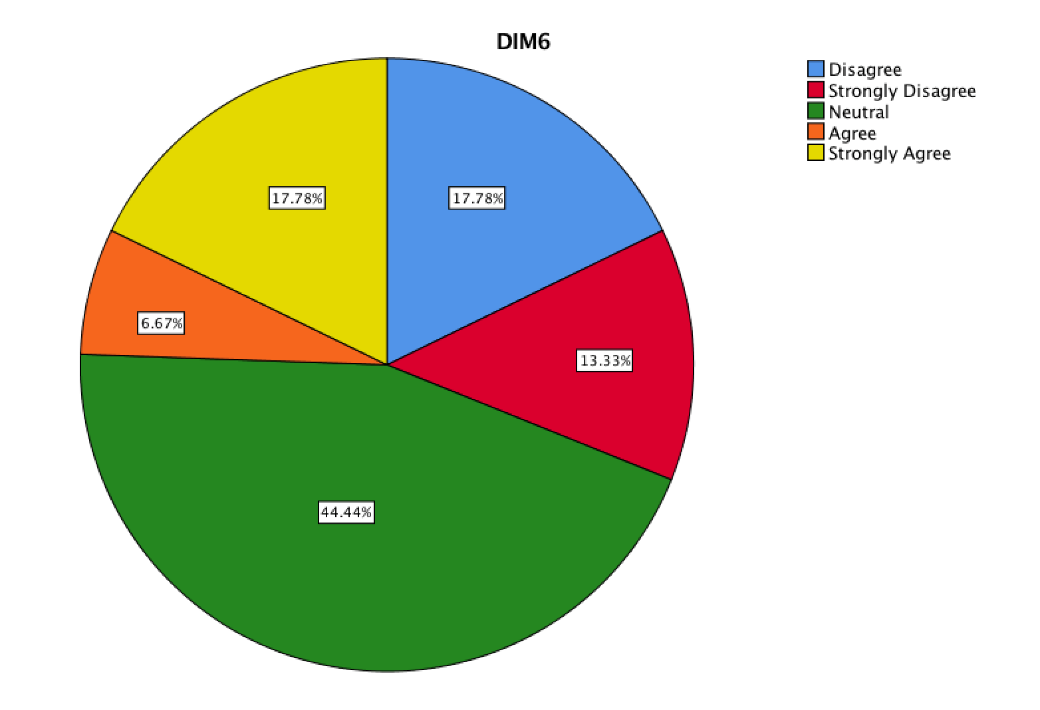
The search of didactic learning assistants while students are the subject of the mathematization and modeling of mathematics teaching strategy allows channeling new sources in search of information to establish cognitive ties with algebraic development. The consulted teaching assistants were specialized software and apps for smartphones. They were able to recreate a problem or establish a visual idea that represents a mathematical function. However, students are still reluctant to consult specialized printed books that generate the scaffolding of knowledge or simply to install applications that could be useful.
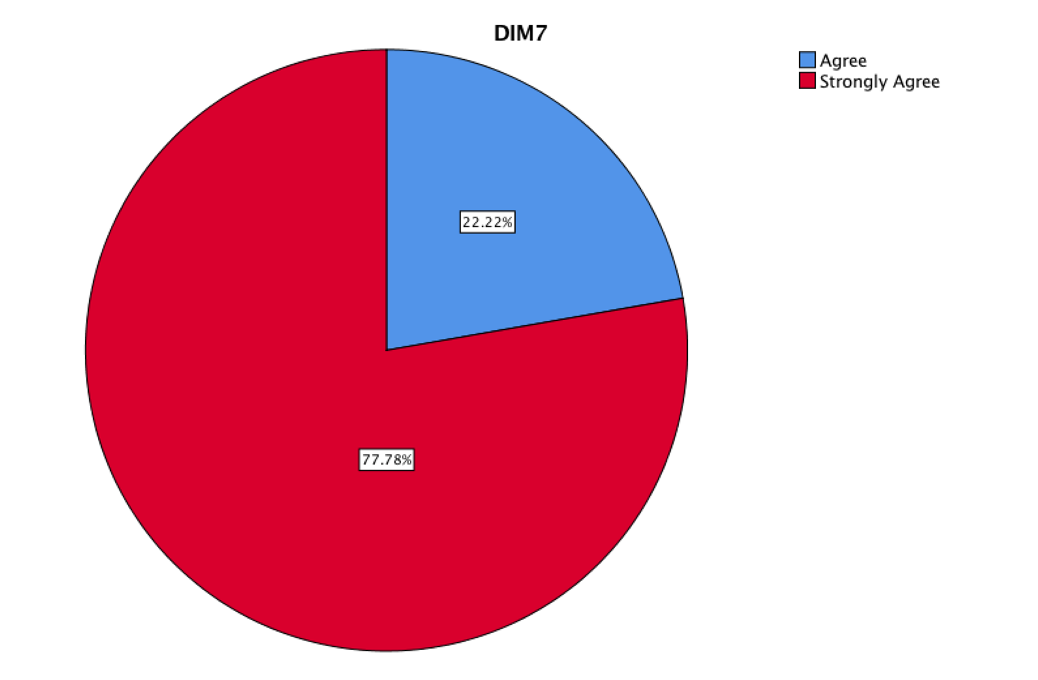
The DIM7 was consider with the item 19.
If the teaching strategy is different, the evaluation model must be different. Therefore, the innovation in evaluation can frame a different way of testing Mathematics in a less aggressive way than in a traditional one, besides it throws more significant data to the teacher when making the decision, if the use of learning was provided. The evaluation consisted on recreating and modeling everyday problems through mathematical functions in order to find critical values that the problem could consider, and in case of taking the critical values that occurred in the mentioned modeling. For this, they could count on specialized software and bibliography search; this strategy is known as problem solving. In this figure, the students show their pleasure with this evaluation model applied to the teaching strategy.
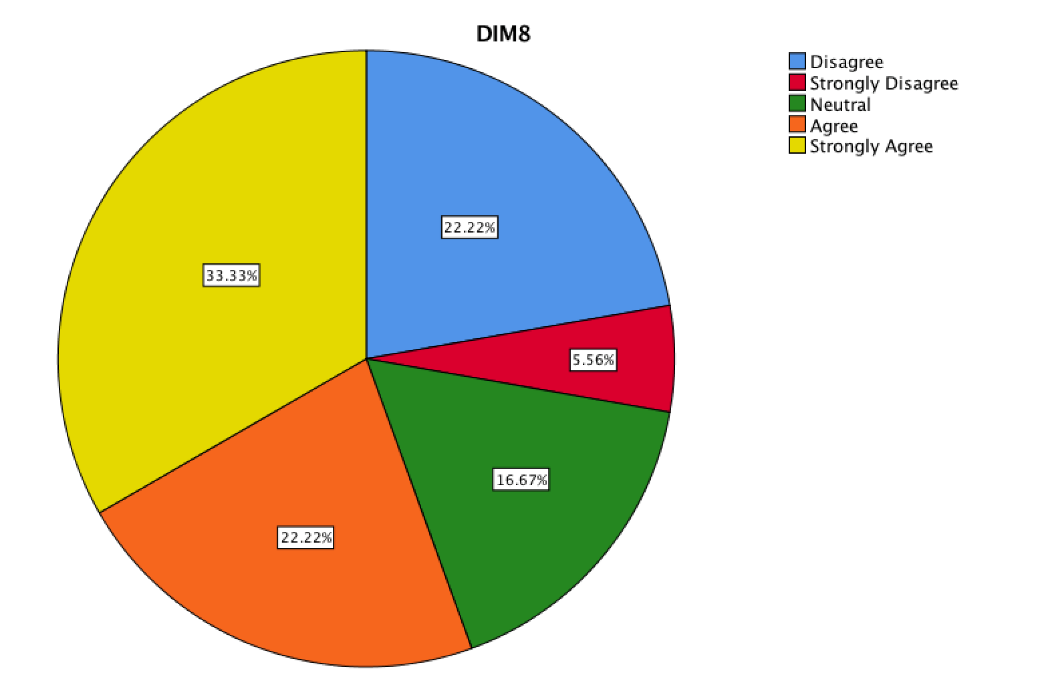
The DIM8 represents the difficulty of learning Mathematics and was considered with the items 11i and 12i.
Students showed a critical and reflective analysis about the learning of their previous Math courses, where they exposed the difficulties to develop and establish Mathematics as a science that would allow to solve a daily problem. Therefore, this figure represents the difficulty with this teaching strategy that students estimated to have compared to their previous Math courses and if that was an obstacle to learn Calculus by strategy. It is impossible to know if they were exposed to innovative strategies in the teaching of Mathematics in their previous courses, but they pointed out in the interviews that it was both a low expository approach and resolution of exercises.
All dimensions interfere in learning, and the results are shown below:
Conclusions
In the educational field, the starting point is a premise: what does the student want to learn.
In order to achieve a meaningful learning, effort is required from the students under the guidance of the teacher, to relate the knowledge they already possess with new knowledge and practices that achieve the retaining of knowledge.
The dissociation of theory and practice is an old question, though it is still present at classrooms (Rojas Maldonado, 2017b). It encourages to look for new teaching strategies that lead to a student professional training.
The exchange of ideas submitted during the mathematical modeling leads the teacher to have a range of information on mathematical concepts that allow to evaluate the learning during the course and to have enough information to make a summative assessment of students, and can help to homogenize the evaluation parameters and criteria that university professors currently establish in a unilateral way as well (Rojas Maldonado, 2017a).
The Mathematics and mathematical modeling teaching strategy was seen as an innovative strategy by students of the Biotechnology degree. By trusting that learning is related to the state of acceptance with the teaching strategy, it can be considered that there was a small improvement of it. The acceptability of the strategy was barely above the average, as per figure 12.
However, it is pertinent to observe that students showed little interest at looking for their own learning. Teaching supports were barely used, even though every student had the technological possibilities to do so, showing indifference or apathy. When they resorted to it, they expected to find an immediate solution to the problem. Even students find difficult to admit technology as a tool -as a means- to help them solve their problems, since they only perceive it as a solution or an end where the result can be magically obtained and copied.
There was a collaborative attitude between the students. They were interested in checking that their modeling was appropriate as well. In addition, mathematization allowed the language to be able to communicate and debate the arguments, allowing to generate new knowledge at the same time.
With this strategy, students were convinced and verified, explained, systematized, and demonstrated, especially the difficulties faced by them, when performing different types of tests and conceptions on what a test is.
The strategy must be considered to be incorporated into Mathematics subjects at the undergraduate level, in order to have an impact on professional training and promote collaborative work.











 text new page (beta)
text new page (beta)