Introduction
Forest ecosystems provide goods and services to humanity (Rendón, Martínez, & Pérez, 2014); however, forests are exposed to anthropogenic disturbances and processes that cause the genetic degradation of many forest species (Guevara-Hernández et al., 2011). It is therefore necessary to develop strategies that allow the conservation of groups of forest species genes, which is of particular importance to the maintenance of an inventory of quality plants for use in forest restoration programs (Bustamante-García et al., 2012).
Seed orchards are a useful and economic means by which to produce genetically improved germplasm in a relatively short time (Gutiérrez-Vázquez, Cornejo-Oviedo, Zermeño-González, Valencia-Manzo, & Mendoza-Villarreal, 2010). In recent decades, seeds produced in such orchards have been used both for commercial forest plantation and reforestation (Muñoz-Gutiérrez et al., 2017). In countries such as Chile, New Zealand and Canada, seed orchards are often used for germplasm production in order to meet the strategic needs of forest plantations (Mead, 2013). According to the Mexican National Forestry Commission (CONAFOR, 2014), Mexico only has 11 seed orchards, located in the states of Veracruz, Chiapas, Durango, Oaxaca and Puebla.
Despite their importance to seed production and the genetic improvement of species, research on seed orchards has been limited. In 2005, two orchards were established in the state of Chihuahua, Mexico. The first in an ejido (a Mexican system of communal land tenure) called El Largo, in which the seed production has not been reported. The second was a clonal orchard of Pinus arizonica Engelm., located in the south of that state, characterized by a promising production of cones (Pérez, Pompa-García, Solís, & Chacón, 2014). Tree size data could help to improve the productive potential of these orchards; however, there is a lack of such data in both cases.
Since geographic data are temporally and spatially variable, it is necessary to use tools other than classical statistics that assume the occurrence of ecological phenomena under identical circumstances and the independence of observations. As a result, increasingly sophisticated geospatial analyses (Carroll et al., 2015) play an important role in the understanding of geographical relationships. For example, spatial analysis allows researchers to determine whether ecological variables are random or clustered (Getis & Ord, 1992) and helps to determine the reasons for such spatial distributions (Fotheringham, Crespo, & Yao, 2015). The use of statistical tools such as geographically weighted regression (GWR) is a useful option for the spatial examination of non-stationary phenomena (Fotheringham, Brunsdon, & Charlton, 2004) and facilitates the measurement and visualization of patterns of variation in relationships between dependent and independent variables (Brunsdon, Fotheringham, & Charlton, 1998). In this sense, geospatial analyses could provide a better understanding of the tree size condition of seed orchards, thus improving their monitoring and management.
The objective of this study was therefore to model, from a geospatial perspective, the cone production and tree size variables of the aforementioned Pinus arizonica Engelm. clonal orchard in northern Mexico. It is hypothesized that the distribution of cone production and tree size variables will follow a non-random spatial pattern, and that cone production will be influenced by both tree size and physical variables.
Materials and methods
Study area
The P. arizonica clonal orchard was established in 2005 by the company Silvicultores Unidos de Guachochi, S.C. (SUG) in the Papajichi ejido, north of the city of Guachochi (27° 8' 57' 'N and 107° 6' 41 '' W; 2400 m asl), Chihuahua, Mexico (Figure 1). The orchard has an almost flat topography with a slope not exceeding 5 %. The climate is semi-humid, semi-cool with rain in summer, and semi-dry, semi-warm in summer. Average annual rainfall is 540.4 mm and the average annual temperature is 10.8 °C. The lowest average temperatures occur in January and December (-6 to -4 °C) and the highest in July and August (16.5 to 17.5 °C). The dominant soils are Regosols and Leptosols with loam textures on broken slopes, described in the 2014 world reference base (Pérez et al., 2014). The land surrounding the orchard is predominantly used for forestry and livestock purposes (González-Cásares, Pompa-García, & Camarero, 2017).
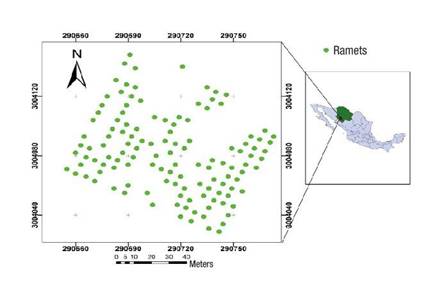
Figure 1 Location of the study area: Pinus arizonica clonal orchard with 126 ramets in the Papajichi ejido, municipality of Guachochi, Chihuahua, Mexico.
The clonal orchard covers an area of 1 ha. To prevent the entry of cattle, a perimeter fence of 2 m in height was placed around the orchard. A large capacity water tank was installed in an area adjacent to the orchard in order to water the trees during the dry season, although the tank is currently not functional. The orchard has 126 surviving ramets, each with an alphanumeric identification code following an ascending order.
Grafts of P. arizonica were made in 2005 using the terminal fissure technique (Muñoz-Flores, Prieto-Ruiz, Flores-García, Pineda-Ojeda, & Morales-Gonzáles, 2013) in the Silvicultores Unidos de Guachochi forest nursery. The grafts came from the apex of the branches located in the upper part of the trees. The orchard design is regular with a square frame layout, in which each tree occupies the vertex of the square angle, so that the distance between the trees and between the rows is constant; the spacing is 6 m between ramets. There are 16 clone lines in the orchard with 17 random positions per line.
Data
Data were obtained in October 2017. All trees were labeled with aluminum foil to facilitate subsequent identification. For each tree, the following measurements were taken: diameter at the base, diameter at breast height (1.30 m from ground level), crown height, total height, and larger, smaller and medium crown diameters, including the azimuth. Photographs were also taken of each tree and the 2016 cone production data were consulted. Each of these variables was entered into a geographic database. In addition, soil depth data were recorded at four sites in the orchard.
Spatial analysis
A geospatial analysis was conducted using the G statistic described by Getis and Ord (1992). This allowed determination of the spatial pattern of the tree size variables and cone production. To find G, we used ArcGis 10.2 software (Environmental Systems Research Institute [ESRI] 2011), where G is defined as:
where:
G |
Getis-Ord statistic |
x ij |
measurement of attributes for units i and j, respectively |
W ij (d) |
one or zero in a symmetric spatial matrix used to detect the proximity between i and j |
d |
distance |
To determine whether the G statistic differed significantly from a random distribution, a test of statistical significance for Z in the G cluster was performed:
where:
Z |
value of the clustering statistic |
G |
random value of the G statistic test |
G E |
expected value of the G statistic test |
StdDev |
standard deviation of G(d) |
The Z test assumes that there is no global autocorrelation, but when autocorrelation exists it has a significant impact on the expected value of G. This impact verifies the validity and accuracy of the clustering. The analysis makes it possible to determine whether or not the spatial randomness hypothesis can be accepted. A high Z score associated with a low P value indicates a statistically significant non-random spatial distribution (Gi_Bin). Three levels of reliability were examined: 90, 95 and 99 %.
Association between cone production and tree size variables
A Pearson correlation analysis (P ≤ 0.05) was performed in order to determine the association between cone production and tree size variables. This correlation also considered the values of the Normalized Difference Water Index (NDWI), commonly used to monitor drought (Gao, 1996). This is a satellite-derived index that uses near infrared (NIR) and shortwave infrared (SWIR) channels. The SWIR reflectance reflects changes in the water content of the vegetation and the spongy mesophilic structure in vegetation canopies, while NIR reflectance is affected by the internal structure of the leaf and its dry matter content, but not by water content. The NDWI was calculated from a Landsat 8 image (Route: 33, Row: 41) using the following formula:
where NIR corresponds to Landsat 8 band 5, and SWIR to Landsat 8 band 6. To eliminate atmospheric effects on the reflectance of the terrestrial surface, an atmospheric correction of the bands that make up the image was necessary, for which the Apparent Reflectance at the Top of the Atmosphere (TOA) method was applied. This method enables conversion of the digital levels of the original image into reflectance percentages and uses a single model of the variation of TOA reflectance with sun and satellite position to adjust to a standard angular configuration. The model implicitly assumes a constant atmosphere, and combines the correction of atmospheric effects and Bidirectional Reflectance Distribution Function (BRDF) effects into a single angular configuration function (Flood, 2014). To improve the resolution of the NDWI pixels, resampling was conducted in ArcGis, producing an NDWI image with a resolution of 5 x 5 m.
The variables that best correlated with cone production and those of greatest statistical importance were examined using an exploratory stepwise regression analysis. This tool evaluates possible combinations of explanatory variables to determine which models fulfill all of the diagnoses of a regression model, and thus allows selection of the model that best complies with all goodness-of-fit parameters. Once the best combination was identified in terms of cone production, it was modeled through a local geographically weighted regression (GWR) analysis (Brunsdon, Fotheringham, & Charlton, 1996). This method evaluates the heterogeneity of the data and estimates the parameters of each location (sampled points) in order to fit each model to each sampled data point, providing more detailed results and a fuller understanding of the process (Duarte-Cunha, Almeida, Cunha, & Souza-Santos, 2016; Pimentel, Lopes, Mexia, & Mumford, 2016).
The GWR model is described as follows:
Yi(u) = β0i(u) + β1i(u)x1i + β2i(u)x2i + … + βmi(u)xmi
where,
Yi |
dependent variable |
β0i and β1i |
parameters describing the relationship among the coordinates (u) of the i-th point in space (specific site) |
xmi |
m-th variable at the i-th point |
In this case, the dependent variable was cone production, while the independent variable was crown diameter. The GWR model was processed using ArcGis 10.2.2 software. This analysis allows mapping of the statistics of the results and can therefore identify the specific geographic space in which the independent variable has the greatest influence on the dependent variable.
Results
Table 1 indicates that there was variation in the tree size variables of the 126 ramets examined. There are 125 live ramets in the orchard, representing a survival rate of 45.95 % since 2005; a low vigor ramet with signs of mortality was included in the analysis. Cones were produced in 35 % of the ramets (44 individuals), ranging from 1 to 587 cones per tree.
Table 1 Descriptive statistics of 126 ramets from the Pinus arizonica clonal orchard in the Papajichi ejido, municipality of Guachochi, Chihuahua, Mexico.
| Descriptive measurement | DB (cm) | DBH (cm) | CH (m) | TH (m) | LCD (m) | SCD (m) |
|---|---|---|---|---|---|---|
| Mean | 19 | 11 | 3.87 | 4.35 | 3.42 | 3.09 |
| Mode | 24 | 11 | 3.50 | 5.00 | 3.60 | 2.60 |
| SD | 6 | 5 | 1.44 | 1.47 | 1.34 | 1.24 |
| Maximum | 36 | 24 | 7.40 | 8.00 | 6.50 | 6.10 |
| Minimum | 6 | 2 | 0.50 | 1.10 | 0.70 | 0.60 |
DB: diameter at base, DBH: diameter at breast height, CH: crown height, TH: total height, LCD: largest crown diameter, SCD: smallest crown diameter, SD: standard deviation of the mean.
Spatial trends of tree size variables
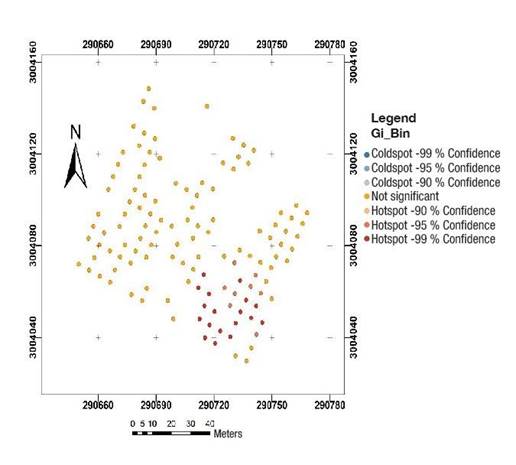
The tree size variables followed a non-random distribution, indicating that the attributes are clustered. According to Figure 2, approximately 25 % of the trees, located in the southeastern section of the orchard, showed statistically significant (P < 0.01) clustering.

Figure 2 Hotspots of the tree size variables of Pinus arizonica: diameter at the base (a), diameter at breast height (b), crown height (c), total height (d), larger crown diameter (e) and smaller crown diameter (f).
Figure 3 shows that cone production also presented a statistically significant (P ≤ 0.01) non-random spatial distribution with clustering. Individual trees with clustered cone production (20.66 %) were distributed in the southeastern section of the orchard, coinciding only partially with the section in which the tree size variables were clustered.
Association between cone production and tree size variables
Pearson's correlation analysis indicated that all tree size variables and the NDWI presented statistically significant (P ≤ 0.05) correlations with cone production (Figure 4). The NDWI revealed differences in moisture levels in some areas of the orchard, specifically in the northern and southern areas, with values from 0.13 to -013. The NDWI has no dimensions and its values range from -1 to 1, depending not only on the water content of the leaf, but also on the vegetation type and cover. In Figure 5, high NDWI values correspond to high vegetation water content, and low values indicate low vegetation water content. In periods of water stress, the NDWI decreases.
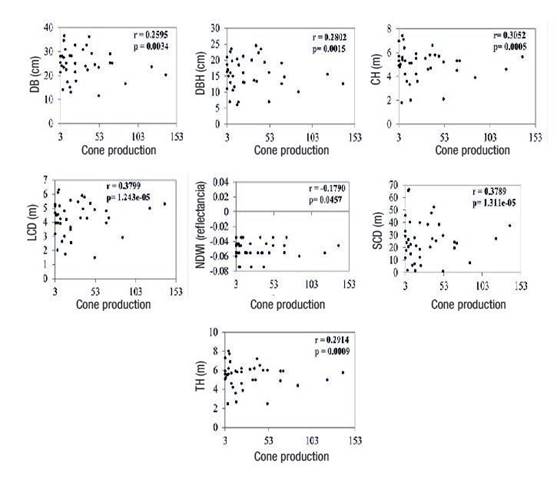
Figure 4 Matrix of the scatter plot between cone production and Pinus arizonica tree size variables (DB: diameter at the base, DBH: diameter at breast height, CH: crown height, LCD: larger crown diameter, NDWI: Normalized difference water index, SCD: smaller crown diameter and TH: total height).
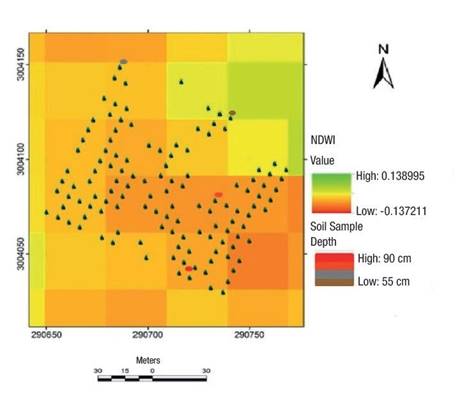
Figure 5 Normalized difference water index (NDWI) of the Pinus arizonica clonal orchard and depth of soil samples from the Papajichi ejido, municipality of Guachochi, Chihuahua, Mexico.
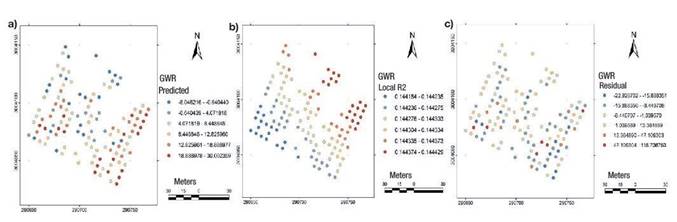
The exploratory regression analysis identified the model that best complied with the goodness of the regression fit as that which integrated the crown diameter variable only. This variable was modeled through GWR and revealed a moderate influence on cone production. The model statistics were mapped in Figure 6.
Discussion
This study reports the spatial pattern of tree size variables, cone production and causal variables of a P. arizonica clonal orchard in Guachochi, Chihuahua. Some studies have modeled tree size variables using spatial analysis (Bozali, Sivrikaya, & Akay, 2015; Corral-Rivas, Wehenkel, Castellanos-Bocaz, Vargas-Larreta, & Diéguez-Aranda, 2010; Elobaid, Shitan, Ibrahim, Ghani, & Daud, 2009; Rubio-Camacho et al., 2017;Silva-Flores, Pérez-Verdín, & Wehenkel, 2014), but this has only been conducted in managed forests to date. Our study is one of the first to use a geospatial approach to better understand a clonal orchard.
Spatial modeling of tree size has been conducted mainly through global autocorrelation models (Aguirre, Hui, von Gadow, & Jiménez, 2003; Elobaid et al., 2009); however, the G statistic can also be used for local spatial analysis, since it allows identification of specific areas where the ecological variables are non-randomly distributed (Rodrigues & de la Riva, 2014). The G statistic has been used in several fields of research, including forest fire studies (Pompa-García & Hernández-González, 2012; Zúñiga-Vásquez, Cisneros-González, Pompa-García, Rodríguez-Trejo, & Pérez-Verdín, 2017), economometrics (Moreno-Serrano & Vayá-Valcarce, 2002), quality of life assessments (Pérez-Valbuena, 2017) and tourism analysis (Lado-Sestayo & Vivel-Búa, 2016).
This work demonstrated the value of the G statistic in terms of understanding the spatial distribution of tree size variables. The use of the G statistic revealed that tree size variables and cone production were both distributed non-randomly with a tendency towards clustering, so special emphasis should be placed on the high clustering or hotspot rates (categories 1, 2 and 3, with reliability percentages of 90, 95 and 99 %, respectively). The spatial pattern of these variables is influenced by one or more physico-environmental and even anthropogenic variables and identification of the clustering pattern is therefore strategic for decision making and consequent analysis, in order to determine the causative variables of the spatial trend. The clustering illustrates the variation in tree size characteristics of individual trees within the orchard.
The local geographically weighted regression model allowed identification of the causes of clustering, specifically in terms of cone production. It should be noted that, under this model, only tree size variables and a moisture index (NDWI) were analyzed, although, according to Viveros-Viveros, Camarillo-Luna, Sáenz-Romero, and Aparicio-Rentería (2013), the clustering of tree size variables is attributable to genetic or environmental factors. In the present study, the use of soil depth data was an indicator of the causes of clustering in the orchard. Coincidentally, the clustering occurred in soils with a depth ≥0.90 m, while there was a lack of clustering in areas where the soil had a depth ≤0.55 m. Similarly, Rodríguez-Laguna, Razo-Zárate, Juárez-Muñoz, Capulín-Grande, and Soto-Gutiérrez (2012) argue that soil type in a particular area influences the clustering of trees with the best phenotypic characteristics and the highest cone and seed production.
Since the grafting of clones in 2005, certain orchard areas have shown high mortality or the absence of individual trees. While determination of the causes of this phenomenon was beyond the scope of this study, this mortality could be attributed to the accumulation of water and the presence of rodents. This finding makes the effective management of the orchard imperative.
While the NDWI values did not contribute significantly to the regression model, the relationship between this variable and cone production was negative (Figure 4). High moisture values were found mainly where there was no clustering of tree size variables (including tree mortality) and spatially coincided with sites of shallower soil depth and thus lower drainage capacity. On the other hand, low moisture values were found in the area of tree size variable cluster grouping and cone production, where the soil was deeper and therefore had better drainage; i.e., excess moisture seems to affect cone production and tree development. This could be explained by water stress in the trees through the effect of excess moisture. Nakai and Kisanuki (2007) state that some tree mortality and growth inhibition are strongly influenced by excess water, specifically by the anaerobic conditions this produces in the soil. This lack of oxygen is related to low root elongation rates, dry mass reduction, and decreased photosynthetic capacity.
In the model of the present study, crown diameter moderately explained cone production. The production also presented clustering, but not in exactly the same area where the tree size variables were clustered. This suggests that cone production does not necessarily coincide with trees that have the best phenotypic characteristics. On the other hand, the results of González-Ávalos et al. (2006) indicate that the increase in the average number of cones per tree is probably caused by increased crown size. This occurs because, as crown size increases, there is a greater number of branches and growth units (bud lengthening sites) in the tree. These authors indicate that, since crown diameter has a greater influence on cone production, the variable is strategic and requires management through pruning and grafting in order to improve cone production in the orchard. In another study, Ávila-Flores and Pompa-García (2008) argue that clones with better phenotypic characteristics should be used for breeding programs because the longevity of the graft carrier helps control the development of propagated vegetative material.
These results establish a basis for future explorations of other causal variables that determine the spatial patterns found. This research will contribute to the design of improved management strategies and can serve as a reference with which to study other seed orchards. In addition, the study clearly shows that the monitoring of seed orchards should not only focus on the genetic material, but also on the dynamics of the tree size and environmental variables of the orchard. For example, the characteristics and conditions of the clonal orchard studied can be compared with those of the El Largo ejido, where cone production has not been documented to date.
Conclusions
The tree size variables of Pinus arizonica, as well as cone production, showed a tendency to cluster, which leads to rejection of the hypothesis of randomness. It was found that crown diameter influences cone production, although in the future some genotypic and environmental variables should be modeled. The use of a geospatial perspective allowed a fuller understanding of the spatial dynamics of the tree size variables in the P. arizonica clonal orchard studied. Geospatial analyses provide an important alternative for generating subsequent knowledge in the management of clonal orchards in Mexico. While these specialized prescriptions are beyond the objectives of this study, management strategies involving experts in the subject are urgently required.





![Modelado espacial histórico y actual del oyamel (Abies religiosa [Kunth] Schltdl. & Cham.) en la Faja Volcánica Transmexicana](/img/pt/next.gif)





 texto em
texto em