Data

The study was carried out at the company named Industria Forestal Tezains (Tezains Forest Industry), property of the San Diego de Tezains ejido, in the municipality of Santiago Papasquiaro, Durango, whose facilities are located in the Western Sierra Madre in northwestern Durango. Its infrastructure includes a sawmill with a main tower and a nationally manufactured HULMAQ^TM resaw (band saw), with a 59.84 inch long flywheel, 8 inch wide, 17 caliber (1.47 mm) band saws, powered by two 100 HP engines, a HULMAQ^TM three-bracket logging carriage with two engines 10 HP one to drive it forward, with 1 425 rpm, and a 7.5 HP one with 1 730 rpm to drive in reverse. This equipment is supplemented with an edger to measure the width (12.70-30.48 cm), a semi- automatic Trimmer and a pendulum to measure the length of the boards. The sawmill has an installed capacity of 120 000 board feet per 8-hour shift; it has 25 workers, and its main product is 7/8”, 5/4”, 6/4” and 2” lumber.

20 logs of each of the following species were analyzed: Pinus durangensis Martínez, P. leiophylla Schltdl. et Cham., P. teocote Schltdl. et Cham. and P. strobiformis Engelm. The sample size was estimated based on the variation in the sawing coefficient, with a 95 % confidence interval of the mean of a pre-sample consisting of 32 logs (eight of each species), using the formula utilized by ^{Barnes (1968)}:

Where:

n = Number of logs.

t = T value for a desired probability level (n-1) degrees of freedom

VC = Variation coefficient (%)

E = Permitted sampling error (%)

The logs had a fixed baseline length of 9.34 m (30 feet) and were selected at random from the pruning areas of the year 2014. Subsequently, logs with lengths of 16, 18 and 20 feet were chosen at the storage yard; certain proportionality in the number of logs per length among the various studied species. Each log was marked with paint in order to differentiate between species and identify these; the diameters without the bark were measured at both ends of the logs.

In order to determine the characteristics of the logs that make it possible to discriminate between the different quality grades of the boards, the following variables were considered: species, mean diameter, length, conicity and quality of the log. The Mexican Norm NMX-C-359-1988 (^{DGN, 1988}) was utilized to classify pine logs, according to the following classification: Mexico 1 = first quality grade; Mexico 2 = second quality grade; Mexico 3 = third quality grade; Mexico 4 = fourth quality grade; Mexico 5 = fifth quality grade. In all cases, the logs must have a minimum diameter of length of 25 cm and 2.44 m, respectively. This classification was utilized because it agrees with the criteria used in the region. Table 1 shows the descriptive statistics of the analyzed logs by species.

Table 1 Descriptive characteristics of the logs analyzed in the study by species. 

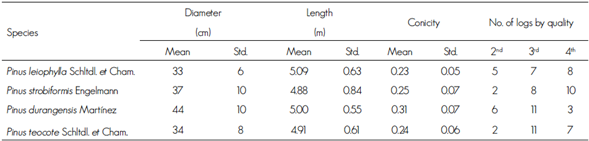
Std= Standard Deviation

Afterward, the logs were debarked and sawn in a sawmill with a main band saw tower and a HULMAQ brand resaw with 1.520 m long flywheels, 20.32 cm wide and 17 caliber (1.47 mm) band saws, powered by 100 HP motors. The sawmill has a log carrier car of three squares, HULMAQ brand with two motors, powered by a one for the advance of 10 HP and 1 425 r.p.m., and for the recoil it uses a 7.5 HP motor and gets 1 730 r.p.m. The trimmer allows to dimension width (12.70 - 30.48 cm), and a semiautomatic Trimmer and a pendulum to do it in the length of the tables.

Once the timber was sawn, it was classified in to the following categories: 2^nd and better, 3^rd, 4^th, 5^th, 6^th and 7^th (short dimensions). However, this work studied only the 2^nd and better, 3^rd, 4^th and 5^th quality grades because these had an apparently appropriate sample size for the statistical analyses (Table 2). This classification corresponds with the categories of the Mexican Norm NMX-C-224-ONNCCE-2001.

Table 2 Volumetric yield by quality grade in percentages and in board feet per m³ of the lumber obtained from four pine species. 

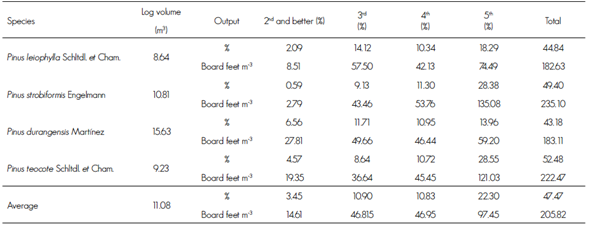
The sawn boards were 7/8”, 5/4”and 6/4” (2.22, 3.18 and 3.81 cm) thick, and broad boards were 3”x 3” and 4”x 4” (7.62 x 7.62 and 10.16 x 10.16 cm) thick. The widths of the timber ranged between 3” and 12” (10.16 a 30.48 cm), and their lengths ranged between 8’ and 20’ (2.4384 to 6.096 m) plus reinforcements. In order to distinguish the classified lumber yielded by each log, a control method based on marking each log with paint was applied. The information was recorded in a control format designed for this purpose.

Methods

The yield of lumber obtained per quality grade was determined based on the ratio of the volume of debarked round wood on the ramp before sawing and the resulting volume of sawn wood (^{Aguilera et al., 2005}; ^{Quirós et al., 2005}; ^{Valério et al., 2007}). The formula used was the following:

Where:

Y = Yield of debarked lumber (%)

Vsc = Volume of sawn boards by quality grade (m³)

Vr = Log volume (m³ roll)

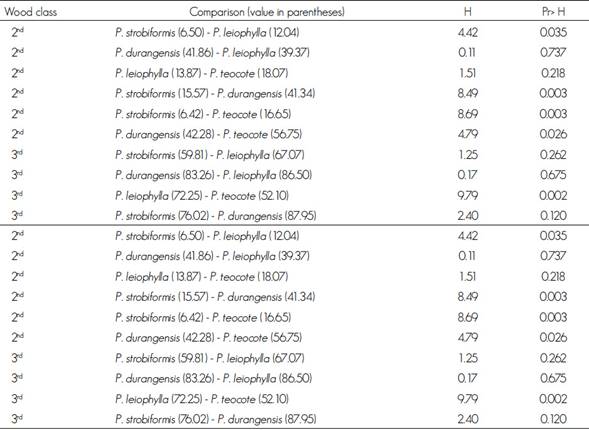
The evaluation of significant differences between species in the yield by lumber quality grade was carried out using the Kruskal-Wallis non-parametric test (^{Kruskal and Wallis, 1952}), as the data were not normally distributed.

In order to identify the characteristics that discriminate between the different classes or quality grades of lumber, a discriminant analysis was carried out, using the DISCRIM procedure of the SAS/STAT system (^{SAS, 2009}). The discriminant analysis allows the disaggregation of sets of data with excluding characteristics in two or more groups (diameter, conicity, and quality of the log, etc.) (^{Khattree and Naik, 2000}). The technique consists essentially in obtaining a classification rule that will maximize the quotient of variance groups in relation to the total of the variance. When the distribution within each group is assumed to be normal multivariate, a parametric method can be used to develop a discriminant function, also known as classification criterion, and it can be determined by means of a generalized squared distance measure (^{Rao, 1973}).

The classification criterion takes into account the probabilities of separation for each group, and can be used as the individual covariance between groups (producing a root mean square function), or as an aggregated covariance matrix (resulting in a linear function). Each observation is carried out for each class, considering the lowest value of the generalized square distance (^{SAS, 2009}).

The discriminant analysis must be performed only when the means of the populations turn out to be statistically different (^{Álvarez et al., 2003}). The MANOVA instruction of the DISCRIM procedure was utilized to carry out the equality of means analysis (^{SAS, 2009}).

The multivariate normality test was carried out using the Mardia’s test for the bias and the kurtosis (^{Khattree and Naik, 1999}), together with the macro %MULTNORM tool of the SAS system ^{(SAS, 2009)}.

The covariance matrix assumption was proved using the plausibility radius; for this purpose, the POOL=TEST instruction of the DISCRIM procedure of SAS/STAT was specified (^{SAS, 2009}).

Since the quality of the adjustment does not necessarily reflect the quality of the prediction, an evaluation of the classification rate of the discriminant function with an independent set of data would be most desirable (^{Myers, 1990}; ^{Wang et al., 2003}; ^{Kozak and Kozak, 2003}). Because these data (an independent sample) are scarce, the cross-validation approach was adopted. This procedure consists in leaving out an observation and building a discriminant rule for the rest of the data -a rule utilized to classify the observation that was left out. This is repeated for each observation, and, finally, the number of erroneously classified observation for each population is counted, and the individual error indices are estimated in the same manner as the respective proportions (^{Khattree and Naik, 2000}).

The performance of the discriminant functions of the data was evaluated using error indices (likelihood of erroneous classification) for the adjustment and the cross-validation with the SAS/STAT procedure (^{SAS, 2009}). The priors utilized were 0.09, 0.23, 0.26 and 0.42 for the lumber quality grades 2, 3, 4 and 5, respectively, according to the production records of the sawmill.

Volumetric yield

The yield of lumber from the four pine species is shown in Table 2. Pinus durangensis had the highest lumber yield of the 2^nd and better grade, with 6.56 % (27.81 board feet per m³), followed by P. teocote, with 4.57 % (19.35 board feet per m³). The mean for the four species was 3.45 % (14.61 board feet per m³). The yield of quality grade 3 boards of P. leiophylla and P. durangensis was 14.12 and 1.71 %, respectively. P. teocote and P. strobiformis had similar volumetric yields in lumber of quality grade 5, with 28.55 and 28.38 %, respectively.

^{Nájera et al. (2011)} assessed the volumetric yield and the dimensional quality of pine wood in five sawmills in El Salto, Durango, Mexico, and obtained averages below those of the present work, with yields of 1.3 % for the 2^nd and better grade and 20.4 % for the 5^th grade.

Another study of pine log sawmills by ^{Zavala and Hernández (2000)} shows an average yield of 12 % for the 2^nd and better grade, 18 % for the 3^rd grade, 12 % for the 4^th grade, and 9 % for the 5^th grade, with an accumulated yield of 51 % of sawn wood. These yields are higher than those of the present research, a difference that may be ascribed to the quality of the logs that were used and to their diameters, which ranged between 30 and 55 cm (85.05 %), and between 25 and 30 cm (3.44 %), while the remaining 1.49 % had diameters of 55 to 70 cm.

The volumetric yield or sawing coefficient of the studied species ranged between 43.18 % and 52.48 %. These sawing coefficients are comparable to those cited by ^{Zavala (1996)} and ^{Zavala (1981)}, in researches on pine log sawmills in Durango (40 to 53 %), and to those observed by ^{Zavala (1987)} in sawmills of Tlaxcala for Pinus spp. (51 to 52 %). However, the estimated sawing coefficients estimated for the four pine species studied were lower than those calculated by ^{Nájera et al. (2012)} for pine logs in two private sawmills located in the El Salto region of Durango (61.64 %). These differences may be attributed, among other factors, to differences in log size (diameter), conicity, or variations in the calibration, the leveling of the flywheels, and the tightening of the band saw, as well as to the expertise of the operator of the main band saw, which has a direct effect on the sawing coefficient.

In this work, a of 20.32 cm (8”) wide, 17 caliber band saw was utilized, whereas the previously mentioned sawmills used a 18.4 cm wide, 16 caliber band saw.

Table 3 shows the results of the Kruskal-Wallis test. Significant differences (P<0.05) were estimated for the volumetric yield by lumber quality grade between 14 of the 25 evaluated species pairs. The analysis indicates that P. durangensis had the highest volumetric yield for the 2^nd and better quality grade; in contrast, P. strobiformis had the lowest volumetric yield.

Table 3 Results of the Kruskal-Wallis test comparing the four evaluated species. 

On the other hand, P. teocote and P. strobiformis are the species with the most significant differences in terms of volumetric yield by sawn wood class in regard to the rest of the studied species (9 and 8 cases, respectively). The low yield registered for P. strobiformis in the 2^nd and better grade (0.59 %) is ascribed to the fact that in the state of Durango this wood is “penalized” due to the reddish graining of its sapwood, which is enough to classify it under the 3^rd, 4^th, and 5^th grade.

The results coincide with those obtained by ^{Erikson et al. (2000)} in aged forests of northern Idaho, where differences in wood quality were found between Pinus contorta Douglas and Pinus ponderosa Douglas ex C. Lawson. More than 65 % of the sawn wood of the former species was rated as 2^nd and better grade or as select, while approximately 50 % of the lumber of the latter species was rated 4^th and 5^th grade. These values are consistent with those obtained by ^{Nocetti et al. (2010)}, who found significant differences between the classes of lumber of six timber-yielding species in Italy. In Mexico, to the date of the present study, no researches assessing the differences in lumber were found between taxa.

Discriminant analysis

The exact value of the F statistic of the Wilks Lambda test to prove the mean equality hypothesis was 7.49 (p value <0.0001); thus, it was assumed that the population means of the wood qualities are statistically different. On the other hand, the Mardia test yielded probabilities for the bias of 0.056, 0.027, 0.032, and 0.13 and for the kurtosis of 0.67, 0.85, 0.58 and 0.82, in the 2^nd, 3^rd, 4^th, and 5^th classes, respectively. Therefore, the hypothesis of mutivariate normality is considered acceptable.

Because the Chi-Square value (25.03) obtained in the equality of covariance matrices test was significant at the level of 0.01 (p value <0.01), the covariance matrices for the four wood qualities were considered to be different within the discriminant function.

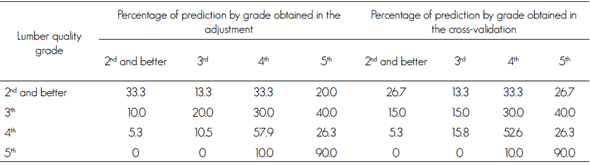
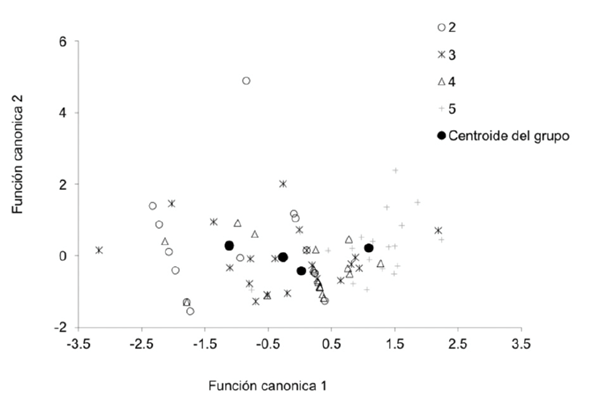
Table 4 shows the values of the discriminant linear function. According to the cross-validation, the discriminant linear function correctly classified 27, 15, 53, and 90 % of the observations as of 2^nd and better, 3^rd, 4^th and 5^th grade, respectively, when the log quality and mean diameter were used as predictive or independent variables. A similar behavior was observed in the results of the adjustment. This suggests that the discriminant function can be utilized to separate the 5^th grade lumber with a very acceptable level of reliability (see aggregation of observations for the 5^th quality grade in Figure 1). In order to classify the remaining lumber quality grades, the model must be either used with caution or avoided altogether, as the precision of the discriminant linear function turned out not to be sufficiently adequate, especially for separating the 2^nd and better grade from the 3^rd grade.

Table 4 Percentage of classified lumber within each grade using the discriminant linear function. 

Figure 1 Graphic classification of the pine boards using the discriminant function. 

Similar results are documented by ^{Zavala and Hernández (2000)}, who registered a direct relationship between log quality and the quality of the sawn wood of six pine species in a sawmill in San Pedro El Alto, Zimatlán, Oaxaca. These results are also consistent with those of ^{Breinig et al. (2015)}, who obtained good adjustments for the classification of certain board quality grades using a discriminant linear function, while major deviations were observed for other grades.

The low reliability of the model for discrimination between these grades may be associated to the low yield of lumber produced by the assessed sample (3 % and 10 %, respectively): the sample size used for these classes may have been insufficient. Therefore, in future researches it is recommended to try the model with a larger board size for these two lumber quality grades. Also, the significant differences observed in the volumetric yield per grade of lumber in the studied species with the Kruskal-Wallis test would indicate the need to use the discriminant function separately for each species (^{Craig et al., 2005}).

Table 5 shows the estimated parameters of the discriminant linear function for the four lumber quality grades.

Table 5 Estimation of the parameters of the discriminant linear functions. 

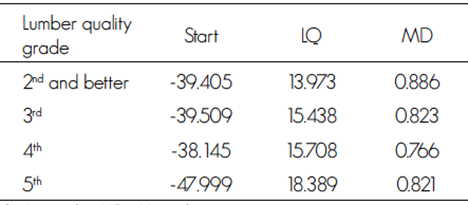
LQ = Log quality; MD = Mean diameter.

The use of the discriminant function for the classification of a board of one of the studied grades is based on the following equation, solved by lumber quality grade:

Where:

D_i = Discrimination percentage estimated for the lumber quality grade of the board

i, X₁ and X₂ = Predictive variables (log quality and mean diameter, respectively)

b_i0 ...b_i1 = Estimated values of the parameters of the discriminant linear function for the lumber quality grade i (Table 4). Each observation is assigned to the group with the máximum D_i value

Figure 1 illustrates a graphic expression of the discriminant function and shows that the average values of the log quality and mean diameter variables can be utilized to classify a new board within one of the four studied lumber quality grades; the discriminant function works well mainly for the 5^th lumber grade.