Artículo

 

Funciones de ahusamiento y volumen comercial para Pinus patula Schltdl. et Cham. en Zacualtipán, Hidalgo

 

Taper and Commercial volume system for Pinus patula Schltdl. et Cham. in Zacualtipán, Hidalgo State

 

Disraeli Hernández Pérez¹, Héctor M. de los Santos Posadas ¹, Gregorio Ángeles Pérez¹, J. René Valdez Lazalde ¹ y Víctor Hugo Volke Haller ²

 

¹Postgrado Forestal, Colegio de Postgraduados. Correo-e hmsantos@colpos.mx

²Postgrado Edafología, Colegio de Postgraduados.

 

Recibido el 24 de noviembre de 2011
Aceptado el 17 de enero de 2013.

 

Resumen

Se presenta un grupo de funciones de ahusamiento y volumen comercial de acuerdo con diversas variables para estimar el diámetro a diferentes alturas del fuste y el volumen total comercial, así como la distribución de productos maderables para Pinus patula, en rodales coetáneos repoblados bajo el sistema de Árboles Padre. Se cosecharon y midieron 78 árboles, en la cubicación se usó el método de trozas traslapadas que permite obtener volúmenes totales y parciales de manera más precisa. La base de datos se utilizó para ajustar 11 sistemas compatibles de ahusamiento-volumen, que incluyeron modelos segmentados. Todos los sistemas se ajustaron mediante la estimación simultánea de parámetros con el método de máxima verosimilitud e información completa que optimiza el ajuste y minimiza los errores de manera conjunta. El sistema segmentado resultó ser el más preciso en el ajuste y explica 97.06 y 98.09% de la variabilidad en el ahusamiento y en el volumen comercial variable, respectivamente. Los puntos de inflexión ocurren a 1.34 y 82.3% de la altura relativa sobre el fuste, lo que sugiere que bajo silvicultura intensiva los fustes son más cilíndricos que en rodales naturales sin manejo intensivo, donde los puntos de inflexión ocurren a 5.7 y 22.4% de altura relativa sobre el fuste.

Palabras clave: Ahusamiento, estimación simultánea, modelos segmentados, Pinus patula Schltdl. et Cham., sistema compatible, volumen comercial.

 

Abstract

A group of taper and commercial volume functions to estimate diameter at different stem heights and total commercial volume, as well as the distribution of timber products for Pinus patula in even-aged regenerated stands under the seed tree method are described in this paper. Seventy eight trees were destructively sampled and measured, and bolt volumes were calculated with the overlapping bolt method which allows to get total and partial volumes in a more accurate way. Data base was used to fit 11 compatible taper-volume systems that included segmented models. All the systems were fitted by the simultaneous estimation of parameters by the with the maximum likelihood and full information method to optimize fitting while simultaneously minimizing the errors in a combined way. The segmented system proposed produced the best fit as it explains 97.06 and 98.09% of the taper and commercial volume variability. The inflection points were estimated at 1.34 and 82.3% of the relative total stem height, which suggests that under intensive forestry, tree stems become more cylindrical than in stands without intensive management, where the inflection points are estimated at 5.7 and 22.4% of relative total stem height.

Key words: Taper, simultaneous estimation, segmented models, Pinus patula Schltdl. et Cham., compatible system, commercial volume.

 

Introducción

En las últimas décadas se han desarrollado diversas ecuaciones para simular el perfil de fuste de los árboles, desde modelos simples de ahusamiento con base en proporciones, hasta estructuras geométricas y trigonométricas que incluyen modelos de tipo polinomial segmentado (Pompa et al., 2009).

La compatibilidad entre funciones de volumen y ahusamiento fue desarrollada por Demaerschalk (1972), con el propósito de que las ecuaciones de ahusamiento compatible, cuando se integren, también sean representaciones realistas de modelos de volumen total y parcial. Cruz et al. (2008) citan que es posible definir un sistema compatible de ahusamiento-volumen a partir de los mismos parámetros y estructura geométrica; esta condición permite distribuir de forma porcentual el volumen por productos y eliminar las discrepancias existentes entre modelos de volumen total y comercial ajustados de manera separada. Si se desea evitar la integración de los modelos de ahusamiento, se pueden ajustar los de volumen comercial (Demaerschalk, 1972; Clutter, 1980; Cao et al., 1980; Cruz et al., 2008). Estas funciones, de forma intrínseca definen una ecuación de ahusamiento, lo que a su vez mediante integración matemática posibilita obtener una ecuación de volumen total compatible (Clutter, 1980; Pompa y Solís, 2008).

Cao et al. (1980) señalan que algunos estudios han mostrado que una ecuación de ahusamiento compleja, como las ecuaciones segmentadas, proporciona una mejor descripción del perfil fustal que una de ahusamiento simple. El ajuste se hace mediante mínimos cuadrados ordinarios (MCO) o como un sistema de ecuaciones simultáneas (Cruz et al., 2008). Si dos ecuaciones son compatibles implica que están relacionadas y, por tanto, los componentes del error están correlacionados; en este caso, el ajuste por MCO producirá estimadores teóricos robustos, pero que ignoran los errores que suceden de manera simultánea a lo largo del fuste entre el ahusamiento y el volumen comercial.

La teoría econométrica ofrece solución a ese problema a través del ajuste, de forma conjunta, del sistema compatible ahusamiento-volumen comercial con ecuaciones aparentemente no correlacionadas y máxima verosimilitud con información completa (SUR y FIML, respectivamente por sus siglas en inglés) donde los estimadores de los parámetros son consistentes, ya que se ajustan de forma simultánea el ahusamiento y volumen acumulado, lo cual representa una ventaja (Borders, 1989; Fang et al., 2000; Cruz et al., 2008).

Por lo tanto, el objetivo del presente trabajo es buscar un sistema compatible de ahusamiento y volumen comercial variable para Pinus patula Schltdl. et Cham., especie que aporta el mayor volumen y valor de la producción maderable en la región de Zacualtipán, Hidalgo (Cruz et al., 2010), en la que no se cuenta con un sistema local de cubicación en pie, que optimice el cálculo de la distribución de los productos del arbolado para el inventario forestal maderable, previo a su aprovechamiento e industrialización.

 

Materiales y Métodos

Área de estudio

La investigación se realizó en rodales coetáneos de Pinus patula que están bajo manejo con el sistema de Árboles Padre en el ejido Atopixco, municipio Zacualtipán, Hidalgo, cuya superficie ejidal es de 1 170.97 ha y se ubica entre las coordenadas 20° 37’ 26" N y 98° 37’ 48" O; y 20° 35’ 20" N y 98° 35’ 23’’O. Su orografía está conformada por pendientes, mesetas y cañones; la altitud media es de 2 100 m; predominio de un clima templado húmedo (C(m)) y templado subhúmedo (C(w₂)), con temperatura media anual entre 12 y 18 °C; la precipitación media anual oscila entre 700 y 2 050 mm (Cruz et al., 2010).

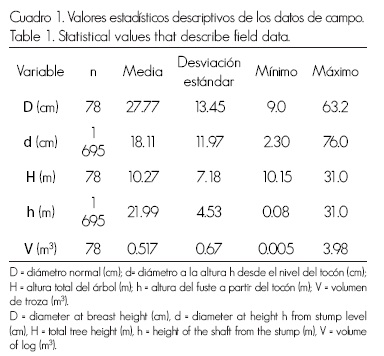
Se obtuvo información de 78 árboles de P. patula dentro de las áreas de aprovechamiento con la técnica de Torres y Magaña (2001) en la que se indica que para mejorar el intervalo de los modelos es necesario captar toda la variabilidad de tamaños y formas posibles del arbolado en una región determinada. La toma de datos se realizó mediante un muestreo destructivo, con ayuda de la cinta métrica los individuos se seccionaron en trozas de un metro de longitud. Las variables registradas fueron diámetro normal, en centímetros (D); altura total, en metros (H); diámetro con corteza a diferentes alturas del fuste, en centímetros (d) y alturas para cada sección con respecto al suelo, en metros (h). Se registró un total de 1 695 pares de diámetro (d) y altura (h). La cubicación de cada muestra se efectuó con el método de trozas traslapadas, que permite estimar volúmenes totales y parciales, en metros cúbicos, (V) más precisos sin considerar el volumen del tocón (Bailey, 1995; Cruz et al., 2008). Los valores medios de las variables en estudio se presentan en el Cuadro 1, además se indican la desviación estándar y los valores mínimos y máximos.

 

Modelos compatibles ahusamiento-volumen

Se analizaron 11 sistemas compatibles de ahusamiento-volumen seleccionados de la bibliografía, mismos que se clasificaron de acuerdo con su función de ahusamiento en modelos compatibles de ahusamiento-volumen y modelos compatibles ahusamiento-volumen segmentados.

El ahusamiento se basa en el supuesto de que la forma del árbol varía a lo largo de su longitud, y el diámetro sobre el fuste es monotónicamente decreciente a medida que la distancia del tocón a la punta comercial se aproxima a la altura total (Lee et al., 2003). Para lograr una verdadera integración que describa de forma simultánea, tanto el perfil completo del árbol como el volumen se necesita un sistema que use los dos componentes: el ahusamiento y el volumen comercial variable, dada la estrecha relación de estos (Pompa et al., 2009).

 

Modelos segmentados

Gallant y Fuller (1973) señalan que un modelo segmentado es uno de regresión que consiste en submodelos injertados; este sistema usa ecuaciones diferentes para distintas partes del fuste e integra tales modelos de forma que sus primeras derivadas son iguales en el punto de intersección (Torres y Magaña, 2001). Husch et al. ( 1982) citan en su trabajo estas funciones y asumen que el fuste de un árbol puede dividirse en tres formas geométricas básicas: cono, paraboloide y neiloide. Algunos modelos como los introducidos por Max y Burkhart (1976) son de ese tipo, en un intento por dar una mejor descripción del perfil del árbol mediante una función de ahusamiento. Otros autores como Parresol (1987) y Fang et al. (2000) han usado esta variante con éxito y sus estructuras se analizan con los datos de campo del presente trabajo.

Las expresiones usadas cumplen con la condición de que h = H cuando d = 0, por lo cual pueden emplearse para predecir diámetros (d) a cualquier altura sobre el fuste del árbol (h). Los sistemas evaluados (Cuadro 2) son: Lenhart y Cutter (1971); Clutter (1980); sistema compatible Cielito I, modificado por Cruz et al. (2008); Diéguez et al. (2006) plasman en su estudio para Pinus silvestris L., los siguientes modelos, que también se analizaron: Kozak et al. (1969); Demaerschalk (1972); Fang y Bailey (1999), con excepción del caso I-b (función compatible de ahusamiento-volumen); debido a que los datos no se ajustaron conforme a la expresión; dentro de los sistemas compatibles segmentados están los de Max y Burkhart (1976); Parresol (1987) y Fang et al. (2000).

Hacer clic para agrandar

Ajuste de los modelos

Si bien en algunos de los sistemas compatibles analizados no se tiene documentado uno de volumen comercial variable, existe un modelo de volumen total cuya estructura matemática es la de uno de forma constante V=αD²H (Kozak et al., 1969; Demaerschalk, 1972; Max y Burkhart 1976; Parresol, 1987), excepto el modelo de Cruz et al. (2008), el cual es de la forma V=αD^δH. Con base en lo anterior se analizaron las ecuaciones y se determinó que los sistemas de ahusamiento propuestos por Kozak et al. (1969); Demaerschalk (1972) y Parresol (1987) generan expresiones de volumen comercial variable (Cuadro 2), que pueden ser utilizadas en conjunto con el ahusamiento en un ajuste de tipo simultáneo. Brooks et al. (2008) registran la ecuación de volumen comercial compatible para el modelo clásico de Max y Burkhart (1976). Para el caso de los sistemas con modelo de volumen total implícito: Lenhart y Clutter (1971); Clutter (1980); Fang y Bailey(1999) ; y Fang et al. 2000 se escaló el parámetro α₀(para aumentar el tamaño absoluto del parámetro estadístico a evaluar) en el modelo de volumen total de Schumacher y Hall, con la función exponencial; esto ayudó a mejorar la estimación y, en consecuencia, a obtener de forma rápida la convergencia del sistema, además de mejorar la significancia de los estimadores.

Para evitar problemas en la estimación de los parámetros, en especial, cuando h = H; es decir, d = 0 se aplicó un valor pequeño en este punto (delta = 0.0001), junto con una variable indicadora en la punta del árbol para evitar que se evaluaran en cero las derivadas parciales de los parámetros que contienen el logaritmo de cero, y que producen datos perdidos y problemas de convergencia; enfoque que fue empleado por Fang et al.(2000) , y que le permitió el uso de todos los datos.

La estimación de los sistemas compatibles se realizó con la técnica de máxima verosimilitud con información completa (FIML, por sus siglas en inglés), la cual es apropiada para el ajuste simultáneo (SAS Institute, 2004). En el desarrollo de los modelos de regresión, el procedimiento asume que el error es independiente y que se distribuye de manera normal con varianza y media igual a cero (Gujarati, 2004); sin embargo, durante la estimación surgen problemas estadísticos que violan los supuestos básicos de regresión; sobre todo la heterocedasticidad, la autocorrelación y la colinealidad, inconvenientes importantes de los modelos de volumen (Kozak, 1997; Pompa et al., 2009), ya que los parámetros se vuelven ineficientes; no hay garantía que sus errores estándar sean mínimos, aunque los parámetros estimados siguen siendo insesgados por haberse ajustado por mínimos cuadrados.

Los criterios para calificar la bondad de ajuste de los modelos se basan en un análisis numérico y de gráficos de los residuales. En el caso numérico se utilizaron tres estadísticos de uso frecuente en biometría: coeficiente de determinación ajustado (R²_adj), la raíz del cuadrado medio del error (RCME) y, el coeficiente de variación (CV) (Prodan et al., 1997; Castedo y Álvarez, 2000; Diéguez et al., 2003; Corral et al., 2007):

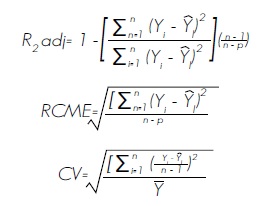
Donde:

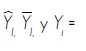= Valor predicho, media de la variable dependiente y valor observado respectivamente

n = Número de observaciones

p = Número de parámetros del modelo.

También se analizaron las gráficas de residuales contra los valores predichos de la variable dependiente, con la finalidad de detectar valores atípicos o tendencias inusuales de los datos. Esto es útil para determinar si los ajustes se adecuan a los datos o se presenta alguna falta de ajuste al sistema empleado.

 

Resultados y Discusión

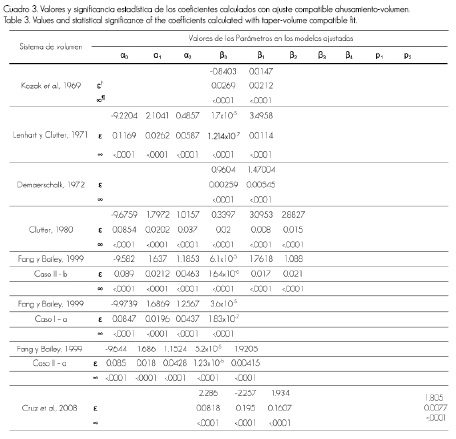
De los sistemas empleados, la función de ahusamiento, en algunos casos, se ajusta a los diámetros y en otros a los diámetros relativos (d/D); por lo tanto, se decidió ajustar todos los modelos como funciones directas del primer diámetro sobre el fuste, a fin de que los estadísticos del ajuste total (R²_adj RCME, CV) para esta variable fueran comparables entre modelos. El ajuste general de los sistemas, bajo la estimación simultánea, a partir de máxima verosimilitud con información completa (FIML) optimiza la predicción de los parámetros de ahusamiento y volumen comercial, además de ser significativos, minimiza los errores de manera conjunta (Cuadro 3). En contraste, cuando se realiza el ajuste de forma independiente, bajo mínimos cuadrados ordinarios (MCO), algunos parámetros presentan un a>005 errores estándar más elevados, aun cuando se escale un parámetro dentro de la función (a₀). Lo anterior coincide con Borders (1989) y Fang et al. (2000), quienes señalan que el ajuste con FIML homogeniza y minimiza el error estándar de los parámetros y permite la compatibilidad total del sistema de ahusamiento y volumen comercial.

Hacer clic para agrandar

Si bien, en algunos modelos como el de volumen comercial de Fang et al. (2000) existe colinealidad en sus parámetros, el cual provoca que algunos de ellos no sean estimables con facilidad, lo que se puede evitar al realizar el ajuste simultáneo del sistema segmentado. De igual forma, con el de Max y Burkhart (1976) la solución implementada a que se llegó fue la de asignar al coeficiente p₂ un valor de 15 para lograr convergencia del sistema compatible, valor que se obtuvo, en parte, de lo registrado en la bibliografía, donde se hace referencia a un intervalo de 1.5 a 2; según datos de Max y Burkhart (1976) en su trabajo para bosques naturales de pino en la costa de Virginia, y más reciente un estudio desarrollado en Turquía, que lo aborda como un sistema compatible de ahusamiento-volumen comercial segmentado para tres especies (Brooks et al., 2008).

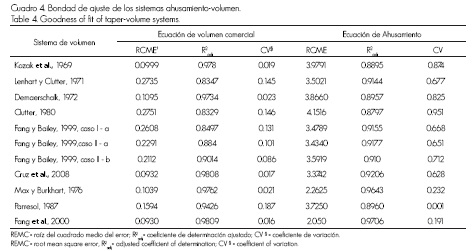
En el Cuadro 4 se muestran los criterios estadísticos de ajuste para la selección del sistema que mejor explica la variabilidad de los datos de ahusamiento y volumen. Primero se seleccionaron los modelos que mejor ajustaban con base en su mayor coeficiente de determinación (R²_adj), RCME más bajo y, finalmente, un bajo coeficiente de variación (CV), con respecto a la media de la variable dependiente.

Hacer clic para agrandar

En primer orden, el sistema que cumple con los criterios de selección fue el segmentado de Fang et al. (2000), seguido del propuesto por Max y Burkhart (1976), también segmentado. La característica de ambos implica que tienen dos puntos de inflexión sobre la altura relativa del fuste. De los no segmentados, el Cielito I modificado por Cruz et al. (2008) resultó ser el más promisorio.

Los puntos de inflexión para el primer sistema (Fang et al., 2000) ocurren a 1.34% de la altura del árbol cerca de la base, y a 82.3% de la altura relativa sobre el fuste. Para el segundo de Max y Burkhart (1976), los segmentos se presentan a 10.7 y 88.3% de altura relativa. No obstante, es necesario comentar que tanto para el modelo de Fang et al. (2000) como para el de Max y Burkhart (1976), contrastados con trabajos anteriores, los puntos de inflexión no se relacionan; por ejemplo, Diéguez et al. (2006) para Pinus sylvestris L., en el noreste de España determinaron segmentos a 10.3 y 60.7% para el sistema de Fang et al. (2000) en la altura relativa del fuste y para el de Max y Burkhart (1976) a 14 y 70% de altura relativa. En el caso particular del trabajo que se documenta el segundo punto de inflexión se calculó por arriba 80% de proporción de h/H. Lo anterior sugiere que tal vez un modelo segmentado con un solo punto de inflexión es más adecuado para modelar a Pinus patula. Si se toma en cuenta que los datos del estudio corresponden a individuos provenientes de un bosque natural manejado de forma intensiva y de rápido crecimiento, se aprecia que tiende a tener un factor de forma constante a lo largo del fuste comercial y, por tanto, a ser cilindrico entre los puntos de inflexión estimados.

A fin de contrastar los resultados, se ajustó el modelo de Fang et al. (2000) a una base de datos integrada a partir de 91 árboles de Pinus patula con 1 039 pares de volumen comercial-ahusamiento obtenidos en rodales naturales recién abiertos al aprovechamiento en la Sierra de Juárez en Oaxaca. Bajo el mismo procedimiento los puntos de inflexión se localizan a 5.7% y 22.4% de altura relativa sobre el fuste, por lo que gran parte del volumen se concentra en una sección de estructura cónica, mientras que solo 16% en una estructura cilindrica.

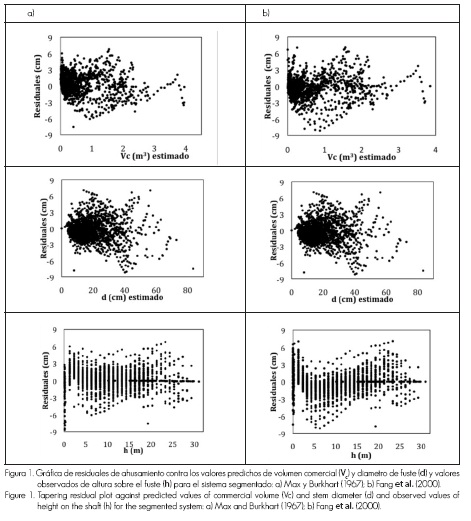
Aunque los estadísticos y sus indicadores son elementos esenciales para calificar la bondad de ajuste de un modelo, el análisis de los residuos es otro de criterio para decidir con mayor precisión cuál de ambos sistemas representa mejor la realidad que se busca modelar y, finalmente, servir como criterio para recomendar alguno de ellos. La tendencia que muestran los residuos del ahusamiento (Figura 1) frente a los valores predichos expone la presencia de cierto nivel de heterocedasticidad y autocorrelación; sin embargo, se decidió no corregir esta aparente violación a los supuestos básicos de regresión, a partir del nivel de ajuste total del sistema compatible (alta R²_adj y coeficientes de regresión altamente significativos). Además, la investigación se efectuó para una sola especie con el enfoque de estimación del volumen comercial, y por la estructura matemática del sistema seleccionado pudiera no representar un problema grave sobre todo al comparar un modelo en su capacidad de predicción, la cual es su principal utilidad (Gujarati, 2004).

Hacer clic para agrandar

Al corregir por autocorrelación y heterocedasticidad se busca mejorar la interpretación de las propiedades estadísticas de un modelo; por lo tanto, al aplicar la estimación de parámetros con presencia de esta violación, de manera práctica no varían de forma exagerada en la predicción del ahusamiento y el volumen comercial. Diéguez et al. (2006) en un trabajo para Pinus sylvestris, corrigieron el problema mediante el uso en los errores de una estructura auto regresiva de segundo orden, y los valores absolutos de los parámetros no difirieron de manera notable al ajuste sin corrección por autocorrelación

 

Conclusiones

De los 11 sistemas compatibles de ahusamiento-volumen comercial explorados, el de Fang et al. (2000) fue el mejor bajo la técnica de ajuste FIML, pues expresa solidez estadística para predecir los volúmenes y diámetros de Pinus patula. En primer término, es consistente en la estimación de volumen comercial y ahusamiento a lo largo del fuste de cada árbol, además de presentar alta significancia en los valores estimados como otra aportación importante en su compatibilidad. En consecuencia, permite estimar de forma directa el diámetro a cualquier altura y viceversa; asimismo referir el volumen a una altura dada, o a un diámetro conocido.

Con los sistemas ilustrados se da la opción de que los manejadores de los bosques coetáneos de la región cuenten con una herramienta más eficiente para el cálculo de la distribución de productos maderables para determinar el valor y uso adecuado de la materia prima de los bosques bajo aprovechamiento. Al contrastar la forma del fuste es evidente que el régimen de manejo afecta la distribución de productos y esta es altamente dependiente de la localidad y de la silvicultura implementada.

 

Referencias

Bailey, R. L. 1995. Upper-stem volumes from stem-analysis data: an overlapping bolts method. Can. J. For. Res. 25: 170-173.         [ Links ]

Borders, B. E. 1989. Systems of equations in forest stand modeling. For. Sci. 35: 548-556.         [ Links ]

Brooks R. J., L. Jiang and R. Ozgelik. 2008. Compatible stem volume and taper ecuations for Brutian pine, Cedar of Lebanon, and Cilicica fir in Turkey. Forest Ecology and Management 256: 147-151.         [ Links ]

Cao O., V., H. Burkhart and T. Max. 1980. Evaluation of two methods for cubic-volume prediction for loblolly pine to any merchantable limit. For. Sci. 26: 71- 80.         [ Links ]

Castedo D., F. y G. Álvarez J. 2000. Construcción de una tarifa de cubicación con clasificación de productos para Pinus radiata D. Don, en Galicia basado en una función de perfil del tronco. Invest. Agrar. Recur. For. 9: 253 - 268.         [ Links ]

Clutter, J. L. 1980. Development of taper functions from variable-top merchantable volume equations. For. Sci. 26: 117-120.         [ Links ]

Corral R., J. J., M. Bario A., A. O. Aguirre C. and U. Diéguez A. 2007. Use of stump diameter to estimate diameter at breast height and tree volume for major pine species in El Salto, Durango (México). Forestry 80: 29-40.         [ Links ]

Cruz C., F., H. M. De los Santos P. y J. R. Valdez L. 2008. Sistema compatible de ahusamiento-volumen para Pinuscooperi Blanco en Durango, México. Agrociencia 42: 473-485.         [ Links ]

Cruz L., I. A., J. R. Valdez L., G. Ángeles P. y H. M. de los Santos P. 2010. Modelación espacial de área basal y volumen de madera en bosques manejados de Pinus patula y P. teocote en el ejido Atopixco, Hidalgo. Madera y Bosque 16: 75-97.         [ Links ]

Demaerschalk, J. P. 1972. Converting volume equations to compatible taper equations. For. Sci. 18: 241-245.         [ Links ]

Diéguez A., U., M. Barrio A., F. Castedo D. y M. Balboa M. 2003. Estimación del diámetro normal y del volumen del tronco a partir de las dimensiones del tocón para seis especies forestales comerciales de Galicia. Invest. Agrar. Sist. Recur. For. 12: 131-139.         [ Links ]

Diéguez A., U., F. Castedo D., J. G. Álvarez G. y A. Rojo. 2006. Compatible taper function for Scotts pine plantations in northwestern Spain. Can. J. For. Res. 36: 1190-1205.         [ Links ]

Fang, Z. and R. L. Bailey. 1999. Compatible volume and taper models with coefficients for tropical species on Hainan Island in Southern China. For. Sci. 45: 85-100.         [ Links ]

Fang, Z., B. E. Borders and R. L. Bailey. 2000. Compatible volume-taper models for loblolly and slash pine based on a system with segmented-stem form factors. For. Sci. 46: 1-12.         [ Links ]

Gallant, A. R. and W. A. Fuller. 1973. Fitting segmented polynomial regression models whose join points have to be estimated. Journal of the American Statistical Association 68:144-147.         [ Links ]

Gujarati, N. D. 2004. Violación de los supuestos del modelo clásico. Traducción al español de Garmendia G., D., Arango M. G. y M. Misas A. In: McGraw Hill Interamericana de México (ed.).Econometría. México, D.F. México. pp. 327-538.         [ Links ]

Husch, B., C. I. Miller and T. W. Beers. 1982. Forest mensuration. 3^rd. ed. Krieger Publishing Company. Malabar, FL USA. 402 p.         [ Links ]

Kozak, A., D. Munro and J. Smith. 1969. Taper functions and their application in forest inventory. For. Chron. 45: 278-283.         [ Links ]

Kozak, A. 1997. Effects of multicollinearity and autocorrelation on the variable-exponent taper functions. Can. J. For. Res. 27: 619-629.         [ Links ]

Lee, W. K., J. H. Seo, M. Y. Son, K. H. Lee and K. Gadow. 2003. Modeling stem profiles for Pinus densiflora in Korea. Forest Ecology and Management. 172: 69-77.         [ Links ]

Lenhart, J. P. and J. L. Clutter. 1971. Cubic-foot yield tables for old-field loblolly pine plantations in the Georgia Piedmont. Ga. For. Res. Council Rep. 22: 12.         [ Links ]

Max, T. A. and H. E. Burkhart. 1976. Segmented polynomial regression applied to taper equations. For. Sci. 22: 283-289.         [ Links ]

Parresol, B. R., J. E. Hotvedt and O. V. Cao. 1987. A volume and taper prediction system for bald cypress. Can. J. For. Res. 17: 250-259.         [ Links ]

Pompa G., M., J. J. Corral R., M. A. Díaz V. y M. Martínez S. 2009. Función de ahusamiento y volumen compatible para Pinus arizonica Engelm. en el suroeste de Chihuahua. Rev. Cien. For. en Méx. 34: 119-136.         [ Links ]

Pompa G., M. y R. Solís M. 2008. Ecuación de volumen para el género Quercus en la región noroeste de Chihuahua, México. Revista de Ciencias Forestales.16: 84-93.         [ Links ]

Prodan, M., R. Peters, F. Cox and P. Real. 1997. Mensura forestal. Instituto Interamericano de Cooperación para la Agricultura (IICA), Costa Rica. 561 p.         [ Links ]

SAS Institute Inc. 2004. SAS/C Online Doc™, Release 7.50. Cary, NC. USA s/p.         [ Links ]

Torres R., J. M. y O. S. Magaña T. 2001. Evaluación de plantaciones forestales. Ed. Limusa. México, D. F. México. 472 p.         [ Links ]