Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Revista mexicana de ciencias pecuarias
versión On-line ISSN 2448-6698versión impresa ISSN 2007-1124
Rev. mex. de cienc. pecuarias vol.7 no.1 Mérida ene./mar. 2016
Articles
Genetic analysis of productive life in Holstein cattle in Mexico
a Facultad de Medicina Veterinaria y Zootecnia de la Universidad Veracruzana. Miguel Ángel de Quevedo s/n esq. Yáñez Col. Unidad Veracruzana, 91710 Veracruz, Ver. México.
b Centro Nacional de Investigación Disciplinaria en Fisiología y Mejoramiento Animal, INIFAP. México.
c Centro de Investigación Regional Golfo Centro, INIFAP. México.
d Universidad Nacional Autónoma de México. México.
Methodology survival analysis model with Weibull proportional hazards was used to study Holstein cattle duration of functional productive life (FPL) in Mexico, using a model sire-maternal grandsire with Survival Kit V3.12 software. The FPL was calculated as the number of days between the date of first calving and the date of culling or censored, with a maximum credit of 305 d per lactation. The FPL was defined as the length of time between first calving and date of culling or death and a maximum of 305 d lactation. The data analyzed were obtained from the Holstein Association of Mexico. The final file consisted of 36,507 records for FPL of cows that calved for the first time between 1995 and 2008. The model included baseline hazard function of Weibull and the following fixed effects: age at first calving, lactation number by stage of lactation with cuts 29, 249 y 305 and standardized production level, with 10 classes with changes in each lactation period included as dependent variables and random effects of herd-year of calving and genetic effects of sire and maternal grandsire. Percentage of censored data was 25.54 %. All analyzed fixed effects were significant (P<0.0001) and had a significant risk of animal culling influence. The heritability calculated logarithmic, original, effective and equivalent scales were 0.08, 0.13, 0.12 and 0.10 respectively, indicating that this character can effectively integrate breeding programs as has been done in other locations of Holstein cattle.
Keywords: Survival analysis; Weibull model; Variable time dependent; Heritability
Se usó la metodología de análisis de supervivencia con un modelo de riesgos proporcionales de Weibull para estudiar la duración de vida productiva funcional (DVPF) de ganado Holstein en México, usando un modelo padre-abuelo materno con el software Survival Kit V3.12. La DVPF se calculó como el número de días entre la fecha de primer parto y la fecha de desecho o censura, con un crédito máximo de 305 días por lactación. Los datos analizados se obtuvieron de la Asociación Holstein de México. El archivo final constó de 36,507 registros para DVPF de vacas que parieron por primera vez entre 1995 y 2008. El modelo incluyó la función de riesgo basal de Weibull y los siguientes efectos fijos: edad al primer parto, número de lactación por fase de lactación con cortes en los días 29, 249 y 305 y nivel de producción estandarizado con 10 clases con cambios en cada lactación, incluidas como variables tiempo dependientes y los efectos aleatorios de hato-año de parto y efectos genéticos de padre y abuelo materno. El porcentaje de censura fue de 25.54 %. Todos los efectos fijos analizados fueron significativos (P <0.0001) y tuvieron una influencia importante en el riesgo de desecho de los animales. Las heredabilidades calculadas en escalas logarítmica, original, efectiva y equivalente resultaron de 0.08, 0.13, 0.12 y 0.10 respectivamente, indicando que este carácter se puede integrar efectivamente a los programas de mejoramiento genético como se ha hecho en otras poblaciones de ganado Holstein.
Palabras clave: Análisis de supervivencia; Modelo de Weibull; Variable tiempo dependiente; Heredabilidades
Introduction
Longevity in dairy cows can be measured as the time from first parturition to animal cull or death, an interval called productive life (PL). In a producing dairy cow, PL is influenced by production level, fertility, health, etc. Of particular interest is involuntary culling, that is, for reasons beyond the control of the farmer (e.g. disease or reproductive problems). This process is known as functional productive life (FPL) when it includes cow production level in the model in an effort to correct for voluntary culling1,2.
The study of FPL using survival analysis techniques allows incorporation of time-dependent covariables, use of incomplete (censured) records, analysis of large data bases and application of mixed models that permit national level genetic evaluations. However, the way these evaluations are done and the models used to do so, can vary depending on circumstances3,4,5.
Previous studies using data from Mexico have analyzed the effect of milk production level on PL either based on a Kaplan-Meier estimator and a Weibull regression model6, or using mixed linear models and treating longevity as the ability to remain in the herd at 48 mo of age with a PL extending to the third lactation7. No studies have been done, however, addressing the use of survival analysis in predicting genetic values in a Holstein population in Mexico under milk recording. Genetic values are needed to develop effective genetic improvement systems for this trait on artificial insemination bulls used in Mexico. This trait is vital to genetic improvement of dairy cows for reasons of economy (e.g. production system sustainability) and animal health (improved PL reduces risk of disease)6,7.
The present study objectives were to estimate heritabilities and predict genetic values for FPL by applying a proportional risk model with a Weibull distribution in a Holstein population in Mexico.
Material and methods
Data was for Holstein cows with first parturition between 1995 and 2008, and was provided by the Mexican Holstein Association (Asociación Holstein de México) from official milk recording and genealogical records. Productive life (PL) was calculated as the number of days between date of first parturition and date of culling or censure. Maximum credit for lactation was 305 d and censured animals were defined as records of cows sold to other farms for production, of live cows in a herd when its production stopped being recorded, or of cows with non-consecutive lactations. For greater accuracy, and to ensure model convergence, lactations were eliminated for any one of four reasons: 1) Abnormal standardized milk production, i.e. <2,500 kg (1st percentile) or >17,000 kg (99th percentile); 2) No data for first lactation; 3) First lactation at <17 mo of age; and 4) Daughters of sires with less than five daughters. The final database consisted of 36,507 PL records.
Parameter estimations and genetic value predictions were calculated with the Survival Kit ver. 3.12 program8,9. A sire-maternal grandsire proportional risk model was used in which a Weibull distribution was assumed for the basic risk function. The FPL analysis model was:
In this model, h(t) represents a cow elimination risk in time t. The basic risk function is λρ(λt)ρ-1, where ρ is the distribution shape parameter and λ corresponds to the distribution scale parameter. HYj (t) is the random effect of the j-th herd-year of first parturition. This had a log-gamma function associated with parameter γ, included to acknowledge that animal elimination is a decision made by comparing animals within similar or contemporaneous groups, the effect of which is not explained in this study8. APk (t) is the k-th effect of age at first parturition in months, divided into four categories (1, ≤23 mo; 2, 24-25 mo; 3, 26-27 mo; and 4, ≥28 mo). LPlm (t) is the time-dependent effect of the l-th lactation phase divided into three times (1-29, 30-249 and 250-305 d after parturition), within the m-th lactation (i.e. 1, 2, 3 and ≥4), assuming that risk does not change within each segment. MPLn (t) is the effect of the n-th milk production level within herd-year of first parturition; production levels were calculated by organizing production records in ascending order to generate the mean and standard deviation. Finally, deciles were calculated based on normal milk production to represent production level per lactation, divided into ten categories, 1 being the lowest and 10 the highest. Sire (S q ) and maternal grandsire (S mg ) were random ancestor effects and were grouped into one vector (S) for analysis, assuming that they followed a normal multivariate distribution with Aσ2s as the variance - covariance matrix.
Heritabilities were calculated on a logarithmic scale (h2log)4,9, that is, the transformation of time (T) in a logarithmic scale, and in the original scale (h2o), following Ducrocq10 as described in Chirinos et al4:
Where: Ψ1 γh, is the trigamma function evaluated in γh ; var(s) is sire’s variance; and π26 is the extreme value distribution’s variance.
Where: υ is the negative Euler number; ρ is the shape of the basic risk function; and h2log is the heritability on a logarithmic scale.
To confirm that the original scale heritability expression depended on the Weibull distribution estimators as reported elsewhere4,10, effective and equivalent heritability were calculated as follows:
Where ρ is the proportion of complete records, which is applied in the present study.
The reliability of the predicted genetic values for sires was calculated based on records of their daughters10:
Where: R is the genetic value reliability of sires; N is the number of daughters with recorded FPL; and h2e is the equivalent heritability.
Model effects were tested with a partial likelihood ratio test, and estimation was done using the maximum likelihood method8.
Results
In the total sample of 36,507 FPL records, censoring rate was 25.5 %, cows had an average of 2.23 lactations, average time to cull/death was 615 d and average time to censoring was 731 d. The data included the daughters of 1,116 sires and 1,684 maternal grandsires.
In terms of relative risk (average risk= 1) under the influence of environmental and genetic effects, the youngest cows (categ. 1, ≤23 mo) had a greater culling risk than the cows in lactation categories 2, 3 and ≥4. Age at first parturition apparently had no effect on FPL (Table 1, Figure 1).
Table 1 Proportion (%) and number (N) of observations by phase within lactation categories and phases
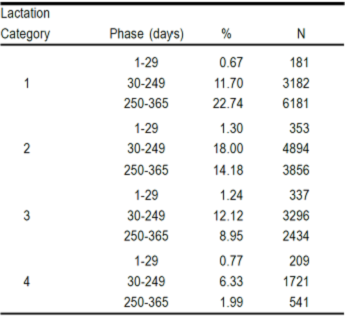
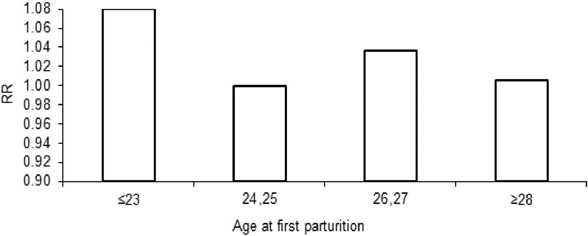
Figure 1 Relative culling risk (RR) in four categories of age (in months) at first parturition for Holstein cattle in Mexico.
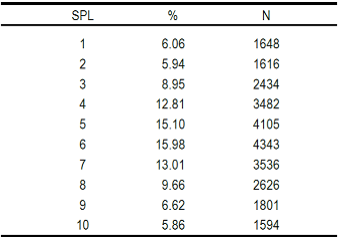
Standardized production level (SPL) data showed the cows in the lowest levels as more likely to be culled than a cow with an average SPL (categ. 6); this was 49 times more probable in SPL 1, 5 times greater in SPL 2 and twice as likely in SPL 3 (Table 2, Figure 2). Risk diminished in levels 7, 8 and 9, and then increased in level 10, the most productive animals.
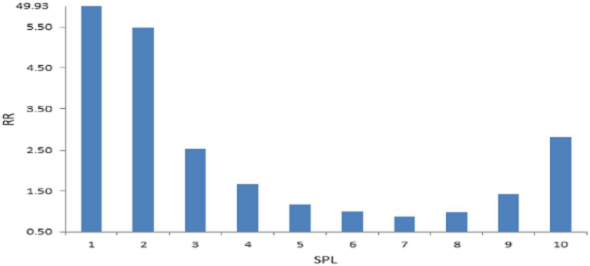
Figure 2 Relative culling risk (RR) in ten standardized production levels (SPL); 1 is lowest production level and 10 is highest.
In cows with consecutive lactations, relative risk of discard tended to increase concurrently with milking days and lactation number, reaching a maximum of 305 d after parturition (Figure 3). The culling rate was particularly intense during the third lactation phase (LP; 250-305 d).
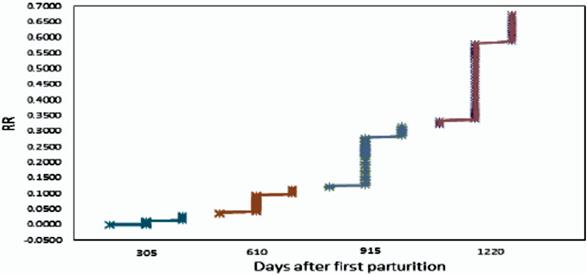
Figure 3 Relative culling risk (RR) in cows with consecutive lactations (1, 2, 3 and ≤4); each lactation is divided into three phases (0-29, 30-249 and 250-305 d).
The estimators for the predicted genetic values varied from -0.68 to 1.62, with a mean of zero. Relative risk of culling for FPL in the daughters of the studied sires ranged from 0.51 to 5.03. Negative genetic values indicated a low cull risk for the daughters of a sire and consequently higher FPL. Among the 2,800 analyzed sires, genetic value reliability varied from 0 to 0.95, with 179 sires having a level ≥0.50 (Figure 4).
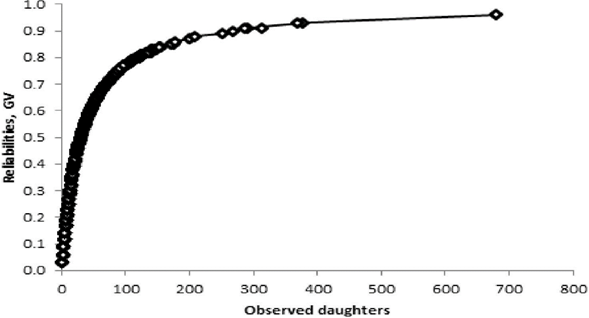
Figure 4 Genetic value (GV) reliabilities for studied sires based on number of daughters with complete records.
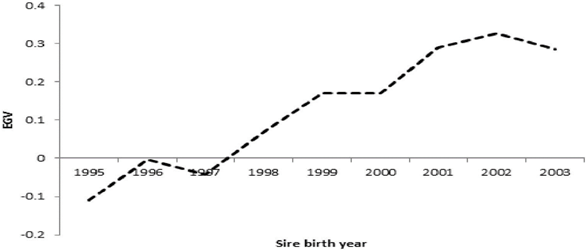
Genetic tendencies for FPL of the studied Mexican Holstein sires by birth year showed increasing risk from 1997 to 2003, followed by a slight decrease in 2003 (Figure 5).
Discussion
Lactations per PL was low on average in the present data, suggesting that the cows had not yet expressed their maximum productive potential11,12,13. This implies that they were discarded shortly after completing two lactations, which coincides with previous reports14-17.
The 25.5 % censoring rate in the records due to incomplete data is within the 9.4 to 73.4 % range reported in other studies using the same methodology in Holstein populations3,4,5.
All the effects analyzed in the model were significant (P<0.0001), although SPL and LP made the greatest contribution to calculating culling risk. Age at first parturition made a lesser contribution. In other studies, this effect has not demonstrated a clear tendency to explain relative culling risk4,11. However, in the present data, it did show a slight increase in cows with first parturition at ≤23 mo. This may be due to the fact that this group includes cows that gave birth at young ages because they were pregnant before 14 mo of age, as well as those that did not complete the full 9 mo of their first gestation, which can cause problems in later parturitions. In older age categories, age at first parturition had no apparent effect on FPL, as has been reported for other Holstein populations4,8.
Relative culling risk associated with standardized production levels (SPL) showed the lowest levels (1, 2 and 3) to have the highest risk. Voluntary culling in response to low SPL is clearly significant in this population. Previous studies done with data from the same population and other Holstein populations also documented greater culling risk in less productive animals4,11. Risk also increased slightly beginning at SPL 8, suggesting that high producing cows experience more intense physiological stress than lower producers, which can affect their FPL8,9.
Culling risk also increased in the final days of a lactation in cows with consecutive lactations. This reflects elimination of non-gestating cows at the end of lactation, possibly due to reproductive or health problems16,17. These tendencies coincide with previous studies reporting increased culling rates at the end of each lactation. The way LP is defined can influence these results since the first LP level will always be more homogeneous than the last ones. At later LP levels, age effects begin to accumulate but this are not included in calculation of the PL by days in lactation beyond 305 d, nor in inter-parturition periods, which are not part of this methodology.
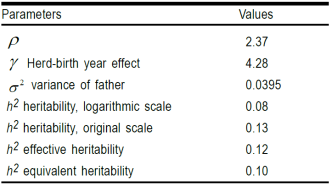
The estimated parameter was 2.37, a value within the 0.36 to 5.0 reported for other Holstein populations4,9,10. This value supports the recorded data since values greater than 1 indicate increased culling risk as animals age. The gamma parameter represents the variance within herd-year. Values greater than 1 indicate heterogeneity in culling practices8. The 4.28 gamma value in the present study is similar to those reported in other Holstein populations3,4,13. Variation in culling practices may be related to varying levels of mechanization throughout Mexico, an aspect requiring further research.
Heritabilities in this study were 0.08 in the logarithmic scale, 0.13 in the original scale, 0.12 in the effective scale and 0.10 for equivalent heritability. All these are within published ranges: 0.02 to 0.11 for the logarithmic scale and 0.038 to 0.22 for the original scale3,4,8; and 0.048 to 0.108 for the effective and equivalent scales4,10,18. However, the estimators were higher than reported in a previous study in the same population using linear models7. These discrepancies in heritabilities occur because the survival model used in the present study is superior to previous models for explaining environmental effects. It can consequently isolate the additive genetic effects associated with the trait of interest, and is better for estimating genetic parameters and predicting FPL genetic values. Calculations done using these procedures produced heritability values similar to those reported elsewhere8,10,18. Recent research has demonstrated extensions of the formulas to other models for the genetic effects of other animal species19. These do not depend on ñ or the extreme value distribution, which was not used in the study.
Reliability of the sires’ genetic values ranged from 0.0 to 0.96. This variability is caused by the fact that the reliability of genetic predictions made using survival models is calculated based on the number of daughters with complete (observed) records and not a sire’s total number of daughters. Because of this, younger sires may be at a disadvantage since most of their daughters will still be alive at the time of evaluation, substantially lowering prediction reliability8,9. The same reliability behavior has been reported in countries such as Spain, France and Switzerland4,10,11, where survival models help produce better predictors of sire FPL genetic values.
Sire FPL genetic values calculated based on daughter longevity in Mexico exhibited an increase in relative culling risk as sire birth year advanced. This increase implies an important decrease in genetic values that may be due to increased selection of sires by breeders for predicted transmission of improved milk production in recent years. Aimed at producing high milk production cows, has affected daughter FPL since high milk production is associated with shorter FPL, probably due to health and fertility problems, as observed in the present study. These genetic tendencies differ from those reported for countries such as France, Germany and Canada where culling risk has declined over time for the daughters of Holstein sires. Most likely this is in response to inclusion of FPL in genetic improvement programs for many years9-12.
Conclusions and implications
The estimated heritabilities observed in the present study (0.08 for logarithmic scale; 0.13 for original scale; 0.12 for effective scale and 0.10 for equivalent scale) indicate that this trait can be effectively integrated into genetic improvement programs, as has occurred in other Holstein populations. The Weibull distribution and associated regression model adequately represented length of functional productive life for Holstein cattle in Mexico and are useful in calculating heritability and predicting genetic values for this trait.
Acknowledgements
The authors thank the Asociación Holstein de México, and Dr. Vincent Ducrocq and Dr. Zuleima Chirinos for assistance with the Survival Kit program. The research reported here forms part of the project “Aplicación de herramientas genómicas en el mejoramiento genético de la fertilidad del ganado Holstein productor de leche” (No. SIGI: 11402733072).
REFERENCES
1. Ducrocq V, Quaas RL, Pollak EJ, Casella G. Length of productive life in dairy cows. 1. Justification of a Weibull Model. J Dairy Sci 1988;71:3061-3070. [ Links ]
2. Ducrocq V, Quaas RL, Pollak EJ, Cassella G. Length of productive life of dairy cows. 2. Variance component estimation and sire evaluation. J Dairy Sci 1988;71:3071-3079. [ Links ]
3. Sewalem A, Kistemaker GJ, Ducrocq V, Van Doormaal BJ. Genetic analysis of herd life in Canadian dairy cattle on a lactation basis using a Weibull proportional hazards model. J Dairy Sci 2005;88:368-375. [ Links ]
4. Chirinos Z, Carabaño MJ, Hernandez D. Genetic evaluation of length of productive life in the Spanish Holstein-Friesian population. Model validation and genetic parameters estimation. Livestock Sci 2007;106:120-131. [ Links ]
5. Roxström A, Ducrocq V, Strandberg E. Survival analysis of longevity in dairy cattle on a lactation basis. Genet Sel Evol 2003;35:305-318. [ Links ]
6. Ruíz LF, Oltenacu PA, Blake RW. Efecto del nivel de producción de leche sobre la duración de vida productiva en ganado Holstein de registro en México. Téc Pecu Méx 1994;32(3):105-112. [ Links ]
7. Valencia MP, Ruiz LF, Montaldo VH. Estimación de parámetros genéticos para características de longevidad y producción de leche en ganado Holstein de México. Interciencia 2004;(29):52-56. [ Links ]
8. Ducrocq V. Statistical analysis of length of productive life for dairy cows of the Normande breed. J Dairy Sci 1994;77(3):855-866. [ Links ]
9. Ducrocq V. Two years of experience with the French genetic evaluation of dairy bull on production - adjusted longevity of their daughter. Proc Inter Workshop in EU. Concerted action for Genetic Improvement of Functional Traits in Cattle (GIFT): Longevity. Jouy-en-Josas, Francia. Interbull Bulletin, 1999;21:60-68. [ Links ]
10. Ducrocq V. An improved model for the French genetic evaluation of dairy bulls on length of productive life of their daughters. Anim Sci 2005;80:249-256. [ Links ]
11. Vukasinovic N, Moll J, Casanova L. Implementation of a routine genetic evaluation for longevity based on survival analysis techniques in dairy cattle populations in Switzerland. J Dairy Sci 2001;84:2073-2080. [ Links ]
12. Dürr JW, Monardes HG, Cue RI. Genetic analysis of herd life in Quebec Holsteins using Weibull models. J Dairy Sci 1999;82:2503-2513. [ Links ]
13. Terawaki Y, Katsumi T, Ducrocq V. Development of a survival model with piecewise Weibull baselines for the analysis of length of productive life of Holstein cows in Japan. J Dairy Sci 2006;89:4058-4065. [ Links ]
14. Vitela MI, Cruz VC, Ramos PM. Identificación de las causas de desecho en cinco establos lecheros de Aguascalientes México. Téc Pecu Mex 2004;42(3):437-444. [ Links ]
15. Bascom SS, Young AJ. A summary of the reasons why farmers cull cows. J Dairy Sci 1998;81:2299-2305. [ Links ]
16. Weigel KA, Palmer RW, Caraviello DZ. Investigation of factor affecting voluntary and involuntary culling in expanding dairy herds in Wisconsin using survival analysis. J Dairy Sci 2003;86:1482-1468. [ Links ]
17. Hare E, Norman HD, Wright JR. Survival rates and productive herd life of dairy cattle in the United States. J Dairy Sci 2006;(89):3713-3720. [ Links ]
18. Yazdi MH, Visscher PM, Ducrocq V, Thompson R. Heritability, reliability of genetic evaluations and response to selection in proportional hazard models. J Dairy Sci 2002;85:1563-1577. [ Links ]
19. Meszaros G, Pálos J, Ducrocq V, Sölkner J. Heritability of longevity in Large White and Landrace sows using continuous time and grouped data models. Genet Select Evol 2010:42:1-13. [ Links ]
Received: June 25, 2013; Accepted: August 15, 2013











 texto en
texto en