Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Revista mexicana de ciencias agrícolas
versión impresa ISSN 2007-0934
Rev. Mex. Cienc. Agríc vol.4 no.2 Texcoco feb./mar. 2013
Artículos
Determinación de las tasas de ventilación natural en un invernadero mediante modelos teóricos y gases trazadores*
Determination of rates of natural ventilation in a greenhouse using theoretical models and tracer gases
Daniel Espejel Trujano e Irineo Lorenzo López Cruz1§
1Posgrado en Ingeniería Agrícola y Uso Integral del Agua, Universidad Autónoma Chapingo. Carretera México-Texcoco. Chapingo km 38.5, México. C. P. 56230. Edificio Efraím Hernández Xolocotzi, Planta Baja. Tel. 01 595 9521551, Fax. 5959521551. (despeje10@hotmail.com). §Autor para correspondencia: ilopez@correo.chapingo.mx.
* Recibido: julio de 2012
Aceptado: enero de 2013
Resumen
La mayoría de los invernaderos en México utilizan ventilación natural como mecanismo principal de controlar el clima. La cuantificación de las tasas de ventilación es difícil porque éstas dependen del efecto de la fluctuación de viento, resistencia de las ventanas al paso del aire y geometría del invernadero en el campo de presiones del viento sobre la estructura. El objetivo del presente trabajo fue determinar las tasas de ventilación natural de un invernadero, bajo tres configuraciones de ventilación: ventanas laterales, cenitales y laterales-cenitales, mediante el método dinámico de gases trazadores. Se compararon mediciones contra predicciones de modelos teóricos de ventilación natural y se analizó el efecto de velocidad del viento sobre las tasas de ventilación. El invernadero está ubicado en el campo experimental San Ignacio en la Universidad Autónoma Chapingo, Chapingo, México. El experimento se realizó en 2010 y el invernadero estuvo libre de cultivo. El gas trazador utilizado fue dióxido de carbono. Para la estimación de parámetros se usó el algoritmo de mínimos cuadrados no lineales. Los resultados mostraron que las tasas de ventilación son dependientes de la velocidad del viento y de la configuración de ventanas existente. Las tasas de ventilación más altas se observaron cuando ambas ventanas laterales y cenitales estuvieron abiertas. Los modelos teóricos predijeron de manera aceptable las tasas de ventilación tomando en cuenta los valores de los estadísticos coeficientes de determinación y cuadrado medio de error, así como el comportamiento de la línea 1:1 entre predicciones y mediciones.
Palabras clave: tasas de ventilación de invernaderos, gases trazadores, método de la caída de la concentración, modelos de ventilación.
Abstract
In Mexico, most greenhouses use natural ventilation as the main mechanism to control the weather. Quantification of ventilation rates is difficult because these depend on the effect of fluctuating wind, resistance to airflow windows and geometry ofthe greenhouse in the field ofwind pressure on the structure. The objective of the present study was to determine the rates of natural ventilation in a greenhouse under three ventilation configurations: side windows, zenith and side-zenith, by the dynamic method of tracer gases. Measurements were compared against predictions of theoretical models of natural ventilation and analyzed the effect of wind speed on ventilation rates. The greenhouse is located at the experimental field of San Ignacio in the University of Chapingo, Chapingo, Mexico. The experiment was conducted in 2010 and the greenhouse was free of crops. The tracer gas used was carbon dioxide. To estimate the parameters the non-linear least squares algorithm was used. The results showed that ventilation rates are dependent on the wind speed and configuration ofthe existing windows. The higher ventilation rates were observed when both side and zenith windows were open. Theoretical models acceptably predicted ventilation rates, taking into account the values of the statistical coefficients of determination and mean square error, as the behavior ofthe 1:1 line between predictions and measurements.
Key words: greenhouse ventilation rates, tracer gases, concentration decay method, ventilation model.
Introducción
En México, desde 1990 se han construido invernaderos en todo el país. La tecnología y los diferentes tipos de estructuras de invernaderos son importados de Israel, Holanda, Canadá y España y adaptados a condiciones ambientales diferentes, con diferentes grados de éxito. La actual área bajo producción refleja la importancia de los diferentes ambientes utilizados, y aunque inicialmente los invernaderos fueron construidos en áreas cercanas a los océanos, particularmente en Sinaloa, desde 1995, aproximadamente, se ha dado una expansión de la industria hacia las zonas más elevadas, donde se tiene un clima más moderado, mejores condiciones de luz, y menor presión por plagas y enfermedades (Steta, 1999).
La ventilación es una de las variables más importantes para controlar el clima dentro del invernadero. Esta tiene un efecto directo en el intercambio de masa y energía con el ambiente exterior. En consecuencia, un buen diseño de los sistemas de ventilación puede mejorar tanto el control climático como el uso de energía. La tasa de ventilación es el intercambio de un volumen de aire por unidad de tiempo. La eficiencia de la ventilación natural depende de la velocidad el viento y la diferencia de temperatura entre el interior y el exterior del invernadero (Katsoulas et al, 2006).
Los primeros estudios de ventilación natural en invernaderos se llevaron a cabo en invernaderos holandeses con cubierta de vidrio (Bot, 1983; Nederhoff et al, 1985; de Jong, 1990) usando modelos matemáticos para predecir las tasas de ventilación y la técnica de los gases trazadores para cuantificarlas experimentalmente. Sin embargo, la teoría básica de la ventilación natural en invernaderos fue elaborada principalmente por Boulard et al. (1996), Baptista et al. (1999), Roy et al. (2002) quienes plantearon que la cantidad de aire a través de una ventana puede ser calculada a partir de las pérdidas de carga usando la ecuación de Bernoulli.
Un segundo enfoque para estudiar la ventilación natural en invernaderos, se ha basado en balances de masa y energía en estado no estacionario (Fernandez y Bailey, 1992; Teitel y Tanny, 1999; Dermati et al, 2001; Dayan et al, 2001; Dayan et al, 2002; Dayan et al, 2004; Majdoubi et al, 2007). En este caso, las tasas de ventilación aparecen en las ecuaciones diferenciales que predicen el comportamiento tanto de la temperatura como la humedad dentro del invernadero. Estas se determinan para estimar el intercambio de calor y de humedad que ocurre entre el aire dentro y fuera del invernadero. Un tercer planteamiento para predecir las tasas de ventilación en invernaderos son los modelos numéricos de Dinámica de Fluidos Computacional (Boulard et al., 2002; Campen y Bot, 2003; Romero et al., 2006; Romero et al, 2010).
La técnica de los gases trazadores es un procedimiento estándar para medir las tasas de ventilación en edificios (Sherman, 1990). Un gas inerte (CO2, N2O) es distribuido en el invernadero y su concentración es determinada para encontrar una relación con las tasas de ventilación.
Esta técnica es el método más usado para validar modelos teóricos de la ventilación, modelos basados en balances de masa y energía o modelos de dinámica de fluidos computacional (Nederhoff et al., 1985; Baptista et al, 1999; Pérez et al, 2004). Una variante de la técnica de los gases trazadores es el método de balance de vapor de agua (Boulard y Draoui, 1995; Mashonjowa et al, 2010) el cual usa el vapor de agua como un trazador. Otro método experimental para determinar las tasas de ventilación en invernaderos es el uso de anemómetros sónicos (Wang y Deltour, 1997; Wang y Deltour, 1999; Wang et al, 1999).
Además de lo anterior, en México existen pocas investigaciones que permitan conocer el comportamiento de las tasas de ventilación en diferentes tipos de invernaderos localizados en diferentes condiciones climáticas (Romero et al., 2006 Romero et al, 2010). Por lo anterior, se planteo el presente trabajo con los siguientes objetivos: 1) determinar las tasas de ventilación mediante el método dinámico de técnica de gases trazadores bajo tres condiciones de ventilación diferentes; 2) comparar los resultados obtenidos con la técnica de gases trazadores y los modelos teóricos; y 3) estudiar la relación que existe entre las tasas de ventilación y la velocidad del viento.
Materiales y métodos
Descripción del experimento
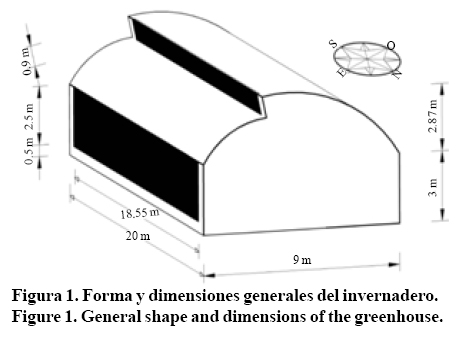
El estudio se realizó en un invernadero ubicado en el campo experimental San Ignacio de la Universidad Autónoma Chapingo en Chapingo, Estado de México. Está localizado a 19° 29' 17'' latitud norte, 98° 53' 16'' longitud oeste y a 2 251 msnm. Como se muestra en la Figura 1, el invernadero es tipo capilla. Tiene 20 m de largo por 9 m de ancho y 5.8 m de alto, con orientación SO-NE y con un volumen de 878.4 m3. El área total de las ventilas cenitales es 17 m2 (9.5% del área de suelo) y de la pared lateral 93 m2 (51% del área del suelo). Las ventanas cenitales están orientadas hacia el este, en dirección contraria de los vientos dominantes. La cubierta es una película de polietileno de una capa calibre 700 ultravioleta con una vida útil recomendada de 2 años. El invernadero cuenta con mallas antiáfidos de 45 x 25 hilos, estas ventanas se cierran por medio de malacates tanto en las ventanas laterales como las cenitales. La ventilación natural fue el único mecanismo para regular la temperatura y la humedad dentro del invernadero.
Se colocaron sensores de temperatura a 1.5 m de altura del suelo a 6 y a 12 m a lo largo del interior del invernadero. Se instaló una estación meteorológica a 2 m sobre el techo el invernadero equipada con sensores de temperatura y velocidad del viento. Los sensores tomaron muestras cada 10 s y registraron el promedio de éstas cada 30 s. Todos los sensores empleados fueron marca HOBO (Onset Company, Bourne, Ma, USA). Las mediciones se realizaron en diferentes días entre los meses de abril a septiembre de 2010, para poder tener diferentes condiciones climáticas. La mayoría de las mediciones se realizaron entre 9 am y 2 pm y se registraron velocidades de viento fuera del invernadero, mayores a 4 ms-1 y menores a 1.5 ms-1 y diferencias de temperatura entre el interior y el exterior mayores a 20 °C. Durante el tiempo de las mediciones, se observó un retraso en el efecto del viento sobre la ventilación del invernadero de entre 2 y 4 min; es decir, un cambio en la velocidad del viento no es instantáneo, sino requiere de cierto tiempo para cambiar las tasas de ventilación del invernadero.
En el presente trabajo se utilizó dióxido de carbono puro (CO2) debido a su bajo costo y que la concentración existente en el aire natural está por debajo de la concentración mínima (400 ppm) que se utilizó. La concentración de CO2 se midió cada 15 s con un sensor marca Telaire modelo 7001 (Onset Company, Bourne, Ma, USA) y un sensor TES1370 NDIR CO2 meter (TES Electrical Electronic Group, Taiwan) . Para mejorar la distribución del gas se utilizaron cinco líneas de manguera de 0.5 pulgadas, a lo largo del invernadero, en un sistema cerrado con orificios de 3/32 pulgadas a cada 2 metros. Se utilizaron ventiladores con el objetivo de homogeneizar el gas. El invernadero estuvo libre de cultivo durante la toma de mediciones.
Las mediciones se llevaron a cabo bajo tres configuraciones de ventanas, la primera consideró únicamente la ventilación lateral, la segunda sólo la ventilación cenital y la última utilizando toda la ventilación (ventanas cenitales y laterales) del invernadero. Antes de inyectar el CO2 se cerraron todas las ventanas del invernadero. En seguida se aplicó CO2 hasta alcanzar un valor de 1100 ppm en promedio. Se activaron los ventiladores para asegurar una distribución uniforme del gas. Posteriormente se abrieron las ventanas y se registró el cambio de concentración del gas junto con las variables temperatura del aire dentro y fuera del invernadero y velocidad del viento externa. Se cerraron nuevamente las ventanas cuando la concentración del gas alcanzó 500 ppm. La concentración de CO2 se incrementó nuevamente hasta 1 100 ppm. Este procedimiento se repitió 3 o 4 veces para diferentes velocidades de viento. Una vez obtenidos los datos de la concentración del gas trazador, la tasa de ventilación se calculó siguiendo el procedimiento propuesto por Baptista et al. (1999).
Modelación de la ventilación natural
La cantidad de fluido a través de una ventana puede ser calculada a partir de las pérdidas de carga usando la ecuación de Bernoulli (Roy et al., 2002). La caída de presión ΔP (Pa) a través de la apertura es calculada por la ecuación:
ΔP= ξpu2 (1)
Donde: ξ (adimensional) es el coeficiente de caída de presión, p (kg m -3) es la densidad del aire y u (m s-1) es la velocidad de aire. La ventilación se puede modelar relacionando la caída de presión con la velocidad media del aire, ya que las diferencias de presión que producen flujos de ventilación pueden deberse a la diferencia de temperatura del aire interior y exterior, y también por el viento que genera diferencias de presión sobre el invernadero (Roy et al., 2002; Bailey, 2000; Kittas et al., 1997):
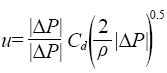 (2)
(2)
Donde de acuerdo con Boulard y Baille (1995), el coeficiente de descarga Cd (adimensional) se define como:
Cd= ξ-0.5 (3)
El efecto del viento tiene dos componentes, un componente medio dado por el promedio de la velocidad del viento y un efecto turbulento (Papadakis et al., 1996).
Efecto térmico de flotabilidad
El efecto térmico de flotabilidad es el resultado de la diferencia entre la temperatura externa e interna la cual crea una distribución de presión entre y sobre las ventanas en dirección vertical (Pérez et al, 2004). Por ello, es posible considerar las ventanas cenitales como aperturas verticales. El nivel de referencia es la mitad de la apertura donde la presión de entrada y salida son iguales y no hay intercambio de aire. En la mitad inferior, la presión de afuera es mayor que la presión dentro. Como un resultado, el aire frio entra por la mitad inferior y el aire caliente sale por la mitad superior (Baptista et al., 1999). El modelo propuesto por Boulard et al. (1996) para estimar las tasas de ventilación natural en invernaderos usando solo ventanas cenitales, está basado en las dos diferentes fuerzas de la ventilación natural: fuerza de flotabilidad y fuerza del viento, es descrito mediante la ecuación siguiente:
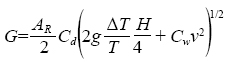 (4)
(4)
Donde: G (m3s-1) es la tasa de ventilación, AR (m2) es el área de ventanas cenitales, H (m) es la altura de la ventana a partir del suelo, g (ms-2) es la aceleración de la gravedad, ΔT (K) es la diferencia de temperatura entre el interior y el exterior del invernadero, T (K) es temperatura exterior, v (ms-1) es la velocidad del viento a una altura de 8 m y Cw (adimensional) es el coeficiente del efecto del viento.
El valor del coeficiente de descarga Cd depende de las características de las ventanas. Roy et al. (2002) presentan los valores para Cd reportados en la literatura, principalmente para ventanas de construcciones verticales continuas o de tipos de invernaderos. Comúnmente los valores para el coeficiente de descarga Cd son de entre 0.6 y 0.8 con un promedio de 0.66. Sin embargo, debe notarse que los valores del coeficiente de descarga corresponden a ventanas sin obstáculos de circulación de aire. Si se consideran obstáculos, el valor de Cd puede ser considerablemente menor, como en el caso de la malla antiáfidos empleada por Fantassi et al. (2002) y Majdoubi et al. (2007). Un estudio detallado del efecto combinado entre el coeficiente de descarga de las aperturas y de la cubierta vegetal esta descrito en Fatnassi et al. (2002).
Efecto del viento
Las fuerzas debidas al efecto viento alrededor de una construcción crean un campo de presiones a las aperturas y por lo tanto produce un flujo de aire a través de ellas. Estas presiones pueden ser positivas, cuando los flujos de aire entran a la construcción, o negativos (succión) cuando los flujos de aire salen.
De acuerdo con Bailey (2000) el coeficiente Cw corresponde a la influencia del viento sobre la tasa de ventilación y parece ser independiente de la superficie del invernadero pero es altamente dependiente de la dirección del viento. Sin embargo, Boulard y Baille (1995) mostraron que decrece significativamente cuando se incrementa la velocidad del viento. Roy et al. (2002) presentan los valores para Cw reportados en la literatura, principalmente para túneles de áreas muy pequeñas. Comúnmente los valores para el este parámetro tienen un rango de entre 0.07 y 0.14. Un modelo para dar cuenta del efecto del viento sobre las tasas de ventilación ha sido propuesto por varios autores (Boulard y Baille, 1995; Papadakis et al., 1996; Kittas et al., 1996; Baptista et al., 1999; Roy et al, 2002).
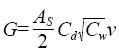 (5)
(5)
Donde: AS (m2) es el área de ventilación.
Efecto combinado del viento y flotabilidad
En la ventilación natural de un invernadero están presentes tanto las fuerzas del viento como las de flotabilidad. En áreas donde el viento alcanza altas velocidades, este efecto es más importante que la diferencia de temperaturas pero domina el efecto de flotabilidad cuando el viento es más débil. Meneses y Raposo (1987) citado por Baptista et al. (1999) consideraron que, para velocidades del viento de 0.5-1.5 (m s-1), la diferencia de temperaturas domina a el efecto del viento en invernaderos con aperturas localizadas en el techo y en las paredes laterales y para velocidades de 1.5 a 2.5 (m s-1) el efecto es combinado. A velocidades más grandes, ocurre lo opuesto y la influencia térmica puede ser ignorada. Sin embargo, estas limitaciones dependen de la geometría del invernadero, la posición de las ventanas y la diferencia de temperaturas entre lo interior y el exterior. Cuando ambas fuerzas actúan juntas, Boulard y Baille (1995), Kittas et al. (1997), Roy et al. (2002), consideraron que el resultado del flujo de aire no es igual a la suma de los dos valores separados. El flujo a través de cualquier apertura está dado por una suma vectorial:
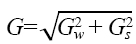 (6)
(6)
Donde: GW (m3 s-1) es el flujo debido al viento y GS (m3 s-1) es el flujo debido a las diferencias térmicas.
De acuerdo con Roy et al. (2002), la hipótesis de un complemento de flujo en lugar de diferencias de presión individuales conduce a un error del orden de 10% en la estimación del flujo combinado.
Kittas et al. (1997) propusieron un modelo que está compuesto del efecto de flotabilidad debido al efecto térmico (producido por la diferencia entre la temperatura del aire interior y exterior) y el efecto del viento debido a la acción de la velocidad del viento en la estructura del invernadero Pérez et al. (2006).
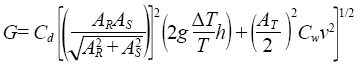 (7)
(7)
Donde: h (m) es distancia vertical ente el punto medio de la ventana lateral y la cenital.
Estimación de parámetros o calibración
La estimación de parámetros o calibración consiste en ajustar o encontrar los parámetros del modelo que permitan obtener el mejor ajuste entre sus predicciones y las mediciones en el sistema real (Peart y Bruce, 1998). El coeficiente que describe el efecto del viento Cw y el coeficiente de descarga Cd son los dos principales coeficientes experimentales involucrados en los modelos de la ventilación natural que se requieren determinar para cada configuración de ventanas. La tasa de ventilación, generalmente se determina midiendo la tasa de flujo volumétrico y las variables velocidad del viento y temperatura del aire dentro y fuera del invernadero junto con el área de ventana. Se utilizó la técnica de mínimos cuadrados del error para determinar los valores del coeficiente de descarga Cd y el coeficiente debido al viento Cw.
Por esto, la función a minimizar fue la suma del cuadrado de la diferencia entre las mediciones de las tasas de ventilación G (m3s-1) y la tasa de ventilación estimada G' (m3s-1) por los modelos. Se usó la función mínimos cuadros no lineales (lsqnonlin.m) disponible en el Optimization Toolbox del ambiente de programación Matlab (The Mathworks INC, 1990-2010). El algoritmo de optimización de Levenberg-Marquardt fue usado para minimizar la función. De acuerdo con información de la literatura (Roy et al., 2002) se definió como región de búsqueda para el coeficiente de descarga 0.6 ≤ Cd ≤ 0.8 y para el coeficiente relacionado con el efecto del viento el intervalo 0.01 ≤ Cw ≤ 0.2.
Análisis de datos
Para evaluar los resultados, se realizó una comparación entre las tasas de ventilación medidas y calculadas con los modelos. Los valores fueron comparados usando el coeficiente de determinación (r2), el Cuadrado Medio del Error (CME) y una línea 1:1. Los primeros dos criterios son definidos por las ecuaciones (8) y (9):
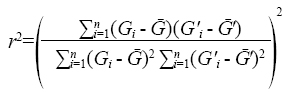 (8)
(8)
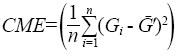 (9)
(9)
Donde: G (m3s-1) es la tasa de ventilación medida y G' (m3s-1) es la estimada y n es el número de observaciones.
Resultados y discusión
Efecto del viento sobre la tasa de ventilación
Las tasas de ventilación tienen una alta dependencia de la velocidad del viento. La tasa de ventilación aumenta conforme se incrementa la velocidad del viento, por lo que esta es muy importante para la renovación del aire dentro del invernadero y es deseable no tener construcciones fuera del invernadero que obstaculicen este flujo. En la Figura 2 se muestran las tasas de ventilación medidas con el método de gases trazadores donde se puede observar que para todas las configuraciones de ventanas abiertas, la tasa de ventilación siempre es afectada considerablemente por la velocidad del viento y en mayor medida para la ventilación lateral.
Katsoulas et al. (2006) encontraron que la configuración de ventanas más eficiente es la combinación de ventanas laterales y cenitales y hay una reducción de 46% cuando sólo se utiliza ventanas laterales y de 71% cuando sólo ventanas cenitales. En el presente trabajo se obtuvo una reducción promedio de 32% cuando sólo existen ventanas laterales y 85% para la situación de sólo ventanas cenitales con respecto a la configuración cenital-lateral. Sin embargo, Papadakis et al. (1996) han reportado que la ventilación más eficiente es cuando se tiene sólo ventilación cenital y la menos deseable es cuando se tiene sólo ventanas laterales. Por su parte, Bailey (2000) observó que existe una considerable reducción de la velocidad dentro del invernadero con la manera que se coloquen las plantas, teniendo una reducción 40% cuando se ponen las filas de plantas perpendiculares a las ventanas y de 10 a 20% cuando se ponen paralelas. Esto no puede verificarse en el caso del invernadero estudiado ya que solo se investigo la ventilación sin presencia de cultivo.
Ventilación cenital
Las tasas de ventilación bajo esta configuración se calcularon con la ecuación (4). Se obtuvo una regresión entre los valores obtenidos con el modelo calibrado y los valores obtenidos con la técnica de gases trazadores (Figura 3) y se obtuvo un coeficiente de determinación de 92.4 %. Para determinar la precisión del modelo se graficó una recta 1:1 junto con la recta de ajuste de regresión de los datos la cual tiene una pendiente de 0.46, esto indica que el modelo está sobreestimando para valores bajos y subestimando para valores altos de tasas de ventilación. El CME fue 0.01. Los valores de los parámetros obtenidos fueron de Cd= 0.799 y Cw= 0.2 siendo más altos a los obtenidos por Katsuolas et al (2006) quienes al igual que en este trabajo analizaron las tasas de ventilación con la presencia de mallas antiáfidos en las ventanas. En el caso del coeficiente Cw resultó ligeramente mayor que los reportados por Roy et al. (2002), lo cual significa que la velocidad del viento tiene una gran influencia sobre las tasas de ventilación en esta configuración y para las condiciones experimentales del presente trabajo.
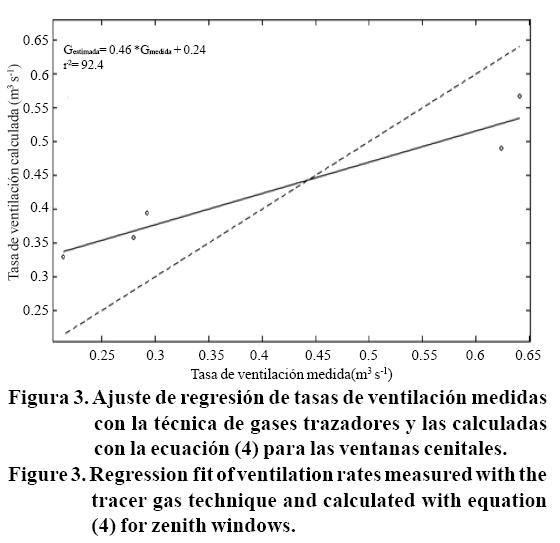
Ventilación lateral
Para la configuración de ventanas laterales abiertas se calcularon las tasas de ventilación con la ecuación (5), la cual solo contempla el efecto del viento. En la Figura 4 se observa la regresión lineal entre los valores obtenidos entre las tasas de ventilación medidas con la técnica de gases trazadores y calculadas con el modelo calibrado obteniendo un coeficiente de determinación de 87.6 %. De acuerdo con la recta de regresión, los valores menores a 2 m3s-1 son subestimados. Se podrían mejorar los resultados con un modelo que contemple el efecto de temperatura puesto que el efecto de la temperatura es mayor para a bajas velocidades de viento.
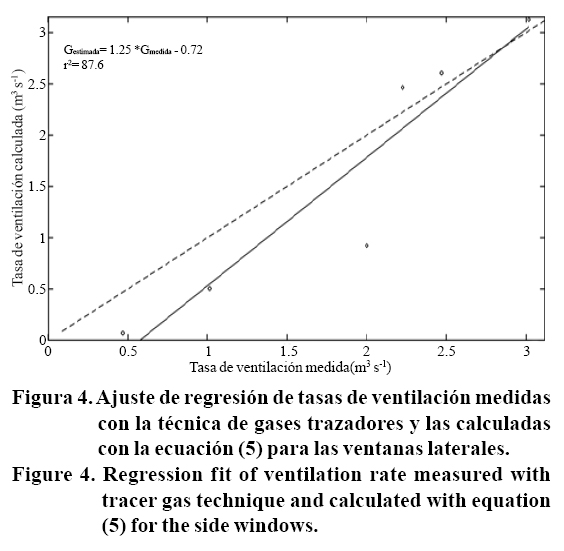
Ventilación cenital y lateral
En la Figura 5 se observa la regresión lineal entre los datos medidos experimentalmente mediante el método de gases trazadores y los valores calculados con la ecuación (7) obteniendo un coeficiente de correlación de 87% y con la recta de ajuste parecida a la recta 1:1, esto significa que el modelo describe en forma aceptable las tasas de ventilación.
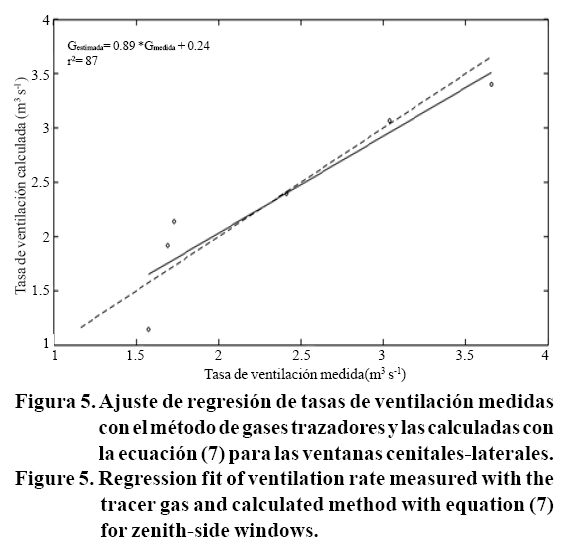
Para verificar este buen ajuste se calculó el cuadrado medio del error (CME) teniendo un valor de 0.078. Este valor corresponde a un error de 0.28 m3s-1 en los valores calculados. El valor de los parámetros para esta configuración después de la calibración resultó para Cd de 0.76 y para Cw de 0.05. Como se puede observar Cd es alto comparando con los obtenidos en Majdoubi et al. (2007) quien estudio ventanas con obstáculos, tales como malla antiáfidos y cultivo. El valor de Cd es cercano a la configuración de ventanas cenitales realizadas en este trabajo y ambos mayor a los de la ventilación lateral, en otras palabras es mayor cuando se tiene ventilación cenital en cualquier configuración. Puede observarse que Cw es menor en esta configuración que cuando solo están abiertas las ventanas laterales y este a su vez es menor que la configuración de solo ventanas cenitales abiertas.
Conclusiones
La medición experimental de las tasas de ventilación se realizó exitosamente mediante el método de la caída de la concentración de la técnica de los gases trazadores, usando dióxido de carbono como gas trazador. Las tasas de ventilación medidas con ventanas cenitales y laterales simultáneamente abiertas se incrementan en 15% y 67% con solo ventanas laterales y solo cenitales respectivamente.
Tres modelos matemáticos de la ventilación fueron usados para determinar las tasas de ventilación con igual número de configuraciones de ventanas en un invernadero, dichos modelos se ajustaron aceptablemente con las mediciones de tasas de ventilación. Se observó que el modelo que contempla tanto el efecto de flotabilidad como el efecto del viento tuvo un mayor ajuste con las mediciones.
El coeficiente debido al viento Cw resultó diferente en cada configuración, siendo mayor con la menor área de ventana abierta decreciendo con mayor área de ventana, teniendo mayor efecto el viento con un área de ventilación menor. Por tanto se tiene que entre mayor sea el área de ventanas, menor es la influencia del efecto del viento sin dejar de ser el efecto dominante en la ventilación.
El coeficiente de descarga Cd es mayor cuando se tiene ventilación cenital en cualquier configuración de ventanas, lo que refuerza la importancia que tiene las ventanas cenitales como mecanismo para mejorar la ventilación natural en un invernadero.
Las tasas de ventilación natural del invernadero estudiado, están en función de la velocidad del viento y de la configuración de ventilación que se utilice. En este estudio se encontró que para la condición de ventanas laterales y cenitales simultáneamente abiertas se tiene una mejor ventilación y circulación del aire interno del invernadero.
Literatura citada
Bailey, B. J. 2000. Constraints, limitations and achievements in greenhouses natural ventilation. Acta Hortic. 534: 21-30. [ Links ]
Boulard, T. and Draoui, B. 1995. Natural ventilation of a greenhouse with continuous vents: measurements and data analysis. J. Agric. Eng. Res 61(1):27-36. [ Links ]
Boulard, T.; Kittas, C.; Roy, J. C and Wang, S. 2002. Convective and ventilation transfers in greenhouses, part 2: determination ofthe distributed greenhouse climate. Biosys. Eng. 83:129-147. [ Links ]
Boulard, T.; Meneses, J. F.; Mermier, M. and Papadakis, G. 1996. The mechanisms involved in the natural ventilation ofgreenhouses.Agric. Forest Meteorol. 79:61-77. [ Links ]
Bot, G. 1983. Greenhouse climate: from physical processes to dynamic model. PhD Thesis. Wageningen Agricultural University. The Netherlands. [ Links ]
Campen, J. B. and Bot, G. P. A. 2003. Determination of greenhouse-specific aspects of ventilation using three-dimensional computational fluid dynamics. Biosys. Eng. 84(1):69-77. [ Links ]
Dayan, E.; Dayan, J. and Strassberg, Y. 2002. The prediction of ventilation rates in greenhouses containing rose crops. Acta Hortic. 593:55-62. [ Links ]
Dayan, J.; Dayan, E.; Strassberg, Y. and Presnov, E. 2004. Simulation and control of ventilation rates in greenhouses. Mathematics and computers in simulation 65:3-17. [ Links ]
Dayan, J.; Strassberg, Y. and Dayan, E. 2001. Simulation and control of ventilation rates in greenhouses. Acta Hortic. 566:67-74. [ Links ]
De Jong, T. 1990. Natural ventilation of large multi-span greenhouses. PhD Thesis. WageningenAgricultural University. The Netherlands. [ Links ]
Dermati, H.; Boulard, T.; Bekkaoui, A. and Bouirden, L. 2001. Natural ventilation and microclimatic performence of a large-scale banana greenhouse J. Agric. Eng. Res. 80(3):261-271. [ Links ]
Fatnassi, H.; Boulard, T.; Dermati, H.; Bouirden, L. and Sappe, G. 2002 Ventilation performance of a large Canarian type greenhouse equipped with insect-proof nets. Bios. Eng. 82(1):97-105. [ Links ]
Fernández, J. E. and Bailey, B. J. 1992. Measurement and prediction of greenhouse ventilation rates Agric. Forest Meteorol. 58:229-245. [ Links ]
Katsoulas, N.; Bartzanas, T; Boulard, T.; Mermier, M. and Kittas, C. 2006. Effect of vent openings and insect screens on greenhouse ventilation. Biosys. Eng. 93(4):427-436. [ Links ]
Kittas, C.; Boulard, T. and Papadakis, G. 1997. Natural ventilation of a greenhouse with ridge and side openings: sensitivity to temperature and wind effects. Transactions of the ASAE. 40(2): 415-425. [ Links ]
Mashonjowa, E.; Ronsse, F.; Milford, J. R.; Lemeur, R. and Pieters, J. G. Measurement and simulation of the ventilation rates in a naturally ventilated Azromtype greenhouse in Zimbabwe. 2010. Appl. Eng. Agric. 26(3):475-488. [ Links ]
Majdoubi, H.; Boulard, T.; Hanaf, A.; Bekkaoui, A.; Fatnassi, H.; Dermati, H.; Nya, M. and Bouirden, L. 2007. Natural ventilation performance of a large greenhouse equipped with insect screens. Transactions of the ASABE 50(2):641-650. [ Links ]
Nederhoff, E. M.; Van de Vooren, J. and Udink ten cate, A. J. 1985. A practical tracer gas method to determine ventilation in greenhouse. J. Agric. Engin. Res. 31:309-319. [ Links ]
Papadakis, G.; Mermier, M.; Meneses, J. F. and Boulard, T. 1996. Measurement and analysis of air exchange rates in a greenhouse with continuous roof and side openings. J. Agric. Eng. Res. 63:219-228. [ Links ]
Peart, R. M. and Bruce, C. R. 1998. Agricultural systems modeling and simulation. 1st Ed. Marcel Dekker, Inc. [ Links ]
Pérez, J.; Berenguel, M.; Rodríguez, F. and Ramírez, A. A. 2006. Ventilation rate models of mediterrean greenhouses for control purposes. Acta Hortic. 719:197-204. [ Links ]
Romero, P.; Choi, C. Y. and López, I. L. 2010. Enhancement of the greenhouse air ventilation rate under climate conditions of central México. Agrociencia. 44:1-15. [ Links ]
Romero P.; Giacomelli G.A.; Choi, C.Y. and López I.L. 2010. Ventilation rates for a naturally-ventilated greenhouse in central Mexico. Acta Hortic. 65-72. [ Links ]
Roy, J. C.; Boulard, T.; Kittas, C. and Wang, S. 2002. Convective and ventilation transfer in greenhouses, Part 1: the greenhouse considered as a perfectly stirred tank. Biosys. Eng. 83(1):1-20. [ Links ]
Sherman, M. H. 1990. Tracer-gas techniques for measuring ventilation in a single zone. Building Environ. 25(4):365-374. [ Links ]
Steta, M. 1999. Status ofthe greenhouse industry in México. Acta Hortic. 481: 735-738. [ Links ]
Teitel, M. and Tanny, J. 1999. Natural ventilation of greenhouses: experiments and model. Agric. Forest Meteorol. 96:59-70. [ Links ]
Wang, S. and Deltour, J. M. 1997. Natural ventilation induced airflow patterns measured by an ultrasonic anemometer in venlo-type greenhouse openings. Agric. Eng. J. 6(3-4):185-196. [ Links ]
Wang, S. and Deltour, J. 1999. Lee-side ventilation-induced air movement in a large-scale multi-span greenhouse. J. Agric. Eng. Res. 74:103-110. [ Links ]
Wang, S.; Yernaux, M. and Deltour, P. 1999. A networked two-dimensional sonic anemometer system for the measurement of air velocity greenhouses. J. Agric. Eng. Res. 73:189-197. [ Links ]














