Artículos

 

Invarianza temporal al escalado de series de tiempo con información pluvimétrica diaria*

 

Temporal invariance to scaling of time series of daily rainfall data

 

Miguel Agustín Velásquez Valle¹, Jaime de Jesús Velásquez García², Jesús Arcadio Muñoz Villalobos¹, Mario Roberto Martínez Menes³, Klaudia Oleschko Lutkova⁴, Ignacio Sánchez Cohen^1§ y Benjamín Figueroa Sandoval³

 

¹Centro Nacional de Investigación Disciplinaria. Relación Agua, Suelo, Planta, Atmosfera (CENID-RASPA). INIFAP. Margen derecha canal Sacramento, km 6.5. Gómez Palacio, Durango. C. P. 35140. Tel. 01 871 1590104. (velasquez.agustin@inifap.gob.mx), (villalobos.arcadio@inifap.gob.mx). ^§Autor para correspondencia: sanchez.ignacio@inifap.gob.mx.

²Campo Experimental Uruapan. INIFAP. Av. Lationoamericana 1101. Uruapan, Michoacán. C. P. 60500. Tel. 01 914 5237392. (jaime_velazquez@prodigy.net.mx).

³Edafología. Colegio de Posgraduados. Carretera México-Texcoco, km 38.5. Montecillo, Texcoco, Estado de México. C. P. 56230. Tel. 01 595 9520200. Ext. 1135. (mmario@colpos.mx), (benjamin@colpos.mx).

⁴Instituto de Geociencias. UNAM. Campus Juriquilla. Bulevard Juriquilla 3001. Querétaro, Querétaro, México. C. P. 76230.

 

* Recibido: mayo de 2010
Aceptado: noviembre de 2010

 

Resumen

La variación en magnitud de los eventos de precipitación pluvial se debe a la ocurrencia de estaciones secas, húmedas y fenómenos extremos. El objetivo de esta investigación, fue determinar el grado de invarianza al escalado (diferente escala) de una series de tiempo de precipitación pluvial, por medio del análisis fractal. Se utilizó la serie histórica de precipitación de 1978 a agosto de 1996 de la estación meteorológica Santa Fé de la Laguna, Quiroga, Michoacán, México. Se elaboraron bases de datos a escala diaria, mensual y anual; se calculó el coeficiente de Hurst con los métodos de referencia de ondoletas y el de rango re-escalado diseñados para el análisis de patrones auto-afines. Se determinó la aleatoriedad de los eventos, la invarianza al escalado y la distribución dinámica de los eventos.

Palabras clave: análisis fractal, bases de datos, coeficiente de Hurst, precipitación.

 

Abstract

Variation in magnitude of events of pluvial precipitation is due to occurrence of dry season, humid season and extreme phenomena. The aim of this investigation was to determine invariance grade at scaling (at different scale) of a series of time of pluvial precipitation, by means of fractal analysis. It was used historical precipitation series from 1978 to August of 1996 from meteorological station Santa Fé de la Laguna, Quiroga, Michoacán, Mexico. Databases were elaborated at daily, monthly and annual scale; the coefficient of Hurst was calculated with the reference methods of wavelets and with re-scaled range designed for the analysis of self-affine patterns. The randomness of events, the invariance to scaling was determined and the dynamic distribution of the events.

Key words: databases, fractal analysis, Hurst coefficient, precipitation.

 

INTRODUCCIÓN

Parte de la aleatoriedad de los fenómenos naturales se debe a causas internas del sistema o a factores externos estocásticos, particularmente si estos no varian en forma lineal. El estudio de las variables y las interacciones de un sistema dinámico a través del tiempo se enfoca a encontrar patrones, estructuras y puntos críticos de estabilidad o inestabilidad así como la sensibilidad al cambio de las condiciones iniciales para lograr cierto grado de control (Balankin et al., 2004). La aleatoriedad de los fenómenos naturales en espacio y tiempo ha sido difícil de caracterizar y cuantificar (Valdez-Cepeda et al., 2003a). La variabilidad de la precipitación pluvial es extrema en tiempo, desde varios minutos a años y en espacio de varios metros a cientos de kilometros (Kumar y Foufoula-Georgiou, 1993; Burlando y Rosso, 1996).

En hidrología, los registros históricos de precipitación constituyen la información fundamental en los estudios de evaluación de impacto y en los relacionados con la predicción (Entekhabi et al., 1999; Arnaud et al., 2002). La problemática del cambio de escala en la extrapolación de información puede ser resuelta mediante el uso de las técnicas de referencia de la teoría fractal, ya que permiten obtener parámetros para determinar el grado de invarianza al escalado de una serie de tiempo determinada.

El estudio de la variabilidad de los eventos de precipitación ha permitido ampliar el conocimiento sobre los procesos hidrológicos, que es fundamental para el manejo adecuado de los recursos naturales de una región (Comrie y Broyles, 2002; Bullock, 2003). La variación en magnitud de la precipitación durante el trancurso de una serie histórica se debe a las fluctuaciones climáticas, la presencia de estaciones secas y húmedas (Lázaro et al., 2001), a la ocurrencia de eventos extremos, entre otros. Por lo anterior, la variabilidad espacio-temporal de la precipitación es interpretada con mayor claridad en la medida en que se disponga de una serie histórica de registros con el máximo número de años posible. A la fecha, se ha utilizado poco el grado de invarianza al escalado de la aleatoriedad de las series de tiempo, en el estudio de los fenómenos meteorológicos y los procesos hidrológicos (Valdez-Cepeda et al., 2003b).

El análisis convencional de los registros pluviométricos generalmente se realiza por medio de métodos estadísticos, para determinar la tendencia de la dispersión de los datos a partir de valores máximos, mínimos, promedios anuales, desviación de la media y número de eventos (Shanan et al., 1967; Bullock, 2003). Para representar de manera espacial la precipitación pluvial, Osborn y Hickok (1968) relacionaron la variabilidad temporal (en tiempo), de los eventos de precipitación con los escurrimientos en cuencas hidrológicas en zonas semi-áridas, determinaron que la variabilidad de la lluvia tiene mayor relación con el escurrimiento en cuencas pequeñas que en cuencas grandes.

En periodos cortos, Richter et al. (1983) observaron que la variación espacial de los valores semanales de precipitación dependieron de los efectos estacionales ocurridos durante el año, el coeficiente de variación para el invierno fue 6.4% comparado con 20.9% en verano. Actualmente, los estudios relacionados con el análisis de series de tiempo de la precipitación pluvial se orientan hacia la predicción (Wight y Hanson, 1991), la variabilidad espacial asociada a la ocurrencia de inundaciones (Arnaud et al., 2002) y su relación con el cambio climático (Rivera, 2000).

Invarianza al escalado

Una propiedad común de los sistemas dinámicos naturales es la invarianza al escalado, esto significa que los momentos centrales de primero, segundo, tercer y cuarto orden se mantienen asintóticamente constantes en el espacio o en el tiempo. Esta es una propiedad que permite escalar información estadística de series de tiempo o eventos a otras escalas (Olsson y Niemczynowicz, 1996). Esto es de gran utilidad cuando la información no está disponible en la escala deseada.

Actualmente se utiliza la geometría fractal para escalar los registros históricos o bases de datos de información pluviométrica, debido que los eventos meteorológicos presentan cierto grado de invarianza al escalado en tiempo y espacio (Mandelbrot 1983; Miranda et al., 2004). La geometría fractal se utiliza para caracterizar sistemas dinámicos con patron estructural irregular y su elaboración se basa en los procesos aleatorios que presentan invarianza de escala (Mandelbrot, 1983; Olsson et al., 1992; Giménez et al., 2000; Morales et al., 2005). Estos conceptos han permitido cuantificar los factores de invariancia escalar contenidos en la estructura o patrón estructural de las series de tiempo (Olsson et al., 1992; Burgos y Pérez, 1999; Miranda et al., 2004).

La teoría fractal se ha utilizado para analizar series de tiempo de precipitación bajo el concepto de trazas auto-afines (Burgos y Pérez, 1999; Miranda et al., 2004). Una de las principales características de las trazas auto-afines, es que independientemente de la forma, la traza puede repetirse de diferente manera en diferentes direcciones y puede presentar o no la persistencia de los datos (tendencia a seguir o no la estructura de la serie de tiempo).

El grado de la aleatoriedad puede ser determinado con el coeficiente de Hurst (H), el cual representa la persistencia de un fenómeno estadístico (Salas et al., 1985; Schroeder, 1991). En el caso de un fenómeno con comportamiento aleatorio puro, el coeficiente de Hurst tiene valor igual a 0.5; es decir, similar a la distribución Gaussiana o al movimiento Browniano clásico (Mandelbrot, 2002). El coeficiente de Hurst es un indicador de la rugosidad de la base de datos y los valores menores de 0.5, indican una tendencia de regresar en si mismos, propiedad que es conocida como anti-persistencia y los valores mayores de 0.5, indican la tendencia a persistir en su progresión en la dirección que se está moviendo y se conoce como persistencia.

El objetivo de esta investigación fue determinar la similitud fractal en diferentes escalas de tiempo (invarianza al escalado), en función del patrón estructural de una serie de tiempo de precipitación pluvial, con el propósito de utilizar esta propiedad para extrapolar información de una escala de tiempo a otra.

 

MATERIALES Y MÉTODOS

El estudio se realizó con información pluviométrica de la estación meteorológica Santa Fé de la Laguna ubicada en la cuenca hidrológica del Lago de Pátzcuaro, Michoacán; cuya localización geográfica está entre los meridianos 101° 25' y 101° 52' de longitud oeste y entre los paralelos 19° 27' y 19° 44' de latitud norte (Figura 1).

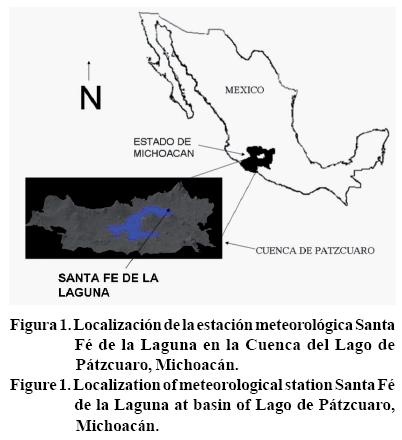
La cuenca de Pátzcuaro es cerrada con superficie de 956.2 km², los escurrimientos superficiales descargan en el Lago de Pátzcuaro, el cual ocupa una superficie 9.3% del área total de la cuenca (Tiscareño et al., 1999). Las laderas de la cuenca tienen pendiente menor de 50% ocupan el 97.6% de la superficie de la cuenca (DETENAL, 1979). La precipitación promedio anual es de 1002 mm con una marcada presencia estacional, donde 91.1% ocurre durante el periodo de mayo a octubre con distribución irregular. La importancia de la cantidad y distribución de la lluvia en la región, radica en la necesidad de satisfacer las necesidades de agua de la agricultura de temporal que cubre 33.8% de la superficie de la cuenca. El resto de la superficie (66.2%) corresponden a áreas urbanas, de uso pecuario, vegetación acuática y agua somera (Amador, 2000). Se utilizó la serie histórica de precipitación entre enero de 1978 a agosto de 1996 del Servicio Meteorológico Nacional (SMN). Se elaboró una base de datos a nivel diario en Excel, a partir de la cual se generaron archivos para cada mes (escala mensual) y para cada año (escala anual). Estos mismos archivos se guardaron como series de tiempo con la extensión "ts", para calcular la dimensión fractal y el coeficiente de Hurst, utilizando los métodos de referencia de ondoletas (D_w) y del rango re-escalado (D_R/S) diseñados para el análisis de los patrones auto-afines con el programa Benoit^®.

Método de ondoletas (D_w)

El método de ondoletas analiza las variaciones localizadas del coeficiente de Hurst, relaciona los datos mediante la descomposición de la serie de tiempo en tres armónicas dentro del espacio frecuencia-tiempo. Esta descomposición es útil para determinar los tipos de variabilidad que dominan en una serie de datos, así como su dinámica en tiempo. El método es válido para el análisis de las trazas auto-afines, donde la varianza no es constante. La forma de la ondoleta se determina en periodos espaciados y cuantifica la forma en que varía o se mantiene constante.

El algoritmo consideran transformadas de ondoleta, cada una con su propio y diferente coeficiente de escalado (a_i); donde: S₁, S₂ .........S_n son las desviaciones estándar a partir de cero de los coeficientes de escalamiento respectivo (a_i).

La tasa de variación de las desviaciones estándar

G₁ , G₂ .......G_n-1 se define como:

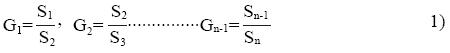
El valor promedio de G_i se estima a partir de la ecuación:

El coeficiente de Hurst se calcula como:

Donde: f= función heurística; que se usa para aproximar el coeficiente de Hurst por G_Promedio para las trazas estocásticas auto-afines. De manera práctica el coeficiente de Hurst es relacionado con la dimensión fractal (D) de la siguiente manera (Carbone et al., 2004):

Método del rango re-escalado (R/S)

Al considerar un intérvalo de una traza o serie de tiempo es posible obtener dos parámetros: el rango de variación de la variable (R_(w)) y la desviación estándar (S_(w)). El primero de ellos se determinó con respecto a la tendencia dentro del intérvalo; esta tendencia se estima como la unión entre el primero y el último valor dentro del intérvalo. El segundo parámetro es la desviación estándar de la primera derivada delta y de los valores de y dentro del intérvalo. Las primeras diferencias entre y' se definen como las diferencias entre los valores de y en algún punto x y otro, ubicado en una posición (x - dx) previa sobre el eje x:

Donde: delta x(dx) es el intérvalo de muestreo, es decir, el intérvalo entre los dos valores consecutivos de x que se están considerando. Una medida confiable de S_(w) requiere que los datos se calculen con un intervalo de muestreo dx constante, porque se busca que las diferencias esperadas entre los valores consecutivos de y sean una función del tipo ley de potencia con la distancia (w) que los separa:

S_(w) en el método de rango re-escalado, se utiliza para normalizar el rango R_(w) para permitir comparaciones de diferentes conjuntos de datos; si no se utiliza S_(w), el rango R_(w) puede calcularse sobre los conjuntos de datos que tienen un intervalo de muestreo no-constante. El rango de re-escalado se define como:

Donde: w= longitud de ventana o intervalo de análisis de los datos y los paréntesis angulados <R_(w) > denotan el promedio de un número considerado de valores de R_(w). En la práctica, para una determinada longitud de ventana w, se subdivide la serie de tiempo analizada en un número de intervalos de longitud w y se determina R_(w) y S_(w) para cada intérvalo y se calcula para cada ventana R_(w)/S_(w) y la tasa promedio de < R_(w)/S_(w)>.

Este proceso se repite en cada longitud de ventana seleccionada por el algoritmo de manera automática. El logaritmo de R_(w)/S_(w) es graficado versus los logaritmos de w. Si la traza es auto-afín, la gráfica debe seguir una línea recta cuya pendiente es igual al coeficiente de Hurst (H). La dimensión fractal de la traza se calcula a partir de la relación mencionada entre el coeficiente de Hurst y la dimensión fractal.

Coeficiente de Hurst

El coeficiente de Hurst determina la intensidad de la dependencia entre los datos y de acuerdo con su magnitud, la serie de tiempo se clasifica como persitente (0.5 < H ≤ 1), que significa que existe dependencia entre un evento y los ocurridos anteriormente; cuando se clasifica como antipersistente (0 ≤ H < 0.5) significa que en la serie persite una tendencia a ser caótica o que sus valores tienen alta volatilidad. En el caso de que H= 0.5 se concluye que la serie de tiempo es aleatoria y los datos no se correlacionan entre sí; es decir, los valores futuros de la serie no son influenciados entre ellos por lo que ocurre en el presente (Palomas, 2002).

Este último caso modela el ruido blanco, la distribución Gaussiana normal o el movimiento Browniano clásico. Los dos casos anteriores describen los movimientos Brownianos fraccionarios. El valor de H permite determinar si el comportamiento de datos de la precipitación es persistente o anti-persistente (Burgos y Pérez, 1999; Miranda et al., 2004) con correlación positiva o negativa entre los eventos.

 

RESULTADOS Y DISCUSIÓN

Variabilidad de la precipitación diaria

Los estadísticos obtenidos para la escala diaria mostraron que el promedio fue 1.85 mm con desviación estándar de 4.65; sin embargo, se han registrado eventos extremos de 46.2 mm (Cuadro 1). La magnitud de los eventos se muestran en el histograma de frecuencias relativas (Figura 2).

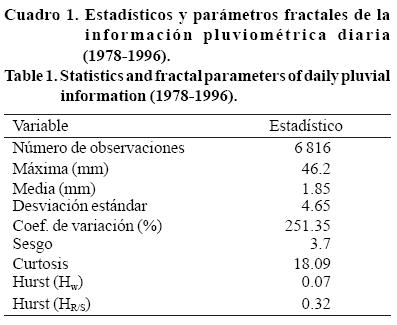
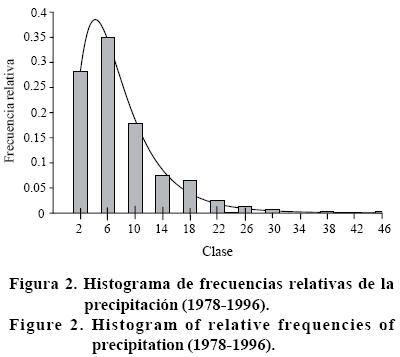
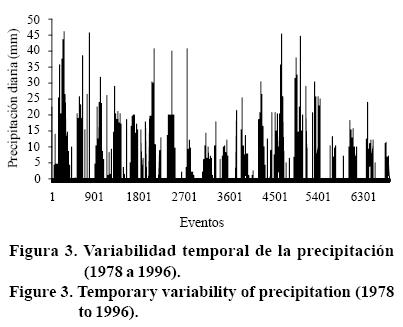
La forma del histrograma es de cola a la derecha lo que significa que gran parte de los datos se encuentran en el extremo izquierdo, esto en términos prácticos indica que la base de datos comprende dos límites contrastantes; por un lado, existe una gran concentración de eventos menores a 8 mm (58%) cuya capacidad erosiva es mínima y eventos mayores a 40 mm, considerados de alta capacidad erosiva. Los eventos de precipitación durante el periodo de 1978 a 1996, mostraron un comportamiento ondulatorio de la magnitud entre años, explicados como precipitación aleatoria a través del tiempo (Figura 3).

Análisis fractal de los eventos diarios

Los parámetros fractales, que estiman la tendencia o rugosidad de la distribución de los eventos de precipitación (H_w y H_R/S), mostraron que las series y los periodos de tiempo estudiados tienden a ser antipersistentes (0≤ H≤ 0.5) o de alta rugosidad debido a la correlación negativa entre los eventos de precipitación a escala de tiempo diaria (Cuadro 1). Cuando el coeficiente de Hurst es mayor que 0.5 los eventos no son independientes, por que cada evento se relaciona con los eventos que le precedieron. Si el proceso es persistente, los eventos recientes tienen más influencia que los anteriores; sin embargo, éstos continuan influyendo en el desempeño general de la serie de tiempo (Palomas, 2002).

La anti-persistencia observada en la serie de tiempo de precipitación diaria sirvió de base para caracterizar el patrón estructural de la información pluviométrica de la región en términos estadísticos. Cabe mencionar que la rugosidad medida en términos del coeficiente de Hurst, fue calculada con la técnica de ondoletas por ser esta de mayor rigor que el de rango re-escalado.

Análisis fractal a escala mensual

La dimensión fractal promedio para los meses que corresponden al periodo de lluvia (mayo a octubre), fue 1.81 para D_w y 1.78 para D_R/S con promedio para los 12 meses de D_w= 1.78 y D_R/S= 1.49 (Cuadro 2). El coeficiente de Hurst obtenido por el método de ondoletas tuvo un promedio mensual de H_w= 0.22, lo cual confirma que las series de tiempo mensuales muestran tendencia a ser anti-persistentes (0≤H≤0.5), similar a los eventos diarios; en contraste, el método de rango re-escalado para la misma serie de tiempo mostró un promedio mensual de H_R/S= 0.51, que corresponde al tipo de ruido blanco, que demuestra la baja precisión para este tipo de análisis.

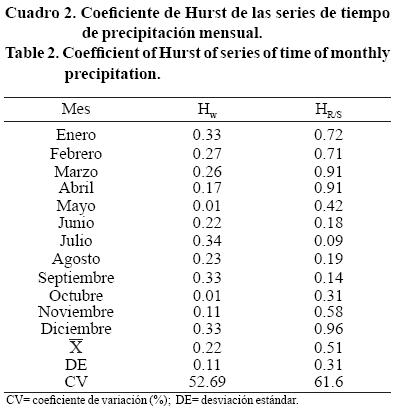
Durante el periodo de junio a septiembre la rugosidad de los eventos de precipitación tiende a la anti-ersistencia con valor promedio de H_w de 0.27; cuya variabilidad no es marcada como al inicio y fin de la época de lluvia. La anti-persistencia de la distribución se relaciona con el tipo de tormentas que se presentan en la región, las cuales se caracterizan por la alta variabilidad en magnitud, pero con mayor frecuencia; lo que se refleja en la rugosidad de la serie de tiempo.

Análisis fractal a escala anual

En general, el método de ondoletas describió la variabilidad promedio de todos los años, mostró correlación negativa a periodos largos entre los eventos de lluvia, que los ubica en el grupo de los anti-persistentes (Cuadro 3).

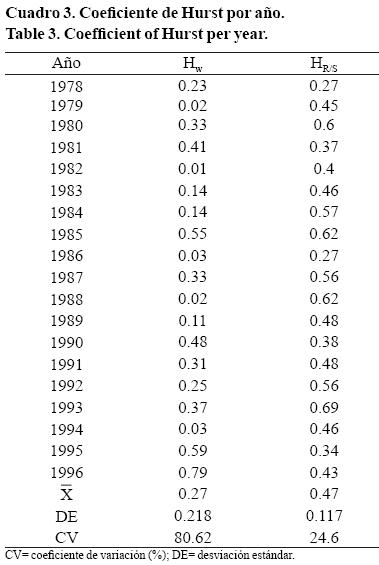
El método R/S tipificó la mayor parte de las series de tiempo como aleatorias o con total independencia entre eventos, con valor promedio del coeficiente de Hurst igual a 0.47. Los valores más altos del coeficiente se estimaron para los años 1985, 1988 y 1993 (H_R/S= 0.62, 0.62 y 0.69, respectivamente). Los resultados anteriores muestran que la técnica de ondoletas, es más rigurosa en la extracción de la rugosidad del patrón estructural de los datos pluviométricos a escala anual (H_w= 0.27), comparada con el método del rango re-escalado (H_R/S= 0.47); el cual no extrajo adecuadamente los valores del coeficiente H, cuya distribución en este caso tiende a un ruido blanco. Los resultados anteriores indican que el método de ondoletas permite una estimación precisa y exacta de la rugosidad en las series de tiempo amplias.

Se infiere que la estructura de la base de datos es importante en la selección del método para el cálculo del coeficiente de Hurst. Se ha reportado que las series de tiempo de precipitación analizadas a escalas anual y mensual, no muestran la diferencia entre estaciones; sin embargo, a escala diaria pueden mostrar independencia entre la magnitud de los eventos (Kipkorir, 2002). El patrón estructural observado en la serie de tiempo de precipitación de Santa Fé de la Laguna es anti-persistente a escalas de tiempo diario (H_w= 0.07), mensual (H_w= 0.22) y anual (H_w= 0.27); es decir, cada evento o periodo de lluvias tiene una gran posibilidad de ser diferente al anterior (Miranda et al., 2004).

Resultados similares fueron reportados por Burgos y Pérez (1999), quienes utilizaron una serie de tiempo de precipitación a escala decenal y obtuvieron un valor de H= 0.21 el cual se interpretó como de gran irregularidad; en el caso del coeficiente de Hurst extraído por el método del rango de reescalado, la tendencia a ser anti-persistente sólo fue detectada a escala diaria (H_R/S= 0.32); mientras que a escala mensual y anual, el patrón estructural se caracterizó como aleatorio H_R/S= 0.51 y H_R/S= 0.47, respectivamente).

Invarianza estadística al escalado en tiempo

El análisis de las series de precipitación a diferentes escalas permitió determinar el grado de invarianza al escalado en tiempo de los parámetros estadísticos. Los resultados mostraron que en las escalas mensual y anual sólo la medida de la tendencia central de la distribución de los datos presentó invarianza al escalado como se muestra en la (Figura 4); en tanto que el coeficiente de variación, sesgo y curtosis presentaron valores bajos del coeficiente de determinación. El ajuste a un modelo de regresión lineal fue R² = 0.82 con el cual es posible estimar el valor promedio de la variable a diferentes escalas temporales y utilizarlo en métodos de extrapolación de información.

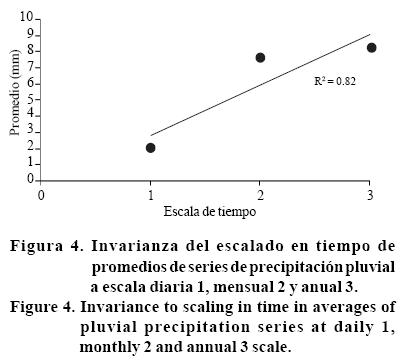
Invarianza fractal al escalado en tiempo

El coeficiente de Hurst extraído por el metodo de ondoletas mostró R²= 0.92 superior al obtenido con rango reescalado (R²= 0.56), lo cual se debió que el método de ondoletas establece correlaciones entre la distribución diaria, mensual, anual y una familia de curvas de forma similar (Gaucherel, 2002); mientras que el método del rango reescalado no estima la variación en forma oscilatoria, sino que considera la longitud de la serie y la divide en un conjunto de sub-series con base en el rango (R_(w)) y la desviación estándar (S_(w)) para cada una de ellas (Figura 5).

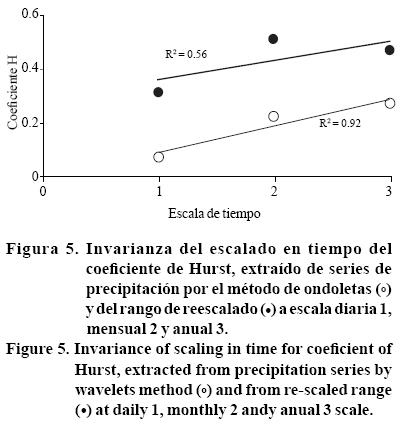
Una posible aplicación de estos resultados en la modelacion hidrológica, es la utilización de la propiedad fractal de la invarianza al escalado de serie de tiempo de la estación de Santa Fé de la Laguna para extrapolar o generar datos diarios a partir de series anuales y viceversa utilizando programas de generadores de trazas o series de tiempo a partir de la rugosidad del patrón estructural de la información disponible.

 

CONCLUSIONES

La aleatoriedad e invarianza al escalado de la información pluviométrica dentro de las series de tiempo, es difícil de cuantificar mediante la estadística convencional o descriptiva. El grado de aleatoriedad obtenido de las series, a través del análisis de las series de tiempo por medio de la geometría fractal y del coeficiente de Hurst, permiten determinar en forma consistente y a diferentes escalas de tiempo el grado de aleatoriedad de la precipitación pluvial.

El método de ondoletas es más riguroso que el método de rango reescalado para determinar el grado de aleatoriedad de las series de tiempo de precipitación pluvial.

Los parámetros fractales H_w y H_R/S son importantes para diferenciar la aleatoriedad y el grado de invariancia a diferentes escalas de tiempo de la precipitación pluvial.

 

AGRADECIMIENTO

Al Consejo Nacional de Ciencia y Tecnología (CONACYT) por el apoyo a través del proyecto nacional "Definición y mapeo de indicadores para el manejo sostenible del suelo" (G-33156-B). Se agradecen las aportaciones de los revisores que mejoraron sustancialmente la calidad de este documento.

 

LITERATURA CITADA

Amador, G. A. 2000. Simulación dinámica del impacto ambiental por actividades agrícolas en la cuenca de Pátzcuaro, Michoacán. Tesis de Maestría. Universidad Michoacana de San Nicolás de Hidalgo, México. 101 p.         [ Links ]

Arnaud, P.; Bouvier, Ch.; Cisneros, L. and Dominguez, R. 2002. Influence of rainfall spatial variability on flood prediction. J. Hydrol. 260:216-230.         [ Links ]

Balankin, A. S.; Morales, M. O.; Gálvez, M. E. and Pérez, A. A. 2004. Crossover from antipersistent to persistent behaviour in time series possessing the generalized dynamic scaling law. Review Ser. 69(3):45-54.         [ Links ]

Bullock, S. H. 2003. Seasonality, spatial coherence and history of precipitation in a desert region of the Baja California peninsula. J. Arid Environ. 53:169-182.         [ Links ]

Burgos, T. R. and Pérez, E. V. 1999. Estimation of the fractal dimension of a rainfall time series over a zone relevant to the agriculture in Havana. SOMETCUBA. Bulletin. Vol. 5. Num. 1. 35 p.         [ Links ]

Burlando, P. and Rosso, R. 1996. Scaling and multiscaling models of depth-duration-frequency curve for storm precipitation. J. Hydrol. 187:45-64.         [ Links ]

Carbone, A.; Castelli, G. and Stanley, H. E. 2004. Analysis of clusters formed by the moving average of a long-range correlated time series. Phys. Rev. E69: 026105.         [ Links ]

Comrie, A. C. and Broyles, B. 2002. Variability and spatial modeling of fine-scale precipitation data for the Sonora Desert of south-west Arizona. J. Arid Envir. 50:573-592.         [ Links ]

Dirección de Estudios del Territorio Nacional (DETENAL). 1979. Descripción de la leyenda de la carta edafológica (DETENAL). SPP. México. 104 p.         [ Links ]

Entekhabi, D.; Asrar, G. R.; Betts, A. K.; Beven, K. J.; Bras, R. L.; Duffy, C. J.; Dunne, T.; Koster, R. D.; Lettenmaier, D. P.; McLaughlin, D. B.; Shuttleworth, W. J.; Van Genuchten, M. T.; Wei, M. Y.; and Wood, E. F. 1999. An agenda for land surface hydrology research and a call for the second international hydrological decade. Bulletin of the Amer. Meteorol. Soc. 80:2043-2058.         [ Links ]

Gaucherel, C. 2002. Use of wavelet transform for temporal characterization of remote watersheds. J. Hydrol. 269:101-121.         [ Links ]

Giménez, D.; Rawls, W. J. and Lauren, J. G. 2000. Scaling properties of saturated hydraulic conductivity in soil. In: Pachepsky, Y. A.; Crawford, J. W. and Rawls, W. J. (eds). Fractals in soil science. Elsevier Science B. V. 115-130 pp.         [ Links ]

Kipkorir, E. C. 2002. Analysis of rainfall climate on the Njemps Flats Baringo District, Kenya. J. Arid Envir. 50:445-458.         [ Links ]

Kumar, P. and Foufoula-Georgiou, E. 1993. A multicomponent decomposition of spatial rainfall fields 1. Segregation of large-and small-scale feactures using wavelets transforms. Water Resour. Res. 29: 2515-2532.         [ Links ]

Lázaro, R.; Rodrigo, F. S.; Gutiérrez, L.; Domingo, F. and Puigdefábregas, J. 2001. Analysis of a 30 - year rainfall record (1967-1997) in semi-arid SE Spain for implications on vegetation. J. Arid Envir. 48:373-395.         [ Links ]

Mandelbrot, B. B. 1983. The fractal geometry of nature. San Francisco, W. H. Freeman, Oxford. 468 p.         [ Links ]

Mandelbrot, B. B. 2002. Gaussian self-affnity and fractals. Globality. The Earth, 1/f Noise, and R/S. Springer. 654 p.         [ Links ]

Miranda, J. G. V.; Andrade, R. S. F.; Da Silva, A. B.; Ferreira, C. S.; González, A. P. and Carrera López, J. L. 2004. Temporal and spatial persistence in rainfall records from Northeast Brazil and Galicia. Theor. Appl. Climatol. 77:113-121.         [ Links ]

Morales, M. O.; Balankin, A. y Hernández, L. M. 2005. Metodología de predicción de precios del petróleo basada en la dinámica fractal. Científica. 9:3-11.         [ Links ]

Olsson, J.; Niemczynowics, J.; Brendsson, R. and Larson, M. 1992. An analisys of the rainfall time structure by box counting-some practical implications. J. Hydrol. 137:261-277.         [ Links ]

Olsson, J. and Niemczynowicz, J. 1996. Multifractal analisys of daily spatial rainfall distributions. J. Hydrol. 187:29-43.         [ Links ]

Osborn, H. B. and Hickok, R. B. 1968. Variability of rainfall affecting runoff from a semi-arid rangeland watershed. Water Resources Res. 4:199-203.         [ Links ]

Palomas, M. E. 2002. Evidencia e implicaciones del fenómeno Hurst en el mercado de capitales. Gaceta de Economía. Año 8. 15:117-153.         [ Links ]

Richter, D. D.; Ralston, C. W. and Harms, W. R. 1983. Chemical composition and spatial variation of bulk precipitation at a coastal plain watershed in South Carolina. Water Resour. Res. 19:134-140.         [ Links ]

Rivera, A. 2000. El cambio climático: el calentamiento de la tierra. Ed. Debate, S. A. Primera edición. Madrid. 165 p.         [ Links ]

Salas, J. D.; Delleur, J. W.; Yevjevich, V. and Lane, W. L. 1985. Applied modeling of hydrologic time series. Water Resources Publications. Littleton, CO. USA. 484 p.         [ Links ]

Schroeder, M. 1991. Fractals, chaos, power laws: Minutes from an infinite paradise. Freeman, W. H. & Co. New York. New York. USA. 288 p.         [ Links ]

Shanan, L.; Evenari, M. and Tadmor, N. H. 1967. Rainfall patterns in the central negev desert. Isr. Exploration J. 17:163-184.         [ Links ]

Tiscareño, L. M.; Báez, G. A. D.; Velásquez, V. M.; Potter, K. N.; Stone, J. J.;Tapia, V. M. and Claverán, A. R. 1999b. Agricultural research for watershed restoration in central México. J. Soil and Water Cons. 36:686-692.         [ Links ]

Valdez-Cepeda, R.; Mendoza, B.; Díaz-Sandoval, R.;Valdés-Galicia, J.; López-Martínez, D. J. and Martínez-Rubin, C. E. 2003a. Power-spectrum behavior of yearly mean grain yields. Fractals. 11:295-301.         [ Links ]

Valdez-Cepeda, R.; Hernández-Ramírez, D.; Mendoza, B.; Valdez-Galicia, J and Maravilla, D. 2003b. Fractality monthly extreme minimum temperature. Fractals.11:137-144.         [ Links ]

Wight, J. R. and Hanson, C. L. 1991. Use of stochastically generated weather records with rangelands simulations models. J. Range Managament. 44:282-285.         [ Links ]