nueva página del texto (beta)
Español (pdf)
Artículo en XML
Referencias del artículo
Traducción automática
Enviar artículo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Las prácticas educativas deben adaptarse a los cambios sociales, con la finalidad de acercarse a los alumnos y aprovechar las ventajas que brindan estos cambios. En la actualidad, la presencia de las tecnologías digitales se puede apreciar en todas las actividades sociales. El Instituto Nacional de Estadística y Geografía, en México y en su encuesta sobre uso de tecnología (INEGI, 2017, p. 1) reporta que “50.6 millones de personas son usuarios de una computadora, y 71.3 millones utilizan Internet”, así que involucrar estas tecnologías en el aula se convierte en una prioridad de la labor docente.
Uno de los objetivos de la Organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura (UNESCO), es el de la “Educación para todos”, y está apoyando para que las personas empleen sus dispositivos móviles en actividades académicas para enfrentar los retos de los diferentes contextos educativos, y sean capaces de poder trabajar contenidos académicos en diferentes formatos (UNESCO, 2013).
El aprendizaje móvil tiene que ver con la forma en cómo el estudiante logra comunicarse, descargar información, resolver actividades y trabajar con diferentes aplicaciones en cualquier lugar y momento. (UNESCO, 2013). El aprendizaje móvil también incluye el esfuerzo que implica apoyar distintas metas educativas como es el caso de la administración efectiva de los sistemas escolares y una mejor comunicación entre las escuelas y las familias.
Por otro lado, uno de los objetivos de las escuelas de nivel superior, consiste en que sus estudiantes alcancen un nivel de desarrollo eficiente para incorporarse al campo laboral, pero una problemática que se está viviendo, es que los estudiantes al ingresar al nivel superior muestran deficiencias en diferentes aspectos. Uno de ellos corresponde al de las matemáticas, lo que se traduce en un incompleto desarrollo de sus competencias y, consecuentemente, en tropiezos durante su trayectoria académica en las distintas asignaturas de formación básica. Como parte de los factores que desencadenan esta situación están: la falta de hábitos de estudio; las estrategias de los profesores; el uso incorrecto de la información y de los recursos obtenidos de internet; y falta de motivación y concentración de los estudiantes, por mencionar algunos.
En la asignatura de Cálculo se ha detectado la falta de significado y sentido (Cuesta, Escalante y Ruiz, 2016) que muchos de los estudiantes de nivel medio y superior tienen de los conceptos involucrados (función, límite, derivada e integral). Algunos autores de la literatura de matemática educativa lo atribuyen a que el estudio del Cálculo se restringe a una manipulación algebraica dejando a un lado las múltiples representaciones que hay (Hitt, 2014., Sánchez, García & Llinares, 2008., Oliveros, 1999., Duval, 1998). El punto de vista de estos investigadores, es que las tareas de conectar las diferentes representaciones de un concepto como la representación numérica, algebraica o analítica y gráfica, ayudan a su comprensión.
Esta problemática, de la falta de otorgamiento de significado y sentido a los conceptos involucrados en el Cálculo, también se refleja en los estudiantes de una de las Unidades Académicas del Instituto Politécnico Nacional (ESCOM-IPN), lo que influye en que no logran enfrentar con éxito las situaciones problemáticas que se les pide resolver en la unidad de aprendizaje de Cálculo Aplicado, trayendo como consecuencia:
Bajo aprovechamiento en la materia
No conectar los conceptos con los de su carrera
Alto índice de reprobación
Falta de interés en aprender
Deserción
Por otro lado, Artigue (2011) señala que aunque los alumnos realizan de manera más o menos mecánica algunos cálculos de derivadas, al resolver algunos problemas estándar tienen dificultades en la comprensión satisfactoria de los conceptos y métodos de pensamiento que conforman el centro del análisis matemático.
Una de las razones principales de este problema es que los alumnos no conectan los conceptos matemáticos con actividades que realizan, y ven en ellos sólo métodos abstractos que deben aplicar cuando se les señala que lo hagan.
Hitt (2013, 2) al realizar un análisis de cómo se utilizan los problemas y contextos físicos en la impartición de una clase, concluye que: “Pareciera que el contexto es importante para introducir un concepto matemático, el mismo es abandonado rápidamente, proporcionado tanto en el libro de texto como en el aula, una primicia a las representaciones algebraicas sobre las otras representaciones”.
Dada la importancia que ha cobrado el aprendizaje electrónico y el móvil, se decidió realizar una investigación, a través de la cual se construyó un escenario de aprendizaje tecnopedagógico, proponiendo como caso de estudio trabajar con una de las asignaturas que tiene un alto índice de reprobación o de fracaso en estudiantes de nivel superior, que es Cálculo Aplicado, en particular se desarrolló este escenario de aprendizaje con la comunidad de estudiantes que cursan la carrera de Ingeniería en sistemas computacionales, en la Escuela Superior de Cómputo en la Ciudad de México (ESCOM-IPN), durante el semestre Agosto-Diciembre de 2018. Se trabajó con un Escenario de Aprendizaje Tecnopedagógico (EATP), el cual se apoyó en lo señalado en la literatura como modelo TPACK, por sus siglas en inglés: Technological Pedagogical Content Knowledge; debido a que interesó abordar la problemática de forma integral, es decir, no solo desde el punto de vista de la asignatura de Cálculo Aplicado, sino entretejida con los aspectos pedagógicos y tecnológicos.
Problema de investigación
El problema que aborda la investigación presentada en este artículo es que hay un alto índice de reprobación en las asignaturas de Cálculo y Cálculo Aplicado en las instituciones de nivel superior del IPN. Se eligió una de las unidades académicas, la Escuela Superior de Cómputo. Se solicitaron al Departamento de Control Escolar las estadísticas de los últimos cinco años y se encontró que de la materia de Cálculo se tiene el 45% de reprobación y de Cálculo Aplicado el 40%. Se propuso como premisa que uno de los motivos de la reprobación de los estudiantes es el hecho de la falta de sentido que le dan al trabajo teórico visto en clase, por lo que el propósito de la investigación fue, primeramente, revisar y entender el motivo de los errores cometidos por los estudiantes al trabajar problemas que son aplicaciones del Cálculo, mediante el análisis de las respuestas dadas a un cuestionario diagnóstico y, después, proponer estrategias de aprendizaje que pudieran llevarse a cabo, para motivar al estudiante a abordar diferentes situaciones, construyendo un Escenario de Aprendizaje Tecnopedagógico (EATP), el cual emplea en la parte tecnológica un sistema computacional desarrollado como parte de la investigación que se muestra en el presente documento y al que se le denominó SIMAATCA, el cual contiene diversos recursos digitales educativos. Este sistema se puede trabajar tanto en la computadora de escritorio como en dispositivos móviles.
La finalidad última de la investigación es que los estudiantes puedan resolver problemas de Cálculo logrando aplicar de forma correcta los conceptos fundamentales y que los estudiantes pudieran enfrentar con éxito los exámenes a título de suficiencia (ETS) que aplica la escuela.
La elección del modelo TPACK como método de trabajo fue debido a que propone un trabajo integral en el salón de clases al considerar no solo el contenido matemático sino el aspecto pedagógico que permite llevar a cabo los diferentes momentos del proceso enseñanza-aprendizaje de los estudiantes (inicio, desarrollo, evaluación, retroalimentación), tomando en consideración teorías psicopedagógicas para el tratamiento de los contenidos, además de que se incorpora el uso de las tecnologías de información y comunicación para poder tratar dichos contenidos buscando el desarrollo de las diferentes habilidades de los estudiantes.
Existen otros métodos reportados en la literatura de matemática educativa para abordar situaciones de matemáticas en el salón de clase, como el método denominado ACODESA propuesto por Hitt (2007) que es una adaptación a un acercamiento sociocultural del aprendizaje de las matemáticas (ver Hitt, González Martín y Morasse, 2008). Con este método, el profesor no dictamina sobre lo realizado por los alumnos en las primeras etapas, salvo al final en donde se da un proceso de institucionalización. El profesor es un guía y es deber de los estudiantes el argumentar y validar sus producciones. Aunque en este método también se toma en cuenta el uso de tecnología educativa, no fue seleccionado en la investigación presentada en este artículo debido a que lo que se buscaba es que el profesor tuviera más actuación en el proceso de enseñanza-aprendizaje, al diseñar un escenario que le permitiera organizar los contenidos de la materia para ser abordados de forma integral por parte del alumno, porque el objetivo final es que los alumnos logren resolver problemas para poder enfrentar los exámenes a título de suficiencia que aplica la escuela.
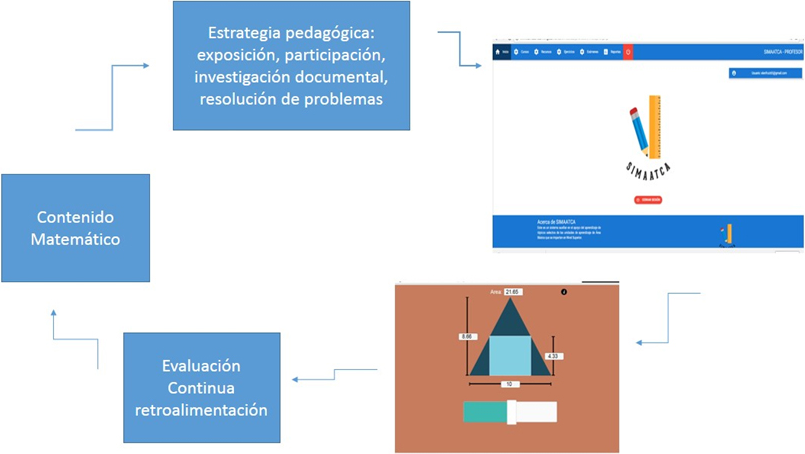
En la parte tecnológica se trabajó con SIMAATCA, que es un sistema que se adapta al estilo de aprendizaje y al nivel de dificultad del estudiante, proporcionándole recursos digitales que son acordes a los perfiles detectados. Los recursos son multimedia: van desde PDF, hasta programas con los que puede interactuar el estudiante. SIMAATCA hasta ahora contiene recursos que corresponden a los temas del plan de estudios de la Unidad de Aprendizaje de Cálculo Aplicado (ESCOM-IPN, 2009). En las Figs. 1, 2 y 3 se muestran interfaces del inicio del sistema, preguntas que tienen que ver con el estilo de aprendizaje y nivel de dificultad de los problemas que logran resolver los estudiantes.
Fuente: Elaboración propia.
Fig. 2 Interfaz que muestra una pregunta del cuestionario, referente a estilos de aprendizaje.
Fuente: Elaboración propia.
Fig. 3 Interfaz gráfica con preguntas para detectar el nivel de dificultad.
Aspectos teóricos a considerar en el trabajo del aula con el Escenario de aprendizaje Tecnopedagógico
El trabajo realizado en el aula con el EATP consideró tomar en cuenta la visualización matemática, ya que ayuda al estudiante en la construcción de una estructura cognitiva sobre el control de la actividad matemática. Además, un alumno que no logra trabajar con las manipulaciones algebraicas, puede encontrar apoyo en la visualización y la aritmética para entender y controlar los resultados obtenidos en los procesos algebraicos.
De acuerdo con este enfoque, la experimentación y el análisis de los resultados se realizaron siguiendo un marco teórico sobre la visualización matemática (según Zimmermann & Cuningham, 1991), sobre los procesos de control (según Saboya, 2010) que los estudiantes desarrollan para llevar a cabo una actividad matemática específica, y alrededor de la transición de la aritmética al álgebra (según Kaput, 2000, 2008; Kieran, 2007; y Artigue, 2011).
Aspectos metodológicos
Sobre el modelo TPACK
Con relación al Escenario de Aprendizaje Tecnopedagógico (EATP), éste se apoyó, para su construcción, en el Modelo TPACK (Technological Pedagogical Content Knowledge). Sobre este modelo se tiene lo siguiente: en la década de los 80, Shulman (1986), introdujo su modelo denominado Pedagogical Content Knowlegde, reducido a PCK, por sus siglas. Él señala que en la enseñanza no solo es requerido el dominio de la materia o de la disciplina con la que se va a trabajar, sino la forma, o las diferentes maneras que encuentra el profesor para representar el contenido que lo haga accesible a los estudiantes, es decir Shulman enfatiza la importancia que tiene la manera en que el tema es transformado para la enseñanza.
Los aspectos o ejemplos que Shulman considera como importantes para PCK son las analogías, ilustraciones, ejemplos, explicaciones y demostraciones, o, en otro palabras, las formas de representar y formular el tema para hacerlo más accesible y comprensible al estudiante.
Koehler y Mishra (2006), observaron que las tecnologías juegan un papel crítico en cada uno de estos aspectos. Desde dibujos en una pizarra, hasta interactivos o simulaciones multimedia o hipertextos basados en la web; por lo que las tecnologías han permitido una gama de representaciones, ejemplos, explicaciones y demostraciones que pueden ayudar a hacer los contenidos de una disciplina más accesible para el alumno.
Por lo tanto, Koehler y Mishra (2006), consideran que el conocimiento de la tecnología se convierte en un aspecto importante del conocimiento general del docente. Lo que es interesante es que las discusiones actuales sobre el papel del conocimiento de la tecnología parecen compartir muchos de los mismos problemas que Shulman identificó en la década de 1980. Por ejemplo, antes del trabajo seminal de Shulman en PCK, el conocimiento del contenido y el conocimiento de la pedagogía fueron considerados separados e independientes el uno del otro. Del mismo modo, hoy, el conocimiento de la tecnología a menudo se considera separado del conocimiento de la pedagogía y contenido.
El conocimiento del contenido pedagógico y tecnológico (TPACK) implica entrelazar el qué enseñar, (contenido), con el cómo enseñar (mediante tecnología) y el para qué enseñarlo (pedagogía); es decir se requiere de que el profesor cuente con una formación en aspectos pedagógicos, pero no generales, sino aquellos que permita darse cuenta de las dificultades que un estudiante enfrenta al abordar una disciplina, además requiere contar con conocimiento de las nuevas tecnologías y su uso en cuestiones educativas.
Por lo tanto, el modelo de integración de la tecnología en la enseñanza y el aprendizaje propicia el desarrollo de un buen contenido mediante un entretejido reflexivo de las tres fuentes clave de conocimiento: tecnología, pedagogía y contenido. El núcleo de esto es que no hay una solución tecnológica única que aplica para cada maestro, cada curso o cada punto de vista de la enseñanza. Para que haya calidad en la enseñanza se requiere desarrollar una comprensión del complejo de relaciones entre tecnología, contenido y pedagogía, y el uso de esta comprensión para desarrollar estrategias apropiadas, específicas al contexto y representaciones.
Estrategia para aplicar el modelo de TPACK
Harris and Hofer (2009) señalan que antes de seleccionar los recursos tecnológicos como parte del proceso de enseñanza aprendizaje, se requiere tener claros los objetivos curriculares que se desean alcanzar en relación a la materia o disciplina con la que se va a trabajar, así como elegir las estrategias que permitirán un involucramiento del estudiante con el contenido a abordar (Harris And Hofer, 2009; Flores, 2013).
Para la implementación del modelo TPACK, Harris y Hofer (2005) proponen una serie de pasos a seguir, los cuales fueron tomados en consideración para el trabajo que se expone en este artículo:
Determinar los objetivos de la disciplina con la que se va a trabajar.
Formular actividades.
Determinar estrategias de enseñanza y de aprendizaje.
Escoger recursos tecnológicos que permitan llevar a cabo las actividades formuladas con las estrategias seleccionadas.
Además Harris y Hofer (2009) proponen una taxonomía de las actividades de matemáticas que se pueden emplear como parte de la planificación de las tareas que un docente lleva a cabo. Esta taxonomía se fundamenta en los 7 géneros relacionados con las actividades propuestas por los estándares del National Council of Teachers of Mathematics (NCTM). Los 7 géneros considerados son:
Método
Descripción del contexto
El estudio se desarrolló en una de las Unidades Académicas del Instituto Politécnico Nacional (ESCOM IPN), con dos grupos de 33 estudiantes cada uno; estos grupos son constituidos por la institución de acuerdo al promedio que obtuvieron los estudiantes en su primer semestre. Los alumnos desde segundo semestre y hasta el octavo, eligen el horario en el que van a cursar las materias establecidas en la currícula, para ello a los estudiantes se les asigna un día y una hora en la que se pueden inscribir, esta asignación obedece al promedio que obtuvieron en primer semestre, de tal forma que el primer día de inscripciones se matriculan los alumnos con más alto promedio y así sucesivamente. Los dos grupos seleccionados correspondían al segundo semestre de la carrera de Ingeniería en Sistemas computacionales. Los estudiantes estaban inscritos en la asignatura de Cálculo Aplicado y como antecedente, habían cursado la materia de Cálculo en su primer semestre. Ambos grupos del estudio estaban formados por estudiantes cuyo promedio en el primer semestre oscilaba entre 4 y 6 (en una escala de 0 a 10), y cerca de la mitad había reprobado la materia de Cálculo en el primer semestre. Se decidió que fuera así para poder revisar cuáles eran sus errores y hacer el seguimiento de los estudiantes, para apoyarlos en la comprensión de conceptos fundamentales, en la resolución de problemas y que lograran enfrentar con éxito los exámenes a Título de Suficiencia. Un grupo se consideró como el grupo de control GC y el otro como el grupo experimental GE. La selección fue aleatoriamente, ya que los estudiantes de ambos grupos se encontraban en situaciones similares académicamente. En el grupo de control, 47% de los alumnos había reprobado la asignatura de Cálculo y del 53% restante, la mitad había acreditado con la mínima calificación que es 6. La situación del grupo Experimental era similar, en éste, el 43% había reprobado la materia de Cálculo y del 57% restante el 37% había obtenido la calificación de 6. Los promedios de los dos grupos eran bajos. El promedio del GC era de 2.6 y el promedio del GE era de 2.7.
Diseño de la investigación
Por las características del diseño del estudio, es decir, el trabajar con dos grupos ya constituidos, aplicar un pre-test y un post-test, se utilizó con un diseño cuasi experimental. Ya que los diseños que carecen de un control experimental absoluto de todas las variables relevantes debido a la falta de aleatorización ya sea en la selección aleatoria de los sujetos o en la asignación de los mismos a los grupos experimental y control, que siempre incluyen una pre prueba para comparar la equivalencia entre los grupos, y que posiblemente poseen dos grupos (el experimental y el control), son conocidos con el nombre de cuasi experimentos. El método cuasi experimental es particularmente útil para estudiar problemas en los cuales no se puede tener control absoluto de las situaciones, pero se pretende tener el mayor control posible, aun cuando se estén usando grupos ya formados. Por ello, una característica de los cuasi experimentos es el incluir "grupos intactos", es decir, grupos ya constituidos. Algunas de las técnicas mediante las cuales se puede recopilar información en un estudio cuasi experimental son las pruebas estandarizadas, las entrevistas, las observaciones, etc. Se recomienda emplear en la medida de lo posible la pre prueba, es decir, una medición previa a la aplicación del tratamiento, a fin de analizar la equivalencia entre los grupos.,
En la búsqueda de la información proporcionada por los estudiantes, se recurrió al diseño y aplicación de dos cuestionarios, los cuales fueron aplicados de forma previa y posterior al trabajo en el aula con el Modelo Tecnopedagógico al que se le denominó Escenario de Aprendizaje Tecnopedagógico (EATP) construido para el grupo experimental (GE), y sin el empleo de éste para el grupo de control (GC). El primer cuestionario tuvo la finalidad de hacer un diagnóstico y el segundo fue de evaluación. Ambos cuestionarios se aplicaron de forma escrita a los dos grupos, y fueron empleados para medir el rendimiento académico de los dos grupos mediante la comparación de ambas calificaciones.
Preguntas de los cuestionarios
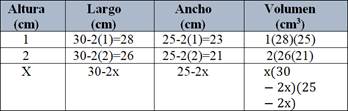
El primer cuestionario tuvo la función de realizar un diagnóstico de los grupos y el segundo permitió evaluar el avance en cada tema de la Unidad 1. En Tabla 1 aparecen las preguntas del cuestionario diagnóstico y en el Cuadro 2 se encuentran las preguntas del cuestionario final. Sobre la fiabilidad y validez de los ítems o problemas del cuestionario, estos fueron extraídos de dos libros de texto que la Academia de Ciencias Básicas de la Unidad Académica donde se realizó el estudio, emplea, y se encuentran en el Plan y Programa de Estudios de la materia de Cálculo Aplicado (Plan de estudios de Cálculo Aplicado, ESCOM-PN, 2009, p. 8). Estos problemas son usados por los profesores en los exámenes que aplican a sus grupos, por ello es que se son considerados para los cuestionarios aplicados a los dos grupos del estudio.
Tabla 1 Problemas del cuestionario diagnóstico.
| Tema | Problema |
|---|---|
| Razones d/e cambio relacionadas | 1.- Un
depósito para agua tiene la forma de un cono circular
invertido, el radio de la base es de 2 m, y la altura es de
4 m. Si el agua se bombea hacia el depósito a una razón de |
| Diferencial de una función | 2.- La
dosis D en miligramos de difenhidramina para un perro de
masa corporal w kg es de |
| Optimización | 3.- Un veterinario cuenta con 30 m de tela de alambre y quiere construir 6 jaulas para perros levantando primero una cerca alrededor de una región rectangular, y dividiendo luego la región en 6 rectángulos iguales mediante 5 rejas paralelas a uno de los lados. ¿Cuáles son las dimensiones de la zona rectangular para las que el área total es máxima? |
| Análisis de una función obteniendo puntos críticos, intervalos de crecimiento y concavidad |
4.- Determinar los puntos críticos de f, los puntos de inflexión de f, los máximos y mínimos locales de f, determinar los intervalos en los que f es creciente o decreciente, determinar los intervalos de concavidad de f y trazar su gráfica. |
| Optimización | 5.- Encuentre las dimensiones de un rectángulo con un perímetro de 100 metros, cuya área sea tan grande como sea posible. |
Fuente: Stewart (2012), Larson & Edwards (2010).
Tabla 2 Problemas del cuestionario final.
| Tema | Problema |
|---|---|
| Razones de cambio relacionadas | 1.- El
automóvil A se dirije hacia el oeste a |
| Diferencial de una función | 2.- Calcule el error relativo cometido en el cálculo del volumen de una esfera de 12.51 mm de diámetro, con un posible error de 0.01 mm, medido con un instrumento que aprecia milésimas de centímetro. |
| Optimización | 3.- Los márgenes superior e inferior de un póster miden 6 cm y los márgenes laterales miden 4 cm. Si el área del póster se fija en 384 cm2, determine las dimensiones del póster cuya área sea la mínima. |
| Análisis de una función obteniendo puntos críticos, intervalos de crecimiento y concavidad |
4.- Determinar los puntos críticos de f, los puntos de inflexión de f, los máximos y mínimos locales de f, determinar los intervalos en los que f es creciente o decreciente, determinar los intervalos de concavidad de f y trazar su gráfica. |
| Optimización | 5.- Un
terreno tiene la forma de un rectángulo con dos semicírculos
en los extremos. Si el perímetro del terreno es de 50 m,
encontrar las dimensiones del terreno para que tenga el área
máxima. 
|
Fuente: Stewart (2012), Larson & Edwards (2010).
Propuesta de trabajo
La duración del trabajo en ambos grupos fue de un mes, y se trabajaron los contenidos correspondientes a la Unidad 1 de la asignatura de Cálculo Aplicado de una Unidad Académica del IPN (ESCOM-IPN). Durante este mes se tuvieron 3 sesiones por semana, de 1.5 horas cada sesión; en total fueron 11 sesiones. El trabajo fue realizado en el semestre de agosto a diciembre de 2018. Con el GE se trabajó con el Escenario de Aprendizaje Tecnopedagógico (EATP), empleando para ello el Sistema SIMAATCA el cual asigna recursos multimedia a los estudiantes, de acuerdo a su estilo de aprendizaje y a su nivel de dificultad, además le permite al estudiante resolver exámenes y revisar su avance registrando toda actividad realizada por él. Para la recolección de los datos, así como la construcción de gráficas se empleó Microsoft Excel. También se llevó a cabo un seguimiento del desarrollo de las competencias digitales de los estudiantes, debido a la integración de las diferentes herramientas tecnológicas dentro de un entorno de aprendizaje.
Contenido matemático abordado
Con ambos grupos se trabajó la Primera Unidad temática de la asignatura de Cálculo Aplicado de la ESCOM. Pero la forma de trabajo fue diferente en cada grupo.
La Unidad 1 se titula Aplicaciones de la derivada y los temas que se trabajaron fueron:
Forma de trabajo con el grupo de control (GC)
Con el grupo de Control se trabajó sin emplear el sistema SIMAATCA, solo se usó la calculadora y, la secuencia de enseñanza no se apoyó en el modelo TPACK. El maestro encargado del grupo permitió al investigador entrar a sus clases durante el mes que duró el trabajo realizado con la Unidad 1 del programa de estudio de la asignatura de Cálculo Aplicado.
En la tabla se describen las estrategias empleadas por el profesor, así como las actividades trabajadas con uno de los temas de la primera unidad y que es el de optimización.
Tabla 3 Actividades y recursos empleados con el GC.
| Actividad | Estrategia de enseñanza | Recurso |
|---|---|---|
| Definición de problemas de optimización por parte del profesor | Expositiva Memorística | Pizarrón y libro de texto |
| El maestro emplea los criterios de la primera y segunda derivada al resolver un problema de optimización como ejemplo | Resolución de problemas | Pizarrón y calculadora |
| El maestro resuelve un segundo ejemplo | Resolución de problemas | Pizarrón, libro de texto y calculadora |
| El maestro deja de tarea ejercicios para resolver | Pizarrón y libro de texto |
Fuente: Elaborada por el autor.
Construcción del Escenario de Aprendizaje Tecnopedagógico (EATP)
El Escenario de Aprendizaje Tecnopedagógico estuvo constituido por 3 componentes: uno correspondiente al contenido de matemáticas, en el presente artículo se muestra el tema de optimización, el segundo componente se refiere al aspecto pedagógico, de tal forma que para abordar el tema se empleó el enfoque de resolución de problemas, así como el uso de diferentes estrategias propuestas por la National Council Teaching of Mathematics (NCTM) y, en relación al tercer componente, que es el tecnológico, se usó el Sistema SIMAATCA que puede ser empleado en una computadora de escritorio, o en una computadora portátil, así como en una tableta o en un celular. En este caso se trabajó con dispositivos móviles, las tabletas y los celulares de los estudiantes (Drijvers, Kieran, Mariotti, Ainley, Andresen, Chan, And Meagher, 2010).
Forma de trabajo con el grupo experimental (GE)
Con el Grupo experimental GE se trabajó empleando las etapas establecidas por Harris y Hofer (2005) para el modelo TPCAK, mencionadas en el apartado previo del presente documento, también se determinaron 2 de los 7 géneros señalados por la NCTM para el trabajo de las actividades.
Primer paso: Determinar los objetivos de aprendizaje de la asignatura con la que se va a trabajar, (Plan de estudios de Cálculo Aplicado, ESCOM-PN, 2009, p. 3).
El objetivo general de esta asignatura es:
Desarrollar habilidades lógico-matemáticas y destrezas, que le permitan al estudiante, mediante el razonamiento, el análisis y la reflexión, manejar las herramientas del Cálculo, para usarlas en la resolución de problemas que lleguen a presentarse en el ejercicio y desarrollo de su profesión.
El objetivo particular de la primera unidad temática consiste en “Aplicar los criterios de la primera y segunda derivada para resolver problemas de optimización”, (ESCOM-IPN, 2009, p.3).
Segundo paso: Selección y secuenciación de las actividades. Para este segundo paso, primero se hizo una planeación de los temas que se trabajarían en cada sesión, así como las actividades que serían empleadas para cada tema. Como se muestra en el Cuadro 4.
Tercer paso: Selección de las estrategias para trabajar con las actividades. En este paso se seleccionaron diferentes estrategias que se emplearían para trabajar cada actividad.
De entre las estrategias empleadas se encuentran:
Realizar una demostración empleando una simulación de la construcción de algún objeto o de la ocurrencia de un fenómeno, que tenga que ver con el contexto de la actividad propuesta.
Leer un texto, referido al contexto del problema.
Discutir en equipo el planteamiento y la propuesta de solución.
Reconocer un patrón al trabajar con aritmética y llegar a una generalización, que sería la función o el modelo matemático del fenómeno o situación del problema que se está trabajando.
Hacer cálculos en el proceso de solución del problema.
Resolver ejercicios relacionados al tema.
Resolver un enigma o reto, lo cual se refiere a que, en equipo o de forma individual, resolverían otro problema con un grado de dificultad más elevado.
Algunas de las estrategias empleadas se muestran en la Tabla 4.
Tabla 4 Organización de los temas y las actividades correspondientes.
| Sesión | Tema | Actividad/ estrategia |
|---|---|---|
| Primera (lunes 6 de agosto de 2018) | Cuestionario diagnóstico | Aplicación del cuestionario. |
| Segunda (miércoles 8 de agosto de 2018) | Razones de cambio relacionadas | Resolución
de problemas, primero empleando la estrategia de ensayo y
error al dar valores para calcular lo que se pretendía, de
ahí se llega a una generalización y se emplean fórmulas. Se
observan animaciones que simulan los fenómenos a los que
hacen referencia los problemas. 
|
| Tercera (jueves 9 de agosto de 2018) | Razones de cambio relacionadas, ejemplos y solución de ejercicios | Se
resuelven problemas empleando diferentes técnicas.
|
| Cuarta (lunes 13 de agosto de 2018) | Diferencial de una función: conceptos y ejemplos | Revisar un
video donde se apliquen las diferenciales de una función y
se concreta la definición. Se resuelven ejercicios que aparecen en el sistema SIMAATCA. 
|
| Quinta (15 de agosto de 2018) | Aplicaciones de la diferencial de una función | Se muestran animaciones donde se aplique el uso de la diferencial de una función. |
| Sexta (16 de agosto de 2018) | Determinación de errores empleando diferenciales |
Se muestra una animación que permita observar al estudiante la determinación de errores en la medición empleando diferenciales.
Se resuelven problemas empleando los conceptos construidos.
|
| Séptima (20 de agosto de 2018) | Extremos de una función, criterio de la primera derivada. Valores críticos, crecimiento y decrecimiento con la primera derivada | Se analizan
algunas gráficas, determinando sus elementos: puntos máximos
y mínimos locales, intervalos de crecimiento y
decrecimiento. Se revisa el criterio de la primera derivada para la obtención de algunos elementos mediante el significado geométrico de la derivada como pendiente de la recta tangente a una curva. El estudiante construye, empleando el programa de Geogebra, diferentes gráficas y ubica sus elementos. 
|
| Octava (22 de agosto de 2018) | Criterio de la segunda derivada Puntos de inflexión. Concavidad. Gráfica de una función | Ahora se trabaja la concavidad en las gráficas construidas por los estudiantes, usando el programa Geogebra. Y se emplea el criterio de la segunda derivada. El estudiante relaciona los registros algebraico, numérico y gráfico. |
| Novena (23 de agosto de 2018) | Optimización, ejemplos y solución de ejercicios | Se plantea
una situación y se resuelve mostrando un video donde aparece
el sólido del cual se pretende obtener su máximo volumen.
|
| Décima (27 de agosto de 2018). | Optimización | Aplica diferentes técnicas en la resolución de problemas de optimización. |
| Décima primera (29 de agosto de 2018) | Resolución del cuestionario final | Resuelve el cuestionario final. |
Fuente: Elaborada por el autor.
Cuarto paso: Selección de las tecnologías más adecuadas para el desarrollo de las actividades propuestas. Explicar las tecnologías usadas.
En la Tabla 5 se muestra un ejemplo, que es con el tema de Optimización, en el que se describe una actividad, las estrategias empleadas y los recursos tecnológicos utilizados con el GE.
Tabla 5 Actividades, estrategias y tecnología usadas en el caso del tema de optimización correspondiente a la unidad 1.
| Estrategia | Actividad | Tecnologías empleadas |
|---|---|---|
| Presenciar una demostración | El docente
mostró a través de una animación del sistema SIMAATCA, la
optimización del volumen de una caja formada por una hoja de
cartón que tenía un área determinada. 
|
Presentación mediante diapositivas. Uso del Sistema SIMAATCA para revisar la animación del problema de la construcción de la caja. |
| Leer textos | Los estudiantes Descargaron en su celular los apuntes que se encuentran en SIMAATCA. Después, extrajeron información del tema de optimización. | Libro electrónico contenido en SIMAATCA |
| Discutir | Los estudiantes discutieron en equipo el concepto de optimización. | Tablet o cuaderno de notas. |
| Reconocer un patrón | Los
estudiantes descargaron en su celular la animación de la
caja, junto con la tabla, interactuaron con ella al dar
valores y observar los volúmenes obtenidos. Observaron el
patrón que se repetía en la tabla, con los casos
particulares que obtuvieron. 
|
Programa interactivo para introducir valores, llenar una tabla y construir una gráfica que se encuentra en SIMAATCA |
| Comprender o definir un problema | Los estudiantes definieron la expresión analítica que generaliza los distintos volúmenes obtenidos probando varios valores. | Uso del programa Geogebra |
Fuente: Contenidos producidos en la investigación del autor.
Desenvolvimiento de los estudiantes del GE
Durante el mes que duró el trabajo de la primera unidad empleando el Escenario de Aprendizaje Tecnopedagógico, que incluyó las estrategias, actividades y tecnología, señaladas en las Tablas 4, 5 y 6, se encontró a los estudiantes motivados e interesados en lo que se presentaba y resolvía en clase, participativos, preguntaban dudas específicas en la resolución de los problemas, pasaban al pizarrón a resolver ejercicios y situaciones planteadas. Todos empleaban su celular con las actividades propuestas en el sistema SIMAATCA, hubo trabajo colaborativo. No se apreció desinterés por el trabajo en el aula ni distracciones. Los alumnos comentan que algunos problemas representaban retos, cuya solución les generaba un estado de satisfacción y los motivaba a continuar con el trabajo. Para poder medir el rendimiento de los estudiantes, se aplicó un cuestionario final y se compararon los resultados de las calificaciones obtenidas entre el primer cuestionario (el de diagnóstico) y el final, lo que se muestra en el siguiente apartado.
Tabla 6 Descripción del uso de algunas estrategas con el apoyo de la tecnología.
| Estrategia | Breve descripción | Posibles tecnologías |
|---|---|---|
| Hacer cálculos | Los estudiantes emplearon la calculadora para obtener los distintos volúmenes de la caja y después usaron el criterio de la primera derivada para determinar los valores que permiten obtener el máximo volumen de la caja. | Calculadoras científicas y graficadoras, hoja de cálculo, Programa Mathematica |
| Hacer ejercicios y prácticas | Los estudiantes resolvieron otro problema de optimización practicando distintas estrategias como el proponer valores numéricos. | Sistema SIMAATCA. Libros digitales. |
| Resolver un enigma | Los estudiantes implementan una estrategia o técnica matemática dentro del contexto de resolución de un enigma atractivo, que puede ser facilitado o planteado a través de tecnología. | Sitios web de juegos matemáticos (por ejemplo, CoolMath) |
Fuente: Contenidos producidos en la investigación del autor.
Resultados
Los datos fueron tratados en Excel, empleando las fórmulas básicas de promedio y varianza, pero básicamente se utilizó una metodología cualitativa para analizar las respuestas dadas por los estudiantes a los cuestionarios aplicados, lo que permitió documentar y analizar los procesos seguidos por los estudiantes en la resolución de los problemas. (Hernández Sampieri, 2014). Moschkovich (2000) señala que los procesos empleados en la construcción de conceptos se dan a través de la práctica, lo que se tomó en cuenta al analizar como los alumnos empleaban los recursos multimedia del Escenario tecnopedagógico. Se emplearon aspectos cuantitativos para establecer la diferencia estadísticamente significativa, se analizaron los datos del Grupo control (GC) y del Grupo de estudio (GE), en una etapa inicial (I), que fue antes de trabajar con el EATP y al final del trabajo en el aula (F). El nombre de las columnas quedó como GC_I, GC_F, GE_I y GE_F.
Primero se analizó la gaussianidad de las muestras, y todas las columnas pasaron la prueba de normalidad de D' Agostino & Pearson (ver Tabla 7). En seguida se aplicó el análisis ANOVA una vía y se encontraron diferencias entre los cuatro casos (p<0.5). Enseguida se analizó si había diferencias significativas bajo tres casos: entre las condiciones iniciales, entre la condición inicial y final de cada grupo y entre las condiciones finales de cada grupo. Empleando la prueba t-student, no pareada con corrección de Welch y considerando dos colas en todos los casos. Se comprobó que ambos grupos al inicio del estudio se encontraban en condiciones similares, con una p < 0.05 (ver Tabla 8.) Posteriormente al comparar las diferencias entre los resultados obtenidos de los cuestionarios, tanto el inicial como final de ambos grupos, los resultados entre las etapas son diferentes (p<0.0001) y al usar la prueba F para determinar diferencias en las varianzas de cada una, se obtuvo que ambos casos tienen una distribución similar con una p>0.05. Se observa que para GE la diferencia entre el inicio y final fue de 4.121 ± 0.4339 y para GC fue de 1.902 ± 0.3843. Finalmente, al comparar las diferencias entre los estados finales de los dos grupos se encontró una diferencia de 2.661 ± 0.4162 con p <0.0001.
Tabla 7 Concentrado de información al aplicar la prueba de normalidad D'Agostino & Pearson para medir la condición inicial del GC y del GE.
| Número de valores | Número de valores>35 | Número de valores>32 | Número de valores>33 | Número de valores>33 |
|---|---|---|---|---|
| Mínimo | 0.0 | 2.000 | 0.0 | 2.000 |
| 25% Percentil | 2.000 | 4.000 | 2.000 | 6.000 |
| Mediana | 2.000 | 4.000 | 2.000 | 6.000 |
| 75% Percentil | 4.000 | 6.000 | 4.000 | 8.000 |
| Máximo | 6.000 | 6.000 | 6.000 | 10.00 |
| 10% Percentil | 0.0 | 2.000 | 0.0 | 4.000 |
| 90% Percentil | 4.800 | 6.000 | 4.000 | 10.00 |
| Significancia | 2.286 | 4.188 | 2.727 | 6.848 |
| Desviación estándar | 1.759 | 1.378 | 1.567 | 1.938 |
| Std. Error de significancia | 0.2972 | 0.2436 | 0.2727 | 0.3374 |
| Abajo del 95% CI de significancia | 1.682 | 3.691 | 2.172 | 6.161 |
| Arriba del 95% CI de significancia | 2.890 | 4.684 | 3.283 | 7.536 |
| Prueba de Normalidad D'Agostino & Pearson | ||||
| K2 | 1.883 | 1.386 | 0.05515 | 0.7290 |
| P valor | 0.3900 | 0.5000 | 0.9728 | 0.6946 |
| Prueba de normalidad (alpha=0.05) | Si | Si | Si | Si |
| P resumen del valor | ns | ns | ns | ns |
| Coeficiente de variación | 76.94% | 32.91% | 57.45% | 28.30% |
| Significancia geométrica | 3.937 | 6.526 | ||
| Oblicuidad | 0.5338 | -0.1226 | 0.06863 | -0.3207 |
| Kurtosis | -0.1652 | -0.7678 | -0.2593 | 0.002105 |
| Suma | 80.00 | 134.0 | 90.00 | 226.0 |
Tabla 8 Caso 1: condiciones iniciales de los 2 grupos.
| Análisis | Grupos | ||
|---|---|---|---|
| Columna C | GE_I | ||
| Vs. | Vs. | ||
| Columna A | GC_I | ||
| Prueba t no pareada con corrección de Welch | |||
| P valor | 0.2777 | ||
| P resumen del valor | ns | ||
| ¿Significativamente diferente? (P < 0.05) | No | ||
| ¿Valor P de una o dos colas? | Dos-colas | ||
| T corregida de Welch, df | t=1.095 df=65.80 | ||
| ¿Qué tan grande es la diferencia? | |||
| Mean ± SEM de la columna A | 2.286 ± 0.2972, n=35 | ||
| Mean ± SEM de la columna C | 2.727 ± 0.2727, n=33 | ||
| Diferencia entre los medios | 0.4416 ± 0.4034 | ||
| 95% intervalo de confianza | -0.3639 to 1.247 | ||
| R cuadrada | 0.01788 | ||
| F prueba de comparación de varianzas | |||
| F,DFn, Dfd | 1.260, 34, 32 | ||
| P valor | 0.5136 | ||
| P resumen del valor | ns | ||
| ¿Significativamente diferente? (P < 0.05) | No | ||
| Modelo de comparación | SS | DF | La probabilidad es correcta |
| Hipótesis Nula: Population means identical | 187.0 | 67 | 61.96% |
| Hipótesis Alternativa: Distinct population means | 183.7 | 66 | 38.04% |
| Razón de probabilidades | 1.629 | ||
| Diferencia en AICc | -0.9753 |
Primero se analizó la gaussianidad de las muestras, y todas las columnas pasaron la prueba de normalidad de D'Agostino & Pearson (ver Tabla 7). Enseguida se analizó si había diferencias significativas entre las 4 columnas por pares, lo que se muestra en la Tabla 8. Al realizar el análisis de las condiciones iniciales de los 2 grupos empleando la prueba t no pareada con corrección de Welch, se comprobó que ambos grupos al inicio del estudio se encontraban en condiciones similares, ya que se obtuvo una p < 0.05.
Resultados del cuestionario diagnóstico
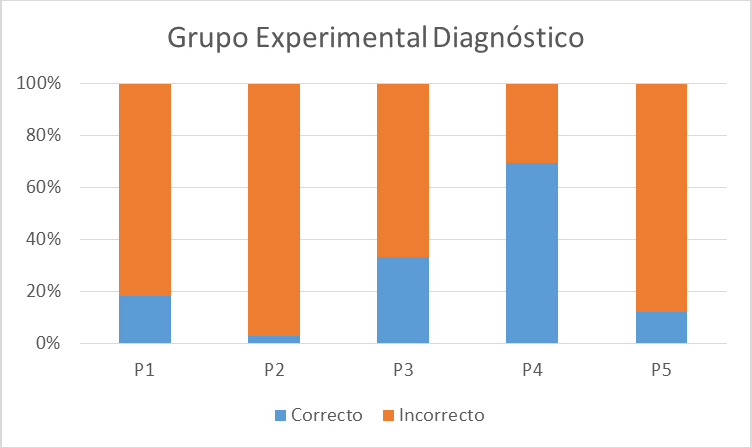
Los resultados obtenidos del cuestionario diagnóstico tanto por el grupo de control (GC) como del grupo experimental (GE) fueron muy bajos como se muestra en las gráficas de las Figs. 5 y 6, respectivamente. Los estudiantes presentaron dificultades en los planteamientos de la mayoría de los problemas. La tarea que tuvo mayor cantidad de respuestas correctas, en ambos grupos, fue la que se refería a la obtención de puntos máximos, mínimos, puntos de inflexión (problema 4 o P4 como aparece en la gráfica), aunque no todos los alumnos tuvieron correcto este problema debido a que no pudieron hacer la gráfica, lo que indica que no han logrado trabajar estableciendo la relación entre los diferentes registros de representación y no han llegado a construir el concepto de función completamente, sólo de forma parcial, como lo señala Duval (1998). La tarea que tuvo menos aciertos, también en ambos grupos, fue la correspondiente al uso de diferenciales para obtener las medidas solicitadas (problema 2 o P2 como se muestra en la gráfica). Los problemas de optimización (problemas 3 y 5 o P3 y P5), como el de razones de cambio relacionadas (problema 1 o P1) también fueron considerados como difíciles por los alumnos, al no poder establecer las relaciones con las variables dadas y con ello llegar a las respuestas solicitadas.
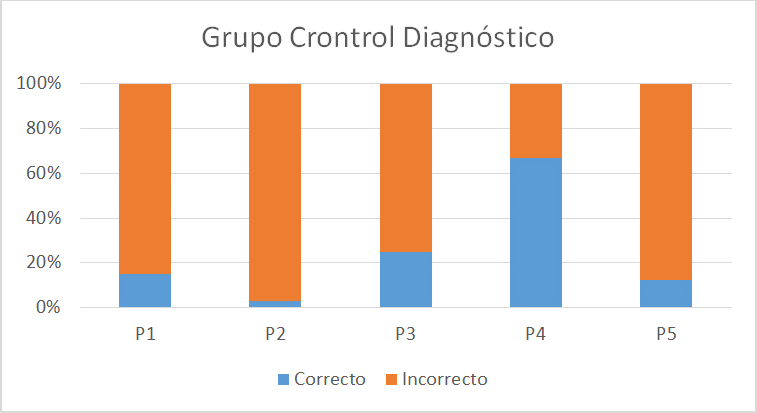
Fig. 5 Gráfica que representa los resultados del cuestionario diagnóstico que corresponden al grupo de control (GC).
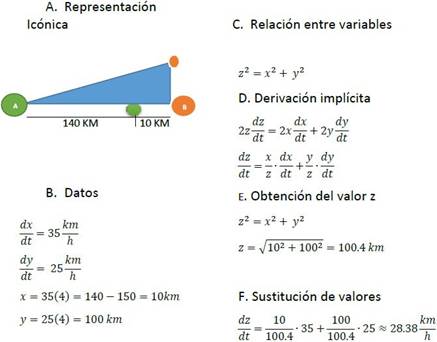
Problemas de Razones de cambio relacionadas
En relación a los problemas de razones de cambio relacionadas, en un inicio los estudiantes tanto del grupo de control como del grupo experimental, no identificaron los datos proporcionados como razones de cambio con respecto al tiempo y tampoco determinaron la ecuación que sufriría una modificación mediante el proceso de la obtención de la derivada, para al final obtener la razón de cambio que se requería encontrar. Los estudiantes no lograban relacionar las variables mediante una función auxiliar, como el establecimiento de triángulos semejantes, “para el problema del depósito que tiene forma de cono invertido”. Esto muestra escaso trabajo en el campo de la geometría y su vinculación con el cálculo.
Problemas de diferenciales
Los estudiantes manifestaron desconocimiento del tema, pero ni siquiera hubo intentos por tener aproximaciones en la resolución; sólo 2 estudiantes, uno de cada grupo (el de control y el experimental), emplearon aritmética para aproximar uno de los errores en la medición solicitados. Para ello, primero encontraron el valor real del volumen del cubo y después el valor aproximado; al primero le restaron el segundo, encontrando tanto el error máximo como el mínimo en la medición del volumen del cubo. Esto implica que el 97% de los estudiantes siguen trabajando con procesos aritméticos sin haber llegado a la transición del conocimiento de los infinitesimales, mediante el cálculo, pero el grueso de los estudiantes no ha logrado construir un modelo matemático que les permita manipular tanto a las variables independientes como dependientes y obtener la diferencial de la función para llegar a responder a la situación planteada.
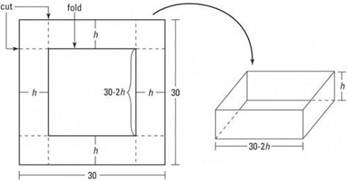
Problemas de optimización
En un inicio los estudiantes tuvieron dificultades para construir el modelo matemático que los ayudaría a encontrar la maximización o minimización de lo que el problema requería obtener. Los estudiantes han tenido durante varios años acercamiento con la aritmética, pero no están haciendo uso de ella para tener aproximaciones en lo que se requiere obtener, tampoco tienen habilidad en el uso de estrategias, como la estrategia de ensayo y error al probar distintos valores hasta llegar a una generalización. Pareciera que los estudiantes están muy mecanizados y se desesperan al no contar con una función a la que le van a aplicar el criterio de la primera o segunda derivada hasta llegar a la determinación del mínimo o máximo.
Análisis de una función y su gráfica
En general los estudiantes resolvieron la situación en la que se requería determinar los puntos críticos, los intervalos de crecimiento y concavidad. Se observa que cuando se da una función de forma analítica, los estudiantes hacen una manipulación algebraica siguiendo una serie de pasos establecidos, aquí la memoria jugó un importante papel, ya que siguieron pasos como derivar la función, igualar a cero, resolver la ecuación para x y determinar qué valor de x represente la abscisa de un punto que es máximo y cual la de un mínimo. Las dificultades encontradas tuvieron que ver con el hecho de no darle sentido al proceso de la determinación de máximos y mínimos, más bien se apoyaron en la memoria y no en el razonamiento.
Resultados del cuestionario final
Después de haber trabajado con el grupo de Control (GC) los temas de la Unidad 1, de forma tradicional, en donde el maestro dictaba la clase empleando el pizarrón y un libro de texto, dando aspectos teóricos y ejemplos de problemas referente a la misma Unidad 1, y después de haber trabajado con el grupo Experimental (GE) a través del Escenario de Aprendizaje Tecnopedagógico, empleando una serie de problemas y el Sistema SIMAATCA, que contiene videos, presentaciones en PowerPoint, programas para hacer cálculos, animaciones y simulaciones, los estudiantes tanto del GC como del GE, resolvieron un cuestionario final, el cual, al igual que el cuestionario diagnóstico, constó de 5 problemas referentes a aplicaciones del Cálculo. En esta ocasión hubo una mejora en los resultados obtenidos por ambos grupos (el de control como el experimental), pero el GE sobresalió en la cantidad de respuestas correctas comparado con el GC.
En las Figs. 7 y 8 se muestran las gráficas de las respuestas correctas de cada grupo correspondientes tanto al cuestionario diagnóstico como al final.
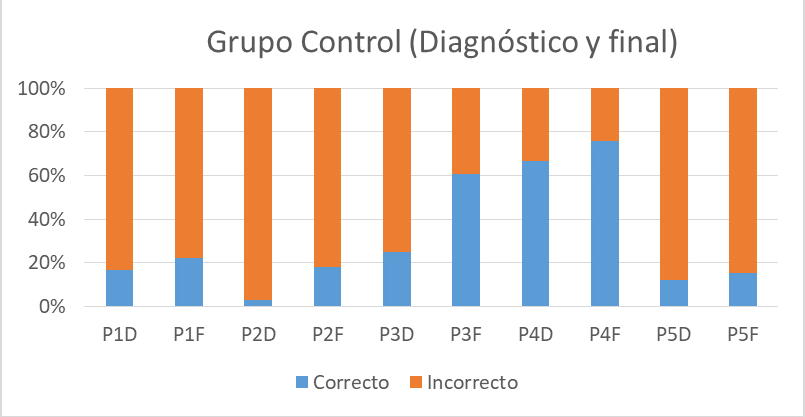
Fig. 7 Gráfica que representa los resultados tanto del cuestionario inicial como del cuestionario final correspondientes al grupo de control (GC).
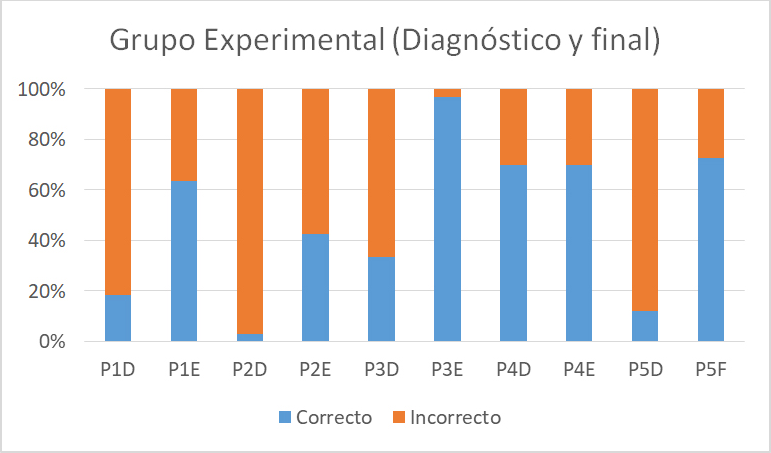
Fig. 8 Gráfica que representa los resultados del cuestionario final correspondiente al grupo experimental (GE).
En el grupo de control los problemas que fueron resueltos de forma correcta, por mayor cantidad de estudiantes, correspondieron a la obtención de puntos críticos (máximos, mínimos), intervalos donde la función es creciente y en donde es decreciente (P4F, es decir, problema 3 del cuestionario final), así como el concerniente al tema de optimización (P3F), aunque en el segundo problema de optimización (P5F) no tuvieron mucho éxito, debido a la construcción geométrica y al uso de fórmulas de geometría que debían conocer y que olvidaron en el momento de la resolución del cuestionario. Los problemas en los que fallaron al rededor del 80 % de los alumnos fueron del tema de razones de cambio relacionadas (P1F) y del de diferenciales (P2F).
En la misma Fig. 7 se muestra la gráfica con el porcentaje de respuestas correctas como incorrectas de los dos cuestionarios aplicados, el de diagnóstico como el final (Fig. 7), para hacer una comparación entre ambos porcentajes, con lo cual se puede decir que hubo un avance y una mejora en el rendimiento de los alumnos del GC pues su promedio, aumentó de 2.4 a 3.7, en una escala de 0 a 10.
Análisis de resultados del grupo de control
Revisando cada uno de los problemas de los cuestionarios aplicados se muestran las dificultades encontradas en un inicio y los aspectos que superaron.
Dificultades superadas por el grupo de control
De manera general hubo mejoras tanto en el GC como en el GE al resolver el cuestionario final, después de un proceso de enseñanza que duró un mes, teniendo distintos acercamientos cada grupo. En este apartado se mencionan las mejoras de cada uno de los grupos.
En el grupo de control (GC), se encontró que hubo un avance en el tema de optimización pues su porcentaje de respuestas correctas tuvo un incremento de más del doble en ambas tareas (problema 3 y problema 5), lo que se debió preferentemente a que los estudiantes emplearon correctamente el criterio de la primera derivada para la obtención de la mínima área que es la que se solicitaba. Se observó que estos estudiantes emplearon más la memoria al seguir cada uno de los pasos para la obtención de los puntos críticos.
Otro tema en el que hubo mejoría por parte del GC fue el de diferenciales, ya que en el cuestionario diagnóstico sólo el 3% de los alumnos resolvió correctamente el problema de diferenciales y en el cuestionario final aumentó al 18%. Los alumnos argumentaron que el tema de diferenciales no lo habían trabajado en el nivel medio superior y tampoco en su primer semestre de cálculo, o al menos no habían resuelto problemas de diferenciales, solo conocían algo de la teoría, pero después de las clases dadas, entre el cuestionario inicial y el final, ya comprendieron en lo que se puede aplicar este tema.
Análisis de resultados del grupo experimental
En relación al grupo experimental (GE) los resultados obtenidos en el cuestionario final en comparación con los del cuestionario diagnóstico, se muestran en la gráfica de la Fig. 8. En donde se observa que los estudiantes tuvieron una notable mejoría en los temas de optimización, seguido del tema de razones de cambio relacionadas, diferencial de una función y obtención de puntos críticos y comportamiento de una función.
Dificultades superadas por el GE
En el grupo experimental (GE) Alrededor del 40 % de los estudiantes, al principio emplearon la estrategia de “ensayo y error”, al dar valores para determinar una aproximación cercana a las dimensiones de la hoja donde se encuentra el póster, lo que significa que estos estudiantes le dieron sentido a la situación planteada en el problema (se ve reflejado el trabajo en clase al usar esta estrategia empleando las simulaciones mostradas), como segunda opción plantearon la función que representaba el área que se iba a minimizar y trabajaron con el criterio de la segunda derivada para concluir que el valor sustituido representaba un mínimo.
En el problema 5, que también era de optimización, algunos alumnos al principio tuvieron dificultad en plantear la función que expresaba algebraicamente la situación, pues se incluían dos semicírculos, la confusión radicó en que trabajaron con dos círculos en lugar de con dos semicírculos. Pero el uso de la estrategia de ensayo y error les ayudó a llegar a la función correcta. Posteriormente emplearon el criterio de la primera y segunda derivada para darle solución.
El porcentaje de incremento en la resolución de los problemas de diferenciales cambió del 3% al 42%, lo que equivale a decir que una catorceava parte de los estudiantes resolvió correctamente el problema en el cuestionario inicial, mientras que en el final aumentó catorce veces la cantidad de estudiantes, lo que se debió a las estrategias de aprendizaje y a los recursos didácticos empleados como parte del Escenario de Aprendizaje Tecnopedagógico (EATP), pues los estudiantes observaban en las simulaciones el cambio que se generaba en la figura de la cual se solicitaba determinar el error de medición. Los estudiantes reconocieron al error como la diferencial de la variable independiente y al error del volumen como la diferencial de la función.
En relación al problema de razones de cambio relacionadas, el porcentaje de estudiantes que logró resolver de forma correcta el problema cambió de 18.2% que obtuvo en el cuestionario inicial, a 63.2% alcanzado en el cuestionario final (más del triple), el éxito se debió al tipo de estrategias empleadas, como esquematizar el problema, colocando las variables identificadas en el texto, así como estableciendo las relaciones adecuadas para obtener una función expresada en términos de una sola variable.
En la Tabla 9 se muestran los resultados finales de ambos grupos, donde se aprecia el efecto del trabajo realizado con el escenario de aprendizaje tecnopedagógico.
Tabla 9 Diferencia en los resultados finales de los dos grupos.
| Análisis de los datos | Grupos | ||
|---|---|---|---|
| Columna D | GE_F | ||
| Vs. | Vs. | ||
| Columna B | GC_F | ||
| Prueba t no pareada con corrección de Welch | |||
| P valor | < 0.0001 | ||
| P resumen del valor | **** | ||
| ¿Significativamente diferentes? (P < 0.05) | Yes | ||
| ¿Valor P de una o dos colas? | Dos colas | ||
| T corregida de Welch, df | t=6.394 df=57.83 | ||
| ¿Qué tan grande es la diferencia? | |||
| Mean ± SEM of column B | 4.188 ± 0.2436, n=32 | ||
| Mean ± SEM of column D | 6.848 ± 0.3374, n=33 | ||
| Diferencia entre los medios | 2.661 ± 0.4162 | ||
| 95% intervalo de confianza | 1.828 to 3.494 | ||
| R cuadrada | 0.4141 | ||
| F test para comparar varianza | |||
| F,DFn, Dfd | 1.979, 32, 31 | ||
| P valor | 0.0606 | ||
| P resumen del valor | ns | ||
| ¿Significativamente diferentes? (P < 0.05) | No | ||
| Modelo de comparación | SS | DF | Probability it is correct |
| Hipótesis Nula: Idénticas poblaciones de medios | 294.2 | 64 | 0.00% |
| Hipótesis Alternativa : Distintas poblaciones de medios | 179.1 | 63 | 100.00% |
| Razón de probabilidades | 0.0 | ||
| Diferencia en AICc | 30.04 |
Al hacer una comparativa entre el grupo de control y el experimental se observa en la Tabla 10 que el GE obtuvo más respuestas correctas en general que el GC.
Tabla 10 Diferencias entre estado inicial y estado final para cada grupo.
| Análisis de los datos | Grupos | ||
|---|---|---|---|
| Columna B | FGC_F | ||
| Vs. | Vs. | ||
| Columna A | GC_I | ||
| Prueba t no pareada con corrección de Welch | |||
| P valor | < 0.0001 | ||
| P resumen del valor | **** | ||
| ¿Significativamente diferente? (P < 0.05) | Yes | ||
| ¿Valor P de una o dos colas? | Dos-colas | ||
| T corregida de Welch, df | t=4.948 df=63.56 | ||
| ¿Qué tan grande es la diferencia? | |||
| Mean ± SEM of column A | 2.286 ± 0.2972, n=35 | ||
| Mean ± SEM of column B | 4.188 ± 0.2436, n=32 | ||
| Diferencia entre los medios | 1.902 ± 0.3843 | ||
| 95% intervalo de confianza | 1.134 to 2.670 | ||
| R cuadrada | 0.2781 | ||
| F test para comparar varianza | |||
| F,DFn, Dfd | 1.628, 34, 31 | ||
| P valor | 0.1737 | ||
| P resumen del valor | ns | ||
| ¿Significativamente diferentes? (P < 0.05) | No | ||
| Modelo de comparación | SS | DF | Probability it is correct |
| Hipótesis Nula: Idénticas poblaciones de medios | 224.5 | 66 | 0.01% |
| Hipótesis Alternativa: Distintas poblaciones de medios | 164.0 | 65 | 99.99% |
| Razón de probabilidades | 0.0 | ||
| Diferencia en AICc | 18.83 |
Discusión o Conclusiones
Sobre lo que se encontró al realizar el análisis a las respuestas dadas por los estudiantes en el grupo experimental y al contrastarlo con lo que señalan los autores de los aspectos teóricos en relación a la visualización y al trabajo de la aritmética para poder llegar a un trabajo algebraico, se tiene lo siguiente.
Después de haber trabajado en el grupo experimental con el modelo TPCAK, se obtuvieron buenos resultados ya que el promedio del grupo aumentó, de 2.7 a 6.3, lo que implica que hubo un mejor rendimiento en este grupo durante el mes de trabajo. La mejoría se atribuye a las diferentes estrategias que emplearon en la resolución de los distintos problemas, predominando la estrategia de “ensayo y error” como primera opción al dar algunos valores que les permitía tener un panorama sobre el aumento o decremento de la situación objeto de que se tratara, es decir los estudiantes pudieron trabajar con la aritmética para visualizar casos particulares para después trabajar con generalizaciones, lo que se asemeja a lo mencionando por Kaput (2000, 2008); Kieran (2007) y Artigue (2011). También la estrategia de “esquematizar el problema” y ubicar las variables reconociendo a las independientes y a las dependientes, mediante las cuales llegaban a determinar la función que representaba el problema y, como parte de esta misma estrategia, el expresar a la función en términos de una sola variable y después determinar una ecuación auxiliar para despejar la variable requerida, para posteriormente, mediante el uso de algún criterio, como el de la primera derivada o segunda, en el caso de problemas de optimización, o la derivación implícita con respecto al tiempo, en el caso de razones de cambio relacionadas, los estudiantes llegaban a obtener las respuestas a los planteamientos realizados. Este trabajo desarrollado por los estudiantes alude a lo señalado por Hitt (2014), Sánchez, García & Llinares (2008), Oliveros (1999), Duval (1998), en relación empleo de diferentes representaciones, no solo el algebraico, sino el icónico, el numérico y el tabular.
En el grupo de control (GC), no hubo mejora en el rendimiento académico pues su promedio cambió de 2.6 a 3.6, lo que se debió al tipo de estrategias empleadas por los estudiantes, las cuales se recostaron en el uso de fórmulas usadas durante la clase pero sin haber adquirido un sentido para los alumnos ya que fue un aprendizaje de carácter memorístico.
Se concluye que el escenario Tecnopedagógico constituye un apoyo para que el estudiante maneje con más soltura y previo entendimiento, las fórmulas implicadas en algunas estrategias de resolución de problemas. La integración de la tecnología productiva en la enseñanza necesita considerar los tres aspectos (Contenido, pedagogía y tecnología) no de forma aislada, sino dentro del complejo de relaciones en el sistema definidas por los tres elementos clave
