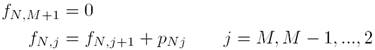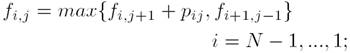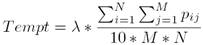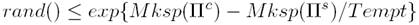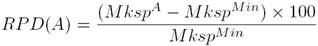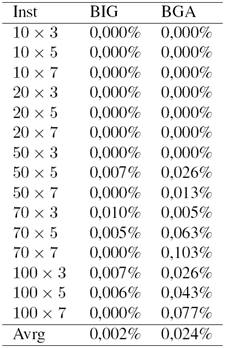I. Problem Description
IN the Blocking Flow Shop Scheduling Problem (BFSP), there is a finite set of N jobs that must be processed on M machines in the same order. Indeed, since there is no buffer storage between each consecutive pair of machines, intermediate queues of jobs waiting for their next process are not allowed. So, a job cannot leave its current machine till the next downstream machine is clear. This blocking state avoids progressing of other jobs on the blocked shop.
Furthermore, each job i (i = 1,2,...,N) ready at time zero and requiring non-negative time p ij as a processing delay has to be processed first on machine M1, then on machine M2 and so on till on machine Mm (j = 1,2,...,M ). That is the sequence in which the jobs are to be processed is identical for each machine. Besides, the processing of a given job at a machine cannot be interrupted once started. Each job can be processed only on one machine at a time and each machine can process at most one job at a time. Based on the above definitions, the final objective is to find out a sequence for processing all jobs on all machines so that its maximum completion time (makespan) is minimized. Formally, the BFSP aborted in this research is the Fm ⎹block⎹Cmax in conformance with the classifications mentioned by Graham et al. [1]. The most popular eccentric work done on this problem is [2] who showed that the F2 ⎹blocking⎹Cmax instance may be reduced to a special case of the traveling salesman problem which may be solved in polynomial time using Gilmore and Gomory algorithm [3]. When the number of machines exceeds two (m > 2), then the problem becomes strongly NP-hard [4]. The BFSP may be sketched in many real-life situations. We may cite the robotic cell [5], the iron and steel production [6], the manufacturing of concrete blocks and other.
As well, let II := (π1 , π2,... πN) be a possible solution for the BFSP, where πi denotes the ith job in the specific sequence; d πi, j (i = 1,2,...,N; j = 0,1,2,...,M) defines the departure time of job πi on machine j, where d πi,0, represents the time job πi, begins its processing on the first machine. The corresponding values of makespan of Π may then be calculated as Cmax(Π) = C πN,M , (Π) in O(nm), where Cπi, M = d πi, M is the completion time of job πi on machine M that can be calculated generally using expressions presented in [7]. We choose in this work to refer to the method based on tails calculation to express the makespan of a given permutation as Cmax (Π) = f 1,1 where fi,j defines the length of time between the latest loading time of operation oij and the end of the operations for j: M, M - 1,...,1; and fi,M+1 is the duration between the latest completion time of operation oiM and the end of the operations [8]. Consequently, we obtain the following recursive equations:
In the beyond recursion, the tails of the last job on every machine are calculated first, then the second last job, and so on up to the first job.
Due to the NP-hardiness of the BFSP, small number of methods have been proposed to solve it. They are ranged from exact methods to meta-heuristic ones. Some of the most important techniques are briefly presented in the following. Solving the BFSP using exact methods has attracted few attention in comparison with other original flow shop problems [9], [10], [11]. In [12], a lower bounding schemes were exposed, next an exact method based on the Branch-and-Bound (B&B) technique which uses a new compounded lower bounds was developed in [13]. Besides, a double B&B algorithm using the reversibility property of the problem is proposed in [14]. As well, two MBIP models and one B&B algorithm were lately presented to solve to optimality the BFSP under the total completion time measure [15]. Certainly, exact methods are unable to solve the problem within a reasonable computational time. Therefore, this incapacity explains the necessity to employ heuristics and meta-heuristics. As constructive heuristics, we may cite the Profile Fitting (PF) [16] and the Nawaz-Enscore-Ham (NEH) technique [17]. Some priority rules and tie breaking strategies were proposed in [18]. In [19] and [20] the NEH-WPT heuristic and a constructive and a GRASP-based heuristics for the BFSP were introduced respectively. Basically, the NEH-WPT sorts all jobs in a non-decreasing order of the sum of their processing times on all machines.
Afterward, meta-heuristics algorithms appear as a comple ment to their counterparts heuristics. The (Ron) algorithm was presented in [13] regarding the blocking constraints, and a Tabu Search (TS) and an enhanced TS techniques were used by Grabowski et al. In [21], we locate an Iterated Greedy (IG) method based on the insertion stage of the NEH. Under the total flow time criterion, we cite the hybrid modified global-best Harmony Search (hmgHS) algorithm and the Discrete Artificial Bee Colony algorithm (DABC_D) technique exposed in [19] and [22], respectively. Under Cmax criterion, an effective Revised Artificial Immune Systems (RAIS) algorithm is proposed in [23], a three-phase algorithm presented in [24], and a Discrete Particle Swarm Optimization algorithm (DPSO) with self-adaptive diversity control was treated in [25]. Subsequently, we refer to the Memetic Algorithm (MA) in [26], the Iterated Local Search algorithm (ILS) coupled with a Variable Neighborhood Search (VNS) in [27], and the Blocking Genetic Algorithm (BGA) and Blocking Artificial Bee Colony (BABC) algorithms in [28]. Experimental results demonstrated that both of the two later proposed algorithms are more efficient in finding better solutions than all other leading techniques.
Now, among meta-heuristics, we focused on the IG algorithm which is being applied to many scheduling problems and subsequently to flow shop variants [29]. It is simple and effective: the approach applies constructive methods iteratively to a selected solution and then uses an acceptance criterion to decide whether the obtained solution substitutes the old one. Indeed, a sequence of solution is obtained using some destruction and construction stages. The destruction phase removes some elements from one selected solution. Next, in the construction phase, a new solution is created by reconstructing a complete solution using a greedy constructive heuristic, which reinserts the removed elements in some order to form a new complete sequence. Facultatively, a local search algorithm may be added to boost the constructed solution.
The basic steps of the IG algorithm are given as shown in Table I. After presenting the problem background, the rest of this paper is organized as follows: In Section 2, the Blocking IG algorithm (BIG) is stated. In Section 3, the computational results and comparisons are provided, and Conclusions are made together with future research direction in Section 4.
II. Solving the Locking Low Shop Problem Based on the Iterated Greedy Algorithm
In this section, the details of the BIG proposed for the problem under discuss is introduced. We recall that the key components of all existing heuristics for the BFSP have been developed based on the NEH heuristic which is made up of two stages: the first stage is the creation of the preliminary sequence of the jobs, and next comes the iterative process of insertion of the resulting jobs depending on the initial sequence obtained in phase 1.
A. Initial solution
To generate the initial solution we have used the PF-NEH(x) heuristic as in [28]. However, instead of generating x solutions at the end of the heuristic we choose only the permutation with the minimum objective value. As well, we employ the insertion-based local search to produce a neighboring solution. In this local search, a job is removed from its original position and reinserted in all other possible places. The local technique is applied with a probability Pls. Next, if the objective value is enhanced then the solution is replaced. The final permutation Πs thus obtained is the seed sequence.
B. Destruction and construction stages
On the basis of an initial solution, the destruction phase is applied. This stage begins with a complete solution Πs and then extracts [q * Πs ] randomly chosen jobs from Πs in an iterative way. The degree of destruction q is in the range [0,1]. This creates two subsequences: the first one contains the removed jobs Πs , and the second subsequence is the rest of the initial sequence obtained after removing some jobs Πs .
Now, based on these resulting subsequences, in the construction phase a final solution Πc is then reconstructed using a greedy constructive algorithm by reinserting the previously removed jobs in the order in which they were extracted.
The pseudo-codes of the destruction and construction steps are as in Table II and Table III.
C. Acceptance criterion
Once a newly reconstructed solution has been obtained, an acceptance criterion is applied to decide wether it will replace the current incumbent solution or not. We consider the Simulated Annealing (SA) acceptance criteria that may be achieved by accepting worse solutions with a certain probability as used in [29], [30]. This acceptance criterion is used with a constant temperature value, which depends on the number of jobs, the number of machines, and on other adjustable parameter λ:
Let Mksp(Π s ) and Mksp(Π c ) be respectively the makespan values of the current incumbent solution and the new reconstructed solution. Also, let rand() be a function returning a random number sampled from a uniform distribution between 0 and 1.
If Mksp(Πc) ≥ Mksp(Π s ) Then Π c is accepted as the new incumbent solution if:
D. Final BIG algorithm
Considering all previous subsections, the proposed BIG algorithm for the BFSP goes as in Table IV.
III. Computational Results
In the following, to confirm the effectiveness and competitiveness of BIG, its performances are compared against some leading methods in the literature. As usually done, we have used the Taillard instances [31] to test our technique. This benchmark include 120 problems of multiple sizes arranged into 12 subsets. Each subset entails ten instances with equal size (20*5, 20*10, 20*20, 50*5, 50*10, 50*20, 100*5, 100*10, 100*20, 200*10, 200*20, and 500*20) where the first number define the job size and the second one represent the machine size.
Each instance is independently run 10 times and in each run we compute the percentage relative difference (PRD) using the following expression:
where, MkspA defines the value of the makespan reached by the BIG algorithm; and MkspMin defines the minimum mekespan value obtained among all the compared algorithms.
The BIG algorithm is coded in C + + 8.0 and the experiments are executed on an Intel Pentium IV 2.4 GHz PC with 512 MB of memory.
The final experimental setup is given in Table V where the main purpose of the experiment was to compare the optimization performances of the algorithm under various system conditions.
A. Results on randomly generated instances
Before testing BIG algorithm on benchmark sets, the computational experiments have been at first carried out on a set of randomly generated instances obtained following the procedure explained in Taillard.
In our tests, the problem sizes are determined by varying the number of jobs and machines from 10 jobs and 3 machines to 100 jobs and 10 machines as was the case in [28].
This choice is fixed such to make comparison between BIG and BGA algorithm under this type of instances. Next, the Cmax values of the best-found solutions for these generated instances were memorized for each of the compared heuristics.
A statistic for the solution quality for each set is given (Average RPD (ARPD)) as in Table VI. According to the above table, the proposed algorithm is more likely to get better solutions than BGA which is outperformed. For small instances, the two algorithms behave in the same way. Difference is observed by increasing the number of jobs.
B. Comparing BIG with leading heuristics
In this subsection, we enlarge the domain of comparison and consider the BIG versus IG [21], MA [26], RAIS [23], and BGA [28] algorithms.
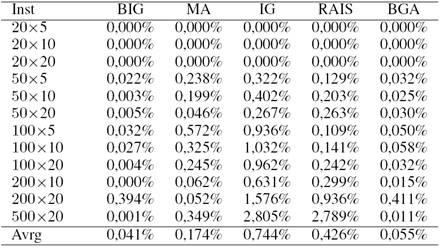
From Table VII, we can observe that the proposed BIG gives the best performance in terms of the overall solution quality, since it yields the minimum overall mean ARPD value equal to 0,041%, which is much better than those by the IG (0.744%), MA (0.174%), RAIS (0.426%), and BGA (0.055%).
More specifically, the BIG gives much better APRD than all compared heuristics and improves 86 out of 120 best-known solutions of Taillard's instances for the BFSP with the makespan criterion. The worst results are given by the IG [21].
Indeed, BIG algorithm behaves much more effective than the BIG algorithm as the size of instances increases. So, regardless its simplicity, we may assert that the BIG algorithm is an efficient heuristic in solving the BFSP and so may be used as a basis of comparison for future research.
IV. Conclusion and Future Work
In our study, BIG algorithm is proposed to solve the BFSP under makespan measure. This greedy method is very simple, and hybridized with a form of local search, enhanced much more the solutions quality.
The algorithm is developed to solve both randomly generated instances and a number of test problems (Taillard instances). The experiment results attest that BIG is better than other leading algorithms on all group instances specifically on high dimensional problems.
In the future, we will hybridize our technique using some hybrid evolutionary heuristics such as SA to improve its performance and design some better NEH heuristic variant to improve its efficiency.











 nueva página del texto (beta)
nueva página del texto (beta)