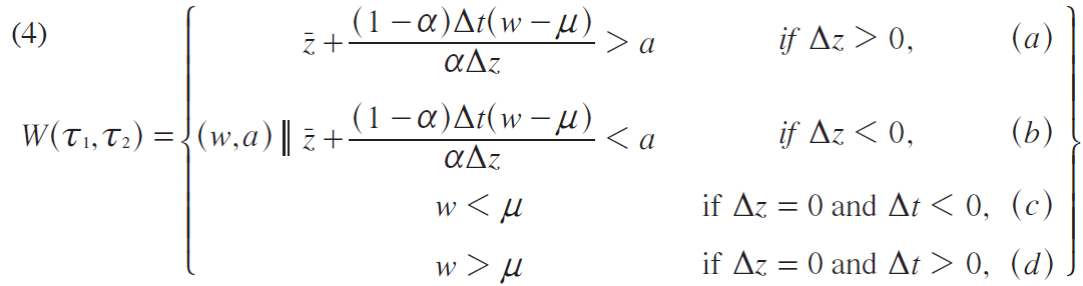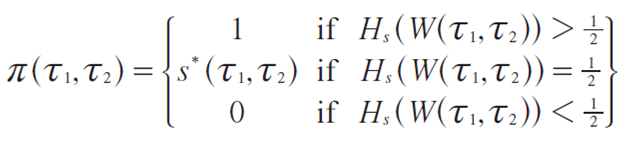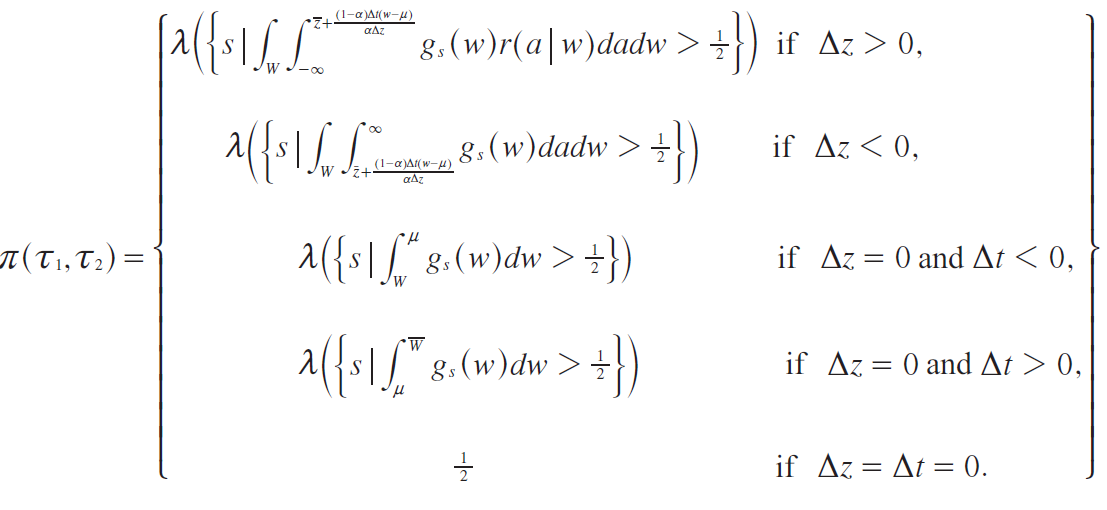Introduction
In a democracy, as citizens above a certain age have the right to vote, we expect economic policies to be designed to benefit the majority. If the median income is less than the mean, the majority of voters are those whose income is less than the mean. Certainly, even in this situation, economic policy is not always designed to benefit the poor.
Apparently, there are factors, other than the income of the voters, affecting economic policy design. Different ideas about ethnicity, religion, nationalism, views or believes about what is fair, and corruption, among others, which we label “ideology”, affect the preferences of the voters, parties, and finally, the equilibrium policy. The same economic policy, tax rate for instance, could appear to be different for a voter depending on the ideological position of the party that proposes it. The preferences of the voters are defined not just by income as people may also care about ideological positions associated with different political parties (Acemoglu and Robinson, 2006).
In this paper we provide a political-economic model that traces the influence of ideology on determining the tax rate in an economy with political competition. There are two dimensions, a proportional redistributive tax rate and ideology. If a party aligns its preferences to those of the poor, we expect such a party to choose a higher equilibrium tax rate. What we found is that when uncertainty is small, ideology plays an important role on the prevailing economic policy.
The model analyzes decision making in a society consisting of two main social groups: the rich and the poor, both having different preferences on tax rate and ideology. The defining features of the political process are that there are two political parties, each having preferences on tax rate and ideology. Parties offer platforms and voters vote for the platform they like most.2
The main analytical result is that, in equilibrium, if the salience of an ideological issue is high and uncertainty is small, regardless of whether the parties align their preferences to those of the poor or the rich, the cohort of voters with the median ideological position become the swing voters.3 Then, the equilibrium tax rate is designed to benefit that cohort of voters.
This paper is related to the work of Roemer (1998) but is, we believe, richer in its objective and in its approach. We adopt the same framework as his, but we focus on the role of ideology in determining the equilibrium tax rate. We focus on different cases: 1) both parties align their preferences to those of the poor; 2) one party aligns its preferences to those of the poor and the other party to those of the rich and vice versa; 3) both parties align their preferences to those of the rich. Note that as Roemer focuses on the conditions that make the party representing the poor selecting a tax rate less than unity, he only explores case 2.4
The study of ideology and its effect on determining economic policy is not new. In this regard, Dixit and Londregan (1998) model the electoral politics of redistribution when voters and parties care about inequality. They find that in presence of ideological concerns about income redistribution, each party adopt a general proportional income tax, adjusted to appeal to the ideological leanings of groups with disproportionately many “swing” voters. Their results suggest that redistributive politics favours middle classes at the expense of both rich and poor. In the same line, Bénabou (2008) develops a model that focus on ideologies concerning the relative merits of the market versus the state. He takes ideology in two senses of the term: as an exercise in the study of ideas and as the interaction of “subjective mental constructs” across agents and with institutions to generate social cognitions that rest on distorted perceptions of reality. He finds that an equilibrium in which people acknowledge the limitations of interventionism coexists with one in which they remain obstinately blind to them. He also finds that history is important: the interaction among beliefs and institutions generate path-dependent dynamics.
The rest of the paper is organized as follows: Section 2 presents the model. Section 3 computes the equilibrium tax rate. Section 4 offers some further discussion. Section 5 concludes. Appendix contains some technical details not provided in the text.
The model
We examine a jurisdiction with two political parties, two social groups, and a space of voters. The model we shall develop builds on Roemer (1998). Our description begins with the economy.
The economy
We consider a society where the space of citizen traits is ,A=W×R, with generic element (w,a). . The set of income is W=[w_,¯w]⊂R. The set of ideological views is given by the real number line, R.
The population is characterized by a joint probability distribution represented by a density h(w,a)=g(w)r(a|w) on A. Where g(w) is a density on W with mean µ (mean income). For each w, r(a|w) is a density on R. In this economy not all the citizens vote. Suppose that the distribution of voters, that is, of citizens who go to the polls on elections day, is g,(w) where s is a random variable (state) uniformly distributed on [0,1] Let G, be the cumulative distribution function of gs We shall suppose that is strictly decreasing in s.5 Then, in state s, the density of voters is given by:
The interpretation is that while s affects only the wealth distribution of the active electorate, a representative sample of ideological views shows up at each wealth level at the polls in every state of the world.
Policies are given by the pair (t,z) where t is an income tax, and z is the ideological position of the government. The utility function of a citizen with traits (w,a) over policies (t,z) is given by
Where x= x(t,w) is net income. The positive number α represents the salience of the ideological issue,α ϵ [0,1].
The political system determines a nonnegative income tax with rate 0 ≤ t ≤ 1 Tax revenues are redistributed via lump sum transfers to all citizens. Assume it is not costly to raise taxes. Then, all the amount collected is redistributed. Given that g(w) is a density on income, per capita taxes collected are t ∫ wg(w)dw=tµ Thus, the net income of a citizen with income w is x(t,w) =(1-t w )w+tµ After substituting this expression into (2), we get the indirect utility function of voter at policy (t,z) which is
Voting behaviour (Probabilistic voting)
From equation (3), the subsection of voters who prefer policy T 1 =(t 1 ,z 1 ) to policy T 2 =(t 2 ,z 2 ) are those who obtain higher indirect utility with policy T 1 that is: v(t 1 ,z 1 ;w,a) >v(t 2 ,z 2 ;w,a) Such a set, denoted by W(T 1 ,T 2 ) is given by:
Were Δz≡z2-z1, ∆t≡t2-t1 and ¯z=(z1+z2)/2
Thus, from equations (1) and (4 (a)), the measure of voters who prefer policy (T 1 ) to policy T 2 if ∆z>0, is given by:
where H is the cumulative probability distribution with density h s .
Let Φ(z,s) be the cumulative distribution function for ideological views in state s; that is,
We assume: ϕ(z,s)= ∫w∫z-∞gs(w)r(a|w)dadw
Assumption (A1) For any z, is Φ(z,s) strictly decreasing in s.6
Policy T 1 defeats policy T 2 in just those states that HS(W(t1,t2))>12. As HS(W(t1,t2))>12 is an event with zero probability, we do not need to worry about it. It follows from A1 and (5) that HS(W(t1,t2))>12 just in case S>S*(T1,T2) where S * (T 1 ,T 2 ) is defined uniquely by:
Thus, the probability that policy T 1 defeats policy T 2 is the probability of the event {S<S * } which is S * (T 1 ,T 2 ), since s is uniformly distributed on [0,1]
That is, letting π(T 1 ,T 2 ) be the probability that policy T 1 defeats policy T 2 where Z 2 >Z 1 we have:
(7)
More completely, we may write the function π(T 1 ,T 2 ) for all possible cases, using (4), as follows. Let λ be Lebesgue (uniform) measure on [0,1]. Then:
(8)
Political parties
There are two partisan parties. They have preferences over policies as well as over whether they come to power. Party 1 (P1) aligns its preferences to those of a constituent with traits (w 1 ,a 1 ) while Party 2 (P2) aligns its preferences to those of a constituent with traits (w 2 ,a 2 ) Each party, j, proposes a policy T j =(t J ,z J ) Given a pair of policies (T 1 ,T 2 ) there is only a probability that P1 will win, denoted π(T 1 ,T 2 ) The function π is given by (8) and is known to both parties. Then, the parties’ pay-off functions are
Π1(T1, T2)=π(T1,T2)v(T1;w2,a2)+(1-π(T1,T2))v(T2;w2,a2)
The pay-off function of a party in a policy pair is the expected utility of its representative constituent for that pair of policies.7
So far we have defined all the elements of the model. Now we proceed to obtain the equilibrium tax rate.
Political equilibrium
In the case when there is no ideology and all that matters to calculate the tax rate is the income of the voters. If a party aligns its preferences to those of the poor, it chooses the tax rate which is of most benefit to the poor, ¯t=1. If the party aligns its preferences to the one of the rich, it, likewise, chooses the best tax rate for them,¯t=0 In the Appendix we also work out this, simpler, one dimensional problem.
Now, we can set the stage for our study. When ideology is included in the preferences, if a party P j aligns its preferences to the ones of the poor, w j <µ, does it choose an equilibrium tax rate of unity to benefit the poor?
Analysis of the Stackelberg equilibrium on taxation and ideology
We compute the equilibrium tax rate when voters and parties alike have preferences over taxation and ideology. Citizens’ preferences are given by (3) while the pay-off functions of the parties are given by (9). We start with case 1, where both parties align their preferences to those of the poor. In the paper we are solving only this case. We include the results for the remaining cases in the next section.8 Then, P1 aligns its preferences to (w 1 ,a 1 ) and P2 to (w 2 ,a 2 ) Where w 1 ,w 2 <µ Parties chose policy platforms to solve the following pair of maximization problems,
P1:MaxΠ1t1,z1(T1,T2;α)=s*v(t1,z1;w1,a1)+(1-s*)v(t2,z2;w1,a1)
P2:MaxΠ2t2,z2(T1,T2;α)=s*v(t1,z1;w2,a2)+(1-s*)v(t2,z2;w2,a2)
Given the two-dimensional nature of the problem, it is difficult to compute the Nash equilibrium. In addition, as we are including ideology in the preferences, we should think of the salience of the parameter α in the utility function as variable, with αϵ[0,1] Then, given the continuity of the payoff functions, for any α there is a Stackelberg equilibrium for the game Ψ a =‹α,(a 1 ,w 1 ),(a 2 ,w 2 ),g,r,{g s },v›
In order to compute the equilibrium tax rate we assume:
Assumption (A2)
In the game Ψ1(i.e., when u(x,z;w,a)=-12(z-a)2 , there is a finite number of Stackelberg equilibria. For any such equilibrium (z*1,z*2) we have ,and a1<z*1<z*2<a2 and 0<π(z*1,z*2)<1[/li]
For any equilibrium policy Z*2 in Ψ 1, P1’s best response is unique.
For any equilibrium policy Z*1 in , Ψ 1, P2’s best response is unique.
Assumption A2 is simply a non-degeneracy axiom about the one-dimensional game Ψ 1 For the analysis of one-dimensional games, which justifies this claim, see Roemer (1999).
Let θ(α) be the Stackelberg equilibrium correspondence, which associates to any of the Stackelberg equilibria of the game Ψ 1 We have the following two facts:
Proposition 3.1 Let A2(b) and A2(c)hold. Then θ(α) is upper-hemi-continuous at .α=1.
Proof: See Appendix.
Let (T 1 (α),T 2 (α)) be a continuum of equilibria for the games Ψ a , α<1 , where T 1 (α)=(t 1 (α), z 1 (α)).
Proposition 3.2 Let A2(a) hold. For sufficiently large α:
∆z(α)>0 and ∆z(α)> is bounded away from 0;
¯z(α)-a1 is positive and bounded away from zero;
¯z(α)-a2 is negative and bounded away from zero.
Proof: See Appendix.
We now proceed to calculate the equilibria in our game. Let (z 1 (1),z 2 (1)) be any equilibrium in the game Ψ 1, and ∆z(1)=z 2 (1)-z 1 (1) Let s * be the probability of victory of P1 at this equilibrium. Define the number ¯μ=¯σ¯ρ where ¯σ≡∫Wwgs*(w)r(¯z(1)|w)dw, and ¯ρ≡∫Wwgs*(w)r(¯z(1)|w)dw. By definition ¯μ is the mean income of the cohort of voters with ideological position in the state .Our condition is:
Assumption (A3) For all Stackelberg equilibria in the game , we have:
(a)
¯μ-μ>∆z(1)(w2-μ)2(z2(1)-a2)
(b)
Assumption A3 states the conditions for the Stackelberg equilibria to exist in the one-dimensional game Ψ 1. Such conditions focus in the difference in the mean income of the population and the mean income of the cohort of voters with ideological position ¯z(1) in the state s * Whether expression (10) holds depends on the value of the right hand side of the inequalities.
Theorem 3.3 Suppose A1, A2, and A3 hold. Then for all sufficiently large α, all Stackelberg equilibria of the game Ψ α have t 1 (α)= t 2 (α)=0
Proof: See Appendix.
Definition 3.4 Let a m (s) be the median ideological view in state s. For any δ>0 we say uncertainty is less than δ if and only if there is a number γ such that, for all s, a m (s) lies in a δ interval around γ.
If uncertainty is sufficiently small, a sufficient condition for the truth of (10) is: the mean income of the cohort of voters with the median ideological view in all states is greater than mean income of the population.
We apply the intuition provided by Roemer (1998) to justify such a condition. If is large, then the game Ψ α is essentially a one-dimensional game on ideology. If uncertainty is small, then the median ideological view varies little across states. In an equilibrium where both parties win with positive probability, both parties must therefore play an ideological position close to the median ideological view. That is, ∆z (1)≈0, as both z 1 (1) and z 2 (1)will be very close to the median ideological view in state s * as will be their average ¯z. But since, ∆z (1)≈0, expression (10) is true as long as ¯μ>μ.9
We state this result in a corollary for further reference:
Corollary 3.5 For sufficiently small uncertainty, if A1 and A2 hold, the mean income of the cohort of voters with the median ideological view in all states is greater than mean income of the population, and the ideological issue is sufficiently salient, then both parties will propose a zero tax rate in all Stackelberg equilibria.
From Corollary (3.5) we may say that the cohort of the population who hold approximately the median ideological view are the swing voters. If that cohort’s income is greater than the mean population income, then their ideal tax rate is zero. Consequently, competition forces the parties to propose a tax rate of zero, to attract the swing voters. We summarize this result in the following corollary:
Corollary 3.6 Consider a set of tax rates tϵ[0,1] and let preferences be given by (3) as a function of tax rate and ideology. Then, the equilibrium tax rate is given by t * which benefits the cohort of voters with the median ideological view. Those voters are the swing voters.
Further discussion
We have shown that the equilibrium tax rate could be significantly less than unity even if both political parties align their preferences to the ones of the poor (w<µ) In fact, as ideology becomes more important (α increases), the tax rate decreases towards zero. The result gives insight about the role of ideology on determining the equilibrium tax rate.
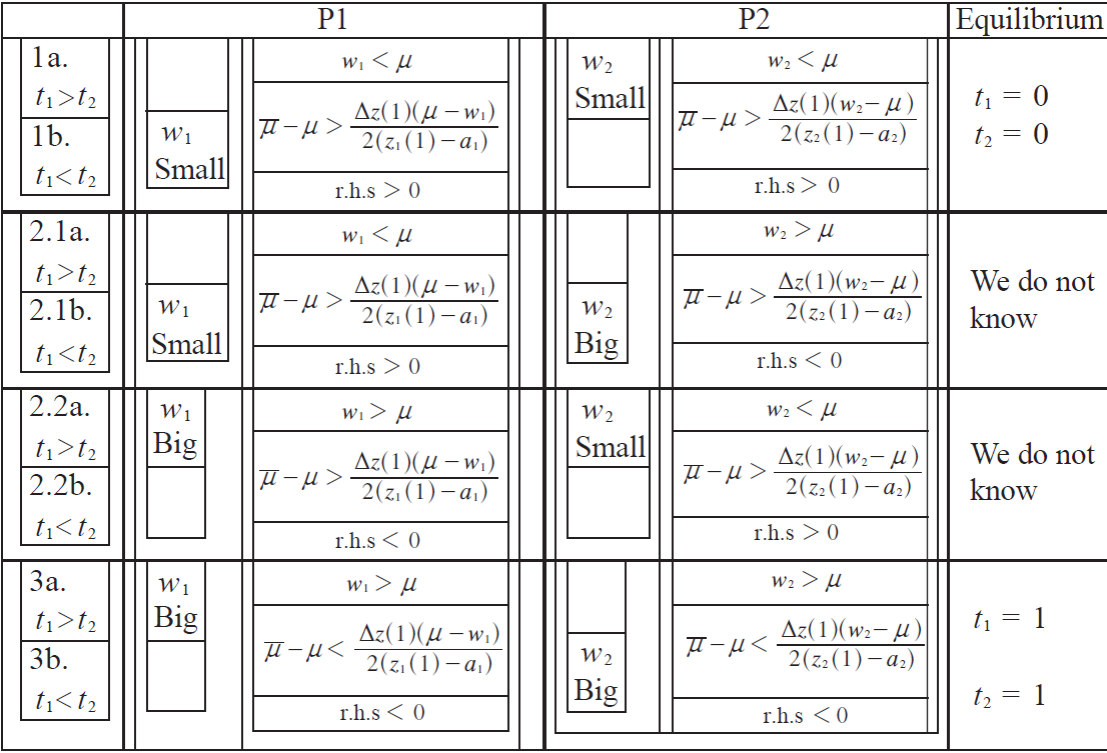
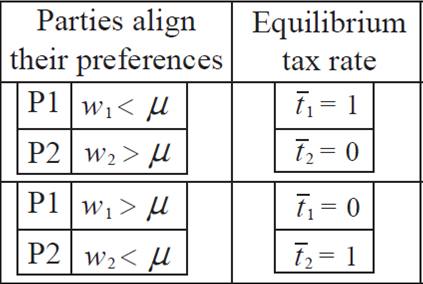
In this paper, we only calculate the equilibrium tax rate for case 1, where both parties align their preferences to those of the poor. Applying the same strategy of analysis used to determine the tax rate in case 1, we now can obtain the equilibrium tax rate for cases 2 and 3. Respectively: 2) one party aligns its preferences to those of the poor and the other party to those of the rich and vice versa; 3) both parties align their preferences to those of the rich. The equilibrium conditions and outcomes are summarized in Table 1.
It is difficult to give an equilibrium condition for each of the cases in the table. However, for case 3, when both parties align their preferences to those of the rich, the resulting equilibrium tax rate equals unity,t 1 =t 2 =1. In that case, the key condition turns out to be: a very small uncertainty, and the mean income of the cohort of voters with the median ideological view in all states less than the mean income of the population.
As for case 1, the voters with the median ideological view are the ones benefitting from political competition. The tax rate is designed according to their income regardless of the parties’ preferences. In equilibrium, a political party, P j , proposes a tax rate of unity (t j =1) if the mean income of the cohort of voters with the median ideological view in all states is less than the mean income of the population ¯μ<μ.10
The previous analysis strongly depends on the assumption of small uncertainty. If we relax that assumption, the equilibrium ideological positions of the parties are not bounded as the median ideological view could vary a lot across states. In fact, the equilibrium of the one-dimensional game on ideology is (z*1,z*2) where z*1 could be considerably different than z*2 Such a situation is described by case 2 in the previous table, when it is not possible to obtain the equilibrium tax rate.
Conclusions
Our analysis shows that, even in democracies, where power is apparently given to the majority, ideology plays an important role on the prevailing economic policy. In equilibrium, if the salience of an ideological issue is high and uncertainty is small, regardless of whether the parties align their preferences to those of the poor or rich, the cohort of voters with the median ideological position become the swing voters. Then, the equilibrium tax rate is designed to benefit that cohort of voters.
When uncertainty is high it is not possible to obtain the equilibrium tax rate.
The analysis suggests that, to some extent, the political parties could choose which ideological issues to emphasize with an eye of pushing the electoral debate towards the economic dimension.











 nueva página del texto (beta)
nueva página del texto (beta)