Services on Demand
Journal
Article
Indicators
Related links
Share
EconoQuantum
On-line version ISSN 2007-9869Print version ISSN 1870-6622
EconoQuantum vol.9 n.2 Zapopan Jul./Dec. 2012
Artículos
On feedback nash equilibrium and cooperation in the neoclassical growth model1
Edgar J. Sánchez Carrera2
2 Facultad de Economía, UASLP, México. E-mail: edgar.carrera@uaslp.mx; http://www.econ-pol.unisi.it/carrera.
Recepción: 26/07/2011
Aceptación: 28/02/2012
Abstract
Far away from any ideological point of view, our aim in this paper is to study, in a differential-game-theoretical approach, the standard growth model. Our baseline model comes from Kaitala y Pohjola (2009) based on the original ideas of Lancaster (1973). We focus on the computation of feedback strategies and we use history-dependent strategies, such as trigger strategies, in which to begin by cooperating and will cooperate as long as the rivals do, and upon observing a defection, it will immediately imply to revert to a period of punishment of specified length in which everyone plays non-cooperatively. We show that trigger strategies are employed by both groups to sustain cooperation as equilibrium. Then, we conclude that players' memory strategies are the key for attaining the maximum economic growth.
Keywords: Differential games, Nash equilibria, Neoclassical Growth model.
JEL Classification: C72, C73, D69, E13, O40, O49.
Resumen
Lejos de cualquier punto de vista ideológico, nuestro objetivo en este trabajo es estudiar, dentro de un enfoque diferencial de la teoría de juegos, el modelo neoclásico de crecimiento económico. Nuestro modelo base viene de Kaitala y Pohjola (2009) sobre la base de las ideas originales de Lancaster (1973). Nos centramos en el cálculo de las estrategias de información y el uso de las estrategias histórico-dependientes, como las estrategias de gatillo en el que empezar por cooperar y colaborar se da siempre y cuando los rivales lo hacen, pero al observar una deserción de tal situación implicará entrar de inmediato a un período de castigo a longitud especificada en donde todo el mundo juega de forma no-cooperativa. Se demuestra que las estrategias de gatillo son empleadas por ambos grupos, firmas y trabajadores, para mantener la cooperación como un equilibrio. Entonces llegamos a la conclusión de que las estrategias con memoria de los jugadores son la clave para lograr el máximo crecimiento económico.
Introduction
Differential games of capitalism were first explored by Lancaster (1973),3 who adopted a two player non-cooperative differential game where the workers control the share of their consumption in total output while the capitalists control the share of investment in the surplus. Comparing the Nash equilibrium with the cooperative solution (from maximizing a weighed sum of worker and capitalist consumption), Lancaster demonstrated that both players obtain more consumption under cooperation, hence resulting in the dynamic inefficiency of capitalism. Lancaster's work has been extended by others. Kaitala and Pohjola (1990) considered a variation on the original Lancaster model in which the politically powerful group of workers controls redistribution, while the economically powerful group of capitalists controls accumulation. Grim trigger strategies are employed by both groups to sustain cooperation as equilibrium. In their model, the workers and capitalists receive returns equivalent to the labor and capital share, respectively. Dockner et al. (2000) surveyed similar models and extensions.
This paper is a short contribution to the literature of game-theoretic framework on economic growth (for a recent summary see, J0rgensen and Zaccour, 2007). Probably, Phelps and Pollak (1968) were the first to consider a game-theoretic approach in economic growth since they modeled economic growth and distribution as an intergen-erational strategic conflict. In their model, a generation derives its utility from the consumption pattern of infinitely many non-overlapping generations, but it can only control its own saving rate. As a result, the Nash equilibrium of this intergenerational game results in undersaving. Comparing the feedback Nash equilibrium with the cooperative solution (that is, maximizing a weighed sum of worker and capitalist consumption), Lancaster demonstrated that both players obtain more consumption under cooperation, hence demonstrating the dynamic inefficiency, in the Pareto sense, of capitalism.4 In the end, this issue has been extended by others in various degrees of sophistication, but the basic conclusion is fundamentally the same (for a survey, see Dockner et al, 2000).
As a caveat, it should be emphasized that such papers should not be perceived as one good or right framework to make inference on economic growth. Indeed, the dynamic inefficiency of the individual capitalism is a real one so that it is always easy and tempting to argue for some collective solution in the face of such inefficiency. In this vein, Benhabib and Rustichini (1996) provide a game-theoretic model of conflict between social groups over the distribution of income. They show how lower wealth can lead to lower growth and even to stagnation when the incentives to domestic accumulation are weakened by redistributive consideration.
Hence, this paper studies growth and redistributive taxation in a differential game model with history-dependent strategies in which the politically powerful government (representing workers' interests) control redistribution, whereas the economically powerful rich (capitalists or firms) control accumulation. In the model, each group is interested in collectively maximizing the sum of its discounted consumption over an infinite horizon.
However, to obtain analytical tractability, we have chosen to make this simplification to the specification in which workers set wages, firms choose employment levels and capitalists control investments. At any case, as a description of a capitalist economy, it is unrealistic in the sense that the labor market is assumed to be competitive, implying full employment at each instant of time.
In this paper, our first task is to reformulate the model of Kaitala and Pohjola (1990) considering a variation on the original Lancaster model in which the politically powerful group of government (workers) controls redistribution, while the economically powerful group of capitalists (firms) controls accumulation. We show that trigger strategies are employed by both groups to sustain cooperation as equilibrium. In our model, the government and capitalists receive returns equivalent to the labor and capital share respectively.
Our paper is organized as follows. Section 2 briefly summarizes the key definitions of differential games. Section 3 presents the model while section 4 and 5 offer the main results of the paper which are based on the feedback equilibrium of the game and the importance of the trigger strategies. Section 6 concludes.
Basic concepts
We focus on situations where there is a large number of "small" followers, such that the actions of any single follower have no impact on the leader's payoff but, in the aggregate, the actions of all followers do have a noticeable impact on the leader's payoff. To have a proper formalization, we invoke the theory of differential games.
Formally, a deterministic differential game defined on a time-interval [to, T], involves (at least) the following elements:
1. A set of players I = {1,...,N}.
2. A vector of controls ui (t)∈ Ui ⊆ Rmi, for each player i ∈ I, and a vector of state variables x(t)∈X ⊆ Rn. Here, X is called the state space and Ui is the set of admissible controls of player i.
3. The state equations describing the motion of the system
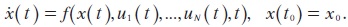
4. A payoff functional of player i,
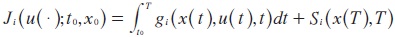
where 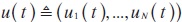 , function gi is players i's instantaneous payoff and function Si is terminal payoff.
, function gi is players i's instantaneous payoff and function Si is terminal payoff.
At any instant of time, player i should select on her control variable ui(t). Suppose that she selects this value according to a strategy, Φi. A strategy (Φi is a decision rule which selects an action as a function of some piece (S) of information. The assumption is that the choice of the decision rule is made at time t = 0 and the player commits to using the decision rule in the game which is about to be played.
Definition 1 A feedback strategy selects the control action according to the rule ui (t) = (Φi (t, x). This means that player i observes the position (t, x) of the system and chooses her action as prescribed by the decision rule Φi.
In games played over infinite time horizons, and where the fundamentals of the game (functions f and gi) do not depend explicitly on time, it is common to confirm one's interest to stationary strategies: ui (t) = (Φi(t, x). The reason is that at any instant of time, players face essentially the same game for the remaining part of the game.
Recall that Nash equilibrium is a A-tuple of strategies (Φ1,Φ2,...,ΦN) such that, given the opponents' equilibrium strategies, no player has an incentive to change his own strategy.
About the notion of memory strategies and a first treatment in the context of differential games, see Tohvinski, Haurie, and Leitmann (1986). Using Friedman's (1971) definition of a differential game as a certain limiting process, the authors discuss a class of two-person (non zero sum) differential games that allow for the enforcement of cooperative outcomes by means of trigger strategies. These strategies are based on the threat to punish a deviator at the moment his deviation from the agreed upon trajectory has been detected. Starting from any possible moment and state of detection, the punisher will try to minimize the deviator's payoff. The best the punished player can obtain is his so-called upper value of the game (see Mehlmann, 1994).
The model
Our model represents a one-sector economy with two agents. That is, an economy with a continuum of identical firms over an interval [0,N] and a continuum of workers over an interval [0,M].
Let us assume that, in this economy, the task of the government is to find a (time-dependent) capital income tax rate (which can be negative) and transfer the tax revenue to the workers as lump sum transfers so as to achieve maximum welfare. If the capital income tax rate is negative, this means the government subsidizes capital income and the subsidy is financed by a lump sum tax on the workers.
The capital-labour ratio at time t is denoted by k(t) and serves as the state variable of the model. Per-capita production at time t is y = f(k( t)) where f is standard neoclassical production function satisfyingand f(0) = 0,f'(k) > 0 and f"(k) < 0 for all k ∈ (0,∞), as well as the Inada conditions limk→0f'(k) = ∞ and limk→∞f'(k) = 0.
The government does redistribution between the two classes by means of lump sum taxes and/or transfers reflected on skill premium denoted by ui (t). Then, ui(t) is a positive number when it is a transfer from the firms, u2, to the skilled working class, u1. This is like a reallocated fiscal policy, i.e. fiscal subsidies on worker's productivity imply a positive ui (t) > 0.
The net income of workers consists of their wage income, w. So the labor force receives an income equal to its marginal product f(k( t)) - k( t )f' (k( t)) while capital a rent equivalent to its marginal product, f' (k( t)) - S, where S is the depreciation rate. A little bit more precise, let R be the rental price for a unit of capital services, and assume that capital stocks depreciate at the constant rate δ≥0. The net rate of return to a household that owns a unit of capital is then R - δ. Households also receive the interest rate r on funds lent to other households. In the absence of uncertainty, capital and loans are perfect substitutes as stores of value and, as a result, they must deliver the same return, so r = R - δ or, equivalently, R = r + δ. The representative firm's flow of net receipts or profit at any point in time is given by π = F(K,L, T) - (r + δ)K - wL. That is, gross receipts from the sale of output, F (K, L, T), less the factor payments, which are rentals to capital, (r + δ)K, and wages to workers, wL. Technology is assumed to be available for free, so no payment is needed to rent the formula used in the process of production. We assume that the firm seeks to maximize the present value of profits. Consider a firm of arbitrary scale; say with level of labor input L. Because the production function exhibits constant returns to scale, the profit for this firm, which is given by equation n(.), can be written as π = L[ f(k) - (r +δ)k - w]. A competitive firm, which takes r and w as given, maximizes profit for given L by setting f' (h) = r + δ, that is, the firm chooses the ratio of capital to labor to equate the marginal product of capital to the rental price. Therefore, in a full market equilibrium, w must be such that profit equals zero; that is, the total of the factor payments, (r + δ) • K + wL, equals the gross receipts in the profit equation given by π= L[f(k) - (r + δ)k - w]. In this case, the firm is indifferent about its scale. For profit to be zero, the wage rate has to equal the marginal product of labor corresponding to the value of K (that satisfies equation f' (k) = r + δ), that is (for deeply details on the overlapping generations model, see Blanchard and Fisher, 1989):
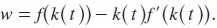
The firm in the model owns the capital and has to decide between retaining its capital earnings for investment and consuming the dividends payments. Its objective is to maximize the stream of dividends payments over time.
We consider that both players (firms and workers) are aware of the state of the system and the economic growth at all times. That is, the interest of the decision makers is centered exclusively on the time interval [0, T ].
It is assumed that workers don't save, thus their income equals consumption. Under the assumption that the utility function is linear with respect to consumption the objective functional of a representative worker can be written as:
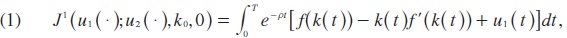
where ρ > 0 is the time preference rate and u2 (•) is the firms' control path described by an investment rate controlled by the representative firm.
Firms act collectively in the sense that they have the same goals, that is, accumulation of capital. Their profits after tax are given by the marginal product of capital f' (k( t)) minus p (t).
Denoting the firms' accumulation rate at time t by u2 (t), we can therefore write their consumption, at time t, as:
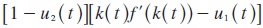
Firms represent, too, persons or consumers, and then we can assume they have a linear utility function and, as the government, they have the same time preference rate p then we can write the firms' (capitalists') objective functional as
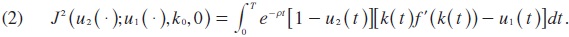
The state of is governed by the dynamic system,
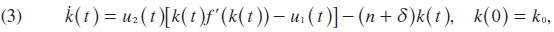
where δ denotes effective depreciation for the capital-labor ratio k, n is the population growth rate and n + δ>0; u1 is a per person lump sum which is controlled by the government, so that f' (k( t)) - u1(t) is the after tax/subsidy profit for the firm. Notice that (n + δ)k( t) is the level of break-even investment per worker, i.e. the amount of investment per worker necessary to leave capital per worker unchanged.
Summarizing, we have a non-cooperative differential two-person game in which each player maintains a strategy (u1 (•); i = 1,2) in order to maximize their respective intertemporal utility function. This is characterized as follows:
Hence, as the redistributive tax can be no greater than profits when it is imposed by firms, and no greater than wages when imposed on government, then the control constraints are given by:
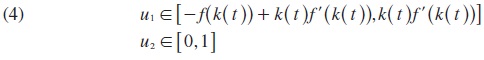
The constraint concerning the firms' accumulation rate u2(t) implies the irreversibility of investment. The constraint concerning the lump sum tax u1(t) ensures that both workers and capitalists have nonnegative consumption. In the absence of a credit market, this is a necessary feasibility condition for any redistributive tax policy. The transfer or tax, u1(t), on the workers must be less than or equal to their incomes while redistribution disbursement cannot exceed the marginal product of workers. Similarly, the tax must be less than or equal to profits when it is imposed on the firm and the subsidy to the firm will not exceed its marginal product. Hence, the above constraint (4) is binding.
We construct the Hamiltonians for each player, firms and workers, with the integrand of his utility function plus a co-estate variable, which will be denoted by λi, i = 1,2, multiplied by the instantaneous variation rate of the state variable (3).
Thus, the Hamiltonian will be as follows for the workers:
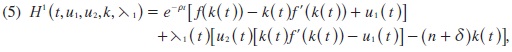
and for the firms:
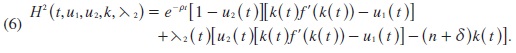
The Pontryagin maximum principle (see for example, Seierstad and Sydsaeter, 1986) guarantees that, given u2, the optimal control u1 will maximize H1 at every point in time, subject to the value restrictions taken by k and λ1 at that time. The same goes for u2 with respect to H2 with k and λ2. Notice that, in our case, the players have no interest in the system beyond T (their payoff is given only in interval [0, T ]).
Recall that, a non-cooperative feedback Nash equilibrium solution is characterized by:
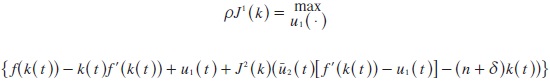
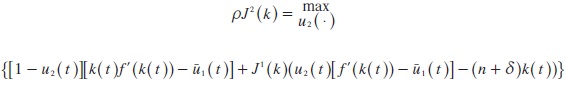
Performing the above maximizations yields:
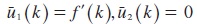
Considering (maxu1(.)) and (maxu2(.)) to solve for the value functions of the workers and the firms respectively:
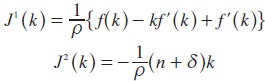
It is straightforward to derive the economic growth rate which is given by:
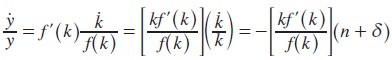
Similarly, the rate of growth of after-transfer profits, denoted by 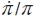 , can be easily obtained:
, can be easily obtained: 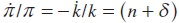 .
.
Both the economic growth rate and the rate of growth after tax profits depend on the level of breakdown investment, denoted by (n + δ), defined as the level of investment needed to keep k at its existing level. If we allow for a negative or zero natural population growth, n ≤ 0,5 then an economy into a below steady state, (n + δ) < 0 has positive growth but will stop growing eventually because the firms are getting subnormal profits and will not be motivated to invest. Those firms in economies which have achieved a steady state growth and beyond, (n + δ) > 0, will break even or enjoy supernormal profits and enter into higher levels of investment.
Capital per person would decline partly due to depreciation of capital at the rate S and partly due to the increase in the number of persons at the rate n. Given the feedback Nash equilibrium (u*1(k), u*2(k)) for the game, the breakdown investment will depend on the capital-labor ratio k. Below steady state, (n + δ) < 0, at steady state, (n + δ) = 0, and above steady state (n + δ) > 0, where the steady-state level of capital is denoted by k*.
Let us briefly discuss the Pareto optimal solutions which can be obtained by devising the pair: (u1 (•), u2(•)), so as to maximize total (workers plus capitalists) consumption, that is a cooperative game between the worker and the firm given some initial state k0. Specifically,
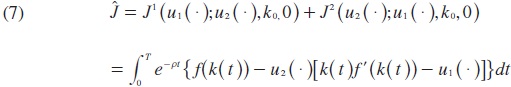
subject to the restrictions (3) and (4). Note that there is no need to assign different weights to J1 and J2 here as it turns out that the same distributional aspect can be brought out by varying the controls in their feasible ranges. In solving this problem, the most rapid approach can be applied because of the simple (linear) structure of the model one can find these solutions without the maximum principle or the HJB equation. Indeed, by using the above state equation (3), then the above integrated (7) becomes:
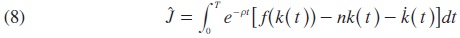
and now to integrate k out and using the initial condition k(0) = k0 yields:
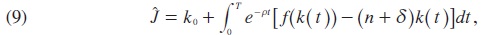
which is concave in k. The solution consequently takes the form of the most rapid approach to the modified golden-rule level k(t) = k* of the capital-labor ratio obtained from f' (k*) = n + δ. Since f(.) is concave and has an infinite slope at the origin, a unique Pareto optimal steady state level k* always exists.
Feedback strategies
The consequences of the feedback Nash equilibrium in terms of economic growth rate, the profitability of the firm and capital accumulation will be more adverse for the developing countries than for relatively more developed countries. Using the above restriction (3), it is straightforward to verify that this is the case if and only if the controls are chosen in such a way that the Pareto optimal strategy pair (u* (.), u2 (.)) can be characterized in feedback form by:
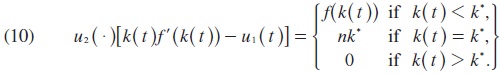
Since the underlying dynamic model is autonomous, the Feedback strategies can be written as functions of the state variable only. Because the definition of k*, concavity of f, and f(0) = 0 imply that f(k*) > nk such that the interval [-f(k*) + (n + r)k*,rk*] is nonempty, then (10) implies, in particular, that, for every a belong to this interval, the stationary feedback strategies are:
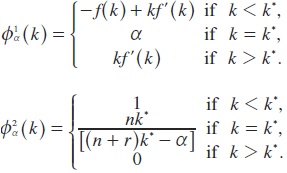
for α∈[-f(k*) + (n + r)k*,rk*].6This meaning that neither class consumes in the first stage of development, which is characterized by smaller than k*. All wages and profits are invested to obtain the most rapid growth.
Also note that for k ≠ k* the strategies are independent of the parameter a which implies that the state trajectory form generated by (Φ1α (k), (Φ2α(k)) is independent of a. Anyway, the solution exhibits some indeterminacy in the steady state: by varying u*i in its feasible range, any feasible distribution of net output among the social classes can be generated.
From now on, we assume that the initial state k0 is positive but smaller than the golden-rule per-capita capital stock k*. This implies that for the Pareto optimal solutions described above, it will always be the case that the state satisfies form for all t∈[0,∞). More specifically, we have:
Since the payoffs are linearly transferable, they can be expressed as:
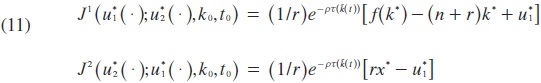
Moreover, we can compute the upper values for both government and firms.
Definition 2 Let ut, (.) ∈ U be an arbitrary but fixed N-tuple of control paths. The upper value of the subgame ΓH (ut (.), t) for player i is defined as:
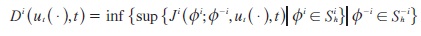
Di(ut, (.), t) is the lowest payoff player i can ensure for himself in the subgame ΓH(ut (.), t) if his opponents announce their strategies before the start of the game. One could also say that Di(ut (.), t) is the highest payoff player i can expect in ΓH(ut (.) t) if his opponents try to minimize his objective functional ji.
To compute the upper values Di(ut, (.), t) for both players i ∈{1,2}, note that, if the workers choose the strategy ui (s) = k( s )f' (k( s)), they could get the utility:
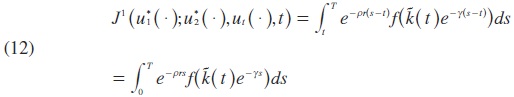
independently of the capitalists' strategy. This implies that:
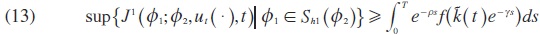
holds for all Φ∈Sh-1. On the other hand, by choosing u2(s) = 0 for all s ∈ [t,∞) the firm can ensure that the government does not get higher utility than that and we therefore conclude that:
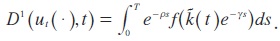
For the calculation of D2(ut, (.), t) we consider the fact that:
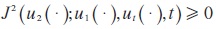
because of the control constraints (4). The case J2 (u2 (.); u1 (.), ut, (.), t) is equal to 0 is when u1 (s) = k(s)f'(k(s)) holds for all s ∈ [t,3), hence, it follows that D2(ut, (.), t) = 0.
Turning from the cooperative mode of play to the non-cooperative one, the government is assumed to choose their redistributive tax strategy so as to maximize their payoff (1), and the firms to choose their savings policy so as to maximize ¿their profits?, subject to the corresponding constraints (3) through (4). Information is assumed to be complete meaning that each player knows the payoff functions and strategy sets of all players. Thus, the non-cooperative feedback Nash equilibrium (u*1 (.), u*2 (.)) is of the form:
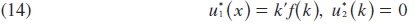
for all values of k.8 If the tax is u*1(k) = k'f(k), the whole rental income of the firm is effectively taxed away and the firm will have to stop investing, thus u*2 (k) = 0. The economic intuition is as follows. In this game, a government may postpone redistribution to later stages so as to facilitate the most rapid economic growth. But the firm predicts as much and being free to optimize on its investment decisions, it will stop investing just before profits are being taxed. But the government is also aware of the firm's reaction: its best response is to impose taxes on capital income earlier. The process will then converge to the feedback Nash equilibrium (u* (k),u*2(k)) = (k'f(k), 0). The strategy pair (14) results in the state trajectory:
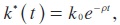
and it generates the following payoffs:
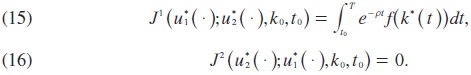
The equilibrium property of (14) can be verified directly. The workers' best response to u*2 (k) = 0 is to transfer all profits to themselves: u*1(k) = k'f(k) for all k. Given that workers play this strategy, the capitalists' saving rate can take any value in the closed unit interval to which u*2(k) = 0 also belongs. The uniqueness of (14) follows from the fact of a positive saving rate. The lack of cooperation between the players has a most severe consequence: there is no growth, but instead the capital stock decays at the constant rate n. Consequently, both social classes have strong incentives to devise mechanisms which would sustain some form of cooperation.
The next proposition summarizes the above result.
Proposition 1 The feedback equilibrium coincides with the minimax threat pair generating payoffs below which players cannot be forced by their opponents.
Thus, in the feedback Nash equilibrium, the economy in a developing country below the steady state has positive growth, but it will stop growing eventually because the firms are getting subnormal profits and will not be motivated to invest. Those firms in countries which have achieved steady state growth and beyond will break even or enjoy supernormal profits and enter into higher levels of investment.
The above results so far are not controversial and are similar to Lancaster (1973) and Kaitala and Pohjola(1990). These authors went on to argue that cooperation between the government and the firm will be more beneficial compared to the dynamic inefficiency in the Pareto sense of capitalism. They assumed implicitly that the cooperative solution will be accepted by all. In the case of Kaitala and Pohjola (1990), the cooperation is enforced by trigger threats that force everyone to cooperate. At any case, one particular way of sustaining cooperation is examined here, namely the use of the feedback strategy pair (14) as a threat to be executed for the rest of the game as soon as one of the players is seen to deviate from an agreed cooperative policy.
Trigger strategies
No binding contracts are allowed or needed and, in this sense, the mode of play is non-cooperative. Instead, it is assumed that the players communicate and use the so-called trigger (memory) strategies (see Mehlmann, 1994).9 This means that, at any time during the game, they can recall all information related to an agreed policy and, in particular, monitor its realization.
Formally, we assume that the players react to a defection by any opponent with a fixed positive time delay δ > 0, that is to say, if a player defects at time s', his opponents will start to punish him at time s = s' + δ. Hence, a trigger strategy Φ for player j with a target profile form and threats θ is given by:

where θ = (θ1,θ2,....,θN)∈ SH is a strategy profile which we call the threats of the punishment strategies. In order for a threat to be credible, it has to be in the punisher's own best interest to carry out the punishment once a defection has occurred.
Considering the above results about the upper values D1(u1(.), t) for both players i ∈{1,2}, we can write the next proposition:
Proposition 2 There exist Pareto optimal target path solutions which are ε - acceptable for some ε > 0. Using the results of D1(u1(.), t) and D2(u1(.), t) and (11), we can conclude that the Pareto efficient strategy profile (φ1α, φ2α) is ε - acceptable if and only if the next two inequalities hold for all :
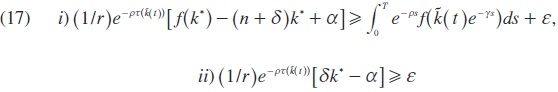
hold for all t ∈[t,∞).
Proof. Without specifying the functional form of the production function f, condition (17) is quite difficult to analyze. However, it can be used to show that there exist some Pareto optimal solutions which are ε - acceptable for some ε > 0.
For example, consider the case where the initial state is equal to the golden-rule, i.e., ko = k*. Of course, this implies τ(k0) = 0 and form for all t ∈[t,∞). It follows that (17) holds for some positive e if, and only if:
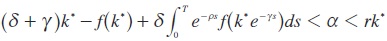
A parameter α satisfying this inequality exists if, and only if:
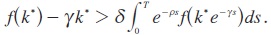
Condition (17) is therefore sufficient for the existence of an e - acceptable and Pareto optimal target path. The continuity assumptions for Di(ut(.), t) are trivially satisfied in this example and we can therefore conclude that there exist Pareto optimal solutions which can be supported as trigger strategy Nash equilibria (more details in Dockner et al., 2000).
Therefore, the players switch from the cooperative mode of play to their feedback strategies for the rest of the game as soon as one of them is observed to deviate from the agreed cooperative policy for an interval of nonzero measure. The threats are credible because they are in equilibrium.
To prove the subgame perfectness, we should consider any intermediate state k(t) reached during play. There are two possibilities: either both sides have cooperated in the past or one of them has cheated for a period of nonzero measure. In the later case, the trigger strategies imply that both sides will play their feedback Nash strategies for the rest of the game and thus be in equilibrium at (t, k(t)). In the former case, if a player unilaterally changes his strategy from time t onwards, it either affects only his control over a set of nonzero measure, in which case Pareto optimal payoff will still be achieved, or it modifies his control over a set of nonzero measure thus triggering the use of feedback Nash relations at time t'>t and, consequently, generating a payoff pair dominated by the Pareto optimal pair.
Concluding remarks
This paper has reformulated the model by Kaitala and Pohjola (2009) under the ideas of Lancaster (1973). Redistribution policy decisions are done by workers and economic decisions of accumulation by capitalist (firms) in the model. We studied strategies to achieve cooperation as equilibrium.
We conclude that in the feedback Nash equilibrium, the economy in a steady state will stop growing eventually because the firms are getting subnormal profits and will not be motivated to invest. This in turn perpetuates a vicious cycle of low capital accumulation level, low growth and maybe some political instability, i.e. characterizing a poverty trap.
Another conclusion is that the results here appear to be that a cooperative or collective solution should be enforced through a "benevolent dictator", since cooperation is enforced by trigger threats that force everyone to cooperate.
References
Alesina, A. and Rodrik, D. (1994). "Distributive Politics and Economic Growth", Quarterly Journal of Economics, 109, pp. 465-449. [ Links ]
Benhabib and Rustichini (1996). "Social Conflict and Growth," Journal of Economic Growth 1, 125-142. [ Links ]
Blanchard, O. and S. Fischer (1989). Lectures on Macroeconomics. The MIT Press. [ Links ]
Dockner, Engelbert J., Steffen Jorgensen, Ngo Van Long and Gerhard Sorger (2000). Differential Games in Economics and Management Science. Cambridge, UK: Cambridge University Press. [ Links ]
Friedman, A. (1971). Differential Games, Wiley, New York, New York. [ Links ]
González-Alcón, C.; Sicilia, J.; Álvarez, J. A. (1999). "Nash Equilibria in a Differential Game of Economic Growth," Journal of Optimization Theory and Applications 103(2), pp. 337-357. [ Links ]
Jørgensen, S. and G. Zaccour (2007). "Developments in differential game theory and numerical methods: economic and management applications," Computational Management Science 4(2), pp. 159-181. [ Links ]
Kaitala, Veijo and Matti Pohjola (1990). "Economic Development and Agreeable Redistribution in Capitalism: Efficient Game Equilibria in a Two-Class Neoclassical Growth Model", International Economic Review, 31(2), 421-438. [ Links ]
Kemp, M. C. and K. Shimomura (1987). "A Differential Game between Organized Labour and Organized Capital", mimeo, The University of New South Wales. [ Links ]
Lancaster, Kelvin (1973). "The Dynamic Inefficiency of Capitalism", Journal of Political Economy, 81, 1092-1109. [ Links ]
Lindner, I. and H. Strulik (2004). "Distributive politics and economic growth: the Markovian Stackelberg solution", Economic Theory, 23, pp. 439-444. [ Links ]
Mehlmann, A. (1994). "On Differential Games with Markov Perfect Triggering," Journal of Optimization Theory and Applications 80(2), 273-288. [ Links ]
Phelps, E. S. and R. A. Pollak (1968). "On Second-best National Saving and Game Equilibrium Growth", Review of Economic Studies, 35, 185-199. [ Links ]
Sierstad, A., and Sydsaeter, K. (1986). Optimal Control Theory with Economic Applications, North Holland, Amsterdam, Holland. [ Links ]
Toewinski, B., Haurie, A., and Leitmann, G. (1986). "Cooperative Equilibria in Differential Games", Journal of Mathematical Analysis and Applications, Vol. 119, pp.182-202. [ Links ]
1Many thanks to two anonymous referees for their feedback to improve this paper. I would really like to thank Elvio Accinelli for his constructive comments; and Jacob Engwerda for his support during my visiting period at Tilburg University in CentER where I started to develop this research. The usual disclaimer applies.
3 Gonzalez-Alcon et al. (1999) aims to integrate the new institutionalist approach with that taken by Lancaster. Since game theory enables us to analyze how the institutional framework (i.e., the game rules) conditions the equilibrium strategies.
4 Lancaster (1973) pointed out that capitalism is dynamically inefficient when compared to a social optimum which can be achieved by both the workers and the capitalism cooperating together.
5 The latest data from the Population Reference Bureau shows that there are twenty countries in the world with negative or zero natural population growth. This negative or zero natural population growth means that these countries have more deaths than births or an even number of deaths and births; this figure does not include the impacts of immigration or emigration (available data: http://www.prb.org/Publications/Datasheets/2011/world-population-data-sheet.aspx).
6 The strategies are feasible, (Φ1α (k), (Φ2α(k)) ∈ Sh, being Sh the set of feasible strategies (Φi,i = 1,...,N.
7 Here 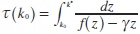 is the terminal time at which the golden-rule capital stock is reached from the initial state.
is the terminal time at which the golden-rule capital stock is reached from the initial state.
8 It is well known that the feedback equilibrium belongs to the class of subgame perfect equilibria.
9 The threats in a trigger strategy equilibrium are intended to prevent defections from the target path. In equilibrium, defections do not occur and the punishment is never executed.