Introducción
La proporcionalidad es una noción clave para la comprensión de otros conceptos como función, ecuación, incluso algunos conceptos de probabilidad. Se encuentra presente en la currícula mexicana desde primaria hasta los niveles superiores de educación (Megginson, Sosa, Padilla-Carrillo, Solares, Martínez & Lozano, 2015) y, es una noción requerida con frecuencia en la resolución de problemas cotidianos. Sin embargo, se ha observado que los estudiantes (incluso de nivel superior) tienen dificultades para comprender operaciones básicas con fracciones, entender lo que son las razones y, por lo tanto, usar la proporcionalidad en el análisis y descripción de situaciones (Valverde, 2012). Esta problemática se observa en el aprendizaje de los estudiantes universitarios que cursan varias licenciaturas, entre ellas la de medicina y enfermería. Por ejemplo, García-Oliveros, Granados-Silva Pinillos-Bohórquez (2009, p. 73) identifican “un serio problema tanto para los profesionales de la salud, responsables de suministrar la medicación, como para las instituciones y para los pacientes debido a la repercusión humana, asistencial y hasta económica” que se deriva de un mal cálculo de dosis y, por lo tanto, de errores de medicación asociados con una falta de desarrollo del razonamiento proporcional. García-Oliveros, Granados-Silva y Pinillos-Bohórquez (2009) describen lo anterior a partir de un estudio realizado con estudiantes de enfermería, vinculado a la administración de medicamentos, donde se reconoce al razonamiento proporcional como un área problemática en la carrera de enfermería que debe atenderse.
En este artículo se busca dar respuestas a las preguntas ¿qué conocimiento y habilidades matemáticas, relacionadas con proporcionalidad, exhiben los estudiantes universitarios de los primeros semestres de la Licenciatura en Medicina al resolver situaciones cercanas a la vida real?, ¿cómo se modifica, extiende y refina este conocimiento y habilidades durante el proceso de resolución de una Actividad Provocadora de Modelos [APM]? Para ello, se diseñaron e implementaron APM en el marco de la perspectiva de Modelos y Modelación (Doerr, 2016; Lesh, 2010; Lesh & Doerr, 2003). Interesaba describir cómo los estudiantes universitarios de la carrera de medicina abordaron una de las actividades; es decir, cómo utilizaron información dada en la situación problemática, cómo organizaron los datos, cómo realizaron el análisis dimensional y las representaciones matemáticas utilizadas. Se documentó el surgimiento de distintos ciclos de entendimiento (Vargas-Alejo, Reyes-Rodríguez, & Cristóbal-Escalante, 2016) asociados con los conceptos y representaciones utilizadas al abordar la situación problemática.
La actividad, que se describe en este artículo, forma parte de un conjunto de cinco actividades diseñadas e implementadas durante el desarrollo de la asignatura Matemáticas Generales en la Universidad de Quintana Roo. El programa de dicha asignatura, sugiere que los estudiantes aprendan a resolver problemas y a modelar situaciones cercanas a la vida real (o profesional) y, de manera simultánea, profundicen en conceptos matemáticos, como proporcionalidad, progresiones aritméticas y funciones. Es decir, se busca que el aprendizaje de los conceptos se asocie con la descripción interpretación, predicción y control del comportamiento de diversos fenómenos.
1 Marco teórico
Enseguida se describen aportes teóricos que sustentaron el análisis, diseño, desarrollo, implementación y evaluación del estudio. Por ejemplo, la Perspectiva de Modelos y Modelación fue importante por la concepción que ofrece sobre aprender matemáticas y el tipo de actividades a utilizar en el aula. Estudios como los de Cramer y Post (1993), Vergnaud (1995) y Lesh, Post y Behr (1988) fueron utilizados para concretar el contenido matemático subyacente de las situaciones problemáticas y contextos diseñados.
1.1 Estudios sobre proporcionalidad
Al ser una noción elemental, la proporcionalidad ha sido objeto de estudio desde muy diversos enfoques dentro de la investigación en didáctica de las matemáticas (Cramer & Post, 1993; García-Oliveros, Granados-Silva, & Pinillos-Bohórquez, 2009; Godino & Batanero, 2002; Lamon, 1993; Lesh & Doerr, 2003; Lesh, Post, & Behr, 1988; Ramírez & Block, 2009; Noelting, 1980 y Vergnaud, 1990; 1994: 1995).
En estudios como los de Cramer y Post (1993) se aborda la necesidad de que los estudiantes resuelvan distintos tipos de problemas en el salón de clases. Por ejemplo, en el Proyecto de Número Racional,1 desarrollaron diferentes tipos de tareas para evaluar de manera diferenciada la comprensión de la proporcionalidad. A partir de los resultados, concluyeron que los estudiantes deberían resolver problemas en los que se utilizaran diferentes contextos reales que incluyeran: valor faltante, comparación numérica, comparación y predicción cualitativa, para mejorar su aprendizaje. La instrucción debería iniciar con contextos familiares y extenderse a aquellos menos familiares. Por otra parte, sugirieron que se deberían enseñar múltiples estrategias, incluyendo la tasa unitaria, el factor de cambio, las fracciones y el algoritmo de producto cruz (regla de tres). Cramer y Post (ibid) pusieron énfasis en la necesidad de promover un aprendizaje basado en los conceptos más que en procedimientos algorítmicos.
De acuerdo con Lesh, Post y Behr (1988), el desarrollo del pensamiento proporcional involucra el sentido de covariación y comparaciones múltiples, y la habilidad para almacenar y procesar mentalmente distintos tipos de información. Señalan la existencia de cierta continuidad desde la multiplicación (suma reiterada) hasta la proporcionalidad. Sugieren la necesidad de diseñar situaciones problemáticas que posibiliten la conceptualización de estructuras multiplicativas que tomen en cuenta el análisis de la variación entre magnitudes, más que la adición repetida de una misma cantidad. Se vuelve importante la realización de análisis dimensionales y tablas de variación asociadas con la resolución de problemas de multiplicación y división para mejorar la comprensión.
Por su parte, Burgos, Giacomone, Beltrán-Pellicer y Godino (2017) identificaron niveles de algebrización que pueden emerger en una tarea de proporcionalidad. Reconocen la existencia de un nivel 0 al cual describen propiamente aritmético, hasta un nivel 4 que caracterizan por el surgimiento de la introducción de parámetros. En estos niveles los estudiantes utilizan procedimientos cada vez más complejos que van desde estrategias aritméticas, uso y cálculo de tasas unitarias, utilización de la regla de tres y diagramas, hasta el uso de la generalización, mediante la utilización de parámetros.
1.1.1 Proporcionalidad de acuerdo con Vergnaud
En el mismo sentido de lo antes expuesto en esta sección, es importante incluir los aportes de Vergnaud (1990) en cuanto a la Teoría de los Campos Conceptuales, la cual da “cuenta de los procesos de conceptualización progresiva de las estructuras aditivas, multiplicativas, relaciones número-espacio, y del álgebra” (p. 1). El campo conceptual de estructuras multiplicativas es, a la vez, el conjunto de las situaciones cuyo tratamiento implica una o varias multiplicaciones o divisiones, y el conjunto de conceptos y teoremas que permiten analizar estas situaciones.
Vergnaud (1994) explica que, en el isomorfismo de la medida establecido entre dos unidades dimensionales distintas (o espacios de medida), existe una relación cuaternaria; es decir, cuatro magnitudes o términos covarían permitiendo hallar el valor de una de ellas para su solución. Esto implica que, incluso en los problemas más simples que involucren realizar operaciones de multiplicación y división, se requiere de la proporción simple entre dos variables, una en relación con la otra. Ello da lugar a cuatro tipos de problemas elementales (Vergnaud, 1990): “la multiplicación, la división-partición, la división cuotición y la cuarta proporcional” (p. 12).
La dificultad de los problemas puede variar; ello depende del tipo de cantidades numéricas que se utilicen como datos, o bien, del tipo de experiencia que requieran por parte del estudiante. La dificultad también depende de la necesidad de establecer una combinación de dos proporciones para resolver el problema, así como, de que se requiera encadenar funciones que liguen a las variables dos a dos o por producto.
Vergnaud (1995) destaca dos procedimientos de solución que nombra como Análisis Vertical o Escalar [AV] y Análisis Horizontal [AH]. El primero se establece ante una relación entre magnitudes de la misma unidad dimensional o mismo espacio de medida, donde el estudiante utiliza al menos un operador razón. El AH se presenta ante una relación entre magnitudes de distinta unidad dimensional (espacio de medida diferente), por lo tanto, el estudiante debe hacer análisis de unidad dimensional o una regla de tres.
En el AV intervienen los operadores escalares (círculos en la Figura 1). Para resolver problemas elementales se pueden aplicar dos operadores de manera sucesiva (uno para multiplicar y, otro para dividir o viceversa, ver flecha en contorno continuo y flecha en contorno punteado en la Figura 1), sin llevar a cabo un análisis dimensional. De acuerdo con Vergnaud (1990), la comprensión de las nociones razón, razón-operador (flecha de relleno sólido en Figura 1) y proporción, están dentro de las dificultades que tienen los estudiantes al resolver problemas utilizando estos operadores.
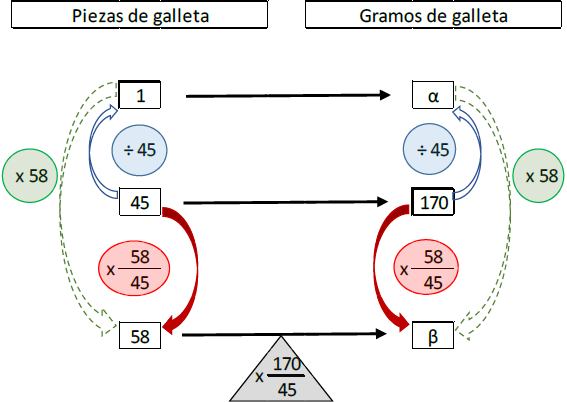
Fuente: Adaptado de Vergnaud (1995).
Figura 1 Diagrama sagital que muestra el Análisis Vertical y Análisis Horizontal del problema del Chef.
El Análisis Horizontal (flechas horizontales en la Figura 1 implica un nivel conceptual más elaborado, por estar centrado en el operador función (triángulo en la Figura 1) y enlazar, por lo tanto, la comprensión de esta noción.
A manera de ejemplo, se analizará el siguiente problema: “Un chef está escribiendo la receta para hacer un pay, ello implica que debe describir los ingredientes utilizados en gramos. Si sabe que aproximadamente 45 galletas pesan 170 gramos (g) y para la base del pay utilizó 58 galletas, ¿cuál es el peso aproximado en gramos de las galletas que debe escribir en la receta?”
Vergnaud explica que el AV se centra en la noción de operador-escalar (sin dimensión) y las resume en dos etapas. En la primera etapa, el procedimiento para pasar de 45 galletas a una galleta (dividiendo entre 45), puede ser el mismo que para obtener el peso de una galleta a partir del peso de 170 g: se debe dividir 170 entre 45 (así se puede obtener α, valor unitario en gramos por galleta). En esta etapa del AV (flechas en contorno continuo en la Figura 1) se podría evitar el manejo de unidades dimensionales distintas (galletas y gramos).
Para la segunda etapa del AV se considera que, así como se transita de una galleta a 58 galletas (multiplicando por 58) se puede calcular, con base en el peso de una galleta (α), el peso de 58 galletas (β). En la Figura 1 se muestra esta etapa con flechas en contorno punteado. Como se observa, tampoco podría requerirse del manejo de unidades dimensionales distintas.
De manera sucinta, podría decirse que es posible transitar directamente de 45 a 58 galletas, multiplicando por el operador fraccionario (58/45), que no es otra cosa que la aplicación sucesiva de dos operadores escalares (÷45) y (x58). El mismo operador fraccionario permite pasar del peso de 45 galletas (170 gramos) al peso de 58 galletas (β). Este paso podría tomarse por trivial, sin embargo, el operador fraccionario (58/45) representa, de manera sintética, la aplicación sucesiva de dos operadores multiplicativos: una división (÷45) y la multiplicación (x58). Lo cual, permite comenzar ya sea por la división o por la multiplicación.
Se puede considerar, también, que el operador fraccionario representa la multiplicación por la razón (ver relación marcada con la flecha de relleno sólido en la Figura 1). Por ejemplo, al intervenir una proporción o igualdad de dos razones:
Por otra parte, el AH está centrado en la noción de como operador-función (razón representada por un triángulo en la Figura 1) que hace pasar de una categoría a otra o unidades dimensionales distintas (cantidad de piezas de galletas al peso de las galletas en gramos). Para este análisis, Vergnaud describe las siguientes etapas:
Primera etapa AH. El operador-función que permite pasar de 58 galletas a β gramos es el mismo requerido para pasar de 45 galletas a 170 gramos (flechas horizontales, Figura 1).
Segunda etapa AH. Este operador-función implica la multiplicación por la razón (dato en un triángulo en la Figura 1). Para ejemplificar lo anterior, tenemos que:
El AH se sitúa en un nivel conceptual más elaborado, dada la comprensión de la noción de función con la cual está relacionada. Vergnaud (1995) relaciona el análisis de unidades dimensionales con la regla de tres y señala que la “regla de tres teórica” plantea dificultades distintas y desiguales para los estudiantes, ya que deja de ser trivial cuando es comprendida como una relación cuaternaria de variables, pues en ocasiones, requiere de un análisis dimensional.
El investigador también menciona las relaciones de doble proporcionalidad, las cuales implican una demanda cognitiva mayor a las relaciones de proporcionalidad simple, Si bien, estas pueden ser resueltas al llevar a cabo, de manera consecutiva, dos relaciones de proporcionalidad simple, la estructura conceptual que subyace en una relación de doble proporcionalidad implica una complejidad mayor.
Para ejemplificar la relación de doble proporcionalidad descrita por Vergnaud retomemos el ejemplo del chef que desea escribir una receta para pay. Supongamos que ahora necesita obtener la cantidad necesaria del ingrediente w (harina, azúcar, sal, etc.) en kilogramos. El problema podría ser el siguiente: “El chef requiere obtener el ingrediente w en kilogramos. Al momento de realizar la receta del pay ha usado α cucharadas de w para la elaboración del postre. Sin embargo, desea escribir la cantidad necesaria w en kilogramos. Para hacer esto, el chef decide calcular a cuántas cucharadas equivale una taza y cuántas tazas equivalen a un kilogramo de w. El chef encuentra la siguiente relación: con 11 cucharadas se llena una taza de ingrediente w y con 4.5 tazas se logra alcanzar el equivalente de un kilogramo de w”.
La relación antes descrita puede ser organizada por los estudiantes de manera tabular como se muestra en la Figura 2.
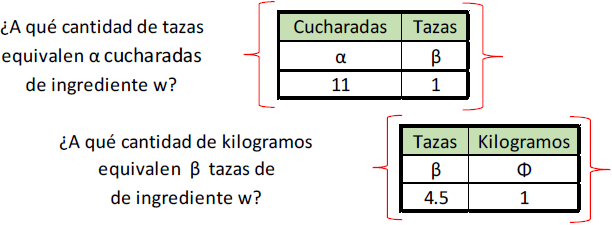
Fuente: elaboración propia.
Figura 2 Preguntas asociadas a la organización tabular de datos en la proporcionalidad simple.
Esto tambien puede ser resumido en una sola organización tabular (Tabla 1).
Tabla 1 Representación tabular que permite visualizar los datos e incógnitas en una relación de doble proporcionalidad
| Doble proporcionalidad | ||
| Cucharadas | Tazas | Kilogramos |
| α | β | Φ |
| 11 | 1 | φ |
| λ | 4.5 | 1 |
Fuente: elaboración propia.
En la Tabla 1 se observan relaciones multiplicativas, las cuales se pueden escribir mediante funciones lineales (donde: α = cantidad en cucharadas del ingrediente w; β = f (α) =cantidad en tazas del ingrediente w; Φ = f (β) = cantidad en kilogramos del ingrediente w).
De lo anterior se puede obtener:
De acuerdo con Vergnaud (1990) este último posible razonamiento muestra un mayor nivel cognitivo de la noción de proporcionalidad.
Vergnaud (1990) considera que “los conceptos de fracción, de cociente, de número racional, de producto y de cociente de dimensiones, de escalares, de función lineal […] toman primitivamente su sentido en los problemas de proporción” (p. 13). Para el investigador, aprender la noción de proporcionalidad implica comprender los conceptos relacionados, entender procedimientos como AH, AV, análisis dimensional, regla de tres y poder utilizarlos al resolver problemas o situaciones reales. Es en este punto, donde Vergnaud (1990) coincide con la Perspectiva de Modelos y Modelación, en el sentido de que los conceptos y procedimientos no están aislados entre sí, están interrelacionados y forman parte de una red o sistema conceptual que el estudiante debe aprender.
1.2 Perspectiva de Modelos y Modelación [PMM]
Desde esta perspectiva (Doerr, 2016; Lesh, 2010; Lesh & Doerr, 2003), el aprendizaje es un proceso de desarrollo de sistemas conceptuales que surgen cuando los estudiantes analizan situaciones que tienen más de una respuesta y cuya solución no es un número o una palabra, sino situaciones que ameritan describir, argumentar y explicar. En PMM, un modelo es definido como un sistema de elementos, relaciones, reglas y operaciones que pueden ser usados para explicar, predecir o describir algún otro sistema. Por lo tanto, el aprendizaje de un concepto matemático ocurre a través del proceso de desarrollar un modelo adecuado a una situación que puede ser usado y reutilizado en cierto rango de contextos (Doerr, 2016).
Aprender matemáticas es un proceso que involucra ciclos progresivos de construcción de entendimiento, modificación, extensión y refinamiento de maneras de pensar (Lesh, 2010); en estos ciclos, los sujetos profundizan un concepto o constructo matemático en distintos niveles al relacionar datos, metas y posibles rutas de solución al enfrentar una situación problemática. Generalmente, los primeros modelos o interpretaciones son burdos, pero paulatinamente van refinándose, esto se debe a que el conocimiento es parecido a un organismo vivo, no es algo inerte, es un sistema dinámico que está adaptándose y autorregulándose continuamente. La evolución involucra diferenciación, integración y refinamiento de sistemas inestables, por lo que también comprende discontinuidad y reorganización conceptual.
Dentro de PMM, pensar de manera matemática es: construir, describir, explicar, calcular, identificar patrones y regularidades en sistemas complejos; realizar representaciones de sistemas relevantes que incluyan una variedad de medios escritos, hablados, construidos y dibujados. La fluidez en las representaciones es crucial para construir modelos y entender conceptos matemáticos. Es por ello que, el proceso se considera como producto del aprendizaje y no el modelo. Este último reside en la mente del individuo y en los medios bajo los cuales es representado donde se ven reflejados los significados asociados con un sistema conceptual determinado (Lesh & Doerr, 2003).
Las actividades, que se utilizan en el aula, son esenciales para propiciar conocimiento (Lesh, 2010); deben permitir a los estudiantes aprender conceptos matemáticos, pero no de manera aislada, sino de manera interrelacionada. Por lo tanto, se propone que los estudiantes realicen cierto tipo de actividades, entre ellas las APM, llamadas así porque permiten que el estudiante, al abordarlas, genere productos que van más allá de respuestas cortas a preguntas específicas (Cpalms, 2018). Las APM propician manipular, modificar, compartir y reutilizar herramientas conceptuales (e.g. modelos) para construir, describir, explicar, manipular, predecir o controlar sistemas matemáticos significativos. Las actividades requieren de la matematización mediante procesos que implican cuantificar, dimensionar, coordinar, categorizar, traducir al lenguaje algebraico y sistematizar objetos relevantes sus relaciones, acciones, patrones y regularidades (Lesh & Doerr, 2003).
Doerr (2016) explica que las Actividades Provocadoras de Modelos permiten, a los equipos de estudiantes, involucrarse en un proceso interactivo donde ellos expresan, prueban y redefinen sus maneras de pensar sobre situaciones problemáticas significativas. Las APM son diseñadas para favorecer la construcción de un modelo generalizable que aclare y delimite la estructura matemática de la situación del problema. La actividad propicia entendimiento matemático nuevo en los estudiantes al estar en un contexto significativo donde exhiben, a lo largo de la tarea, su conocimiento actual proveniente tanto de su experiencia como de su conocimiento matemático. Este conocimiento se expresa, usualmente, mediante el uso de medios de representación como: modelos concretos, metáforas basadas en la experiencia, lenguaje hablado, diagramas o dibujos, símbolos escritos, tablas, gráficas y ecuaciones (Lesh & Doerr, 2003). Cuando los estudiantes realizan las APM pueden pasar por varios ciclos de entendimiento conceptual. El entendimiento conceptual se relaciona con el proceso de matematización de los estudiantes, es decir, con las ideas cualitativas que emergen, la forma de cuantificar información, atribuir dimensiones, organizar y analizar datos y hacer operaciones.
Algunas APM (e.g. Lesh & Yoon, 2004) propician que los estudiantes realicen sus primeras descripciones de manera cualitativa. Identificando la existencia de variables y cierta relación entre ellas, mediante el uso de metáforas basadas en la experiencia, sin utilizar representaciones tabulares, gráficas o algebraicas. El estudiante caracteriza las relaciones con términos como “es más pequeño”, “es más grande”.
Las descripciones pueden evolucionar y las características cualitativas o comparaciones se pueden volver numéricas. Es posible que en un segundo ciclo de entendimiento los estudiantes exhiban ambos tipos de descripciones (cualitativas y cuantitativas), pero ahora los datos y las relaciones tienden a expresarse numéricamente, mediante tablas y gráficas. Vargas-Alejo, Reyes-Rodríguez y Cristóbal-Escalante (2016) propusieron, con base en la interpretación dada a PMM (Lesh & Doerr, 2003), que los estudiantes pueden exhibir ciclos de entendimiento cualitativos, cuantitativos y algebraicos (Tabla 2) al resolver situaciones problemáticas; al ciclo algebraico lo caracterizan de la siguiente manera:
El ciclo de entendimiento algebraico, es aquel en el cual los estudiantes ya han pasado por diferentes fases de diferenciación, integración y refinamiento de los distintos sistemas o modelos. En este ciclo los estudiantes muestran un uso fluido de las representaciones (tabulares, gráficas, verbales, etc.), así como la manipulación de símbolos algebraicos para resolver una situación (p. 70).
Tabla 2 Resumen de los ciclos de entendimiento
| Ciclo | Se
caracteriza porque el estudiante |
Posibles
representaciones que emergen en la resolución |
Observaciones |
|---|---|---|---|
| Cualitativo | Da sentido a la situación en la que se desarrolla el problema, así como a las variables involucradas y la posible relación entre ellas. | El estudiante no utiliza representaciones matemáticas (números, tablas, gráficas o expresiones algebraicas). | El estudiante puede expresar el comportamiento y la relación entre variables mediante términos lingüísticos. |
| Cuantitativo | Es capaz de establecer cuantitativamente qué significan las expresiones lingüísticas y las comparaciones se vuelven numéricas. | El alumno expresa los datos y sus relaciones entre sí mediante representaciones tabulares y gráficas. | El manejo de estas representaciones puede permitir al estudiante comprender y describir el problema o situación. |
| Algebraico | Puede llegar a mostrar fluidez en las representaciones (tabulares, gráficas, verbales, etc.) y manejo de símbolos algebraicos al resolver una situación. | El estudiante, para describir e interpretar un fenómeno, construye, usa, transita y coordina distintas representaciones matemáticas. | Es posible que los estudiantes que alcancen este ciclo hayan diferenciado, integrado y refinado distintos sistemas conceptuales o modelos previos. |
Fuente: Descripción tomada y adaptada de Vargas-Alejo, Reyes-Rodríguez y Cristóbal-Escalante (2016).
El hecho de que los estudiantes puedan usar distintas representaciones (Tabla 2) para explicar, describir e interpretar las APM es un indicador del entendimiento del conocimiento matemático porque de acuerdo con Lesh y Doerr (2003, p. 12): “los significados asociados con un sistema conceptual dado, tienden a estar distribuidos a través de una variedad de medios representacionales”.
Los aportes antes descritos fueron el sustento teórico que marcó las directrices para esta investigación. Se tomó en cuenta principalmente la Perspectiva de Modelos y Modelación (sección 1.2), dado que, en esta investigación interesó identificar el desarrollo del conocimiento y habilidades de los estudiantes en relación con el sistema conceptual de la noción de proporcionalidad. Fue importante que las actividades implicaran la resolución de problemas de proporción cercanos a contextos reales (tal como lo sugieren Cramer & Post, 1993) y el manejo interrelacionado de conceptos (Vergnaud, 1995). Se determinó que las actividades iniciales serían aquellas que permitieran el uso de relaciones cuaternarias, y la proporción simple entre dos variables, una en relación con la otra. En el análisis de resultados se utilizó la caracterización de los ciclos de entendimiento (Tabla 2), dado que dichos ciclos, de manera simultánea a la evolución en la habilidad para comunicarlos, se asocian con la profundización de un concepto matemático.
2 Metodología
Este estudio fue cualitativo porque se documentó y analizó información asociada con el conocimiento y habilidades matemáticas relacionadas con la proporcionalidad, que exhiben los estudiantes de la Licenciatura en Medicina, al resolver situaciones cercanas a la vida real; así como se identificó y analizó cómo se modifica, extiende y refina este conocimiento y habilidades durante el proceso de realización de una APM. Para ello, se detectaron ciclos de entendimiento, el tipo de representaciones y conceptos utilizados, así como, los procedimientos en los que el Análisis vertical y el Análisis horizontal fueron fundamentales por su relación con el uso de razones y relaciones funcionales.
2.1 Población de estudio
La población en este estudio fue un grupo de 21 estudiantes de primer ingreso a la Licenciatura en Medicina impartida en la División de Ciencias de la Salud de la Universidad de Quintana Roo. Las edades de los alumnos variaban entre los 18 y 21 años. Los estudiantes se encontraban cursando la asignatura de Matemáticas Generales, la cual, forma parte de las materias del tronco común en los planes de estudio de carreras profesionales tanto en Licenciaturas como en Ingenierías de la Universidad de Quintana Roo. La asignatura tiene entre sus objetivos principales orientar a los estudiantes para utilizar los conocimientos matemáticos adquiridos a lo largo de su trayectoria académica en la resolución de problemas y modelación de situaciones cercanas a la vida real. Esta asignatura está dividida en cuatro unidades: Álgebra, Progresiones, Funciones y Probabilidad y Estadística. A lo largo del curso se promueven los conocimientos matemáticos básicos necesarios para la vida académica y profesional del estudiante.
La noción de proporcionalidad se incluye en la unidad de Funciones, pero no únicamente guarda relación con los demás temas de la asignatura de Matemáticas generales, también es básica para la comprensión y resolución de problemas en otras disciplinas como: Epidemiología, Dosificación de fármacos, Salud pública, Química molecular o Nutrición, por mencionar algunas asignaturas del actual plan de estudios. Es decir, los estudiantes requieren desarrollar razonamiento proporcional para estar en condiciones de resolver problemas más complejos o bien de otras disciplinas. Un ejemplo de problemas podría ser el caso hipotético de suministro de medicamento propuesto por Barrera-Mora y Santos-Trigo (2000) que en una versión más sencilla se encuentra en el libro editado por National Council of Teachers of Mathematics (2003).
Los participantes en este estudio, previo a la implementación de la actividad que se describe en este artículo, habían revisado en clases de la asignatura conceptos matemáticos como: razón, progresiones aritméticas y geométricas, entre otros. Sin embargo, de acuerdo con los comentarios de su profesor habitual, estos temas habían sido abordados mediante métodos expositivos y con la resolución de ejercicios o problemas descontextualizados que requerían respuestas únicas y/o cortas. No habían realizado, durante el curso, actividades semejantes a las APM (ver punto 2.2); tampoco habían tenido oportunidad de resolver problemas que implicaran la formulación de conjeturas, presentación de argumentos y comunicación de resultados.
2.2 Actividad
A diferencia de García-Oliveros, Granados-Silva y Pinillos-Bohórquez (2009) cuya propuesta se orienta a la resolución de problemas con respuestas únicas y cortas, en este estudio se consideró importante utilizar APM, diseñadas con base en las sugerencias derivadas de la PMM (Doerr, 2016). Una descripción detallada de los principios que rigen el diseño se puede revisar en Vargas-Alejo, Reyes-Rodríguez y Cristóbal-Escalante (2018).
La APM constó de una actividad de calentamiento (Figura 3) y una situación problemática a resolver (Figura 4). La actividad de calentamiento constaba de un artículo informativo respecto a las dietas hospitalarias, cuyo título fue: Importancia de la calidad alimentaria en las clínicas y hospitales. El objetivo de la actividad era introducir el contexto en el cual se desarrollaba la situación problemática (Figura 4), así como, aclarar dudas respecto a términos utilizados como: costo, logística, dieta, entre otros.
La APM se denominó “Dieta blanda hospitalaria” y trata de una posible prescripción médica del platillo de dieta blanda de un hospital. Incluía datos relevantes para la resolución del problema como: la cantidad requerida por ingrediente para la realización de la dieta blanda de un paciente adulto (se incluían datos en cantidades discretas y continuas, como la cantidad exacta de taza de puré de manzana para cada dieta de un adulto o la cantidad de galletas por paciente adulto); cantidad esperada de pacientes en el hospital que podrían requerir alimentos (se estimaba un número de pacientes por día de una semana específica); costo aproximado de los ingredientes por presentación comercial (se proporcionaban costos aproximados, como el precio del kilo de manzanas para hacer puré o el costo del paquete de galletas) y cantidades equivalentes por ingrediente (por ejemplo, se incluía el dato de cuántas manzanas se requerían para hacer una taza de puré, así como, una aproximación respecto a las unidades de manzanas a las que equivalía un kilogramo)2, lo cual, implicaba la conversión de una unidad dimensional a otra. La APM solicitaba la construcción de un procedimiento compartible, modificable y reutilizable para estimar la cantidad de ingredientes a comprar y posible costo; de tal manera que se satisficiera la demanda alimenticia del hospital, para una situación particular y cualquiera en general. Lo anterior, es planteado en el problema de la siguiente manera (Figura 4): “Es importante que consideres que la información con la que cuentan está basada en estimaciones y puede llegar a cambiar, esto significa que puede verse modificada la cantidad de pacientes en el hospital, o en los costos de las presentaciones de los alimentos, etc. Por ello, sugiere un procedimiento que les permita (a los interesados) hacer modificaciones cuando sean necesarias”. A partir de la solución particular, se esperaba que los estudiantes construyeran una general o bien, transitaran del ciclo de entendimiento cuantitativo al algebraico.
2.3 El trabajo en el aula
La implementación de las actividades se llevó a cabo en cuatro fases.
Fase 1: Entrega de actividad de calentamiento (trabajo en equipo). Esta fase comenzó, tal como la PMM lo sugiere, con la lectura de la actividad de calentamiento (la cual se realizó en equipo) y terminó con la discusión grupal de las respuestas a las preguntas incluidas en el artículo (al final de la actividad se encontraban preguntas de comprensión relacionadas con términos como “costo” y “logística”, ejemplo: ¿a qué crees que se refiera la lectura cuando menciona que los costos y la logística representan un reto en la gestión hospitalaria?). Enseguida, los estudiantes se organizaron en siete equipos, compuestos por tres integrantes cada uno, para resolver las actividades en un ambiente colaborativo.
Fase 2: Entrega del problema (trabajo en equipo). En esta fase se entregó el problema a los alumnos para ser resuelto en un ambiente colaborativo. Los estudiantes conformados en equipo, construyeron modelos, los modificaron y evaluaron. Finalmente, los prepararon para presentar en una discusión grupal. Esta fase sirvió para identificar los conocimientos previos de los estudiantes.
Fase 3: Discusión grupal y cierre de la sesión. En esta fase los equipos de estudiantes presentaron sus modelos al grupo; los describieron, argumentaron y explicaron. Se llevó a cabo una discusión grupal con el objetivo de ampliar y extender los modelos. La discusión permitió la reflexión y, en algunos casos, la reformulación. Además, los estudiantes modificaron, extendieron y refinaron sus conocimientos previos con el apoyo del profesor-investigador.
Fase 4: Trabajo individual. Esta fase consistió en realizar la APM de manera individual como tarea extra clase. El objetivo fue que el estudiante integrara y refinara su conocimiento al reconstruir un modelo propio de solución. El modelo individual permitiría al profesor-investigador observar y comparar si el estudiante, había refinado su conocimiento previo.
El profesor-investigador participó como observador durante la realización de la actividad y facilitó la discusión grupal. Intervino con el planteamiento de preguntas que permitieran al estudiante tener claridad de la situación, más que para explicar contenidos matemáticos o dar sugerencias para la resolución del problema. Tres investigadores más participaron en el estudio. Uno de los tres participó durante el proceso del diseño, desarrollo, implementación y evaluación del estudio. Los otros dos investigadores apoyaron en el análisis de los datos.
2.4 Recolección de datos
Los instrumentos de recolección de datos fueron las hojas de trabajo con las producciones escritas por los alumnos, fotografías de las producciones de los estudiantes tomadas durante el trabajo grupal y la bitácora del profesor-investigador, la cual se realizó al término de la sesión. Se tomaron, también, algunos audios durante la sesión. Estos instrumentos de recolección de datos fueron útiles debido a que se usaron estrategias de triangulación para verificar las hipótesis planteadas a partir de las observaciones descritas por el profesor-investigador.
Los productos de análisis principales, esperados y obtenidos en cada fase (de la dos a la cuatro) fueron las cartas con los modelos de solución construidos por los estudiantes. El contenido de estas cartas, usualmente, se refinó mientras los estudiantes realizaron la actividad: surgió una primera versión de solución propuesta por el equipo, la cual fue validada, modificada o ampliada cuando la presentaron ante el grupo y, finalmente, los estudiantes propusieron otra carta, escrita de manera individual, cuyo contenido fue influenciado por la discusión grupal.
En la fase 1 se esperaba que los estudiantes comprendieran el contexto del problema, reflexionaran en términos de experiencias personales. Lo anterior se revisó en las producciones escritas y verbalizadas de los estudiantes, que se obtuvieron a partir de las respuestas a las preguntas incluidas en las hojas de calentamiento y del audio.
En la fase 2 se esperaba que los estudiantes incluyeran en sus modelos de solución (contenidos en las cartas) representaciones matemáticas diversas, en las cuales se observara la identificación de datos, relaciones de comparación y variación, descripciones de tipo cualitativo, cuantitativo y quizás algebraico. En la Tabla 3 se puede revisar el tipo de procedimientos y conceptos matemáticos que se analizaron.
Tabla 3 Categorías de análisis agrupadas en ciclos de entendimiento3
| Ciclos | Representación | Procedimientos | Conceptos Matemáticos |
|---|---|---|---|
| Cualitativo | Verbal | Comparación | |
| Cuantitativo | Aritmética sin organización tabular | Aplicación sucesiva de dos operadores |
Fracción Razón Proporción Variación Porcentaje |
| Tabular | Uso de operador razón (AV) | ||
| Análisis de
unidad dimensional: Producto de medidas (AH) Regla de tres | |||
| Tabular- Geométrica |
Identifica la constante de proporcionalidad y variables | Variables
dependientes e independientes Constante de proporcionalidad |
|
| Algebraico | Algebraica | Uso de simbolismo algebraico | Variable
dependiente Variable independiente Función lineal |
Fuente: elaboración propia.
En la fase 3 se esperaba que los equipos de estudiantes modificaran y ampliaran sus modelos (representaciones, procedimientos y conceptos matemáticos) al escribirlos en el pizarrón y comunicarlos al grupo. Finalmente, en la fase 4 se esperaba que de manera individual los estudiantes modificaran y ampliaran sus cartas y, por lo tanto, los modelos de solución propuestos, lo anterior, como consecuencia de haberlos discutido en grupo, con apoyo del profesor-investigador.
2.5 Análisis de los datos
Los datos fueron analizados con base en aportaciones de la PMM (Lesh & Doerr, 2003) y de Vergnaud (1990). Se detectaron los conocimientos matemáticos previos relacionados con la proporcionalidad (exhibidos por los estudiantes universitarios al resolver la actividad), la transición (cuando la hubo) entre los ciclos de entendimiento cualitativo y cuantitativo (Tabla 2), las representaciones matemáticas y los procedimientos utilizados. La Tabla 3 resume los criterios o categorías de análisis: ciclos de entendimiento, representaciones (tablas, gráficas y ecuaciones) y factores de complejidad cognitiva relacionados con las aportaciones de Vergnaud (1990). Se consideraron dos factores de complejidad cognitiva dentro del ciclo cuantitativo: a) Conceptos matemáticos asociados al concepto de proporcionalidad: valores numéricos, razón, tasa, número entero, decimal, fracción, porcentaje, variación, proporción, función lineal y constante de proporcionalidad; b) Dominio de experiencia de los estudiantes para resolver problemas: estrategias, algoritmos y procedimientos utilizados durante la resolución del problema (multiplicación, división, algoritmo de la regla de tres, análisis de unidad dimensional, búsqueda del valor unitario, razones, operadores AV y AH).
3. Resultados y discusión
Los resultados de la actividad implementada se han dispuesto de acuerdo con las fases de implementación explicadas en la sección 2.3. Se describe el surgimiento y evolución de los ciclos de entendimiento de los estudiantes con base en los productos generados durante su trabajo en equipo, exhibido en las fases uno a tres y, finalmente, se señala el ciclo de entendimiento que caracterizó su trabajo individual.
3.1 Primera fase, surgimiento del ciclo de entendimiento cualitativo
La Actividad de calentamiento despertó inquietudes en todos los estudiantes respecto al tema. Ello permitió el libre intercambio de opiniones entre los integrantes de cada equipo, las cuales, después de ser compartidas verbalmente, fueron plasmadas por escrito en sus hojas de trabajo. Acto seguido, las ideas que habían sido discutidas en equipo, fueron compartidas en la sesión grupal. Por ejemplo Las ideas discutidas incluyeron descripciones cualitativas relacionadas con los costos de los alimentos. Por ejemplo: algunas de las expresiones obtenidas en relación a la pregunta mencionada en la Fase 1 del punto 2.3 fueron: “¡Imagínate el costo de hacer una dieta para cada enfermo según sus características!”, “cada insumo tiene un costo en específico que se debe cubrir”, “el hospital administra sus recursos monetarios distribuyéndolos en cada área… [incluso, debe tomar en cuenta] los insumos para cubrir los costos y gastos correspondientes a la gestión alimentaria”, “Presenta un gran gasto al hospital ya que cada paciente requiere de una dieta adecuada a él, los ingredientes, etc”. Es importante mencionar que en sus comentarios se observa cómo identificaron variables y la relación entre ellas, pero en un ciclo de entendimiento cualitativo (Vargas-Alejo, Reyes-Rodríguez, & Cristóbal-Escalante, 2016).
3.1 Segunda fase, surgimiento del ciclo de entendimiento cuantitativo
Entrega del problema y trabajo en equipo. Las expresiones verbales se convirtieron en expresiones cuantitativas, por ejemplo, la expresión “cada insumo tiene un costo especifico” cambió a “el costo del ingrediente es de 10 pesos por paquete”. Los estudiantes identificaron datos y empezaron a operar con ellos. Es decir, durante la resolución del problema los alumnos pasaron de un ciclo de entendimiento cualitativo a un ciclo de entendimiento cuantitativo (Vargas-Alejo, Reyes-Rodríguez, & Cristóbal-Escalante, 2016). A continuación se describen los procedimientos realizados.
3.2.1 Interpretación errónea de los datos
De los siete equipos, cinco (1, 3, 4, 5 y 7) identificaron de manera correcta los datos. Los equipos 2 y 6 no los interpretaron bien. Aún y cuando sus procedimientos fueron correctos, los resultados fueron erróneos, pues los estudiantes trabajaron los datos de manera equivocada desde el principio, como se describe a continuación.
Los estudiantes confundieron el dato semanal con el diario. Utilizaron el dato de los pacientes por semana como el número de pacientes por día e hicieron lo siguiente (Figura 5). El dato de las dos piezas de huevo (proporcionado en el problema) lo multiplicaron por 19 (número de pacientes adultos por semana). Es decir, los estudiantes realizaron operaciones que, de acuerdo con Vergnaud (1995), reflejaron el uso de operadores escalares y no funcionales Por ejemplo, escribieron como procedimiento para encontrar la porción diaria requerida de huevo por platillo para los pacientes adultos: 19 veces 2; donde, la única cantidad con dimensión fue el 2 (piezas), lo cual se refleja en el resultado final: 38 piezas. El equipo 6 realizó un procedimiento similar.

Fuente: trabajo de los estudiantes.
Figura 5 Estimación semanal de consumo de alimentos realizada por Equipo 2.
Los equipos 2 y 6 realizaron operaciones innecesarias. Posiblemente, debido a que con frecuencia los estudiantes aplican procedimientos algorítmicos memorizados que no saben cuándo o cómo utilizar en la resolución de problemas; tal como está documentado en la literatura de investigación (NCTM, 2003; Santos, 2014).
3.2.2 Representación aritmética sin organización tabular
Como se observa en la Figura 6, el equipo 4 llevó a cabo operaciones de multiplicación y división realizando un Análisis Vertical (Vergnaud, 1995) centrado en la noción de operador-escalar (sin dimensión). En el procedimiento exhibido por el equipo no se observó el uso del concepto de razón-operador.
La Figura 6 muestra las operaciones realizadas. Nótese que no hay comprensión del uso del signo igual (error detectado en la literatura de investigación, por ejemplo por Kieran, 2006). Para calcular la cantidad de galletas que consumirían cuatro pacientes infantes un determinado día, multiplicaron cuatro (cantidad de porciones a calcular) por nueve (cantidad de galletas requerida para una dieta para adulto), obteniendo como resultado 36 galletas para cuatro porciones de alimento de un adulto. Dado que los infantes consumían la mitad de la porción de un adulto, dividieron 36 entre dos para obtener el total correspondiente a los pacientes infantes. Es decir, los estudiantes primero multiplicaron y luego dividieron reflejando el uso de operadores escalares: “4 veces 9” y “36 veces ½”. Esto muestra el manejo de la fracción como operador escalar (Vergnaud, 1995). Puesto que la única cantidad con dimensión era 9 (piezas de galletas), los estudiantes escribieron 18 piezas como resultado. Este equipo fue el único que organizó sus datos siguiendo este esquema, mientras que los otros seis equipos organizaron los datos de manera tabular, lo cual se explica a continuación.
3.2.3 Representación tabular
Seis de los siete equipos incluyeron en su procedimiento una tabla para resolver el problema (ejemplo, Figura 7). En la tabla, realizada por el equipo 5, se muestran cinco columnas y seis renglones. De izquierda a derecha, la primera columna representa los ingredientes que requiere el platillo. En la segunda columna, se registran las cantidades requeridas para satisfacer la demanda de platillos durante la semana. La tercera columna especifica las cantidades por presentación (paquetes) de producto que se requieren comprar para satisfacer la demanda de los platillos. La cuarta columna, representa el costo de comprar los paquetes requeridos. Finalmente, la quinta columna, representa las posibles piezas sobrantes al comprar una presentación o un paquete de alimentos que exceden la demanda para satisfacer la dieta.
En la Figura 7 se observa el modelo propuesto por el equipo 5 donde, por ejemplo, para satisfacer la demanda de huevo de los 26 pacientes (19 pacientes adultos y 7 pacientes infantes) se requerían 45 huevos. Los equipos propusieron comprar el producto en paquetes por docena, por ello, los alumnos estimaron necesario comprar 4 docenas (lo que implicaba comprar 48 unidades de huevo), con un costo aproximado de 82 pesos por las cuatro docenas. Dado que, sólo se requerían 45 unidades (piezas) de huevo, se estimaron tres piezas de huevo sobrantes (columna 5, Figura 7) al comprar las cuatro docenas.
Este arreglo tabular es informativo y conceptos como variación, no son evidentes. Sin embargo, se utilizaron conceptos relacionados con proporcionalidad como son las magnitudes discretas, las fracciones (algunos de los ingredientes estaban considerados en fracciones y fueron expresados en fracción, como se observa en la Figura 7), la razón como operador y la proporción en el procedimiento para obtener los datos que se observan en la tabla de la Figura 7.
Lo anterior, se observó en los procedimientos de seis de los siete equipos quienes utilizaron la regla de tres (Vergnaud, 1990; Giacomone, Beltrán-Pellicer, & Godino, 2017) para identificar la unidad dimensional de las cantidades. Por ejemplo, 9 galletas era la porción requerida para cada platillo de un paciente adulto, sin embargo, al comprar las galletas era necesario conocer a cuánto equivalían en gramos dicha porción. El equipo 1 realizó un análisis dimensional (Figuras 8 y 9) donde explicó los pasos necesarios para encontrar equivalencias.

Fuente: trabajo de los estudiantes.
Figura 9 Análisis de unidad dimensional realizado por el Equipo 1.
El equipo 1 recurrió a la regla de tres para llevar a cabo el análisis de unidades dimensionales (tza, pza, etc.), esto evidencia una comprensión de la regla de tres como una relación cuaternaria de variables que requirió de un análisis dimensional.
3.2.4 Representación algebraica
Del total de los equipos, sólo el 43% (equipos 1, 2 y 3) mostró en su procedimiento un tránsito hacia una representación algebraica (ciclo de entendimiento algebraico). Por ejemplo, el equipo 3 escribió una relación lineal (Figura 10) e identificó en ella los siguientes elementos: una variable independiente, una constante de proporcionalidad y una variable dependiente. Sin embargo, el equipo 3 tuvo dificultades para nombrar y usar la variable independiente, así como la constante de proporcionalidad (Figura 10). Aunque los estudiantes identificaron patrones de comportamiento, no lograron generalizar las relaciones en un lenguaje algebraico.
3.2 Tercera fase, continúa ciclo de entendimiento cuantitativo
Discusión grupal y cierre de la sesión. Aquí todos los equipos escribieron en el pizarrón cada uno de sus modelos (Figura 11) y los explicaron al grupo. Esto permitió a los integrantes de los equipos 2 y 7 darse cuenta de que habían interpretado los datos de manera errónea y esto había afectado sus resultados finales. Presentaron sus dudas en relación con los conceptos de razón, fracción, decimal y porcentaje y con apoyo del profesor-investigador las aclararon, por ejemplo, el problema presentaba la información escrita en números fraccionarios, sin embargo, al momento de trabajar con los datos, los estudiantes expresaban las cantidades como números decimales o porcentajes. Al momento de socializar los modelos de solución alcanzados en equipo (ver Figura 11) surgían dudas entre los estudiantes sobre si la expresión de 4/5 de taza de puré de manzana era equivalente a .8 de taza de puré de manzana o a 80% de taza de puré de manzana, los cuestionamientos giraban en torno a si era correcto utilizar cualquiera de los tres valores y porqué. Los estudiantes también tuvieron dudas en cuanto como representar algebraicamente la solución del problema (la forma algebraica de la función lineal) y la utilidad de la estrategia del valor unitario para encontrar la constante de proporcionalidad.

Fuente: evidencia del trabajo de los estudiantes.
Figura 11 Procedimientos escritos en el pizarrón por los estudiantes durante la discusión grupal.
La doble proporción fue parte de las dificultades discutidas en la sesión grupal. Los estudiantes debían calcular el posible costo del puré de manzana, para ello, debían estimar cuántas piezas se requerían para satisfacer la demanda de tazas de puré de las dietas de adulto; a cuántos kilogramos de manzanas equivalían dichas piezas; y, finalmente, el alumno debía estimar el posible costo de la totalidad de puré requerido. Esto implica varios cambios de unidad dimensional. La estrategia que todos los estudiantes utilizaron fue la aplicación, de manera consecutiva, de la proporción simple, en lugar de escribir relaciones lineales como las mostradas en la Tabla 1.
3.3 Cuarta fase, indicios del ciclo de entendimiento algebraico
Trabajo individual. En las cartas de los estudiantes (por ejemplo, los integrantes de los equipos 2 y 7) mostraron cambios en sus procedimientos y, por lo tanto, en su conocimiento matemático con respecto a los inicialmente planteados en su equipo. Se observó en 20 de os 21 estudiantes que, a pesar de identificar patrones que pudieran permitirles generalizar, los alumnos continuaron en un ciclo de entendimiento cuantitativo, no exhibieron el uso del lenguaje algebraico. Sin embargo, el procedimiento de un estudiante perteneciente al equipo 5 (Figura 12), incluyó una relación algebraica para describir el proceso de solución del problema.
4 Reflexiones y conclusiones
Los ciclos de entendimiento que emergieron antes de la discusión grupal fueron cualitativos y cuantitativos (Tabla 4). Las representaciones utilizadas fueron verbales, aritméticas sin organización tabular y con organización tabular donde la variación no estaba presente (Figura 7). La representación más compleja y cercana al proceso de generalización fue la tabular con el uso de análisis dimensional (Figuras 8 y 9).
Tabla 4 Ciclos de entendimiento que emergieron ante la resolución de la APM
| Ciclos | Representación | Procedimientos | Conceptos matemáticos |
Equipos |
|---|---|---|---|---|
| Cualitativo | Verbal | Comparación | 1, 2, 3, 4, 5, 6 y 7 (equivale al 100%) | |
| Cuantitativo | Aritmética
sin organización |
Aplicación sucesiva de dos operadores | Fracción Razón Proporción Variación |
4 (equivale al 14%) |
| Tabular | Uso de operador razón (AV) | 1, 2 y
3 (equivale al 43%)4 5, 6 y 7 (equivale al 43%) |
||
| Análisis de unidad
dimensional Producto de medidas (AH) Regla de tres |
Fuente: elaboración propia.
A pesar de que la discusión grupal posibilitó que los estudiantes reflexionaran sus procedimientos y los modificaran, con respecto a los inicialmente planteados en su equipo, en el trabajo individual final entregado por los estudiantes no se exhibió el uso de lenguaje algebraico en 20 de los 21 estudiantes.
Con base en las preguntas de investigación planteadas inicialmente: ¿qué conocimiento y habilidades matemáticas, relacionadas con proporcionalidad, exhiben los estudiantes universitarios de los primeros semestres de la Licenciatura de medicina al resolver situaciones cercanas a la vida real? y ¿cómo se modifica, extiende y refina este conocimiento y habilidades durante el proceso de resolución de una APM?, podemos concluir lo siguiente.
Inicialmente, los modelos de los equipos de estudiantes permitieron observar el ciclo de entendimiento cualitativo y cuantitativo, con ello, el uso de conceptos como fracción, razón y proporción en la resolución de los problemas, así como el uso de la regla de tres. Se encontró que el 100% de los equipos de estudiantes utilizaron el procedimiento de AV mencionado por Vergnaud (1990) o bien operadores escalares para resolver el problema (asociados con la multiplicación como suma reiterada). No se observó que los estudiantes utilizaran simbolismo algebraico en los modelos inicialmente planteados.
Una de las principales causas que pudieron dificultar el planteamiento de representaciones algebraicas fue la ausencia del surgimiento de los operadores funcionales o procedimientos de AH (Vergnaud, 1990) para encontrar solución a la actividad. Sin embargo, la construcción, interpretación, comunicación y análisis de los modelos durante la discusión grupal favoreció el desarrollo de ciclos de entendimiento de los equipos de estudiantes. Se modificaron tanto la interpretación inicial de la situación como el entendimiento de los conceptos matemáticos.
Se evidenció un cambio en las descripciones y comparaciones, las cuales, pasaron de ser verbales a numéricas y evolucionaron a representaciones tabulares, denotando la identificación de patrones, procesos de generalización e indicios de expresiones algebraicas. El uso de distintas representaciones permitió dar significado al concepto de proporcionalidad.
Durante la discusión grupal también se observó mejoría en la habilidad de comunicación, en relación con la comunicación inicial que se dio al interior de los equipos, lo cual, de acuerdo con la perspectiva de Modelos y Modelación (Lesh & Doerr, 2003), está asociada con la profundización de conceptos matemáticos como lo es la proporcionalidad.
Una actividad podría pensarse insuficiente para apoyar el desarrollo de conocimiento proporcional en los estudiantes, sin embargo, tal como señala la perspectiva de modelos y modelación, con la cual coincidimos, se encontró que durante el periodo de realización de la actividad los modelos creados por los estudiantes evolucionaron. Como se mencionó inicialmente, se desarrollaron cuatro actividades más, las cuales no se describen en este artículo debido a los límites en cuanto a extensión del documento y a la descripción que interesaba mostrar.
En resumen, con base en los resultados presentados en este documento, se observó que el proceso de desarrollo del conocimiento de proporcionalidad por los equipos de estudiantes fue un proceso continuo, que se efectuó en varias dimensiones, acordes con las interacciones con el entorno que experimentaron los alumnos con sus compañeros y el grupo. Durante estas interacciones desarrollaron sistemas conceptuales, que les permitieron describir, comunicar, predecir el comportamiento de la situación (Lesh y Doerr, 2003). El significado del concepto (objeto, evento o situación) lo fueron construyendo al relacionarlo con otros conceptos, en su forma de operar o funcionar, en los usos que pudieron hacer con ellos.











 nueva página del texto (beta)
nueva página del texto (beta)










