PACS: 01.40.Fk; 03.65.Ca; 41.20.Gz
1. Introduction
Nowadays, there are many techniques to observe and analyze the inside of the human body in order to obtain a better diagnosis. One non-invasive and high-resolution technique is the Magnetic Resonance Imaging (MRI), which takes advantage of hydrogen nuclei, a powerful static magnetic field, and a computer system to process and get images.
The Nuclear Magnetic Resonance is a physical phenomenon in which certain atomic nuclei (with an odd number of protons or neutrons) are placed under a high-intensity magnetic field and can selectively absorb energy from electromagnetic waves in the radio-frequency range. Once the nuclei have absorbed the energy, the excess energy returns to the surroundings through a process called relaxation which is accompanied by a local magnetic variation, which induces a signal to a receiving antenna for digital processing and thus obtain an image or to perform a spectrometric analysis 6.
MRI equipment consists of a magnet (usually superconductor), radio frequency coils, magnetic field gradients, a bore or tunnel, and a computer for signal processing. MRI requires the use of a high-intensity magnetic field. Clinical equipment use field strengths ranging from 0.5-3.0 T, which have been achieved by replacing the permanent magnets by superconducting electromagnets resulting in a very wide line research. BCS theory 12-14 is the dominant physical theory of superconductivity and was proposed by John Bardeen, Leon Cooper, and Robert Schrieffer. The theory is based on the fact that the charge carriers are not free electrons but, rather, pairs of electrons known as Cooper pairs. Although electrons are fermions and are subject to the Pauli exclusion principle, being in a crystal lattice, the energy between them becomes negative (attractive) so that pairs are created to minimize the energy and behave as bosons.
In this paper we discuss the basic physics involving magnetic resonance, providing an analysis from the viewpoint of quantum mechanics.
2. The Hydrogen atom
MRI uses the properties of hydrogen nuclei when they are exposed to a high magnetic field and a radio-frequency field, so it is important to analyze the physical characteristics of the hydrogen atom 11.
The hydrogen atom is the simplest atom since, there is a proton in its core and an electron orbiting it experimenting an attractive Coulomb potential.
To perform the analysis, the Schrödinger equation indepen- dent of time is used:
where µ is the reduced mass of the system and p, the momentum operator
Because there is a central potential V (r), natural coordinates are spherical coordinates, and Eq. (2) becomes:
re-arranging the equation above:
To solve Eq. (6) the separation of variables is:
replacing the solution proposed in Eq. (6) and dividing by R(r)Y (θ,φ) we obtain:
We can separate the Eq. (8) into two with a separation constant. For reasons that will eventually become clear, we will write this separation constant as l(l + 1), i.e.
For the solution of Eq. (9) the separation of variables method is used again, this time making Y (θ,φ) = Θ(θ) · Φ(φ), to get:
multiplying the above equation by sin2 θ: sen
separating the azimuth part,
The solution to Eq. (13) is given as:
where A and B are constants. Equation (12) is as follows:
multiplying the equation by Θ(θ) we get:
Making the following change in the Eq. (16) cos θ → x and Θ → y, to get:
Performing the above changes, Eq. (16) is written as:
Equation (17) is known as Associated Legendre Differential Equation, and also reveals why we chose the constant above to be l(l+1). That is, its solutions are given by the Associated Legendre Polynomials:
The solution Y (θ,φ) = Θ(θ) · Φ(φ), comprising the angular part of the Eq. (8) is of the form:
where N is a normalization constant defined as:
and thus it ensures that the functions Y l,m (θ,φ) are orthonormal. Equation (19) is known as Spherical Harmonics. Returning to the radial part of Schrödinger Eq. (10), rearranging it to be:
whole solution is given by the Associated Laguerre Polynomials, which meet the following normalization condition:
so the solution of Eq. (8) for the radial part is expressed as:
where ρ = 2r/na0 y a0 = ℏ/me2.
Since we have the solutions of each of the equations depending only on one variable, we proceed to build the exact solution of the Schrödinger equation independent of time for the hydrogen atom,
explicitly writing in terms of the spherical harmonics:
where the principal, azimuthal, and magnetic (n,l,m) quantum numbers take the following values:
The wave function Ψ(r,θ,φ) by itself has no physical meaning, but the expression |Ψ|2 calculated for a place and a given time is proportional to the probability of finding an electron in that place, at that instant.
3. Nuclear magnetic resonance
Nuclear magnetic resonance is a physical phenomenon associated with the intrinsic angular momentum of the spin and the magnetic properties of atomic nuclei. When a nucleus is placed in a magnetic field an interaction occurs between the magnetic moment of the nucleus and the field, resulting in an energy splitting. By the absorption and emission of photons with the right frequency, transitions between these energy states may occur.
Local magnetic changes produced by the absorption and emission of photons are detected by an antenna that sends the signal to a computer for decoding and image generating.
3.1. Nuclear Spin
The particles that make up the atomic nuclei (protons and neutrons) have the intrinsic quantum mechanical property of spin. In nuclear physics the total angular momentum that the nucleus has is called nuclear spin 18, though the term should not be confused with spin of each nucleon or total spin as the sum of all nucleons, because this is just one of the two contributions to the nuclear spin, the other is the angular momentum of the nucleons. So each nucleon will have a net angular momentum such that:
then the nuclear spin will be:
or just:
Each of these vectors have a similar quantum number. The magnitude of orbital angular momentum satisfies:
The direction of the angular momentum vector L is associated with the quantum number m. For a given quantum orbital momentum number l, there are 2l +1 integral magnetic quantum numbers m ranging from −l to l. Along the z axis the component of angular momentum is given as:
For the vector of spin angular momentum S, its quantum number s can take integer or half-integer values:
and for the z component, we find that sz = msℏ, there are 2s + 1 values of ms. To exhibit the property of MRI, the nucleus must have a non-zero value of s. In medical applications, the proton (1H) is the nucleus of most interest, due to its high natural abundance, however other nuclei have been studied.
The proton is a fermion whose value of s is 1/2, therefore there will be two possible values for Sz, i.e. ±ℏ/2. The eigenfunctions describing the nucleus can be written as |+1/2〉 and |−1/2〉, and since in quantum mechanics every physical observable has an associated operator, we can write an eigenvalue equation to describe the observation of the spin state as:
where Sz is the operator describing the measurement of angular momentum along the z axis.
3.2. Voxel magnetization
To measure the energy of the spin system it is necessary to construct a Hamiltonian operator.
The shape of the Hamiltonian can be derived from classical electromagnetism, for
the energy of a magnetic moment placed in a magnetic field 15. The nuclei have a magnetic moment
where γ is a constant of proportionality called gyromagnetic ratio, which for the proton it has a value of 2.675×108 rad/s·T. When this magnetic moment is placed in a magnetic field B its ground state is degenerated and the energy of a particular level will be:
combining Eqs. (6), (7) the Hamiltonian is obtained:
and since the field B is oriented in the z direction, the Hamiltonian becomes:
now using Schrödinger’s equation, the energy eigenstates are found
and they will be:
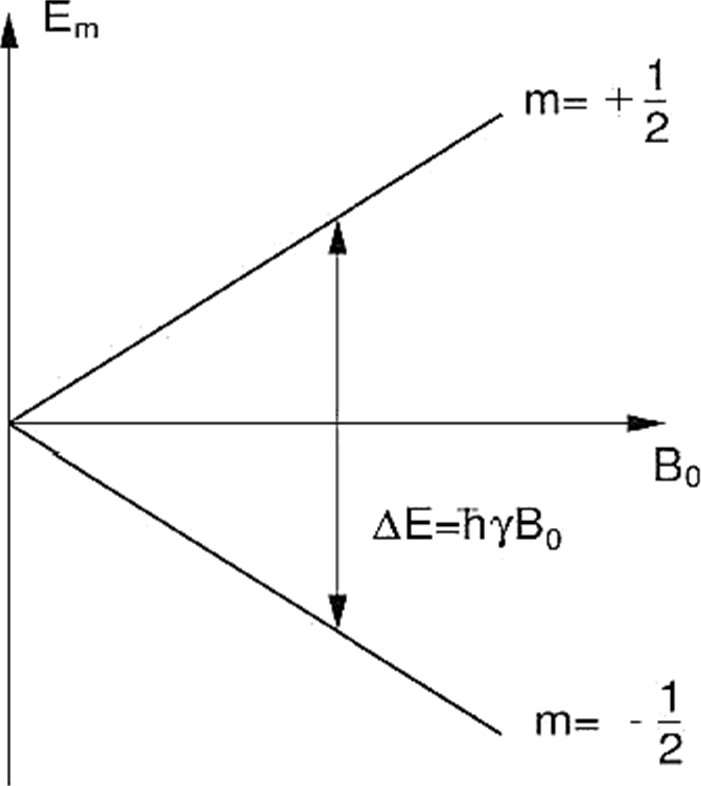
For the proton ms = ±1/2, a transition between the two states represents a change in energy. This is called Zeeman splitting17 and is shown in Fig. 1, where it shows that as the intensity of the magnetic field increases, the energy difference between the states is bigger. The two possible states are more commonly known as “spin−up” and “spin−down”, where the latter has a higher energy state than the “spin−up” state. Transitions between the two states can be induced by absorption or emission of a photon such that:
Thus obtaining the Larmor equation which underpins the whole phenomenon of Nuclear Magnetic Resonance.
The characteristic frequency ω0 is called Larmor frequency and B0 = Bz. In a real system there is not only an isolated nucleus, but many nuclei which may occupy a particular spin state. This means that our development must be extended to consider an ensemble of spins. To do this we define a Ψ eigenstate, which is a linear combination of possible spin states for a single nucleus as:
When performing a measurement on the system, the expected value of the operation on this superposition of states is:
where the value |ams|2 represents the probability of finding a single nucleus in the ms state. For the case of a proton, which is the particle of interest, with two spin states we have:
The ratio of the population in the two energy states follows the Boltzmann statistics 4,
and since kBT ≫ ℏγB0, expanding the first order exponential we have
and the difference in the number of spins between the spin-up state and the spin-down state will be:
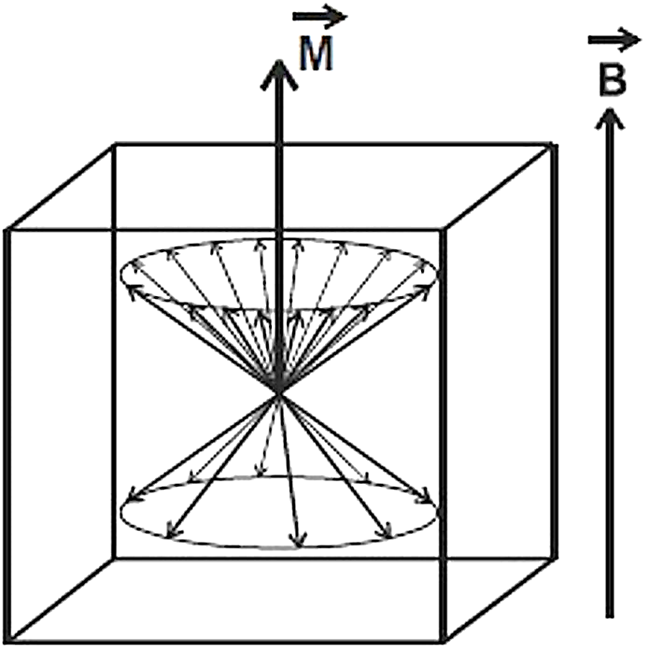
The magnitude of the magnetization of a voxel containing a nucleus density ρ is obtained by multiplying the density by the difference between the number of spins in both states and the magnetic moment of the nuclei µz = ±(γℏ/2)
The magnetization of the volume element also has a direction which is equal to the orientation of the main magnetic field for that reason it should be considered as a vector quantity, as it shown in Fig. 2.
3.3. Excitation of the Magnetization by radio-frequency pulse
A volume element of the sample is defined as a voxel. Having placed a transmitting antenna in the direction of maximum emission to the voxel in the vertical plane and changing the transmission frequency, when we emit the frequency of precession (Larmor frequency), the nuclei are able to absorb energy, i.e. enter resonance.
When the nuclei of the voxel are entering into resonance, the magnetization vector M travels performing a spiral rotational movement relative to the direction of the field B 0. Each nucleus entering into resonance at a specific frequency specified by the Larmor Law, depending on B 0 perceived and biochemical environment in which it is located. Therefore, the radio-frequency emission contains an approximate bandwidth of 100 kHz.
Separation of M with respect to its equilibrium position is determined by the angle of inclination or FLIP angle. Its value depends on the power and time of radio-frequency emission, among other factors.
The process of the radio-frequency emission is of the order of microseconds called radio-frequency pulse and quantified by the value α. A 90° pulse moves the magnetization vector about the xy plane, and a 180° pulse inverts the magnetization respect to its equilibrium position.
After a 90° pulse, the longitudinal component of the magnetization vector is zero, in this position the number of nuclei in the lower energy state equals the number of nuclei in the higher energy state, it is called a state of saturation.
3.4. MRI selectivity
If we have multiple voxels placed under different magnetic fields, we can selectively excite either by simply changing the transmission frequency of the antenna.
A magnetic gradient enables atomic nuclei to perceive a distinct magnetic field. In addition to changes in biochemical environment, one can selectively resonate all nuclei within positions that are being excited by the frequency bandwidth used in the pulse emitter. Therefore all voxels contained in a plane perpendicular to the direction of the gradient plane and whose thickness depends, once defined the value of the gradient, on the bandwidth used on the pulse emitter, will be excited.
Magnetic resonance images are obtained by sending pulses to different spaced time intervals with suitable values, which is a pulse sequence.
3.5. Evolution of magnetization under temporal variation of the magnetic field
Taking a volume element (Voxel) that has a magnetization vector M, the set of equations describing the temporal evolution of said vector are called Bloch equations1 and are defined as follows:
where γ is the gyromagnetic ratio of the proton and M0 = M is the magnitude of the magnetization in equilibrium, T1 and T2 are time constants that will be discussed later. The above equations can be solved with the appropriate conditions; for example, immediately after when the radio-frequency pulse is turned off:
3.6. Nuclear relaxation
Once the radio emission is completed, the magnetization vector, M, returns to its initial position by releasing energy through a process called relaxation. Relaxation occurs because nuclei emit the excess energy absorbed when entering resonance. Relaxation ends when the proportion of nuclei voxel between higher energy states and lower energy states match the Boltzmann equilibrium.
The return to the equilibrium position of M produces magnetic field modifications that may be collected by a receiving antenna, since the magnetic field variations induce an electrical signal called Free Induction Decay (FID) 16, which is a damped sinusoidal signal. The frequency of the sinusoid is the precession frequency imposed by the value of the magnetic field during relaxation.
Given the definition for the electromotive force (fem) and the magnetic flux through a coil:
On the other hand, for the magnetization vector M of a sample, there is an associated magnetic field from the current
density
the vector potential derived from a source is defined as:
with this, the magnetic field can be calculated as
Substituting the vector potential in the term for the current density and later in the line integral, we have:
simplifying the above equation and performing integration by parts:
The expression in the parentheses of Eq. (60) can be compared with the vector potential A, obtaining an expression for circuits:
thus the curl of the line integral is indeed the magnetic field per unit current that would be produced by the coil at point r'
The magnetic flux through the coil can be written as:
Finally, the electromotive force is expressed as:
Two voxels placed under different magnetic fields in the moment of relaxation, will have different relaxation frequencies and, therefore, their signals may be differentiated through a frequency analysis such as Fourier analysis. By studying signals of relaxation, one can obtain information on the density (D) of hydrogen nuclei in the voxel and information related with the medium by the parameters T1, T2, and T2 *.
3.7. Spin-lattice relaxation (T1 relaxation)
During the relaxation, the hydrogen nuclei release their excess energy. Once reaching complete relaxation, the magnetization vector M recovers its initial value aligned with the direction of the main magnetic field B0. An analysis after a pulse of radio-frequency of the variations in time of the projection of the magnetization vector on the longitudinal axis (Mz), called longitudinal relaxation, once the value of the projection is identical to the initial value of M, the relaxation will be over. Thus the study of the longitudinal relaxation gives an idea of the rapidity with which it again reaches its initial state.
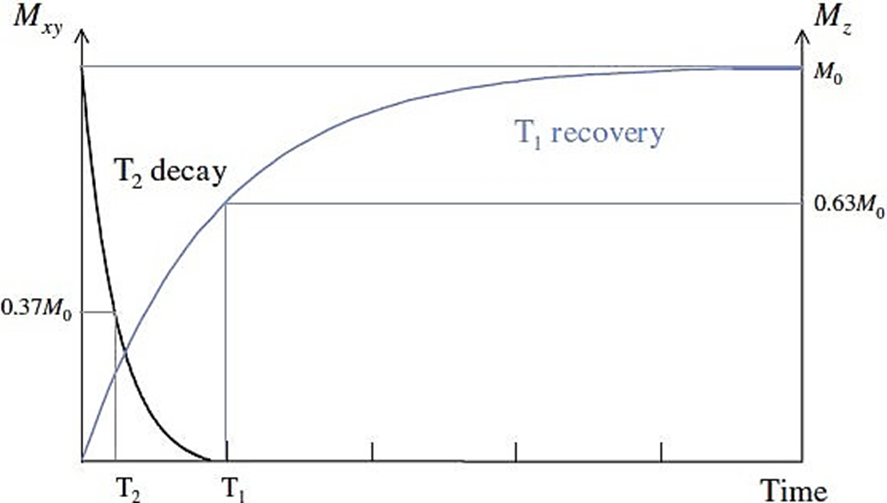
As we can see in the Fig. 3, the longitudinal relaxation has the form of a growing exponential regulated by a time constant expressed in milliseconds called T1, which is also called Longitudinal Relaxation Time.

Figure 3 The recovery of Mz to M0 is controlled by an exponential. T1 is the necessary time to recover the 63% of the equilibrium value of the magnetization 4.
The values of T1 increases with the value of the magnetic field.
3.8. Spin-spin relaxation (T2 Relaxation)
We can get information related to the biochemical structure of the medium, by studying the variations over time of the component for the magnetization vector in the vertical plane (x,y) during the transverse relaxation.
When Mx,y is zero it implies that the magnetization vector is aligned on the z-axis with the main magnetic field. Immediately after excitation, part of the spins precess synchronously, these spins have a 0° phase and are said to be in phase, this state is called coherent phase.
The coherent phase is gradually lost as the spins advance and others are delayed on their way precession. In other words the transverse relaxation is the decay of transverse magnetization due to loss of coherence in the spins.
The transverse relaxation differs from longitudinal ralaxation in that the spins do not dissipate energy to the surroundings but, rather, exchange energy with each other.
The evolution of the transverse magnetization over time, until it vanishes, corresponds to a sinusoid with a dampened relaxation frequency generating an exponential decay (see Fig. 4). This exponential decay of the surroundings is regulated by a parameter T2* 2. When we take into consideration all factors that influence the asynchronism of the nuclei, or T2 if neither are influenced by the external magnetic field’s inhomogeneities or local magnetic variations acting permanently on the nuclei. Therefore T2 indicates asynchronism of nuclei of the voxel during relaxation due to spin-spin random influences which depend on the composition and structure of the tissue. T2 is the time that must elapse before the transverse magnetization loses 63% of its value. The time constant T2 is called the Transverse Relaxation Time.
Returning to the coherence, it is lost in two ways:
4. Conclusions
MRI is a technique for visualizing tissues that takes use of the physical phenomenon of nuclear magnetic resonance, which is the union of quantum mechanics with classical electrodynamics, that uses the quantum-mechanical properties of the hydrogen atom to produce high resolution images that help with medical diagnosis. Nowadays, there are many MRI machines used for both medicine and research, where, for the second case it is essential to have knowledge of the facets at a quantum level of the physical process involved. Likewise there is a wide variety of research topics such as digital processing of images acquired during a study, magnetic resonance spectroscopy, designing new radio frequency coils, pulse frequency design, etc., thus the broad field for the development and monitoring of research.











 nueva página del texto (beta)
nueva página del texto (beta)