1. Introducción
Históricamente, la demanda internacional de petróleo crudo y las fluctuaciones de sus precios han sido muy importantes debido al gran impacto en el desempeño macroeconómico mundial, Liu, Lu y Li (2019). El análisis del posible efecto spillover que se puede generar por la volatilidad de los precios del petróleo en el mercado de valores es importante para comprender el comportamiento de las economías. En tiempos recientes variables intrínsecas del mercado petrolero internacional, los rendimientos y su volatilidad, han cobrado relevancia para explicar las condiciones internas de los países, en un entorno creciente de integración y de globalización, lo cual ha motivado a comprender la forma en cómo se transmiten los desequilibrios entre los mercados, Fowowe (2017).
Desde esta perspectiva, un incremento de los precios del petróleo aumenta el nivel de los precios internos, reduce el poder adquisitivo de los residentes, inhibe el consumo, desincentiva el crecimiento económico e impacta negativamente al mercado de valores. Además, conduce a un aumento en los costos de las pequeñas y medianas empresas, reduce las ganancias corporativas y desalienta la producción, obstruyendo el crecimiento económico y el desarrollo del mercado de valores.
Existe una vasta literatura empírica que ha investigado los efectos de las fluctuaciones en los precios del petróleo en una amplia gama de variables macroeconómicas. Hamilton (1983, 2003), Gisser y Goodwin (1986), Mork (1989), Bohi (1989), Rotemberg y Woodford (1996), Hooker (1996), Bachmeier (2008), Lee, Lee y Ning (2017) argumentan que mayores precios del petróleo traen consigo incrementos en la gasolina y en una variedad de combustibles que elevan los costos de producción y por ende los bienes de consumo. De hecho, este ha sido uno de los principales argumentos para explicar la desaceleración económica que ha seguido al incremento de los precios del petróleo en 1973-74, 1978 y a principios de las décadas de los años ochenta y de los noventa del siglo pasado, Chen (2010). La mayoría de esos estudios muestran que la actividad económica de los países objeto de estudio es afectada por las variaciones del precio del petróleo. Más recientemente, el análisis se ha enfocado en determinar si las fluctuaciones del precio del petróleo y su volatilidad impactan los rendimientos de los mercados bursátiles y a su variabilidad.
Este estudio estima los efectos spillovers de los rendimientos y de volatilidad- entre los principales mercados accionarios y el mercado internacional del petróleo en América Latina y el de los Estados Unidos (EE.UU). Usamos datos semanales para el periodo comprendido entre enero de 1990 y octubre de 2019 mediante la metodología propuesta por Diebold y Yilmaz (2009 y 2012). En las líneas que siguen presentamos una revisión de la literatura empírica; enseguida explicamos la metodología a emplear. Posteriormente realizamos un análisis econométrico con el fin de suministrar evidencia empírica a favor del objetivo de este artículo. La sección final concluye.
2. Revisión de los trabajos empíricos
Diversos estudios han analizado los efectos de la transmisión de distintos tipos de choques entre el mercado del petróleo y los mercados de valores. Jones y Kaul (1996) fueron los primeros en ofrecer evidencia sobre la reacción de los mercados bursátiles internacionales (Canadá, Reino Unido, Japón y EE.UU.) ante las perturbaciones de los precios del petróleo. Con base en el modelo estándar de valuación de dividendos de flujo de efectivo, encuentran que para Canadá y EE.UU., existe una reacción que es explicada completamente por el impacto de los choques petroleros en los flujos de efectivo.
Huang et al. (1996) muestra a través de un modelo Autorregresivo Vectorial
(VAR) no restringido un vínculo significativo entre los rendimientos de las acciones de ciertas compañías petroleras estadounidenses y las variaciones en los precios del petróleo. Sin embargo, no encuentran evidencia de un nexo entre los precios del petróleo y los índices de mercado como el S&P 500. En contraste, Sadorsky (1999) a través de esta misma metodología, muestra que los precios del petróleo juegan un papel importante en la actividad económica, sus resultados sugieren una relación asimétrica, ya que las variaciones de la actividad económica no parecen tener un impacto en los precios del petróleo.
Ciner (2001) con el empleo de pruebas de causalidad no lineal, proporciona evidencia empírica de que los choques petroleros afectan significativamente y de forma no lineal los rendimientos de los índices bursátiles en los Estados Unidos, y que éstos también tienen un impacto en en el mercado de futuros del petróleo crudo.
Gomes y Chaibi (2014) examinan los mecanismos de transmisión de volatilidad entre los índices bursátiles de los “mercados frontera”, los índices generales MSCI Frontier Markets y el MSCI World, y los precios del petróleo a través de modelos bivariados BEKK-GARCH (1,1) con los cuales estiman simultáneamente la media y la varianza condicional. Sus resultados muestran una transmisión significativa de choques y volatilidad entre los precios del petróleo y algunos de los mercados examinados, inclusive en algunos casos el efecto indirecto es bidireccional.
Fowowe (2017) examina los efectos spillovers de rendimientos y de volatilidad entre el mercado internacional de petróleo y los mercados bursátiles de Nigeria y Sudáfrica. Los resultados de volatilidad muestran que el mercado bursátil de Nigeria y el petrolero son independientes, mientras que se encontraron efectos débiles entre las volatilidades del mercado accionario de Sudáfrica y el del petróleo.
Agren (2006) emplea un modelo BEKK-GARCH(1,1) asimétrico para investigar los spillovers de volatilidad de los precios del petróleo en los mercados bursátiles en cinco economías desarrolladas, los Estados Unidos, el Reino Unido, Noruega, Suecia y Japón, y encuentra evidencia de que la volatilidad se propaga hacia casi todos los mercados accionarios de EE.UU., el Reino Unido, Noruega y Japón con excepción de Suecia.
Malik y Hammoudeh (2007) investigaron la transmisión de la volatilidad entre el mercado mundial del petróleo, los mercados bursátiles de EE.UU. y los mercados bursátiles de los países petroleros del Golfo, Bahrein, Kuwait y Arabia Saudita, y encontraron que la volatilidad se extiende del mercado del petróleo hacia los tres mercados analizados por estos autores. De igual forma, la volatilidad del mercado de valores de Arabia Saudita impacta al mercado mundial del petróleo, destacando con ello la gran importancia que tiene este mercado accionario en el petrolero.
Chang, McAleer y Tansuchat (2009) analizan la transmisión de la volatilidad entre los rendimientos de los futuros del petróleo crudo West Texas Intermediate (WTI) y los rendimientos de diez compañías mundiales de petróleo y gas a través de diferentes especificaciones de modelos GARCH, como son el CCC, VARMA-GARCH y VARMA-AGARCH. Mediante el uso del modelo CCC, Chang et al. (2009) encuentran que las correlaciones condicionales entre los rendimientos de los futuros del petróleo crudo y los rendimientos de las acciones de las compañías petroleras son muy bajas. Sorprendentemente, en cualquier par de series de rendimientos, los resultados empíricos muestran la ausencia de efectos de transmisión de volatilidad.
Arouri, Jouini, y Nguyen (2011) emplean varios modelos GARCH multivariados para investigar la transmisión de la volatilidad del mercado del petróleo a los mercados de valores de Europa y de los Estados Unidos a nivel sectorial. Sus hallazgos revelan que la propagación de la volatilidad del mercado del petróleo a los mercados bursátiles europeos es unidireccional, pero en el caso de los EE.UU. es bidireccional. También demuestran que el modelo VAR-GARCH es el que mejor se ajusta para analizar la efectividad de la cobertura y la diversificación vis à vis otros modelos multivariados; como son el CCC-GARCH, BEKK-GARCH y el DCC-GARCH. Los resultados de Arouri et al. (2012) sugieren la presencia de transmisión de volatilidad significativa entre los precios del petróleo y los rendimientos bursátiles sectoriales de Europa, donde los efectos de la transmisión son más evidentes de los precios del petróleo a los mercados bursátiles. Xu et al. (2019) encuentran evidencia sólida de asimetrías entre los mercados accionarios representativos de China y Estados Unidos ante choques del precio internacional del petróleo.
3. Metodología
La metodología empleada fue inicialmente propuesta por Diebold y Yilmaz (2009) quienes introdujeron una medida de
spillover de volatilidad que se basa en la descomposición de la varianza
del error de pronóstico de un vector autoregresivo. Ésta registra cuánto de la varianza del
error de pronóstico
Diebold y Yilmaz (2009) consideran un
No obstante, Diebold y Yilmaz (2012) destacan que el uso de la factorización de Cholesky posee el problema de que la descomposición de varianza resultante depende del orden de las variables, Fowowe (2017). Por esta razón, Diebold y Yilmaz (2012) proponen emplear la metodología del VAR generalizado de Koop et al. (1996) y Pesaran y Shin (1998), comúnmente abreviada como KPPS, la cual produce una descomposición de la varianza que no depende del de las variables. En lugar de ortogonalizar las perturbaciones, el procedimiento de KPPS permite que tales perturbaciones estén correlacionadas y toma en cuenta este hecho para explicarlas adecuadamente a través de la distribución histórica observada de los errores.
Diebold y Yilmaz (2012) definen las proporciones de
la varianza de cada variable como las fracciones de la varianza del error
Donde
Con
De esta manera, las contribuciones de volatilidad de la descomposición de la varianza KPSS se pueden emplear para construir distintos índices de spillovers.
El índice de spillover total se construye a partir de
el cual mide la contribución de los efectos colaterales de los choques de volatilidad en
varias clases de activos a la varianza del error de pronóstico total. Es la suma de las
proporciones de la varianza del error de pronóstico de
Por otra parte, debido a que las funciones de impulso-respuesta d generalizadas y la
descomposición de varianza no son sensibles al orden de las variables, es posible construir
el índice de spillover direccional usando los elementos normalizados de la
matriz de descomposición de varianza generalizada. Es decir, los spillovers
de volatilidad direccional recibidos del mercado
De forma similar, los spillovers de volatilidad direccional transmitidos
del mercado
Se pueden concebir al conjunto de spillovers direccionales como los que provienen de una descomposición del spillover total a aquellos provenientes desde, o hacía, una fuente particular, Fowowe (2017).
Por último, es posible calcular el índice de spillover de volatilidad neto
del mercado
El cual proporciona información sintética sobre cuánto contribuye cada mercado a la volatilidad en otros mercados, en términos netos, Tamakoshi y Hamori (2018).
4. Datos
Empleamos datos semanales para el periodo comprendido entre el 19 de enero de 1990 y el 25 de octubre de 2019 con un total de 1554 observaciones. Arouri et al. (2011), Arouri et al. (2012) y Fowowe (2017) señalan que los datos semanales capturan mejor la interacción dinámica entre los mercados accionarios y el petrolero, ya que el uso de datos diarios puede ocasionar sesgos por: i) los rebotes que se pueden presentar en la oferta y la demanda; ii) la falta de sincronización en los días de negociación; y iii) la falta de liquidez en los precios accionarios; mientras que el uso de datos mensuales pueden ocultar algunos mecanismos de transmisión de volatilidad atribuible a la agregación temporal y a efectos de compensación, Fowowe (2017).
Los índices de precios de los mercados bursátiles de América Latina que analizamos se encuentran en dólares y corresponden a los siguientes países: Brasil (Ibovespa), Chile (Ipsa), México (IPyC), Argentina (Merval), y el de Estados Unidos (S&P 500) provienen de Economatica. Mientras que el precio del West Texas Intermediate (WTI) es considerado como el precio internacional del petróleo y se obtuvo de la Administración de Información de Energía (EIA, por sus siglas en inglés).
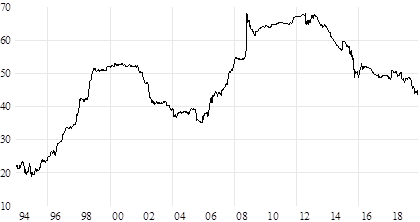
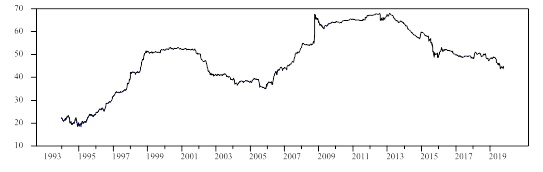
Los rendimientos accionarios y del precio internacional del petróleo se obtuvieron como la primera diferencia del logaritmo natural de dos precios sucesivos, es decir, como el cambio en el logaritmo de los precios y de los índices representativos de cada mercado. Los rendimientos de los mercados accionarios de América Latina analizados, del S&P 500 y del West Texas Intermediate se presentan en la gráfica 1.
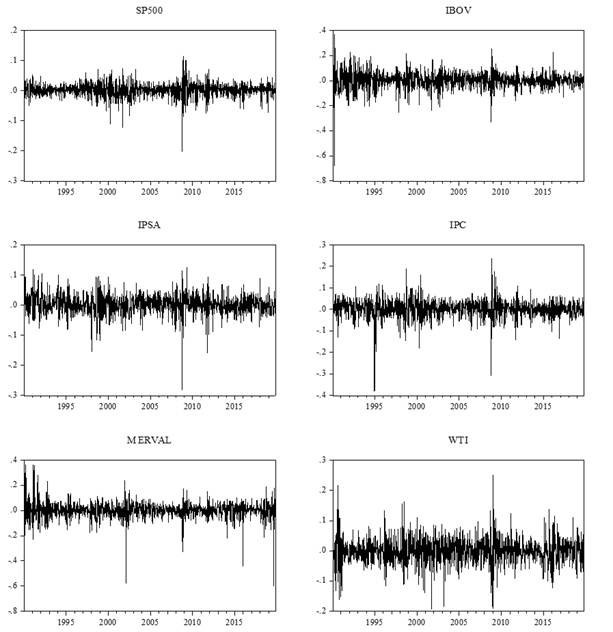
Gráfica 1 Rendimientos del Precio Internacional del Petróleo y de los principales Mercados Accionarios de América Latina y de Estados Unidos: ene -1990 - oct -2019.
En la gráfica 1 se puede apreciar la evolución de los rendimientos accionarios de los países de América Latina y de Estados Unidos, así como la del precio internacional del petróleo en el periodo de estudio. En dicha gráfica observamos la presencia de ciertos clústers de volatilidad, los cuales corresponden a las fechas en la que se presentaron crisis en los mercados y las economías analizados.
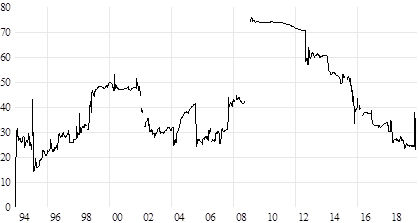
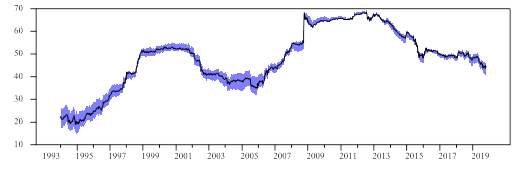
La gráfica 2 muestra las volatilidades estimadas del precio internacional del petróleo y de los mercados accionarios de Estados Unidos y América Latina en el periodo de estudio.
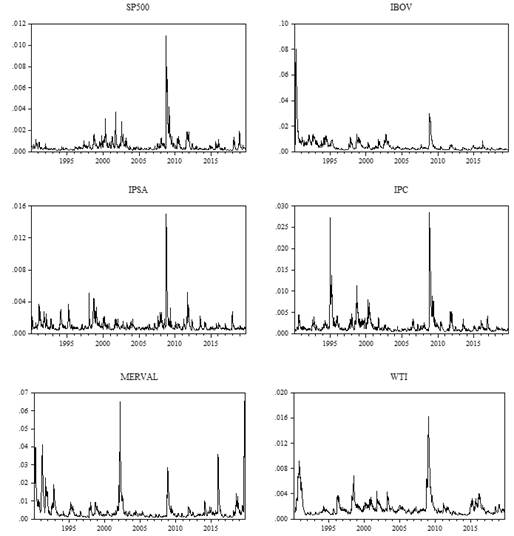
Gráfica 2 Volatilidades estimadas del precio internacional del petróleo y de los principales Mercados Accionarios de América Latina y de Estados Unidos a través de un GARCH(1,1): ene -1990 - oct -2019.
Las volatilidades se estimaron a través de un
Donde
5. Resultados
En esta sección, mostramos los resultados de las pruebas de raíces unitarias con rupturas aplicadas a las series de los rendimientos así como los correspondientes a los modelos VAR estimados.
Los cuadros 1 y 2 presentan los resultados de las pruebas de raíces unitarias con una ruptura,
Zivot y Andrews (1992), y con dos rupturas, Lumsdaine y Papell (1997), con diversos tipos de
quiebres: en intercepto, en tendencia y en intercepto y tendencia aplicadas a las series de
los rendimientos de los principales mercados accionarios de América Latina considerados, de
Estados Unidos y de los del precio internacional del petróleo. Como se puede apreciar del
cuadro 1, la penúltima columna, correspondiente al
parámetro estimado
De igual forma, los resultados de la prueba de Lumsdaine y Papel (1997) con dos rupturas estructurales, los cuales se muestran en el cuadro 2, revelan que todas las series de rendimientos accionarios analizados, así como los rendimientos del precio internacional del petróleo son estacionarios bajo distintos tipos de quiebres como se puede ver a partir de los valores de la prueba que se presentan en la última columna del cuadro 2.
Cuadro 1 Resultados de la prueba de Zivot-Andrews (1992):
| Quiebre |
|
|
|
|
|
|
|
SSR |
|---|---|---|---|---|---|---|---|---|
| Sp500 | ||||||||
| Intercepto | 2009:03:06 | 6 | 0.0048 | 0.0082 | -0.0000 | - | -1.1631 | 0.7559 |
| (3.51)*** | (3.82) *** | (-3.39) *** | (-15.99)*** | |||||
| Tendencia | 2008:07:24 | 6 | 0.0032 | - | -0.0000 | 0.0000 | -1.1217 | 0.7618 |
| (2.29) ** | (-1.52) | (1.61) | (-15.57)*** | |||||
| Ambos | 2009:03:06 | 6 | 0.0047 | 0.0084 | -0.0000 | -0.0000 | -1.1630 | 0.7559 |
| (3.25) *** | (3.52) *** | (-3.06) *** | (-0.17) | (-15.99)*** | ||||
| IBOVESPA | ||||||||
| Intercepto | 2002:10:11 | 1 | 0.0051 | 0.0133 | -0.0000 | - | -0.9473 | 6.5132 |
| (1.48) | (2.06) ** | (-1.99) ** | (-26.58)*** | |||||
| Tendencia | 1994:07:15 | 1 | -0.0034 | - | 0.0000 | -0.0000 | -0.9430 | 6.5275 |
| (-0.44) | (0.87) | (-0.91) | (-26.48)*** | |||||
| Ambos | 1994:09:23 | 1 | -0.0113 | -0.0199 | 0.0001 | -0.0001 | -0.9493 | 6.5078 |
| (-1.34) | (-2.20) ** | (2.22) ** | (-2.22)** | (-26.60)*** | ||||
| IPSA | ||||||||
| Intercepto | 2002:10:11 | 5 | 0.0059 | 0.0096 | -0.0000 | - | -0.8429 | 1.5364 |
| (3.41)*** | (3.01) ** | (-3.51) ** | (-15.07)*** | |||||
| Tendencia | 1996:03:08 | 5 | 0.0103 | - | -0.0000 | 0.0000 | -0.8309 | 1.5410 |
| (3.08)*** | (-2.34)** | (2.10)** | (-14.89)*** | |||||
| Ambos | 1998:09:11 | 5 | 0.0129 | 0.0111 | -0.0001 | 0.0000 | -0.8517 | 1.5324 |
| (4.08)*** | (3.11)*** | (-3.80) ** | (3.36)*** | (-15.19)*** | ||||
| IPC | ||||||||
| Intercepto | 2003:03:07 | 7 | 0.0048 | 0.0077 | -0.0000 | - | -0.8531 | 2.5628 |
| (2.14)** | (1.87)* | (-2.15)** | (-13.27)*** | |||||
| Tendencia | 1994:10:28 | 7 | 0.0098 | - | -0.0000 | 0.0000 | -0.8472 | 2.5651 |
| (1.99)** | (-1.55) | (1.45) | (-13.21)*** | |||||
| Ambos | 1995:03:10 | 7 | 0.0194 | 0.0216 | -0.0001 | 0.0001 | -0.8919 | 2.5410 |
| (3.58)*** | (3.86)*** | (-3.95)*** | (3.81)*** | (-13.74)*** | ||||
| MERVAL | ||||||||
| Intercepto | 2002:06:14 | 8 | 0.0069 | 0.0200 | -0.0000 | - | -0.9812 | 5.7575 |
| (2.09)** | (3.23)*** | (-3.29)** | (-14.08)*** | |||||
| Tendencia | 1994:08:26 | 8 | 0.0143 | - | -0.0001 | 0.0000 | -0.9505 | 5.7877 |
| (1.89)* | (-1.63) | (1.54) | (-13.77)*** | |||||
| Ambos | 2002:06:14 | 8 | 0.0129 | 0.0231 | -0.0000 | 0.0000 | -0.9929 | 5.7479 |
| (2.57)** | (3.56)*** | (-3.05)*** | (1.59) | (-14.18)*** | ||||
| WTI | ||||||||
| Intercepto | 2008:07:04 | 7 | -0.0018 | -0.0081 | 0.0000 | - | -0.7622 | 2.6380 |
| (-0.70) | (-1.99)** | (1.55) | (-12.28)*** | |||||
| Tendencia | 2004:07:16 | 7 | -0.0010 | - | -0.0010 | -0.0000 | -0.7491 | 2.6431 |
| (-0.36) | (-0.36) | (-1.00) | (-12.15)*** | |||||
| Ambos | 2002:06:14 | 7 | -0.0017 | -0.0081 | 0.0000 | 0.0000 | -0.7622 | 2.6380 |
| (-0.64) | (-1.86)* | (1.39) | (0.03) | (-12.28)*** | ||||
Notas: Los números entre paréntesis son los t-estadísticos.
***, ** y * denota significancia del parámetro
estimado al 1%, 5% y 10%, respectivamente.
Cuadro 2 Resultados de la prueba de Lumsdaine-Papell (1997) con dos rupturas:
| Quiebre |
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|---|---|
| Sp500 | ||||||||
| Intercepto | 1994:12:09 | 6 | 0.0033 | 0.0063 | 0.0115 | - | - | -1.1903 |
| 2009:03:06 | (2.21) | (2.77) | (4.69) | (-16.25)*** | ||||
| Tendencia | 1997:02:14 | 6 | 0.0001 | - | - | -0.0000 | 0.0000 | -1.1477 |
| 2001:07:20 | (0.05) | (-2.49) | (2.87) | (-15.78)*** | ||||
| Ambos | 2003:03:14 | 6 | 0.0048 | 0.0115 | 0.0171 | -0.0001 | 0.0001 | -1.2352 |
| 2009:03:06 | (2.74) | (3.72) | (5.30) | (-4.03) | (3.87) | (-16.65)*** | ||
| IBOVESPA | ||||||||
| Intercepto | 1997:07:04 | 1 | -0.0000 | -0.0146 | -0.0173 | - | - | -0.09507 |
| 2008:05:30 | (2.34) | (-2.20) | (-2.39) | (-26.64)*** | ||||
| Tendencia | 1997:02:14 | 6 | 0.0001 | - | - | -0.0000 | 0.0000 | -1.1477 |
| 2001:07:20 | (0.05) | -2.49 | 2.87 | (-15.78)*** | ||||
| Ambos | 2003:03:14 | 6 | 0.0048 | 0.0115 | 0.0171 | -0.0001 | 0.0001 | -1.2352 |
| 2009:03:14 | (2.74) | (3.72) | (5.30) | (-4.02) | (3.87) | (-16.65) | ||
| IPSA | ||||||||
| Intercepto | 2002:10:11 | 5 | 0.0089 | 0.0115 | 0.0077 | - | - | -0.8626 |
| 2008:12:05 | (4.21) | (3.50) | (2.47) | (-15.29)*** | ||||
| Tendencia | 1998:05:29 | 5 | 0.0108 | - | - | 0.0001 | 0.0108 | -0.8459 |
| 2003:10:03 | (3.58) | (2.86) | (3.58) | (-15.04)*** | ||||
| Ambos | 2002:10:11 | 5 | 0.0094 | 0.0175 | 0.0110 | -0.0000 | 0.0000 | -0.8749 |
| 2008:12:05 | (3.67) | (3.98) | (2.49) | (-1.65) | (2.04) | (-15.43)*** | ||
| IPC | ||||||||
| Intercepto | 1998:09:11 | 7 | 0.0063 | 0.0128 | 0.0118 | - | - | -0.8680 |
| 2009:03:06 | (2.48) | (2.96) | (2.60) | (-13.50)*** | ||||
| Tendencia | 1994:12:23 | 7 | 0.0116 | - | - | 0.0001 | -0.0000 | -0.8615 |
| 2004:10:29 | (2.33) | (2.21) | (-1.72) | (-13.33)*** | ||||
| Ambos | 1995:03:10 | 7 | 0.0196 | 0.0257 | 0.0102 | 0.0001 | 0.0000 | -0.9064 |
| 2003:03:07 | (3.63) | (3.94) | (2.08) | (2.81) | (1.19) | (-13.88)*** | ||
| MERVAL | ||||||||
| Intercepto | 2002:06:14 | 8 | 0.0137 | 0.0255 | 0.0173 | - | - | -1.0148 |
| 2009:03:06 | (3.35) | (3.94) | (2.80) | (-14.38)*** | ||||
| Tendencia | 1994:08:26 | 8 | 0.0156 | - | - | 0.0001 | -0.0001 | -0.9647 |
| 2015:03:20 | (2.05) | (1.94) | (-1.61) | (-13.87)*** | ||||
| Ambos | 2002:06:14 | 8 | 0.0134 | 0.0357 | 0.0243 | -0.0001 | 0.0001 | -1.0275 |
| 2009:03:06 | (2.66) | (4.27) | (2.88) | (-1.75) | (1.99) | (-14.51)*** | ||
| WTI | ||||||||
| Intercepto | 1998:12:25 | 7 | 0.0028 | 0.0110 | 0.0078 | - | - | -0.7701 |
| 2009:02:13 | (1.10) | (2.49) | (1.70) | (-12.38)*** | ||||
| Tendencia | 2010:07:09 | 7 | -0.0004 | - | - | -0.0000 | 0.0001 | -0.7539 |
| 2014:12:12 | (-0.18) | (-1.40) | (1.26) | (-12.19)*** | ||||
| Ambos | 2004:07:02 | 7 | -0.0009 | 0.0114 | 0.0199 | -0.0001 | 0.0001 | -0.7737 |
| 2008:12:26 | (-0.28) | (1.83) | (3.07) | (-3.03) | (2.53) | (-12.48)*** | ||
Notas: Los números entre paréntesis son los t-estadísticos.
***, ** y * denota significancia del parámetro
estimado al 1%, 5% y 10%, respectivamente.
Teniendo en cuenta que todas las series de rendimientos consideradas son estacionarias,
estimamos un modelo VAR para los rendimientos para formar los indicadores que constituyen la
base del análisis empírico. El cuadro 3 muestra los
spillovers (índices de derrame) para los rendimientos, la entrada
Cuadro 3 Spillovers entre los Rendimientos del Precio Internacional del Petróleo y los principales Mercados Accionarios de América Latina y de Estados Unidos.
| S&P 500 | IBOVESPA | IPSA | IPC | MERVAL | WTI | De otros | |
|---|---|---|---|---|---|---|---|
| S&P 500 | 53.21 | 10.10 | 11.25 | 18.24 | 6.08 | 1.11 | 46.80 |
| IBOVESPA | 10.88 | 55.43 | 11.81 | 14.04 | 7.34 | 0.49 | 44.60 |
| IPSA | 11.58 | 11.98 | 54.16 | 14.88 | 6.66 | 0.75 | 45.80 |
| IPC | 17.07 | 11.95 | 12.74 | 49.76 | 7.78 | 0.70 | 50.20 |
| MERVAL | 8.09 | 8.36 | 7.53 | 11.06 | 64.30 | 0.65 | 35.70 |
| WTI | 1.67 | 1.38 | 1.45 | 1.95 | 1.40 | 92.15 | 7.90 |
| Contribución a otros | 49.30 | 43.80 | 44.80 | 60.20 | 29.30 | 3.70 | 231.00 |
| Contribución a otros* | 102.50 | 99.20 | 99.00 | 109.90 | 93.60 | 95.80 | 38.5% |
Notas: * Incluyendo los propios spillovers.
Los resultados del cuadro 1 muestran que los índices de spillovers de los rendimientos propios de cada mercado son mayores que los índices cruzados entre los mercados. Por ejemplo, un choque en los rendimientos del S&P 500 impacta en 53.21% al error de pronóstico de sus propios rendimientos. En forma similar, innovaciones en el mercado accionario IBOVESPA dan cuenta del 55.43% de la varianza del error de pronóstico de sus propios rendimientos. Un resultado a destacar es que los spillovers de los rendimientos de los mercados bursátiles de América Latina bajo estudio a los rendimientos del precio internacional del petróleo (7.90%) son mayores a los spillovers de los rendimientos del precio internacional del petróleo a los mercados bursátiles de la región (3.70%). De igual forma, los resultados muestran spillovers bidireccionales, evidenciando de este modo, causalidad en ambos sentidos: del mercado internacional del petróleo a los mercados de valores de América Latina y viceversa. No obstante, la contribución en términos de spillovers de los rendimientos del precio internacional del petróleo a los rendimientos accionarios de los principales mercados de América Latina bajo estudio así como al de Estados Unidos es mucho menor (3.70) en comparación con la contribución de spillovers de los rendimientos de estos mercados accionarios a los rendimientos del precio internacional del petróleo (7.90). Lo anterior también puede interpretarse como evidencia empírica de la relación entre los rendimientos bursátiles y los del precio internacional del petróleo, sin embargo el efecto las contribuciones en términos de spillovers es relativamente bajo en comparación de lo que podría esperarse, principalmente en el caso del mercado accionario de Estados Unidos (S&P 500) por su tamaño en comparación con el resto de los mercados accionarios analizado.
Otro resultado que es digno de destacarse es que la contribución de spillovers de los rendimientos del mercado accionario de México (IPC) a los rendimientos accionarios de Estados Unidos y de Latinoamérica es mayor a la contribución proveniente de cualquier otro mercado de la región, incluso es mayor a cualquier otra contribución del resto de los mercados considerados. Un resultado similar ocurre con los spillovers que recibe de los otros mercados. Lo cual sugiere que el mercado accionario de México desempeña un papel crucial en la transmisión y recepción de choques provenientes de los mercados accionarios de la región.
Una de las principales implicaciones de estos resultados es que no muestran evidencia de que mayores precios del petróleo casi no estimulan a los mercados accionarios de América Latina, lo cual puede atribuirse a una baja presencia de acciones relacionadas con el petróleo en los mercados de la región. De hecho, son mayores los choques provenientes de los mercados accionarios de la región al precio internacional del petróleo que los de este último a los mercados bursátiles, muy probablemente debido a la presencia de dos países exportadores de petróleo de la región en la muestra: México y Brasil.
El cuadro 4 presenta los resultados de los índices de spillovers para las volatilidades, de manera similar a los resultados obtenidos para los rendimientos, las estimaciones muestran una magnitud mucho mayor cuando se trata de los que recibe cada mercado de sí mismo que de los spillovers que provienen de otros mercados.
Cuadro 4 Spillovers entre las Volatilidades del Precio Internacional del Petróleo y las de los principales Mercados Accionarios de América Latina y de Estados Unidos.
| S&P 500 | IBOVESPA | IPSA | IPC | MERVAL | WTI | De otros | |
|---|---|---|---|---|---|---|---|
| S&P 500 | 56.15 | 3.20 | 26.02 | 10.46 | 0.37 | 3.81 | 43.90 |
| IBOVESPA | 6.13 | 77.61 | 9.81 | 3.24 | 3.12 | 0.10 | 22.40 |
| IPSA | 26.01 | 4.08 | 55.70 | 11.08 | 1.05 | 2.13 | 44.30 |
| IPC | 23.79 | 3.77 | 22.98 | 47.69 | 0.52 | 1.25 | 52.30 |
| MERVAL | 2.97 | 4.93 | 6.28 | 1.27 | 84.10 | 0.45 | 15.90 |
| WTI | 5.08 | 1.64 | 0.95 | 0.92 | 0.21 | 91.21 | 8.80 |
| Contribución a otros | 64.00 | 17.60 | 66.00 | 27.00 | 5.30 | 7.70 | 187.50 |
| Contribución a otros* | 120.10 | 95.20 | 121.70 | 74.70 | 89.40 | 98.90 | 31.3% |
Notas: * Incluyendo los propios spillovers.
En efecto, los mayores spillovers de volatilidad estimados son los que provienen del propio mercado. Por ejemplo, para el mercado accionario de Argentina (MERVAL) las innovaciones en volatilidades dan cuenta del 84.1% de la varianza del error de pronóstico de la volatilidad en el mercado argentino. Un resultado similar muestra el caso del mercado accionario de Brasil, en el cual los choques contra la varianza del error de pronóstico de su propia volatilidad es del 77.61%. No obstante, el índice de spillovers total es de 187.5%, sugiriendo de este modo una fuerte interdependencia entre las volatilidades de los mercados accionarios de América Latina y de Estados Unidos con la del mercado internacional del petróleo. Sin embargo, esta condición puede atribuirse más a la interdependencia entre los mercados accionarios que a la de éstos con el mercado petrolero.
El mayor índice de spillovers de volatilidad del precio internacional del petróleo a los mercados accionarios es el de Estados Unidos, representado por el S&P 5000, el cual asciende a 3.81%, seguido por el de Chile con un 2.13% en este mismo indicador. Mientras que los mercados de Argentina (MERVAL) y de Brasil (IBOVESPA) muestran una menor dependencia de la volatilidad del precio internacional del petróleo.
Otro resultado derivado de este análisis es que el mercado accionario de Chile (IPSA) es el que tiene una mayor contribución en spillovers de volatilidad hacia el resto de los mercados con un 66%, el cual supera al de Estados Unidos (S&P 500) que asciende a 64%. Por el contrario, el mercado accionario que más spillovers de volatilidad recibe es el mercado de México (IPC) con un 52.3%, lo cual sugiere que es el mercado bursátil de la región que tiene una mayor interdependencia con el resto de los mercados considerados.
Los resultados presentados en los cuadros 3 y 4 proporcionan información relevante sobre los spillovers entre los mercados analizados. No obstante, los índices de spillovers estimados se basan en valores promedio del periodo muestral, los cuales pueden ocultar movimientos seculares o cíclicos, o simplemente la respuesta a eventos relevantes ocurridos en el periodo analizado. Por tanto, cabe la posibilidad de que los spillovers fluctúen considerablemente a lo largo del periodo de estudio. Con el fin de mostrar la evolución de éstos a lo largo del tiempo, efectuamos la estimación con una ventana corrediza de 200 semanas para evaluar la evolución a través del tiempo de los spillovers estimados.
Como se puede apreciar en la gráfica 3, el índice de spillovers total de los rendimientos inicialmente fluctúa entre el 20 y 25% y tiende a incrementarse a finales de 1995, fecha en la que se registró la crisis cambiaria en México y que dio lugar al efecto Tequila. Posteriormente, de fines de 1999 a principios del 2000 se estabiliza alrededor de 50% y luego tiende a caer hasta el 2006 para luego incrementar. Con la aparición de la crisis financiera del 2008-09 este índice se incrementó abruptamente y continúo estable en años posteriores alrededor de 65% para posteriormente, a partir de 2013, mantener una tendencia decreciente.
El índice de spillovers total de las volatilidades (Gráfica 4) de los mercados estudiados también tiende a incrementarse en los periodos de crisis. Sin embargo, luego de la crisis cambiaria en México registrada en 1994-95 cayó drásticamente hasta el 15% después de rondar el 30% a principios de 1994. Después registró una tendencia creciente hasta 1999, fecha en que se estabilizó en cerca de 50% y después presentó nuevamente una caída a los niveles de 30% hasta el 2008, año en el que se incrementó drásticamente a alrededor de 75%. Desde finales del año 2008 y hasta mediados del 2012 se mantuvo relativamente estable y a partir de este último año ha mantenido una tendencia decreciente que tiende a revertirse a finales del periodo de estudio.
De manera análoga al procedimiento de Diebold y Yilmaz (2012), con el fin de determinar qué tan robustos son los resultados a el número de rezagos del VAR, calculamos el índice de spillovers para el caso de los rendimientos en un intervalo de rezagos, de 2 a 6, y graficamos la mediana así como los valores máximos y mínimos obtenidos, los cuales se muestran en la gráfica 5.
Repetimos el mismo procedimiento para evaluar la sensibilidad del índice al horizonte de pronóstico, para tal fin obtuvimos la mediana y los valores máximos y mínimos del índice de spillovers de los rendimientos para horizontes de pronóstico de 4 a 10 semanas, los cuales se presentan en la gráfica 6. Como se puede apreciar en las gráficas 5 y 6, el índice de spillovers total de los rendimientos no es sensible a la elección del orden del VAR ni a la elección del horizonte de pronóstico, lo anterior permite concluir que nuestros resultados son los suficientemente robustos.
6. Conclusiones
En este trabajo analizamos empíricamente la relación entre el precio internacional del petróleo y los principales mercados accionarios de América Latina y de Estados Unidos, a nivel de rendimientos y de sus volatilidades, con el fin de cubrir la brecha que han dejado los trabajos empíricos sobre el tema ya que éstos se han concentrado principalmente en los mercados bursátiles de las economías desarrolladas.
Con tal fin empleamos los índices de spillovers propuestos por Diebold y Yilmaz (2009) y (2012), los cuales permiten estimar la contribución neta de un mercado en el mecanismo de transmisión de información de otro mercado, Fowowe (2017), y así calcular el impacto de los choques de rendimientos y de volatilidad del mercado petrolero internacional en los mercados bursátiles de esta región con datos semanales del periodo comprendido entre el 19 de enero de 1990 y el 25 de octubre de 2019.
Los resultados obtenidos en el caso de los spillovers de los rendimientos muestran una interdependencia débil entre los principales mercados accionarios de América Latina, de Estados Unidos y el precio internacional del petróleo. En términos generales, los spillovers de los mercados bursátiles al mercado petrolero son mayores (7.9%) que los del mercado petrolero hacia los mercados bursátiles de América Latina (3.7 por ciento). Estos resultados son consistentes a lo encontrado por Fowowe (2017) para los mercados accionarios de Sudáfrica y de Nigeria, a lo reportado por Mohanty et al., (2011) y Awartani y Maghyerek (2013) para los mercados accionarios del Consejo de Cooperación del Golfo (CCG) y a los hallazgos de Arouri, Jouini y Nguyen (2011) y de Malik y Hammoudeh (2007) para el mercado bursátil de Estados Unidos y los del CCG.
Por otro lado, los resultados empíricos obtenidos para las volatilidades muestran que el índice de spillovers promedio es de 31.3%, lo cual sugiere una menor interdependencia entre las volatilidades de los principales mercados bursátiles de América Latina y de Estados Unidos con la del precio internacional del petróleo que el índice estimado para los rendimientos de estos mismos mercados.
Un resultado interesante, es el hecho de que el mercado bursátil de México es el que más recibe choques del resto de los mercados considerados y del precio internacional del petróleo, tanto a nivel de rendimientos como de volatilidades. En tanto que los mercados que más choques de rendimientos emiten son el mercado accionario mexicano (IPC) con 60.2% y el que más emite choques de volatilidad es el de Chile (IPSA) con 66%. Este último resultado es relevante en virtud de que los mercados bursátiles de estos países han experimentado en las últimas décadas un mayor grado de integración financiera internacional.











 nova página do texto(beta)
nova página do texto(beta)