Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista mexicana de ingeniería química
versão impressa ISSN 1665-2738
Rev. Mex. Ing. Quím vol.10 no.3 Ciudad de México Dez. 2011
Fenómenos de transporte
Modeling conventional and ultrasound–assisted extraction of oil–containing materials
Modelado de extracción convencional y asistida con ultrasonido de materiales que contienen aceite
R.S. Ruiz*, C. Martínez and M.G. Vizcarra
Universidad Autónoma Metropolitana–Iztapalapa. Área de Ingeniería Química, Av. San Rafael Atlixco 186. Col. Vicentina. 09340, México, DF. *Corresponding author. E–mail: rmr@xanum.uam.mx Tel.: +52 58044648, Fax: +52 58044900.
Received 22 of June 2011.
Accepted 9 of September 2011.
Abstract
A two–zone model based on broken and intact cells has been presented and applied to the experimental results on oil extraction obtained by various authors and on several species of seeds where the operation were based solely on solvent extraction or aided by ultrasound. The model a ssumes that oil contained within disrupted cells tobe extracted by a solvent washing process and to be described by a convective mass transfer mechanism. Oil contained within intact cells is assumed to diffuse towards the particle surface as described by Fickean diffusion within a semi–infinite slab. The resulting model consists of algebraic equations that; permit readily interpretation of experimental data in terms of relevant model parameters such as transport parameters and particle fractions of damaged and sound cells, among others. Results showed good agreement between calculated and experimental data for both conventional and ultrasound–assisted extraction. The model was found to be sensitive to the presence of ultrasound irradiation as it resulted in relatively higher convective mass–transfer rate constants and larger damaged cells proportions as compared to 1he corresponding conventional extraction.
Keywords: oil extraction, model, solvent, ultrasound, mass transport parameters, cells.
Resumen
Se presenta un modelo de extracción de aceite que supone la presencia de tanto células dañadas como intactas, Se interpretan datos experimentales reportados en la literatura para distintas semillas extraídas con solvente o en sistemas asistidos con ultrasonido. Se supone que el aceite contenido en las células dañadas se extrae por un proceso de lavado con el solvente, y se describe mediante un mecanismo convectivo de transferencia de masa, mientras que el aceite en la estructura celular intacta se supone que se desplaza hacia la superficie de la partícula siguiendo un mecanismo de difusión que puede describirse como un sólido semi infinito. El modelo resultante consiste en ecuaciones algebraicas que al ser ajustadas a cinéticas de extracción permite determinar parámetro relevantes del proceso tales como los de transporte y las fracciones del solido con células rotas e intactas, entre otras. Se encontró que el modelo se ajusta relativamente bien tanto a datos de extracción convencional como a los procesos asistidos por ultrasonido. De acuerdo a las predicciones del modelo el ultrasonido puede favorecer la extracción al incrementar tanto los coeficientes de transferencia de masa en el lavado de células rotas como la cantidad relativa de estas.
Palabras clave: extracción de aceite, modelo, solvente, ultrasonido, parámetros de transporte, células.
1 Introduction
The solvent extraction of a vegetable oil from a crushed, sliced, or flaked oil seed involves solution of the free oil from the broken cells and mass transfer of the oil in the undamaged cellular structure of the seed. Adequate design of an efficient extraction procedure from biomass materials requires a thorough knowledge of all the factors which may influence the extraction process (Del Valle and De la Fuente, 2006; Sacramento–Rivero, J.C. et al., 2010). Several oil extraction models have been reported in the literature. Some of them are empirical in nature and are not adequate for scaling–up since they do not provide a description of underlying mass transfer phenomena that occur in industrial–size extraction vessels (Seth et al., 2007). For design purposes, mass transfer models on solvent extraction may facilitate the scale–up of laboratory data.
Oil extraction has sometimes been modeled by assuming the solid as a single phase, homogeneous matrix, for which diffusion is considered as the only internal mass transfer mechanism. In this case, no distinction is made between the solute concentrations in the solid matrix and in its pores, and it is implicitly assumed that all the cells have similar physical characteristics and therefore, the variation of the oil concentration in the solid particle is assumed to follow Fick's second law as the sole transport mechanism. This type of model has been utilized for describing oil extraction from seeds by means of a hydrocarbon solvent (Alvarez et al., 2001; Fan et al., 1948; Krasuk et al., 1967; Martinez et al., 2010), as well as for describing supercritical carbon dioxide oil extraction (Esquivel et al., 1999).
One of the first attempts of introducing a physical description of vegetable substrate was proposed by Sovova (1994) in modeling supercritical carbon dioxide extraction. This model takes into consideration that as a result of seed physical manipulation such as chopping and crushing the extracted solid contains both broken and intact cells. It is then assumed that microstructurally, a seed particle contains: i) "free oil", which is extracted at a rate that is controlled by the external resistance to mass transfer, and is localized in fractured cells in the particle surface; and, ii) "tied oil," which is extracted at a rate that is determined by internal mass transfer mechanisms, and is localized in undamaged cells and/or partially damaged cells in the inner portions of the particle. Marrone et al. (1998) developed a more fundamental adaptation of Sovova's model for supercritical fluid extraction. They proposed that the rate of extraction of oil was equal to the sum of the rates of extraction of free oil and tied oil. The rate of extraction of free oil was assumed to be proportional to an external mass transfer coefficient and a driving force equal to the difference between the density of the oil (ρsol, concentration of oil in a pure oil phase) and its concentration in a saturated supercritical fluid phase, whereas that of tied oil was assumed to be proportional to an internal mass transfer coefficient and a driving force equal to the difference between the averaged concentration of tied oil in the solid, and its equilibrium concentration when in contact with the loaded supercritical phase. Although the use of such internal mass transfer coefficient can facilitate the solution of their model the equations, it remains questionable that a constant value, as imposed by the authors, can adequately describe the internal transport (Cussler, 1997; Del Valle and De la Fuente, 2006).
Similar models that consider both external and internal mass transport have also been reported for solvent oil extraction from olive foot cake (Meziane et al., 2006) and from canola seeds (So and Macdonald, 1986). However, these models are based on kinetic constants that implicitly include the particularities of the solid structure and hence do not explicitly take into consideration the relative proportions between the amount of damaged and intact materials.
For the case of ultrasound–assisted extraction only few papers report modeling of the extraction process. Stanisavljevic et al. (2007) studied ultrasound–aided oil extraction from tobacco seeds and modeled the extraction kinetics using the transient diffusion through plant material model. For ultrasonic extraction of waste solid residues from the Salvia sp. Velickovic et al. (2008) also report description of the kinetics by the unsteady–state diffusion through the plant material and the film theory. Although these models were fitted to data in the relatively slow extraction period, they appear to be inadequate for modeling the initial and comparatively faster extraction period. It is evident that more comprehensive models are required for describing ultrasound–assisted solvent extraction systems.
It appears that several models are found in the literature for oil extraction with different degree of complexity in terms of the description of the solid structure and material transport within and between phases. Those models that recognize the heterogeneity nature of the material and hence the possible existence of different oil transport mechanisms are expected to reflect closer the extraction phenomena than the comparatively simpler homogeneous models. The former models, however, are frequently based on questionable transport expressions or employ kinetic–reaction–type rate expressions that lump together in single constants both transport properties and geometric characteristics. In order to deal with these limitations a heterogeneous model is presented in this work that employ fundamentally based transport equations that explicitly consider both transport and physical solid characteristics. It consists of a the two–stage mass transfer model that considers the presence of both free and tied oil, the former within damaged cells in the external layers of the particle, and the latter within intact cells in the particle core. In comparison with previously cited models, the present model describes the extraction process in terms of more fundamental assumptions, mainly those concerning internal transport within the particle. In this regard, tied oil is assumed to diffuse within the intact cell structure by Fickian transport. Furthermore, the model assumes that oil in broken cells is extracted away by solvent washing.
The present model is based on a number of assumptions that are found applicable to both conventional and ultrasound–assisted extraction and therefore it has been tested for both types of systems. Fitting of the model equations to an extraction kinetics curve permits direct calculation of the effective diffusion coefficient, the solid volume fractions containing free and tied oils, and the washing rate, for both systems based solely on solvent extraction and systems where solvent extraction is aided by ultrasound.
2 Mathematical model
The modeling of the extraction process is based on the following assumptions.
1. Vegetable oil consists predominantly of a mixture of triglycerides, but in terms of mass transfer behavior oil is represented by a single seudo–component.
2. Oil in the extracted sample can be found within the structure of intact cells or as part of disrupted superficial cells. The latter can be produced by physical manipulation and exacerbated by ultrasound. Extraction of the oil stored in the cell structure requires trespassing of the cell wall while oil in damaged cells can be considered as being essentially unbound.
3. The rate extraction of oil from disrupted cells is comparatively faster than the oil within intact cells. The extraction rate of the former is assumed to occur by a washing phenomenon and that it can be described by a mass transfer expression.
4. Extraction of oil within the cell structure is assumed to occur by diffusion and to follow Fick's second law.
5. Both free and bound oil extractions occur simultaneously.
6. Diffusion of oil is a relatively slow process that can be considered as a semi–infinite slab at short enough times.
2.1 Mathematical presentation of the model
According to the basic hypothesis of the model the following definitions and mass balance equations can be written for free and bound oils.
The total amount of oil within sample corresponds of oil in disrupted cell (free oil) and within the intact cell structure (bound oil), that is:
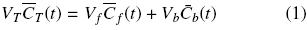
where sub–indices T, f and b respectively correspond to total, free, and bound oils. In terms of the volumetric fractions of damaged cells,  f, and of the intact cell structure,
f, and of the intact cell structure,  b:
b:
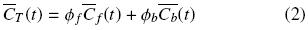
where  f +
f +  b = 1.
b = 1.
The extraction rate of free oil is described by convective mass transfer by:
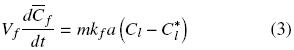
where Cl and is the oil bulk concentration in the solvent and Cl* is the oil concentration in the solvent at the solid surface, and which is assumed to correspond to the saturation concentration in the solvent at the temperature of extraction, and kf is the mass transfer coefficient. In the particular case of a batch system for which the mass of the solid extracted is much smaller than that of the mass of solvent, as well as for extraction systems involving a continuous flow of fresh solvent, the bulk liquid oil concentration can be expected to be significantly lower than the corresponding equilibrium value, that is Cl 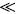 Cl*, and hence Eq. (3) reduces to:
Cl*, and hence Eq. (3) reduces to:
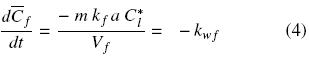
where kwf can be seen as a pseudo zero–order washing rate constant with respect to free oil concentration. Assuming that the initial oil concentration, Co, applies to both disrupted and intact cells, integration of Eq. (4) gives the oil concentration in disrupted cells as a function of time and the normalized washing rate
constant, 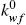 :
:
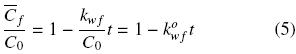
Equation (5) is valid for 0 < t < tcr, where tcr corresponds to time period that it takes for the oil in damaged cells to be completely extracted.
At this point it is worth mentioning that the different experimental extracting systems considered in this work all correspond to seed slices physically prepared so as to promote one dimensional oil transport. Therefore, for oil within the undisrupted cell structure extraction is assumed to occur by diffusion and can be described for a slab by the following equation (Cussler, 1997):
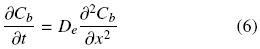
where the effective diffusion coefficient, De, is assumed to be constant. At a given time, the space mean oil concentration is related to Cb by:
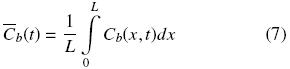
At the beginning of the extraction process all the mean oil concentrations in the solid are equal to the initial value, which is: 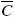 T =
T = 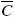 f =
f = 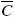 b = C0 .
b = C0 .
Assuming short enough times the diffusion process can be seen as to occur in a semi–infinite slab and the initial and boundary conditions for Eq. (6) are given by
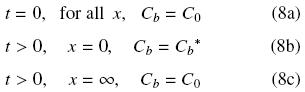
where equilibrium between oil at the solid matrix and oil in the solvent is assumed to exist at the solid surface. Solution for Eq. (6) subject to given initial and boundary conditions can be obtained in terms of the error function (Cussler, 1997)
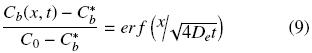
The oil flux at the interface of intact cells with the solvent can be obtained by combining Fick's law with
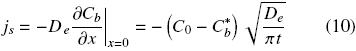
The cumulative extracted oil, Js,cum, from time t = 0 to time t can be obtained from a time integration of Eq. (10):
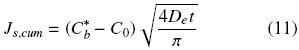
The cumulative extracted oil can be expressed in terms of the mean oil concentration and the volume of the intact cell structure, Vb = Asls
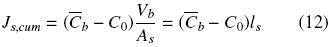
where As and ls are respectively the superficial area and half thickness of the diffusion slab (slice of thickness 2ls). By combining eqs. (11) and (12) the mean oil concentration in the cell structure can be obtained as a function of time
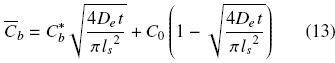
For the case in which the total volume of solvent is much greater than the volume of the solid sample, the bulk oil concentration in the solvent is negligible and hence the equilibrium oil concentration at the solid surface can be assumed as zero. Combining then eqs. (2), (5), and (13) gives the mean concentration oftotal oil in the extracted sample as a function of time:
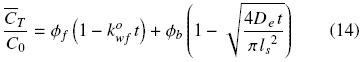
This equation can be expressed in terms of the amount of oil per unit volume of solid, q, commonly utilized in extraction:
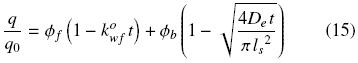
For t > tcr it is assumed that extraction occurs only by diffusion and for this conditions the variation of q with time is given by
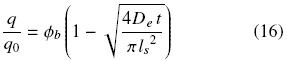
3 Experimental data
3.1 Solvent extraction systems
For the purpose of validation of the proposed model, conventional oil extraction data reported in the literature for commercial peanut kernels, and tung fruit seeds (Aleurites fordii), were chosen for the present work (respectively by Fan et al., 1948, and Krasuk et al., 1967). In general terms, the experimental extraction process reported was similar for both seeds, which consisted in extracting slices of seed and evaluating the progress of extraction by a weighing procedure. The oil was extracted by an organic solvent (both pure solvents and mixtures were utilized) at different temperatures and atmospheric pressure. Seed samples of up to 2 mm thick were prepared so as to have one–dimensional mass transport. For peanut slices the authors reported that this was easily obtained and that oil transport occurred basically through the exposed face areas, something that was possible because the edge of the slices consisted of intact surface layer cells that greatly retarded extraction by the solvent. For tung seed slices one–dimensional transport was secured by sealing the edges with an epoxy resin.
3.2 Comparison of conventional and ultrasound assisted extraction
Data reported by Lou et al. (2010) for oil extraction from chickpea with and without the aid of ultrasound were also analyzed with the present model. Two different extraction systems were utilized: a conventional batch solvent extraction apparatus and a so called dynamic extraction chamber, both of which were operated with and without the aid of ultrasound. In the batch solvent extraction system, grounded chickpea were extracted at 60° C in an agitated flask. In the experiments with the dynamic extraction system a relatively small bed of ground seed particles was placed within the extraction chamber and through which a given flow of solvent was made to circulate. For temperature control the extraction chamber was immersed in a constant temperature bath at 60°C. For the ultrasound–assisted experiments, the extraction vessels were immersed in an ultrasonic cleaner (40 kHz) and operated at different ultrasonic powers. The data used in the present work corresponds to ground chickpea with a particle range of 0.2–0.8 mm and the solvent consisted of a mixture of hexane and isopropanol in a proportion 75:25% (v/v). After extraction, the extracts were filtered under vacuum, the oil concentrated with a rotary evaporator, and finally dried in a vacuum dryer to remove residual solvent.
3.3 Statistical analysis
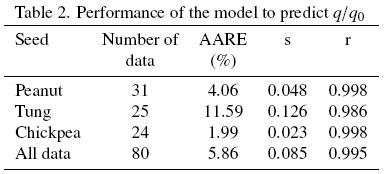
Oil extraction data reported in the abovementioned experimental works have been fitted to the present model and its performance evaluated based on the following descriptors: (a) the average absolute relative error (AARE) between q/qo predictions and experimental values; (b) the standard deviation (s) of the relative errors and the mean relative error; and (c) the correlation coefficient to assess the quality of the fit by the model. This was done for each of the three seeds considered as well as for the whole ensemble of data.
4 Results and discussion
As mentioned above, experimental oil extraction data for the following seeds peanut, tung, and chickpea (conventional and ultrasound–assisted), have been interpreted in terms of the present model. The information that is obtained from the model consists mainly of the oil effective diffusion coefficient within the solid structure (De), the washing kinetic constant of oil from disrupted cells (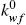 ), the sample volume fraction of oil–containing disrupted cells (
), the sample volume fraction of oil–containing disrupted cells ( f), and the time period that it takes for the oil in damaged cells to be completely extracted (tcr).
f), and the time period that it takes for the oil in damaged cells to be completely extracted (tcr).
4.1 Extraction of peanut oil
Figure 1 shows the extraction curves for peanut slices obtained with a solvent that consisted essentially of hexanes at 25°C (Fan et al, 1948). The data correspond to peanut slices 0.32, 0.26, and 0.2 mm thick, with similar moisture contents. It is evident from Fig. 1 that two distinct extraction periods exist; at the beginning a relatively high extraction rate followed by a clearly lower rate, and which is consistent with observations often reported in the literature.
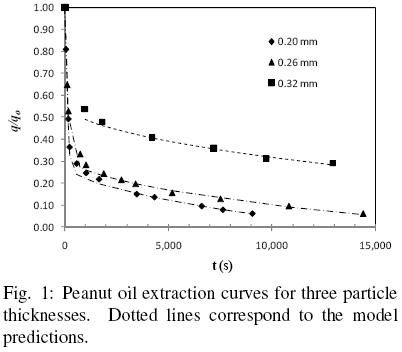
According to the assumptions of the proposed model the first and faster period corresponds basically to oil extraction from disrupted cells, while the slower rate is controlled by oil diffusion in the intact cell structure. According to the present model, the first extraction period is assumed to be described by Eq. (15), which considers simultaneous extraction by convective and diffusion transport. Furthermore, by the end of this period all the oil present in disrupted cells is assumed to have been washed away. The second extraction period is then described by Eq. (16), which considers only oil transport by diffusion and from which the effective diffusion coefficient and the volume fraction of intact cells can be obtained. Fig. 2 shows the experimental data for a 0.2 mm slice for the second extraction period, as well as Eq. (16) fitted to the data by linear regression. It is clear from the fitted line that  b is equal 0.30, and hence that
b is equal 0.30, and hence that  f is 0.70, that is to say that 30 per cent of the slice volume corresponds to intact cells and 70 percent to damaged cells. It is evident from Table 1 that the fraction of oil within damaged cells,
f is 0.70, that is to say that 30 per cent of the slice volume corresponds to intact cells and 70 percent to damaged cells. It is evident from Table 1 that the fraction of oil within damaged cells,  f, decreases with an increase of particle size, which is somewhat expected if one considers that the damaged material corresponds basically of the particle superficial cells and hence, an increase in particle size essentially increases the fraction of undamaged material.
f, decreases with an increase of particle size, which is somewhat expected if one considers that the damaged material corresponds basically of the particle superficial cells and hence, an increase in particle size essentially increases the fraction of undamaged material.
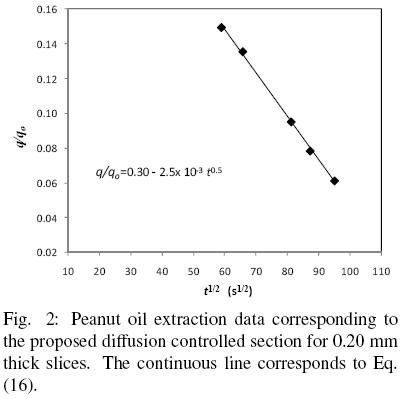
Table 1 presents the effective diffusion coefficients, De, obtained from the slope of Eq. (16) as shown in Fig. 2 for 0.2 mm slices. Although for peanut slices the values of De obtained appear to be of similar magnitude, when De values for 0.2 and 0.32 mm samples are compared an effect of particle thickness on De cannot be discarded, especially if the diffusion coefficient happens to depend on oil concentration. As can be seen from Fig. 1, the diffusion–controlled period occurred for 0.32 mm slices at a higher oil content ((q/qo)av = 0.343) than for 0.2 mm ((q/qo)av = 0.104) , which seems to suggest that the diffusion transport coefficient can be negatively affected by an oil content reduction, as it has been reported in the literature (Krasuk, et al. 1967, Martínez et al., 2010). In order to evaluate such possible effect, for each diffusion–control period the effective diffusion coefficients and the respective average dimensionless oil content (q/qo)av have been correlated in terms of the following exponential expression:
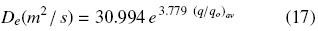
which is valid for 0.104 < (q/q0)av < 0.343, with determination coefficient, r2 = 0.992, and from which the dependency between the diffusion coefficient and the solid oil content becomes evident.
Analysis of the first extraction period is presented next. As was mentioned above, Eq. (15) has been assumed to describe the first oil–extraction period. The first term on the right side of this equation corresponds to the convective washing of oil from disrupted superficial cells. The normalized pseudo zero–order washing rate constant, 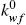 , as defined by Eq. (5), can be obtained from Eq. (15) once the parameters De,
, as defined by Eq. (5), can be obtained from Eq. (15) once the parameters De,  b, and
b, and  f are known. For every pair of q/qo and t data in the first extraction period, the values for (1 –
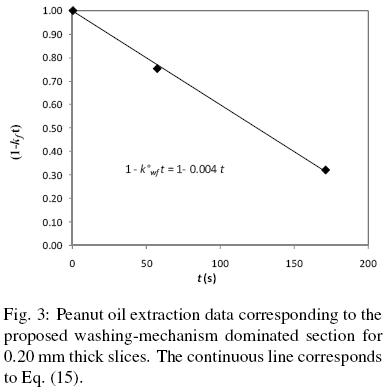
f are known. For every pair of q/qo and t data in the first extraction period, the values for (1 – 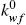 ) were calculated from Eq. (15) and then plotted against time, as shown in Fig. 3 for 0.2 mm slices. For the experimental conditions considered, that is when the mass of the solid extracted is much smaller than that of the mass of solvent; it is clear from the fitted line that a constant
) were calculated from Eq. (15) and then plotted against time, as shown in Fig. 3 for 0.2 mm slices. For the experimental conditions considered, that is when the mass of the solid extracted is much smaller than that of the mass of solvent; it is clear from the fitted line that a constant 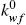 value can describe the assumed extraction phenomena from disrupted cells. The corresponding
value can describe the assumed extraction phenomena from disrupted cells. The corresponding 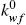 values for the 0.20 and 0.26 mm thick peanut slices are presented in Table 1. The
values for the 0.20 and 0.26 mm thick peanut slices are presented in Table 1. The 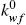 value for 0.32 mm slices could not be satisfactorily determined due to fact that only two data points were available (see Fig. 1). Table 1 also shows tcr, the time period that it takes for the oil in damaged cells to be completely extracted. This critical time was calculated from Eq. (5) astcr = 1 /
value for 0.32 mm slices could not be satisfactorily determined due to fact that only two data points were available (see Fig. 1). Table 1 also shows tcr, the time period that it takes for the oil in damaged cells to be completely extracted. This critical time was calculated from Eq. (5) astcr = 1 /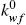 . It is apparent from these results that washing of disrupted cells consists of a relatively fast process that did not exceed 5 minutes for 0.20 and 0.26 mm extracted samples, and according to the present model for t > tcr solvent extraction of the samples appear to be described by Fick's law.
. It is apparent from these results that washing of disrupted cells consists of a relatively fast process that did not exceed 5 minutes for 0.20 and 0.26 mm extracted samples, and according to the present model for t > tcr solvent extraction of the samples appear to be described by Fick's law.
Finally, the values of the model parameters De,  b,
b,  f, and
f, and 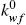 (Table 1) were substituted into eqs. (15) and (16) and the extraction curves calculated; the segmented lines in Fig. 1 correspond to the model predictions, which are in relatively good agreement with the experimental extraction curves as it is suggested by a correlation coefficient of 0.998 (see Table 2). Also shown in Table 2 are the average absolute relative error (AARE) and its corresponding standard deviation (s), and from which an average 4.06 per cent error is observed for the fitted model.
(Table 1) were substituted into eqs. (15) and (16) and the extraction curves calculated; the segmented lines in Fig. 1 correspond to the model predictions, which are in relatively good agreement with the experimental extraction curves as it is suggested by a correlation coefficient of 0.998 (see Table 2). Also shown in Table 2 are the average absolute relative error (AARE) and its corresponding standard deviation (s), and from which an average 4.06 per cent error is observed for the fitted model.
4.2 Oil extraction oftung seeds
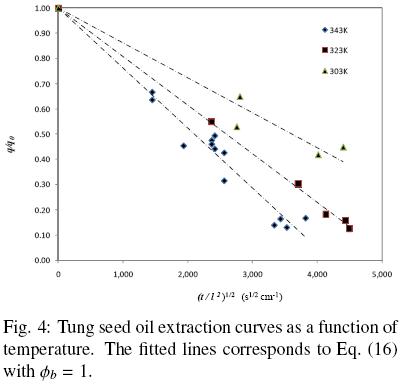
Figure 4 presents oil extraction curves for slices of tung seeds with initial moisture contents below 6.0 per cent at 30, 50, and 70°C (Krasuk et al., 1967). The authors utilized different petroleum distillation products as the extraction solvent, however no apparent effect of the solvent was observed for the considered experimental conditions. Slices of different thicknesses of 0.7 to 2.0 mm were used in the experiments, and hence, in order to make the extraction curves comparable with each other the oil content in the samples was expressed as a function of the single variable (t/l2) as shown in Fig. 4.
The experimental data has been interpreted in terms of the equations of the present model as it has been done above for peanut slices, and the resulting parameters De,  b,
b,  f, and
f, and 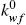 are shown in Table 1.
are shown in Table 1.
The fitted lines corresponds to Eq. (16) with  b = 1, that is for case in which all the extractable oil is found within intact cells and the oil extraction process is assumed to occur solely by diffusion. Although a fraction of damaged cells could be expected to be present at the surface of the sample, it is apparent from Fig. 5 that the experimental data is somewhat dispersed so as to allow for a more precise estimation of
b = 1, that is for case in which all the extractable oil is found within intact cells and the oil extraction process is assumed to occur solely by diffusion. Although a fraction of damaged cells could be expected to be present at the surface of the sample, it is apparent from Fig. 5 that the experimental data is somewhat dispersed so as to allow for a more precise estimation of  b. Such data dispersion also resulted in a 0.986 correlation coefficient and in 11.59% AARE, the latter being significantly larger than those obtained for both peanut and chickpea (Table 2).
b. Such data dispersion also resulted in a 0.986 correlation coefficient and in 11.59% AARE, the latter being significantly larger than those obtained for both peanut and chickpea (Table 2).
It is often assumed that the effective diffusivity, De, follows exponential temperature dependence as that given by the Arrhenius equation:
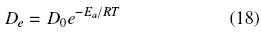
where Do is a constant, Ea the activation energy, R the ideal gas constant, and T absolute temperature. The logarithm of the effective diffusion coefficients listed in Table 1 for tung seeds have been plotted against 1/T and an activation energy of 23.6 kJ mol–1 was obtained from the slope of the fitted straight line (determination coefficient, r2 = 0.991). This value is similar to those reported in the literature for solvent oil extraction from other oilseeds (e.g., 24.4 kJ mol–1 for hazelnuts (Schneeberger et al. 1988), 25.4 kJ mol–1 for zapote mamey seeds (Alvarez et al., 2001), and 21.8 kJ mol–1 for sun flower collets (Baumler et al., 2010)).
The fraction of the particles that corresponds to damaged material can be related to the size of oil–containing cells. For the peanut and tung data utilized in this work, it can be expected that cells were broken in the preparation of the extracted samples, basically by the cutting process of the seeds, and hence damaged cells would be located mainly on the sample surfaces. The shape of the experimental slice samples was that of a plate with two symmetrical extraction surfaces. Accordingly, the product of the volume fraction of damaged cells by half of the sample thickness would correspond to the length from the surface of damaged material. For the case of peanut samples the length of damaged material for the 0.20 and 0.26 mm particles would be, respectively, (0.70x0.20 mm/2) and (0.69x0.26 mm/2), that is 70 μm and 88 μm. Fan and co–workers found by microscopy that the size of peanut cells was approximately 70 jm, which appears to be similar in magnitude to the length of damaged material calculated with the present model. Similarly, Krazuk and co–workers report an average cell size of 22 m for tung seed cells, which for sample thicknesses between 0.7 and 2.0 mm yields volume fractions of damaged cells between 2.2% and 6.3%. That is, only a relatively small fraction of the sample appears to correspond to damaged material, which in general terms is in accordance with the prediction that the extraction is controlled basically by diffusion transport.
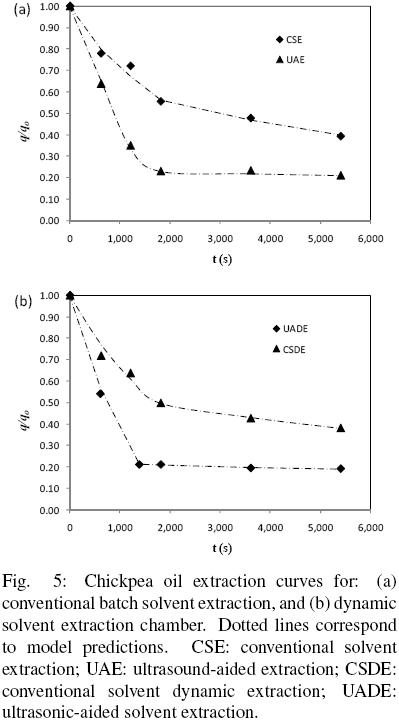
4.3 Oil extraction of chickpea particles with and without ultrasound
The data presented in Fig. 5(a) and (b) correspond to 1.0 g of ground chickpea particles extracted batch wise and by a recirculating solvent flow, respectively. It is clear from Fig. 5(a) that, for both systems, at the beginning of the process a relatively fast extraction rate occurs which is then followed by a comparatively much moderate one. The ultrasound–aided global extraction rate and yield (UAE) are clearly higher than those for conventional solvent extraction of (CSE), as for instance, after 1.5 h extraction period the percentage yields of chickpea oil were 78.6% and 60.7%, respectively for UAE and CSE (Lou et al, 2010). The highest yield for conventional extraction was reported to be 70.21% at 4h, 8% lower compared with ultrasound–aided extraction.
Figure 5(b) shows the extraction kinetics for particles extracted by a flowing solvent (conventional solvent dynamic extraction, CSDE) and by the same system operated under ultrasonic irradiation (ultrasound aided dynamic extraction, UADE). Here too it appears that ultrasound assisted operation can significantly reduce the extraction time and improve the extraction yield, compared with conventional extraction. The yields of chickpea oil by CSDE and UADE were 62.02% and 80.66% after 1.5 h extraction, respectively. Furthermore, UADE and CSDE techniques were found to significantly shorten extraction time by 10 min and 30 min, when compared with UAE and CSE techniques, respectively (Lou et al., 2010). Similar findings with regard to the effect of ultrasound have been reported in the literature, which suggest that in liquid–solid extraction ultrasound enhances mass transfer mainly by cavitation forces. In such systems, the collapse of cavitating bubbles can generate intense localized pressure causing rupture of cell walls and improving the release of intracellurar material into the solvent (Knorr et al., 2002). Therefore, it seems that application of ultrasound can have an impact on the amount of damaged cells, which can then be expected to be larger for ultrasound treated material than for the corresponding non–irradiated one, and hence, a corresponding increase of the oil extraction rate can also be foreseen.
The experimental data for chickpea oil extraction have been interpreted in terms of the proposed model and the dotted lines in figs. 5 (a) and (b) correspond to the predictions of the fitted model. It is evident from Fig. 5 that the model reasonably fits the experimental data as it is suggested by a correlation coefficient of 0.998 (see Table 2). Also shown in Table 2 are the average absolute relative error (AARE) and its corresponding standard deviation (s), and from which an average 1.99 per cent error is observed for the fitted model. The corresponding parameters, De,  b,
b,  f, and
f, and 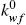 , are presented in Table 1.
, are presented in Table 1.
An analysis of the values of the parameters obtained is presented next, starting with the particle volume fractions of damaged and intact cells for the systems shown in Fig. 5 (a). The particle volume fraction with free oil,  f, was found to be 0.22 and 0.74 for CSE and UAE, respectively, which suggests that a significant increase in the amount of damaged cells has occurred by the effect of ultrasound. The depth of superficial damaged material as well as the inner diameter of intact cells (db) can be estimated from
f, was found to be 0.22 and 0.74 for CSE and UAE, respectively, which suggests that a significant increase in the amount of damaged cells has occurred by the effect of ultrasound. The depth of superficial damaged material as well as the inner diameter of intact cells (db) can be estimated from  b = 1 –
b = 1 –  f = (db/dp)3, by assuming spherical shape 0.5 mm diameter particles. The diameter of the inner core of intact material has been calculated to be 0.46 mm and 0.32 mm for CSE and UAE, respectively, while the corresponding superficial layers of damaged material were 20 m and 90 μm. The depth of damaged material for grounded chickpea, 20 μm, is of the order of magnitude of the size of cells reported for other seeds (Reverchon and Marrone, 2001), which seems to suggest that chopping and cutting have an effect on the integrity of the external layer of cells. According to the present model, the depth of damaged material clearly increases by the effect of ultrasound to 90 μm, which suggests that ultrasound can affect several external cell layers. Similar results were obtained for the recirculating flow cells (Fig. 5 (b)) in terms of a significant increase of damaged material produced by the effect of ultrasound as can be seen from the obtained particle volume fraction of damaged cells,
f = (db/dp)3, by assuming spherical shape 0.5 mm diameter particles. The diameter of the inner core of intact material has been calculated to be 0.46 mm and 0.32 mm for CSE and UAE, respectively, while the corresponding superficial layers of damaged material were 20 m and 90 μm. The depth of damaged material for grounded chickpea, 20 μm, is of the order of magnitude of the size of cells reported for other seeds (Reverchon and Marrone, 2001), which seems to suggest that chopping and cutting have an effect on the integrity of the external layer of cells. According to the present model, the depth of damaged material clearly increases by the effect of ultrasound to 90 μm, which suggests that ultrasound can affect several external cell layers. Similar results were obtained for the recirculating flow cells (Fig. 5 (b)) in terms of a significant increase of damaged material produced by the effect of ultrasound as can be seen from the obtained particle volume fraction of damaged cells,  f , which was 0.34 and 0.77 for CSDE and UADE, respectively.
f , which was 0.34 and 0.77 for CSDE and UADE, respectively.
The normalized pseudo zero–order oil washing rate constants, 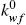 , as defined by Eq. (5), are presented in Table 1 for the chickpea extraction kinetics, and from which it appears that the largest and smallest washing rate constants correspond to UADE and CSE, respectively. According to Luo et al. (2010) the dynamic extraction system showed better liquid–solid mass transfer conditions compared to that of the batch conventional extractor. Therefore, the larger rate constant observed for UADE can be explained by a combined effect of ultrasound and larger liquid–solid mass transfer in the flow extractor. As can be seen from Table 1, under UADE operation the amount of oil extracted by washing mechanism was 3.5 times that for CSE operation (0.77/0.22), and which was accomplished in a smaller period of time (1111s against 1818s). In terms of Eq. (5) ultrasound appears to have an impact on the washing rate constant by generating violent shock waves and high–speed jets that disrupt the cell walls and hence increase the effective surface area available for mass transfer, a, and also reduce the boundary layer mass transfer resistance which in turn increases kf.
, as defined by Eq. (5), are presented in Table 1 for the chickpea extraction kinetics, and from which it appears that the largest and smallest washing rate constants correspond to UADE and CSE, respectively. According to Luo et al. (2010) the dynamic extraction system showed better liquid–solid mass transfer conditions compared to that of the batch conventional extractor. Therefore, the larger rate constant observed for UADE can be explained by a combined effect of ultrasound and larger liquid–solid mass transfer in the flow extractor. As can be seen from Table 1, under UADE operation the amount of oil extracted by washing mechanism was 3.5 times that for CSE operation (0.77/0.22), and which was accomplished in a smaller period of time (1111s against 1818s). In terms of Eq. (5) ultrasound appears to have an impact on the washing rate constant by generating violent shock waves and high–speed jets that disrupt the cell walls and hence increase the effective surface area available for mass transfer, a, and also reduce the boundary layer mass transfer resistance which in turn increases kf.
Finally, from both Fig. 5 and the effective diffusivities in Table 1, it appears that extraction from damaged material was the main mechanism for extraction under ultrasound conditions. For UADE and UAE the effective diffusion coefficients were an order of magnitude smaller than those for conventional extraction, which can probably be attributed to an oil–concentration dependence of the diffusion coefficient. The effective diffusion coefficients for conventional solvent chickpea extraction were of the same order of magnitude of those obtained for peanut oil extraction.
4.4 Applicability of the model
The present model is based on several assumptions listed above in Section 1. One of these assumptions considers transport within the intact cell structure as Fickean diffusion, and also, that it can be dealt with as a semi–infinite slab. It is not rare to find works on oil extraction that report the use of Eq. (6) to describe the process, however what is not so common is to find works that treat the solid as a semi–infinite slab. This assumption is valid in cases for which either transient diffusion transport occurs at relatively short periods of time or where the transport process is relatively slow so that Eq. (8) is satisfied. This condition can be taken into account by the mass transfer Fourier number, Fom = Det/ls2, and can be expected to be satisfied at relatively small values of it. In order to identify such values Eq. (6) was solved numerically with the following initial and boundary conditions:
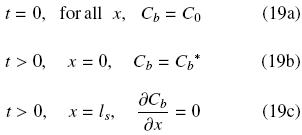
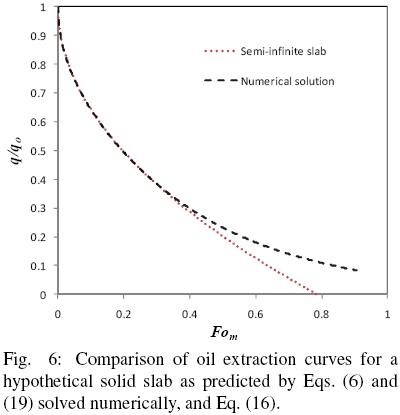
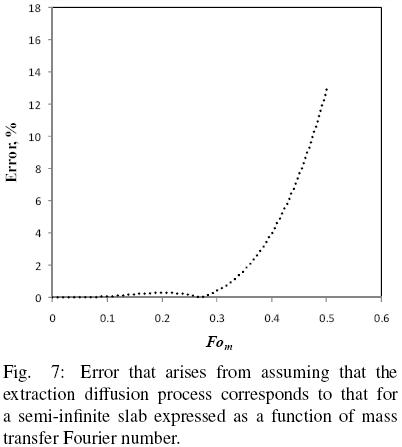
and the results reported in terms of q/qo and compared with those of Eq. (16) with  b = 1. Fig. 6 shows the numerical solution for the evolution in time of the mean oil content of a hypothetical slice and the corresponding solution assuming semi–infinite slab behavior. It is apparent that for Fom smaller than about 0.4 the predictions of both solutions coincide fairly well, however, as the mass Fourier number is further increased both solutions tend to depart from each other. Fig. 7 presents the corresponding error from assuming semi–infinite slab behavior, and from which it is found that for Fom < 0.32 the error is smaller than 1%, while for Fom = 0.4 the error is about 4%. For the data of all three seeds utilized in the present work the mass transfer Fourier numbers were calculated and found that Fom was smaller than 0.30.
b = 1. Fig. 6 shows the numerical solution for the evolution in time of the mean oil content of a hypothetical slice and the corresponding solution assuming semi–infinite slab behavior. It is apparent that for Fom smaller than about 0.4 the predictions of both solutions coincide fairly well, however, as the mass Fourier number is further increased both solutions tend to depart from each other. Fig. 7 presents the corresponding error from assuming semi–infinite slab behavior, and from which it is found that for Fom < 0.32 the error is smaller than 1%, while for Fom = 0.4 the error is about 4%. For the data of all three seeds utilized in the present work the mass transfer Fourier numbers were calculated and found that Fom was smaller than 0.30.
Conclusions
A model for oil extraction that considers simultaneous extraction from disrupted and intact cells is presented and applied to conventional and ultrasound–assisted extraction. When compared with some previously reported models, the present one describes the extraction process in terms of more fundamental assumptions, mainly those concerning internal transport within the particle. It is assumed that washing of oil from broken cells and diffusion of oil through the intact cell structure occurs. Simple algebraic equations describe the model which when applied to experimental data permitted determination of relevant system parameters such as: the so called washing mass transfer coefficient for oil extraction from broken cells; the effective diffusivity mass transfer coefficient for oil extraction from intact cells; the particle fractions of damaged and sound material; the critical time which corresponds to the transition from transport dominated by washing extraction to that controlled by diffusion. For design or simulation purposes of an extraction system that follows the assumptions of the present model, Eq. (15) and (16) can be utilized in combination with the corresponding batch or continuous solvent mass balance equation.
The model was found to fit well experimental solvent extraction curves reported in the literature for peanut, tung and chickpea seeds, and also for ultrasound–assisted chickpea extraction. In contrast with other models that utilize the fraction of damage material as external information for solution of the model, the present model could directly estimate the fraction of extracted sample that corresponded to damaged and intact materials. Furthermore, from the fraction of particle damaged material the depth of superficial damaged material was calculated, which in turn was found to be similar in magnitude to the size of oil containing cells for conventional extraction.
The fraction of damaged material appears to be affected when a conventional extraction system is irradiated by an ultrasonic field as it was observed for cheakpea extraction data. The effect of ultrasound not only significantly increased the surface depth of damaged cells as compared to that for conventional extraction, it also showed to increase the oil extraction rate mass constant from broken cells, both of which can be probably attributed to cavitating bubbles that produce violent shock waves and high–speed jets that disrupt the cell walls and promotes surface mixing at the particle surface.
The model considers transport within the intact cell structure as described by diffusion in a semi–infinite slab, which results in a relatively simple algebraic equation of readily application for determining the oil effective diffusion coefficient as well as the sample volume fraction that corresponds to intact cells. The semi–infinite slab assumption was found to be valid at the beginning of the extraction process, for a mass Fourier number below 0.30, for which the corresponding error would be less than one percent, as it was case in the present work.

References
Alvarez, R.A., Solis, F.J. and Duran de Bazua, C. (2001). Coeficientes de difusividad aparente durante la extracción de aceite de almendras de zapote mamey (Pouteria sapota). Tecnología, Ciencia, Educacion, (IMIQ) 16, 20–27. [ Links ]
Baümler, E.R., Crapiste, G.H., and Carelli, A.A. (2010). Solvent Extraction: Kinetic Study of Major and Minor Compounds. Journal of the American Oil Chemical Society 87(12), 1489–1495. [ Links ]
Cussler, E.L. (1997). Diffusion: Mass transfer in fluid systems, (2nd ed.). Cambridge, University Press, New York. [ Links ]
Del Valle, J.M. and De la Fuente, J.C. (2006). Supercritical CO2 Extraction of Oilseeds: Review of Kinetic and Equilibrium Models. Critical Reviews in Food Science and Nutrition 46, 131–160. [ Links ]
Esquivel, M.M., Bernardo–Gil, M.G. and King M.B. (1999). Mathematical models for supercritical extraction of olive husk oil. Journal of Supercritical Fluids 16, 43–58. [ Links ]
Fan, H.P. and Morris, J.C. (1948). Diffusion phenomena in solvent extraction of peanut oil. Industrial and Engineering Chemistry 40(2), 195–199. [ Links ]
Krasuk, J.H., Lombardy, J.L. and Ostrovsky, C.D. (1967). Diffusion extraction of oil–containing materials. Industrial and Engineering Chemistry Process Design and Development 6(2), 187–195. [ Links ]
Knorr, D., Ade–Omowaye, B.I.O. and Heinz, V. (2002). Nutritional improvement of plant foods by non–thermal processing. Proceedings ofthe Nutrition Society 61, 311–318. [ Links ]
Lou, Z., Wang, H., Zhang, M. and Wang, Z. (2010). Improved extraction of oil from chickpea under ultrasound in a dynamic system. Journal of Food Engineering 98, 13–18. [ Links ]
Marrone, C., Poletto, M., Reverchon, E. andStassi A. (1998). Almond oil extraction by supercritical CO2: experiments and modelling. Chemical Engineering Science 53, 3711–3718. [ Links ]
Martínez–Vera, C. Ruiz–Martínez, R.S., Vizcarra–Mendoza, M.G. and Álvarez–Calderón, J. (2010). Apparent diffusion model assessment in extraction processes by means of a Luenberger observer. Jounal of Food Engineering 101, 1622. [ Links ]
Meziane, S., Kadi, H. and Lamrous, O. (2006). Kinetic study of oil extraction from olive foot cake. Grasas y Aceites 57(2), 175–179. [ Links ]
Reverchon, E. and Marrone, C. (2001). Modeling and simulation of the supercritical CO2 extraction of vegetable oils. Journal of Supercritical Fluids 19, 161–175. [ Links ]
Sacramento–Rivero, J.C., Romero, G., Cortés–Rodríguez, E., Pech, E., Blanco–Rosete, S. (2010). Diagnostico del desarrollo de biorefinerías en México. Revista Mexicana de Ingeniería Química 9(3), 261–283. [ Links ]
Schneeberger, R., Villarroel, M., Drapela, N., Caire, F. and Castillo, M. (1988). Cinética de extracción de aceite de avellana. Grasas y Aceites 39(3), 151–154. [ Links ]
Seth, S., Agrawal, Y.C., Ghosh, P.K., Jayas, D.S. and Singh, B.P.N. (2007). Oil extraction rates of soya bean using isopropyl alcohol as solvent. Biosystems Engineering 97, 209–217. [ Links ]
So, G.C. andMacdonald, D.G. (1986). Kinetics of oil extraction from canola (Rapeseed). Canadian Journal ofChemical Engineering 64, 80–86. [ Links ]
Sovová, H. (1994). Rate of the vegetable oil extraction with supercritical CO2 –I. Modelling of extraction curves. Chemical Engineering Science 49, 409–414. [ Links ]
Stanisavljevic, I.T., Lazic, M.L. and Veljkovic, V.B. (2007). Ultrasonic extraction of oil from tobacco (Nicotiana tabacum L.) seeds. Ultrasonic Sonochemestry 14, 646–652. [ Links ]
Velickovic, D.T., Milenovic, D.M., Ristic, M.S. and Veljkovic, V.B. (2008). Ultrasonic extraction of waste solid residues from the Salvia sp. essential oil hydrodistillation. Biochemical Engineering Journal 42, 97–104. [ Links ]














