Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista mexicana de ingeniería química
versão impressa ISSN 1665-2738
Rev. Mex. Ing. Quím vol.10 no.3 Ciudad de México Dez. 2011
Fenómenos de transporte
Effective thermal properties at the fluid–porous medium interfacial region: role of the particle–particle contact
Propiedades térmicas efectivas en la región interfacial entre un medio poroso y un fluido: el papel del contacto partícula–partícula
C.G. Aguilar–Madera1, F.J. Valdés–Parada1, B. Goyeau2 and J.A. Ochoa–Tapia1*
1 División de Ciencias Básicas e Ingenierías, Universidad Autónoma Metropolitana–Iztapalapa. San Rafael Atlixco 186. Col. Vicentina 09340. Iztapalapa, D.F., México. * Corresponding author. E–mail: jaot@xanum.uam.mx Tel: +52 55 5804 4648, Fax: +52 55 5804 4900
2 Laboratoire EM2C, UPR–CNRS 288, Ecole Centrale Paris, Grande Voie des Vignes, (92295), Châtenay–Malabry, Cedex, France
Received 27 of May 2011.
Accepted 19 of October 2011.
Abstract
In this work, we studied the role played by the particle–particle contact over the effective properties appearing in upscaled thermal models, for heat transport at the fluid–porous medium interfacial region under conductive regime. Using closure problems recently reported in the literature, the various effective properties were predicted as functions of position in rhe inter–region and of the degree of interconnection between solid particles. To this end, the associated closure problems were solved in unit cells containing squares connected by rectangular ramifications. It is shown that the existence of contact between particles yields results significantly different from those without contact. This may be an important source of error in modeling, specially when the solid (or the fluid) is highly conductive in comparison with the other phase.
Keywords: upscaled thermal models, one–domain approach, effective properties, particle–particle contact.
Resumen
En este trabajo, se estudió el papel del contacto partícula–partícula sobre las propiedades efectivas que aparecen en los modelos escalados, para el transporte de calor en la región interfacial entre un medio poroso y un fluido bajo régimen conductivo. Utilizando problemas de cerradura reportados recientemente en la literatura, se predijeron las propiedades efectivas en función de la posición en la inter–región y del grado de interconección entre las partículas sólidas. Para esto, los problemas de cerradura se resolvieron en celdas unitarias que contienen cuadrados conectados entre sí por medio de brazos rectangulares. Se encontró que la existencia de contacto entre las partículas produce resultados significativamente diferentes a aquellos originados sin contacto. Esto puede representar una importante fuente de error en el modelamiento, especialmente cuando el sólido (o el fluido) es mucho más conductivo en comparación con la otra fase.
Palabras clave: modelos térmicos escalados, modelo de un solo dominio, propiedades efectivas, contacto partícula–partícula.
1 Introduction
Accurate characterization for heat transport taking place between homogeneous media, as those composed by a porous medium adjacent to a free fluid region, plays a crucial role in modeling and designing in several practical applications. Some examples are packed bed reactors (Pereira–Duarte et al., 1984), modified heat exchangers (Alkam et al., 2001; Chen and Sutton, 2005), drying processes (Jimenez–Islas et al., 2004; Carrera–Rodríguez et al., 2009), transport in biological tissues (Khaled and Vafai, 2003) and transpiration cooling processes (Cho and Eckert, 1994). In this type of systems, one of the main challenges lies in accurately describing transport phenomena at the vicinity of the fluid–porous boundary. In this zone, the effective properties in the bulk of homogeneous regions can not be used due to the drastic changes of the microstructure of the phases. To overcome this issue there are two different alternatives (Goyeau et al., 2003):
• The first one is the One Domain Approach (ODA) (Valdes–Parada et al., 2007; Aguilar–Madera et al., 2011). Here the entire system, i.e., porous medium and free fluid region, is considered as a single domain and the modeling is carried out with effective equations valid everywhere. Such effective equations are expressed in terms of position–dependent parameters, which are constant in the bulk of homogeneous media and undergo rapid and continuous changes through the so–called inter–region. To use this methodology it is required to know the spatial dependency of the effective properties.
• The second one is the Two Domain Approach (TDA) (Ochoa–Tapiaand Whitaker, 1998,1997; Valdes–Parada et al., 2009). Here each homogeneous medium is considered as a single domain and the modeling is carried out with effective equations for each domain. In this case, the effective equations are expressed in terms of position–independent parameters and the inter–region is replaced by a singular dividing surface. To use this method it is required to know the position of the dividing surface, which is still a matter of investigation (Jamet and Chandesris, 2009; Veran et al., 2009), and the jump boundary conditions for coupling effective equations at the dividing surface.
In modeling heat transport between homogeneous media, the majority of works in literature use the TDA with conventional boundary conditions, i.e., continuity of heat flux and temperature (Alkam et al., 2001; Chen and Sutton, 2005). This type of boundary conditions are not formally derived from the rigorous upscaling of pore–scale governing equations, and they might be inconsistent with the phenomenon at the microscale (Prat, 1989). In this regarding, some efforts have been devoted to theoretically (Ochoa–Tapia and Whitaker, 1997, 1998) and empirically (Sahraoui and Kaviany, 1993, 1994) obtain appropriate boundary conditions. A summary of several boundary conditions reported in the literature for momentum and heat transport can be found in the work of Alazmi and Vafai (2001).
Recently, Valdes–Parada et al. (2009) pointed out that in order to compute the jump coefficients (unknown coefficients appearing in the associated jump boundary conditions) it is necessary to account for the spatial functionality of transport properties involved in the effective equations under the ODA. This means that both types of formulations above described, are related mainly due to the phenomenon taking place at the vicinity of the fluid–porous boundary. This stresses the importance of developing closed models under the ODA context, since these are crucial previous steps toward the derivation of closed and complete boundary conditions for the TDA.
One geometrical feature that crucially drives heat transfer through multiphase media, besides the physical properties, concerns the way in which phases are distributed at the microscale. Heat is preferentially transported through the more conductive phase and the remaining (less conductive) phases act as thermal insulators. Thus, one has that, depending of the thermal conductivities of materials, the existence of continuous and dispersed phases may contribute to favor (or hinder) the heat propagation through the entire multiphase system.
In this work, we predict the effective thermal coefficients appearing in the closed ODA models recently developed by Aguilar–Madera et al. (2011) under local thermal equilibrium and non–equilibrium assumptions. Particularly, we study the role played by the particle–particle contact on the spatial functionality of the effective thermal tensors and the interstitial heat transfer coefficient within the inter–region. The analysis is bounded to purely conductive cases, in which the particle–particle contact is represented through interconnection–arms. The use of this type of geometrical models, generally, yields results in excellent agreement with experimental data when the solid matrix is highly conductive (Nozad et al., 1985; Yang and Nakayama, 2010).
2 Upscaled models
For purely–conductive heat transport, the governing equation at the continuum scale for the fluid (β–phase) is given by, whereas for the solid (σ–phase) is
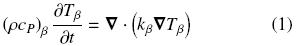
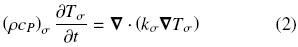
where (ρcP)β and (ρcP)σ are the heat capacities per volume at constant pressure for the fluid and the solid, respectively; Tβ and Tσ are the fluid and solid pore–scale temperatures, respectively; kβ is the thermal conductivity for the fluid phase and kσ the corresponding one for the solid. To complete the microscale heat transport description, it is required to specify the boundary conditions at the macroscopic limits of the whole domain presented in Fig. 1, the initial conditions and the interfacial conditions applying at the fluid–solid interface (these are continuity of heat flux and temperature). The difficulty associated in solving the microscale heat transport problem is outlined in the complex microstructure sketched in Fig. 1. Note that one needs to know the distributions of phases in detail. This gives rise to the necessity of describing the transport from the macroscale in terms of average temperatures and effective coefficients, i.e., an upscaling process must be done.
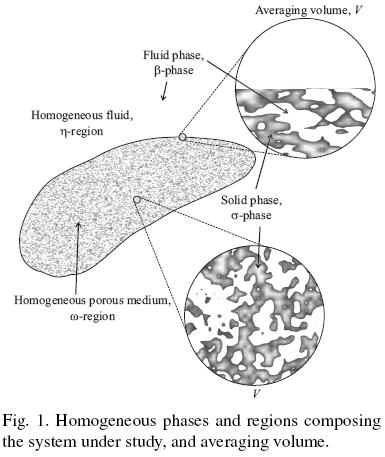
Recently, Aguilar–Madera et al. (2011) carried out the upscaling process for the heat transport problem by using the method of volume averaging (Whitaker, 1999). They derived the volume averaged model under local thermal non–equilibrium conditions and within the ODA framework, which in turn is composed by the governing equations for the β– and σ –phases,
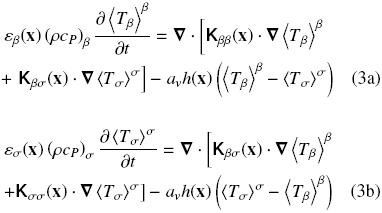
where εβ and εσ are the volume fraction of fluid and solid respectively. The above equations contain several effective transport coefficients, which arose from the upscaling process. These are the thermal tensors Kij (i, j = β, σ) and the interstitial heat transfer coefficient avh, which depend on the position x. In this case, as we are dealing with the non–equilibrium model we require two governing equations, one for each phase present in the system. In the above equations the fluid intrinsic average temperature is defined as,
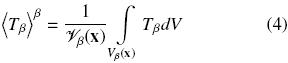
with Vβ being the space occupied by the β–phase within the averaging domain V showed in Fig. 1, and 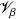 represents the volume of Vβ. It is understood that there is an analogous definition for the solid intrinsic average temperature
represents the volume of Vβ. It is understood that there is an analogous definition for the solid intrinsic average temperature  Tσ
Tσ σ. It is worth stressing that the effective coefficients involved in the above equations have constant values in the bulk of the homogeneous regions (sketched in Fig. 1), and undergo continuous and rapid changes through the inter–region. Additionally, it is mentioned that Eqs. (3) represent a more simplified model in comparison with that one originally derived by Aguilar–Madera et al. (2011) [see Eqs. (13) and (16) in there] as some less–relevant effective parameters were discarded.
σ. It is worth stressing that the effective coefficients involved in the above equations have constant values in the bulk of the homogeneous regions (sketched in Fig. 1), and undergo continuous and rapid changes through the inter–region. Additionally, it is mentioned that Eqs. (3) represent a more simplified model in comparison with that one originally derived by Aguilar–Madera et al. (2011) [see Eqs. (13) and (16) in there] as some less–relevant effective parameters were discarded.
When the local thermal equilibrium assumption is valid, a model with a single governing equation is enough for modeling heat transport and Eqs. (3) can be appropriately added to obtain,
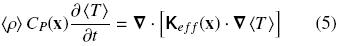
where,
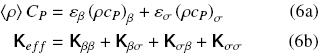
and the single average temperature is defined as,
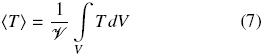
with T being the pore–scale temperature, which can be Tβ or Tσ.
In order to use the upscaled models it is necessary to predict the effective coefficients from experimental or theoretical procedures. Using the method of volume averaging, Aguilar–Madera et al. (2011) derived the associated closure problems involving convective and conductive heat transport; these closure problems are solved in representative samples of the microscale (unit cells). For the case at hand, the corresponding closure problems are slightly different from those of Aguilar–Madera et al. (2011) since only conductive heat transport is considered. These problems are given in the Appendix along with the definitions of the effective coefficients.
3 On the solution of closure problems
As stated above, the closure problems required to predict the effective properties can be solved in reduced domains capturing essential features from microescale. Indeed, the best procedure involves using real micrographs, i.e., Transmission Electron Microscopy images (TEM) from the porous medium under study. However, the usage of simplified geometric models, as those represented by periodic arrays of particles is, generally, enough to obtain results in excellent agreement with experimental values (Ryan et al., 1980; Nozad et al., 1985; Wood, 2007; Yang and Nakayama, 2010).
In this work, we model the microstructure of the porous medium as a periodic array of touching squared cylinders. Following the method of Nozad et al. (1985), the degree of inter–connection between particles is quantified through the ratio c/a showed in Fig. 2. Thus, in the porous region the continuous phase is the solid whereas the dispersed phase is the fluid. In Fig. 2 we have also sketched a periodic model that consists in a non–touching array of cylinders. Such a periodic model was recently used by Aguilar–Madera et al. (2011) in the study of steady convective–conductive heat transport between a porous medium and a fluid within a ODA framework, and their results for conductive regime will be compared in this work.
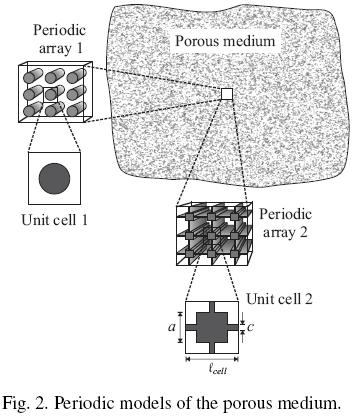
The closure problems were solved using the commercial finite element solver Comsol Multiphysics 3.5a, which implements a direct linear method for inversion of matrices (UMFPACK solver) to solve the associated non–local steady boundary–value problems [Eqs. (A–2) in the Appendix]. The whole domain was discretized in numerous triangular elements as those showed in Fig. 3 (finite elements), where unit cells in the bulk of the porous medium and in the inter–region are presented. As discussed by Valdes–Parada et al. (2007), the size of unit cells (i.e. the number of particles in the cell) in the inter–region must be large enough so that results are independent on this parameter. In this case, we found that a cell including 10 solid particles satisfies this requirement. As the large cell in Fig. 3 contains 5 particles (of 10 possibles), then the results computed from this cell correspond to y = 0 if the cell centroid is assigned to the center. In addition, it is worth noting that results computed with this method are independent of the number of triangular elements used.
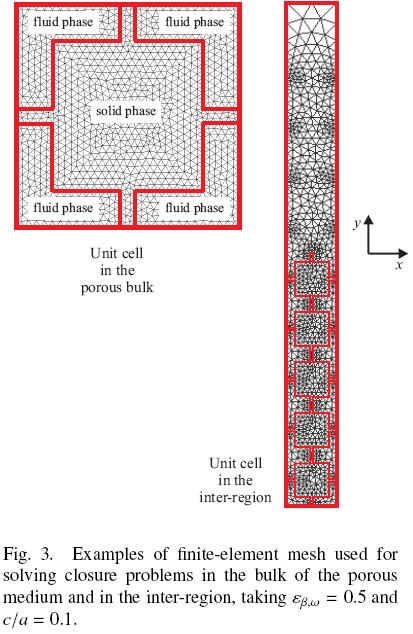
Particularly, the number of triangular elements rapidly grows when c/a  0, causing that computational demands significantly increase due to the thin interconnection arms. For this reason, the results of next section are bounded for c/a = 0.04 as minimum value for computations in the inter–region, and 0.005 in the porous bulk. Despite of this limitation, the tendency of results will clarify the role played by the particle–particle contact in the effective medium equations under the ODA framework.
0, causing that computational demands significantly increase due to the thin interconnection arms. For this reason, the results of next section are bounded for c/a = 0.04 as minimum value for computations in the inter–region, and 0.005 in the porous bulk. Despite of this limitation, the tendency of results will clarify the role played by the particle–particle contact in the effective medium equations under the ODA framework.
4 Results and discussion
4.1 Predictions in the porous bulk
Firstly, we focus upon the behavior of the most significant effective properties in the bulk of the porous medium. Particularly, we analyze the influence of the particle–particle contact over the effective thermal tensors and the interstitial heat transfer coefficient. The effect of varying parameters as the porosity and the ratio of thermal conductivities, k = kσ/kβ, can be found elsewhere (Quintard and Whitaker, 1993, 1995; Quintard et al., 1997). As sketched in the discretization mesh presented in Fig. 3, cells located at the porous bulk allows us to perform computations for lower values of the ratio c/a, in comparison with cells in the inter–region. For this reason, in this section we present results up to c/a = 0.005 as minimum value, from which one can infer the corresponding tendency within the inter–region.
In Fig. 4 the dependency of the longitudinal components (xx–elements) of Kββ and Kσσ evaluated in the bulk of the porous region, o, with the ratio c/a are presented. Notice that increasing the degree of interconnection causes that (Kββ, ω)xx decreases for k < 1, whereas for k > 1 this parameter is insensitive. The opposite behavior for (Kσσ,ω)xx is true. This situation is congruent with the physics at the microscale; if the solid is more conductive than the fluid (k > 1), then increasing the degree of interconnection favors the thermal tensor associated with the solid, i.e., Kσσ.
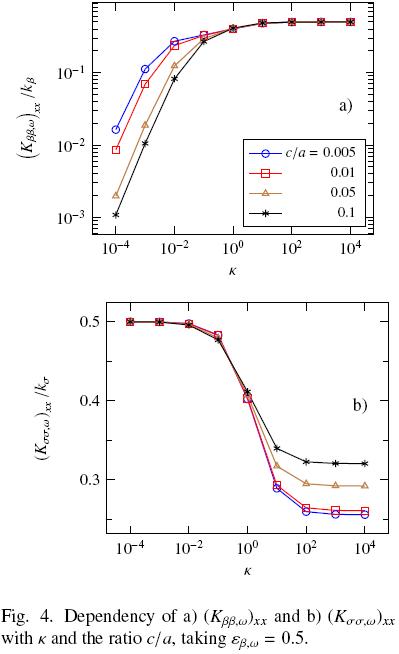
In the case when the fluid is more conductive than the solid (k < 1), decreasing the grade of interconnection favors Kββ since the resistance to heat transport offered by the solid diminishes.
From our computations we found that all the off–diagonal elements of thermal tensors are negligible in comparison with their diagonal counterparts. For example, we have that
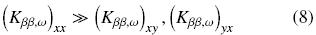
In addition, since the unit cell used in calculations is symmetric with respect to the x– and y–coordinates, it is easy to demonstrate that the diagonal elements of the thermal tensors are equal, for example
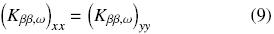
It is pointed out that the isotropy expressed in later equation is broken under "asymmetric conditions" that might take place for cases with convective heat transport and/or the microstructure is preferentially oriented (for instance, a porous medium composed by laminated solids).
The following thermal tensors that we study are the crossed ones Kβσ and Kσβ. Particularly, from our simulations, and according to Quintard and Whitaker (1993), it was found that both tensors are equal in the porous bulk, i.e.

As showed in Fig. 5a), the longitudinal element of Kβσ increases when c/a  0, specifically for k > 1. Note that for k
0, specifically for k > 1. Note that for k  1 this effective parameter vanishes, and the degree of interconnection is not significant.
1 this effective parameter vanishes, and the degree of interconnection is not significant.
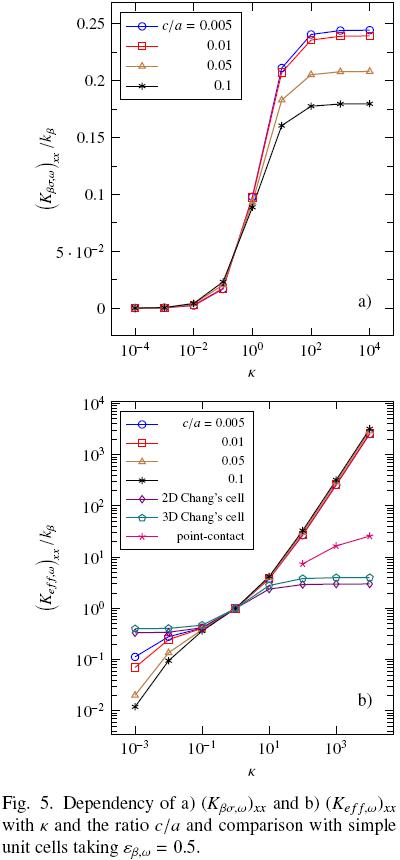
With the effective thermal tensors involved in the non–equilibrium model being available, we can use Eq. (6b) in order to predict the effective thermal conductivity in the equilibrium model. In Fig. 5b) we show the dependency of the longitudinal component of Ke f f with k and the grade of interconnection. Notice that the ratio c/a plays an important role mainly for k < 1 and, eventually, the effective conductivity vanishes when c/a  1. In this limit, the solid matrix acts as thermal insulator enclosing portions of fluid hindering the capability of the porous medium for heat transport. In the opposite case (k > 1), the effective conductivity slowly tends to the corresponding value when c/a
1. In this limit, the solid matrix acts as thermal insulator enclosing portions of fluid hindering the capability of the porous medium for heat transport. In the opposite case (k > 1), the effective conductivity slowly tends to the corresponding value when c/a  0. Moreover, for comparison purposes, we also plot the analytical expression reported by Batchelor and O'Brien (1977).
0. Moreover, for comparison purposes, we also plot the analytical expression reported by Batchelor and O'Brien (1977).
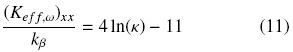
which is valid for large values of k and when there is point–contact between particles. Notice that the tendency of our results agrees with the behavior of the point–contact curve. In addition, in Fig. 5b) we present the results when there is no interconnection between particles, i.e., the β–phase is continuous. For a periodic array of cylinders as those presented in Fig. 2, Ochoa–Tapia et al. (1994) reported the analytical expression,
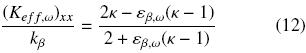
whereas for a periodic array of spheres the corresponding equation is (Maxwell, 1873),
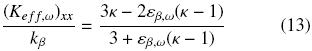
As these equations result from the solution of the corresponding closure problems in non–periodic Chang's cell (Chang, 1982), they are conveniently labeled as 2D and 3D Chang's cell in Fig. 5b). Additionally to Eqs. (11)–(13), we refer the reader to the Chapter 4 in the book of Vafai (2000) where several analytical expressions of the effective conductivity for different geometrical models are summarized.
In Fig. 5b) the importance of the particle–particle contact is manifested through the three types of curves showed: with contact, with point–contact and without contact. It should be stressed that in cases when k 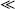 1 or k
1 or k 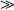 1, the differences between curves are more noticeable, and under these circumstances, the accurate characterization of the porous microstructure becomes relevant.
1, the differences between curves are more noticeable, and under these circumstances, the accurate characterization of the porous microstructure becomes relevant.
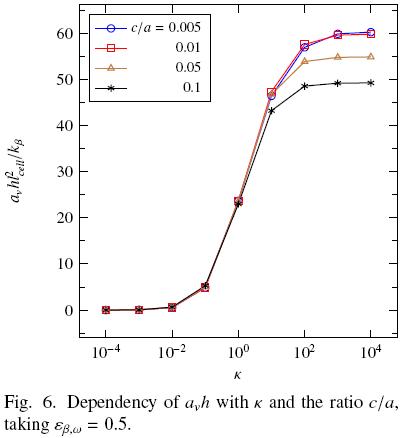
To finalize this section, in Fig. 6 we show the effect of the ratio c/a and k over the interfacial heat transfer coefficient avh normalized with kβ/l2cell, where lcell is the unit cell width. For cases with k 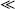 1 this coefficient vanishes and the influence of the particle–particle contact is negligible. This is a topic consistent with physics at the microscale; as k
1 this coefficient vanishes and the influence of the particle–particle contact is negligible. This is a topic consistent with physics at the microscale; as k 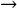 0 the solid acts as a thermal insulator and the heat exchanged between phases (quantified with avh) eventually decreases. When the solid is more conductive than the fluid, it seems that increasing the ratio c/a reduces the heat exchanged between phases. However, it should be mentioned that avh represents the heat exchanged per unit volume; as c/a decreases, the interfacial area av also do it and consequently avh too.
0 the solid acts as a thermal insulator and the heat exchanged between phases (quantified with avh) eventually decreases. When the solid is more conductive than the fluid, it seems that increasing the ratio c/a reduces the heat exchanged between phases. However, it should be mentioned that avh represents the heat exchanged per unit volume; as c/a decreases, the interfacial area av also do it and consequently avh too.
4.2 Predictions in the inter–region
Now we focus over the spatial transitions of effective coefficients through the inter–region. Particularly, our interest is centered on the influence of the degree of interconnection over effective parameters evaluated at different positions. The influence of others parameters such as k and the porosity can be found elsewhere (Aguilar–Madera, 2011). In the inter–region, the redistribution of phases makes it necessary to consider this zone as an heterogeneous zone which encompasses variations in geometrical properties (εβ sp and av). This makes us use larger unit cells as the one shown in Fig. 3, in such a way that changes in the microstructure are taken into account (Valdes–Parada et al., 2007, 2009; Aguilar–Madera et al., 2011).
The spatial evolutions of (Kββ)xx and (Kβσ)xx as functions of c/a are presented in Fig. 7a) keeping thermal conductivities and porosity fixed. The first thermal coefficient hardly depends on the particle–particle contact and all results computed collapse in the same curve, for this reason we just present for c/a = 0.04. As the results correspond to k = 100, they are in agreement with those presented in Fig. 4a), in which the ratio c/a practically does not influence (Kββ)xx. Here the position y has been normalized with the cell radius r0. In addition, we also present the results recently reported by Aguilar–Madera et al. (2011) where the porous medium is represented as a periodic array of non–touching solid cylinders (periodic array 1 showed in Fig. 2). Regarding the effective coefficient (Kβσ)xx, the degree of interconnection has a moderate influence mainly in the vicinity of the porous bulk, i.e., when y/r0 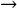 –1. Nevertheless, geometries considering particle–particle contact give rise different results with respect to non–touching particles. Notice that using a periodic array of cylinders, (Kβσ)xx is a linear function of position being equal to (Kββ)xx in the porous bulk and 0 in the fluid region.
–1. Nevertheless, geometries considering particle–particle contact give rise different results with respect to non–touching particles. Notice that using a periodic array of cylinders, (Kβσ)xx is a linear function of position being equal to (Kββ)xx in the porous bulk and 0 in the fluid region.
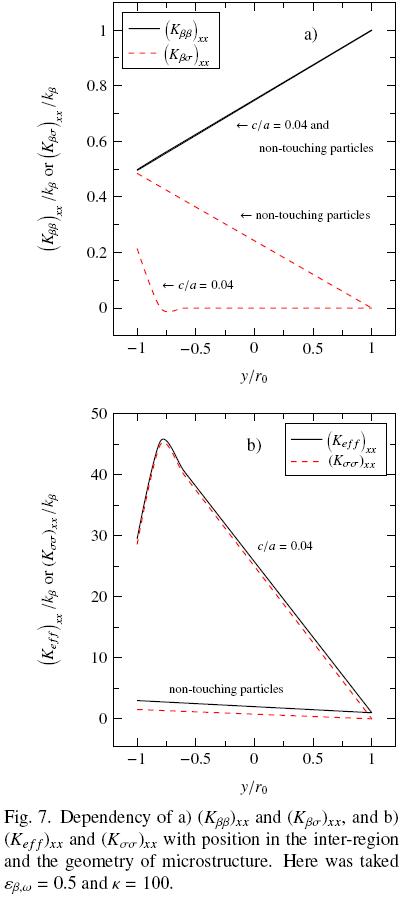
In Fig. 7b) the spatial dependence of (Kσσ)xx involved in the non–equilibrium model, and (Ke f f )xx the unique effective parameter in the equilibrium model are presented. In this case, as k = 100 both effective parameters have similar values through the inter–region and within the porous medium. As mentioned above, high values of k favor the coefficient associated to the solid, and consequently, the thermal tensor Kσσ mainly contributes to the effective thermal conductivity [remember that Ke f f involves all the thermal tensors of the non–equilibrium model, see Eq. (6b)]. The results presented are in agreement with those shown in Figs. 4b) and 5b), in the sense that particle–particle contact significantly influences the effective parameters leading to evident differences with respect to non–touching particles. In addition, it should be noted that in cases with particle–particle contact the spatial dependency is nonlinear as opposed to those corresponding to non–touching particles.
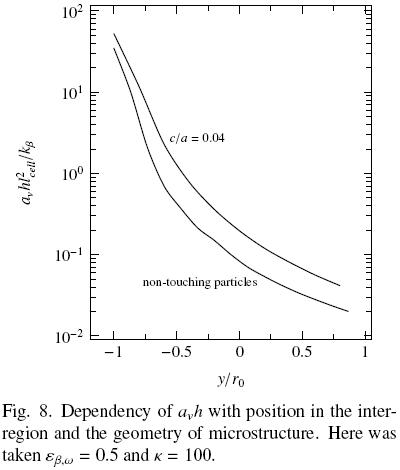
Finally, in Fig. 8 we show the spatial evolution of avh. In this case the tendency with and without particle–particle contact are similar. Nevertheless, as showed in Fig. 6, the interconnection between particles causes larger values of avh (in comparison with non–touching particles) in the porous bulk and this trend continues through the inter–region. Notice that results present maximum values in the porous bulk and rapidly decrease to 0 in the fluid region. This is consistent with the physics at the microscale since eventually the solid volume fraction decreases, and therefore, also the heat exchanged between phases.
4.3 Comparison between predictions of the average temperature
In order to exemplify the error that one can make when the particle–particle contact is not taken into account, in this section we present comparisons between numerical steady–state solutions of the equilibrium model [Eq. (5)] using different types of interconnection. Thus, we define a purely conductive heat transport problem taking place in the one–dimensional domain –yω < y < + yn. Here y is the coordinate normal to the macroscopic boundary dividing the porous domain from the fluid region; yη and yω are the size of the fluid region and the porous medium, respectively. We assume that the free fluid–porous boundary is located at y = 0 and the limit of the porous medium at y = –yω, hence, the fluid region encompasses the positive side of the domain, i.e., 0 < y < + yη. It is important to mention that despite the fact we specify the location of the virtual boundary separating the homogeneous regions, we do not need to specify boundary conditions there, as we are using the one–domain approach with position–dependent effective conductivity.
Now, we define the Dirichlet–type conditions at the boundaries of the domain,
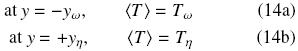
In this way, introducing the non–dimensional temperature
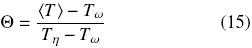
the solution field is bounded by 0 < Θ < 1. In addition, the dimensionless length

is used in the analysis and, therefore, the inter–region is given by –1 < ŷ < +1
In Table 1 we present the percentage of error
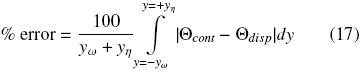
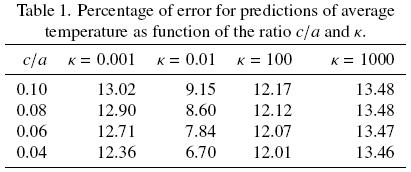
for several values of the ratio c/a and k keeping fixed εβ,ω = 0.5 and yω = yη = 20r0. In Eq. (17) the subscript cont refers to the field solution when the solid is a continua phase (periodic array 1 in Fig. 2) and disp when the solid is a dispersed phase (periodic array 2). As expected, the larger error (around 13.0–13.5) is observed as long as the ratio of connectivity increases and the thermal conductivities between phases differ significantly, i.e., k 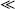 1 or
1 or 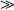 1. Notice that the largest error occurs when the solid is more conductive than the fluid phase.
1. Notice that the largest error occurs when the solid is more conductive than the fluid phase.
The numerical results given in Table 1 quantitatively illustrate the possible source of error if the microstructure of a specific heat transport problem is not taken into account for prediction of the effective coefficients. Undoubtedly, in order to gain precision in modeling some particular problem, the previous knowledge of the spatial distribution of phases is conveniently required, specially in cases where physical properties of materials, as the thermal conductivity, are clearly different.
Conclusions
In this work, we analyze the role played by the particle–particle contact over the effective coefficients appearing in upscaled thermal equations under conductive conditions. Particularly, models with and without local thermal equilibrium assumptions, and in the context of the one–domain approach for heat transport in the porous–fluid inter–region, were considered. The contact between solid particles was modeled through interconnection arms, and therefore, the fluid phase was considered as dispersed. In cases when the solid is more conductive than the fluid, the particle–particle contact favors effective parameters related to the solid–phase; whereas when the fluid is more conductive, minimizing contact between particles favors the effective parameters related to the fluid–phase. In general, it was found that the existence of contact between particles give rises larger values, compared to the case when there is no contact, for the effective thermal conductivity and the interstitial heat transfer coefficient. This could be a serious source of error in modeling, specially when the porous medium is composed with a highly (or poorly) conductive solid in comparison with the fluid. The results of this work provide the background for further derivations of closed jump boundary conditions in the two–domain approach in systems with dispersed phases.

References
Aguilar–Madera, C.G. (2011). Heat transfer between a porous medium and a fluid (in spanish). Doctoral dissertation, Universidad Autónoma Metropolitana– Iztapalapa, Mexico. [ Links ]
Aguilar–Madera, C.G., Valdes–Parada, F.J., Goyeau, B. and Ochoa–Tapia, J.A. (2011). One–domain approach for heat transfer between a porous medium and a fluid. International Journal of Heat and Mass Transfer 54, 2089–2099. [ Links ]
Alazmi, B. and Vafai, K. (2001). Analysis of fluid flow and heat transfer interfacial conditions between a porous medium and a fluid layer. International Journal ofHeat and Mass Transfer 44, 1735–1749. [ Links ]
Alkam, M.K., Al–Nimr, M.A. and Hamdan, M.O. (2001). Enhancing heat transfer in parallel–plate channels by using porous inserts. International Journal of Heat and Mass Transfer 44, 931–938. [ Links ]
Batchelor, G.K. and O'Brien, R.W. (1977). Thermal or electrical conduction through a granular material. Proceedings of the Royal Society A 355, 313–333. [ Links ]
Carrera–Rodrííguez, M., Martíínez–Gonzaílez, G.M., Navarrete–Bolanos, J.L., Botello–Alvarez, E., Rico–Martínez, R. and Jimenez–Islas, H. (2009). Numerical study of the effect of the environmental temperature in natural two–dimensional convection of heat in grain stored at cylindrical silos. Revista Mexicana de Ingeniería Química 8(1), 77–91. [ Links ]
Chang, H.C. (1982). Multi–scale analysis of effective transport in periodic heterogeneous media. Chemical Engineering Communications 15, 83–91. [ Links ]
Chen, X. and Sutton, W.H. (2005). Enhancement of heat transfer: Combined convection and radiation in the entrance region of circular ducts with porous inserts. International Journal of Heat and Mass Transfer 48, 5460–5474. [ Links ]
Cho, H.H. and Eckert, E.R.G. (1994). Transition from transpiration to film cooling. International Journal of Heat and Mass Transfer 37, 3–8. [ Links ]
Goyeau, B., Lhuillier, D., Gobin, D. and Velarde, M. (2003). Momentum transport at a fluid–porous interface. International Journal ofHeat and Mass Transfer 46, 4071–4081. [ Links ]
Jamet, D. and Chandesris, M. (2009). On the intrinsic nature of jump coefficients at the interface between a porous medium and a free fluid region. International Journal of Heat and Mass Transfer 52, 289–300. [ Links ]
Jimenez–Islas, H., Navarrete–Bolanos, J.L. and Botello–Álvarez, E. (2004). Numerical study of the natural convection of heat and 2–D mass of grain stored in cylindrical silos. Agrociencia 38(3), 325–342. [ Links ]
Khaled, A.R.A. and Vafai, K. (2003). The role of porous media in modeling flow and heat transfer in biological tissues. International Journal of Heat and Mass Transfer 46, 4989–5003. [ Links ]
Maxwell, J.C. (1873). A treatise on electricity and magnetism (1st ed., Vol. 1). Londres: MacMillan and Co. [ Links ]
Nozad, I., Carbonell, R.G. and Whitaker, S. (1985). Heat conduction in multiphase systems–I: Theory and experiment for two–phase systems. Chemical Engineering Science 40(5), 843–855. [ Links ]
Ochoa–Tapia, J.A., Stroeve, P. and Whitaker, S. (1994). Diffusive transport in two–phase media: Spatially periodic models and Maxwell's theory for isotropic and anisotropic systems. Chemical Engineering Science 49, 709–726. [ Links ]
Ochoa–Tapia, J.A. and Whitaker, S. (1997). Heat transfer at the boundary between a porous medium and a homogeneous fluid. International Journal of Heat and Mass Transfer 40(11), 2691–2707. [ Links ]
Ochoa–Tapia, J.A. and Whitaker, S. (1998). Heat transfer at the boundary between a porous medium and a homogeneous fluid: The one–equation model. Journal of Porous Media 1(1), 31–46. [ Links ]
Pereira–Duarte, S.I., Ferretti, O.A. and Lemcoff, N.O. (1984). A heterogeneous one–dimensional model for non–adiabatic fixed bed catalytic reactors. Chemical Engineering Science 39(6), 1025–1031. [ Links ]
Prat, M. (1989). On the boundary conditions at the microscopic level. Transport in Porous Media 4, 259–280. [ Links ]
Quintard, M., Kaviany, M. and Whitaker, S. (1997). Two–medium treatment of heat transfer in porous media: Numerical results for effective properties. Advances in Water Resources 20, 77–94. [ Links ]
Quintard, M. and Whitaker, S. (1993). One–and two–equation models for transient diffusion processes in two–phase systems. Advances in Heat Transfer 23, 369–464. [ Links ]
Quintard, M. and Whitaker, S. (1995). Local thermal equilibrium for transient heat conduction: Theory and comparison with numerical experiments. International Journal ofHeat and Mass Transfer 38(15), 2779–2796. [ Links ]
Ryan, D., Carbonell, R.G. and Whitaker, S. (1980). Effective diffusivities for catalyst pellets under reactive conditions. Chemical Engineering Science 35, 10–16. [ Links ]
Sahraoui, M. and Kaviany, M. (1993). Slip and no–slip temperature boundary conditions at the interface of porous plain media: Conduction. International Journal of Heat and Mass Transfer 36, 1019–1033. [ Links ]
Sahraoui, M. and Kaviany, M. (1994). Slip and no–slip temperature boundary conditions at the interface of porous plain media: Convection. International Journal of Heat and Mass Transfer 37, 1029–1044. [ Links ]
Vafai, K. (2000). Handbook ofporous media (1st ed.). New York: Marcel Dekker, Inc. [ Links ]
Valdes–Parada, F.J., Alvarez–Ramirez, J., Goyeau, B. and Ochoa–Tapia, J.A. (2009). Computation of jump coefficients for momentum transfer between a porous medium and a fluid using a closed generalized transfer equation. Transport in Porous Media 78, 439–457. [ Links ]
Valdes–Parada, F.J., Ochoa–Tapia, J.A. and Ramirez, J. Alvarez. (2007). Diffusive mass transport in the fluid–porous medium inter–region: Closure problem solution for the one domain approach. Chemical Engineering Science 62, 6054–6068. [ Links ]
Veran, S., Aspa, Y. and Quintard, M. (2009). Effective boundary conditions for rough reactive walls in laminar boundary layers. International Journal ofHeat and Mass Transfer 52, 3712–3725. [ Links ]
Whitaker, S. (1999). The method of volume averaging. Netherlands: Kluwer Academic Publishers. [ Links ]
Wood, B.D. (2007). Inertial effects in dispersion in porous media. Water Resources Research 43, W12S16, doi: 10.1029/2006WR005790. [ Links ]
Yang, C. and Nakayama, A. (2010). A synthesis of tortuosity and dispersion in effective thermal conductivity of porous media. International Journal of Heat and Mass Transfer 53, 3222–3230. [ Links ]














