Fenómenos de transporte

 

Formulaciones integrales para ecuaciones reacción–difusión generalizadas

 

Integral formulations for generalized reaction–diffusion equations

 

E. Hernández–Martínez*, F.J. Valdés–Parada y J. Alvarez–Ramírez

 

Universidad Autónoma Metropolitana–Iztapalapa. Departamento de Ingeniería de Procesos e Hidráulica. Av. San Rafael Atlixco 186. Col. Vicentina 09340. Iztapalapa, D.F. *Autor para la correspondencia. E–mail: cbi206380874@xanum.uam.mx Tel. 52–55–58044650, Fax 52–55–58044900

 

Recibido 10 de Enero 2011.
Aceptado 5 de Agosto 2011.

 

Resumen

Las formulaciones integrales son metodologías que consisten en transformar los operadores diferenciales a operadores integrales incorporando de manera exacta las condiciones de frontera. Este trabajo se extiende el uso de formulaciones de ecuaciones integrales (FEI) para el desarrollo de esquemas numéricos para sistemas generales tapo reacción–difusión. Debido a la propiedad de incorporación exacta de las condiciones de frontera, los esquemas numéricos resultantes no requieren de aproximaciones en las fronteras, lo que conduce a esquemas numéricos con ordenes globales de aproximación de O(h²). Las FEI se caracterizan por su metodología sistemática y su estructura matemática que permite la fácil interpretación física de los procesos involucrados en los sistemas reacción–difusión. Para evaluar la capacidad de aproximación numérica del esquema propuesto se consideraron diferentes condiciones que surgen en el estudio de las pastillas catalíticas. Las simulaciones numéricas realizadas muestran que las FEI exhiben mejores aproximaciones numéricas que los esquemas clásicos de diferencias finitas (DF).

Palabras clave: sistema reacción–transporte, función de Green, solución numérica.

 

Abstract

Integral equation formulations are methodologies that consists on transforming the differential operators into integral operators exactly incorporating the boundary conditions. This work extends the use of integral equations formulations (IEF) for the development of numerical schemes for generalized reaction–diffusion systems. Due to the property of exact incorporation of the boundary conditions, the numerical schemes resulting do not require approximations at the boundaries, which leads to numerical schemes with global orders approximation O(h²). IEF schemes are characterized by their systematic methodology and its their mathematical structure that allows easy physical interpretation of the processes involved in the reaction–diffusion systems. To evaluate the ability of numerical approximation of the proposed scheme different conditions that arise in the study of catalytic pellets were considered. The numerical simulations carried out show that the IEF exhibit better numerical approximations than classic finite differences schemes (FD).

Keywords: reaction–transport system, Green's function, numerical solution.

 

1 Introducción

En este trabajo, se consideran ecuaciones diferenciales parciales (EDP) de reacción–difusión (RD) como

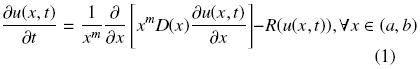
con condiciones de frontera du (a, t)

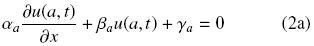
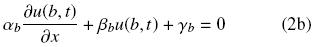
y condición inicial

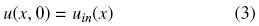
donde α_i, β_i, γ_i, i = a, b son constantes, R(u(x, t)) describe la reacción química, D(x) es el coeficiente de difusión como función de la posición y el parámetro m índica el sistema coordenado (e.g., m = 0 para coordenadas rectangulares, m = 1 para cilíndricas y m = 2 para esféricas). La Ec. (1) puede representar las interacciones reacción–transporte en una pastilla catalítica (Aris, 1975). Para el estudio de pastillas catalíticas el parámetro m no está restringido a valores enteros. Valores fraccionales de m pueden modelar el comportamiento de pastillas catalíticas con formas irregulares (Burghardt & Kubaczka, 1996; Papadias y col., 2000). Por otro lado, las condiciones de frontera (2a) y (2b) pueden simplificarse para describir los fenómenos físicos que se llevan a cabo en la frontera de las pastillas catalíticas. Por ejemplo, en x = α condición de simetría y en x = b resistencia al transporte externo. Típicamente en el estudio de las interacciones entre el transporte difusivo con las reacciones químicas, los parámetros del sistema son considerados contantes. Sin embargo, estudios teóricos y experimentales muestran que el coeficiente de difusión puede ser función de la concentración, temperatura y/o posición. Por ejemplo, Barrer (1945) presentó una metodología para el cálculo del coeficiente de difusión (másico y terrífico) como una función de la concentración y de la posición. Sus resultados mostraron que cuando el coeficiente es no homogéneo es posible reproducir con mayor precisión los resultados experimentales. Los mecanismos de reacción–difusión con formación de patrones surgen en ambientes espacialmente heterogéneos (Page y col., 2005). Algunos estudios han demostrado que los coeficientes de difusión variables son un importante regulador de patrones tanto biológicos (Schnackenberg, 1979; Othmer and Pate, 1980; Maini y col., 1992) como en interacciones ecológicas (Segel and Jackson, 1972; Benson y col., 1992). Por otro lado, en procesos químicos, tales como en sistemas fluidos en medios porosos los coeficientes de difusión variable son empleados para descripción más exacta de los fenómenos de transporte en las zonas de cambio rápido (Valdes–Parada y col., 2007b).

La gran mayoría de los sistemas RD con aplicación práctica en ingeniería están descritos mediante EDP no lineales. Para dichos sistemas, generalmente no se cuentan con soluciones analíticas por lo que es necesario el uso de aproximaciones numéricas. Las FEI son metodologías que consisten en transformación de los operadores diferenciales a operadores integrales incorporando de manera exacta las condiciones de frontera, conduciendo a la disminución de los errores de aproximación debido a las derivadas numéricas en todo el dominio. Esta metodología ha sido aplicada en la solución de EDP en diferentes campos de la ingeniería, tales como, en la física y mecánica cuántica (Kadanoff y Baym, 1962), ciencia de los materiales (Pan, 1997; Wapenaar, 2004), electromagnetismo (Duffin y Mcwhirter, 1974), electrónica (Janicki, 2002), entre otros. A diferencia de los métodos clásicos de discretización, la literatura reportada sobre el uso de las FEI aplicadas a problemas donde intervienen interacciones reacción–transporte, es escasa. Sin embargo, se ha demostrado que las formulaciones integrales son una alternativa de aproximación numérica que proveen ventajas sobre los métodos clásicos de discretización (e.g., Kesten, 1969; Dixit y Tavlarides, 1982; Onyejekwe, 2002; Valdes–Parada y col., 2007a; 2008; Mansur y col., 2009; Valdes–Parada, 2010).

El propósito de este trabajo es demostrar que las formulaciones integrales están basadas en metodologías sistemáticas y se pueden extender fácilmente a una gran cantidad de procesos en ingeniería química. Para ello hacemos uso de la fórmula de Green, que permite hacer la inversión analítica del operador diferencial a un operador integral. Para la solución de la ecuación integral resultante es necesario el cálculo de la función de Green correspondiente. Para ilustrar la habilidad sistemática del método se abordaron diferentes problemas de reacción–difusión, tales como, sistemas reacción–difusión involucrando el coeficiente de difusión variable, condiciones de frontera generales y diferentes geometrías. Los resultados obtenidos se compararon con esquemas de diferencias finitas tradicionales.

El trabajo está organizado de la siguiente manera: en la siguiente Sección se describe el desarrollo de las formulaciones integrales a partir de EDP tipo reacción–difusión, posteriormente se calcula la función de Green general correspondiente. En la Sección 3 se presentan las metodologías numéricas para la aproximación de los perfiles u(x, t) en los sistemas RD (FEI y DF). En la Sección 4 se presentan las simulaciones numéricas de diversos sistemas RD que surgen en problemas en ingeniería química y finalmente en la Sección 5 se presentan las conclusiones del trabajo.

 

2 FEI para sistemas reacción–difusión

Si en la Ec. (1) definimos a Lu(x, t) = 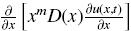como el operador diferencial espacial. Entonces, Lu(x, t) describe los procesos de transporte y R(x, u(x, t)) describe la reacción química. Una condición importante para el desarrollo exitoso de la formulación integral es que el operador diferencial L sea un operador auto adjunto. En el caso que el operador no sea auto adjunto, existen metodologías para transformar dichos operadores en auto adjuntos (Greenberg, 1971). Por conveniencia en el desarrollo, re–escribimos a la Ec. (1) como

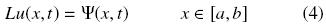
donde 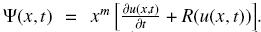. Ahora, se multiplica a la Ec. (4) por la función G(z, x) e integramos por partes, así

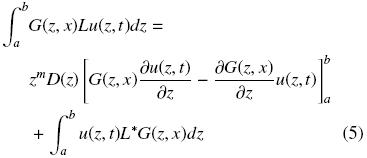
La Ec. (5) es conocida como la forma integral de la identidad de Lagrange o la formula de Green, donde L^* es el operador diferencial adjunto asociado con L. De acuerdo a la Ec. (4), la Ec. (5) se puede escribir como

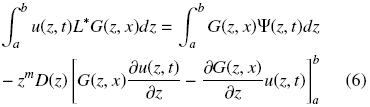
Nótese que la Ec. (6) ahora solo depende de G(z, x). La función G(z, x) es llamada la función de Green y satisface el problema de valor a la frontera original reemplazando el término fuente por la función delta de Dirac (δ(z – x)) y tomando las condiciones de frontera en su forma homogénea, tal que

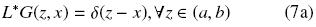
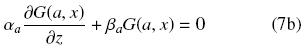
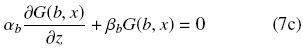
La función de Green describe la solución del problema de valor a la frontera a través una fuente localizada en x = z. En ese sentido, la solución del problema original con fuente Ψ(x, t) está dada por la respuesta impulso G(z, x). Sustituyendo la Ec. (7a) en la Ec. (6), obtenemos

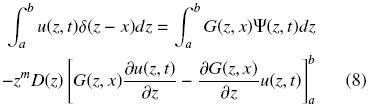
Haciendo uso de la propiedad de filtración de la función delta de Dirac, 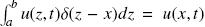(Greenberg, 1971; Haberman, 2004), tenemos que la Ec. (6) se reduce a

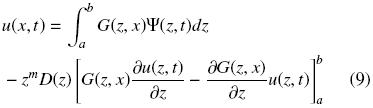
Evaluando las condiciones de frontera dadas en las Ecs. (2a)–(2b) y (7b)–(7c) en la Ec. (9), se obtiene la siguiente expresión

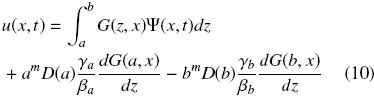
o bien

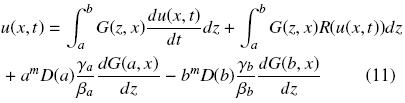
A diferencia de los métodos tradicionales para la solución numérica de problemas de valor a la frontera (e.g., diferencias finitas, colocación ortogonal), las formulaciones integrales basadas en funciones de Green proveen una interpretación acerca de cómo se llevan a cabo los procesos de transporte y reacción. Siguiendo el desarrollo presentado arriba, podemos identificar lo siguiente:

• En el problema de valor a la frontera original, el transporte difusivo es descrito por el operador diferencial. Mientras que en las formulaciones de ecuaciones integrales los fenómenos de transporte son descritos a través de la función de Green.

• La formulación integral permite identificar que el perfil u(x, t) se compone de la interacción de los fenómenos involucrados (transporte y reacción).

• El primer término del lado derecho de la Ec. (11) es la memoria del sistema e indica como cambia el perfil de concentración a través del tiempo, los cambios temporales son distribuidos en el espacio mediante la función de Green. Si = 0, el campo no depende del tiempo, es decir, describe el perfil en estado estacionario de la Ec. (4).

• La segunda integral denota como la función de Green (fenómenos de transporte) distribuye el término fuente (reacción) a través de todo el dominio.

• El tercer termino describe la influencia de los terminos no homogéneos en las fronteras.

2.1 funciones de Green para sistemas reacción–difusión

Algunos métodos han sido reportados para calcular la función de Green G(z, x), tales como variación de parámetros y expansión en funciones propias (Greenberg, 1971; Haberman, 2004). En este trabajo, se usa el método de la función delta de Dirac para calcular la función de Green, G(z, x). Considerando las Ecs. (7a)–(7c), tenemos que

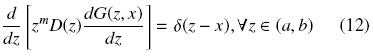
con sus correspondientes condiciones de frontera. Teniendo en cuenta que

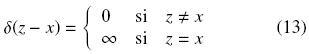
e integrando dos veces la Ec. (12), obtenemos a G(z, x) como

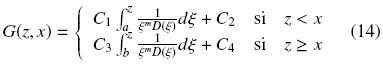
Evaluando las condiciones de frontera (7b) y (7c) en la Ec. (14) obtenemos

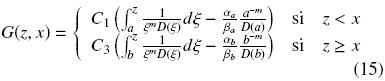
Para obtener los parámetros C₁ y C₃, necesitamos imponer dos condiciones adicionales. La primera condición surge del hecho que el campo de concentraciones es continuo en z = x, entonces

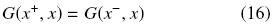
La segunda condición resulta de integrarla Ec. (12) en los límites z = x^– y z = x⁺ para dar

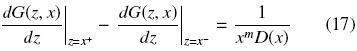
Después de evaluar la Ec. (15) en las Ecs. (16) y (17) se obtiene

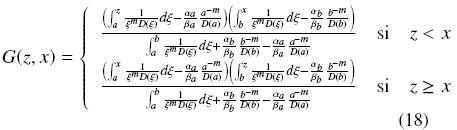
La Ec. (18) es la función de Green correspondiente al problema reacción–difusión dado por la Ec. (1). La expresión analítica completa de la función de Green depende directamente de la función para el coeficiente de difusión. Si D(x) es una función compleja y no es posible obtener la solución exacta de las integrales en la Ec. (18), podemos aproximar la función de Green mediante métodos de cuadratura. Por otro lado, en procesos donde el coeficiente de difusión es constante, no es difícil demostrar que la función de Green para dichos procesos es: para m ≠ 1

y para m = 1

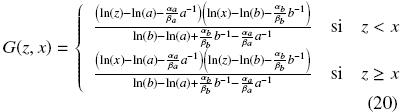
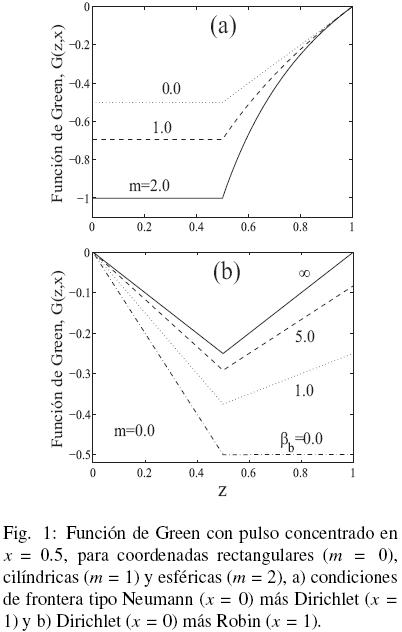
Considerando la Ec. (19) con a = 0 y b = 1.0, la Fig. 1 muestra los efectos tanto de la geometría como de las condiciones de frontera sobre la distribución de la función de Green. Para condiciones de frontera tipo Dirichlet (α_a = α_b = 0 y β_a = β_b = 1), el valor de la función de Green se hace cero en las fronteras, esto es debido a que para condiciones de frontera Dirichlet los valores en las fronteras están fijos. Mientras que para condiciones de frontera Neumann y Robin (α_a = α_b = 1 y β_a = 0) la función de Green no desaparece en las fronteras, en el caso de condiciones tipo Robin la tendencia de la función de Green va a depender del parámetro β_b. Si β_b 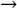0, la condición de frontera tiende a ser de tipo Neumann y si β_b ∞ tiende a ser de tipo Dirichlet.

 

3 Esquemas numéricos

La formulación integral del sistema reacción–difusión generalizado dado por las Ecs. (1)–(3) está descrito por las Ecs. (11) y (18), donde las integrales son función de u(x, t), por lo que no es posible obtener una solución analítica explícita. Esto hace necesario el uso de metodologías numéricas. En ésta sección se presentan los esquemas numéricos generales para solución del sistema (1)–(3) mediante el esquema propuesto y mediante el esquema de DF.

3.1 ecuaciones integrales

Si consideramos un tamaño de malla equidistante, h = (b – a)/(N + 1), con x_i = a + ih y u_i(t) = u(x_i, t) para i = 1,2,..., N. Entonces, podemos re–escribir la Ec. (11) como

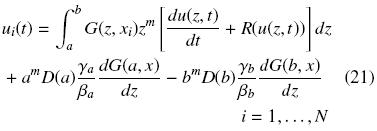
Nótese que, los nodos de la frontera x₀ y x_N+1 no son considerados en la Ec. (21), esto es porque la metodología incorpora exactamente las condiciones de frontera. La discretización de la ecuación integral puede ser estimada mediante aproximaciones numéricas. Por ejemplo, usando la regla del trapecio para aproximar la integral, se obtiene el siguiente sistema de ecuaciones

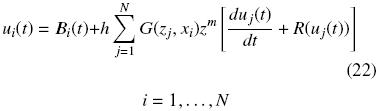
donde

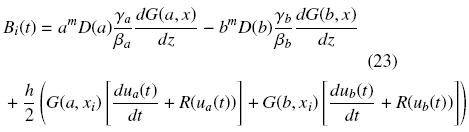
Si u(t)=(u₁,...,u_N)^t, B(t)=(B1(t),...,B_N(t))^T y R(u(t))=(R(u₁(t)),...,R(u_N(t))^T. Entonces, la Ec. (22) se puede escribir como

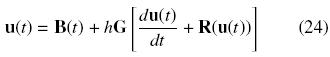
donde G es la matriz de NxN con componentes g_i,,j = z^mG(x_j, x_i), i, j = 1,..., N. Por lo tanto, el conjunto de N ecuaciones de valor a la frontera está dado por

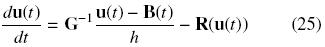
La solución del sistema de ecuaciones diferenciales (EDO) puede llevarse a cabo mediante métodos numéricos, tales como los métodos de Runge–Kutta. Una alternativa es hacer una discretización total que incluya la derivada temporal. En ese sentido, definimos δ = Δt como el paso de integración, t_k = t₀ + kδ y u_i^k = u_i(t_k). Para la derivada temporal en la Ec. (25) se propone un esquema de Euler implícito, esto es, 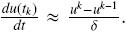Esto conduce a la siguiente ecuación

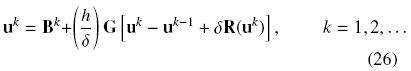
La Ec. (26) es un sistema de ecuaciones algebraicas no lineales (EAN), el cual para cada tiempo t^k puede ser resuelto usando métodos iterativos (e.g. Newton Raphson, punto fijo). La ventaja del esquema dado en la Ec. (26) sobre el esquema de la Ec. (25) es que no se requiere la inversión de la matriz G.

3.2 Diferencias finitas

Considerando una malla regular X_N+2 = x₀, x₁, x₂,...,x_N, x_N+1 de tamaño N en el dominio Ω = [a,b], donde x_i = ih, i = 0,..., N + 1, y h = (b – a)/(N + 1). Por conveniencia, definimos y(x, t) = P(x)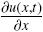y u_i = u(x_i, t). Entonces, la Ec. (4) es

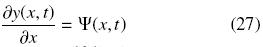
si en la derivada espacial usamos un esquema de diferencias finitas centrales en los puntos i ± 1/2, obtenemos para el nodo x_i

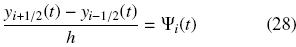
donde Ψ_i(t) = Ψ(x_i, t) y Ψ(x_i, t) y = y_i(t). Si D_i = D(x_i) y sustituimos a y_i en la Ec. (28), tenemos

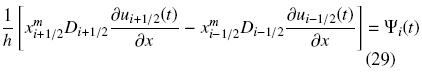
Ahora usando el esquema de diferencias finitas centrales en las derivadas, tenemos

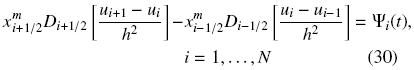
o bien

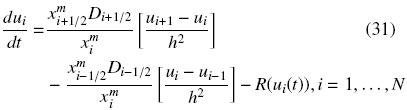
Como las Ecs. (25), las Ecs. (31) constituyen un conjunto de N EDO que puede ser resuelto numéricamente mediante métodos estándar de Runge–Kutta o bien se puede hacer la discretización de la derivada temporal y resolver un conjunto de EAN. Por ejemplo, si empleamos un esquema implícito en 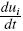, tenemos

donde h_t es el tamaño del paso de integración, t^k = t₀ + kh_t y u_i^k = u_i (t_k). Para incorporar las condiciones de frontera (2a) y (2b) es necesario aproximarlas. Tradicionalmente la aproximación de las derivadas en las condiciones de frontera se hace mediante diferencias hacia atrás o hacia adelante (primer orden), ya que las diferencias centradas introducen un nodo ficticio a una distancia h antes y/o Después del dominio en cuestión (en este caso en a – h ó b + h) y en muchos casos los nodos artificiales pueden no ajustarse a las situaciones físicas del problema. Una alternativa para la obtención de esquemas de DF con ordenes de aproximación globales de h² es el uso de diferencias hacia atrás o hacia adelante de segundo orden. Dicha discretización puede ser obtenida mediante series de Taylor e incluso pueden ser obtenidos en forma natural a partir de formulaciones integrales (Hernandez–Martinez y col., 2011).

 

4 Resultados numéricos

Para evaluar la capacidad de aproximación numérica de las FEI para sistemas reacción–difusión, se resolvieron diversos problemas típicos que surgen en el análisis de pastillas catalíticas. Los resultados numéricos son comparados con esquemas clásicos de diferencias finitas (con aproximación de las derivadas en las condiciones de frontera mediante diferencias de orden h y h²) y con las soluciones analíticas. En los casos donde no se dispone de la solución analítica, los resultados se compararon con los obtenidos mediante Comsol Multiphysics 3.5a usando 2000 nodos en la malla computacional. Como un índice del error de aproximación numérica se considero el error cuadrático medio, el cual está definido como

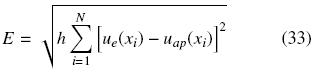
donde u_ap(x_i) es la aproximación del perfil de concentración y u_e(x_i) es el perfil de concentración exacto o calculado mediante diferencias finitas usando 2000 nodos. Considerando el modelo de la pastilla catalítica (1) normalizado en x 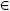[0, 1], con las siguientes condiciones de frontera

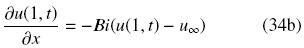
y con condición inicial

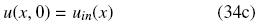
En x = 0 la condición de frontera indica simetría, mientras que en x = 1 indica que existe resistencia al transporte de masa en la superficie de la pastilla catalítica. Bi es el numero de Biot y relaciona el transporte externo entre el transporte interno y u_∞ = 1.0 es la concentración normalizada en la fase fluida externa.

4.1 Caso 1: Coeficiente de difusión constante

Considerando la Ec. (1) en estado estacionario, es decir con 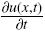= 0 y con una velocidad de reacción de primer orden, R(u(x)) = 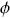²u(x), donde 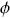es el módulo de Thiele, que relaciona la reacción química y la difusión interna. Para m = 0, m = 2 y Bi = 1.0, la Fig. 2 muestra la comparación del error cuadrático medio E, obtenido mediante los esquemas de DF y la formulación integral para dos valores del modulo de Thiele ( 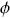= 0.5 y 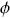= 5.0).

Es posible observar, que en el esquema de DF, la incorporación de las condiciones de frontera discretas mediante diferencias de primer orden reduce el orden global del método. Por otro lado, si las condiciones de frontera son aproximadas mediante diferencias de segundo orden, el esquema de DF conserva un orden global de 2. Sin embargo, la formulación integral exhibe mejor desempeño numérico que los esquemas de DF. Es importante resaltar que los errores de aproximación para las FEI incrementan cuando el proceso es controlado por la transferencia de masa, es decir cuando 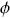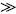1. Debido a que la formulación integral se basa en la inversión analítica del operador diferencial, el desempeño numórico de FEI es mayor cuando el transporte difusivo domina sobre los mecanismos de reacción (Valdés–Parada y col., 2007a; 2008).

Para evaluar el desempeño del esquema propuesto para valores fraccionales de m, se considera una velocidad de reacción tipo Langmuir–Hinshelwood,

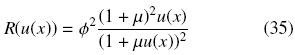
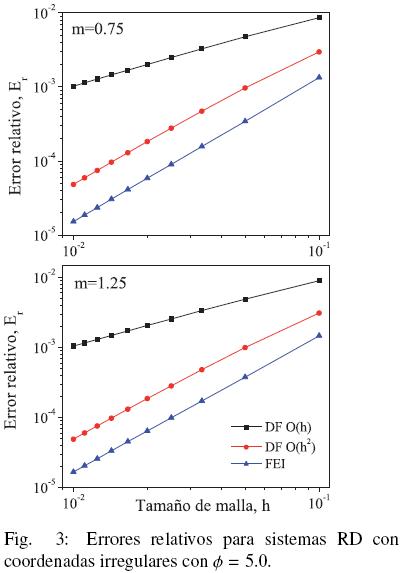
Para μ = 0.5 y 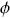= 5.0, la Fig. 3 muestra los errores relativos a diferentes valores de m, donde se observa que para cualquier valor de m el método integral preserva ordenes de aproximación de O(h²) mientras que DF se mantiene con ordenes de aproximación de O(h) y O(h²), respectivamente.

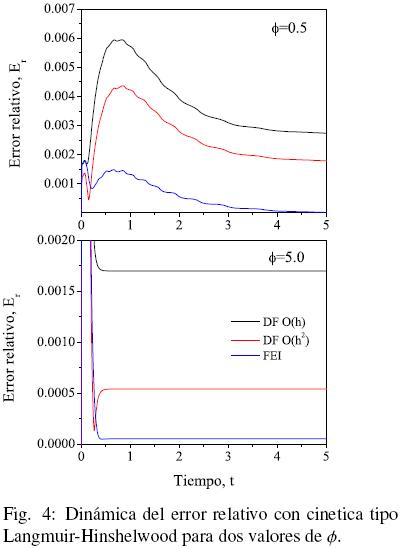
El caso dinámico se analiza para la Ec. (1) con u(x, 0) = 0.5, m = 1.0 y bajo las mismas condiciones que el caso anterior. En este caso el error relativo se calcula con la Ec. (33) en intervalos de tiempo de Δt = 0.01. Empleando los esquemas dados en las Ecs. (26) y (32) para FEI y DF, respectivamente y usando 50 nodos, la Fig. 4 muestra la dinámica del error de aproximación hasta t = 5.0, donde se observa lo siguiente: (i) el error relativo muestra una dinámica que corresponde al estado transitorio de la pastilla catalítica en estudio. Por ejemplo, cuando 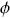= 5.0 el procesos llega súbitamente al estado estacionario, ya que la los fenómenos difusivos dominan el proceso, es decir, la reacción química es muy rápida con respecto a la difusión. Mientras que, cuando 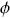= 0.5 el proceso llega al estado estacionario a t > 5, en este caso la reacción es la que domina el proceso global. (ii) Como era de esperarse, los errores relativos obtenidos con FEI son menores que los obtenidos mediante DF, particularmente son mas pequeños cuando 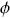> 1a cualquier tiempo.

4.2 Caso 2: Coeficiente de difusión variable

En este caso iniciamos el análisis en estado estacionario y consideramos un coeficiente de difusión como una función lineal D(x) = D₀(1 + δx) con D₀ = 0.3 y δ = 5/6 (Barrer, 1945) y con la siguiente velocidad de reacción no isotérmica (Aris, 1975),

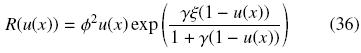
Para ξ = 20.0 y γ = 0.2, la Fig. 5 muestra el efecto de la resistencia al transporte externo sobre el desempeño de los esquemas numéricos. Considerando m = 0 y m = 1.0, el esquema integral exhibe menores errores de aproximación numérica que los esquemas de DF. Es importante resaltar que el E obtenido mediante DF disminuye cuando Bi 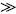1. Esto es debido a que la condición de frontera en x = 1 depende de valor del Bi, si Bi 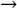0 la condición de frontera tiende a tipo Neumann y cuando Bi 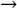∞ tiende a tipo Dirichlet. El esquema de DF incorpora las condiciones de frontera tipo Neumann y Robin mediante la aproximación de la derivada, mientras que las condiciones tipo Dirichlet se incorporan directamente. Para el caso dinámico, sustituimos el coeficiente de difusión por la función no lineal reportada en Maini y col. (1992),

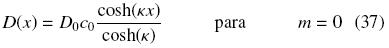
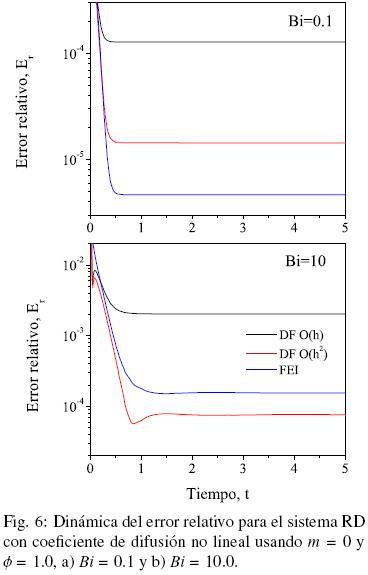
Para los experimentos numéricos, se consideró = 50, Δt = 0.01, u(x, 0) = 0.5, m = 0 y las Ecs. (36) y (37) con D₀ = 1.0, κ = 3.4008 y c₀ = 15.0 (Maini y col., 1992). En la Fig. 6 se muestra el efecto de Bi en las dinámicas del error de aproximación numérica, donde se observa, como en el caso anterior, que las mejores aproximaciones numéricas son cuando Bi 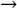0. Aunque para valores de Bi 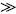1, el esquema de DF errores de aproximación numérica ligeramente menores que FEI, en general, los resultados numéricos muestran que las formulaciones integrales son una buena alternativa para la solución numérica de modelos reacción–difusión generales a diferentes condiciones (i.e., condiciones de frontera, geometrías irregulares, coeficiente de difusión anisotrópico, estado transitorio, etc.).

De acuerdo a los resultados descritos arriba, se hacen los siguientes comentarios: (i) en general, para sistemas reacción–difusión la formulación integral exhibe un O(h²) para cualquier valor de m, esto debido a la propiedad de incorporación exacta de las condiciones de frontera. Por otro lado, en diferencias finitas, el operador de difusión es aproximado mediante diferencias centrales con O(h²). Sin embargo, el orden global de aproximación del método depende del tipo de discretización de las condiciones de frontera. Por ejemplo, si se incorporan mediante diferencias de O(h), entonces el orden global del método disminuye. Los errores relativos para DF se aproximan a los calculados por FEI cuando 0 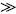1. Esto es, porque los mecanismos de reacción tienen mayor importancia en el proceso y la aproximación de la condición de frontera es incorporada en el operador de difusión discreto. (ii) Los esquemas basados en funciones de Green presentan mejor aproximación numérica cuando en los procesos los fenómenos de transporte tienen mayor importancia (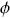 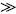1). Esto es debido a que la formulación integral se basa en la inversión analítica del operador diferencial, siendo la función de Green la encargada de representar la distribución de los fenómenos de transporte en todo el dominio. (iii) Los fenómenos de transporte externos afectan directamente al transporte difusivo interno, por lo tanto el desempeño numórico de las FEI también se ve afectado. A medida que la resistencia al transporte externo incrementa los errores relativos calculados también incrementan. Es decir, cuando el proceso es controlado por los fenómenos difusivos internos, las FEI exhiben mejor desempeño numérico. (iv) La fórmula de Green puede ser extendida a sistemas con más de una dimensión (i.e., 2D ) (Haberman, 2004). Por lo tanto, la metodología propuesta puede ser extendida a problemas bidimensionales.

 

Referencias

Aris, R. (1975). The mathematical theory of diffusion and reaction in permeable catalysts, Vol. I. Clanderdon Press, Oxford.         [ Links ]

Barrer, R.M. (1945). Measurement of diffusion and thermal conductivity constants in non–homogeneous media, and in media where these constants depend respectively on concentration or temperature. Proceedings of the Physics Society 58, 321–331.         [ Links ]

Benson, D. L., Sherratt, J. A. y Maini, P. K. (2008). Diffusion driven instability in an inhomogeneous domain. Bulletin of Mathematical Biology 1992, 55(2), 365–384.         [ Links ]

Burghardt, A. y Kubaczka, A. (1996). Generalization of the effectiveness factor for any shape of a catalyst pellet, Chemical Engineering Progress 35, 65–74.         [ Links ]

Dixit, R.S. y Tavlarides, L. (1982). Integral Method of analysis of Fischer–Tropsch synthesis reactions in a catalyst pellets. Chemical Engineering Science 37, 539–544        [ Links ]

Duffin, R.J. y Mcwhirter, J.H. (1974). An Integral Equation Formulation of Maxwell's Equations. J. of The Franklin Institute 298 (5), 385–394.         [ Links ]

Greenberg M. D. (1971). Applications of Green's Functions in Science and Engineering. Prentice Hall, New York        [ Links ]

Haberman, R. (2004). Applied Partials Derivatives Equations with Fourier series and boundary problems. New Jersey, Prentice Hall, USA        [ Links ]

Hernandez–Martinez, E., Valdes–Parada, F.J. y Alvarez–Ramírez, J. (2011). A Green's Function Formulation of Nonlocal Finite–Differences Schemes for reaction–Diffusion Equations. Journal of Computational and Applied Mathematics 235, 3096–3103.         [ Links ]

Janicki, M., De–Mey G. y Napieralski, A. (2002). Application of Green's functions for analysis of transient thermal states in electronic circuits.Microelectronics Journal 33, 733–738        [ Links ]

Kadanoff, L.P. y Baym G. (1962). Quantum statistical mechanics: Green's function methods in equilibrium and nonequilibrium problems. Benjamin, New York.         [ Links ]

Kesten, A.S. (1969). An integral equation method for evaluating the effects of film and pore diffusion of heat and mass on reaction rates in porous catalyst particles. AICHE Journal 15, 128–131        [ Links ]

Maini, P.K., Benson, D. L. y Sherratt, J. (1992). Pattern formation in reaction–diffusion models with spatially inhomogeneous diffusion coefficients. Journal of Mathematics Applied in Medicine and Biology 9, 197–213.         [ Links ]

Mansur W.J., Vasconcellos C.A., Zambrozuski N.J. y Rotunno O.C. (2009). Numerical solutions for linear transcient heat conduction equation using an explicit Green's approach. International Journal of Heat and Mass Transfer 52, 694–701.         [ Links ]

Onyejekwe, O. (2002). Green element solutions of nonlinear diffusion–reaction model. Computers and Chememical Engineering 26, 423–427.         [ Links ]

Othmer, H.G. y Pate, E. (1980). Scale–invariance in reaction–diffusion models of spatial pattern formation. Procedings of the National Academy of Sciences 77, 4180–4184.         [ Links ]

Page, K.M., Maini, P. y Monk A.M. (2005). Complex pattern formation in reaction diffusion systems with spatially varying parameters. Physica D 202, 95–115.         [ Links ]

Pan L. (1997). Boundary element strategies and discretized Green's functions: applications in composite materials and wave mechanics. phD thesis, Iowa, USA.         [ Links ]

Papadias, D., Edsberg, L. y Bjornbom, P. (2000). Simplified method of effectiveness factor calculations for irregular geometries of washcoats: A general casein a 3D concentration field. Catalyst Today 60, 11–20.         [ Links ]

Schnackenberg, J. (1979). Simple chemical reaction systems with limit cycle behaviour. Journal Theorical Biology 81, 389–400        [ Links ]

Segel, L.A. y Jackson, J.L. (1972). Dissipative structure: an explanation and an ecological example. Journal Theorical Biology 37, 545–559.         [ Links ]

Valdés–Parada, F.J., Alvarez–Ramírez, J. y Ochoa–Tapia, J.A (2007a). Analisis de problemas de transporte de masa y reacción mediante funciones de Green. Revista Mexicana de Ingenería Química 6(3), 283–294.         [ Links ]

Valdés–Parada, F.J., Ochoa–Tapia, J.A y Alvarez–Ramírez, J. (2007b). Diffusive mass transport in the fluid–porous medium inter–region: Closure problem solution for the one–domain approach. Chemical Engineering Science 62, 6054–6068.         [ Links ]

Valdés–Parada, F.J., Sales–Cruz, M., Ochoa–Tapia, J.A. y Alvarez–Ramírez, J. (2008). On Green's function methods to solve nonlinear reaction–diffusion systems. Computer and Chemical Engineering 32, 503–511.         [ Links ]

Valdés–Parada, F.J. (2010). Formulación integral para la solución de problemas de cerradura en procesos de escalamiento. Revista Mexicana de Ingenería Química 9(1), 53–66.         [ Links ]

Wapenaar, K. (2004). Retrieving the Elastodynamic Green's Function of an Arbitrary Inhomogeneous Medium by Cross Correlation. Physical Review Letters 93, 254–301.         [ Links ]