Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista mexicana de ingeniería química
versão impressa ISSN 1665-2738
Rev. Mex. Ing. Quím vol.10 no.1 Ciudad de México Abr. 2011
Simulación y control
Adaptive smooth observer design for state estimation in Desulfovibrio alaskensis 6SR cultures
Diseño de un observador suave adaptivo para estimación de estados en cultivos de Desulfovibrio alaskensis 6SR
M.I. Neria–González1, J.C. Figueroa–Estrada1, M.R. Cruz–Diaz1 and R. Aguilar–López2*
1 División de Ingeniería Química y Bioquímica, Tecnológico de Estudios Superiores de Ecatepec. Av. Tecnológico S/N. CP 55120, Ecatepec, Edo. de México, México.
2 Departamento de Biotecnología y Bioingeniería, CINVESTAV–IPN Av. Instituto Politécnico Nacional, No. 2508, San Pedro Zacatenco, D.F. México. *Autor para la correspondencia. E–mail: raguilar@cinvestav.mx
Received 9 of September 2010.
Accepted 2 of January 2011.
Abstract
In this work the dynamics of a sulfate reducing bacteria is predicted by estimating the biomass concentration and sulfide production using only sulfate (substrate) concentration measurements. The estimation process is developed on batch, fed–batch and continuous cultures of Desulfovibrio alaskensis 6SR, where a mathematical dynamic model of the bioreactor is presented and tuned with experimental data. The design of the adaptive smooth state observer takes into account the model's system structure and an adaptive gain of the output feedback which contain a hyperbolic tangent of the estimation error, an theoretical frame is provide in order to show the convergence characteristics of the proposed method. The results of the proposed estimation methodology are generated via numerical simulation in order to show its performance.
Keywords: bounded error observer, hyperbolic tangent feedback, adaptive observer gain, bioreactor model, Desulfovibrio alaskensis 6SR.
Resumen
En este trabajo la dinámica de una bacteria sulfato reductora es predicha vía estimación de la concentración de la biomasa y la producción de sulfuro usando únicamente mediciones de la concentración de sulfato (sustrato). El proceso de estimación es aplicado en cultivos por lotes, lote alimentado y continuo de Desulfovibrio alaskensis 6SR, donde el modelo dinámico del biorreactor es presentado y sintonizado con datos experimentales. El diseño del observador de estados adaptable toma en consideración la estructura del modelo del sistema y una retroalimentación con una ganancia adaptable que contiene una tangente hiperbólica del error de estimación, un marco teórico es propuesto con el fin de mostrar algunas de las característica de la convergencia del observador propuesto. Los resultados de la estrategia de estimación propuesta son generados por medio de simulaciones numéricas con el fin de mostrar su desempeño.
Palabras clave: observador con error acotado, retroalimentación con tangente hiperbólica, ganancia del observador adaptable, modelo del biorreactor, Desulfovibrio alaskensis 6SR.
1 Introduction
In standard bioprocess operation, on–line measurements are often limited to basic variables such as temperature, pH, and dissolved oxygen O2. Measurements of component concentrations, i.e. essential substrates, biomass and products of interest are obtained for off–line laboratory analysis at different discrete times. In recent years, on–line probes for measuring component concentrations, e.g. biomass probes based on capacitance measurements, have been developed, but their use is still very limited due to high costs. In particular, in sulfate–reducing bioreactors the biomass growth and products are difficult of measure on–line, given the anaerobic process conditions. Different methods for detection and enumeration of sulfate reducing bacteria (SRB) in natural and industrial environments have been developed, they have been grouped in: (i) direct detection methods and (ii) culture methods (APHA, 1989). The detection direct involved the using antibodies raised against SRB (Daly et al., 2000), and the uses of molecular biology tools as 16S rRNA, both techniques may be using in situ but required of a bigger knowledge and in some case is not possible by the nature of the considered sample (Vester and Ingvorsen, 1998). Culture methods for enumeration of SRB requires of strict anaerobic conditions and special culture medium, experience of handling of these bacterial, the incubation times are sometimes very large, etc (Neria–González et al., 2006).
In this context, the design of "software sensors" based on state estimation techniques takes on particular importance (Bastin and Dochain, 1990). Software sensors allow the online reconstruction of non–measured variables (i.e. component concentrations) based on a process model and some available measurements (from "hardware sensors" or from on–line sampling).
From kinetic studies point of view, is important to determine the kinetic parameters and especially of kinetic rates inside bioreactor (Soroush, 1997). The estimates of these rates are used for advanced control strategies (Aguilar–López, 2003). The procedure to estimate the kinetic rates based on the adaptive systems theory, consist of the estimation of unmeasured state with asymptotic observers (software sensor); later, the measurements (hardware sensor) and the estimates of the state variables (software estimator) are used for on–line estimation (Kazantzis and Kravaris, 1998; Aguilar–López et al., 2010; Espinoza–Salgado et al., 2008). This method is useful, but in some cases, when many reactions are involved, the implementation requires the calibration of too many parameters. A relative modern approach (Marin, 2002; Ohsumi et al., 2002) is the distribution based on identification method. In this approach the set of nonlinear differential equations that describe the state evolution is mapped into a set of linear algebraic equations respect to the model parameters.
The design of a stable and convergent state estimator appropriates for a particular bioprocesses is a complex task, and an adequate response is only obtained studying each bioprocess (Aguilar et al., 2004). For example, sliding mode control can be used to design an observer that brings one estimated state's error to zero in finite time even in the presence of measurement error (Seli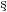 teanu, et al., 2007; Hong, et al., 2002); the other states have error that behaves similarly to the error in a Luenberger observer after peaking has subsided. Sliding mode observers also have attractive noise resilience properties that are similar to a Kalman filter. As discussed for the linear case above, the peaking phenomenon present in Luenberger observers justifies the use of a sliding mode observer. The sliding mode observer uses non–linear high–gain feedback to drive estimated states to a hypersurface where there is no difference between the estimated output and the measured output (Levant, 2001). The non–linear gain used in the observer is typically implemented with a scaled switching function, like the signum (i.e., sign) of the estimated–measured output error. Hence, due to this high–gain feedback, the vector field of the observer has a crease in it so that observer trajectories slide along a curve where the estimated output matches the measured output exactly. So, if the system is observable from its output, the observer states will all be driven to the actual system states. Additionally, by using the sign of the error to drive the sliding mode observer, the observer trajectories become insensitive to many forms of noise (Boiko and Fridman, 2005). Hence, some sliding mode observers have attractive properties similar to the Kalman filter but with simpler implementation. However, as it is well known, this switching happens at any instant the state trajectories cross the switching hyper–plane, this leads to the named chattering phenomenon caused by the discontinuity of the input injection, undesirable in most applications (Davila, et al., 2006). In order to avoid the named chattering phenomenon, several methodologies have been proposed, as the high order sliding–mode observers, which provides some smoothness to the estimation methodology diminishing the corresponding chattering, however to avoid the presence of the sign function (i.e., discontinuous function) a continuous one have been proposed (Bertoni and Punta, 2000).
teanu, et al., 2007; Hong, et al., 2002); the other states have error that behaves similarly to the error in a Luenberger observer after peaking has subsided. Sliding mode observers also have attractive noise resilience properties that are similar to a Kalman filter. As discussed for the linear case above, the peaking phenomenon present in Luenberger observers justifies the use of a sliding mode observer. The sliding mode observer uses non–linear high–gain feedback to drive estimated states to a hypersurface where there is no difference between the estimated output and the measured output (Levant, 2001). The non–linear gain used in the observer is typically implemented with a scaled switching function, like the signum (i.e., sign) of the estimated–measured output error. Hence, due to this high–gain feedback, the vector field of the observer has a crease in it so that observer trajectories slide along a curve where the estimated output matches the measured output exactly. So, if the system is observable from its output, the observer states will all be driven to the actual system states. Additionally, by using the sign of the error to drive the sliding mode observer, the observer trajectories become insensitive to many forms of noise (Boiko and Fridman, 2005). Hence, some sliding mode observers have attractive properties similar to the Kalman filter but with simpler implementation. However, as it is well known, this switching happens at any instant the state trajectories cross the switching hyper–plane, this leads to the named chattering phenomenon caused by the discontinuity of the input injection, undesirable in most applications (Davila, et al., 2006). In order to avoid the named chattering phenomenon, several methodologies have been proposed, as the high order sliding–mode observers, which provides some smoothness to the estimation methodology diminishing the corresponding chattering, however to avoid the presence of the sign function (i.e., discontinuous function) a continuous one have been proposed (Bertoni and Punta, 2000).
From the above in this work it is proposed a class of adaptive smooth bounded observer, where the feedback term is related with the hyperbolic tangent of the estimation error, coupled with an adaptive gain which is close to high order sliding–mode observers but avoiding the discontinuous structure of the sliding–modes, which allows a smooth convergence of the proposed observer, avoiding the chattering phenomena. The considered observer allows infers biomass and product concentrations under the assumption that the substrate measurements are available. The proposed observer is applied to kinetic model for cell growth for Desulfovibrio alaskensis 6SR. Desulfovibrio alaskensis was described in the first time by Feio (Feio et al., 2004) and subsequently studies of bacteria associated at biocorrosion, have reported that D. alaskensis is present in oil fields from Gulf of Mexico (Neria–González et al., 2006, Hernández–Gayoso et al., 2004; Padilla–Viveros et al., 2006). The strain 6SR was isolated of biofilm in oil pipeline, which have high resistance to heavy metals (Cd+2 and Cr+6) in relation at other species, is tolerant at oxygen, grows at pH 5.5–9 (7), 15–55 (45) °C and in 30% (w/v) NaCl, and produces extracellular polymeric substances. These bacterial characteristics are important in environmental process and other as corrosion.
2 Experimental
2.1 Organism, culture maintenance and purity test
Desulfovibrio alaskensis 6SR was isolated of a developed biofilm inside face of oil pipeline (Neria–González et al., 2006). The strain was maintained routinely in Hungate tubes with 5 mL of Postgate's medium B (Hungate, 1969). To evaluate the organism purity decimal dilution in plates of anaerobic agar supplemented with 6 mL of lactate (60% w/w), 4.5 g of NaSO4, 0.004 mg of FeSO4, and 27.5 g of NaCl were carried–out. The plates were placed in anaerobic jar (BBLTM GasPakTM Anaerobic Systems) and incubated until to colonies appear. The presence of black colonies indicated the growth of sulfate reducing bacteria. One black colony well definite and isolated was picked and quickly transferred at 45 mL sterile Postgate's C medium in anaerobic conditions (Postgate, 1979), and subcultures ware made subsequently.
The media was inoculated with 5 mL of culture and incubated at 37 ºC. Each medium was prepared and dispended in anaerobic conditions under a N2 (99.998% purity) atmosphere, 120 and 160 mL serum bottles were filled with 45 and 95 mL of medium, respectively, and autoclaved at 121ºC.
2.2 Growth kinetics
The inoculum for kinetic study was cultured in 45 mL of Postgate's C medium for 25 h at 37°C (logarithmic phase). A 5 mL aliquot was taken from Postgate's C medium to inoculate 95 mL of fresh medium at 37 ºC. The experiment was done using two series of triplicate independent cultures; each set of triplicate cultures were inoculated with12 hours separated each other, the experimental run time was 72 hours.
2.3 Analytic methods
The bacterial growing, consuming of sulfate and the sulfide production were monitored each 3 or 4 hours, the samples were taken carefully, avoiding contact with oxygen. The bacterial growing was followed through Optical Density (OD) methodology, the OD reading for cell growing was transformed into dry mass (mg/L) through a standard growth curve. The consuming sulfate in the medium was measured by the turbid metric method based on the precipitation of barium (Kolmert et al., 2000). Also, the production of sulfide was measured by a colorimetric method (Cord–Ruwisch, 1985).
2.4 Data analysis and mathematical model
The experimental data of biomass, sulfate, and sulfide from two series of sulfate reducing culture were analyzed using the average values of each measurement point. As is well known, in sulfate reducing culture the accumulation of sulfide (product) in the medium has an inhibitory effect on bacterial growth. Therefore, to approximate the average experimental data of bacterial growth in batch bioreactor, the Levenspiel's inhibition product model (Levenspiel, 1999) be used to represent the specific growth rate (Eq. 1). Basically, this is an unstructured model that describes the bacterial growth rate as a function of substrate, product and biomass concentrations as the unique biological state variable.
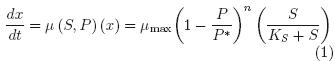
Where: μmax represents the maximum growing rate; KS represents the affinity substrate; P* corresponds to inhibition concentration product, and n is the reaction order; meanwhile S, P, and x are substrate, product, and biomass concentrations, respectively.
2.5 Estimation of the kinetic parameters
Levenspiel growth kinetic parameters ware estimated by the rate of change of biomass production, using central finite differences according to the following equation:
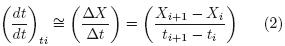
and a nonlinear multivariable regression for the rates of change of biomass production and experimental data (X, S, and P) was done. POLYMATH 6.0 Professional software was used, the program allow applying effective numerical analysis techniques, and Levenberg–Marquardt algorithm was using for this case (see Table 1).
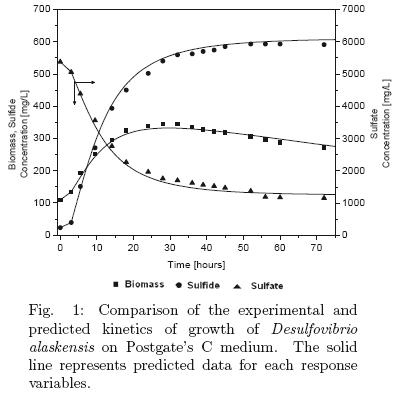
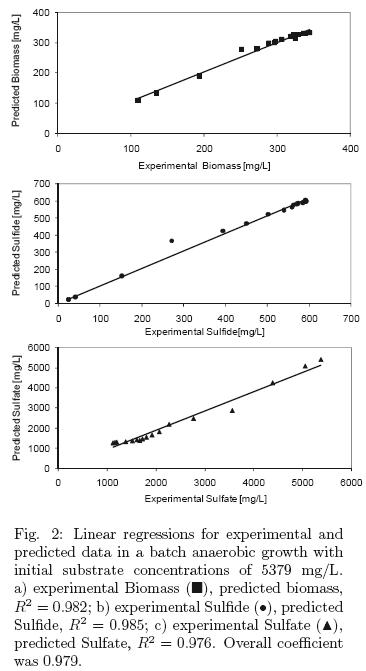
The mathematical model was simulated using the same software. Besides, a linear regression between the experimental and the predicted data were obtained, and overall correlation coefficient was calculated, see figs. 1–2 (Tejeda, 2007).
3 Bioreactor mathematical model
The unstructured models are using nowadays as the main tool for the bioprocess modeling, but also for being applied in overall computer control. Considering the above kinetic model, it is proposed by following the mathematical model for a class of continuous stirred bioreactor, which is based on classical mass balances for biomass, sulfate (substrate) and sulfide (product) concentrations: Sulfate (S).–
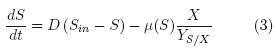
Biomass (X).–
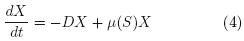
Sulfide (P).–
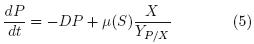
Here D is the dilution rate, μ is the specific growth rate, YS/X is the sulfate coefficient yield and YP/X is the sulfide coefficient yield. In accordance with the specific experimental setup the following initial conditions are considered for the batch culture and model validation purposes Xo = 100 mg/L, So = 5200 mg/L, Po = 10 mg/L. Figure 1 shows the performance of the kinetic model considering a comparison with the experimental data which looks satisfactory. The above model predicts batch operation when D = 0, the fed–batch operation is considered when D = f(t) and the output flow terms are null and finally the continuous operation which considers inputs and outputs flow terms.
4 Methodology observer design
Consider a canonical control representation form of the bioreactor model:

Now, the following state observer is proposed:
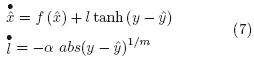
where the observer's gain l is given by an update adaptation algorithm and α is a parameter design. To prove the convergence of the proposed observer, let us to consider the dynamic equation of the estimation error (ε = x — 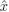 ), as follows:
), as follows:
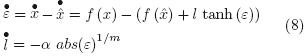
under the following assumptions:
A1. f (x) — f (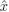 ) —
) — 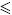 L(x —
L(x — 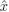 ) Taking norms to both sides of Eq. (8) and applying A1 it is obtained:
) Taking norms to both sides of Eq. (8) and applying A1 it is obtained:
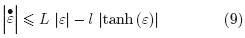
Now, suppose that the function abs(ε)1/m is a positive continuous function on the integration interval [a, b]; then H is the maximum of the function on the domain [(δ,γ)], then abs (ε) is bounded, i.e. abs (ε) 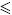 H
H 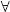 t
t 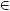 [(δ,γ)], such that: abs(ε)1/n
[(δ,γ)], such that: abs(ε)1/n 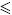 H1/n n > 0
H1/n n > 0 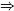
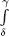 abs(ε)1/n
abs(ε)1/n 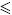 H1/n (γ – δ) considering n an odd number i.e. n = 2p + 1, p
H1/n (γ – δ) considering n an odd number i.e. n = 2p + 1, p 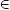 Z+ therefore; lim sup
Z+ therefore; lim sup 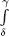 abs(ε)1/(2p+1)
abs(ε)1/(2p+1) 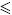 lim sup H1/(2p+1)(γ – δ) for p large enough.
lim sup H1/(2p+1)(γ – δ) for p large enough.
From the above, Eq. (9) can be rewritten as:
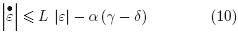
Solving Eq. (9) and considering t  ∞, can be concluded that the estimation error belongs to ball:
∞, can be concluded that the estimation error belongs to ball:
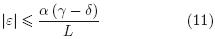
5 Numerical experiments and discussion
Besides to show the performance of the proposed estimation methodology, an important additional issue concerns with the evaluation of the capacities Desulfovibrio alaskensis 6SR for biotechnological applications. Both two of these possible applications are related with wastewater treatment for degradation of sulfate compounds and heavy metal mobility. From the kinetic model presented in Section 3, the proposed observer is applied to batch, continuous and fed–batch operating modes; each one of the above mentioned operating modes is related with a specific process task, on the batch operation an optimal trajectory must to be reached in order to provide an adequate performance, besides a finite time operation politics must be considered; related with the continuous operation process the main tasks is to lead the bioreactor trajectories to an optimal and stable steady state, where the convergence of observers and controllers can be designed with asymptotic convergence and finally the feed–batch operation can be considered as a batch operation with input disturbances, therefore a robust monitoring and controlling methodologies are needed. The initial concentration conditions for the batch culture was above mentioned and the corresponding for the continuous and fed–batch operating modes are Xo = 980 mg/L, So = 6850 mg/L and Po = 15 mg/L. The initial conditions imposed to the proposed observer are 5000 mg/L, 96 mg/L and 8 mg/L, respectively, for the batch operation and 950 mg/L, 6250 mg/L and 20 mg/L for biomass, sulfate and sulfide concentrations, respectively, for continuous and fed–batch operation modes. The estimation procedure considers the sulfate concentration (substrate) as measured output in order to infer the biomass and sulfide concentrations.
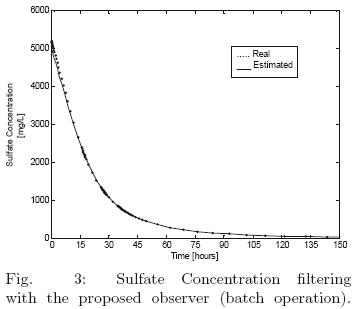
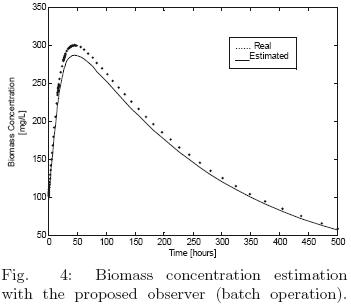
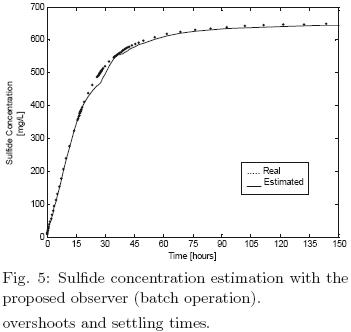
Batch operation is considered from figs. 3–(4)–5, where the performance of the proposed observer is satisfactory, a fast convergence to the named real concentrations is achieved, without large overshoots and settling times.
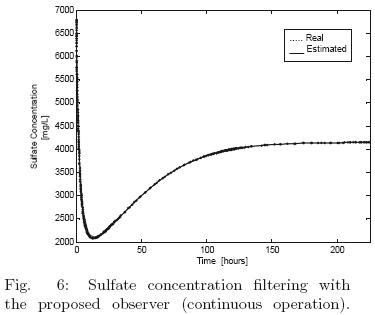
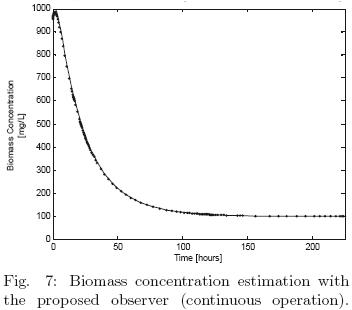
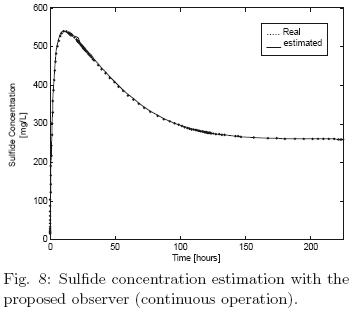
Figures 6–(7)–8 concern to continuous operating mode can be observed an adequate performance of the proposed estimation methodology from the time series.
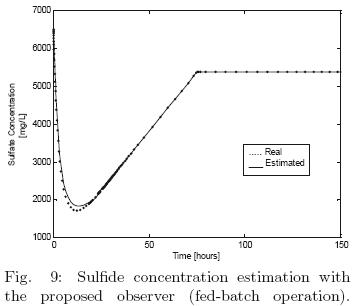
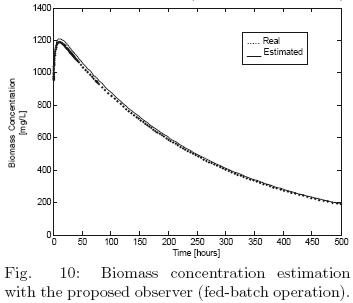
Finally, figs. 9–(10)–11 are related with the observer's performance when a fed–batch operation is considered; for this case a dilution rate of D = 0.01 1/h is considered from the start–up of the bioreactor operation to 75 hours, later the input flow is null (D = 0). Despite of this sudden disturbance the proposed observer keeps a satisfactory performance following the named real concentrations.
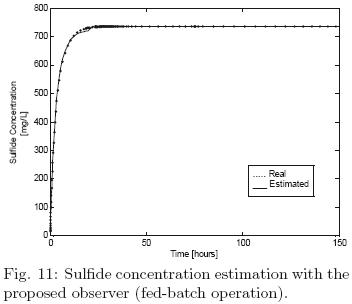
Conclusions
In this work is modeled the biomass growth and sulfide production of a sulfate reducing bacteria Desulfovibrio alaskensis, which has been recently described, and its biotechnological properties are not studied yet enough. For the above mentioned, a nonlinear state observer to infer biomass and sulfide concentration from sulfate concentration measurements is implemented for a batch, fed–batch and continuous operating bioreactor modes, where can be observed a satisfactory performance. A mathematical analysis to show the convergence characteristics of the proposed methodology is done. Future work will be oriented to analyze the effect of model uncertainties and noisy measurements in order to try to design robust estimation methodologies.
Acknowledgment
JCFE is grateful with CONACyT for the corresponding support via a postgraduate scholarship.
Nomenclature

Referencias
Aguilar–López, R. (2003). Integral observers for uncertainty estimation in continuous chemical reactors: differential–algebraic approach. Chemical Engineering Journal 9, 113–120. [ Links ]
Aguilar, R., Soto, G., Martínez, S., Maya–Yescas, R. (2004). Substrate regulation in fixed bed bioreactors via feedback control. Revista Mexicana de Ingeniería Química 3, 1–11. [ Links ]
Aguilar–López, R., López–Pérez, P. A., Neria–González, M.I., Domínguez–Bocanegra, A.R. (2010). Observer based adaptive model for a class of aerobic batch bioreactor. Revista Mexicana de Ingeniería Química 9, 1, 29–35. [ Links ]
APHA. (1989). Estimation of bacterial density. In standard methods for the examination of water and waste–water. American Public Health, Pp. 977–980. Association Washington D.C. [ Links ]
Bastin, G., Dochain, D. (1990). On–line estimation and adaptive control of bioreactors. Elsevier Science Ltd. Amsterdam. [ Links ]
Bertoni, G., Punta, E. (2000). Chattering elimination with second order sliding–modes robust to Coulomb friction. Journal of Dynamics, Measurement and Control 122, 679–684. [ Links ]
Boiko, I., Fridman, L. (2005). Analysis of chattering in continuous sliding–mode controllers. IEEE Transactions on Automatic Control 50, 1442–1446. [ Links ]
Cord–Ruwisch, R. (1985). A quick method for determination of dissolved and precipitated sulfides in cultures of sulfate–reducing bacteria. Journalof Microbiololy Methods 4, 33–36. [ Links ]
Daly, K., Sharp, R.J., McCarthy A.J. (2000). Development of oligonucleotide probes and PCR primers for detecting phylogenetic subgroups of sulfate–reducing bacteria. Microbiology 146, 1693–705. [ Links ]
Dávila, J., Fridman, L., Levant, A. (2005). Second order sliding–mode observer for mechanical systems. IEEE Transactions on Automatic Control 50, 1785–1789. [ Links ]
Espinoza–Salgado, S., Reyes–Reyes, J. Alvarez–Castillo, A., Astorga–Zaragoza, C. M., Mendizabal–Mijares, E., Cadenas–Pliego, G. (2008). High gain adaptive nonlinear observer for emulsion copolymerization process. Revista Mexicana de Ingenierí a Química 7, 1, 89–98 [ Links ]
Feio, M.J., Zinkevich, V., Beech, I.B., Llobet–Brossa, E., Eaton, P., Schmitt, J., Guezennec, J. (2004). Desulfovibrio alaskensis sp. nov., a sulphate–reducing bacterium from a soured oil reservoir. International Journal of Systems, Evolution and Microbiology 54,1747–1752. [ Links ]
Hernández–Gayoso, M. J., Zavala–Olivares, G., Ruiz–Ordaz, N., Juárez–Ramírez C., García–Esquivel, R., Padilla–Viveros, A. (2004). Microbial consortium influence upon steel corrosion rate, using polarization resistance and electrochemical noise techniques. Electrochemistry Acta 49, 4295–4302. [ Links ]
Hong, Y., Xu, Y., Huang, J. (2002). Finite–time control for robot manipulators. Systems & Control Letters 46, 243–253. [ Links ]
Hungate, R.E. (1969). A roll tube method for cultivation of strict anaerobes. In: Methods in Microbiology (J.R. Norris and D.W. Ribbons eds.), Pp. 117–32. London: Academic Press. [ Links ]
Kazantzis, N. y Kravaris, C. (1998). Nonlinear observer design using Liapunov's auxiliary theorem. Systems & Control Letters 34, 241–247. [ Links ]
Kolmert, Å., Wikström, P., Hallberg, K. (2000). A fast and simple turbidimetric method for the determination of sulfate in sulfate–reducing bacterial cultures. Journal Microbiology Methods 41, 179–184. [ Links ]
Levant, A. (2001). Universal single–input–single–output (SISO) sliding–mode controllers with finite–time convergence. IEEE Transaction on Automatic Control 46, 1447–1451. [ Links ]
Levenspiel, O. (1999). Chemical Reactor Engineering. John Wiley & Sons, New York. [ Links ]
Marin, C. (2002). System Identification Based on Distribution Theory. June 25–28, Crete, Greece. Proceedings of IASTED International Conference on Applied Simulation and Modelling. (ASM 2002), 1125–1131. [ Links ]
Neria–González, I., Wang, E.T., Ramírez, F., Romero, J.M., Hernández–Rodríguez, C. (2006). Characterization of bacterial community associated to biofilms of corroded oil pipelines from the southeast of Mexico. Anaerobe 12, 122–133. [ Links ]
Ohsumi, A., Kameyama, K. y Yamaguchi, K. (2002). Subspace identification for continuous–time systems via distribution–based approach. Automatica 38, 63–79. [ Links ]
Padilla–Viveros, A., Garcia–Ochoa, E., Alazard, D. (2006). Comparative electrochemical noise study of the corrosion process of carbon steel by the sulfate–reducing bacterium Desulfovibrio alaskensis under nutritionally rich and oligotrophic culture conditions. Electrochimica Acta 51, 3841–3847. [ Links ]
Postgate. J.R. (1979). The sulphate–reducing bacteria. Cambridge University Press, New York . [ Links ]
Seli teanu, D., Petre, E., R?svan, V. (2007). Sliding mode and adaptive sliding–mode control of a class of nonlinear bioprocesses. International Journal of Adaptive Control and Signal Processing 21, 795–822. [ Links ]
teanu, D., Petre, E., R?svan, V. (2007). Sliding mode and adaptive sliding–mode control of a class of nonlinear bioprocesses. International Journal of Adaptive Control and Signal Processing 21, 795–822. [ Links ]
Soroush, M. (1997). Nonlinear state–observer design with application to reactors. Chemical Engineering Science 52, 387–404. [ Links ]
Tejeda, P. A. (2007). Estadística para Ciencias Sociales, del comportamiento y de la salud. Edit. CENGAGE Learning, 3ª Edición, México. [ Links ]
Vester, V. y Ingvorsen, K. (1998). Improved most–probable–number method to detect sulfate reducing bacteria with natural media and a radiotracer. Applied Environmental Microbiology 64, 1700–1707. [ Links ]














