Fenómenos de transporte

 

Formulación integral para la solución de problemas de cerradura en procesos de escalamiento

 

Integral formulation for the solution of closure problems in upscaling processes

 

Francisco J. Valdés-Parada*

 

Área de Ingeniería en Recursos Energéticos. Universidad Autónoma Metropolitana-Iztapalapa Av. San Rafael Atlixco 186, Col. Vicentina, 09340, México, D.F., México. *Autor para la correspondencia. E-mail: iqfv@xanum.uam.mx Tel. 58044648 ext.238

 

Recibido 4 de Noviembre 2009;
Aceptado 18 de Diciembre 2009

 

Resumen

El desarrollo de modelos de transporte a escalas macroscópicas puede llevarse a cabo mediante técnicas de escalamiento como el método del promedio volumétrico. Esta técnica consiste en promediar las ecuaciones de transporte que describen fenómenos a escalas microscópicas para llegar a modelos de medio efectivo. Dichos modelos se expresan en términos de coeficientes efectivos que pueden calcularse a partir de la solución de los problemas de cerradura correspondientes. En este trabajo se presenta una formulación integral basada en funciones de Green para llevar a cabo la solución formal de problemas de cerradura. Esta metodología no sólo proporciona una interpretación física de las variables de cerradura, sino que además permite extender el escalamiento a modelos de transporte no lineales. Además, la formulación integral requiere únicamente la solución de un problema de valor a la frontera para el cálculo de las variables de cerradura; lo cual representa un avance respecto al método de superposición. Los resultados de este trabajo amplían el rango de aplicación del método del promedio volumétrico a problemas no lineales al asociar la parte lineal del problema de cerradura a la función de Green y considerando a la parte no lineal como una fuente no homogénea.

Palabras clave: formulación integral, función de Green, escalamiento, problema de cerradura.

 

Abstract

The derivation of transport models at macroscopic scales can be carried out using upscaling techniques such as the method of volume averaging. This upscaling technique consists on averaging the transport equations that describe phenomena at the microscale. The result is the so-called effective medium models, which are expressed in terms of effective coeffcients that can be computed from the solution of the corresponding closure problems. In this work, we present an integral formulation based on Green’s functions to carry out the formal solution of closure problems. This methodology not only provides a physical interpretation of the closure variables, but it also allows solving nonlinear closure problems. In addition, the integral formulation only requires the solution of one boundary-value problem; this represents an advantage with respect to the traditional approach. The results from this work extend the range of applicability of the method of volume averaging to nonlinear problems by associating the linear part of the closure problem to the Green’s function and considering the nonlinear part as a nonhomogeneous source.

Keywords: integral formulation, Green’s function, upscaling, closure problem.

 

1. Introducción

El modelado de sistemas que involucran el transporte a través de diversas escalas puede llevarse a cabo mediante el escalamiento de las ecuaciones que gobiernan el transporte a escala microscópica (Bear, 1972). En este tipo de sistemas, es sabido que los procesos a una escala microscópica pueden tener una influencia directa en la escala macroscópica (Whitaker, 2009). Entre las diversas metodologías reportadas en la literatura, se encuentra el método del promedio volumétrico (Whitaker, 1999). Este método no sólo per-mite obtener las ecuaciones de transporte en la macroescala (ecuaciones de medio efectivo), sino que además proporciona las restricciones que indican el rango de validez del modelo. Más aún, el conjunto de suposiciones y restricciones de escala que llevan a la reducción sistemática de grados de libertad del modelo microscópico que permiten llegar al modelo macroscópico ha sido recientemente identificado por Wood (2009) como reglas de escalamiento. Una característica de los modelos promedio es que contienen coeficientes de medio efectivo, los cuales son la conexión con la microescala. Como lo ha mostrado Whitaker (1999), para cerrar las ecuaciones macroscópicas es necesario plantear y resolver un problema de valor a la frontera para las desviaciones espaciales de la propiedad a estudiar. Cuando el problema es lineal, la solución de este problema se expresa como una superposición de soluciones resultantes de otros problemas de valor a la frontera que suelen ser igual o menos complicados que el problema original. Las funciones que representan a dichas soluciones se denominan variables de cerradura (ver por ejemplo, Crapiste y col., 1986) y su dominio corresponde a una región representativa de la microestructura del sistema (celda unitaria). El significado físico de los coeficientes efectivos resultantes del método del promedio volumétrico suele ser claro y característico del tipo de transporte que se está estudiando; sin embargo, las variables de cerradura no suelen siempre compartir estas propiedades. De acuerdo con Whitaker (1999), una variable de cerradura es una función auxiliar que mapea a las fuentes promedio en los campos de las desviaciones. A pesar de que esta interpretación es correcta desde un punto de vista matemático, deja algunas preguntas sin responder desde el punto de vista físico. Por ejemplo, esta interpretación no nos informa si una variable de cerradura captura o no el efecto de la microestructura de la celda unitaria. Más aún, la superposición en variables de cerradura y fuentes promedio sólo es posible para problemas lineales. En otras palabras, si el problema de las desviaciones involucrara términos no lineales, no sería posible utilizar el método de superposición. De manera que si no hacen aproximaciones en el término no lineal, el proceso de escalamiento queda limitado a problemas lineales. Lo cual constituye una seria limitación del método del promedio volumétrico.

En este trabajo se presenta una formulación integral basada en funciones de Green para obtener la solución formal del problema de las desviaciones espaciales. El uso de funciones de Green para la solución de problemas en ciencias e ingeniería tiene una larga tradición que puede ir desde problemas de transporte y reacción (ver por ejemplo, Mukkavilli y col., 1987a,b; Arce y col., 1996) hasta dinámica cuántica, como lo ejemplifican Mishra y col. (1991). En la formulación integral, una variable de cerradura es, en general, la integración (en espacio y tiempo) de la función de Green que describe la influencia de la microestructura y de las fuentes promedio concentradas en una determinada posición a un tiempo dado sobre el campo de las desviaciones espaciales. Lo anterior se traduce en que para calcular los campos de las variables de cerradura solo es necesario integrar los campos de las funciones de Green que resultan de resolver un problema de valor a la frontera. Esto constituye un avance respecto al método de superposición, en donde es necesario resolver tantos problemas de cerradura como fuentes promedio existan en el problema de las desviaciones. Algunas de las ventajas que proporciona este tipo de formulaciones para el estudio de transporte de calor en medios porosos pueden encontrarse en el reciente trabajo de Haji-Sheikh y col. (2004). Por otro lado, cuando el problema de las desviaciones no es lineal, la formulación integral permite obtener soluciones implícitas del campo de las desviaciones, con las cuales es posible cerrar los modelos macroscópicos. El uso de formulaciones integrales para la solución de problemas de transporte y reacción ha sido explorada recientemente por Valdés-Parada y col. (2007, 2008a) obteniendo una rápida velocidad de convergencia con respecto a métodos tradicionales como el de diferencias finitas.

El trabajo está organizado como sigue: en la Sección 2 se presentan algunas generalidades sobre formulaciones integrales. Posteriormente, se aborda la solución de problemas de cerradura lineales (Sección 3) y no lineales (Sección 4) en términos de funciones de Green. Por último se presentan las conclusiones y perspectivas del trabajo.

 

2. Introducción a las formulaciones integrales

En esta sección se presentan algunos conceptos fundamentales de las formulaciones integrales para la solución de problemas de valor a la frontera basados en funciones de Green. Para propósitos de ilustración, los desarrollos se limitan a problemas lineales unidireccionales, en los cuales es relativamente simple obtener expresiones analíticas de las funciones de Green. Sin embargo, esto de ninguna manera limita las aplicaciones de la formulación integral.

2.1. Fórmula de Green

Considere la siguiente ecuación diferencial ordinaria

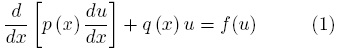
siendo p y q funciones continuas conocidas de x ∈ [a, b] y f es un término fuente que puede o no ser función de la variable dependiente u. Para los desarrollos que siguen, es conveniente introducir el siguiente operador diferencial

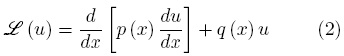
donde v es otra función continua en el dominio de x. Aplicando el operador 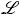(·) a las funciones u y v puede obtenerse la siguiente expresión,

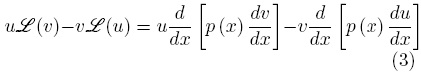
Sin embargo, de la regla de la derivada del producto entre dos funciones, resultan las siguientes relaciones

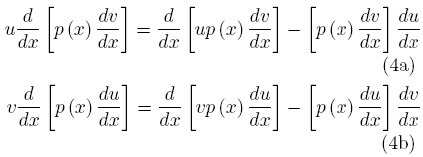
Usando estos resultados en la Ec. (3) se obtiene lo siguiente

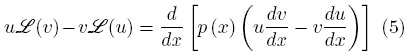
la cual se conoce como la identidad de Lagrange.

Por otro lado, al integrar la Ec. (5) se obtiene la fórmula de Green en una dirección, es decir

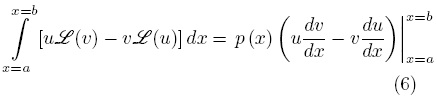
El uso de la fórmula de Green no está limitado al desarrollo de soluciones analíticas, de hecho esta fórmula fue usada por Li y Evans (1991) para resolver problemas de convección de calor en sistemas bidimensionales usando el método de elemento a la frontera. Más aún, Kim y col. (2008) recientemente propusieron descomponer sistemáticamente un operador elíptico multidimensional en operadores unidimensionales basados en la fórmula de Green y en la solución analítica de la función de Green asociada del problema unidimensional.

Para concluir esta parte del trabajo es pertinente escribir la fórmula de Green para el Laplaciano en dos y tres dimensiones (ver página 416 en Haberman, 2004), respectivamente

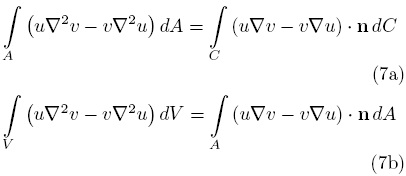
siendo n el vector unitario normal a la frontera correspondiente.

2.2. Solución de problemas de transporte y reacción con funciones de Green

Regresando al problema original, la Ec. (1) puede tomar la siguiente forma:

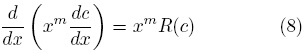
donde m = 0, 1, 2 se refiere a un sistema coordenado cartesiano, cilíndrico o esférico, respectivamente y x ∈ [0, 1] es la posición adimensional, c es la concentración adimensional y R(c) denota la cinética de reacción. Cabe mencionar que al escribir la ecuación anterior se supuso que los cambios importantes ocurren en una sola dirección. Para completar el planteamiento del problema, se imponen las siguientes condiciones de frontera

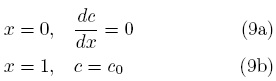
la primera condición de frontera es consecuencia de imponer la condición de simetría en el centro del dominio, mientras que la segunda condición de frontera supone que no hay resistencias externas a la transferencia de masa. Asociado a este problema de valor a la frontera se propone el siguiente problema lineal

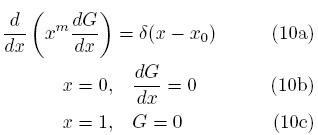
En este problema, la variable x₀ tiene el mismo dominio que x; además δ(x − x₀) es la función delta de Dirac, la cual satisface la siguiente propiedad de filtración,

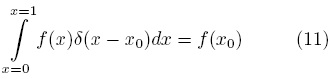
Usando ahora la fórmula de Green unidireccional [Ec. (6)] y tomando u = c y v = G se obtiene

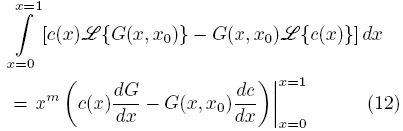
O bien con base en los problemas de valor a la frontera para c (x) y G (x, x₀).

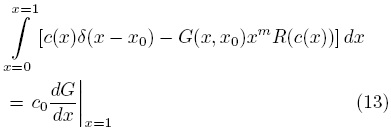
Resolviendo para la concentración y haciendo la sustitución formal x → x₀ resulta lo siguiente

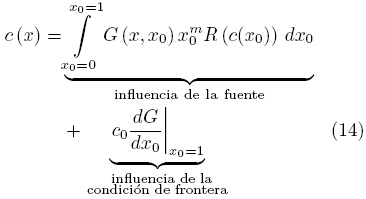
donde se impuso la condición de simetría para la función de Green alrededor de x₀, G(x₀, x) = G(x, x₀). Este resultado es relevante desde un punto de vista tanto matemático como físico. A continuación se explica cada punto de vista

• Matemáticamente, la Ec. (14) es relevante debido a que la solución de problemas de valor a la frontera lineales y no homogéneos consiste en la superposición de una solución general y otra particular. Al utilizar las condiciones de frontera se obtienen las correspondientes constantes de integración que resultan en la solución general. Mientras que la solución particular se propone para tratar con el término fuente en la ecuación diferencial. En la Ec. (14), el primer término denota la influencia de la fuente en la ecuación diferencial, es decir, denota la solución particular, mientras que el segundo término resulta de la aplicación de las condiciones de frontera por lo que representa a la solución general.

• Físicamente, la Ec. (14) es relevante porque conserva los mismos principios involucrados en el problema de valor a la frontera original. Es decir, en este caso el transporte de masa se debe tanto a la difusión como a la reacción química. Además, se ha supuesto que existe una fuente constante de alimentación en la frontera x = 1. De esta forma, el primer término en el lado derecho de la Ec. (14) representa la influencia de la fuente reactiva en todo el dominio de la concentración, mientras que el segundo término representa la influencia de la concentración en la frontera x = 1 sobre el campo de c(x).

Cabe mencionar que la Ec. (14) solo representa una solución explícita del problema cuando el término fuente es independiente de la concentración. Cuando este no es el caso, la solución es evidentemente implícita y constituye la base de un método iterativo para la solución de problemas no lineales. Dicha metodología ha sido empleada por Valdés-Parada y col. (2007, 2008a,b) para la solución de problemas de transporte tanto puramente difusivo como difusivo y convectivo de masa y reacción con cinéticas no lineales.

2.3. Solución analítica de funciones de Green

Para concluir esta sección se ilustra el cálculo de funciones de Green para una placa. Sin embargo este mismo procedimiento puede aplicarse directamente a problemas en otros sistemas coordenados e incluso para el cálculo de funciones de Green en dos y tres dimensiones. Para una placa (m = 0), el problema de valor a la frontera asociado es

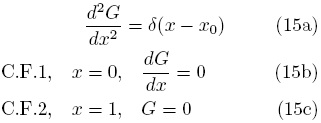
Cuya solución general es

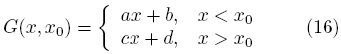
Usando las condiciones de frontera resulta que a = 0 y c = −d, por lo que,

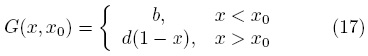
Para determinar las constantes b y d se impone primeramente la condición de continuidad de la función de Green en x = x₀, es decir,

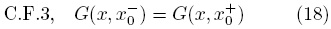
de la cual resulta que

Y la función de Green es ahora función de una sola constante de integración,

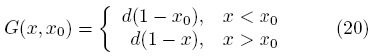
Para cerrar este resultado, es necesaria una última condición de frontera, la cual resulta de integrar la Ec. (15a) desde x = x₀^– hasta x = x₀⁺ ; y está dada por

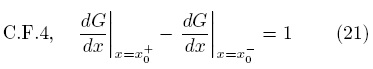
Aplicando esta condición de frontera se obtiene que

De esta forma, la expresión final de la función de Green es

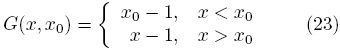
la cual, como se puede notar, satisface la condición de simetría G(x, x₀) = G(x₀, x).

Los resultados en coordenadas cilíndricas (m = 1) y esféricas (m = 2) son, respectivamente:

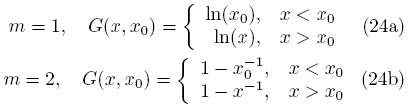
los detalles de estos resultados están disponibles en la literatura (ver por ejemplo el Apéndice en Valdés-Parada y col., 2007).

 

3. Interpretación de las variables de cerradura en el proceso de escalamiento

3.1. Problemas puntual y promedio

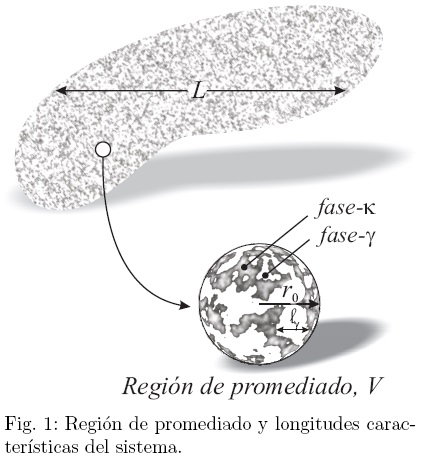
Considere ahora el siguiente problema que describe el transporte de una propiedad ψ_γ a través de un medio poroso rígido y homogéneo (es decir, de porosidad constante en el tiempo y espacio),

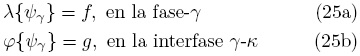
donde λ{·} y φ{·} son operadores diferenciales lineales conocidos (ver, por ejemplo, Whitaker, 1999) y ψ_γ una función (escalar o vectorial) continua en la fase-γ, mientras que f y g son términos fuentes conocidos. Para llevar a cabo el proceso de escalamiento, es necesario definir una región de promediado como la mostrada en la Fig. 1 (Whitaker, 1999). En términos de esta región se introducen los operadores de promediado superficial

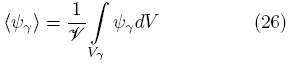
e intrínseco

 

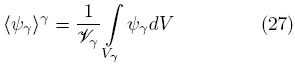
En las ecuaciones anteriores 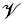y 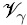representan los volúmenes de la región de promediado, V , y de la fase γ, V_γ, respectivamente. Ambos operadores están relacionados de acuerdo a la siguiente expresión

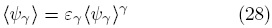
siendo ε_γ la fracción volumétrica de la fase-γ en la región de promediado. En la literatura es común encontrar que el promedio de la velocidad se expresa como un promedio superficial en la ley de Darcy, mientras que para otras variables como la temperatura y concentración, se suele preferir el promedio intrínseco (Whitaker, 1999).

La aplicación del operador de promedio superficial a la Ec. (25a), da lugar a

Intercambiando diferenciación e integración en el lado izquierdo de la ecuación anterior y usando la relación de los operadores de promediado [Ec. (28)] resulta

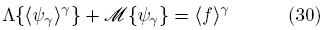
los detalles y suposiciones detrás de esta operación pueden encontrarse en Whitaker (1999). En la Ec. (30), Λ{·} es un operador diferencial conocido y 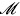{·} es un operador integral que aplica sobre la interfase sólido-fluido y también es conocido. De hecho, este operador es consecuencia de la aplicación del teorema del promediado espacial (Howes y Whitaker, 1985),

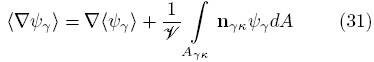
El siguiente paso en el análisis es descomponer a la función ψ_γ de acuerdo con (Gray, 1975)

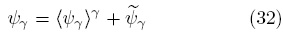
donde 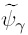representa las desviaciones espaciales de la variable puntual ψ_γ con respecto a 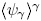. De esta forma, aprovechando la linealidad de los operadores Λ{·} y 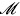{·}, la Ec. (30) toma la siguiente forma

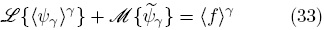
donde, en general, 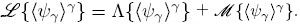Sin embargo, en casos en que puedan despreciarse los cambios espaciales de ε_γ (por ejemplo en el seno de un medio poroso homogéneo), se cumple la restricción de escala r₀ << L por lo que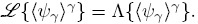

3.2. Problema de cerradura

Para cerrar la Ec. (33), es necesario contar con el campo de las desviaciones, 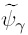. Con este fin, se resta la Ec. (33) a la Ec. (25a) para obtener

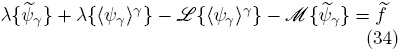
Basados en las restricciones de escala usuales, es decir,

donde 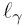y L denotan las longitudes características de la fase-γ y de la macroescala, respectivamente; es razonable, en muchos casos, despreciar a los términos no locales con respecto a sus contrapartes locales, es decir

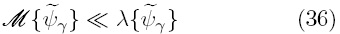
La condición de frontera interfacial para el campo de las desviaciones espaciales resulta de sustituir la descomposición espacial [Ec. (32)] en la Ec. (25b); y puede expresarse como sigue

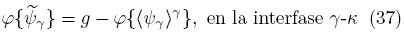
Más aún, el problema de valor a la frontera para 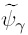se resolverá en una celda unitaria periódica, como la mostrada en la Fig. 2; por lo que se impone la condición de periodicidad en las entradas y salidas de dicha celda (Crapiste y col., 1986),

 

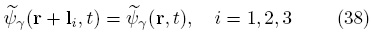
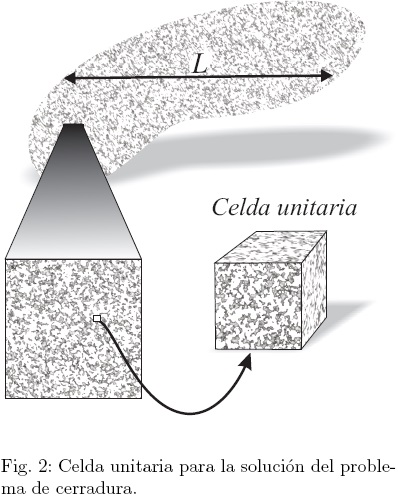
De esta forma, el problema de las desviaciones espaciales es

donde, para simplificar la notación, se usaron las siguientes definiciones,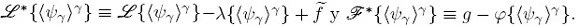

Note que para casos en que se puedan despreciar los cambios espaciales de ε_γ , se tiene que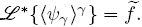

Por otro lado, si no se impone la suposición de estado cuasiestacionario, es necesario contar con una condición inicial para 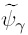, la cual puede expresarse como sigue

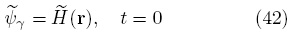
donde 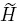(r) representa la distribución inicial del campo de las desviaciones espaciales. En algunos problemas de cerradura (ver capítulos 3-5 en Whitaker, 1999) es además necesario imponer la siguiente condición

con la que se completa el planteamiento del problema de las desviaciones espaciales.

3.3. Solución formal del problema de cerradura

Siguiendo los desarrollos de la Sección 2, el problema asociado para el cálculo de las funciones de Green es

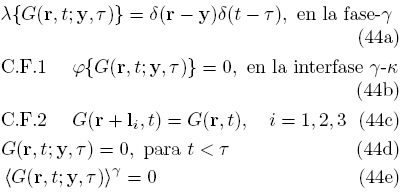
La Ec. (44d) representa el principio de causalidad, el cual establece que la función de Green es la respuesta (en la posición r al tiempo t) a una fuente concentrada en r = y al tiempo t = τ.

Para obtener la solución formal del problema de las desviaciones espaciales, es necesario expresar la fórmula de Green para un campo tridimensional transitorio; la cual está dada por (ver Capítulo 11 en Haberman, 2004)

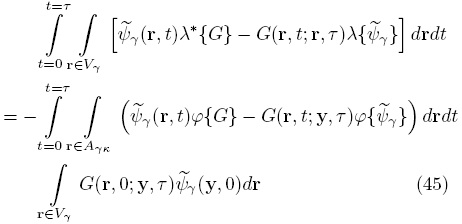
donde λ*{·} es la versión adjunta del operador λ{·}. Siguiendo el procedimiento de la Sección 2, a partir de la ecuación anterior se puede obtener el campo de las desviaciones como sigue:

donde se han identificado las fuentes de no homogeneidad del problema de 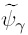, las cuales comprenden fuentes superficiales y volumétricas así como a la condición inicial.

Más aún, si se satisfacen las restricciones de escala, 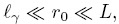los términos que involucran propiedades promedio pueden considerarse como constantes en las integrales correspondientes y por tanto, la Ec. (46) se puede expresar como sigue

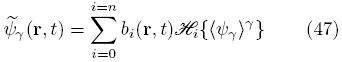
donde n denota el número de fuentes promedio y

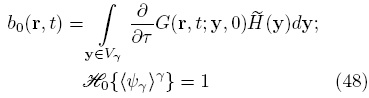
En la Ec. (47), los coeficientes b_i son las variables de cerradura definidas por (Whitaker, 1999) y 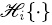es un operador algebraico-diferencial que es función de los operadores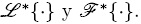

La importancia de la Ec. (46) es que expresa al campo de las desviaciones espaciales en función de integrales de la función de Green asociada. Más aún, dado que el problema de valor a la frontera para la obtención de las funciones de Green [Ecs. (44a)-(44e)] se resolverá en la celda unitaria representativa de la microestructura; es razonable pensar que los campos de G cambiarán de acuerdo a la geometría de la celda unitaria. En otras palabras, de acuerdo a la formulación integral dada por la Ec. (46), las funciones de Green son las encargadas de capturar la información esencial de la microestructura del medio poroso. Un corolario de esta observación es que una variable de cerradura es la integral (en espacio y tiempo) de las funciones de Green asociadas. Es decir, gracias a las funciones de Green, las variables de cerradura son capaces de describir la influencia de las fuentes y la microestructura en los campos de las desviaciones espaciales y por tanto en el modelo macroscópico, como se mostrará más adelante.

Para concluir esta parte del trabajo, se debe cerrar el modelo macroscópico; para ello se sustituye la Ec. (47) en la Ec. (33), el resultado es

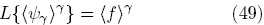
donde .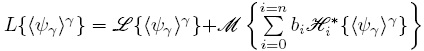

Cabe mencionar que en el operador diferencial L están incluidos los coeficientes de transporte efectivos.

3.4. Consistencia con el método de superposición

De acuerdo con Whitaker (1999), la solución del problema de las desviaciones puede expresarse directamente como se muestra en la Ec. (47), es decir aplicando el método de superposición. Sin embargo, este procedimiento es válido únicamente para problemas lineales. Cuando este no es el caso, la idea de una superposición no es evidente. El análisis de problemas de cerradura con fuentes no lineales se discutirá en la siguiente sección. Debe notarse que en el método de superposición, es necesario resolver, en general, n + 1 problemas de cerradura; mientras que en la formulación integral es necesario resolver únicamente un problema de valor a la frontera para calcular el campo de la función de Green. Por supuesto, existen situaciones en que es necesario resolver sólo un problema de cerradura, en cuyo caso la complejidad del método de superposición es comparable a la de la formulación integral.

Para ilustrar este punto y mostrar la consistencia de la formulación integral con el método de superposición, considere el proceso de transferencia difusiva de masa con reacción química homogénea de primer orden en un medio poroso. Suponiendo que la fase sólida es impermeable, las Ecs. (25a) y (25b) toman la siguiente forma

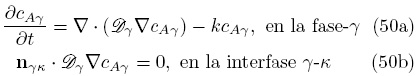
donde, c_Aγ es la concentración molar del reactivo (especie A) en la fase-γ, n_γκ es el vector unitario dirigido de la fase-γ hacia la fase-κ, mientras que 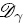y k son los coeficientes de difusión molecular y de reacción de primer orden, respectivamente. Comparando las Ecs. (50a) y (50b) con las Ecs. (25a) y (25b), se observa que en este caso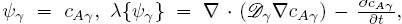

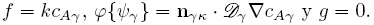
Aplicando el operador de promediado superficial [Ec. (26)] a la Ec. (50a) resulta lo siguiente

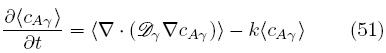
para obtener esta ecuación se tomó en cuenta la suposición de que el medio poroso es rígido, por lo que 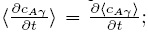además se han despreciado los cambios espaciales del coeficiente de reacción, k, dentro de la región de integración. Aplicando el teorema del promedio espacial [Ec. (31)] para intercambiar diferenciación e integración en la Ec. (51) resulta el siguiente modelo macroscópico no cerrado,

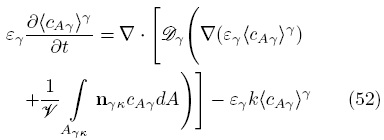
donde se usó la relación de operadores de promediado [Ec. (28)]; además se despreciaron los cambios espaciales de 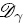y se aplicó la condición de frontera interfacial. Sustituyendo la descomposición espacial de la concentración 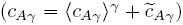en la Ec. (52), se obtiene lo siguiente

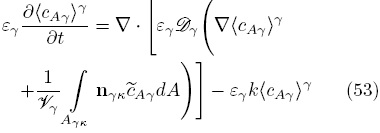
O bien, despreciando los cambios espaciales de ε_γ (esto es posible debido a la restricción r₀ << L, Whitaker, 1999),

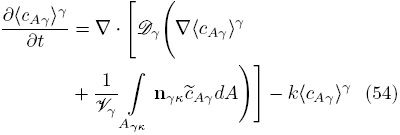
Comparando las Ecs. (54) y (33) se observa que en este caso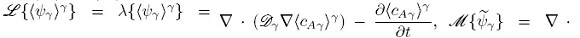

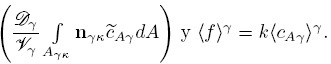
Siguiendo los desarrollos presentados anteriormente, para cerrar el modelo macroscópico es necesario contar con el campo de las desviaciones espaciales de la concentración. Para obtener el respectivo problema de valor a la frontera, se resta la Ec. (54) a la Ec. (50a) para llegar a

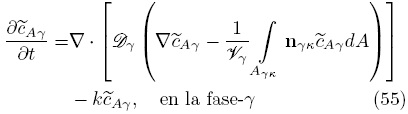
Para simplificar está ecuación se hacen las siguientes suposiciones

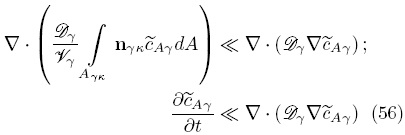
las cuales se justifican cuando se satisfacen las restricciones de escala

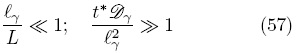
De esta forma, la Ec. (55) se simplifica a

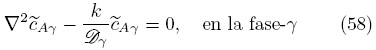
Si se siguen los mismos pasos detallados arriba, se puede demostrar que las ecuaciones que completan el planteamiento del problema de 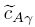son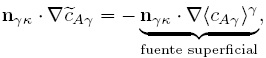

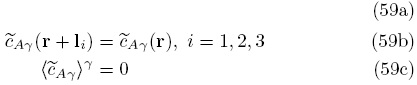
Note que, en este caso, no es necesario indicar la condición inicial ya que se ha impuesto la suposición de estado cuasiestacionario, la cual es razonable para transporte difusivo (Moyne, 1997). Como se ha considerado una cinética de primer orden, ésta puede incluirse en el operador para la función de Green, de manera que el problema asociado al problema de 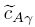es

En este caso, 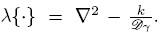Usando la fórmula de Green en tres dimensiones,

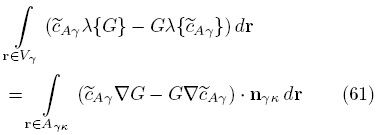
La Ec. (61) se simplifica notablemente al sustituir las ecuaciones diferenciales y condiciones de frontera interfaciales para 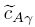y G, para dar lugar a la siguiente solución

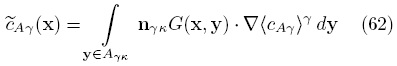
Sin embargo, si se satisface la restricción de escala 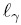<< L, el término promedio puede salir de la integral de área de manera que la Ec. (62) puede escribirse de la siguiente manera simplificada

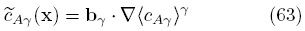
la cual corresponde a la superposición propuesta por Whitaker (1999), donde el vector de cerradura bγ está definido como

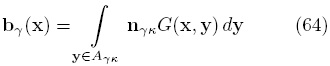
Por ultimo, se sustituye la solución del campo de las desviaciones en el modelo macroscópico [Ec. (53)], para llegar al modelo deseado de medio efectivo

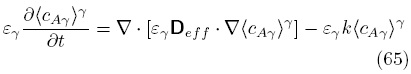
donde se recuperó la definición del tensor de difusividad efectiva propuesto por Whitaker (1999), como

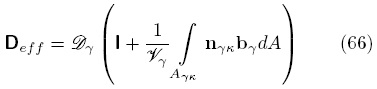
O bien, en términos de la función de Green asociada

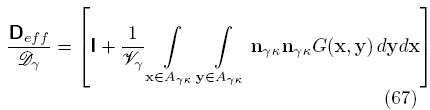
Dado que la función de Green captura el efecto de la geometría usada en la celda unitaria, la Ec. (67) muestra la relación entre el tensor de difusividad efectiva y la microestructura del medio. Más aún, dado que la función de Green depende, en este caso, del valor del coeficiente k; D_eff es función de la velocidad de reacción. Esto constituye una diferencia respecto al resultado presentado por Whitaker (1999) en donde la reacción química es heterogénea, es decir, tiene lugar en la interfase sólido-fluido. En ese caso, el problema de valor a la frontera para las desviaciones de la concentración es

donde a_v es el área interfacial por unidad de volúmen. El problema asociado sigue estando dado por las Ecs. (60a)-(60d) tomando λ{·} = ∇². Usando la fórmula de Green para el Laplaciano en tres dimensiones [Ec. (7b)] resulta que

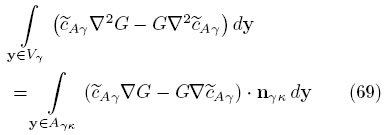
A partir de la cual se obtiene la siguiente solución

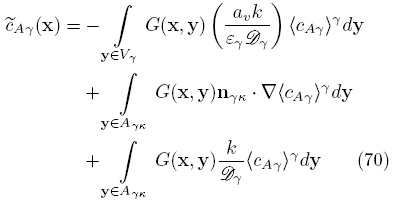
en base en los problemas de valor a la frontera para 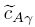y G. O bien, tomando a los términos promedio como constantes en las regiones de integración,

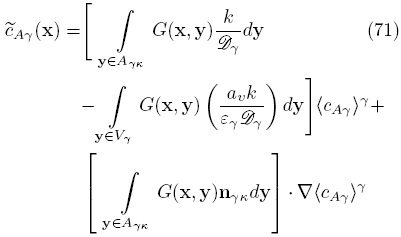
Los términos entre paréntesis rectangulares de la ecuación anterior corresponden a las variables de cerradura s_γ y b_γ de acuerdo a

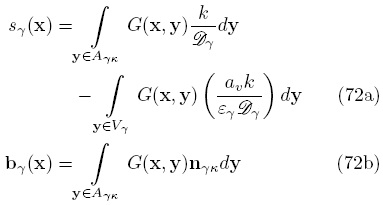
De manera que la Ec. (71) puede expresarse en la siguiente forma simplificada

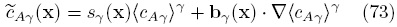
la cual corresponde a la Ec. (1.4-57) de Whitaker (1999) tomando ψ_γ = 0. Más aún, la sustitución de la Ec. (73) en el modelo no cerrado conduce a la siguiente ecuación de medio efectivo

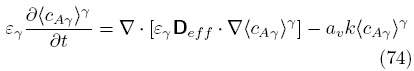
Este resultado difiere de la Ec. (65) no sólo en el último término del lado derecho, sino que además el tensor de difusividad efectiva no es, en este caso, función de k. Debe notarse que la definición de D_eff sigue estando dada por la Ec. (66). Sin embargo, en este problema λ{G} = ∇²G, a diferencia del caso donde la reacción química es homogénea y se tiene que λ{G} = ∇·(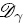∇G) − kG. En otras palabras, cuando la reacción química es homogénea la función de Green (y por tanto el coeficiente de difusividad efectiva) depende tanto del transporte por difusión como por la reacción química, mientras que en el caso en que la reacción es heterogénea, G sólo depende del transporte difusivo y por ende D_eff es independiente de k. La discusión detallada de la funcionalidad del tensor de difusividad efectiva con el tipo de reacción química se discutirá en otro trabajo. Por el momento, es suficiente remarcar que, dada la naturaleza lineal de los problemas que gobiernan el campo de las desviaciones espaciales, la formulación integral permite recuperar la misma estructura de solución que la que se obtiene por el método de superposición. Más aún, como se puede notar de las Ecs. (72a) y (72), al calcular la función de Green se pueden determinar las dos variables de cerradura involucradas en la Ec. (73), mientras que por el método de superposición es necesario resolver un problema de valor a la frontera para cada variable de cerradura.

 

4. Escalamiento de problemas no lineales

Con el fin de ilustrar la extensión de la formulación integral discutida en las dos secciones anteriores al escalamiento de problemas de transporte no lineales, y sin pérdida de generalidad, considere el transporte difusivo de masa con reacción química homogénea en un medio poroso. Las ecuaciones que describen el transporte del reactivo en la microescala son

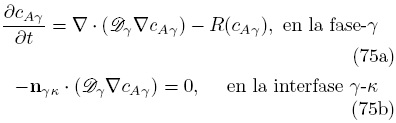
donde R(c_Aγ) representa la expresión de la cinética de reacción, la cual es no lineal en este caso.

Llevando a cabo el proceso de promediado y haciendo el intercambio de diferenciación e integración descrito anteriormente, resulta el siguiente modelo macroscópico no cerrado

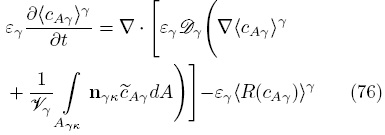
Para que la Ec. (76) pueda ser usada, es necesario contar con expresiones de 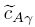y 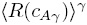en términos de 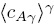. Para lograrlo, es necesario plantear y resolver formalmente el problema de cerradura. La ecuación diferencial que gobierna el campo de 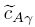resulta de restar la Ec. (76) de la Ec. (75a), y puede expresarse como sigue

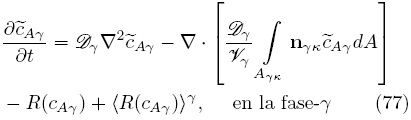
Al igual que en el caso anterior, las restricciones de escala 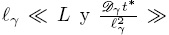1 permiten despreciar el término no local de transporte difusivo con respecto al término de transporte local e imponer la suposición de estado cuasiestacionario. De esta forma, usando la descomposición espacial en los términos de reacción, la Ec. (77) toma la siguiente forma

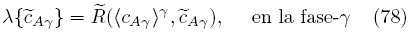
La cual está expresada en términos de la función no lineal 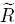, definida como

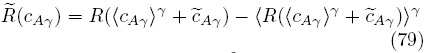
y del operador 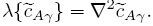Siguiendo los pasos de la sección anterior, las condiciones de frontera que completan el problema de 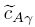son

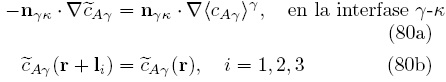
Como se cuenta con el planteamiento completo del problema de 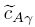, es posible escribir el problema asociado para la función de Green, el cual es

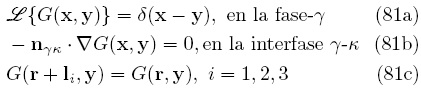
Note que, a diferencia de la Ec. (78), la Ec. (81a) corresponde a la ecuación de Poisson, la cual es lineal. Dado que el problema de las desviaciones de la concentración ha sido planteado en estado cuasiestacionario, la fórmula de Green es, para una celda unitaria tridimensional, la siguiente

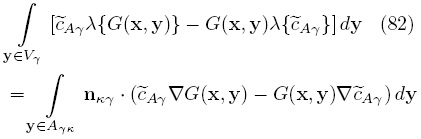
de la cual se obtiene la siguiente expresión para ,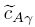

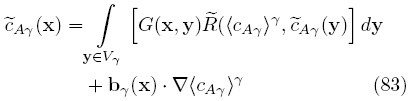
En la Ec. (83) se recuperó la definición del vector de cerradura b_γ (Whitaker, 1999) y es, en este caso, independiente de la reacción química,

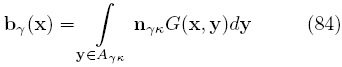
Para expresar la Ec. (83) en una forma más compacta se introduce la siguiente variable de cerradura

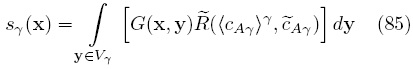
Por lo que la Ec. (83) se simplifica a

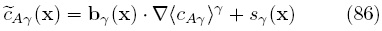
donde el primer término representa la influencia de la parte difusiva del transporte y el segundo representa la influencia de la fuente reactiva. Por supuesto, la Ec. (86) es una solución implícita, pues sγ depende del campo 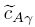. Sin embargo, en trabajos anteriores (Valdés-Parada y col., 2007, 2008a) se ha mostrado que la velocidad de convergencia de la formulación integral puede superar a los esquemas típicos de diferencias finitas. Esto se debe principalmente a que en una formulación integral, los errores de aproximación son suavizados en el paso de integración, a diferencia de esquemas basados en la discretización de operadores diferenciales, en los que el error se propaga por todo el dominio. Además, en una formulación integral las condiciones de frontera (ya sean de tipo Dirichlet, Neumann o Robin) se incorporan en forma exacta en la solución, mientras que en el método de diferencias finitas es necesario reducir en un orden de magnitud la aproximación de las derivadas en la frontera.

Cabe mencionar que, si el problema de cerradura se resuelve en la celda de Chang (Chang, 1982, 1983; Ochoa-Tapia y col., 1994) en una sola dirección, se pueden usar las soluciones analíticas de las funciones de Green presentadas arriba [Ecs. (23), (24a) y (24b)], lo cual facilita el proceso iterativo. Actualmente se está trabajando en esta dirección y los resultados se presentarán en una publicación futura.

Para finalizar esta sección, se sustituye la Ec. (86) en el modelo macroscópico no cerrado [Ec. (76)], para llegar a la siguiente ecuación de medio efectivo

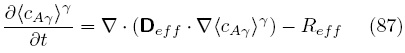
donde D_eff está dada por la Ec. (66). La Ec. (87) contiene un coeficiente de reacción efectiva, el cual se puede calcular a partir del campo de s_γ (x) de acuerdo con la siguiente expresión

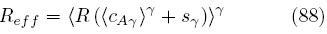
Siguiendo esta metodología puede demostrarse que el modelo de medio efectivo [Ec. (87)] no tiene, en general, la misma forma que el modelo microscópico [Ec. (75a)]. Lo anterior quiere decir, por ejemplo, que en el caso en que la reacción química fuese de segundo orden 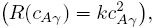es posible que el modelo macroscópico involucre términos de orden cero, así como de primer y segundo orden.

Debe notarse que la metodología aquí propuesta no implica ningún tipo de aproximación de la expresión cinética. En otras palabras, se ha mostrado que es posible desarrollar modelos de medio efectivo cerrados sin necesidad de linealizar la expresión cinética o restringir el análisis a casos particulares que limiten el rango de aplicación del modelo, lo cual constituye un avance significativo en los procesos de escalamiento.

 

Conclusiones

En este trabajo se presentó una formulación integral basada en funciones de Green para la solución formal de los problemas de cerradura involucrados en procesos de escalamiento usando el método del promedio volumétrico. Bajo este enfoque se encontró que si el problema que gobierna los campos de las desviaciones espaciales de alguna propiedad es lineal, se pueden recuperar los resultados del método de superposición. De esta manera se determinó que una variable de cerradura es, en general, el resultado de un proceso de integrar (en el espacio y tiempo) las funciones de Green que describen la influencia de las fuentes promedio en los campos de las desviaciones espaciales en una determinada posición y tiempo. Además, se mostró que las funciones de Green representan la información esencial de la geometría involucrada en la celda unitaria. Esto hizo posible llegar a expresiones del tensor de difusión efectiva como función de la microestructura a partir de la función de Green asociada.

Entre las ventajas que presenta la formulación integral respecto al método de superposición se encuentran las siguientes:

• Al plantear la solución del problema de las desviaciones espaciales mediante la formulación integral se puede identificar directamente el significado físico de cada variable de cerradura. Esto se traduce en un mejor entendimiento de los términos que componen el campo de las desviaciones espaciales y en los coeficientes efectivos que resultan en los modelos macroscópicos.

• Para cerrar una solución formal es necesario resolver sólo el problema de valor a la frontera que determina el campo de las funciones de Green. Por otro lado, en el método de superposición es necesario, en general, resolver tantos problemas de valor a la frontera como fuentes de desviaciones existan.

• La formulación integral puede extenderse para el estudio de modelos de transporte que involucren términos de fuente no lineales sin necesidad de aproximar dichos términos. En este caso, el resultado es una solución implícita con la cual se puede cerrar el modelo macroscópico.

Actualmente se está trabajando en la aplicación de esta metodología a una variedad de situaciones de interés en ciencias e ingeniería. Entre ellas se encuentra la discusión de la funcionalidad del tensor de difusión efectiva con el tipo de reacción (homogénea o heterogénea) que se lleva a cabo en el medio poroso. Además, se están investigando metodologías numéricas eficientes y paquetes computacionales comerciales que permitan calcular las funciones de Green en celdas unitarias simples (medios homogéneos y ordenados) y complejas (en regiones de cambios geométricos drásticos, medios aleatorios, dominios resultantes del procesamiento digital de microfotografías de sistemas reales, etc.).

 

Agradecimientos

Parte de este trabajo fue presentado en el XXX Encuentro Nacional de la AMIDIQ y en el Seminario sobre la Predicción de Coeficientes Efectivos en Problemas de Escalamiento organizado por el área de ingeniería en recursos energéticos de la UAM-Iztapalapa. El autor está agradecido a los asistentes de ambos eventos, así como a los doctores Brian Wood y Mark Porter (Oregon State University) por sus valiosos comentarios.

 

Referencias

Bear J. (1972). Dynamics of Fluids in Porous Media. Elsevier.         [ Links ]

Chang H-C. (1982). Multiscale analysis of effective transport in periodic heterogeneous media. Chemical Engineering Communications 15, 83-91.         [ Links ]

Chang H-C. (1983). Effective diffusion and conduction in two-phase media. AIChE Journal 29, 846-853.         [ Links ]

Crapiste G.H., Rotstein E., Whitaker S. (1986). A general closure scheme for the method of volume averaging. Chemical Engineering Science 41, 227-235.         [ Links ]

Gray W. (1975). A derivation of the equations for multiphase flow. Chemical Engineering Science 30, 229-233.         [ Links ]

Haberman R. (2004). Applied Partial Differential equations with Fourier series and boundary value problems. Prentice Hall, New Jersey.         [ Links ]

Haji-Sheikh A., Minkowycz W.J., Sparrow E.M. (2004). Green's function solution of temperature field for flow in porous passages. International Journal of Heat and Mass Transfer 47, 4685-4695.         [ Links ]

Howes F.A., Whitaker S. (1985). The spatial averaging theorem revisited. Chemical Engineering Science 40, 1387-1392.         [ Links ]

Kim D. W., Park S.K., Jun S. (2008). Axial Green's function method for multidimensional elliptic boundary value problems. International Journal for Numerical Methods in Engineering 76, 697-726.         [ Links ]

Li B.Q., Evans J.W. (1991). Boundary element solution of heat convection-diffusion problems. Journal of Computational Physics 93, 255-272.         [ Links ]

Mishra M., Peiperl L., Reuven Y., Rabitz H., Yetter R.A., Smooke M.D. (1991). Use of Green's functions for the analysis of dynamic couplings: Some examples from chemical kinetics and quantum dynamics. Journal of Physical Chemistry 95, 3109-3118.         [ Links ]

Moyne C. (1997). Two-equation model for a diffusive process in porous media using the volume averaging method with an unsteady-state closure. Advances in Water Resources 20, 63-76.         [ Links ]

Mukkavilli S., Tavlarides L. L., Wittmann C.V. (1987a). Integral method of analysis for chemical reaction in a nonisothermal finite cylindrical catalyst pellet-I. Dirichlet problem. Chemical Engineering Science 42, 27-33.         [ Links ]

Mukkavilli S., Tavlarides L. L., Wittmann C.V. (1987b). Integral method of analysis for chemical reaction in a nonisothermal finite cylindrical catalyst pellet-II. Robin problem. Chemical Engineering Science 42, 35-40.         [ Links ]

Ochoa-Tapia J. A., Stroeve P., Whitaker S. (1994). Diffusive transport in two-phase media: spatially periodic models and Maxwell's theory for isotropic and anisotropic systems. Chemical Engineering Science 49, 709-726.         [ Links ]

Valdés-Parada F.J., Alvarez-Ramírez J., Ochoa-Tapia J.A. (2007). Análisis de problemas de transporte de masa y reacción mediante funciones de Green. Revista Mexicana de Ingeniería Química 6, 283-294.         [ Links ]

Valdés-Parada F.J., Sales-Cruz M.A., Alvarez Ramírez J., Ochoa-Tapia J.A. (2008a). On Green's funcions methods to solve reaction-diffusion systems. Computers and Chemical Engineering 32, 503-511.         [ Links ]

Valdés-Parada F.J., Sales-Cruz M.A., Alvarez Ramírez J., Ochoa-Tapia J.A. (2008b). An integral equationformulation for solving reaction-diffusion-convection boundary-value problems. International Journal of Chemical Reactor Engineering 6, article A61.         [ Links ]

Whitaker S. (1999). The Method of Volume Averaging. Kluwer Academic Publishers.         [ Links ]

Whitaker S. (2009). Chemical engineering education: Making connections at interfaces. Revista Mexicana de Ingeniería Química 8(1), 1-32.         [ Links ]

Wood D.D. (2009). The role of scaling laws in upscaling. Advances in Water Resources 32, 723-736.         [ Links ]