Serviços Personalizados
Journal
Artigo
Indicadores
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista mexicana de ingeniería química
versão impressa ISSN 1665-2738
Rev. Mex. Ing. Quím vol.9 no.1 Ciudad de México Abr. 2010
Control
Observer based adaptive model for a class of aerobic batch bioreactor
Modelo adaptable basado en un observador para una clase de bio-reactor aerobio por lotes
R. Aguilar-López1*, P. A. López-Pérez1, M.I. Neria-González2 and A.R. Domínguez-Bocanegra1
1 Departamento de Biotecnología y Bioingeniería CINVESTAV-IPN Av. Instituto Politécnico Nacional, No. 2508, San Pedro Zacatenco, D.F. México. * Corresponding author. E-mail: raguilar@cinvestav.mx.
2 División de Ingeniería Química y Bioquímica Tecnológico de Estudios Superiores de Ecatepec.
Received 26 of August 2009;
Accepted 12 of January 2010
Abstract
The main issue of this work is to design a nonlinear observer (soft sensor) with finite convergence time for a class of batch bioreacting systems. Considering the necessity to fast response for monitoring and control issues for batch processes a finite time high order sliding-mode observer is considered. It is presented a theoretical analysis to provide a sketch of proof to demonstrate the convergence properties of the proposed observer and the finite time of convergence is calculated from the same analysis. A simple model for a batch aerobic wastewater bioreactor, experimentally corroborated, is proposed as application example and numerical experiments show the adequate observer performance compared to a standard nonlinear Luenberger observer.
Keywords: batch processes, bioreactors, finite time convergence, observer design.
Resumen
El principal objetivo de este trabajo el diseñar un observador no lineal (sensor suave) con tiempo de convergencia finito para un tipo de biosistemas por lotes. Considerando la necesidad de respuestas ra6pidas en cuestiones de monitoreo y control para procesos por lotes se considera un observador de estados de modos deslizantes de alto orden de convergencia a tiempo finito. Se presenta un análisis teórico para demostrar las características de la convergencia del observador propuesto y el tiempo finito de convergencia es determinado a partir de este análisis. Un modelo simple de un birreactor aerobio por lotes para tratamiento de aguas residuales, experimentalmente validado, es propuesto como un ejemplo de aplicaci6on y experimentos num6ericos muestran el desempeño adecuado del observador propuesto en comparacio6n con un observador esta6ndar no lineal de tipo Luenberger.
Palabras clave: procesos por lote, biorreactores, convergencia de tiempo finito, diseño de observador.
1. Introduction
One the major bottlenecks in the application of computer monitoring and control for biological process is the lack of reliable, sterilizable and robust sensors for the on-line measurements of process key variables, such as biomass, precursors and product concentrations. In particular the biomass concentration (or cell activity) is generally measured via optical techniques, electrochemical detection and by viscosity, filtration and fluorescence methods, but these approaches frequently do not properly address the most important industrial problems and necessities. On other hand, the monitoring and control designs are related with a class of continuous process where the synthesis of observers and controllers is done considering asymptotic (t → ∞) convergence. However, in chemical industry the batch processes are up-to-date very important in pharmaceutics, polymer, and wastewater, so on. These kinds of processes present serious problems for on-line monitoring and control issues, for their dynamic behavior nature, where a non steady-state is reached, such that the observation and control actions must be implemented in a finite time.
For this topic, observers' theory for nonlinear systems is a developing scientific field; hence important and interesting results have been presented for nonlinear systems with different characteristics, such as continuous and discrete dynamics, several types of nonlinearities, non modeled dynamics and so on (see Raghavan et al., 1994; Aguilar et al., 2003; Aguilar, 2003). However, despite of these great theoretical advances several issues remain unsolved; for example, most of the observers in continuous time setting are designed for asymptotic convergence (Kazantzis and Kravaris, 1998; Nijmeijer and Fossen, 1999; Thau, 1973). In contrast, convergence in finite time is an attractive feature which is very important for industrial applications.
Up-to-date, for batch processes the control issues have had more attention, the control problem in batch process is related to tracking issues, where optimal and deadbeat controllers have been successfully employed. On this topic, continuous time-invariant feedback controllers have been studied and finite time controllers involving terms containing fractional powers were constructed (At-hans and Falb, 1966; Bhat and Berstein, 2000). Furthermore, also output feedback control design in finite time has been studied (Haimo, 1986). However, as it is well known, control problems are parallel to estimation issues; therefore observer design with finite time convergence must be considered for on-line monitoring, fault detection and other related control issues of batch processes.
Finite time observers have been presented in several papers, for example Engel and Kreisselmeier designed a finite time observer for linear systems, where the convergence time can be assigned independent of the observer eigenvalues. In particular, the named high order sliding-mode techniques claim robustness to deal with uncertainties, disturbances, chattering reduction and finite time convergence (Engel and Kreisselmeier, 2005); this techniques have been applied to control design and observer design for triangular systems (Levant, 2001; Bertoni and Punta, 2000). Almost all finite time controllers and observers have been applied to robot manipulators (Hong et al., 2001; Hong et al., 2002), secure data transmission (Feki, 2003) but the process control and estimation applications are up-to-date, very few.
The objective of this paper is to present an observer design procedure for the class of nonlinear batch system, where the application example related with a wastewater batch bioreactor is presented in Section 2; Section 3 develops observer design and the convergence properties founded from theoretical analysis, besides the convergence time is presented. Section 4 comments about numerical experiments and finally Section 5 is the conclusion of this work.
2. The aerobic wastewater batch bioreactor
A wastewater from petrochemical industry which is generated in the different chemical processes is considered in this work. The wastewater contains volatile organic carbon's substances classified as toxics (SEMARNAP, 1997) like 1,2 dichloroethane, chloroform, benzene, among others volatile compounds, (VOC's). The petrochemical wastewater treatment plant is located near the Mexican coast, where the mean weather temperature in the hottest months (April to August) is nearly 35° C and in extreme conditions it reaches up to 38° C. Such high temperatures affect the air temperature at the compressor exit producing a significant air temperature rise at the diffusers up to 82°C or more. This provokes an increase in the bioreactor wastewater temperature within the biological reactor. As a matter of fact, the actual temperature conditions within the bioreactor are 32°C in October-November reaching up to 41°C in August-September. Due to this effect, the microorganism's activity is affected and this must be considered in the dynamic modeling of the system. As a first approach to process analysis a kinetic model of the process was carried out. Some models have been developed to describe the effect of temperature on bacterial growth (Zwieterig et al., 1991; Heitzer et al., 1991). The temperature effect on the maximum specific growth rate, mass transfer coefficient for oxygen (kla) and death coefficient (kd), were incorporated in the mass balance equations of the process.
2.1. Experimental
Experimental data were obtained from the petrochemical biological wastewater plant. Different samples were taken out daily (after 8 hours), from the influent and bioreactors during the period from October 2002 to September 2003. Bench-scale bioreactor was utilized. These units are made of Plexiglas with a volume capacity of 15 liters. The air was supplied using air diffusers stone in the reactor bottom to keep the dissolved oxygen (DO) concentration at values higher than 4.0 mg/L. The bubbles produced during the aeration kept the contents of the bioreactor well mixed and homogeneous. Start-up was performed with wastewater and inoculated with biological sludge. Samples were taken out from the wastewater reservoir. Chemical oxygen demand (COD) and the volatile suspended solids (SSV) were determined in each sample employing the methodology proposed in (Eckefelder, 2000). The mean of three analyses was taken, in order to obtain the results reported as below.
2.2. Modeling
The model structure is based on the IWA 1 model (Dochain, 2001). The chemical oxygen demand (COD) was measured (Ramalho, 1999) in the laboratory plant. The kinetic parameters were obtained in laboratory bioreactors following the method by Ramalho (1999).
Bioreactor temperature is a very important factor, such that it affects the microorganism growth, generally the microorganism growth between 30 a 40° C, independently if the microorganism are psicrophyles, mesophyles or thermophyles. The temperature affect directly the specific growth rate, the corresponding metabolism and the coefficient yields, besides, several of the bacterial population can not floculate and can not degrade substrate, therefore an important fraction of the microorganism dead.
The temperature effect on the maximum specific growth rate was evaluated, where b = 0.05 (K)-1 h-0'5 K in Kelvin and h in hours (Zwieterig et al., 1991) and c = 0.005 (K)-1 (which is a parameter to fit the experimental data to the model), the mass transfer coefficient for the oxygen ( kla) with Eq. (7) which is an empirical function of the air flow (Dochain, 2001), the death coefficient (kd) with Eq. (6), the evaporation flux of VOC's (KevS) is also considered in the COD balance, together with the inactivate biomass kd(1 —fn)X which contributes to growth the substrate concentration in the bioreactor, all were incorporated in the mass balance equations of the process. The bioreactor behavior was assumed as completely mixed reactor. As usual, the follow equations were used to obtain the biokinetic coefficients (Dochain, 2001):
Substrate (S) concentration mass balance:
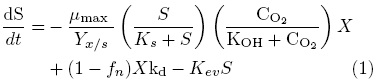
Biomass (X) concentration mass balance:
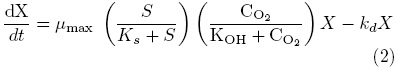
Oxygen (CO2) concentration mass balance:
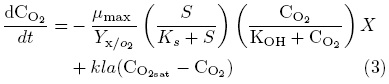
As can be noticed the mathematical model of the considered bioreactor consist of three coupled nonlinear ordinary differential equations; this model is based on the corresponding mass balances for substrate, biomass and disolved oxygen concentrations in the bioreactor. The model consider endogenus methabolism, in order to introduce a microorganism death rate, evaporation subtrate rate and disolved oxygen mass transfer coefficient, all of them temperature depended The model validation is tuned with industrial data, as is presented in (Martínez et al., 2005; Maqueda et al., 2006). See the nomenclature section for variables definition. The goal of this model is to be employed as a virtual plant to infer substrate and biomass concentration (state variables of hard determination) from on-line dissolved oxygen concentration which is considered as the measured process output.
3. Methodology for the observer design
In a vector compact form the reactor model can be expressed as the following system:
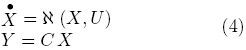
In general, X ∈ ℜn is the vector of states; U ∈ ℜq is the control input vector; ℵ (o) : ℜn → ℜn is a nonlinear vector field; the measured output coefficient C ∈ ℜn; and Y ∈ ℜm is the linear system measured output.
Proposition 1. The dynamic system described by Eq. (9) is a finite time observer for system (4).
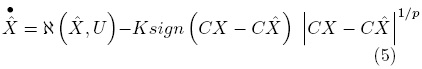
Here K is the observer gain and p ∈ Z+,p > 1 being p an odd number.
3.1. Proof of Proposition 1
From eqs. (4) and (5), the dynamics of the estimation error (e = X — 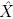 ) can be constructed as follows:
) can be constructed as follows:
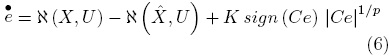
Now, consider the following assumption:
A1. The function ℵ (o) complies with Lipschitz condition with respect to X, i.e., 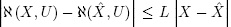 ; the Lipschitz constant is L > 0; therefore Eq. (6) can be expressed as:
; the Lipschitz constant is L > 0; therefore Eq. (6) can be expressed as:
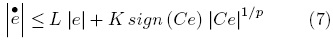
Applying the equality:
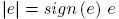
The following is obtained:
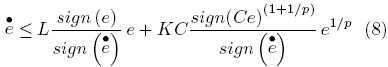
Now, it is possible to define the following change of variable, then for each component of the vector e we define:
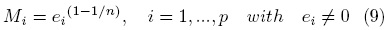
Expressing the estimation error in the new variable, it is possible to find its dynamics as shown by Eq. (10).
Combining eqs. (8-9) the following equation system is generated:
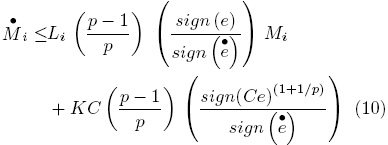
A2. Considering e ≠ 0 and p ∈ Z+ , (p — 1)/p > 0.
By solving and performing algebraic manipulations of Eq. (10), it is possible to find some relationships among the variable Mi and the sign of its dynamics then by assuming A2, we obtain the general solution of Eq. (10) for t0 = 0:
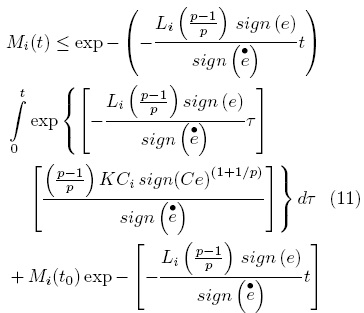
After algebraic manipulations of Eq. (11) the following equation is obtained:
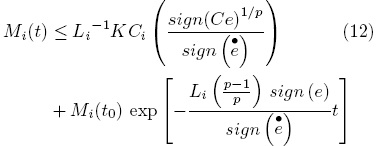
If 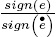 > 0 and t is large enough and considerign (12) then:
> 0 and t is large enough and considerign (12) then:
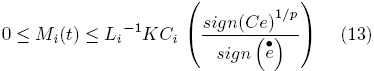
If KCi is small enough Mi(t) → εi with εi > 0 as small as be desired. Furthermore ei = 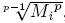 , then ei =
, then ei = 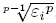 , we choose ē = maxi ei and
, we choose ē = maxi ei and 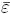 = maxiεi. It can be concluded that ē ∈
= maxiεi. It can be concluded that ē ∈ 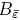 (0).
(0).
3.2. Convergence time calculation
In order to determine the convergence time of the proposed observer, let's consider Eq. (12). As it can be seen the second term of the right side of the above equation is time dependent, at steady state condition this term must exhibit a numerical value close to zero (Eq. 14).
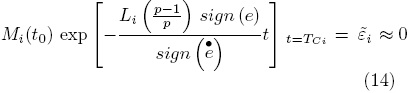
Here, TC is the convergence time of the observer to the open ball ē ∈ 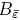 (0); after algebraic manipulations, the following equation for the convergence time is calculated as:
(0); after algebraic manipulations, the following equation for the convergence time is calculated as:
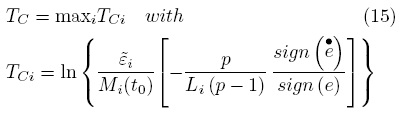
4. Estimation performance index for the substrate concentration.
In order to show the performance of the observer proposed, the mathematical model of batch bioreactor given in Section 2 was employed as application example. For comparison purposes a standard nonlinear Luenberger observer is implemented too. The initial condition of the batch reactor was considered as So = 2200 mg/L; Xo = 800 mg/L and O2o = 4 mg/L, the initial condition for both two observers are 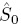 = 2000 mg/L;
= 2000 mg/L; 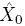 = 750 mg/L;
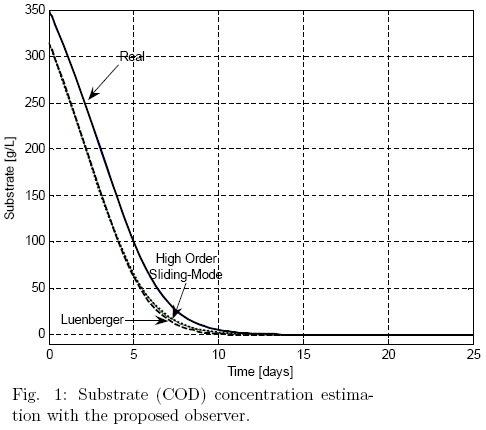
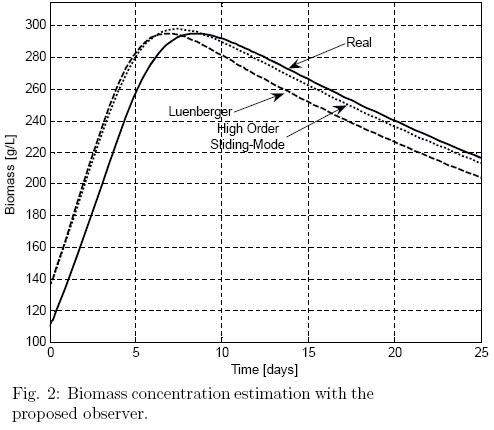
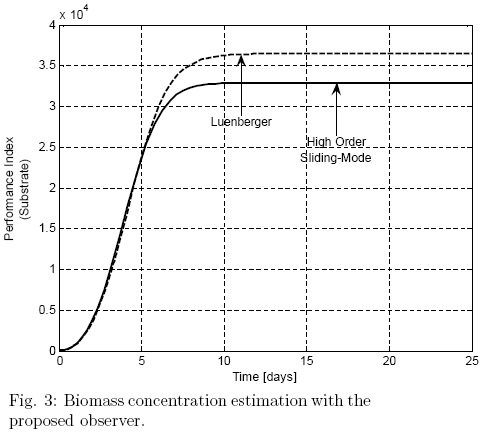
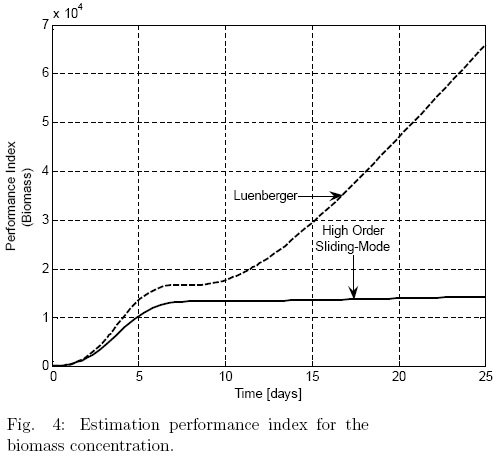
= 750 mg/L; 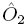 = 3.4 mg/L. The observer gains are considered the same for the entire variables estimated and for both observers, the values Ki = 1 day-1 are chosen for simulation purposes. The dissolved oxygen concentration is considered as the corresponding measured output, it is justified such that dissolved oxygen is one of the reactor's variables more common and easy to measuring, besides from a standar observability test, the substate and the biomass are observable from dissolved oxygen measurements. In the case of the proposed estimation methodology, it is possible to note faster convergence rate and small steady-state error (Fig. 1 to Fig. 3) (Fig.2), which is very important for the transient nature of the (batch) bioreactor; this situation is in accordance to the theoretical properties of the observer. Figs. 4 and 5 are related to the estimation error behavior for the proposed observer and the nonlinear Luenberger observer, where can be appreciated the asymptotic convergence of the classical observer in comparison with a faster response of the proposed methodology. Note that the proposed methodology can show a satisfactory performance despite of any set of initial conditions.
= 3.4 mg/L. The observer gains are considered the same for the entire variables estimated and for both observers, the values Ki = 1 day-1 are chosen for simulation purposes. The dissolved oxygen concentration is considered as the corresponding measured output, it is justified such that dissolved oxygen is one of the reactor's variables more common and easy to measuring, besides from a standar observability test, the substate and the biomass are observable from dissolved oxygen measurements. In the case of the proposed estimation methodology, it is possible to note faster convergence rate and small steady-state error (Fig. 1 to Fig. 3) (Fig.2), which is very important for the transient nature of the (batch) bioreactor; this situation is in accordance to the theoretical properties of the observer. Figs. 4 and 5 are related to the estimation error behavior for the proposed observer and the nonlinear Luenberger observer, where can be appreciated the asymptotic convergence of the classical observer in comparison with a faster response of the proposed methodology. Note that the proposed methodology can show a satisfactory performance despite of any set of initial conditions.
Conclusions
A methodology for the design of a finite time nonlinear observer has been presented for on-line monitoring purposes. For the case of bounded systems, such as the case of bioreacting systems, it was possible to find convergence properties of the observer proposed and to estimate its convergence time. The observer proposed exhibits finite convergence time, as it was presented in section 3, and its performance is more satisfactory than the one obtained when we use a classical nonlinear Luenberger observer. Note that the proposed observer avoids the high gain observer approach, in order to improve the convergence rate; it is very important issue such that the high gain observers tend to amplify the noise measurements. This characteristic is appreciated for state estimation in nonlinear plants with finite time operation and faster dynamics. The proposed methodology can be employed for biomass and substrate estimation from dissolved oxygen measurements for aerobic biological systems.

References
Aguilar-López R. (2003) Integral observers for uncertainty estimation in continuous chemical reactors: differential-algebraic approach. Chemical Engineering Journal 9, 113-120. [ Links ]
Aguilar R., Martínez-Guerra R. and Maya-Yescas R. (2003) State Estimation for Partially Unknown Nonlinear Systems: A Class of Integral High Gain Observers. IEE Proceedings Control Theory and Applications 150 (3), 240-244. [ Links ]
Athans M., Falb P. (1966) Optimal Control: An introduction to theory and Applications. Mc-Graw Hill, New York. [ Links ]
Bertoni G., Punta E. (2000) Chattering elimination with second order sliding-modes robust to Coulomb friction. Journal of Dynamics, Measurement and Control 122, 679-684. [ Links ]
Bhat S., Berstein D. (2000) Continuous finite time stability of continuous autonomous systems. SIAM Journal of Control and Optimization 38, 751-766. [ Links ]
Dávila J., Fridman L., Levant A. (2005) Second order sliding-mode observer for mechanical systems. IEEE Transactions on Automatic Control 50 (11), 1785-1789. [ Links ]
Dochain, D. and Vanrolleghem, P. (2001). Dynamic modeling and estimation in wastewater treatment process. IWA Publishing. U.K. [ Links ]
Eckefelder, W. (2000) Industrial water pollution control. Environmental Engineering Series. McGraw Hill. 3rd Ed. 34 [ Links ]
Engel R., Kreisselmeier G. (2002). A continuous-time observer which converges in finite time. IEEE Transactions on Automatic Control 47 (7), 1202-1204. [ Links ]
Feki M. (2003) Observer-based exact synchronization of ideal and mismatched chaotic systems. Physics Letters A 309, 53-60. [ Links ]
Haimo V. (1986). Finite time controllers. SIAM Journal of Control and Optimization 24 (4), 760-770. [ Links ]
Heitzer, A., Hans-Peter E., Reichert, P. and Hamer, G. (1991). Utility of phenomenological models for describing temperature dependence of bacterial growth. Applied Environmental Microbiology 57, 2656-2665. [ Links ]
Hong Y., Huang J., Xu Y. (2001) On an output feedback finite-time stabilization problem. IEEE Transactions on Automatic Control 46 (2), 305-309. [ Links ]
Hong Y., Xu Y., Huang J. (2002) Finite-time control for robot manipulators. Systems and Control Letters 46, 243-253. [ Links ]
Kazantzis N., Kravaris C. (1998) Nonlinear observer design using Liapunov's auxiliary theorem. Systtems and Control Letters 34, 241-247. [ Links ]
Levant A. (2001). Universal single-input-single-output (SISO) sliding-mode controllers with finite-time convergence. IEEE Transactions on Automatic Control 46 (9), 1447-1451. [ Links ]
Maqueda M.A.M., Martínez S.A., Narvffez D., Rodríguez M.G., Aguilar-López R., Herrero V. M. (2006) Dynamical modeling of an activated sludge system of a petrochemical plant operating at high temperatures. Water Science and Technology 53, (11), 135-142. [ Links ]
Martínez S., Rodríguez M., Morales M., Aguilar R. (2005) Effect of the temperature in the performance of a biological system for the treatment of wastewater in a petrochemical industry. Ingeniería Hidráulica en México November - December. [ Links ]
Ministry of the Environment, Natural Resources and Fisheries SEMARNAP (1997). NOM001-ECOL-1996. México D.F., México. [ Links ]
Nijmeijer H., Fossen T.I. (1999). New directions in nonlinear observer design. Springer. [ Links ]
Raghavan S., Hendrick J.K. (1994) Observer design for a class of nonlinear systems. International Journal of Control. 59, 515-528. [ Links ]
Ramalho, R. (1999) Wastewater Treatment. Ed. Reverte. Spain. [ Links ]
Thau F.E. (1973). Observing state of nonlinear dynamic systems. International Journal of Control 17, 471-479. [ Links ]
Zwieterig, M.H., De Koos, J.T., Hasenack, B.E., De Wit, J.C. and Van 'Triet, K. (1991). Modeling of bacterial growth as a function of temperature. Applied Environmental Microbiology 57, 1094-1101. [ Links ]














