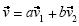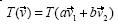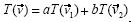Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista latinoamericana de investigación en matemática educativa
versión On-line ISSN 2007-6819versión impresa ISSN 1665-2436
Relime vol.9 no.3 Ciudad de México nov. 2006
Transformaciones lineales en un ambiente de geometría dinámica 1
Rocío Uicab 2 Asuman Oktaç 3
2 Facultad de Matemáticas Universidad Autónoma de Yucatán México E–mail: uballote@tunku.uady.mx
3 Cinvestav–IPN México E–mail: oktac@cinvestav.mx
Fecha de recepción: Marzo de 2006
Fecha de aceptación: Septiembre de 2006
RESUMEN
Este artículo reporta la presencia o ausencia de un pensamiento sistémico en los estudiantes, al resolver el problema de extensión lineal, el cual consiste en determinar una transformación lineal por medio de las imágenes de los vectores de una base. Este problema se plantea geométricamente, haciendo uso de las herramientas del software Cabri–géomètre II. Las dificultades que presentan los estudiantes cuando hacen frente a este problema pueden deberse a que ellos no realizan las conexiones adecuadas entre los conceptos involucrados. Este fenómeno puede estudiarse desde el punto de vista de la aproximación teórica el pensamiento teórico versus el pensamiento práctico (Sierpinska, 2000). Uno de los rasgos del pensamiento teórico es que intenta enfocarse en el establecimiento y estudio de las relaciones entre los conceptos y su caracterización dentro de un sistema que también contiene otros conceptos (Sierpinska, et al. 2002).
PALABRAS CLAVE: Transformaciones lineales, conexiones, pensamiento teórico, álgebra lineal, geometría dinámica.
ABSTRACT
This paper reports the presence or absence of a systemic thinking in students, when they solve the linear extension problem, which consists of determining a linear transformation through the images of the vectors of a basis. The problem is formulated geometrically, making use of the tools of the Cabri–géomètre II software. The difficulties that students present when face this problem, probably are due to that they do not carry out the adequate connections among the concepts involved. This phenomenon can be studied from the point of view of the theoretical approximation the theoretical thinking versus the practical thinking (Sierpinska, 2000). One of the characteristics of the theoretical thinking is that tries to be focused in the establishment and study of the relations between the concepts and its characterization inside a system that also contains other concepts (Sierpinska, et al. 2002).
KEY WORDS: Linear transformations, connections, theoretical thinking, linear algebra, dynamic geometry.
RESUMO
Este artigo reporta a presença ou a ausência de um pensamento sistêmico nos estudantes, ao resolver o problema de extensão linear, no qual consiste em determinar uma transformação linear por meio das imagens dos vetores de uma base. Este problema se coloca geometricamente, fazendo uso das ferramentas do software Cabri–géomètre II. As dificuldades que apresentam os estudantes quando fazem frente a este problema pode ser devido a que eles não realizam as conexões adequadas entre os conceitos envolvidos. Este fenômeno pode–se estudar desde o ponto de vista da aproximação teórica e pensamento teórico versus o pensamento prático (Sierpinska, 2000). Uma das características do pensamento teórico é que tenta enfocar o estabelecimento e estudo das relações entre os conceitos e sua caracterização dentro em um sistema que também contém outros conceitos (Sierpinska, et al. 2002).
PALAVRAS CHAVE: Transformações lineares, conexões, pensamento teórico, álgebra linear, geometria dinâmica.
RÉSUMÉ
Cet article reporte la présence ou l'absence d'une pensée systémique chez les étudiants, au moment de résoudre le problème d'extension linéale, qui consiste à déterminer une transformation linéale à travers les images des vecteurs d'une base. Ce problème se pose géométriquement, en faisant usage des outils du software Cabri–géomètre II. Les difficultés que présentent les étudiants quand ils font face à ce problème peuvent trouver leur origine au fait que les étudiants ne font pas les connections adéquates entre les concepts impliqués. Ce phénomène peut s'étudier depuis le point de vue de l'approximation théorique la pensée théorique versus la pensée pratique (Sierpinska, 2000). Une des caractéristiques de la pensée théorique est qu'elle essaye de se concentrer dans l'établissement et dans l'étude des relations entre les concepts et leurs caractérisation a l'intérieur d''un système qui contient aussi d'autres concepts (Sierpinska, et al. 2002).
MOTS CLÉS: Transformations linéales, connections, pensée théorique, algèbre linéale, géométrie dynamique.
1. INTRODUCCIÓN
Durante el aprendizaje escolar suele ocurrir que los estudiantes se apropian de los conceptos de manera aislada y no de manera estructurada. Esto hace que tengan dificultades cuando abordan situaciones completamente nuevas cuya resolución no se puede realizar sólo recordando algún procedimiento enseñado por el profesor.
Poseer una estructura conceptual da lugar a que el estudiante no sólo trabaje con los conceptos como objetos aislados y aplique procedimientos, sino también a que reflexione de manera general sobre ellos, que los vea como elementos de un todo coherente y establezca conexiones. En este trabajo, nuestro enfoque se centrará en esta forma integradora de pensar, la cual está relacionada con el pensamiento teórico (Sierpinska, 2000) y en particular con el pensamiento sistémico.
Un pensamiento sistémico implica pensar sobre sistemas de conceptos, donde el significado de un concepto está basado en sus relaciones con otros, no con cosas o eventos (Sierpinska et al., 2002); de acuerdo con los investigadores, se divide en definicional, demostrativo e hipotético. Consideramos que la presencia de un pensamiento sistémico en la adquisición de conceptos desempeña un papel importante en la didáctica de las matemáticas.
Algunos errores de los alumnos cuando resuelven un problema podrían explicarse mediante la falta de conexiones que deberían hacer entre los conceptos que forman un sistema. La detección de tal fenómeno por profesores e investigadores podría llevarlos a enfocarse en las conexiones que deberían desarrollarse en los estudiantes para una comprensión adecuada de los conceptos de matemáticas.
Para este trabajo elegimos el tema de transformación lineal, que concierne al álgebra lineal, por ser un tópico central relacionado con conceptos como espacio vectorial, combinación lineal, base, valores y vectores propios, entre otros. Además, las transformaciones lineales juegan un papel importante en muchas áreas de las matemáticas, así como en numerosos problemas aplicados en las ciencias físicas, económicas y sociales.
El problema central que seleccionamos para llevar a cabo nuestra experimentación fue tomado de los trabajos de Sierpinska y sus colaboradores (Sierpinska et al., 1999; Sierpinska, 2000; Trgalová & Hillel, 1998). Se le denomina como problema de extensión lineal, y consiste en determinar una transformación lineal por medio de las imágenes de los vectores de una base; para resolverlo, se hace uso de herramientas del software Cabri–Géomètre II. El problema de extensión lineal nos permite explorar los vínculos que hacen los estudiantes entre diferentes conceptos de álgebra lineal, así como observar las estrategias que usan cuando están trabajando ante una situación no familiar.
2. ANTECEDENTES
2.1. La investigación en la enseñanza y aprendizaje del álgebra lineal llevada a cabo por Sierpinska y colaboradores.
Un grupo de investigadores, bajo la dirección de Sierpinska, en su afán por explicar ciertos aspectos que afectan el razonamiento de los estudiantes en el álgebra lineal, inició una investigación cuyo objetivo era detectar las dificultades de los estudiantes sobre las nociones de esta rama de las matemáticas.
De 1993 a 1996, la investigación se enfocó en los modelos de estructura general del comportamiento matemático de los estudiantes, al interactuar individualmente con tutores y textos de álgebra lineal. En el período 1996–1999, se centró en el diseño de una introducción al álgebra lineal, que estuvo basado en un modelo geométrico de espacio vectorial bidimensional. El principal problema que se intentó resolver con tal diseño fue disminuir en los estudiantes el desarrollo del obstáculo de formalismo (cuando el estudiante manipula las representaciones formales simbólicas, pero no tiene las suficientes aptitudes para comprenderlas).
Como parte de su justificación por su inclinación a la geometría, algunos aspectos que los investigadores señalan es que habitualmente los vectores en R2 o R3 son presentados a los estudiantes como coordenadas y las transformaciones como matrices; posteriormente, se hace el vínculo con la geometría analítica. Esta aproximación tiene varias deficiencias y en muchas ocasiones crea confusión en los estudiantes. Por su parte, una aproximación geométrica permite fácilmente considerar las transformaciones no lineales, donde el concepto de las imágenes es formado sobre la base de ejemplos y no ejemplos (Dreyfus, et al., 1998).
En nuestra opinión, aunque una aproximación analítica también permite la consideración de transformaciones no lineales, implica la definición analítica de la transformación lineal, mientras que en la aproximación geométrica resulta más fácil brindar, de manera intuitiva, dos grupos de transformaciones al mismo tiempo: unas que sean lineales y otras que no lo sean, usando sus propiedades geométricas.
Dicho grupo de trabajo se dio entonces a la tarea de investigar la opción de usar una introducción geométrica al álgebra lineal; más específicamente a las nociones de vector, transformación, transformación lineal y vector propio en dos dimensiones. Para facilitar esta aproximación y ofrecer a los estudiantes un ambiente exploratorio, seleccionaron para su diseño el software Cabri–Géomètre II, que fue usado como ayuda pedagógica, no como herramienta para resolver problemas de álgebra lineal. Su función consistió en proporcionar una base conceptual sobre la que pudiera ser construida la representación de vectores y transformaciones lineales como objetos geométricos.
La experimentación de tal diseño se llevó a cabo tres veces. Los investigadores llegaron a la conclusión de que, sin importar cuánto intenten aproximarse al contenido del álgebra lineal, las dificultades de los estudiantes parecen persistir. Sierpinska (2000) argumenta que los estudiantes podrían no entender la teoría porque quieren comprenderla con una mente más práctica que teórica4. Señala también que los modos de pensamiento teórico y práctico difieren fuertemente en la manera en que constituyen el significado de las palabras:
Para la mente práctica, los objetos matemáticos son "objetos naturales", no "objetos discursivos" (a estos últimos sólo las definiciones y teorías pueden describirlos, no crearlos o construirlos). Consecuentemente, un término matemático es interpretado, primariamente, a través de su denotación o referente, como representación de una colección de objetos particulares, y la connotación, o propiedad de definición, aparece así solamente como una propiedad (Sierpinska, 2000).
2.2. El problema de extensión lineal en las experimentaciones desarrolladas por el grupo de Sierpinska
En la primera experimentación se planteó a los estudiantes el siguiente problema: Dadas las imágenes bajo una transformación lineal de un par de vectores no colineales, encuentra la imagen bajo esa transformación de un vector arbitrario. Más precisamente, se les pidió que construyeran cinco vectores partiendo del origen. Los vectores fueron etiquetados como 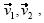
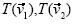 y
y 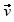 (Fig. 1). Se les dijo a los estudiantes que supusieran que
(Fig. 1). Se les dijo a los estudiantes que supusieran que 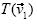 y
y 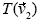 eran imágenes de
eran imágenes de 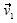 y
y 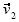 , respectivamente, bajo cierta transformación lineal. La pregunta fue: De acuerdo con la información dada, ¿podrían saber dónde debería estar situado
, respectivamente, bajo cierta transformación lineal. La pregunta fue: De acuerdo con la información dada, ¿podrían saber dónde debería estar situado 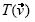 (Haddad, 1999). El problema fue etiquetado como problema de extensión lineal porque, en efecto, consistía en extender una transformación lineal de una base a todo el plano vectorial. Se esperaba que los estudiantes construyeran un sistema de coordenadas en la base
(Haddad, 1999). El problema fue etiquetado como problema de extensión lineal porque, en efecto, consistía en extender una transformación lineal de una base a todo el plano vectorial. Se esperaba que los estudiantes construyeran un sistema de coordenadas en la base 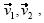 (Fig. 1) y así hallaran las coordenadas (a,b) de
(Fig. 1) y así hallaran las coordenadas (a,b) de 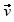 Como
Como 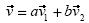 y la transformación era lineal, entonces:
y la transformación era lineal, entonces:
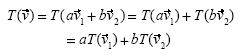
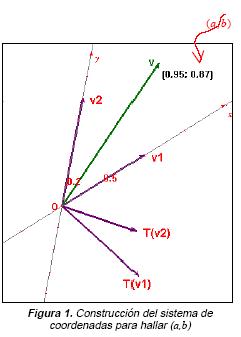
Los estudiantes podrían dilatar 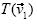 y
y 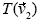 por los factores a y b, respectivamente (Fig. 1). El vector
por los factores a y b, respectivamente (Fig. 1). El vector 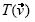 sería la suma de los vectores resultantes (Haddad, 1999).
sería la suma de los vectores resultantes (Haddad, 1999).
Como conclusiones finales a este primer experimento, los autores precisaron que, además de algunas fallas del diseño, hay aspectos epistemológicos serios relacionados a la noción de función y al uso de definiciones axiomáticas.
En el tercer experimento, los investigadores detectaron los síntomas del obstáculo de formalismo. Cuando los estudiantes abordaron el problema de extensión lineal sus intentos revelaron una dificultad, pues mostraron tendencia a pensar conceptos matemáticos en términos de ejemplos prototipo en lugar de definiciones. La actividad del experimento consistió en lo siguiente: se pidió a los estudiantes que abrieran un nuevo archivo en Cabri y pusieran dos rectas numéricas en él (estas macros5 permiten a los estudiantes producir dos escalares independientes), el origen y los vectores etiquetados 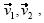
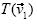 y
y 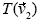 partiendo del origen.
partiendo del origen.
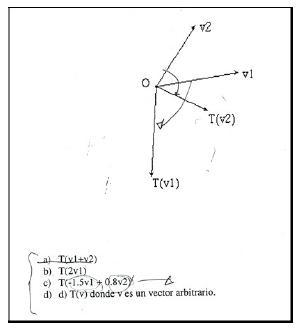
Después de esto, el problema fue planteado así: vamos a asumir que los vectores 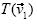 y
y 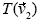 son las imágenes de los vectores
son las imágenes de los vectores 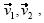 respectivamente, bajo alguna transformación lineal T. Sólo con esta información, ¿puedes construir a)
respectivamente, bajo alguna transformación lineal T. Sólo con esta información, ¿puedes construir a) 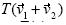 , b)
, b) 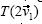 , c)
, c) 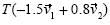 y d)
y d) 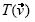 donde
donde 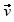 es un vector arbitrario?
es un vector arbitrario?
Para llevar a cabo la actividad, también se proporcionó a los estudiantes las macros adición de vectores, multiplicación escalar y combinación lineal, que podían ser aplicadas a los vectores y escalares.
Las respuestas obtenidas de los siete estudiantes fueron divididas por los investigadores en 3 tipos principales:
1. La solución formal (3 de 7)
2. La solución prototipo (3 de 7)
3. La solución teórica (1 de 7)
En las soluciones formales los estudiantes presentaron síntomas del obstáculo del formalismo. La prototipo es aquella donde los estudiantes consideraron el concepto de transformación lineal en términos de ejemplos prototipos. Por ejemplo, intentaron encontrar T como una de las transformaciones lineales conocidas, una rotación por un ángulo, una dilatación, una reflexión, o posiblemente alguna combinación de éstas, solamente investigando la relación que guardaban los vectores en la pantalla. Una estudiante resolvió el inciso c) en la manera esperada y luego se dio cuenta que, al mover los puntos en la línea numérica, los escalares podían hacerse variables, así que cualquier vector podía ser obtenido de esta forma, lo cual resolvía el inciso d), aunque la estudiante estaba insegura si era correcto. Esta solución fue clasificada como teórica.
Las conclusiones a que llegó este grupo de investigadores respecto a los resultados de esta actividad fueron expresadas de la siguiente manera. Existen dificultades en los estudiantes para hallar las imágenes de combinaciones lineales y la de un vector cualquiera, que pueden ser generadas a) por una necesidad de construir una representación del objeto "cualquier vector", que no es dado en el problema; b) por la necesidad de tener una noción de definiciones axiomáticas. Los estudiantes perciben la condición definida de transformación lineal sólo como propiedades de una transformación, por lo que para ellos una transformación debe ser dada por algún otro significado, como una macro o fórmula (es decir, necesitan una definición descriptiva); no aprecian que al decir "T es una transformación lineal con tales y tales valores en la base" se está definiendo la transformación.
3. OBJETIVO DE NUESTRA INVESTIGACIÓN
Es de particular interés para nosotros el problema de extensión lineal porque, cuando se les pide a los estudiantes que construyan la imagen de un vector arbitrario v , en realidad se les está pidiendo que determinen una transformación lineal por medio de las imágenes de los vectores de una base. Consideramos que para elaborar dicha construcción los estudiantes necesitan hacer una conexión entre varios conceptos, en especial entre los de base y transformación lineal; también están implícitos los de espacio vectorial y combinación lineal.
Tal reflexión nos lleva a conjeturar que, además de las consideraciones expuestas por Sierpinska, la principal causa de que los estudiantes no tengan éxito en la resolución del problema de extensión lineal se debe a que no efectúan las conexiones adecuadas entre los conceptos involucrados. Por ello, el objetivo de nuestra investigación es ofrecer una explicación acerca de dicho fenómeno, basándonos en observaciones empíricas. Aunque nuestro enfoque está en un problema específico (el de la extensión lineal), consideramos que es un fenómeno general que se manifiesta en varias situaciones de enseñanza en álgebra lineal y en otras ramas de las matemáticas que vale la pena investigar.
4. JUSTIFICACIÓN
En el ambiente escolar la información que recibimos puede registrarse como información factual, la cual puede ser extraída y procesada de manera mecánica, o bien abstraerse como información conceptual, que puede ser obtenida y procesada de manera significativa. La segunda se apreciará cuando hagamos frente a un problema no cotidiano, porque es ahí donde los conceptos son forzados a reunirse en un todo coherente con el objetivo de dar solución al nuevo problema.
Sin embargo, la mayoría de los problemas que resolvemos en la escuela son similares a los que el profesor ha hecho, de modo que sólo necesitamos reproducir un algoritmo aprendido. La repetición constante de ejercicios prototipo puede llevarnos a una habilidad y un dominio, pero de procedimientos; más aún, puede engañar a los profesores y estudiantes de que los conceptos han sido comprendidos. Es preciso sustituir algunos de estos problemas por otros novedosos, que motiven al estudiante a reflexionar sobre sus conceptos adquiridos.
Steinbring (1991) indica que el profesor en ocasiones asume una forma de conocimiento matemático que él mismo ha organizado ordenadamente, e intenta desarrollar el conocimiento del estudiante desde esta perspectiva recurriendo a métodos indirectos de enseñanza. No obstante, mientras los estudiantes no asuman un punto de vista sistémico integrarán los elementos proporcionados indirectamente, de forma individual. Solamente la caracterización de conocimiento como un sistema relacional, en vez de un orden lineal de aprendizaje, podría ser de ayuda en caso de que emerjan dificultades de entendimiento.
Zazkis (2001) afirma que los vínculos que matemáticamente parecen claros y sencillos pueden representar una red compleja para los estudiantes; sus aproximaciones al resolver problemas pueden ser la señal de que no utilizan totalmente las conexiones adecuadas de los conceptos involucrados. Ella sugiere que teorías como APOS (Acción–Proceso–Objeto–Esquema), donde aparece la idea de esquema (Asiala et al., 1996), podrían servir como perspectiva teórica para clarificar el reaprendizaje, así como para dar forma a la noción de vínculo y su papel en el aprendizaje de las matemáticas.
Apreciamos que la presencia de un pensamiento sistémico en la adquisición de conceptos desempeña un papel importante en la didáctica de las matemáticas. Algunos errores que cometen los alumnos cuando resuelven un problema podrían explicarse mediante la falta de conexiones que deberían hacer entre los conceptos que forman un sistema. La detección de tal fenómeno por profesores e investigadores podría llevarlos a enfocarse en las conexiones que tendrían que fomentarse en los estudiantes para una comprensión adecuada de los conceptos de matemáticas. Asimismo, con este trabajo queremos propiciar una reflexión sobre las estrategias para hacer que los estudiantes realicen tales conexiones.
5. CONSIDERACIONES TEÓRICAS
Contemplamos entonces dos acercamientos como marcos de referencia para nuestro trabajo. El primero corresponde, de acuerdo con Sierpinska (2000), al pensamiento teórico versus pensamiento práctico. El segundo se refiere al obstáculo de formalismo, término denotado por Dorier et al. (1997).
5.1. Pensamiento teórico versus pensamiento práctico
Sierpinska (2000) manifiesta que, a pesar de los esfuerzos por mejorar la enseñanza del álgebra lineal, persistían las dificultades en los estudiantes. Ante esta situación, el grupo de investigadores conjeturó que quizá los alumnos no entendían la teoría porque querían comprenderla con una mente práctica en lugar de hacerlo con una mente teórica. A partir de ahí, comenzaron a desarrollar las nociones de pensamiento teórico y pensamiento práctico.
Aclara Sierpinska que el planteamiento del pensamiento teórico versus pensamiento práctico fue inspirado por la distinción vigotskiana entre conceptos cotidianos y científicos. Ella asume que:
El pensamiento teórico se caracteriza por una reflexión concienzuda sobre significados semióticos de representación del conocimiento, así como sobre sistemas de conceptos y no sólo de acumulación de ideas. Suponemos además que en el pensamiento teórico el razonamiento está basado en conexiones semánticas y lógicas entre conceptos dentro de un sistema; las conexiones entre los conceptos se hacen con base en sus relaciones hacia conceptos más generales, de los cuales los anteriores son casos especiales, en lugar de asociaciones empíricas. Las relaciones entre los conceptos y los objetos se dan a través de las relaciones entre unos y otros conceptos. En particular, las definiciones de los conceptos, comparaciones entre conceptos y sus diferencias se construyen sobre la base de las relaciones entre estos conceptos con conceptos más generales y no, por ejemplo, sobre la base de sus ejemplos más comunes (Sierpinska, 2000).
Luego de esta primera aproximación, Sierpinska et al. (2002) se dan a la tarea de describir más precisamente el pensamiento teórico versus pensamiento práctico, así como a identificar cuáles son sus características específicas para el aprendizaje del álgebra lineal. Para ello:
a)Detallan un modelo de pensamiento teórico
b)Desarrollan una metodología para evaluar en forma individual o grupal la inclinación6 a pensar teóricamente en el sentido del modelo postulado.
La elaboración de esta teoría, al igual que la metodología para evaluar la inclinación a pensar teóricamente, se dio a través del estudio de los datos empíricos obtenidos de las entrevistas con 14 estudiantes que lograron altas calificaciones en un primer curso de álgebra lineal (algunos también tuvieron altas calificaciones en un segundo curso). Los datos proporcionaron a los investigadores información para refinar el modelo y establecer los distintos comportamientos teóricos7. Caracterizaron al pensamiento teórico en tres categorías principales, aclarando que el pensamiento teórico es reflexivo, sistémico y analítico (Fig. 2), mas al clasificar las respuestas distinguieron ciertas particularidades, las cuales fueron denotadas específicamente para un mejor análisis. Esto les llevó a insertar subcategorías específicas de comportamientos teóricos a partir de las ya establecidas como marco de referencia.
Nuestro énfasis, sobre todo, reside en detectar en los estudiantes un pensamiento sistémico porque creemos que es la clave para solucionar el problema de extensión lineal, en torno al cual gira nuestra investigación. Destacamos esta característica del pensamiento, sin restar importancia a las otras dos, por la misma naturaleza del problema, ya que su esencia consiste en que los estudiantes utilicen estrategias que los conduzcan a determinar una transformación lineal por medio de las imágenes de los vectores de una base.
Ante nuestra postura, es necesario tener características que nos permitan apreciar si en el desempeño de la actividad los estudiantes dan muestras de un pensamiento sistémico.
Para abordar la categoría sistémica del pensamiento teórico, el grupo de investigadores coordinado por Sierpinska utilizó como base una referencia de Vigotsky, quien al introducir su noción de concepto científico enfatiza que los conceptos son siempre parte de un sistema de conceptos:
La diferencia clave en la naturaleza psicológica de los conceptos científicos y cotidianos es la presencia o ausencia de un sistema. Los conceptos permanecen en una relación diferente respecto a los objetos cuando existen fuera de un sistema que cuando están dentro. Fuera de un sistema, las únicas conexiones posibles son aquellas que existen entre los objetos por sí mismos, esto es, conexiones empíricas. Esta es la fuente del dominio de la lógica de acción y de conexiones sincréticas de las imitaciones en los niños. Con un sistema, las relaciones entre los conceptos emergen. Estas relaciones median las relaciones de los conceptos hacia el objeto a través de sus relaciones con otros conceptos (Vigotsky, 1987, pp.234–235; citado en Sierpinska et al., 2002).
Podemos argumentar al respecto que el pensamiento teórico es consciente de los conceptos con los que opera, mientras que el pensamiento práctico centra su atención en los objetos concretos y no repara en sus conceptos relacionados. Entonces, las conexiones entre conceptos sólo podrán hacerse cuando el estudiante tome conciencia de los conceptos con los que opera; es decir, cuando adquieran significado para él.
Los conceptos pueden ser aprendidos como entidades individuales, pero cuando se asocian a sistemas de significados forman parte de una estructura conceptual; aquí se hacen presentes las conexiones.
Cuando aprendemos un concepto, lo que aprendemos es resultado de un proceso de significación para quienes lo crearon, del cual no fuimos parte. Podríamos decir que somos bombardeados de conceptos que deben ser aprendidos mediante definiciones (un vector v en un espacio vectorial V se denomina combinación lineal de los vectores 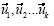 en V si
en V si 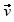 puede expresarse como
puede expresarse como 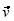 =
=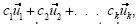 donde c1, c2 ,... cK son escalares, no todos cero), teoremas ( una matriz cuadrada A es invertible si v sólo si det A ≠ 0 ), notaciones (
donde c1, c2 ,... cK son escalares, no todos cero), teoremas ( una matriz cuadrada A es invertible si v sólo si det A ≠ 0 ), notaciones ( 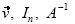 ) y procedimientos ( dado
) y procedimientos ( dado 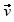 = (–2,5) , entonces
= (–2,5) , entonces 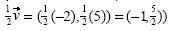
La información aprendida puede añadirse a la mente como entidad individual, aunque también puede asociarse a sistemas de significados, con lo que se convierte en parte de una estructura conceptual.
Por ejemplo, 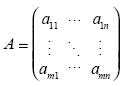 se puede ver como un arreglo de números, pero si sabemos que
se puede ver como un arreglo de números, pero si sabemos que 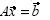 donde A es la matriz (de orden m x n) de coeficientes en un sistema de ecuaciones
donde A es la matriz (de orden m x n) de coeficientes en un sistema de ecuaciones 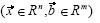 y que si A es invertible implica que el sistema de ecuaciones representado por
y que si A es invertible implica que el sistema de ecuaciones representado por 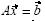 tiene solución única dada por
tiene solución única dada por 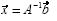 entonces A forma parte de una estructura conceptual.
entonces A forma parte de una estructura conceptual.
Durante el aprendizaje resulta común que los estudiantes adquieran conocimientos mediante series de pasos, que observan y luego reproducen. Suelen adaptar ciertas técnicas para dar solución a los problemas, que pueden ser familiares o desconocidos para el estudiante. Ante uno familiar, hará algo parecido a lo ya realizado; sólo tiene que recordar cómo resolverlo. Pero ante una situación desconocida, el alumno debe reflexionar sobre las instrucciones del problema y recurrir a sus conceptos previamente adquiridos, efectuando posiblemente las relaciones o conexiones válidas que lo conduzcan a una solución adecuada.
Steinbring (1991) hace notar que existe una distancia entre el conocimiento del profesor y el conocimiento del estudiante. El profesor posee una teoría matemática y es consciente de vínculos conceptuales, mientras que los estudiantes tienen un conocimiento local (material), por lo cual sus conceptos adquiridos quedan aislados. Entonces, el profesor –cuyo conocimiento es global–, al desempeñar su papel de transmitir el conocimiento, recurre a múltiples formas didácticas para guiar al estudiante en su aprendizaje, de modo que les construye una trayectoria a seguir y trata de desarrollar en ellos un estado de conocimiento, pero desde su perspectiva.
Respecto a los métodos de enseñanza, Steinbring (1991) indica que, aunque tengan la mejor intención de organizar el aprendizaje paso por paso y deductivamente, es necesario tener en cuenta que las relaciones conceptuales de conocimiento requieren de una conexión sistémica–holística, donde un nuevo concepto se constituye por su posición dentro de un sistema, no surge como resultado de deducciones metódicas o lógicas.
Además, Steinbring (1991) dice que hay una tensión entre el conocimiento local que maneja el estudiante y el conocimiento global que atañe al profesor. Para este último, el conocimiento tiene un carácter teórico o autorreferente, lo cual indica que la visión epistemológica de estudiantes y profesores ante un mismo conocimiento matemático suele ser diferente.
Por su parte, Zazkis (2001) afirma que los conceptos matemáticos no deben ser estudiados aisladamente, sino en relación con otros conceptos matemáticos, de manera que expresa al conocimiento conceptual como una red porque la idea de red sugiere no sólo conexión, sino también complejidad del conocimiento.
A medida que se avanza en el contenido del álgebra lineal, los conceptos previos se vinculan con los posteriores. Cuando un estudiante se enfrenta a este tipo de ejercicios, su estrategia debe considerar qué conceptos están involucrados y cómo se relacionan. Entonces, se ponen en juego los significados de los conceptos que le permiten al estudiante, además de generar hipótesis y establecer conjeturas, llevar a cabo diferentes decisiones pertinentes frente a la resolución de un problema. Sus argumentos tienen que ser razones válidas que le permitan justificar el planteamiento de su solución.
El significado de los conceptos y las conexiones entre ellos son elementos estrechamente relacionados. Por ejemplo, podríamos pensar en un estudiante que da una definición aceptable de un concepto, que es capaz de resolver ejercicios haciendo uso correcto del concepto y sus propiedades, que puede interpretar geométricamente su significado y que siempre tiene éxito ante problemas prototipo; sin embargo, ante una situación nueva que requiera hacer uso de ese concepto, no puede hacer los vínculos adecuados para llegar a la solución correcta. En forma contraria, podría darse el caso que las experiencias del estudiante y su intuición le permitan pisar el terreno apropiado para llegar a la solución de un problema, haciendo las conexiones adecuadas en cada paso, pero titubeando, inseguro de que la solución sea la correcta; esto podría reflejar la debilidad en la apropiación de los significados de los conceptos.
Cuando un estudiante se enfrenta a una situación nueva, el primer paso hacia una solución exitosa es que reflexione sobre los elementos que tiene a su alcance y sobre los que están involucrados, aunque no sean explícitos en el problema. Después, tiene que organizar su conocimiento de manera tal que busque hacer conexiones entre sus conceptos, valiéndose de sus significados.
Para poder apreciar la presencia de un pensamiento teórico en los estudiantes que enfrentan el problema de extensión lineal, consideramos que deben estar presentes los siguientes comportamientos:
• Reflexión sobre los datos explícitos y aquellos que podrían estar involucrados implícitamente en la interpretación del problema.
• Actitud indagadora respecto a posibles conceptos involucrados.
• Desarrollo de estrategias con un propósito, haciendo uso de los conceptos involucrados en un problema.
• Toma de decisiones pertinentes que involucren conceptos relacionados para llegar a la solución de un problema, ofreciendo argumentos válidos que permitan justificar el planteamiento de su solución, con una coherencia que haga ver un sistema de conceptos.
5.2 El obstáculo de formalismo
Por otra parte, como quisimos observar de qué manera se presenta el obstáculo de formalismo en un ambiente geométrico, el segundo acercamiento que tomamos en cuenta fue el obstáculo de formalismo, un término introducido por Dorier et al. (1997).
A través de distintas investigaciones de tipo diagnóstico hechas por el grupo de Dorier (entre 1987 y 1994), se muestra que las dificultades de los estudiantes en álgebra lineal revelan un mismo obstáculo, macizo, el cual aparece en todas las generaciones sucesivas y prácticamente en todos los métodos de enseñanza –los empleados en las investigaciones–, al cual llaman obstáculo de formalismo (Dorier et al., 1997).
Los estudios realizados en 1989 y 1990 (Robert y Robinet, 1989; Rogalski 1990, citados en Dorier, 1997) indican una dificultad especialmente fuerte en los estudiantes para poder hacer funcionar los conceptos del álgebra lineal en marcos formales, y no en tareas donde una técnica precisa podía establecerse. Estos análisis les permitieron precisar la naturaleza del obstáculo de formalismo, pues ponen de manifiesto que la teoría de los espacios vectoriales aparece como un ámbito abstracto y formal a los estudiantes, quienes se sienten ahogados por las nuevas definiciones y tienen dificultades de hacer el vínculo con lo que anteriormente aprendieron. Las respuestas de algunas tareas, relacionadas con espacios vectoriales, parecen mostrar una falta total de control de las herramientas de lógica y lenguaje conjuntista.
Otro grupo que trabajó con esta noción fue el de Sierpinska, pero hace una adaptación a la noción introducida por Dorier, et al. En términos de Sierpinska, un estudiante que se encuentra bajo el hechizo del obstáculo de formalismo es aquel que se comporta como si las representaciones simbólicas formales de los objetos del álgebra lineal fueran los objetos en sí mismos. Todavía no tiene suficiente aptitud para comprender la estructura de estas representaciones y, por tanto, las manipula de manera tal que no es compatible con su gramática; el estudiante no ve las relaciones entre distintas representaciones formales y recurre a un número inmanejable de objetos.
Podemos comentar al respecto que cuando los estudiantes no entienden los conceptos (independientemente de las razones de porqué no lo hacen), muestran signos del obstáculo de formalismo, lo cual da pie a que trabajen en el nivel de manipular las expresiones, pero ignoran los significados o las reglas de las matemáticas. De acuerdo con Haddad (1999), en sus soluciones los alumnos escriben una gran cantidad de símbolos y notaciones matemáticas porque esto se ve matemático, aunque no tenga sentido.
Consideramos que, aunque la actividad está situada esencialmente en un ambiente geométrico, lo que permite la manipulación de objetos y no de símbolos, tal obstáculo puede hacerse presente debido al carácter teórico de los conceptos involucrados.
Al incorporar las características abstractas y teóricas de los conceptos a las actividades, se da una incorporación de lo analítico en lo sintético (para las descripciones de los modos de pensamiento, ver Sierpinska, 2000), con lo que ocurre el obstáculo de formalismo, razón por la cual consideramos también esta aproximación teórica.
6. METODOLOGÍA
Como mencionamos anteriormente, conjeturamos que el problema de extensión lineal requería de hacer conexiones entre diferentes conceptos para su resolución exitosa, lo que nos condujo a plantear nuestro objetivo de investigación: observar la presencia de conexiones entre conceptos y su naturaleza, basándonos en observaciones empíricas. Para tal fin, contemplamos tres etapas en nuestra investigación:
• En la primera etapa se llevó a cabo un curso con ocho estudiantes de primer semestre, inscritos en el programa de maestría del Departamento de Matemática Educativa. El objetivo principal del curso fue dar a los estudiantes la oportunidad de ver y analizar ejemplos del uso de la tecnología en la clase de matemáticas en el nivel superior. La rama elegida como enfoque matemático fue álgebra lineal y como ambiente tecnológico el Cabri–Géomètre II.
6.1. La dinámica del curso
En dicho curso, la dinámica fue: a) aplicación de las actividades diseñadas por Sierpinska y su grupo, pertenecientes al segundo rediseño, a los participantes del curso; b) discusión teórica sobre el tema; c) análisis didáctico de las actividades y su diseño; d) consideraciones técnicas en el diseño de las actividades. Así, se trató que los estudiantes, por un lado, trabajaran directamente sobre las actividades; por otro, analizaran el uso didáctico, pretendiendo que reflexionaran en torno a los fenómenos observados desde el punto de vista de sus experiencias. Aunque durante el curso se llevaron a cabo seis módulos, explicamos con detalle el 5 y 6 porque abordan las transformaciones lineales.
Módulo 1: Familiarizarse con los comandos de Cabri. Vectores, igualdad de vectores y operaciones sobre los vectores.
Módulo 2: Aplicaciones del lenguaje de los vectores en la geometría.
Módulo 3: Coordenadas de un vector en una base.
Módulo 4: Cambio de base.
Los vectores, desde el inicio de curso, fueron abordados como vectores libres. En un principio tanto las combinaciones lineales como los cambios de base se trataron bajo construcciones geométricas, y conforme iba avanzando el contenido del curso algunas se convirtieron en macros. Asimismo, el módulo 3 atendió al tema de coordenadas de un vector en una base, lo cual permitió no sólo la construcción geométrica, sino también la inclusión de elementos numéricos.
Soto (2003), quien efectuó una investigación cuyo propósito fue identificar las dificultades de los estudiantes para construir y utilizar estos conceptos reducidos a R2 y R3, y de qué manera estas dificultades están relacionadas con la conversión de representaciones gráficas en algebraica y viceversa, mostró actividades diseñadas en Cabri para introducir el tema de las transformaciones lineales mediante la matriz de transformación. Esto tuvo como intención que el estudiante se familiarizara con el significado gráfico y numérico que tiene la evaluación de una transformación lineal. A diferencia del trabajo de Soto –uno de los pocos estudios que abordan el tema de las transformaciones lineales en Cabri–, el tratamiento que tienen las transformaciones lineales en nuestro escenario se da en un contexto más geométrico. Las entradas numéricas (como la macrorrecta numérica) son proporcionadas con la intención de que, al generar un vector en una base dada, se genere una familia de vectores que le pertenecen.
6.1.1. Módulos 5 y 6: transformaciones lineales
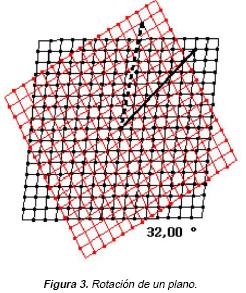
Las actividades que detallaremos a continuación pertenecen a los módulos 5 y 6, alusivos a las transformaciones lineales. El módulo 5 inició con la definición de espacio vectorial y sus axiomas, luego se presentó a los estudiantes la idea de transformación de todo el plano vectorial, mediante archivos hechos en Cabri con una parte de cuadrícula finita, que operaba el instructor. Se mostró el hecho de que una transformación del plano vectorial tiene que entenderse como definida para todos los vectores del plano; una transformación del plano vectorial no es lo mismo que la de un vector o una figura aislada en el plano (los investigadores hacen hincapié en tal fenómeno, pues es una dificultad que observaron en las aplicaciones anteriores de sus actividades, como se reporta en Dreyfus, et al., 1998).
Por ejemplo, en la Figura 3 podemos observar que las cuadrículas finitas representan planos vectoriales: una al plano vectorial dado, la otra al plano vectorial transformado (en este caso, por una rotación). Asimismo, se ha construido un par de vectores, uno punteado y otro no punteado, a fin de indicar que parten de un origen y también den la idea de que hay una infinidad de vectores en el plano vectorial, mediante el modo de arrastre del software. El vector punteado es la imagen del no punteado bajo dicha transformación.
Otra de las actividades consistió en proporcionar a los alumnos macros que permitieron una transformación T del plano vectorial, poniendo un vector libre 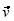 sobre la pantalla y construyendo su imagen bajo T, según la regla que definía a la transformación (Figuras 4 y 5). Luego, moviendo el punto terminal del vector
sobre la pantalla y construyendo su imagen bajo T, según la regla que definía a la transformación (Figuras 4 y 5). Luego, moviendo el punto terminal del vector 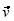 , las imágenes de muchos otros vectores bajo T se pudieron visualizar. Algunos ejemplos fueron reflexión, proyección, rotación, una transformación semilineal (rotación de 90°, combinada con una dilatación por un factor variable), trasquilado (su elaboración depende de dos parámetros, q y L, donde q ≠ 0 y L es una recta que pasa por el origen; entonces, la imagen de un vector
, las imágenes de muchos otros vectores bajo T se pudieron visualizar. Algunos ejemplos fueron reflexión, proyección, rotación, una transformación semilineal (rotación de 90°, combinada con una dilatación por un factor variable), trasquilado (su elaboración depende de dos parámetros, q y L, donde q ≠ 0 y L es una recta que pasa por el origen; entonces, la imagen de un vector 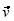 es tal que la recta que une los puntos finales del vector
es tal que la recta que une los puntos finales del vector 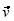 y su imagen es paralela a L, mientras que la distancia entre los puntos finales de
y su imagen es paralela a L, mientras que la distancia entre los puntos finales de 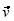 y su imagen es igual a
y su imagen es igual a 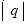 veces la distancia entre el punto final de
veces la distancia entre el punto final de 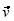 y la recta L), traslado–punto–terminal (traslación por un vector). Notamos que se hace una referencia al mismo espacio de trabajo (la pantalla), pues se hace uso en las actividades de los ejes horizontales y perpendiculares, aunque no son propiamente elementos de la estructura matemática, donde no se emplean coordenadas o referencias.
y la recta L), traslado–punto–terminal (traslación por un vector). Notamos que se hace una referencia al mismo espacio de trabajo (la pantalla), pues se hace uso en las actividades de los ejes horizontales y perpendiculares, aunque no son propiamente elementos de la estructura matemática, donde no se emplean coordenadas o referencias.

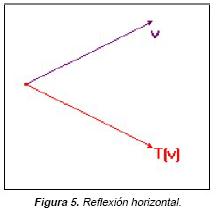
Para concluir el módulo 5, se dio la definición de una transformación lineal como aquella que conserva combinaciones lineales, es decir, para cualesquiera vectores 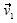 y
y 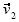 cualesquiera escalares k1 , y k2 ,
cualesquiera escalares k1 , y k2 , 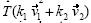 =
= 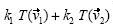 8. Como equivalente a esta definición, una transformación es lineal si y sólo si conserva la suma de vectores y la multiplicación por un escalar, o sea
8. Como equivalente a esta definición, una transformación es lineal si y sólo si conserva la suma de vectores y la multiplicación por un escalar, o sea 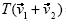 =
= 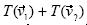 para cualesquiera vectores
para cualesquiera vectores 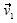 y
y 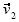 , y
, y 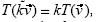 cualquier vector
cualquier vector 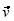 y cualquier escalar k.
y cualquier escalar k.
Con el fin de mostrar ejemplos de transformaciones lineales y no lineales, el instructor hizo uso de dos macros: lin basis (su nombre en español es lin–base; sin embargo, durante el curso se mantuvo el nombre en inglés) y semilineal. La primera macro fue construida para obtener la imagen de cualquier vector v bajo una transformación lineal, haciendo uso de dos vectores linealmente independientes, 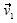 y
y 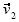 sus imágenes
sus imágenes 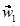 y
y 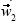 respectivamente, bajo la misma transformación lineal. La segunda macro daba la imagen de un vector cualquiera bajo una transformación que cumplía solamente la condición de multiplicación por un escalar, no la de la suma. En cada caso, el instructor averiguó geométricamente si
respectivamente, bajo la misma transformación lineal. La segunda macro daba la imagen de un vector cualquiera bajo una transformación que cumplía solamente la condición de multiplicación por un escalar, no la de la suma. En cada caso, el instructor averiguó geométricamente si 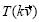 y
y 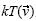 así como
así como 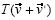 y
y 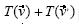 para cualesquiera vectores
para cualesquiera vectores 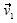 y
y 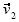 , coincidían.
, coincidían.
Para finalizar el módulo 5, se pidió a los estudiantes que examinaran si las transformaciones dadas por ciertas macros eran lineales, verificando si  =
= 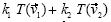 para cualesquiera vectores
para cualesquiera vectores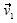 y
y 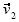 cualesquiera escalares k1 y k2 .
cualesquiera escalares k1 y k2 .
El problema de extensión lineal formó parte del módulo 6. Por tanto, sólo describiremos la parte que corresponde a dicho módulo, antes de presentar el problema.
Al inicio del módulo 6, a manera de repaso, se empezó verificando si cierta transformación, definida nuevamente por la macro lin–basis, era lineal. Primero, se observó qué estaba haciendo la transformación al plano, creando tal representación por el uso de una cuadrícula (Figura 6).
También se mostró una nueva manera de averiguar la linealidad de una transformación, usando la condición de conservación de combinaciones lineales.
El instructor puso dos rectas numéricas y dos vectores,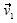 y
y 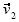 , aplicó alguna de las macros vistas con anterioridad (aquellas que proporcionan una transformación T del plano vectorial), colocó un vector libre
, aplicó alguna de las macros vistas con anterioridad (aquellas que proporcionan una transformación T del plano vectorial), colocó un vector libre 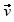 sobre la pantalla y elaboró su imagen bajo T, según la regla que define a la transformación. Al aplicar la macro, construyó entonces
sobre la pantalla y elaboró su imagen bajo T, según la regla que define a la transformación. Al aplicar la macro, construyó entonces 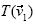 y
y 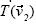 . Después, usando la macro combinación lineal hizo un vector
. Después, usando la macro combinación lineal hizo un vector 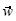 tal que
tal que 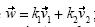 ; a este vector le aplicó la macro de transformación, generando el vector
; a este vector le aplicó la macro de transformación, generando el vector  . Finalmente, construyó un vector
. Finalmente, construyó un vector 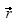 tal que
tal que 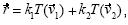 observándose que
observándose que 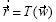 , independientemente de las posiciones de
, independientemente de las posiciones de 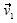 ,
, 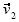 y k1 y k2.
y k1 y k2.
Posteriormente, se dieron ejemplos donde sólo una o ninguna de las condiciones (suma de vectores y multiplicación por un escalar) se satisfacía. Estas tareas de alguna manera prepararon a los estudiantes para el siguiente paso: la realización del problema de extensión lineal, que fue nuestro enfoque de interés para los fines de esta investigación.
En la segunda etapa se aplicó un cuestionario diagnóstico, conformado por 12 reactivos comprendidos en 6 secciones, cuyo contenido estuvo relacionado con las transformaciones lineales. Al contestar dicho instrumento, los estudiantes ya habían cursado los módulos 1–5 y parte del módulo 6. Nuestro objetivo era caracterizar el pensamiento de los estudiantes en forma general.
6.2. Características de los estudiantes
Para proteger la identidad de los participantes, cuyas edades iban de los 23 a los 26 años, les dimos los pseudónimos de Estudiante 1 hasta Estudiante 8. Los estudiantes 1, 2, 3, 4, 5 y 8 terminaron una licenciatura en Enseñanza de las Matemáticas (LEM). Los estudiantes 3, 4, 5 y 8 sólo tomaron un curso trimestral en diferentes periodos: el 3 y el 4 en 1998, el 5 en 1999 y el 8 en 2000.
Los estudiantes 1 y 2, antes de ser alumnos de la LEM, cursaron cinco semestres de la licenciatura en Matemáticas (LM), ambas pertenecientes a la misma facultad, donde tomaron dos cursos semestrales correspondientes a Álgebra Lineal I (1997) y Álgebra Lineal II (1998). El Estudiante 1 dijo que no los acreditó en periodo ordinario y los volvió a cursar: el de Álgebra Lineal I en 1998 y el de Álgebra Lineal II en 1999. También llevó un curso trimestral en la LEM en 2001. Por último, el Estudiante 6 es Ingeniero Metalúrgico y el 7 licenciado en Economía; de acuerdo con la información proporcionada, no llevaron curso alguno de álgebra lineal, de manera que nuestro curso fue la primera experiencia que tuvieron con esta asignatura.
6.3. Análisis del cuestionario diagnóstico y respuestas de los estudiantes
Como hemos mencionado, antes de llevar a cabo la entrevista se aplicó un cuestionario diagnóstico, en una sesión del curso, con una duración de 2 horas. Cada estudiante tuvo a su disposición una computadora.
Presentaremos los análisis de algunas secciones y luego haremos una descripción general del desempeño de los estudiantes con base en los resultados.
6.3.1. Sección 1. Pregunta 1 (ver Cuadro 1). Como las respuestas de los estudiantes varían, las copiaremos textualmente para poder apreciarlas en su totalidad. Aquí, queríamos saber cómo percibían a una transformación, sin considerar el término lineal.
Podemos apreciar que los estudiantes hacen referencia a las transformaciones basándose en intuiciones relacionadas con su propia experiencia, las cuales son cercanas o distantes a la definición. Los estudiantes 1, 2 y 3 ofrecen una definición que involucra a un espacio vectorial y a la noción de función. La definición del Estudiante 8 no contempla el espacio vectorial, sino que hace mención de un conjunto; el 4 posiblemente nota que afecta a un solo vector y no a todo el espacio; el 5 y 6 la entienden como una modificación de todos los vectores, pero parece que el 6 también considera al elemento original y a su respectiva imagen bajo la transformación como diferentes, por lo cual podríamos pensar que la función identidad no está contemplada para él como una transformación. El 7 la percibe en términos de una combinación lineal.
6.3.2. Sección 1. Pregunta 1. 2 (ver Cuadro 2). En esta pregunta, donde contemplamos la palabra lineal, nuestro interés se centró en observar si los estudiantes hacían referencia a las dos propiedades que involucran la suma y multiplicación por un escalar de vectores. Decidimos copiar sus respuestas textualmente y ver cómo las asociaban con la pregunta 1.
La mayoría de los estudiantes consideró a una transformación lineal como aquella que satisface dos condiciones, 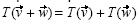 y
y 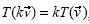 , mas sin la presencia de un modo de empleo; por ejemplo, omitiendo los cuantificadores. Parece que su definición de transformación lineal se centra sólo en las dos propiedades que la satisfacen, olvidando a qué campo pertenecen sus elementos.
, mas sin la presencia de un modo de empleo; por ejemplo, omitiendo los cuantificadores. Parece que su definición de transformación lineal se centra sólo en las dos propiedades que la satisfacen, olvidando a qué campo pertenecen sus elementos.
Apreciamos que el Estudiante 2 piensa que la preservación de los vectores sobre una recta bajo una transformación es equivalente a que tal cambio cumpla con las dos condiciones de la linealidad. El 3 se refiere a la transformación lineal como una combinación lineal. El 4 da tres condiciones, aunque la primera es equivalente a las dos últimas juntas. El 5 considera a la propiedad de la suma como combinación lineal. El 7 indica que hay tres condiciones, que asociamos con actividades hechas en el curso.
El Estudiante 6 parece señalar el cambio de un plano. Por ello, para tratar de relacionar su respuesta anterior con ésta, e interesados en saber cuál sería su solución ante la transformación identidad, posteriormente construimos una macro llamada transformación 3, definida por la expresión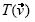 =
=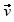 , que proporciona la imagen de un vector construido en la pantalla al hacer click en él, y durante la entrevista le pedimos al alumno que verificara si era o no una transformación lineal. El 5 fue invitado a participar en esta actividad como su pareja de entrevista. Resultó interesante observar que ambos estudiantes –con mayor énfasis el 5– consideraban a una transformación como generadora de un cambio. Notamos que, a pesar de satisfacerse las condiciones de suma y multiplicación por un escalar, el hecho de los alumnos vieran al vector imagen encima del vector inicial, y no en otra posición, los hacía dudar. El 6 finalmente identifica que es la transformación identidad.
, que proporciona la imagen de un vector construido en la pantalla al hacer click en él, y durante la entrevista le pedimos al alumno que verificara si era o no una transformación lineal. El 5 fue invitado a participar en esta actividad como su pareja de entrevista. Resultó interesante observar que ambos estudiantes –con mayor énfasis el 5– consideraban a una transformación como generadora de un cambio. Notamos que, a pesar de satisfacerse las condiciones de suma y multiplicación por un escalar, el hecho de los alumnos vieran al vector imagen encima del vector inicial, y no en otra posición, los hacía dudar. El 6 finalmente identifica que es la transformación identidad.
6.3.3. Sección 3. En esta parte se presentó a los estudiantes dos columnas con figuras; las segundas eran las imágenes bajo alguna transformación. Les pedimos que indicaran si era posible que hubiera una transformación lineal que convirtiera a la Figura 1 en la Figura 29. El objetivo consistía en analizar sus argumentos ante la ausencia de alguna expresión analítica que permitiera formular una transformación. A continuación, mostramos los tres incisos que conformaban dicha actividad.
Inciso a). Para este inciso (ver Cuadro 3) sí podría existir una transformación lineal; por ejemplo, los alumnos podrían argumentar que observan la composición de una rotación y una dilatación. También, en un sentido más formal, partiendo de dichas figuras podrían verificar las dos propiedades, al comprobar que en la Figura 1 el vector 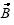 se puede escribir como
se puede escribir como 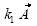 , y en la Figura 2 el vector
, y en la Figura 2 el vector 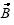 se puede escribir como
se puede escribir como 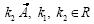 .
.

Para este inciso, el Estudiante 1 dijo que sí podría haber una transformación lineal, basándose sólo en la dilatación de los vectores. El 2 consideró bases en cada figura; tomó a la segunda como imagen de la primera y de ahí planteó la posible existencia. El 3 afirmó que no era posible, argumentando que, para que se definiera una transformación lineal, él necesitaba dos vectores linealmente independientes y dos escalares que cumplieran con la combinación lineal y generaran otro espacio vectorial. Nosotros percibimos ante tal respuesta que quizá el Estudiante 3 sentía necesidad de tener siempre dos vectores para verificar si había una transformación lineal, más aún que fueran linealmente independientes, aunque era posible que tampoco hubiera considerando una combinación lineal de vectores colineales.
Para confirmar estas conjeturas, durante la entrevista a este alumno le pusimos tres actividades. Con base en el esquema del cuestionario diagnóstico, le proporcionamos primero dos figuras, cada una con un vector, y le preguntamos si era posible que existiera una transformación lineal del plano que convirtiera al vector de la Figura 1 en el vector de la Figura 2. Efectivamente, como lo imaginábamos, respondió que no porque era necesario tener dos vectores (Figura 7).
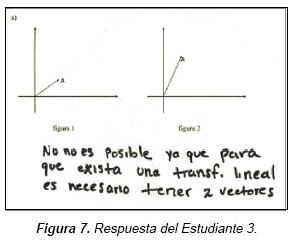
Seguidamente le planteamos de nuevo el inciso a) del cuestionario diagnóstico porque ahí sí se encontraban dos vectores. Y argumentó que no porque los vectores eran linealmente dependientes.
El Estudiante 4 anotó la fórmula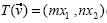 con
con 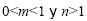 y verificó que fuera lineal, comprobando si se satisfacían las propiedades de suma y multiplicación por un escalar. El 5 señaló la posible existencia de una transformación lineal; sin embargo, al igual que el 1, sólo percibió la dilatación de vectores, de ahí que sus argumentos se basaran en un sentido visual. El 6 también indicó que sí podría existir una transformación lineal y se percató además de la dilatación, una rotación. El 7 y el 8 no abordaron este inciso.
y verificó que fuera lineal, comprobando si se satisfacían las propiedades de suma y multiplicación por un escalar. El 5 señaló la posible existencia de una transformación lineal; sin embargo, al igual que el 1, sólo percibió la dilatación de vectores, de ahí que sus argumentos se basaran en un sentido visual. El 6 también indicó que sí podría existir una transformación lineal y se percató además de la dilatación, una rotación. El 7 y el 8 no abordaron este inciso.
6.3.4. Descripción general del desempeño de los estudiantes con base en los resultados del cuestionario diagnóstico.
• Estudiantes 1 y 2: Podemos advertir a lo largo del desarrollo de las actividades que muestran elementos de un pensamiento teórico. No tienen dificultades con las nociones involucradas en las preguntas.
• Estudiante 3: No presenta una estructura conceptual sólida, de ahí que, en su mayoría, ofrezca respuestas intuitivas pero erróneas, basándose en sus experiencias previas. Notamos elementos de un pensamiento práctico en sus soluciones.
• Estudiante 4: Podemos apreciar que tiene elementos de un pensamiento teórico. Sin embargo, nos llama la atención que cuando cierta situación se sale de un esquema prototipo adapta sus técnicas, que suelen no conducirlo a los resultados correctos.
• Estudiante 5: Podemos considerar que su pensamiento es más práctico que teórico. Aborda los ejercicios que guardan relación con procedimientos de actividades anteriores, mientras que tiene dificultades para abordar aquellos cuya solución requiere de procedimientos nuevos.
• Estudiante 6: Aunque su conocimiento respecto al álgebra lineal era limitado, consideramos que su intuición le guía hacia soluciones adecuadas.
• Estudiante 7. Sus conocimientos previos en álgebra lineal son limitados y lo conducen a desarrollar el obstáculo de formalismo. Sus respuestas presentan incongruencias.
• Estudiante 8: Dejó sin contestar la mayoría de las preguntas, lo cual nos impide sacar información acerca de su pensamiento.
Finalmente, en la tercera etapa se llevó a cabo una entrevista, conformada por tres actividades, que incluía al problema de extensión lineal. Los estudiantes trabajaron en binas (1 con 2; 3 con 4; 5 con 6, y 7 con 8) con la intención de poder observar las discusiones entre ellos y los argumentos correspondientes. Presentamos a continuación sólo la tercera actividad.
6.4. Entrevista. Tercera actividad .
La tercera actividad consistió en el problema de extensión lineal. Aquí, les proporcionamos a los estudiantes una copia escrita de la actividad (Figura 8).
6.4.1. Estatus de los elementos que intervienen en el problema de extensión lineal .
Los vectores 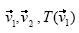 y
y 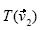 son libres; el estudiante los construye partiendo de un punto 0, denotado origen. Por el enunciado del problema, está implícito que los vectores
son libres; el estudiante los construye partiendo de un punto 0, denotado origen. Por el enunciado del problema, está implícito que los vectores 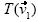 y
y 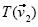 son imágenes de
son imágenes de 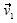 y
y 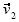 , y al cambiar su posición resultaría otra transformación lineal. El vector
, y al cambiar su posición resultaría otra transformación lineal. El vector 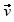 , construido como combinación lineal de
, construido como combinación lineal de 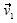 y
y 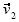 será dependiente de los vectores
será dependiente de los vectores 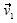 y
y 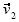 . Cada línea numérica presenta un escalar independiente uno del otro.
. Cada línea numérica presenta un escalar independiente uno del otro.
6.4.2. La actividad .
Como la actividad pertenecía al segundo rediseño (Sierpinska, 2000), se le añadieron los tres primeros incisos –sobre todo el c)– con la intención de inducir a los estudiantes a que establecieran la respuesta del inciso d). En este último, el paso esencial para obtener la solución correcta era considerar al vector 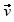 como combinación lineal de
como combinación lineal de 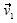 y
y 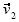 "por ser linealmente independientes" formaban una base para el plano; a partir de ahí, se tenía que aplicar la definición de transformación lineal para obtener la imagen de
"por ser linealmente independientes" formaban una base para el plano; a partir de ahí, se tenía que aplicar la definición de transformación lineal para obtener la imagen de 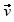 . Como las instrucciones del problema no hacían explícito que
. Como las instrucciones del problema no hacían explícito que 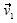 y
y 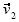 formaban una base, entonces el alumno debía recurrir a estrategias que involucrara conexiones entre sus conceptos para dar la solución adecuada. Nuestra intención era observar sus estrategias para percibir de qué manera vinculaban estos conceptos.
formaban una base, entonces el alumno debía recurrir a estrategias que involucrara conexiones entre sus conceptos para dar la solución adecuada. Nuestra intención era observar sus estrategias para percibir de qué manera vinculaban estos conceptos.
7. PRINCIPALES RESULTADOS
A excepción de los estudiantes 1 y 2, los demás tuvieron dificultades al resolver el inciso d). Explicaremos a continuación nuestras percepciones al respecto.
De manera sintética, el procedimiento para llegar a la solución deseada constaba de los siguientes pasos:
1. Construir
como combinación lineal de
y
2. Escribir la relación
3. Aplicar la transformación lineal a la expresión del paso 2 y obtener
4. Finalmente, construir
como se indica en la última relación del paso 3.
Podemos decir que este era un algoritmo corto y no algebraicamente complicado; sin embargo, los estudiantes no lo plantearon. Creemos que el paso esencial radica en establecer la combinación lineal de 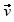 respecto a
respecto a 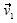 y
y 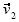 ; mientras los estudiantes no perciban tal relación no podrán avanzar en la resolución.
; mientras los estudiantes no perciban tal relación no podrán avanzar en la resolución.
Lo que posiblemente les impide dar ese primer paso es que no hacen una conexión entre los conceptos de base y transformación lineal. Es como si pensaran sólo en el concepto de transformación lineal y todas sus estrategias giraran únicamente en torno a dicha noción; tal es el caso de la pareja conformada por los estudiantes 3 y 4, quienes en sus intentos trataron de encontrar la regla de la transformación lineal o intentaron partir de las propiedades para despejar 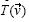 y llegar a la solución. Pero cuando sus estrategias se agotaron, concluyeron que no era posible hallar
y llegar a la solución. Pero cuando sus estrategias se agotaron, concluyeron que no era posible hallar 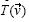 , lo cual se puede apreciar en el siguiente extracto:
, lo cual se puede apreciar en el siguiente extracto:
[197]Estudiante 4: A ver... ese es mi vector v [dibuja en la pantalla al vector v]
[198]Figura
[199]Estudiante3: Mm... tendrías que saber qué hace la...
[200] Estudiante 4: La transformación.
[201]Estudiante 3: La transformación para poder buscar su imagen. [...]
[210] Estudiante 4: ¿Te acuerdas que había uno? bueno, pero ese estaba en la macro... este... donde poníamos éste [señala al vector v] y lo movíamos y coincidía con cualquiera
[211] Estudiante 3: Pero tenías que tener la regla de las transformaciones para hacerlos coincidir.
[212]Estudiante 4: Acá, ajá, acá no la tenemos... Entonces, acá, vamos a ir al revés... la imagen del vector v... construir la imagen de v donde v es un vector arbitrario [relee la actividad].
[213]Estudiante 3: Mj... Fíjate, parece ser que lo que hace la transformación es rotar –90 grados el vector y multiplicarlos por un escalar porque este vector tiene su imagen acá y este vector tiene su imagen acá [señala los vectores imágenes en la hoja donde está escrita de la actividad]
[214]Estudiante 4: Mj... sí...
[215]Estudiante 3: ¿Sí es la regla?
[216]Estudiante 4: Por como está la figura en la hoja, sí... [...]
En otro intento, los mismos alumnos trataron de hallar la regla de transformación por combinación de dos movimientos simples, rotación y dilatación. Sin embargo, observaron que dicha transformación no se satisfizo para los dos vectores 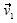 y
y 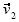 , por lo cual descartaron esa posibilidad:
, por lo cual descartaron esa posibilidad:
[227]Estudiante 4: [...] Ahora, si hago lo que tú es... ¿qué rotar?
[228]Estudiante 3: Rotar –90 y multiplicarlo por un escalar, pero ¿qué escalar?
[229]Figura
[230]Estudiante 4: Mm, fíjate, si dices eso, que es rotar... la transformación de v2
[231]Estudiante 3: Ah, más o menos, o sea, no es exacto igual. ¿Ya lo viste?
[232]Estudiante 4: Sí, esto [refiriéndose al vector T(v2)] se ve un poco más pequeño que éste [vector v2], pero es un escalar menor que 1, mas para v1 se ve mayor éste [vector T (v1)]. Entonces el escalar tiene que ser mayor que 1... no coinciden con el escalar... ¿Ya?... ¿Qué más podemos hacer?... Mm, no veo...
Un pequeño vínculo puede crear un puente entre los conceptos involucrados dentro de un problema. Nosotros esperábamos que el inciso c) pudiera crear ese puente para llegar al inciso d), mas no fue así. Contemplábamos que el hecho de resolver correctamente el inciso c) permitiría a los estudiantes generalizar 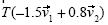 y así hallar
y así hallar 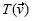 .Fue interesante observar, respecto a dicho vínculo esperado entre el inciso c) y el d), que los estudiantes 3 y 4 no sintieron la necesidad de alguna regla para trabajar el inciso c); de hecho, en ninguno de los tres primeros incisos. Este aspecto nos hace pensar que trabajar con un caso general –el inciso c)– puede causar dificultades que no se observan en casos particulares, tomando a los incisos a), b) y c).
.Fue interesante observar, respecto a dicho vínculo esperado entre el inciso c) y el d), que los estudiantes 3 y 4 no sintieron la necesidad de alguna regla para trabajar el inciso c); de hecho, en ninguno de los tres primeros incisos. Este aspecto nos hace pensar que trabajar con un caso general –el inciso c)– puede causar dificultades que no se observan en casos particulares, tomando a los incisos a), b) y c).
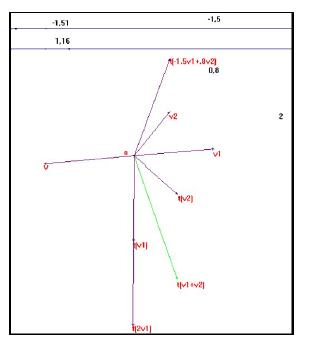
Los estudiantes 6 (de la bina 6 y 7) y 8 (de la bina 7 y 8) se apoyaron en otras relaciones, ya que consideraron combinaciones lineales en sus estrategias y tras algunos intentos llegaron a la solución deseada. Sin embargo, los significados de sus conceptos no jugaron el papel adecuado porque no les permitieron tomar decisiones pertinentes y justificar el desarrollo de la solución, a diferencia de los estudiantes 1 y 2, quienes desde el inicio de la Actividad 3 trataron el problema considerando una estructura global, pues partieron del caso general, al elaborar una construcción que obedeció al inciso d) y fueron resolviendo los incisos a), b) y c). En cambio, a pesar de que llegaron a la solución esperada, el Estudiante 6 no mostró seguridad en su planteamiento y el 8 consideró 2 vectores arbitrarios, sin percibir una equivalencia entre ellos (el significado de base para él no estuvo presente).
Observemos el siguiente extracto, correspondiente al Estudiante 8:
[388]Estudiante 8: Entonces, a ver... Hacemos la combinación lineal de este escalar con este vector y éste con éste [construye el vector
Esto lo etiquetamos y esto va a ser nuestro
. ¿Está bien?
[389]Estudiante 7: Mj.
[390]Estudiante 8: Ahora, este
, si le aplicamos la transformación, que es esto que está acá [señala la expresión T(k1 v1 + k2 v2)] nos debe dar esto [indica la expresión T (V1) + K2 T (V2)] pero nosotros tenemos T(v1) y T(v2) . Entonces, sería la suma del producto escalar de éstos [señala en la pantalla a los vectores t(v1) y t(v2)], que sería también la combinación lineal de estos dos vectores [t(v1) y t(v2)].
[391]Estudiante 7: Con los escalares.
[392] Estudiante 8: Aja... [construye en la pantalla la combinación lineal de k1, t(v1), k2, t(v2) y eso es esto [etiqueta ese vector resultante como t(k1v1+k2v2)] .
[393]Figura
[...]
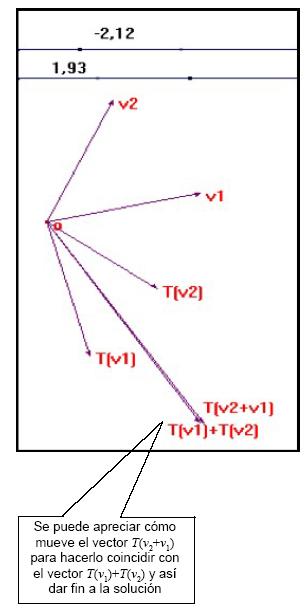
[404]Estudiante 8: [...] Si hacemos coincidir este vector v, arbitrario con este vector [apunta al vector k1v1+k2v2] entonces la imagen bajo la transformación de este vector [v] va a ser ésta [señala al vector t(k1v1+k2v2)] . El vector que esté acá, ya cuando hagamos variar esto y sean otros vectores, si volvemos a hacer coincidir acá [apunta al vector v], entonces la imagen que aparezca debe coincidir con la imagen de esta... sería la transformación.
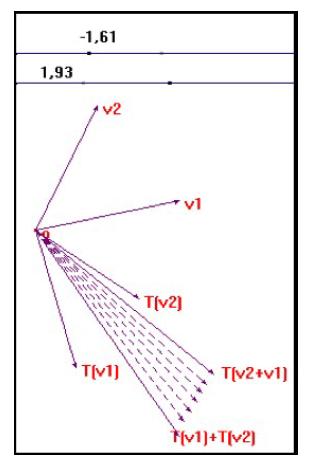
Otro punto importante radicó en la intencionalidad, ya que sin ella los significados no desempeñan ningún papel. Quizá eso fue, en parte, el caso del Estudiante 5, en quien se pudieron apreciar planteamientos correctos a lo largo de la entrevista, mas sin reflexionar sobre las estrategias; hizo acciones basado en hechos memorísticos. Por ejemplo, no se percató del error cometido en el inciso a) de la tercera actividad, cuando el Estudiante 6 dio una solución en la que se notó que buscaba representar geométricamente la expresión 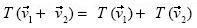 mediante construcciones en Cabri. Es decir, tomando los datos que tenían, por un lado construyó
mediante construcciones en Cabri. Es decir, tomando los datos que tenían, por un lado construyó 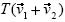 ; por otro, elaboró un vector (al que le llamaremos
; por otro, elaboró un vector (al que le llamaremos 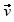 10) como combinación lineal de los vectores
10) como combinación lineal de los vectores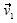 y
y 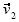 los escalares de las rectas numéricas
los escalares de las rectas numéricas 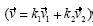 y movió los escalares, de tal forma que ese vector
y movió los escalares, de tal forma que ese vector 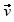 coincidiera con el vector suma
coincidiera con el vector suma 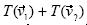 Así, él cree que ha construido el vector
Así, él cree que ha construido el vector 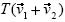 , cuando en realidad ha hecho
, cuando en realidad ha hecho 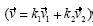 equivalente a
equivalente a 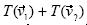 para algún k1,k2 . El siguiente extracto muestra lo que hemos señalado en este párrafo:
para algún k1,k2 . El siguiente extracto muestra lo que hemos señalado en este párrafo:
[248]Estudiante 6: ¿T de v1 más v2? transformación... o sea...
[249]Estudiante 5: La transformación de v1 más v2
[250]Estudiante 6: Hago la suma de estos dos [señala T(v1) y T(v2) ] y a ver dónde cae, entonces después construimos la suma de estos dos v1 y v2]
[251]Estudiante 5: Mj
[252]Estudiante 6: Como combinación lineal de estos [parece indicar con el cursor a T(v1) y T(v2)] y luego los movemos.
[253]Estudiante 5: Mj, ok.
[254]Estudiante 6: ¿Estás de acuerdo?
[255]Estudiante 5: A ver, pérate, pérate...
[256]Estudiante 6: ¿Estás de acuerdo? Sino, ahorita lo deshacemos.
[257]Estudiante 5: No, sí, sí...
[258] Estudiante 6: Adición de vectores [suma T(v1) con T(v2)].
[259] Estudiante 6: Ahora, combinación lineal [realiza la combinación lineal de los vectores v1 y v2utilizando los escalares que tiene en la pantalla y los mueve para que el vector resultante de dicha combinación coincida con el vector suma T(v1) + T(v2). Lo etiqueta como T(v1+T(v2)].
[260]Figuras
7.1. Manifestaciones del obstáculo de formalismo
El obstáculo de formalismo fue estudiado por Dorier, et al. (1997) y Sierpinska (2000) en un contexto algebraico, al observar que los estudiantes manipulaban símbolos y notaciones, pero ignoraban los significados o las reglas de las matemáticas.
Nuestra investigación se situó en un contexto geométrico, por lo que la manipulación no siempre fue de símbolos, sino también de objetos concretos, como los vectores y las construcciones geométricas involucradas con ellos. Por ello, cuando conjeturamos que el obstáculo de formalismo podía hacerse presente, no consideramos de qué manera se manifestaría y hasta cierto punto pensamos que había poca probabilidad de que ocurriera; sin embargo, se hizo presente en los alumnos 6 y 7. El Estudiante 6, en el inciso a) de la tercera actividad, intentó verificar geométricamente la igualdad 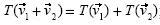 ; con los datos del problema pudo construir el vector suma
; con los datos del problema pudo construir el vector suma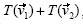 ,pero no el vector
,pero no el vector 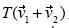 . Entonces, construyó un vector con los elementos disponibles y lo denotó como
. Entonces, construyó un vector con los elementos disponibles y lo denotó como 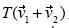
En el caso del Estudiante 7 se notaron muchas manifestaciones del obstáculo de formalismo. Aunque había en él una necesidad de hacer, sus planteamientos carecieron de sentido, pues intentó adecuar ejemplos de sus experiencias pasadas a las situaciones que tenía enfrente, cayendo en una serie de pasos ilógicos. Si bien dichos pasos no fueron apreciados en su totalidad por la intervención de su compañero –el Estudiante 8–, se pudo observar en sus participaciones acciones sin sentido. Por ejemplo, en las primeras dos actividades, aun cuando el Estudiante 8 había verificado las propiedades que satisfacían una transformación lineal, insistió en verificar otras condiciones (que calificó como colinealidad, paralelismo y suma). En el inciso b) de la tercera actividad construyó el vector 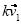 , pero no supo qué hacer con él, mientras que en el inciso d), para hallar,
, pero no supo qué hacer con él, mientras que en el inciso d), para hallar, 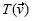 hizo una construcción que era completamente ajena a las condiciones del problema.
hizo una construcción que era completamente ajena a las condiciones del problema.
[294]Estudiante 7: Lo que nos están pidiendo es su trasformación. entonces, si yo aquí tengo una recta [empieza a hacer nuevamente trazos, reproduciendo la figura de la línea 291; dibuja una recta horizontal, a la que le llamaremos L1], trazo la perpendicular de esta recta [L2] y la paralela de esta recta [dibuja una tercera recta, L3]. Se supone, bueno, si esta es una recta, la perpendicular es igual, se supone que esta es su transformación [señala el vector que se encuentra sobre la recta L2]... de este vector [refiriéndose al otro vector, que no se encuentra en la recta L2]
[295] Figura
[296]Estudiante 8: ¿Transformación?
[297]Estudiante 7:¿No es esto lo que estoy buscando? [repinta el vector que se encuentra sobre la recta perpendicular]
[298] Estudiante 8: ...Mm no sé... yo no...
[299]Estudiante 7: ¿No?... Es que están pidiendo la transformación de un vector v, nada más.
8. CONCLUSIONES
Los resultados nos llevan a plantear la siguiente pregunta: ¿cómo ayudar a los estudiantes a pensar teóricamente y a hacer conexiones entre diferentes conceptos? Responderla no es tan sencillo, pero nos invita a reflexionar porque tiene muchas implicaciones en la enseñanza.
Consideramos que dos ingredientes nos permiten llevar a cabo conexiones entre los conceptos: su abstracción y la práctica constante de problemas nuevos. Poner en marcha el segundo elemento quizá no sea difícil de realizar, mas realizar actividades que garanticen la abstracción de los conceptos no es una labor fácil. Ahora bien, el carácter formal de los conceptos siempre debe estar presente durante el proceso de enseñanza–aprendizaje y quizá como punto de partida. El empleo de un buen método de enseñanza que evite empezar con el aspecto formal tiene que cuidar de no dar lugar a que los conceptos sean apreciados sólo por sus características o carácter funcional.
Para Steinbring (1991), el conocimiento matemático no puede ser reducido a la reproducción exitosa de algoritmos. Es necesario hacer frente a las dificultades conceptuales que los estudiantes puedan manifestar, en vez de trazarles un camino plano con la mejor de las intenciones, usando simplificaciones metódicas. Tal reflexión es muy pertinente en áreas como el álgebra lineal, cuya naturaleza compleja hace que se recurra a estrategias de simplificación.
Otra cuestión importante, de acuerdo con Steinbring (1991), es que la visión epistemológica de estudiantes y profesores ante un mismo conocimiento matemático suele ser diferente. La postura de profesores y estudiantes sobre el conocimiento no es la misma: el estudiante por lo general se encuentra en una etapa anterior al conocimiento, por lo cual siempre está en un estado de revolución, mientras que el profesor es como un científico de la matemática escolar cuyo conocimiento está hecho. Ello conduce a tomar en cuenta que profesores y estudiantes son, ante todo, individuos diferentes que tienen sus propios contextos, sus propios significados y sus propias actividades.
Es fundamental para el aprendizaje que se pueda reducir la distancia entre el conocimiento del profesor y el del estudiante (Steinbring, 1991) porque ambos tendrían una misma visión epistemológica para el conocimiento. Sin embargo, consideramos que el conocimiento del profesor puede también mostrar ciertas deficiencias que pueden afectar el aprendizaje de los estudiantes.
Además, cuando se recurre a aspectos intuitivos y analíticos de los conceptos hay que buscar un equilibrio entre ambos, a fin de lograr una apropiación adecuada de los significados que están involucrados. Tal vez dicho equilibrio haya estado presente en los estudiantes 1 y 2; es posible que en sus cursos anteriores su ambiente de aprendizaje fue más algebraico y el nuestro complementó aspectos geométricos que no habían apreciado, provocando así un equilibrio.
Enfatizamos la importancia de considerar dentro de la enseñanza problemas novedosos que permitan a los estudiantes poner en juego su conocimiento adquirido, donde diferentes conceptos deban vincularse para una solución adecuada. También opinamos que, si los estudiantes reciben una experiencia en la que no sean estrictamente dependientes del profesor en el proceso de enseñanza–aprendizaje y se les conduzca a generar su propio conocimiento, podría ayudarles a desarrollar las conexiones para solucionar los problemas que las requieran.
La motivación de un pensamiento teórico en los estudiantes debe ser un tema que preocupe a profesores e investigadores, sobre todo en las ramas de las matemáticas como la de álgebra lineal, donde el estudio de muchos conceptos abstractos da lugar a su algoritmización para un manejo más fácil por parte de profesores y estudiantes. Cabe mencionar que habría que marcar una diferencia respecto a establecer conexiones entre conceptos particulares y el desarrollo de un pensamiento conectivo que permitiría tener elementos para aplicar en cualquier caso. Por tanto, enfatizamos un modo de pensamiento y no la resolución correcta de cualquier problema.
En una futura investigación, dentro del pensamiento teórico podría contemplarse el establecimiento de una subcategoría del pensamiento sistémico, llamándola pensamiento conectivo, para darnos cuenta de la presencia o ausencia de vínculos entre los conceptos que manejan los estudiantes.
Podríamos sugerir que la enseñanza del álgebra lineal debe contemplar estrategias que permitan combinar aspectos intuitivos y analíticos de los conceptos, cuidando el aspecto formal y organizando el contenido de tal manera que los conceptos previos lleven a la adquisición de los posteriores. En particular, en el aprendizaje del concepto de transformaciones lineales es importante hacer hincapié, por un lado, en el aspecto intuitivo, considerando el aspecto geométrico de sus propiedades; por otro, atender el aspecto formal, incluyendo el uso de los cuantificadores y el espacio vectorial en su definición. Asimismo, hay que incluir más situaciones del tipo problema de extensión lineal para ayudar a los estudiantes a hacer conexiones con otros conceptos del álgebra lineal, de manera que puedan apreciar una estructura global.
Tal vez no sea una tarea fácil ayudar a los estudiantes a que construyan conexiones entre conceptos matemáticos. Sin embargo, metodologías que permitan precisar empezar a realizar actividades con ese estrategias tendientes a lograr esas propósito puede ayudar al desarrollo de conexiones.
1 Este trabajo forma parte del proyecto CONACYT 2002–C01 –41726S
9. BIBLIOGRAFÍA
Asiala, M., Brown, A., DeVries, D., Dubinsky, E., Mathews, D., & Thomas, K. (1996). A framework for research and curriculum development in undergraduate mathematics education. En Kaput, A. H. Schoenfeld & E, Dubinsky (Eds.), Research in collegiate mathematics education (pp. 1–32). Providence, RI: American Mathematical Society.
Dorier, J–L. (1997). Exemples d'interaction entre recherches en didactique et en histoire des mathématiques à propos de l'enseignement de l'algèbre linéaire. Fascicule de Didactique des Mathématiques et de l'EIAO (pp. 53–74). Rennes, France : IREM de Rennes. [ Links ]
Dorier, J–L., Robert, A., Robinet, J. et Rogalski, M. (1997). L'algèbre linéaire: l'obstacle du formalisme à travers diverses recherches de 1987 a 1995. En J–L. Dorier (Ed.), L'enseignement de l'algèbre linéaire en question (pp. 105–147). Grenoble, France : La Pensée Sauvage Editions. [ Links ]
Dreyfus, T., Hillel, J. & Sierpinska, A. (1998). Cabri–based linear algebra: transformations. Artículo presentado en CERME–1 (First Conference on European Research in Mathematics Education, Osnabrück). Obtenido de http://www.fmd.uni-osnabrueck.de/ebooks/erme/cerme1-proceedings/papers/g2-dreyfus-et-al.pdf. [ Links ]
Haddad, M. (1999). Difficulties in the learning and teaching of linear algebra. A personal experience. Tesis de maestría, Concordia University, Montreal, Canadá. [ Links ]
Molina, G. (2004). Las concepciones que los estudiantes tienen sobre la transformación lineal en contexto geométrico. Tesis de maestría, Cinvestav, México. [ Links ]
Resnick, L. B. (1987). Education and learning to think. USA: Washington, DC: National Academy Press. [ Links ]
Robert, A. y Robinet, J. (1989). Quelques résultats sur l'apprentissage de l'algèbre linéaire en première année de DEUG. Paris, France: IREM de Paris VII, Cahier de Didactique des Mathématiques 53. [ Links ]
Rogalski, M. (1990). Pourquoi un tel échec de lénseignement de l'algèbre linéaire? In Enseigner autrement les mathématiques en DEUG Première Année (pp. 279–291). Paris, France: Commission Inter–IREM Université. [ Links ]
Sierpinska, A. (2000). On some aspects of students thinking in linear algebra. En J–L. Dorier (Ed.), On the Teaching of Linear Algebra (pp. 209–246). Dortrecht/Boston/London: Kluwer Academic Publishers. [ Links ]
Sierpinska, A.; Dreyfus, T. & Hillel, J. (1999). Evaluation of a teaching design in linear algebra: the case of linear transformations. Recherches en Didactique des Mathématiques, 19 (1), 7–40. [ Links ]
Sierpinska, A., Hillel, J. & Dreyfus, T. (1998). Evaluation of a teaching design in linear algebra: the case of vectors (Technical Report). Montreal, Canada: Concordia University. [ Links ]
Sierpinska, A., Nnadozie, A. & Oktaç, A. (2002). A study of relationships between theoretical thinking and high achievement in linear algebra (Research Report). Montreal, Canadá: Concordia University. [ Links ]
Soto, J. L. (2003). Un estudio sobre las dificultades para la conversión gráfico–algebraica relacionadas con los conceptos básicos de la teoría de espacios vectoriales en R2 y R3. Tesis de doctorado, Cinvestav, México. [ Links ]
Steinbring, H. (1991). Mathematics in teaching processes. The disparity between teacher and student knowledge. Recherches en Didactique des Mathématiques, 11 (1), 65–108. [ Links ]
Trgalová, J. et Hillel, J. (1998). Une ingénierie didactique à propos de notios de base de l'algèbre linéaire intégrant l'outil informatique : Cabri–Géomètre II. In Actes du Colloque du Groupe de Didactique des Mathématiques du Québec (pp. 138–149). Montreal, Canada. [ Links ]
Vigotsky, L. S. (1987). The collected works of L. S. Vigotsky (Vol. 1, Problems of General Psichology. Including the volume Thinking and Speech). New York & London: Plenum Press. [ Links ]
Vinner, S. (1983). Concept definition, concept image and the notion of function. International Journal of Mathematics Education in Science and Technology, 14, 239–305. [ Links ]
Zazkis, R. (2001). Múltiplos, divisores y factores: explorando la red de conexiones de los estudiantes. Revista Latinoamericana de Investigación en Matemática Educativa, 4 (1), 63–92. [ Links ]
4 En el apartado Consideraciones Teóricas daremos información más amplia respecto a estos modos de pensamiento.
5 La macro es una herramienta del software que permite la realización automática de una secuencia de construcciones interdependientes, según su programación.
6 Los autores utilizan el término disposition (en inglés) en el sentido de Resnick (1987, p. 41, citado en Sierpinska et al., 2002): "El término disposition no debería ser considerado como implicación de un rasgo biológico o hereditario. Como se usa aquí, es más bien semejante al hábito del pensamiento, mismo que puede ser aprendido, y por lo tanto, enseñado.
7 Comportamientos observables a través de las respuestas de los estudiantes.
8 Cabe mencionar que todas las transformaciones lineales que se trabajaron fueron transformaciones del espaciobidimensional, representado por la pantalla.
9 Estas actividades fueron diseñadas por Molina (2004). Dos de ellas fueron consideradas en su tesis de maestría y la otra la discutimos en una charla que sostuvimos.
10 El Estudiante 6 está haciendo construcciones en la pantalla, de modo que el vector resultante de la combinación lineal de los vectores 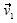 y
y 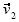 y los escalares de las rectas numéricas (o sea,
y los escalares de las rectas numéricas (o sea,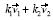 no es etiquetado. Portal motivo, decidimos denotar al dicho vector como
no es etiquetado. Portal motivo, decidimos denotar al dicho vector como 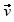 .
.