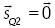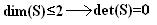Estudios e investigaciones recientes

 

Análisis cinemático directo de un manipulador paralelo esférico asimétrico

 

J. Gallardo–Alvarado¹, J.M. Rico–Martínez² y M. Caudillo–Ramírez¹

 

1 Departamento de Ingeniería Mecánica, Instituto Tecnológico de Celaya

2 FIMEE, Universidad de Guanajuato

 

E–mails:
gjaime@itc.mx
mrico@itc.mx
cmartin@itc.mx

 

Recibido: abril de 2005
Aceptado: febrero de 2006

 

Resumen

Este trabajo se enfoca al análisis cinemático directo de un manipulador paralelo de tres grados de libertad, cuya plataforma móvil puede experimentar sólo movimientos de rotación. El análisis directo de posición, una tarea retadora en la mayoría de los manipuladores paralelos, se presenta en forma cerrada. El análisis directo de velocidad se aborda por medio de la teoría de tornillos siendo de especial utilidad la forma de Klein del álgebra de Lie e(3). Finalmente, se proporciona una interpretación geométrica de las llamadas singularidades locales del manipulador paralelo propuesto.

Descriptores: Movimiento esférico, manipulador paralelo, teoría de tornillos, singularidad, análisis cinemático.

 

Abstract

This work is devoted to the forward kinematics of a three–degree–of –freedom parallel manipulator whose moving platform can undergo only spherical motions. The forward position analysis, a challenging task for most parallel manipulators, is presented in closed–form solution. Afterwards, the forward velocity analysis is approached by means of the theory of screws being of special utility the Klein form of the Lie algebra e(3). Finally, a geometric interpretation of the so–called local singularities of the proposed parallel manipulator is provided.

Keywords: Spherical motion, parallel manipulator, screw theory, singularity, kinematics.

 

Introducción

Una plataforma general Gough–Stewart es un manipulador paralelo de seis grados de libertad que consta de una plataforma móvil unida a una plataforma fija por medio de seis cadenas cinemáticas o extremidades, las cuales se accionan de manera independiente. El análisis directo de posición del mecanismo, introducido por Gough hace más de medio siglo, como un mecanismo para probar neumáticos de avión bajo diferentes condiciones de carga, y retomado por Stewart como un simulador de vuelo en 1965, es una tarea compleja que conduce a 40 posibles soluciones, (Raghavan, 1993), las cuales se pueden resumir en un polinomio de grado cuarenta, (Innocenti, 1998). No es de sorprender que el primer algoritmo, no iterativo, propuesto para determinar los coeficientes de dicho polinomio data de hace menos de diez años y se le atribuye a Husty (1996).

A fin de simplificar el análisis directo de posición, la plataforma Gough–Stewart puede descomponerse en dos manipuladores paralelos ensamblados en serie, uno para la rotación y el otro para la translación, y con ello, es posible obtener la solución en forma cerrada, (Gallardo, 2005). Por otra parte, si se reconoce que muchas aplicaciones industriales no requieren de los seis grados de libertad de un manipulador paralelo, entonces es posible recurrir a lo que se denomina como un manipulador paralelo deficiente. Un ejemplo del éxito industrial de un manipulador paralelo con menos de seis grados de libertad, es el llamado manipulador Delta, una invención de Clavel (1988).

Dentro de los manipuladores paralelos con menos de seis grados de libertad, se ubican los llamados manipuladores esféricos, y seguramente el más estudiado de ellos es el manipulador conocido como el ojo ágil, un mecanismo sobre restringido que fue introducido por Gosselin y Angeles (1988). Con dichos mecanismos un punto fijo de la plataforma móvil sólo puede experimentar movimientos de rotación, por lo tanto, las demás partículas de la plataforma móvil se mueven sobre esferas concéntricas. Los manipuladores esféricos, dadas sus arquitecturas, tienen aplicaciones interesantes, como por ejemplo, en dispositivos mecánicos que orientan antenas de radar y telescopios.

En este trabajo se realiza el análisis cinemático del manipulador paralelo esférico, compuesto por tres cadenas cinemáticas asimétricas que se muestran en la figura 1.

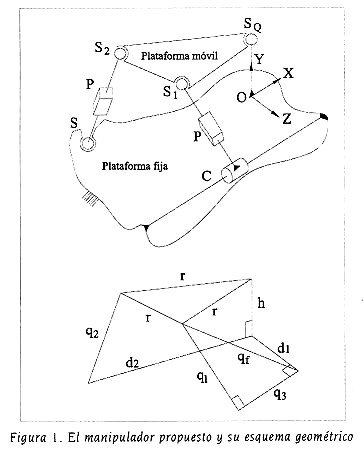
La plataforma móvil se une a la fija por medio de una cadena cinemática tipo CPS, por sus siglas en el idioma Inglés de Cylindrical + Prismatic + Spherical, otra tipo Spherical + Prismatic + Spherical, o por brevedad simplemente SPS, y un par esférico pasivo que por sí solo constituye la tercer extremidad.

El análisis directo de posición se obtiene en forma cerrada, y con ello, se prescinde del uso de una técnica numérica para su solución, como lo es el método de Newton–Raphson, (Gallardo et al., 2004). Por su parte, el análisis de velocidad, así como el análisis de singularidades locales, se resuelve por medio de la teoría de tornillos infinitesimales.

Finalmente, se proporciona un ejemplo numérico, y los resultados obtenidos vía teoría de tornillos se comparan con los generados con el programa de simulación de análisis cinemático y dinámico ADAMS©.

 

Análisis de posición

El análisis directo de posición consiste en determinar las coordenadas, de acuerdo al sistema de referencia fijo o global XYZ, de los centros de los pares esféricos, {S_Q, S₁, S₂}, que conectan la plataforma móvil con las tres cadenas cinemáticas cuando se dispone de un conjunto de coordenadas generalizadas {q₁, q₂, q₃}, así como de los parámetros del manipulador. Este análisis requiere, definitivamente, del cálculo correcto del grado de libertad del mecanismo, por lo que esta sección inicia con dicho análisis de movilidad.

El grado de libertad F de un mecanismo espacial de acuerdo a la clásica fórmula de Kutzbach–Grübler, viene dado por

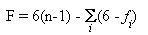
donde n es el número de eslabones y f_i representa el grado de libertad del par cinemática en turno. De esta manera, puesto que el manipulador paralelo bajo estudio se compone de 6 eslabones, 1 par cilíndrico, 2 pares prismáticos y 4 pares esféricos; entonces, aparentemente, el mecanismo es de 4 grados de libertad, como bien lo menciona uno de los revisores. Sin embargo, nótese que la rotación a lo largo de la extremidad SPS, debida a los dos pares esféricos, no afecta el movimiento de la plataforma móvil, es decir, dicha rotación debe considerarse como un grado de libertad pasivo que debe restarse de los 4 ya calculados, dando como resultado el grado de libertad del mecanismo que es en realidad 3.

Una vez que se ha determinado el grado de libertad del mecanismo, se prosigue con el análisis directo de posición.

De la figura 1 es evidente que

S_Q=(0,h,0).

Por otra parte, a fin de calcular las coordenadas del centro de la junta esférica

S₁ = (X₁, Y₁, Z₁)

es necesario considerar las ecuaciones de clausura asociadas a la cadena cinemática CPS y el par esférico pasivo de la tercer extremidad, la cual actúa como un simple poste. De la arquitectura del mecanismo, es posible escribir las ecuaciones de restricción

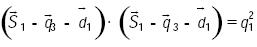....................................(1)

y

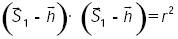....................................................(2)

donde • denota al producto escalar usual del álgebra vectorial de tres dimensiones. Si se toma en cuenta que el par prismático asociado al par cilíndrico de la extremidad CPS, denotado por la coordenada generalizada q₃, se mueve en una dirección paralela al eje X, entonces de acuerdo con las expresiones (1) y (2) se obtiene una ecuación cuadrática con la cual es posible determinar Z₁ Esto es

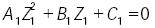.........................................................(3)

donde los coeficientes se proporcionan en la tabla 1. Más aún, dada la topología del manipulador, si el sistema de referencia XYZ se ubica de tal forma que el eje X se encuentra a lo largo de la coordenada generalizada q₃, entonces es evidente que X₁ = q₃. Por su parte, la componente Y₁ se obtiene a partir de la ecuación (1) como

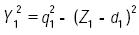.............................................................(4)

y con ello, se completa el cálculo de las coordenadas del centro del par esférico S₁.

A fin de calcular las coordenadas del centro de la junta esférica

S₂= (X₂, Y₂, Z₂)

se consideran las ecuaciones de restricción dadas por

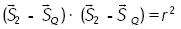....................................................(5)

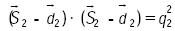.....................................................(6)

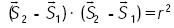.....................................................(7)

De las expresiones (5), (6) y (7), es posible obtener un sistema lineal de dos ecuaciones con tres incógnitas {X₂, Y₂, Z₂}. Por lo tanto, expresando X₂ y Y₂ en términos de la variable Z₂ se obtiene que

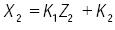.................................................................(8)

y

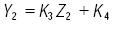.................................................................(9)

Donde, los coeficientes se listan en la tabla 2.

La sustitución de las expresiones (8) y (9) en la (5) conduce a la siguiente ecuación cuadrática, cuya variable es precisamente Z₂

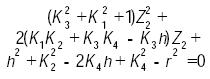...............................................(10)

Una vez que se calcula Z₂, las componentes restantes del centro del par esférico S₂= (X₂, Y₂, Z₂), se determinan directamente de las expresiones (8) y (9), y con ello, se completa el análisis directo de posición en forma cerrada.

 

Conceptos básicos de teoría de tornillos en los análisis de primer orden

Como una consideración para aquellos lectores que no están familiarizados con la teoría de tornillos infinitesimales, a fin de darle coherencia a las secciones posteriores, en esta sección se proporciona una revisión, necesariamente breve de algunos conceptos relacionados con la aplicación de esta herramienta matemática en el análisis de velocidad de cadenas cinemáticas abiertas y cerradas.

Un tornillo, $, es un vector de seis dimensiones dado por una componente primaria, 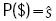, y una componente dual, 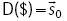, y se representa en coordenadas de Plücker, Duffy (1996), como

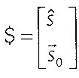........................................................................(11)

El vector unitario o normalizado 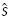representa un vector a lo largo del eje del tornillo, mientras que el vector 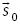es el momento producido por 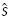en relación a un punto O fijo al sistema de referencia. El momento 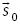se determina como

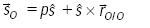..........................................................(12)

donde, 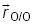es un vector que inicia en un punto O del eje instantáneo del tornillo y termina en el punto de interés O', mientras que p es el paso del tornillo. Por su parte, x, denota al producto cruz usual del álgebra vectorial de tres dimensiones.

Cualquier par cinemático inferior puede representarse por un tornillo o conjunto de tornillos. Si el tornillo representa a un par de revoluta, entonces el paso p es igual a cero y el tornillo viene dado por

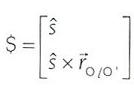.............................................................(13)

Si el paso del tornillo tiende a infinito, entonces el tornillo representa a un par prismático y se reduce a

..........................................................................(14)

Un par cilíndrico es la combinación de un par de revoluta y un par prismático, mientras que un par esférico resulta de la acción de tres pares de revoluta, cuyos ejes concurren a un punto común.

Sean

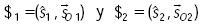
dos tornillos infinitesimales o elementos del álgebra de Lie e(3). La forma de Klein se define como

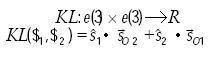............................................(15)

El estado de velocidad 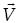de un cuerpo rígido representa el giro sobre un tornillo (Ball, 1900), y se determina como

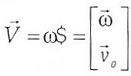..............................................................(16)

donde 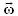es la velocidad angular del cuerpo rígido mientras que 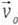es la velocidad del punto O, fijo al cuerpo rígido en movimiento bajo estudio, y que en el instante de tiempo considerado coincide con un punto fijo al sistema de referencia.

En un manipulador serie, el estado de velocidad del órgano terminal cuerpo m, con respecto al eslabón fijo cuerpo O, puede expresarse, según Sugimoto y Duffy (1982), en términos de los tornillos infinitesimales, asociados a los pares cinemáticos del manipulador como la siguiente combinación lineal

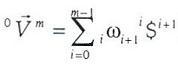....................................................(17)

donde _iω_i+1 representa los cambios instantáneos de velocidad entre los cuerpos indicados.

La expresión (17) es un elemento esencial en el análisis de velocidad de manipuladores serie y puede extenderse sin esfuerzo considerable al análisis de velocidad de cadenas cinemáticas cerradas y manipuladores paralelos, (Rico et al., 1999).

 

Análisis de velocidad

En esta sección se formula el análisis directo de velocidad del manipulador paralelo propuesto. Dicho análisis consiste en determinar la velocidad angular de la plataforma móvil, con respecto a la fija, dado un conjunto de velocidades generalizadas instantáneas.

En el manipulador propuesto, el estado de velocidad de la plataforma móvil cuerpo 6, con respecto a la plataforma fija cuerpo 0, puede expresarse a través de cualesquiera de las tres cadenas cinemáticas conectoras. Por ejemplo, el estado de velocidad de la plataforma móvil de acuerdo a la expresión (17), (Sugimoto y Duffy, 1982), tomando como referencia el punto Q indicado en la figura 1, y de acuerdo a la cadena cinemática CPS vendrá dado por

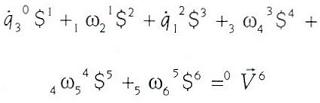........................(18)

donde, los tornillos infinitesimales indicados en la expresión (18) se muestran en la figura 2. Nótese que los tornillos ⁰$¹ y ¹$² representan, respectivamente, al par de revoluta y al par prismático del par cilíndrico de la cadena CPS.

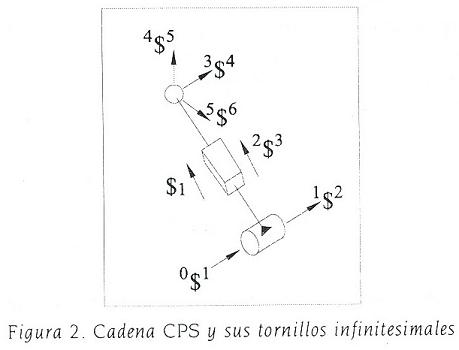
Más aún, puesto que el punto Q carece de movimientos de translación, entonces es evidente que la componente dual del estado de velocidad es nula, (Ball, 1900). Esto es

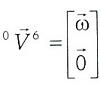....................................................................(19)

donde

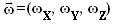
es la velocidad angular de la plataforma móvil de acuerdo al sistema de referencia fijo.

Considere la línea en coordenadas de Plücker,

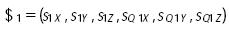
(Duffy, 1996), a lo largo de la extremidad CPS. Esta línea es recíproca a todos los tornillos que representan los pares de revoluta de la extremidad CPS. Por lo tanto, la aplicación de la forma de Klein, Rico y Duffy (2000), entre $₁ y ambos lados de la expresión (18) conduce a

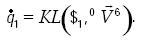............................................................(20)

Considere ahora la extremidad SPS, figura 3. Siguiendo un procedimiento similar al de la extremidad CPS, se obtiene que

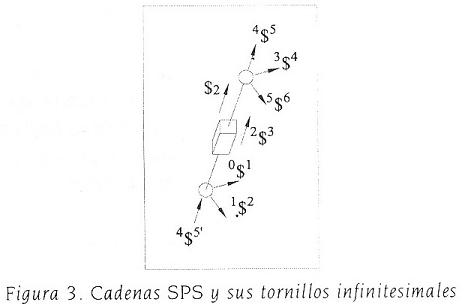
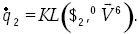............................................................(21)

donde

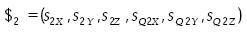
es la línea a lo largo de la extremidad SPS.

Con la finalidad de completar las ecuaciones necesarias para el análisis directo de velocidad, se introduce una cadena cinemática ficticia SPS que inicia en el punto de intersección de las líneas d₁ y q₃ que termina en el centro del par esférico S₁, tal y como se indica en las figuras 1 y 4. De esta manera, es posible escribir la siguiente expresión

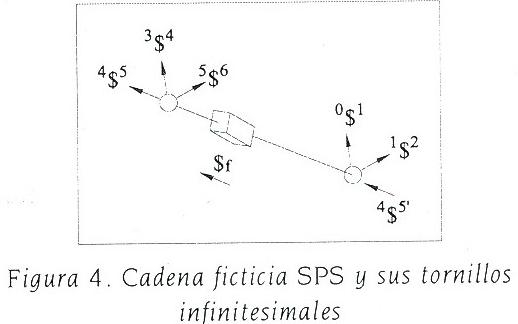
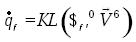.............................................................(22)

Donde

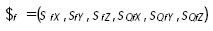
es una línea en coordenadas de Plücker a lo largo de la extremidad ficticia. Más aún, puesto que de acuerdo a la figura 1 se tiene que

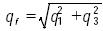
Entonces, la velocidad 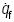se obtiene por simple derivación como

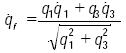...............................................................(23)

Finalmente, ordenando en forma matricial las expresiones (20), (21) y (22) se obtiene que la velocidad angular de la plataforma móvil, como se observa desde la plataforma fija, puede calcularse directamente de la expresión

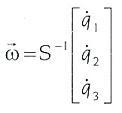................................................................(24)

donde S es una matriz especial dada por las componentes duales de las líneas a lo largo de las extremidades CPS, SPS y la línea ficticia $_f como

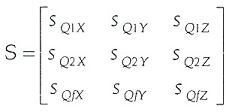
Vale la pena destacar que la expresión (24) permite calcular la velocidad angular de la plataforma móvil a partir de las velocidades generalizadas y las componentes duales de las coordenadas de las líneas a lo largo de las extremidades del manipulador, incluyendo la extremidad ficticia. Más aún, la expresión (24) muestra cómo el análisis directo de velocidad puede ser resuelto sistemáticamente aplicando las propiedades de tornillos recíprocos a través de la forma de Klein, sin necesidad de calcular las velocidades pasivas del manipulador, algo que sin duda representa un ahorro considerable de tiempo de cómputo.

 

Análisis de singularidades locales

En esta sección el análisis de singularidades se aborda por medio de la teoría de tornillos infinitesimales y se toma como referencia la extremidad tipo CPS, aun así, los resultados son aplicables a la extremidad SPS.

La expresión (18) puede ser rescrita como

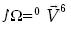..........................................................................(25)

donde

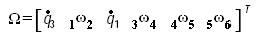
es la matriz de las velocidades pasivas y generalizadas de la extremidad CPS, mientras que J es la matriz Jacobiana generada por el subespacio de los correspondientes tornillos infinitesimales. Esto es

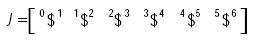
Una singularidad local ocurre cuando no existe una relación uno a uno en la expresión (25), (Di Gregorio, 2004), y puede presentarse tanto en el análisis directo de velocidad como en el inverso.

El primer tipo de singularidad en ser analizada es la asociada al análisis inverso de velocidad. Suponga que la velocidad angular de la plataforma móvil se anula, esto es

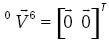
Esta condición se satisface si:

• Ω=[O^6x1] La cual es una situación trivial y por lo tanto, cualquier análisis posterior es tiempo perdido.

• El rango de la matriz Jacobiana J es deficiente, lo cual implica que su dimensión es incompleta y det(J) = 0. Bajo estacondición, la matriz Ω puede admitir valores arbitrarios reales, siendo de especial interés los correspondientes a las velocidades generalizadas y . Si o el manipulador esférico experimenta desplazamientos infinitesimales y la plataforma móvil se encuentra en un punto muerto.

El otro tipo de singularidad en ser analizada, es la asociada con el análisis directo de velocidad. Estas singularidades son más interesantes que las primeras y la ecuación clave para su estudio es la expresión (24).

Una breve inspección de la expresión (24) revela que el análisis directo de velocidad no tiene solución o significado físico cuando el rango de la matriz es deficiente, es decir, cuando det(S) = 0. Varias situaciones pueden caer en esta posibilidad y a continuación se estudian algunas de ellas.

• Si una extremidad del manipulador se anula, por ejemplo si q₂=0, entonces la componente primaria de la línea $₂ no queda definida de manera única, provocando la singularidad de la matriz S.

• Suponga que el centro del par esférico S_Q se encuentra en la dirección del vector . Entonces es evidente el que

y con ello, se anula el segundo renglón de la matriz S, lo cual evidentemente provoca que

Un resultado similar se obtiene si el centro del par esférico S_Q se encuentra en la dirección de , lo cual, implica además que q₃=0.

• Si las componentes primarias de las líneas $₁ y $₂ son coplanares, entonces las componentes duales de dichas líneas son linealmente dependientes, provocando la singularidad de la matriz S.

• Si las componentes primarias de las líneas $₁ y $₂ concurren a un mismo punto, entonces si dicho punto se toma como referencia para el cálculo de las respectivas componentes duales, éstas se anulan y todos los elementos de la matriz S son iguales a cero. Bajo tal situación es evidente que det (J) = 0.

Finalmente, las singularidades locales indicadas en esta sección seguramente son las más representativas e interesantes del manipulador propuesto. Sin embargo, es importante mencionar que un mayor número de singularidades locales pueden ser detectadas e interpretadas recurriendo al concepto de dependencia lineal de la matriz S. Por ejemplo, la condición de no singularidad de la matriz S ocurre cuando se genera con unicidad al vector cero de tres dimensiones, es decir, si se satisface que

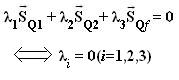
donde, por supuesto, se descarta la solución trivial.

 

Ejemplo numérico

A fin de mostrar la versatilidad de las expresiones derivadas en la presente contribución para el análisis cinemático directo del mecanismo propuesto, en esta sección se proporciona un ejemplo numérico.

Los parámetros asignados al mecanismo son los siguientes

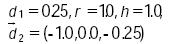
donde todos los valores están en metros. Por su parte, las coordenadas generalizadas se rigen por las funciones periódicas

Es decir, la plataforma móvil inicia su movimiento en el tiempo t=0 y 2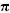, segundos más tarde regresa a su posición original. Por otra parte, las velocidades generalizadas se obtienen como simples derivadas temporales de las coordenadas generalizadas. Con esta información se desean determinar todas las posibles orientaciones instantáneas de la plataforma móvil, vía el cálculo de las coordenadas de los tres pares esféricos que se ubican sobre ésta, así como el historial de la velocidad angular instantánea de la plataforma móvil, con respecto a la plataforma fija, tomando como posición inicial del manipulador una solución del análisis directo de posición.

Las expresiones requeridas para resolver el ejemplo numérico se introdujeron en una hoja Maple© y en la tabla 3 se listan las cuatro posibles soluciones resultantes del análisis directo de posición.

Finalmente, la velocidad angular de la plataforma móvil, tomando como posición inicial la primera solución del análisis directo de posición, se muestra en la figura 5. Más aún, con la finalidad de validar los resultados numéricos del ejemplo propuesto, se generó un modelo con el programa de simulación de análisis cinemático y dinámico ADAMS© y los resultados de dicho modelo se incluyen en la misma figura.

 

Conclusiones

En este trabajo se propone un manipulador esférico con una topología, hasta donde los autores esperan, inédita. El manipulador propuesto se compone de una plataforma fija y una móvil, unidas por medio de dos extremidades, una tipo CPS y la otra tipo SPS, y un par esférico pasivo cuya función es la de restringir el movimiento de translación de un punto fijo a la plataforma móvil, por lo que dicho punto sólo puede experimentar movimientos de rotación, mientras que los restantes puntos, fijos a la plataforma móvil, se mueven sobre esferas concéntricas de acuerdo a la posición fija del punto.

El análisis directo de posición del mecanismo propuesto se obtiene en forma cerrada, y con ello, se evita el uso de una técnica numérica con sus respectivos inconvenientes, como lo es el método de Newton–Raphson para su solución. El análisis revela que existen, cuando mucho, cuatro soluciones diferentes del manipulador esférico, lo cual contrasta con las posibles cuarenta soluciones del análisis directo de posición de una plataforma general Gough–Stewart.

El análisis directo de velocidad del manipulador esférico se aborda por medio de la teoría de tornillos infinitesimales. Para un mejor entendimiento de este análisis, se incluye una sección con conceptos preliminares relacionados con el análisis de velocidad de cadenas cinemáticas abiertas y cerradas por medio de la teoría de tornillos infinitesimales. El estado de velocidad, o giro infinitesimal sobre un tornillo, se expresa como un vector de seis dimensiones, y a su vez, en forma de tornillos infinitesimales a través de cada una de las dos cadenas cinemáticas de que consta el mecanismo propuesto. Posteriormente, la aplicación de la forma de Klein entre la línea en coordenadas de Plücker a lo largo de la extremidad CPS con el estado de velocidad de la plataforma móvil, permite calcular la velocidad generalizada asociada al par prismático de dicha extremidad. Un procedimiento similar conduce al cálculo de la velocidad generalizada asociada al par prismático de la cadena cinemática SPS. A fin de completar las expresiones requeridas para el análisis directo de velocidad, se introduce una cadena cinemática ficticia tipo SPS y de igual forma, se determina la velocidad generalizada del par prismático ficticio. Ordenando en forma matricial las expresiones así generadas, y tomando en cuenta que la componente dual del estado de velocidad de la plataforma móvil es el vector cero, se obtiene una expresión simple y compacta para el cálculo de la velocidad angular de la plataforma móvil, con respecto a la plataforma fija. Es interesante mencionar que dicha expresión no requiere de los valores de las velocidades pasivas del manipulador, lo cual sin duda representa un ahorro significativo en tiempo de cómputo. Adicionalmente, se provee una interpretación geométrica sobre las singularidades locales más significativas del manipulador propuesto.

Finalmente, se proporciona un ejemplo numérico y los resultados obtenidos con las expresiones derivadas en la presente contribución, vía teoría de tornillos, se comparan con resultados generados con el programa de simulación de análisis cinemático y dinámico ADAMS©.

 

Agradecimientos

Los autores expresan su más sincero agradecimiento al Consejo de Ciencia y Tecnología del Estado de Guanajuato (Concyteg), ya que este trabajo fue apoyado por medio de un proyecto de fondos mixtos, cuyo convenio es el 03–09–A–016. De igual forma, se agradece la cuidadosa revisión que los árbitros realizaron en la presente contribución.

Asimismo, los autores 1 y 3 desean dedicar este trabajo a la memoria del Profesor Fidencio López Navarro. Sus amigos, colegas y estudiantes estamos consternados por el sensible fallecimiento de este hombre ejemplar, quien con sus enseñanzas, coraje y característico buen humor influyó fuertemente de manera positiva en decenas de generaciones de estudiantes, q.e.p.d.

 

Referencias

Ball R.S. (1900, reimpreso en 1998). A Treatise on the Theory of Screws, Cambridge University Press, Cambridge.        [ Links ]

Clavel R. (1988). DELTA, A Fast Robot with Parallel Geometry. Proceedings 18th International Symposyum on Industrial Robots, Lausanne, pp. 91–100.        [ Links ]

Di Gregorio R. (2004). Analytic Form Solution of the Direct Position Analysis of the SP–2RS Architectures. Proceedings ASME DETC'04, CD–ROM Paper DETC2004–57037, Salt Lake City.        [ Links ]

Duffy J. (1996). Statics and Kinematics with Applications to Robotics, Cambridge University Press, Cambridge.        [ Links ]

Gallardo J. (2005). Kinematics of a Hybrid Manipulator by Means of Screw Theory. Journal of Multibody System Dynamics, Vol. 14, pp. 345–366.        [ Links ]

Gallardo J., Rico J.M., y Orozco H. (2004). Un algoritmo para resolver la cinemática directa de plataformas Gough Stewart, tipo 6–3. Computación y Sistemas, Vol. 8, pp. 132–149.        [ Links ]

Gosselin C. and Angeles J. (1988). The Optimum Kinematic Design of a Planar Three–Degree–of–Freedom Parallel Manipulator. ASME Journal of Mechanisms, Transmissions and Automation in Design, Vol. 110, pp. 35–41.        [ Links ]

Husty M.L. (1996). An Algorithm for Solving the Direct Kinematics of General Stewart–Gough Platforms. Mechanism and Machine Theory, Vol. 31, pp. 365–380.        [ Links ]

Innocenti C. (1998). Forward Kinematics in Polynomial Form of the General Stewart Platform. Proceedings ASME 1998. Design Engineering Technical Conferences, CD–ROM, Paper DETC98/MECH–5894, Atlanta.        [ Links ]

Raghavan M. (1993). The Stewart Platform of General Geometry has 40 Configurations. ASME Journal of Mechanical Design, Vol. 115, pp. 277–282.        [ Links ]

Rico J.M. and Duffy J. (2000). Forward and Inverse Acceleration Analyses of In–Parallel Manipulators. ASME Journal of Mechanical Design, Vol. 122, pp. 299–303.        [ Links ]

Rico J.M., Gallardo J. and Duffy J. (1999). Screw Theory and Higher Order Kinematic Analysis of Open Serial and Closed Chains. Mechanism and Machine Theory, Vol. 34, pp. 559–586.        [ Links ]

Romdhane L., Affi Z. and Fayet M. (2002). Design and Singularity Analysis of a 3–Translational–DOF In–Parallel Manipulator. ASME Journal of Mechanical Design, Vol. 124, pp. 419–426.        [ Links ]

 

Semblanza de los autores

Jaime Gallardo-Alvarado. Obtuvo el título de ingeniero industrial mecánico, así como el grado de maestro en ciencias en ingeniería mecánica, ambos en el Instituto Tecnológico de Celaya en los años 1985 y 1989, respectivamente. También adquirió el grado de doctor en ciencias en ingeniería eléctrica en el Instituto Tecnológico de la Laguna en el año 1999. A partir del año 1993, se incorporó como profesor–investigador de tiempo completo en el Departamento de Ingeniería Mecánica del Instituto Tecnológico de Celaya. Es miembro del Sistema Nacional de Investigadores, de la Asociación Mexicana de Robótica y de la International Federation for the Theory of Machines and Mechanisms. Su principal área de interés es el modelado cinemático y dinámico de manipuladores serie y paralelo por medio de la teoría de tornillos.

José María Rico-Martínez. Titulado como ingeniero industrial mecánico en el Instituto Tecnológico de Celaya en el año 1974, se graduó como maestro en ciencias en ingeniería mecánica en el Instituto Tecnológico y de Estudios Superiores de Monterrey en el año 1977. Asimismo, se graduó como doctor en ingeniería mecánica en la Universidad de Florida en el año 1988. A partir de 1975, se incorporó como profesor–investigador de tiempo completo en el Departamento de Ingeniería Mecánica del Instituto Tecnológico de Celaya. Ha realizado estancias posdoctorales en la Universidad de Florida, la Universidad Estatal de Arizona y la Universidad de California en Davis. Es miembro del Sistema Nacional de Investigadores, de la American Society of Mechanical Engineers y de la International Federation for the Theory of Machines and Mechanisms. Sus principales áreas de interés comprenden la cinemática y dinámica, teórica y aplicada, así como vibraciones mecánicas.

Martín Caudillo-Ramírez. Obtuvo el título de ingeniero industrial mecánico en el Instituto Tecnológico de Celaya en el año 1985, y el grado de maestro en ingeniería mecánica en la Facultad de Ingeniería Mecánica, Eléctrica y Electrónica de la Universidad de Guanajuato, en el año 1992. Durante varios años trabajó en el Centro de Investigación y Asistencia Técnica del Estado de Querétaro, centro fundado por el CONACYT, como diseñador de maquinaria pesada. A partir del año 1992, se incorporó como profesor de tiempo completo al Departamento de Ingeniería Mecánica del Instituto Tecnológico de Celaya. Su principal línea de investigación es el diseño para manufactura y ensamble.