nueva página del texto (beta)
Español (pdf)
Artículo en XML
Referencias del artículo
Traducción automática
Enviar artículo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Las estimaciones de biomasa aérea resultan importantes para conocer la contribución de la vegetación en el almacenamiento de carbono en distintos ecosistemas. Las estimaciones se realizan mediante la aplicación de ecuaciones alométricas específicas de cada especie, las cuales implican proporcionalidad entre las tasas relativas de crecimiento de dos variables en un organismo (Zianis, Spyroglou, Tiakas y Radoglou, 2016).
Las relaciones de escala entre el tamaño, peso y circunferencia de un individuo son comúnmente descritas en estudios ecológicos mediante ecuaciones potenciales (Marquet et al., 2005). En la teoría de escala metabólica, West, Brown y Enquist et al. (1997) afirmaron que, a partir de una ecuación potencial, se puede derivar una regla general de escala para un gran número de especies y ecosistemas. Esta teoría confronta los resultados de Zianis et al. (2016) y Jenkins, Chojnacky, Heath y Birdsey (2003), los cuales afirman que existen diferencias entre los parámetros debido a la variabilidad geográfica donde fueron realizadas, por lo tanto, la regla de escala provoca resultados sesgados cuando se aplica en zonas distintas.
El método de mínimos cuadrados ordinarios (MCO) se usa para ajustar ecuaciones alométricas en diferentes especies de importancia forestal (Picard, Saint-André y Henry, 2012). Sin embargo, el enfoque bayesiano ha tomado auge en este ramo en los últimos años debido a que incorpora conocimiento a priori acerca de los datos, lo que el MCO ignora por completo (Zhang, Duan y Zhang, 2013). Por ejemplo, Zapata-Cuartas, Sierra y Alleman (2012) utilizaron valores de los parámetros a y b de diversas investigaciones para introducir el enfoque bayesiano (EB), sus resultados indicaron que el EB puede predecir con alta certidumbre la biomasa en muestras de seis individuos en comparación con MCO que necesita mínimo 40 a 60 árboles. Estos resultados fueron corroborados en las investigaciones de Zhang et al. (2013), Kuyah, Sileshi y Rosenstock (2016) y Zianis et al. (2016).
Los ajustes de ecuaciones alométricas específicas para cada especie son importantes para aplicarlas en datos de inventarios regionales (Intergovernmental Panel on Climate Change [IPCC] (2003). No obstante, la colecta de datos puede ser costosa en tiempo y en dinero (Sileshi, 2014). La investigación de Roxburgh, Paul, Clifford, England y Raison (2015) indica que es necesario cosechar entre 19 y 95 árboles para obtener desviaciones estándar por debajo de 5%; por su parte, Méndez-González, Turlan-Medina, Ríos-Saucedo and Nájera-Luna (2012) indicaron que necesitan mínimo 40 árboles de Prosopis laevigata para ajustar el modelo y que la varianza de lo estimado sea mínima.
La parte operativa en la aplicación de ecuaciones alo-métricas necesita evaluar la confiabilidad de las estimaciones por el hecho de que la fuente de error más importante es la elección del modelo alométrico (Chave et al., 2004). Por ejemplo, es común que, al no encontrar ecuaciones alo-métricas de una especie de interés, se usen ecuaciones alternas ajustadas a otras zonas (IPCC, 2003), donde los parámetros de estas capturan las condiciones medioam-bientales y de competencia del sitio donde fueron hechas, mas no de donde se aplican (Zhang et al., 2013).
El almacén de carbono más importante de México se ubica en el ecosistema semiárido (Masera, Ordóñez y Dirzo, 1997); sin embargo, existen pocos estudios en los cuales se desarrollen ecuaciones alométricas específicas para este tipo de ecosistema (Méndez-González, Santos Méndez, Nájera-Luna y González-Ontiveros, 2006). El género Prosopis spp. es típico de estas regiones y está representado por 11 especies (Palacios, 2006).
La investigación de Méndez-González et al. (2012) ajustó ecuaciones alométricas de Prosopis laevigata en siete sitios del norte de México. En cada sitio se ajustaron los parámetros correspondientes de una ecuación potencial mediante el método clásico de MCO, además, se determinó un tamaño óptimo de cosecha de árboles para realizar el ajuste. Sin embargo, en esta investigación no se menciona la cantidad de repeticiones de las submuestras para determinar un tamaño ideal de muestreo, con la cual se puede dar idea de la variabilidad del error en cada una de ellas. La hipótesis de este trabajo fue que el enfoque bayesiano reducirá la incertidumbre asociada a la estimación de biomasa en menores tamaños de muestra con respecto al MCO y a los ajustes de Méndez-González et al.(2012)
Objetivos
Los objetivos de esta investigación fueron generar ecuaciones alométricas para estimar la biomasa de Prosopis laevigata mediante un enfoque bayesiano y cuantificar el error en distintos tamaños de muestra para comparar el marco bayesiano con el método de mínimos cuadrados ordinarios y el ajuste obtenido de la investigación de Méndez-González et al. (2012).
Materiales y métodos
Fuente de datos
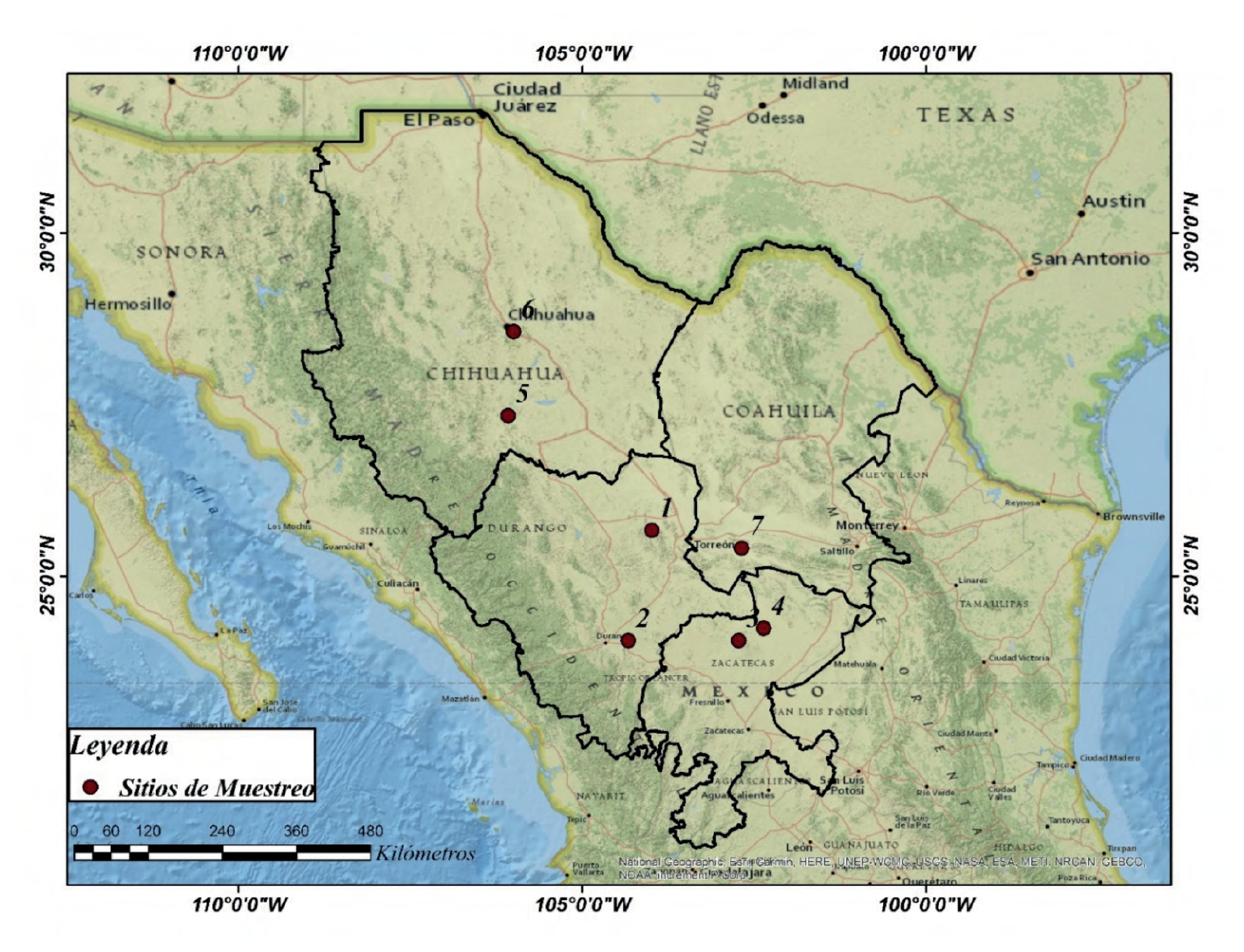
Los registros del diámetro basal (cm) y biomasa (kg) se obtuvieron de Turlan-Medina (2011), los cuales ajustaron ecuaciones potenciales de Prosopis laevigata para siete sitios en el Norte de México (Méndez-González et al., 2012) (Fig. 1). La tabla 1 presenta un resumen de las principales características de los sitios de muestreo. El número total de árboles observados en los sitios fue de 144, donde cada dato representa el diámetro basal (Db) y la biomasa (B). Los parámetros a y b se ajustaron con el método de mínimos cuadrados mediante una ecuación
Tabla 1 Descripción de los valores usados para aplicar el enfoque bayesiano, los datos y ajuste se pueden ver en Turlan-Medina (2011) y Méndez-González et al. (2012).
| Sitio | Estado/Municipio | Árboles | DB (cm) | B (kg) | Parámetros | ||||
| (n) | mín | máx | mín | máx | a | Ln(a) | b | ||
| 1 | Durango/Nazas | 10 | 11.0 | 20.7 | 3.0 | 16.2 | 0.346 | -1.06 | 1.679 |
| 2 | Durango/Dgo. | 30 | 5.2 | 31.5 | 3.1 | 229.1 | 0.056 | -2.88 | 2.383 |
| 3 | Zacatecas//Río Grande | 14 | 6.8 | 26.0 | 10.3 | 265.5 | 0.108 | -2.23 | 2.200 |
| 4 | Zacatecas/Nieves | 15 | 7.3 | 27.0 | 11.3 | 367.5 | 0.127 | -2.06 | 2.161 |
| 5 | Chihuahua/Satevo | 27 | 5.9 | 41.8 | 8.1 | 558.7 | 0.041 | -3.19 | 2.513 |
| 6 | Chihuahua/Aldama | 22 | 6.0 | 39.0 | 7.7 | 490.6 | 0.018 | -4.01 | 1.458 |
| 7 | Coahuila/Viesca | 26 | 5.2 | 32.1 | 4.7 | 117.7 | 0.751 | -0.28 | 2.166 |
DB= Diametro basal, B= Biomasa.
Al hacer comparaciones en unidades reales es necesario transformar la ecuación (1) a su escala aritmética; sin embargo, existe un sesgo producido por la transformación logarítmica. Para evitar esto se aplicó un factor de corrección como lo indica Zianis et al. (2016).
Teoría bayesiana
La regla de Bayes se expresa como un vector de datos y = (y1, y2, y3…yn), datos de biomasa, y un vector de parámetros
donde
La distribución de probabilidad a priori de los parámetros para alguna ecuación alométrica están dados por
Implementación bayesiana en la estimación de biomasa de Prosopis
La elección de las distribuciones a priori de los parámetros es crítica para el desarrollo del método bayesiano, por lo que en este trabajo se partió del supuesto que los parámetros de la ecuación (1) están normalmente distribuidos, por lo que se calculó la media y la varianza.
Los valores de la media y desviación estándar para el parámetro a (escala logarítmica) introducidos al modelo bayesiano fueron -2.2472 y 1.2383, respectivamente, mientras que para el parámetro b los valores fueron µ= 2.2103 y σ = 0.4438.
La ventaja de tener conocimiento informativo de los parámetros es que se define el dominio que deben tener estos y, de esta manera, la distribución de los parámetros puede generar miles de soluciones antes de converger en su distribución posterior. Para lograr lo último, es necesario recurrir a métodos numéricos por la gran cantidad de simulaciones requeridas para lograr tener datos confiables. Este procedimiento fue programado en el lenguaje Python 2.7, el cual se apoya del módulo PYMC3, que posee librerías especializadas en la implementación de modelos bayesianos (Patil, Huard y Fonnesbeck, 2010). Dicho módulo incorpora el método NUTS (muestreador sin giro en U, por sus siglas en inglés) para actualizar los parámetros. El método NUTS es una extensión del algoritmo de cadenas de Markov Montecarlo que elimina las imprácticas ejecuciones de ajuste e intervenciones del usuario (Hoffman y Gelman, 2014). El concepto es simple, a medida que se iteren más muestras (con el método NUTS) los valores de los parámetros a posteriori convergerán a valores más precisos. Dentro del programa se ajustó a que se realizaran 25 000 iteraciones del muestreador NUTS para asegurar una máxima convergencia de los parámetros estimados (el código de programación puede solicitarse a los autores de esta investigación).
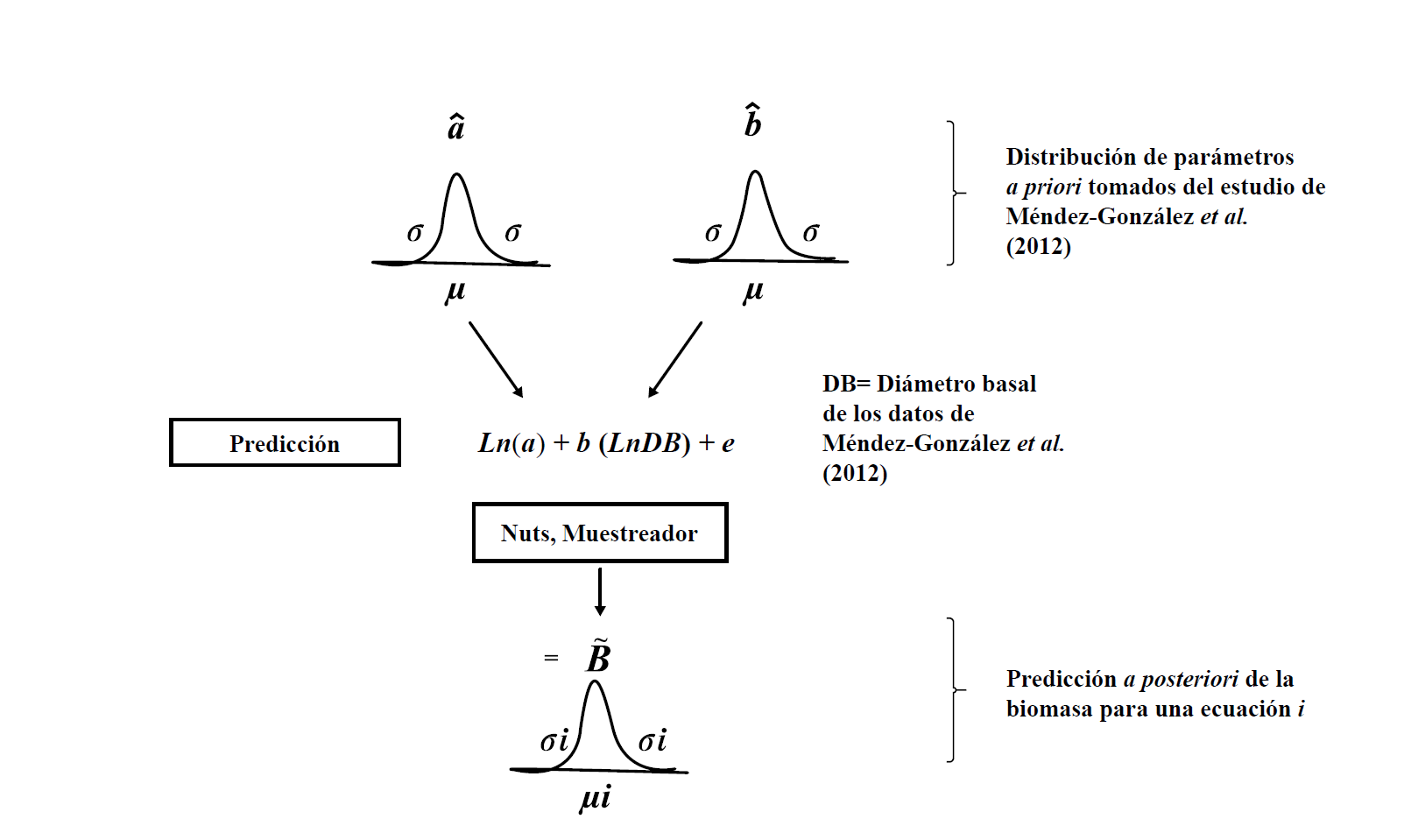
La figura 2 presenta el esquema de ajuste de parámetros con el esquema bayesiano; en la primera parte se tiene que definir la media (μ) y desviación estándar (σ) de los parámetros a y b de la ecuación (1). El modelo lineal generalizado (MLG) empleado para ajustar parámetros asume una distribución normal bivariada en los dos parámetros. Se supuso que los errores están normalmente distribuidos
Evaluación de los modelos
La evaluación del enfoque bayesiano, MCO y las ecuaciones generadas por Méndez-González et al. (2012) se llevaron a cabo con los 144 datos de diámetro basal y biomasa descritos anteriormente (población objetivo). Se utilizó el programa SQLite 3.0 para definir los tamaños de muestra (TM) de 10, 30, 60, 90, 120 individuos. Cada TM se muestreó aleatoriamente, sin remplazo, 1000 veces y se ajustaron con los tres enfoques propuestos. El conjunto de parámetros ajustados en las diferentes TM se usó para calcular la biomasa de la población objetivo (144 datos de biomasa) y con ello poder determinar la eficiencia para los diferentes tamaños de muestra. La eficiencia en términos del error se calculó con el error absoluto medio (EMA) y la raíz cuadrada media del error (RCME):
donde B es la biomasa observada (kg),
Resultados
Ajuste bayesiano y mínimos cuadrados ordinarios
Los valores de los parámetros muestran una tendencia descendente al incrementarse el tamaño de muestra en los dos enfoques propuestos (Fig. 3). Las 1000 repeticiones mostraron que, para un tamaño de muestra de 120 individuos, el coeficiente de variación (CV) del parámetro a en EB y MCO fue 3.74% y 3.90%, respectivamente. En lo que respecta al parámetro b el CV para EB y MCO fue de 1.25% y 1.29%. La mediana de los valores de a y b para EB y MCO resultó similar en este tamaño de muestra, EB: a = -1.85, b = 2.08; MCO: a = -1.83, b = 2.04. Lo anterior indica que en muestras grandes los resultados de los ajustes de EB y MCO tienden a ser iguales.
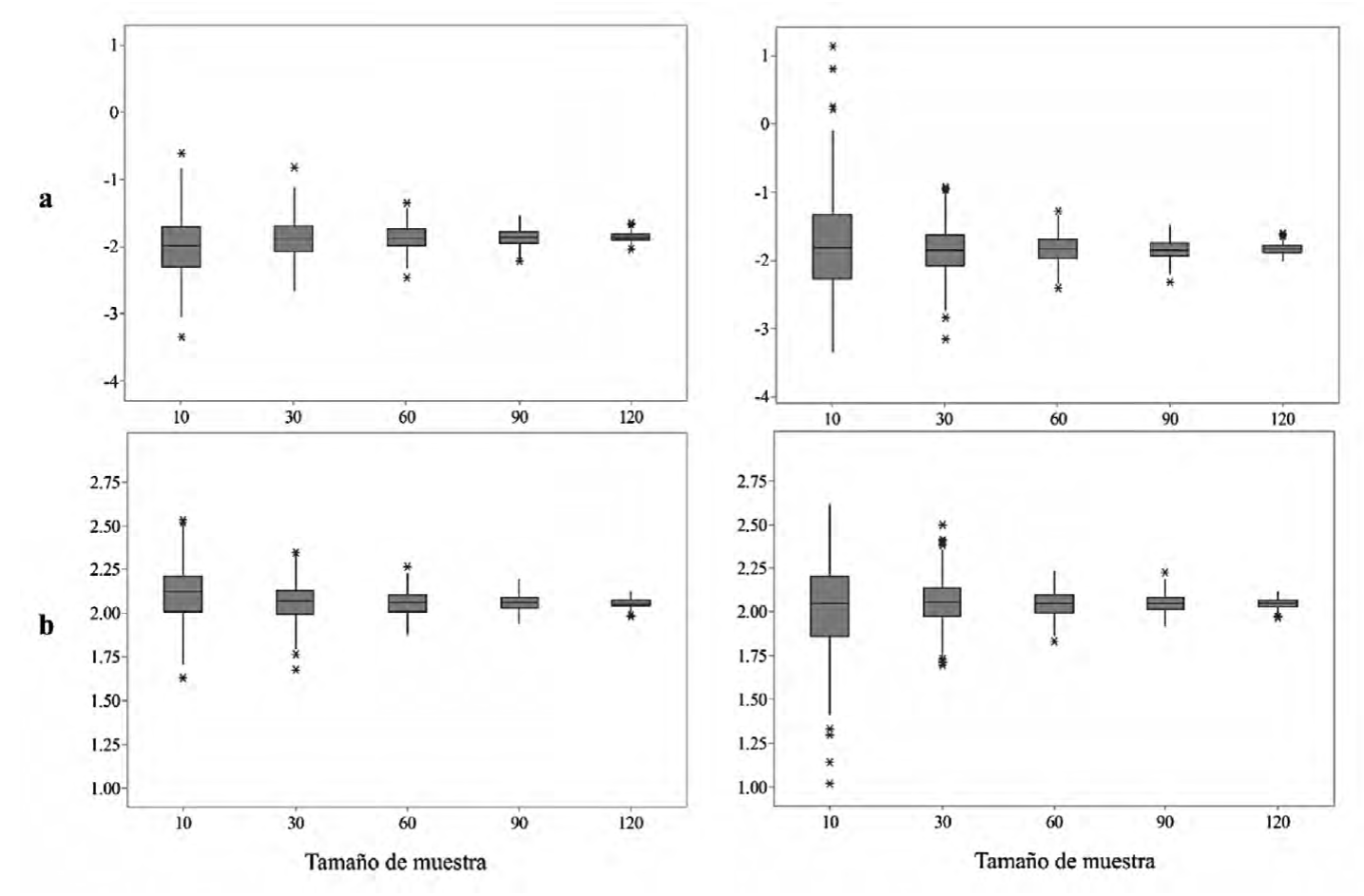
Las figuras de la izquierda son los valores para EB y las de la derecha son de MCO, los asteriscos muestran los valores atípicos.
Figura 3 Resultados del ajuste de los parámetros para las 1000 repeticiones en diferente tamaño de muestra.
Las diferencias entre los enfoques se logran apreciar en tamaños de muestras menores donde los valores de MCO presentan un rango superior a EB. Los coeficientes de variación del parámetro a en la muestra de 10 árboles fueron de 21.19% y 36.21% en EB y MCO, respectivamente. Las diferencias entre el CV del parámetro b fueron bajas en comparación con a (7.32% y 11.78% para EB y MCO), lo que mostró que los valores de la pendiente del modelo fueron más estables que el intercepto en las repeticiones procesadas.
Validación de los métodos propuestos
La tabla 2 presenta los resultados promedios en la validación del EB, MCO y los valores ajustados por Méndez-González et al. (2012) en las diferentes muestras y 1000 repeticiones analizadas. La validación se realizó transformando las predicciones de la ecuación (1) a su escala original. La incertidumbre promedio de EMA y RCME del error fue similar para los tres enfoques propuestos y los diferentes tamaños de muestra. Sin embargo, se observó que a medida que el tamaño de muestra disminuyó, el coeficiente variación de EMA y RCME aumentó proporcionalmente en los tres métodos. La figura 4 muestra la incertidumbre de cada método, donde se observó que el enfoque bayesiano es el más estable, aunque el MCO mostró una tendencia similar, pero con mayores valores atípicos. Al usar el ajuste de Méndez-González et al. (2012) se observó que en TM de 10 árboles, su porcentaje de error en comparación con el EB fue de 497.6%. En el caso de MCO el porcentaje de error fue de 55% con respecto a EB. Se necesitan entre 90 y 120 árboles del ajuste de Méndez-González et al. (2012) para obtener CV similares al EB, que lo obtiene con tan solo 10 individuos. Al mantener la incertidumbre del error más baja en los diferentes tamaños de muestra, se determinó que el EB es mejor para aplicarse en TM grandes o pequeños.
Tabla 2 Resumen de la validación de 1000 repeticiones para los tres enfoques propuestos en diferente tamaño de muestra.
| Estadísticos | 10 | 30 | 60 | 90 | 120 |
| E. bayesiano | |||||
| EMA | 19.79 | 19.87 | 19.36 | 19.28 | 19.30 |
| CV(EMA) | 11.34 | 4.11 | 2.56 | 1.96 | 1.19 |
| RCME | 36.81 | 36.79 | 36.98 | 36.79 | 36.91 |
| CV(RCME) | 13.34 | 7.85 | 4.98 | 3.74 | 2.16 |
| MCO | |||||
| EMA | 20.39 | 19.50 | 19.40 | 19.37 | 19.35 |
| CV(EMA) | 16.19 | 5.04 | 2.89 | 1.99 | 1.23 |
| RCME | 38.62 | 37.11 | 37.11 | 37.08 | 37.05 |
| CV(RCME) | 20.71 | 9.49 | 5.70 | 3.82 | 2.26 |
| Méndez-González et al. (2012) | |||||
| EMA | 17.55 | 19.87 | 20.83 | 20.26 | 20.38 |
| CV(EMA) | 55.03 | 26.08 | 14.73 | 9.91 | 5.77 |
| RCME | 27.80 | 34.24 | 38.23 | 36.97 | 38.09 |
| CV(RCME) | 66.39 | 31.64 | 17.49 | 12.19 | 7.10 |
(CV) representa el coeficiente de variación, EMA es el error medio absoluto promedio, RCME es la raíz cuadrada media del error promedio.
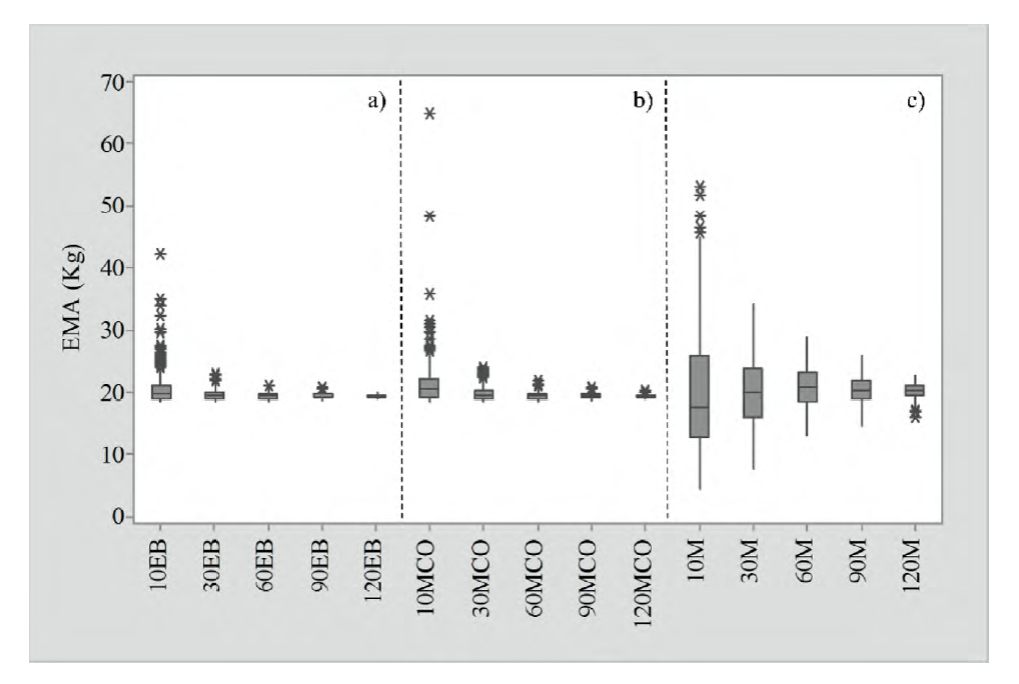
Las letras después de los números indican el método propuesto: bayesiano (EB), mínimos cuadrado (MCO) y Méndez-González et al. (2012) (M).
Figura 4 Comparación del error absoluto medio (EMA) para los enfoques bayesiano (a), mínimos cuadrados ordinarios (b) y el ajuste de Méndez-González et al. (2012) (c) para cada tamaño de muestra.
Discusión
La publicación de parámetros de ecuaciones alométricas en conjunto con los datos de biomasa medida proveen la oportunidad de contrastar hipótesis referentes al mejor ajuste de los datos ante el escaso recurso destinado para la investigación. Con base en las inconsistencias metodológicas y los supuestos que producen diferentes resultados en el ajuste alométrico esta investigación propuso el uso de un enfoque bayesiano para evaluar nuevas ecuaciones a través de datos de diámetro basal y biomasa medidos por Turlan-Medina (2011) y Méndez-González et al. (2012).
Los resultados son consistentes con los encontrados por Zapata-Cuartas et al. (2012) y Zhang et al. (2013), donde se observó que el enfoque bayesiano, con información a priori presentó mayor certidumbre en comparación con métodos clásicos. Las simulaciones hechas en este trabajo permitieron analizar el ajuste de los parámetros con respecto a la población de Prosopis en diferente tamaño de muestra, donde los resultados mostraron que, al disminuir el tamaño de muestra, la variación del error aumentó en los enfoques propuestos. Sin embargo, dicha variación fue menor en el enfoque bayesiano, similar a lo presentado por Zapata-Cuartas et al. (2012) y Zell, Bösch y Kändler (2014), los cuales afirmaron que un tamaño de muestra de seis árboles es suficiente para ajustar un modelo alométrico. El ajuste con el método de mínimos cuadrados presentó ajustes similares a los del bayesiano, aunque en el tamaño de muestra de 10 individuos mostró valores atípicos, lo que incrementó su incertidumbre.
El enfoque bayesiano (EB) demostró que tiene un mecanismo de optimización para reducir la incertidumbre de un modelo potencial aplicado a la especie de Prosopis laevigata. Como lo mencionan Dietze, Wolosin y Clark (2008), el EB reduce la incertidumbre total porque aprovecha la información de especies bien representadas.
En zonas áridas de México son pocas las mediciones para calcular biomasa (Turlan-Medina, 2011), por lo que resulta crítico en la elección de un modelo para hacer predicciones de biomasa dentro de un inventario nacional (Sileshi, 2014). El trabajo realizado por Méndez-González et al. (2012) fue un esfuerzo para proveer información inexistente de la especie Prosopis laevigata en el norte de México, de acuerdo con las buenas prácticas del IPCC (IPCC, 2003), por lo que esta información puede usarse cuando no existan modelos de esta especie en una región en particular. No obstante, los resultados del enfoque bayesiano difieren en la variabilidad del error a lo propuesto por Méndez-González et al. (2012). Por ejemplo, ellos recomiendan 40 especies como mínimo para ajustar ecuaciones de biomasa en Prosopis; sin embargo, con las simulaciones hechas en esta investigación, se mostró que el ajuste de Méndez-González et al. (2012) necesita entre 90 y 120 muestras para obtener una variabilidad del error similar a las del ajuste bayesiano, que solo necesita 10 individuos.
Una ventaja de usar el EB y simulaciones para cada tamaño de muestras, es que permite observar la variabilidad del error con respecto a la población que se analiza con gran veracidad. Esto elimina cualquier suspicacia acerca de cómo fueron elegidos los datos para ajustar un modelo (Kruschke y Vanpaelmel, 2015).
Los resultados de este trabajo concuerdan con Zhang, Zhang y Duan, 2015, en que el enfoque bayesiano (EB) permite integrar distintas fuentes de información para mejorar las predicciones de biomasa; también coincide con Zapata-Cuartas et al. (2012) en que el EB es adecuado para estimar la biomasa con pocas muestras y alta certidumbre al compararla con enfoques clásicos. Asimismo, es congruente con lo planteado por Henry et al. (2014), donde el EB se plantea como una alternativa para usarse en inventarios forestales nacionales.
Los resultados de la presente investigación resaltan la importancia de usar información existente como variables de entrada para inferir sobre el enfoque bayesiano. En el caso de no haber información a priori de las especies a trabajar, los estudios de Zapata-Cuartas et al. (2012) y Zianis et al. (2016) usaron información a priori sobre género obteniendo resultados aceptables.
Conclusiones
Se ajustaron nuevas ecuaciones de biomasa a la especie Prosopi laevigata a través de la implementación de un enfoque bayesiano. Los datos para alimentar el modelo se colectaron de un trabajo de investigación donde levantaron siete sitios y estimaron la biomasa para la especie mediante MCO. Los parámetros ajustados en estos sitios (a y b) permitieron que se construyeran distribuciones de probabilidad a priori para ajustar el enfoque bayesiano (EB).
El uso de 1000 simulaciones permitió hacer comparaciones entre los diferentes enfoques de ajuste a diferente tamaño de muestra. La comparación realizada entre el EB y mínimos cuadrados ordinarios presentó resultados similares; solo en tamaños de muestra bajos, la variabilidad del error fue mayor en MCO, además de que presentó mayores datos atípicos. En el caso de las ecuaciones propuestas por Méndez-González et al. (2012), se observó que la variabilidad del error fue grande para diferentes tamaños de muestra, en comparación al EB. Las simulaciones mostraron que el ajuste de una ecuación con parámetros fijos tendieron a sobrestimar los valores medidos hasta cuatro veces más que el EB.
De acuerdo con los resultados obtenidos para Pro-sopi leavigata, es factible la aplicación del EB para otras especies de interés forestal. También explorar otras perspectivas del enfoque bayesiano, como los modelos jerárquicos bayesianos, los cuales son una tendencia reciente en investigaciones sobre el tema.
