Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Madera y bosques
versión On-line ISSN 2448-7597versión impresa ISSN 1405-0471
Madera bosques vol.15 no.1 Xalapa ene. 2009
Artículo de investigación
Aplicación de técnicas multicriterio en el manejo integral forestal en Durango, México
Application of multi-criterion techniques on integral forest management in Durango, México
Gustavo Pérez-Verdín1*, José Ciro Hernández-Díaz2, Marco Antonio Márquez-Linares1 y Aregai Tecle3
1 CIIDIR-IPN Unidad Durango. Sigma s/n, Frac. 20 de Nov II, C.P. 34220 Durango, Dgo. Tel. (618) 823-33-20. *Autor para correspondencia. Correo electrónico: gusperver@gmail.com.
2 ISIMA. Universidad Juárez del Estado de Durango. Blvd. Guadiana 501; C.P. 34120, Durango, Dgo., México.
3 School of Forestry, Northern Arizona University, P.O. 5018, Flagstaff, AZ.
Manuscrito recibido el 18 de octubre del 2007
Aceptado el 28 de enero del 2009
RESUMEN
Tradicionalmente, la capacidad del bosque para producir bienes y servicios se ha enfocado principalmente a maximizar los beneficios económicos únicamente de la producción de madera. Este enfoque no toma en cuenta otras funciones del bosque, ni las interacciones del ecosistema, provocando eventualmente la degradación de algunos de sus componentes. En este estudio se propone una metodología para analizar y resolver un problema forestal que involucra el manejo de varios bienes y servicios del bosque, tomando en cuenta la opinión de productores y técnicos forestales. Se usaron datos de inventario forestal de un ejido del estado de Durango y se recurrió a la técnica de consulta a expertos para construir funciones de respuesta para diez objetivos. Se utilizaron tres variables independientes: área basal, número de árboles por hectárea y diámetro cuadrático medio, para evaluar cada uno de estos objetivos. Se usó la técnica multicriterio de programación por compromisos para determinar la mejor combinación de esas variables que respondan al manejo simultáneo de dichos objetivos. Mediante un simulador silvícola y sistemas de información geográfica se evaluaron las soluciones considerando la dinámica de crecimiento de los bosques. Las estructuras forestales encontradas normalmente fueron superiores a las condiciones actuales de los rodales. Estas diferencias podrían deberse a prácticas de manejo anteriores o a otros disturbios ambientales que han reducido los inventarios y la calidad de las masas forestales. El uso de este tipo de herramientas puede ayudar a entender la dinámica de los bosques y el manejo simultáneo de varios usos y servicios del bosque en el largo plazo.
Palabras clave: Dinámica forestal, estructura forestal deseada, Los Altares, programación por compromisos, toma de decisiones multicriterio.
ABSTRACT
Traditionally, the forest capacity to produce multiple goods and services has been overlooked in favor of developing alternatives that maximize timber production or economic profit alone. This approach is suboptimal, it fails to address ecosystem interactions, and occasionally leads to degradation of some of its components. In this study, a technical framework to analyze and solve a multiobjective forest problem in an ejido of Durango, Mexico is presented. Forest inventory data and expert consultation were used to construct ten objective response functions expressed in terms of tree basal area, number of trees per hectare, and quadratic mean diameter. Compromise programming, a multiobjective decision-making technique was used to determine the most preferred solution of forest structures. Forest vegetation simulator and geographical information systems were used in order to evaluate the solutions for various clusters. The simulated optimal forest structures were typically above current stand conditions. These differences can be due to past management practices and other forest disturbances that reduced stocking and quality of residual trees. The use of this type of multiobjective decision making approach can help understand forest stand dynamics and long-term management of forest goods and services.
Keywords: Forest stand dynamics, desired forest structures, Los Altares, compromise programming, multiobjective decision-making.
INTRODUCCIÓN
Tradicionalmente, la capacidad del bosque para producir múltiples bienes y servicios se ha enfocado más hacia la producción de madera (Mendoza-Briseño, 1993), que al corto plazo proporciona altos beneficios económicos, pero a largo plazo causa un detrimento a los recursos asociados al bosque. Este enfoque no considera las interacciones presentes en los ecosistemas forestales y eventualmente provoca la degradación de algunos de sus componentes. Los esquemas de manejo en la década de los 1960's ejercieron excesiva presión sobre los recursos forestales, hasta el punto de que muchas áreas se caracterizaron por tener estructuras y especies no deseables y a menudo sobreexplotadas (Gingrich, 1993). Ese esquema prevaleció hasta finales de los 1970's, cuando se introdujeron nuevos métodos para el cultivo del bosque, con el propósito de usar con más eficiencia la capacidad productiva de las áreas forestales (Caballero, 2000).
Los nuevos métodos, por ejemplo, abordaron el tratamiento de rodales jóvenes y sobrepoblados, aplicando aclareos y garantizando una mejor calidad de la regeneración natural, al dejar en pie los mejores árboles semilleros (Caballero, 2000). Sin embargo, la capacidad del bosque para proveer bienes y servicios múltiples, incluyendo productos no maderables, no se reconoció en México hasta hace algunos años. Los cambios recientes en la administración federal y local, motivados parcialmente por esfuerzos internacionales relacionados con el concepto de sustentabilidad en el uso y manejo de los recursos naturales, generaron nuevos programas institucionales, como el de Servicios Hidrológicos, el de Servicios Ambientales y el de Biodiversidad, en un intento de ayudar a los dueños y poseedores del recurso a incrementar el número de fuentes alternativas de ingresos y empleos (Muñoz-Piña et al., 2008). Estos programas incluyen el fortalecimiento de bienes y servicios, como la recreación, ecoturismo, manejo de la fauna silvestre, captura de carbono atmosférico, producción de agua y biodiversidad, así como la capacitación a los dueños del recurso forestal y a los prestadores de servicios técnicos y el reforzamiento a la investigación y asistencia técnica (CONAFOR, 2000; SEMARNAT,2003).
Recientemente se ha mostrado más interés en desarrollar planes o líneas de acción estratégicas que contribuyan a atender la complejidad del manejo de ecosistemas forestales, de tal forma que se logren varias metas sociales y ambientales en forma simultánea, apartándose del modelo que se basaba casi exclusivamente en el crecimiento económico y reconociendo la necesidad de integrar completamente la protección ambiental y el manejo sano de los recursos naturales en todas las actividades (Kazana et al., 2005). Este enfoque holístico debe mejorar la capacidad productiva de los recursos y diversificar la economía regional. Uno de los primeros enfoques multicriterio en el manejo forestal en México fue presentado por Pérez-Verdín y Tecle (2002), quienes determinaron el área basal que podría satisfacer el manejo simultáneo de cinco objetivos de manejo forestal. Este estudio, basado en técnicas no paramétricas, consideró una sola variable de decisión y no se incluyeron simulaciones a través del tiempo.
En el presente trabajo se usó al ejido Los Altares como caso de estudio para formular y resolver un enfoque de manejo forestal con varios objetivos, considerando la dinámica del recurso. Este ejido se localiza en el noroeste del estado de Durango y posee alrededor de 17 800 ha arboladas, de las cuales 93 por ciento está cubierto con bosques templados, principalmente de pino-encino. Las especies principales son: Pinus arizonica, P durangensis y P. teocote, que se mezclan con vegetación caducifolia como Quercus spp. y Populus tremuloides, entre otros (Figura 1). Los bienes de este ejido se distribuyen de manera común entre 108 ejidatarios.
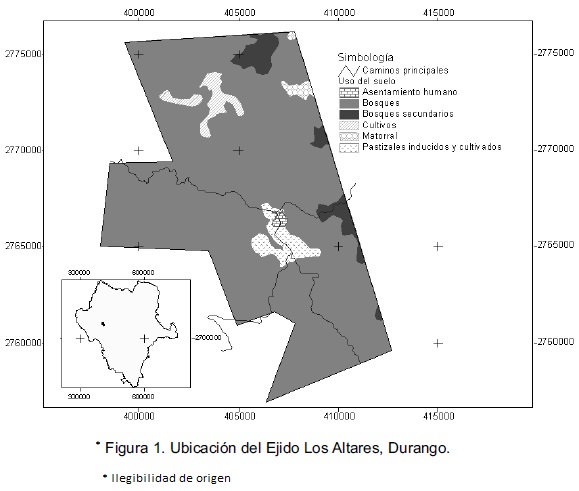
Los bosques del ejido se han manejado por más de 40 años, principalmente con fines maderables. El aprovechamiento forestal se ha realizado bajo esquemas de manejo de bosque regular e irregular, que incluyen tratamientos de selección, aclareos y árboles padres. La corta anual permisible ha decrecido en forma constante desde los 16 000 m3 en el año 1985 hasta los 6 000 m3 actuales. Esta disminución se explica en parte por el uso de métodos más refinados de inventario forestal, la exclusión o restricción de diversas áreas para proteger cuerpos de agua, caminos, suelos frágiles, hábitat de fauna, etc., y la disminución de la productividad por disturbios naturales y antropogénicos (UAF Santiago Papasquiaro, 2005).
Los objetivos planteados en este trabajo son: (i) proveer y demostrar un enfoque integral para formular y resolver problemas de manejo de un ecosistema forestal que involucre la opinión de los productores y técnicos forestales, (ii) evaluar la dinámica del bosque bajo un esquema de análisis multicriterio, y (iii) determinar estructuras forestales deseables que satisfagan varios objetivos, simultáneamente.
METODOLOGÍA
En el estudio se usaron datos del último inventario forestal del ejido, la consulta a expertos y una técnica multicriterio denominada programación por compromisos. En esta sección se describen los métodos utilizados, los objetivos de manejo detectados, las variables de decisión (atributos dasométricos) y el uso de un simulador silvícola para evaluar la dinámica del recurso.
Programación por compromisos
La programación por compromisos es una técnica multicriterio basada en minimizar la distancia entre el nivel de desempeño de dos o más objetivos y un punto ideal (Yu, 1973; Zeleny, 1974). Alas soluciones más cercanas al punto ideal se les considera no dominadas y juntas constituyen el juego de soluciones compromiso (Goicochea et al., 1982; Rodríguez-Cotilla, 2000). Una solución no dominada es aquella que es factible para un problema multiobjetivo y que, siendo la mejor, no existe otra solución factible que pueda mejorar un objetivo sin afectar negativamente alguno de los otros (Tecle et al., 1998; Duckstein y Tecle, 2006). Las variaciones del nivel de prioridad entre 0% y 100% producen un juego de soluciones compromiso, también conocido como 'frontera eficiente' o 'frontera de Pareto' (Yu, 1973).
La figura 2 muestra la relación de un problema multiobjetivo (en este caso, de dos objetivos) desde la perspectiva de programación por compromisos. Si en el proceso de optimización, el objetivo y1 tiene 100% de prioridad (o peso relativo) sobre el objetivo y2 , la solución al problema será el eje horizontal. El objetivo y1 tendrá el mejor desempeño mientras que el objetivo y2 tendrá el peor desempeño. De manera similar, si el objetivo y2 tiene 100% más prioridad que el objetivo y1, la solución será entonces el eje vertical. El punto ideal representa el mejor desempeño de los dos objetivos involucrados, pero por lo general es imposible de lograr (Goicochea et al., 1982). Por lo regular, un objetivo tiende a ceder hacia el otro sin que esto provoque soluciones dominadas. El problema entonces es determinar qué punto, a lo largo de la frontera eficiente, resulta ser el más efectivo para ambos objetivos sin tener una utilidad negativa (Yu, 1973). Normalmente, ese punto es el que se encuentra más cerca al punto ideal (Zeleny, 1982).
En problemas multicriterio que involucran tres o más objetivos la solución se torna más complicada, debido a las dificultades de expresar gráficamente esa relación y a la dificultad para encontrar el punto ideal. Además, todos los objetivos de manejo tienen tendencias diferentes, aunque su dirección sea similar. Por ejemplo, la biodiversidad y secuestro de carbono tienen una relación positiva y directa con el diámetro de los árboles. Pero el objetivo secuestro de carbono por lo general requiere árboles aún más grandes (mayor diámetro) que la biodiversidad. Otras diferencias son más evidentes: la recreación y belleza escénica se perciben mejor en rodales abiertos (Perez-Verdín et al., 2008), mientras que el control de la erosión y la productividad del bosque tienen mejores calificaciones en bosques cerrados. Para solventar este tipo de conflictos, el uso de técnicas multicriterio como la programación por compromisos puede ayudar significativamente. En estos casos, la distancia más cercana al punto ideal puede calcularse por una familia de distancias dp expresada como sigue (Zeleny, 1982):
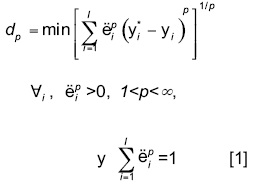
donde p es un parámetro de distancia, y*i es el mejor valor o máximo encontrado para el objetivo i, mientras yi es el valor observado del objetivo i, e l es el número de objetivos considerados. El parámetro λ1 es el nivel de prioridad o importancia del objetivo i con relación a los otros. El valor p es un indicador de escala y representa el nivel de importancia que se le otorga a las desviaciones individuales entre el punto ideal y la frontera eficiente, y depende del analista. El concepto de distancia para cualquier valor de p, se utiliza aquí como una medida para expresar preferencias individuales y no como un concepto puro de distancia geométrica. La distancia, en este caso, representa comparaciones, similitudes o proximidad con respecto a coordenadas individuales, dimensiones y atributos (Tecle, 1992; Srinivasa Raju and Pillai, 1999). El analista puede considerar desde minimizar la suma de esa desviación (i.e., tener una compensación perfecta entre los objetivos) hasta minimizar la desviación máxima (i.e., sin importar la compensación entre los objetivos) (Yu, 1973; Tecle et al., 1988). Sin embargo, los valores más comúnmente utilizados en la programación por compromisos son cuando p=1, 2 e ∞. Cuando p=1, es decir, la mayor distancia finita entre dos puntos en sentido geométrico (Zeleny, 1982) o comúnmente conocida como distancia Manhattan o rectilínea, dp resulta ser:
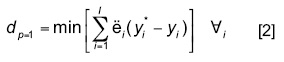
La mínima distancia entre dos puntos es una línea recta; esto se logra cuando p=2 y se representa básicamente por la ecuación [1]. Cuando p tiende a ∞, la ecuación [1] se convierte en un problema míni-máx (minimizar la máxima distancia) y la solución se determina de la manera siguiente:
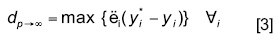
A fin de estandarizar valores, la ecuación [1] se puede expresar como sigue:
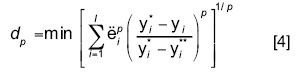
donde y*i* representa el peor o mínimo valor (mínimo local) del objetivo i. El análisis de sensibilidad de esta técnica se basa precisamente en evaluar la desviación al punto ideal considerando los valores más comunes para p y, además, evaluando el peso relativo del objetivo i en comparación con el resto de los objetivos (parámetro λi) (Goicochea et al., 1982; Zeleny, 1982; Krcmar et al., 2005). Todos los cálculos, incluyendo el análisis de sensibilidad, fueron realizados en hojas de cálculo de Excel®.
Objetivos de manejo
Un objetivo de manejo expresa la dirección deseada del cambio con respecto a una situación actual (Duckstein y Tecle, 2006). Por lo general indica una de tres posibles orientaciones: maximizar, minimizar, o mantener su status quo (Tecle, 1992; Duckstein y Tecle, 2006). En el presente estudio se eligieron objetivos de manejo para atender varios usos del bosque que se espera se produzcan en el sistema forestal ejidal. Los objetivos seleccionados, sin orden jerárquico, son: (1) Mantener la biodiversidad o riqueza biológica (BIOVID), (2) Incrementar el secuestro de carbono y provisión de oxígeno (CARBON), (3) Reducir el riesgo de incendios (FUEGO), (4) Incrementar la producción de no maderables (NO-MAD), (5) Aumentar la productividad forestal (PROD), (6) Incrementar la recreación (REC), (7) Incrementar belleza escénica (BELLEZA), (8) Disminuir erosión del suelo (SUELO), (9) Maximizar beneficios económicos de la madera (MADERA) y (10) Elevar la calidad y cantidad del agua (AGUA).
Estos objetivos fueron considerados tomando en cuenta la Ley Forestal y otros documentos normativos (SEMARNAT, 2003), la opinión de los dueños y otros interesados, así como trabajos previos relativos al manejo forestal con objetivos múltiples (Pérez-verdín y Tecle, 2002). Para evaluar su nivel de importancia, cuatro grupos de personas conocedoras del ámbito forestal participaron mediante encuestas asignando un nivel de prioridad o peso relativo a cada uno de los objetivos (Tabla 1). Los grupos de expertos fueron: dueños y/o propietarios de bosque, especialistas forestales, representantes de gobierno y organizaciones no gubernamentales. En total, se entrevistaron 144 personas.
Consulta a expertos
Muchos autores sugieren que en ausencia de información empírica que permita construir expresiones matemáticas para explicar el comportamiento de bienes y servicios del bosque con respecto a ciertos atributos dasométricos, puede usarse la consulta a expertos (ver Alho y Kangas, 1997; Leskinen y Kangas, 1998; Kangas et al., 2000; Kazana et al., 2005; Ray Burgman, 2006; Zadnik, 2006).
La opinión de expertos permite generar o respaldar opciones viables en una cierta área de interés. La consulta a expertos también se ha utilizado para determinar los rangos de variables ambientales que son apropiados para un determinado uso del suelo (Bojórquez- Tapia et al., 2001), ordenamiento ecológico (Márquez-Linares et al., 2006), o para tomar decisiones consensuadas cuando existen conflictos por el uso del territorio (Bojórquez-Tapia et al., 1994; Mendoza et al., 2005). Sin embargo, es frecuente preguntarse cómo identificar los expertos a ser consultados. En este sentido, Kazana et al. (2005, p. 20) señalan que los expertos pueden seleccionarse de acuerdo a grado de escolaridad, experiencia, membresías profesionales, reconocimiento de sus colegas o inclusive por autoproclamación.
Dada la falta de información empírica sobre la relación de los bienes y servicios ambientales y los atributos dasométricos en Durango, se realizaron 29 entrevistas personales con especialistas forestales que trabajan en la entidad. El nivel de educación de los especialistas fue desde licenciatura hasta doctorado y experiencia profesional desde 14 hasta 45 años en el campo del manejo forestal. La consulta a expertos, junto con la información dasométrica, fue usada para determinar funciones de producción que eventualmente expresaran estructuras forestales deseables para cada uno de los objetivos de manejo.
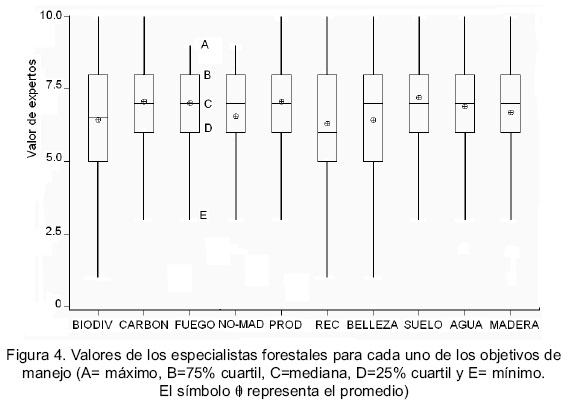
La pregunta base que se hizo a los expertos consultados fue acerca de su opinión respecto a cierta condición del bosque para maximizar, minimizar o mantener cierto objetivo forestal. Para ello, se tomaron fotografías de rodales con varias condiciones forestales y se mostraron las fotos a los expertos para obtener sus preferencias y construir una ecuación (función de producción) en cada objetivo. Las fotografías fueron tomadas dentro del ejido tratando de representar la diversidad de condiciones forestales características del área. Así por ejemplo, el área basal varió desde 18,6 m2/ha hasta 43,9 m2/ha; el número de árboles fue desde 160 hasta los 2 400 árboles por hectárea y el diámetro cuadrático medio cubrió una diversidad desde 11.1 cm hasta 43.3 cm. Las fotografías editadas contenían información dasométrica como área basal, número de árboles por hectárea y diámetro cuadrático medio (Figura 3). Las preferencias de los expertos consultados se basaron en una escala de 10 puntos donde 1 significa muy bajo o muy malo y 10 significa muy alto o excelente (Figura 4).

Variables de decisión
Las variables de decisión son aquellos atributos dasométricos que pueden ser modificadas por el técnico forestal para lograr los objetivos de manejo deseados, pudiendo ser discretas o continuas (Duckstein y Tecle, 2006). En este estudio se consideraron tres atributos de rodal: área basal (ba),número de árboles por hectárea (nth) y diámetro cuadrático medio (qmd). Estas tres variables reflejan la diversidad de las condiciones ecológicas (productividad, densidad y volumen del arbolado), son comunes a todos los objetivos de manejo y fáciles de manejar por el técnico forestal en el campo. Introducir más variables al sistema hubiera resultado en cierta redundancia dado que muchas otras variables dasométricas resultan de la interacción de una o más de las seleccionadas. Las variables seleccionadas se expresan en m2/ha, número de árboles por hectárea y centímetros, respectivamente.
Funciones de producción
A partir de la información recabada con la consulta a expertos, se derivaron funciones de producción para cada objetivo del manejo i. Como se mencionó, la función de producción yi se expresó en función de tres variables de decisión como sigue:
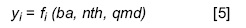
donde yi es la calificación de los expertos para el objetivo i, ba es el área basal (m2/ha), nth es el número de árboles por hectárea, y qmd es el diámetro cuadrático medio (cm). Se usó la primera derivada parcial de cada función yi para determinar los valores locales máximos y mínimos, usando las expresiones siguientes:
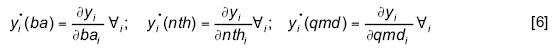
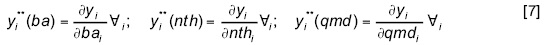
La búsqueda de los valores máximos o mínimos consiste en encontrar los puntos en los que se presenta un cambio en la pendiente a lo largo de la función de producción de cada objetivo. Dado el carácter multivariado de la expresión, se requirió un análisis individual de cada variable para obtener los valores de la ecuación (5). El paquete Solver de Excel® fue usado para determinar dichos valores para todos los objetivos de manejo, sin importar el carácter lineal o no lineal de las ecuaciones (Baker, 2006). Una vez estimados estos datos, los valores resultantes fueron substituidos en la ecuación [4] para determinar la distancia mínima y eventualmente las estructuras forestales deseadas.
Clasificación y simulación silvícola
En virtud del alto número de rodales que existen en el ejido y con fines prácticos de manejabilidad, se usó la técnica de análisis por conglomerados para agrupar rodales con estructuras similares en cuanto a número de árboles por hectárea, diámetro cuadrático medio, área basal, edad y composición de especies. Los rodales se agruparon en 15 conglomerados usando el método de relación de promedios por grupos, medido por distancias euclidianas (Romesburg,1990). En cada conglomerado se identificó un rodal tipo que sirvió como representante de las características promedio del conglomerado. Cada rodal tipo se usó posteriormente en el análisis temporal de los datos. La información de los rodales tipo incluyó datos generales como índices de sitio, índices de densidad, pendiente y elevación. Los datos a nivel árbol incluyeron especie, diámetro y altura de los árboles.
Se usó el Simulador de Vegetación Forestal (FVS) del Servicio Forestal de Estados Unidos para simular el crecimiento del bosque, la regeneración y la mortalidad en los rodales en cada conglomerado. Estas simulaciones permitieron conocer las estructuras forestales deseables a lo largo del tiempo con base en la técnica de multicriterio. El FVS consiste en una familia de modelos de simulación de árboles individuales, independientes de la distancia, y puede ser aplicado a una amplia variedad de tipos de bosques, estructuras de rodales y composición de especies (Crookston y Dixon, 2005). Se usó la variante de las Montañas Rocallosas del FVS debido a las similitudes de los tipos de bosques y a su flexibilidad para ajustarse a condiciones específicas. Aunque no existen datos comparativos, los ecosistemas en esa región y los del norte de México comparten características similares en especies, géneros y patrones de crecimiento (Richardson, 1998). Por ejemplo, Pinus arizonica, la especie dominante en el norte de Durango, se ha considerado como una variedad del P. ponderosa, la especie dominante en el suroeste de E.U. (Farjon y Styles, 1997; Perry, 1991). Por otro lado, el FVS puede también autocalibrarse a nuevos datos si se incluyen atributos del arbolado, como índice de sitio, densidad y competencia. Las ecuaciones de crecimiento y las prescripciones de manejo también pueden ajustarse fácilmente usando comandos específicos del FVS (Dixon, 2002).
Para las simulaciones se usó un periodo de planeación de 100 años dividido en ciclos de 10 años. El periodo de 100 años es el tiempo promedio que un árbol típico requiere para alcanzar la madurez en el área de estudio. La regeneración de las especies dominantes Pinus arizonica y Quercus spp., se calculó en 840 y 346 árboles por hectárea a la edad de cinco años, respectivamente. El ciclo de corta para rodales incoetáneos se determinó en 13 años, con una pendiente de la distribución diamétrica igual a -1,4 (UAF Santiago Papasquiaro, 2005).
Usando el FVS se simularon numerosas condiciones y se examinaron los resultados al término del periodo de planeación (100 años). La solución óptima se determinó usando la ecuación 4, substituyendo los valores resultantes de las simulaciones de cada una de las tres variables de decisión. Si cierta simulación daba valores consistentes para p=2 (la distancia más corta entre dos puntos), los mismos valores de las variables de decisión se calculaban al azar para p=1 y p → ∞ o para evaluar su consistencia. El criterio para determinar la mejor solución consistió en encontrar el mínimo valor de dp (la menor distancia al punto ideal) considerando la dinámica de crecimiento de los rodales en cada conglomerado. Para evaluar la variabilidad temporal de los conglomerados se usaron mapas de distribución de estados de vegetación basados en el sistema de clasificación de dinámica de rodales de Oliver and Larson (1996). Las cuatro fases de vegetación, definidas parcialmente por la magnitud de las variables de decisión, son etapa de iniciación del dosel, exclusión o eliminación por competencia, reiniciación del dosel inferior y madurez. La etapa de madurez es la culminación del estado sucesional de la vegetación y comúnmente se le conoce como bosque clímax (ver detalles de esta clasificación en Oliver and Larson, 1996 y Mendoza et al., 2005).
RESULTADOS Y DISCUSIÓN
Los valores de la opinión de los expertos acerca de las condiciones iniciales del bosque con respecto a las tres variables de decisión (ba, nth, y qmd) se usaron para construir las funciones de respuesta para cada objetivo de manejo. Se usó una prueba de normalidad de los residuales para determinar la bondad de ajuste de los modelos, calculando el parámetro Shapiro-Wilk y otros parámetros estadísticos como R2 y nivel de significancia. Se calcularon las derivadas parciales de las diversas funciones objetivo para encontrar los valores máximos y mínimos. Los resultados del ajuste de modelos y valores máximos y mínimos se muestran en la tabla 2. En esta tabla se observa que los objetivos recreación, belleza escénica y productos no maderables tienen coeficientes negativos en cuanto a número de árboles por hectárea, lo cual sugiere que, en la opinión de los especialistas forestales consultados esta variable se ve favorecida en bosques abiertos. Esto coincide con los resultados de trabajos similares donde se ha reportado que, por lo general, la gente prefiere doseles abiertos y árboles grandes al momento de seleccionar sitios para la recreación (Tecle et al., 1998; Perez-Verdín et al., 2008). Una situación similar fue observada para el objetivo venta de madera, donde bosques cerrados son generalmente percibidos como masas con árboles de diámetros menores, menos volumen y eventualmente menos ingresos por venta de productos maderables.
Una vez construidas las funciones de respuesta y determinados los valores locales máximos y mínimos para todos los objetivos, se usó la ecuación 2 para determinar la solución compromiso para cada conglomerado en cada simulación. La tarea consistió en encontrar la menor distancia entre el juego de soluciones no dominadas y el punto ideal en cada simulación. Se usó un proceso iterativo para cada periodo de 10 años y para todos los conglomerados, simulando diferentes escenarios de manejo forestal hasta determinar la mejor solución. Además, se buscó obtener una mayor diversidad de estados de la vegetación al final del periodo de planeación.
Este procedimiento no fue fácil. Algunos conglomerados se encontraban por abajo en términos de área basal, pero por arriba con respecto al número de árboles por hectárea. Además, el FVS no soporta más de una variable a la vez durante la simulación, así que en algunos conglomerados el proceso se repitió para las otras variables. Las simulaciones con el FVS incluyeron varios tratamientos silvícolas, como aclareos por lo bajo y por lo alto, selección individual, árboles padres, así como diferentes niveles de densidad residual. Tratamientos de no corta fueron desechados debido a la necesidad de seguir proveyendo un flujo constante de recursos económicos a los miembros del ejido. Esta diversidad de escenarios de manejo generó un esfuerzo considerable para estimar y comparar cada una de las dp. Los resultados de las simulaciones se analizaron mediante los reportes estadísticos que incluyen, entre otros, los promedios de las variables de decisión y el sistema de visualización de rodales que genera esquemas tridimensionales de los resultados (Crookston y Dixon, 2005).
La tabla 3 muestra las estructuras actuales y deseables para las tres variables de decisión. Así por ejemplo, las estructuras iniciales del rodal tipo 1309 del conglomerado uno son: 28,2 cm de diámetro cuadrático medio, 10,5 m2/ha de área basal, y 171 árboles por hectárea. Las estructuras deseables, de acuerdo a la información del inventario y la técnica de programación por compromisos, para este mismo conglomerado son: 38,1 de diámetro cuadrático medio, 17,2 m2/ha de área basal y 151 árboles por hectárea. En general, al aplicar promedios ponderados a todos los conglomerados, se observa que el área basal deseable es mayor que la actual en un 31%, el diámetro cuadrático medio es mayor en un 24% mientras que el número de árboles por hectárea es menor en un 5%. La tabla 3 muestra también el tratamiento inicial aplicado y los valores de la técnica de programación por compromisos ajustados para p =2 (Ecuación 4). Estos valores corresponden a la distancia mínima entre la estructura actual y la deseable (punto ideal) para todos los objetivos manejados simultáneamente. La estructura deseable consideró no sólo una amplia variación de prescripciones silvícolas sino también la dinámica de crecimiento de los rodales.
La figura 5 muestra la condición actual, a la mitad y al final del periodo de planeación (100 años) de las fases de vegetación. En la etapa inicial es evidente la dominancia de la fase de exclusión (88% del área forestal total) y en menor escala la fase de iniciación (12% del área forestal total). La fase de exclusión se caracteriza por una relativa dificultad para el establecimiento y desarrollo de nuevos individuos (Mendoza et al., 2005). A través de aclareos selectivos, el ejido y los servicios técnicos han mantenido esta fase a lo largo de los años para hacer más eficiente la producción maderable. A la mitad, y sobre todo al final del periodo de planeación, se pueden observar otras fases de la vegetación como reiniciación del dosel inferior y madurez. La presencia de otras fases vegetativas garantiza una mayor diversidad vegetal y animal, y como señalan Oliver y Larson (1996), es muy importante también para proveer valores recreacionales. Al final del periodo de planeación, los porcentajes de distribución de las fases vegetativas son: exclusión 51%, reiniciación del dosel inferior 24%, madurez con un estrato 11% y madurez con varios estratos 14%. Valores muy similares fueron encontrados por Mendoza et al. (2005) en una región del estado de Jalisco, donde la aplicación de varios tratamientos silvícolas ha generado una mayor diversificación de fases vegetativas sin reducir el volumen de producción maderable.
Análisis de sensibilidad
Se realizó un análisis de sensibilidad para probar la fortaleza de los algoritmos con respecto a cambios en p y en el peso relativo de los objetivos. Dado que el proceso incluyó el examen simultáneo de tres variables de decisión continuas, se usó nuevamente la herramienta Solver del paquete Excel®. El primer paso de sensibilidad consistió en evaluar el algoritmo de la técnica de multicriterio con respecto a los valores de p= 1, 2 e ∞. Los resultados del análisis en este caso no mostraron diferencias en las soluciones excepto en los valores de nth cuando p = 1. Esto muestra que el algoritmo demulticriterio no es altamente sensible a cambios en los valores de p.
El segundo análisis se realizó para determinar la sensibilidad del algoritmo a cambios en los valores del nivel de prioridad (expresados en porcentaje) de los objetivos (λ1). En este caso, se separó la prioridad asignada por cada uno de los grupos participantes, es decir, los representantes del ejido Los Altares, los especialistas forestales, funcionarios del gobierno y los integrantes de organizaciones no gubernamentales. De esta manera, el algoritmo fue evaluado con relación a la prioridad de los objetivos de manejo otorgada por cada grupo. Sin embargo, no hubo diferencias significativas en las soluciones preferidas al modificarse dichas prioridades. Los cuatro grupos participantes tienen preferencias similares en las ponderaciones asociadas con respecto a los objetivos del manejo, de tal forma que ninguno de ellos, individualmente o combinados, afectan los resultados. Para verificar que la solución no fue sensible a los cambios en las ponderaciones, se realizaron dos pruebas adicionales: (1) se incluyó un conjunto de prioridades asignadas de manera arbitraria y (2) se aplicaron prioridades iguales para cada objetivo y luego se estimaron las soluciones de compromiso bajo estos dos escenarios. En ambos casos, tampoco hubo cambios significativos en las soluciones compromiso. Por consiguiente, los resultados obtenidos muestran que el algoritmo de la técnica de programación por compromisos no es sensible a cambios en los valores de p ni de λi. Una de las razones por las que no se detectaron cambios sustanciales en el análisis de sensitividad puede deberse a las grandes diferencias entre los valores actuales y deseados de las estructuras forestales. Es decir, la distancia entre la frontera eficiente (dada por las estructuras actuales) y el punto ideal es tan amplia que cambios en p o λi no afectan significativamente las soluciones compromiso. Si las estructuras forestales actuales, particularmente el área basal y el diámetro cuadrático medio fueran mayores, entonces las soluciones compromiso podrían verse afectadas por cambios en los valores de p y/o en la ponderación otorgada a los objetivos de manejo por los grupos participantes.
RESUMEN Y CONCLUSIONES
En este estudio se formuló y solucionó un problema de toma de decisiones aplicando técnicas multicriterio en el manejo integral de recursos naturales, usando como caso de estudio el ejido forestal Los Altares del estado de Durango. Con base en la opinión de especialistas forestales se evaluaron diez objetivos forestales y tres atributos dasométricos. Para determinar el nivel de importancia (prioridades) de los objetivos de manejo, se consultaron a 144 personas agrupadas en cuatro categorías que fueron: dueños y/o propietarios, especialistas forestales, representantes de gobierno y organizaciones no gubernamentales. Se realizaron numerosas simulaciones de manejo de los recursos forestales, evaluando el comportamiento dinámico de los tres atributos dasométricos, con el fin de encontrar las mejores estructuras forestales que satisficieran los objetivos de manejo. Para determinar el juego de soluciones no dominadas, se usó la técnica de programación por compromisos que se ha utilizado con éxito para resolver problemas similares en el manejo de cuencas hidrográficas y recursos forestales.
Los resultados de este trabajo indican que las estructuras forestales deseables, particularmente área basal y el diámetro cuadrático mínimo, generalmente estuvieron por encima de las condiciones actuales observadas en los rodales tipo. Es decir, los bosques actuales del ejido son en su mayoría rodales jóvenes con una alta densidad de árboles por hectárea, de diámetros pequeños y área basal baja. Dichos bosques se encuentran mayoritariamente en una sola etapa vegetacional (exclusión) y carecen de rodales maduros y sobremaduros que puedan balancear la presencia de hábitat para la flora y fauna silvestre. Este tipo de estructuras difícilmente puede facilitar el manejo de varios objetivos de manejo y proteger la integridad del ecosistema.
Muchos factores pueden contribuir a esas diferencias; por ejemplo, el manejo individual de un solo recurso (madera) puede reducir el nivel de existencias y la calidad de los árboles residuales generando distribuciones diamétricas desequilibradas (Gingrich, 1993). Eventualmente, este tipo de manejo forestal afecta la dinámica de crecimiento de las masas forestales al excluir la presencia de otras fases vegetativas. Excluyendo los incendios forestales que dentro del ejido se limitan a áreas pequeñas y de baja intensidad, otros factores que afectan la dinámica de los bosques son la actividad humana, al deforestar áreas para la agricultura, caminos y pastoreo. La presencia de ganado, la cual es evidente en toda el área de estudio, frecuentemente afecta la regeneración. La interacción de todos estos factores genera riesgos para la integridad y sustentabilidad de los ecosistemas forestales.
Los resultados sugieren que el manejo forestal enfocado a lograr objetivos múltiples es diferente al punto de vista tradicional, en el que la madera ha sido el producto más importante para maximizar ganancias. Pero lo más importante es que el manejo forestal tradicional ha ignorado muchos valores no económicos, culturales y ambientales, como la biodiversidad, recreación y el mantenimiento del ciclo hidrológico. Se espera que la adopción del manejo de multirecursos y la dinámica de los bosques genere una mayor colaboración entre los administradores del recurso forestal, los grupos ecologistas y otros interesados en el manejo de los ecosistemas forestales para la producción de bienes y servicios ambientales. Se espera también que el ejemplo presentado aquí propicie un mejor entendimiento, así como la aceptación y el uso de técnicas multicriterio en el manejo de los ecosistemas forestales. Las opiniones de expertos o consultores, si bien han probado su utilidad en muchos estudios, siguen siendo opiniones personales y pueden reflejar aspiraciones, no necesariamente situaciones reales. Para mejorar la confiabilidad de este enfoque se requiere más investigación, especialmente en la evaluación de los bienes y servicios ambientales que dependen de ciertos atributos del rodal. Es necesario el establecimiento de parcelas experimentales para generar más conocimiento en las variables para evaluar los bienes y servicios que ofrece el recurso forestal.
RECONOCIMIENTOS
Agradecemos a los ejidatarios de Los Altares, Durango y a Fernando Salazar Jiménez por permitirnos usar los datos de inventario del Ejido y su información cartográfica. Gracias también a Ramón Silva Flores, Jesús Soto Rodríguez y J. Guadalupe Barrios Téllez por su apoyo en la obtención de opiniones sobre las prioridades de los objetivos de manejo, externadas por varios sectores de la sociedad. Le agradecemos al Dr. Shafiu Jibrin su asesoría para resolver el problema de optimización y derivadasparciales. Nuestro agradecimiento también a los dos revisores anónimos y a los editores de la revista por sus valiosas sugerencias en este trabajo. Una parte del apoyo financiero para este proyecto provino del CONACYT y de la Propuesta 301 del estado de Arizona, EUA.
REFERENCIAS
Alho, J. y J. Kangas. 1997. Analyzing uncertainties in experts' opinions of forest plan performance. Forest Science 43: 521-528. [ Links ]
Baker, K.R. 2006. Optimization modeling with spreadsheets. Thomson Brooks/Cole, Belmont, CA. [ Links ]
Bojórquez-Tapia, L., E. Ongay-Delhu-meau y E. Ezcurra. 1994. Multivariate approach for suitability assessment and environmental conflict resolution. Journal of Environmental Management 41:187-198. [ Links ]
Bojórquez-Tapia, L., S. Díaz-Mondragón y E. Ezcurra. 2001. GIS based approach for participatory decision making and land suitability assessment. International Journal of Geographical Information Science 45(2): 129-151. [ Links ]
Caballero D., M. 2000. La actividad forestal en México. Universidad Autónoma Chapingo, Chapingo, Mex. [ Links ]
CONAFOR. 2000. Decreto de creación de la Comisión Nacional Forestal. Disponible en: http://conafor.gob.mx; consultada el 25 de junio de 2008. [ Links ]
Crookston, N.L. y G.E. Dixon. 2005. The forest vegetation simulator: A review of its structure, content, and applications. Computers and Electronics in Agriculture 49, pp. 60-80. [ Links ]
Dixon, G. 2002. Essential FVS: A user's guide to the Forest Vegetation Simulator. Internal Report. Fort Collins, CO. USDA Forest Service, Forest Management Center. 196 p. [ Links ]
Duckstein, L. y A. Tecle. 2006. Multi-criterion analysis in water resources management. In: Savenije, H.G. and Hoeksta, A.Y. (Eds) Encyclopedia of life support systems (EOLSS). pp. 1-20. UNESCO, EOLSS publishers. Oxford, Reino Unido. [ Links ]
Farjon, A. y B. Styles. 1997. Pinus (Pinaceae). Flora Neotrópica, Monograph 75, New York Botanical Gardens, Nueva York. [ Links ]
Goicochea, A., D.R. Hansen y L. Duckstein. 1982. Multiobjective decision analysis with engineering and business applications. John Wiley & Sons, Nueva York. [ Links ]
Gingrich, R.W. 1993. The political ecology of deforestation in the Sierra Madre Occidental of Chihuahua. Master of Science Thesis. The University of Arizona. Tucson, AZ. [ Links ]
Kangas, J., R. Store, P. Leskinen y Mehtãtalo. 2000. Improving the quality of landscape ecological forest planning by utilizing advanced decision-support tools. Forest Ecology and Management 132: 157-171. [ Links ]
Kazana, V., F. Bonnieux, P. Campos Palacin, A. Caparrós, L.Croitorou, P. Gatto, A. Kazaklis, M. Merlo, J. C. Paoli y L. Zadnik. 2005. MEDMONT: Tools for evaluating investment in the mountain Mediterranean areas -An integrated framework for sustainable development. Final Report Edited by the Mediterranean Agronomic Institute of Chania (MAI.Ch), Alsyllion Agrokepion, Chania, Grecia. [ Links ]
Krcmar, E., G.C. van Kooten y I. Vertinsky. 2005. Managing forest and marginal agricultural land for multiple tradeoffs: compromising on economic, carbon and structural diversity objectives. Ecological Modeling, 185: 451-468. [ Links ]
Leskinen, P. y J. Kangas. 1998. Analyzing uncertainties of interval judgment data in multiple-criteria evaluation of forest plans. Silva Fennica 32: 363-372. [ Links ]
Márquez- Linares, M. A., A. Esparza R., M. González-Elizondo, L. López Enriquez, D. Pámanes G. y D. García M. 2006. Estudio Técnico para el Ordenamiento Ecológico del estado de Durango, fase de pronóstico y propuesta. Inédito. 62 p. [ Links ]
Mendoza-Briseño, M.A. 1993. Conceptos básicos de manejo forestal. Limusa- UTEHA, Mexico, D.F. 161 p. [ Links ]
Mendoza, M. A., J.J. Fajardo y J. Zepeta. 2005. Landscape based forest management, a real world case study from Mexico. Forest Ecology and Management 209(1-2): 19-26. [ Links ]
Muñoz-Piña, C., A. Guevara, J.M. Torres, y J. Braña. 2008. Paying for the hydrological services of Mexico's forests: Analysis, negotiations and results. Ecological Economics 65: 725-736. [ Links ]
Oliver, C.D. y B.C. Larson. 1996. Forest stand dynamics. John Wiley & Sons, Nueva York. 520 p. [ Links ]
Pérez-Verdín, G. y A. Tecle. 2002. Multiobjective forest management in San Miguel, Mexico. Hydrology and Water Resources in Arizona and the Southwest 32: 63-70. [ Links ]
Pérez-Verdín, G., M.E. Lee y D. J. Chávez. 2008. Planning forest recreation in natural protected areas of southern Durango, Mexico. Madera y Bosques 14(1): 53-67. [ Links ]
Perry, J.P. 1991.The pines of Mexico and Central America. Timber Press, Portland, OR. [ Links ]
Ray, N. y M.A. Burgman. 2006. Subjective uncertainties in habitat suitability maps. Ecological modelling 195: 172-186 [ Links ]
Richardson, D.M. 1998. Ecology and biogeography of Pinus. Cambridge University Press, Nueva York. [ Links ]
Rodríguez-Cotilla, Z. 2000.Teoría de la decisión multicriterio: un enfoque para la toma de decisiones. Economía y Desarrollo 1 (126): 41-57. [ Links ]
Romesburg, C.H. 1990. Cluster analysis for researchers. Robert E. Krieger Publishing Company, Malabar, FL. [ Links ]
SEMARNAT (Secretaría de Recursos Naturales y Medio Ambiente). 2003. Ley General de Desarrollo Forestal Sustentable, y su Reglamento. [Disponible en http://www.conafor.gob.mx/documentos_conafor/pdfs/LGDFS.pdf] [ Links ]
Srinivasa Raju, K. y C.R.S. Pillai. 1999. Multicriterion decision making in river basin planning and development. European Journal of Operational Research 112: 249-257. [ Links ]
Tecle, A., M. M. Fogel y L. Duckstein. 1988. Multicriterion analysis of forest watershed management alternatives. Water Resources Bulletin 24(6):1169-1178. [ Links ]
Tecle, A. 1992. Selecting a multicriterion decision making technique for watershed resources management. Water Resources Bulletin 28 (1): 129-140. [ Links ]
Tecle, A., B.P. Shrestha y L. Duckstein. 1998. A multiobjective decision support system for multiresource forest management. Group Decision and Negotiation 7: 23-40. [ Links ]
UAF Santiago Papasquiaro. 2005. Propuesta del plan de manejo forestal para el Ejido Los Altares, municipio de Santiago Papasquiaro, Dgo. Reporte no publicado. [ Links ]
Yu, P.L. 1973. A class of solutions for Zeleny, M. 1982. Multiple criteria decision group decision problems. Manage- making. McGraw-Hill Book ment Science 19 (8): 936-946. [ Links ]
Zadnik, S. L. 2006. Integrating the fuzzy analytic hierarchy process with dynamic programming approach for determining the optimal forest management decisions. Ecological Modeling 194: 296-305. [ Links ]
Zeleny, M. 1974. A concept of compromise solutions and the method of the displaced ideal. Computers and Operations Research 1 (3-4): 479-496. [ Links ]
Zeleny, M. 1982. Multiple criteria decision making. McGraw-Hill Book Company, Nueva York. [ Links ]
Nota
Este documento se debe citar como: Pérez Verdín, G., J. C. Hernández-Díaz, M. A. Márquez-Linares y A. Tecle. 2009. Aplicación de técnicas multicriterio en el manejo integral forestal en Durango. Madera y Bosques 15(1):27-46.














